7. fejezet - KIDOLGOZOTT PÉLDÁK
7.1. Feladat
Szórásanalízis, egyszeres osztályozás
Kidolgozta: Pintér Ádám, PhD ösztöndíjas hallgató
Ellenőrizte: Dr. Wenzel Klára
Szakítószilárdság mérést végzünk négy különböző (A, B, C és D) anyagon. Minden mérést 4-szer ismétlünk meg, de utólag kiderült, hogy az egyik mérési adatot a mérés közben beállt műszerhiba miatt nem vehetjük figyelembe.
A N/mm2-ben mért mérési adatok az alábbiak:
|
mérés |
A anyag |
B anyag |
C anyag |
D anyag |
|
1 |
23,014 |
23,121 |
23,085 |
25,415 |
|
2 |
21,508 |
23,802 |
24,445 |
25,809 |
|
3 |
23,766 |
22,690 |
23,802 |
25,666 |
|
4 |
- |
22,548 |
24,161 |
24,958 |
Szórás analízis segítségével határozza meg, hogy
1. Van-e szignifikáns különbség az A, B, C és D anyag szakító szilárdsága között?
2. Ha van, melyik a legerősebb?
3. Adjon becslést a mérés hibájára!
A megoldás menete:
1.)
Bemenő adatok:
|
Szakító szilárdság mérési eredmények σm [N/mm2] (xti) |
Megjegyzés |
||||
|
mérés (i) |
A anyag |
B anyag |
C anyag |
D anyag |
|
|
1 |
23,014 |
23,121 |
23,085 |
25,415 |
egy mérés hibás volt, ezt elhagytuk |
|
2 |
21,508 |
23,802 |
24,445 |
25,809 |
|
|
3 |
23,766 |
22,690 |
23,802 |
25,666 |
|
|
4 |
|
22,548 |
24,161 |
24,958 |
|
Származtatott adatok (az ismert, témakörhöz tartozó elemi képletekkel):
|
at |
22,763 |
23,040 |
23,873 |
25,462 |
csoport átlag |
|
s* |
1,150 |
0,563 |
0,588 |
0,373 |
korrigált tapasztalati szórás |
|
A |
23,853 |
a teljes átlag |
|||
|
k |
4 |
a csoportok száma |
|||
|
N |
15 |
a teljes mérésszám |
|||
Végzünk egy előzetes F-próbát, hogy megállapítsuk, a csoportok szórása megegyezik-e. Ezt a legrosszabb esetre nézve (A és D csoport szórása tér el leginkább egymástól ránézésre) azt az eredményt kapjuk, hogy adott, 5%-os szignifikancia szinten a szórások megegyeznek.
|
Előzetes F-próba a legrosszabb esetre (A-D csoport): F-szám 9,5 ; Fkrit: 19,2 tehát OK! |
Ezek után elkezdjük kiszámolni az ANOVA-tábla kitöltéséhez szükséges értékeket:
|
xti-A |
-0,839 |
-0,732 |
-0,768 |
1,562 |
mérések teljes átlagtól való eltérései |
|
-2,345 |
-0,051 |
0,592 |
1,956 |
||
|
-0,087 |
-1,163 |
-0,051 |
1,813 |
||
|
|
-1,305 |
0,308 |
1,105 |
|
zti |
0,251 |
0,081 |
-0,788 |
-0,047 |
mérések csoport átlagtól való eltérése |
|
-1,255 |
0,762 |
0,572 |
0,347 |
||
|
1,003 |
-0,350 |
-0,071 |
0,204 |
||
|
|
-0,492 |
0,288 |
-0,504 |
|
Bt |
-1,090 |
-0,812 |
0,021 |
1,609 |
csoportátlagok teljes átlagtól való eltérései |
|
Gt |
22,763 |
23,040 |
23,873 |
25,462 |
a csoportátlag várható értéke |
Táblázatos formában összefoglalva az eddigiek:
|
|
HATÁSOK t=1 …4 |
ÖSSZES ADAT |
|||
|
21,508 |
23,802 |
24,445 |
25,809 |
||
|
23,766 |
22,690 |
23,802 |
25,666 |
||
|
|
22,548 |
24,161 |
24,958 |
||
|
ÁTLAGOK |
22,763 |
23,204 |
23,777 |
25,630 |
28,853 |
Ezekből az értékekből már meg tudjuk határozni a jegyzet szerint definiált négyzetösszegeket:
|
Q (xti-at) |
21,616 |
teljes négyzetösszeg |
|
Q1 (Bt) |
16,566 |
csooprtok közötti négyzetösszeg |
|
Qe (zti) |
5,050 |
csoporokon belüli négyzetösszeg |
A szórásnégyzetek meghatározásához a négyzetösszegeket osztanunk kell a szabadságfokok számával. A csoportok közötti eltérés négyzet összeg szabadságfoka k-1, mert k csoport van, és a csoport átlagok képzéséhez 1 szabadságfokot felhasználtunk. A csoporton belüli négyzetösszegek szabadságfoka N-k, mert az összes N adatból k csoport átlagot képeztünk, tehát k szabadságfokot használtunk fel. A totál négyzetösszeg szabadságfoka N-1, mert N adatból képeztük és az N adat átlagához 1 szabadság fokot használtunk fel.
Így a szabadságfokok, illetve ezek felhasználásával a szórásnégyzetek:
|
k-1 |
3 |
Q1 szabadság foka (k-1) |
|
N-k |
11 |
Qe szabadságfoka (N-k) |
|
N-1 |
14 |
Q szabadságfoka (N-1) |
|
s12 |
5,522 |
csoportok közötti eltérés szórásnégyzete |
|
se2 |
0,459 |
csoportokon belüli eltérés szórásnégyzete |
|
F-szám |
12,028 |
a két szórásnyégyzet hányadosa (F-szám) |
Az eredményeket az egyszeres osztályozás ANOVA táblájában összefoglalva:
|
A szóródás oka |
Eltérés négyzetösszeg |
Szabadságfok |
Szórásnégyzet |
|
Csoportok közötti eltérés |
16,566 |
3 |
5,522 |
|
Csoportokon belüli eltérés |
5,050 |
11 |
0,459 |
|
Total |
21,616 |
14 |
F-szám: 12,028 |
Azt kell megvizsgálni, hogy az adott f-paraméterek (melyek: k-1 = 3 és N-k = 11) mellett megkapott Fkrit értéknél nagyobb-e a számolás során kapott F-szám:
|
Fkrit (3,11) |
3,6 |
F-próba táblázatából |
Megállapíthatjuk tehát, hogy 12,028 > 3,6:
|
A CSOPORTHATÁS SZIGNIFIKÁNS (VAN SZIGNIFIKÁNS KÜLÖNBSÉG A CSOPORTOK KÖZÖTT) |
2.)
Számba vesszük az egyes anyagok szakító szilárdságát a mérnöki gyakorlatban szokásos módon, amely szerint az adott érték (több mérésből számítva) egyelő az átlaggal, plusz-mínusz a szórás kétszerese:
|
Anyagok |
A |
B |
C |
D |
|
|
σm [N/mm2] |
22,763 ± 2,300 |
23,040 ± 1,126 |
23,873 ± 1,176 |
25,463 ± 0,746 |
mérési eredmény a műszaki gyakorlatban szokásos " átlag ± 2 x s* " alapján |
Ebből egyértelműen leolvasható, hogy:
|
A D anyagnak a legnagyobb a szakító szilárdsága |
3.)
A mérés hibájára a műszaki méréstechnikában megszokott 95%-os szignifikancia szinthez tartozó konfidencia-intervallumot fogjuk tekinteni.
Tehát azt fogjuk kiszámolni, hogy az adott - ebben az esetben egymástól függetlennek tekintett - mérési sorozatok alapján mekkora sugarú intervallumot kellene felvennünk a mérési sorozatok átlaga körül ahhoz, hogy a valós érték (ami a valóságban soha nem ismerhető pontosan) 95%-os valószínűséggel beleessen az így kijelölt intervallumba.
|
p |
0,95 |
szignifikancia szint |
|||
|
f |
2 |
3 |
3 |
3 |
szabadsági fokok |
|
λ |
4,303 |
3,182 |
3,182 |
3,182 |
Student eloszlás táblázatából (p=0.95) |
|
a |
2,856 |
0,896 |
0,935 |
0,594 |
konfidencia intervallum sugara |
|
A mérési sorozatok becsült hibája |
|||||
|
Anyagok |
A |
B |
C |
D |
a várható érték és az átlag maximális eltérése 0.95-ös valószínűségi szinten |
|
Mérési hiba |
± 2,856 |
± 0,896 |
± 0,935 |
± 0,594 |
|
7.2. Feladat
Szórásanalízis, egyszeres osztályozás
Kidolgozta: Manhertz Gábor, PhD ösztöndíjas hallgató
Ellenőrizte: Dr. Wenzel Klára
Műanyag csiszolatokat kell minősítenünk a reflexiós tényező alapján. (A felületi simaság azonosan tükrös). A csiszolatokat jelöljük A , B, C és D-vel! A mérések egy része a körülmények miatt értékelhetetlennek bizonyult (jelölés: „-”). Az értékelhető mérési adatok a következők:
|
A |
B |
C |
D |
|
|
mérés |
195 |
45 |
230 |
110 |
|
mérés |
150 |
40 |
115 |
55 |
|
mérés |
205 |
195 |
235 |
120 |
|
mérés |
120 |
65 |
225 |
50 |
|
mérés |
160 |
145 |
- |
80 |
|
mérés |
- |
195 |
- |
- |
Szórás analízis segítségével állapítsa meg, hogy egyforma minőségűek-e a csiszolatok?
A megoldás menete:
A mérési adatokból látszik, hogy egy adott csiszolaton hiába lett végrehajtva 6 mérés, vannak olyan esetek, amelyek értékelhetetlenek. Ilyen esetben több megoldást kínálkozik. Az egyik módszer, hogy az adatsort ritkítjuk, a másik pedig, hogy változatlanul hagyjuk.
Az adatsor ritkítás csak úgy lehetséges, ha pl. minden csiszolatnál csak 4 mérést veszünk figyelembe – mivel ez az egy csiszolathoz (C-hez) tartozó mérési adatszám minimuma. Ekkor a randomizálás folyamatát kell alkalmazni azon csiszolatoknál, ahol a mérési adat több mint 4.
A feladat megoldásánál nem ez a módszer lesz terítéken, hanem az adatsort változatlanul hagyjuk, és a különböző számú adatból álló csoportokat egyedileg vizsgáljuk meg..
A szórás analízis elvégzéséhez szükség lesz a csoportok összegeire, négyzetösszegeire, a mérés teljes átlagára, valamint az egyes csoportok átlagtól való eltéréseire.
Az értékekre azért van szükség, mert az alábbi táblázat feltöltésével válaszolható meg a kérdés, végezhető el a szórás analízis. Ez a táblázat az egyszeres osztályozás ANOVA táblája, mivel jelenleg egy faktor szerepel a feladatban. Ez a faktor a reflexiós tényező.
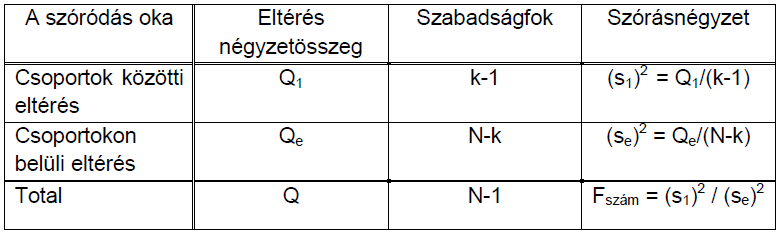
Jelen feladatban a szabadságfokok a következő képen alakulnak:
k=4 (csoportok száma) és N=20 (összes mérés száma)
Az eltérések összegeit az alábbi két képlet alapján lehet számítani:
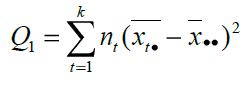
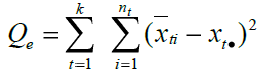
ahol:
-
nt az egy adott csoportban kiértékelhető mérések száma (jelen esetben A: 5, B: 6, C: 4, D: 5)
-
k a csoportok száma
-
i az adat sorszáma
-
t a csoport sorszáma
-
t-edik csoport átlaga
-
a teljes mérési sorozat átlaga
-
xti a t-edik csoport i-edik adata
Q1 értékének meghatározására szükség van az adott csoportok átlagaira:
Az egyes csoportok átlagainak számítása
ahol:
-
nt a kiértékelhető mérések száma
-
i az adat sorszáma
-
j a csoport sorszáma
-
a csoport i-edik adata
-
a csoport átlaga
Ezek alapján a csoportok átlagai a következők:
A csoport:
B csoport:
C csoport:
D csoport:
A teljes mérési sorozat átlaga:
ahol:
-
nt az egy adott csoportban kiértékelhető mérések száma
-
k a csoportok száma
-
i az adat sorszáma
-
t a csoport sorszáma
-
a t-dik csoport i-edik adata
-
a mérési adatsor átlaga
Tehát:
Ezen értékek felhasználásával:
A kapott eredményekkel az ANOVA táblázatot feltöltve
|
A szóródás oka |
Eltérés négyzetösszeg |
Szabadságfok |
Szórásnégyzet |
|
Csoportok közötti eltérés |
|
|
|
|
Csoportokon belüli eltérés |
45439,6 |
|
|
|
Total |
|
|
|
meghatározásával elvégezhető az F-próba, mellyel a kérdés megválaszolása lehetséges. Amennyiben , akkor a szórásnégyzetek szignifikánsan különböznek. az F-próba segédtáblázatából kereshető ki. F-próba a jelen esetben:
Végkövetkeztetés:
Mivel , ezért a szórásnégyzetek szignifikánsan különböznek, így a csiszolatok nem egyforma minőségűek.
7.3. Feladat
Szórásanalízis, kétszeres osztályozás kereszthatás vizsgálata nélkül Kidolgozta:
Gárdonyi Gábor, PhD ösztöndíjas hallgató
Ellenőrizte: Dr. Wenzel Klára
A, B, C és D jelű új szerszámgép teljesítményét vizsgáljuk 5 napon át. A gépek teljesítményét a rajtuk elkészült munkadarabok számával jellemezzük. Az adatok az alábbi táblázatban láthatók.
Szórás analízis segítségével határozza meg, hogy van-e szignifikáns különbség a gépek teljesítménye között?
-
tapasztalható-e bejáratási jelenség?
Kísérleti beállítások és a kísérleti eredmények
|
Mérés |
Gép megnevezése |
Sorösszeg |
Sornégyzetösszeg |
||||||
|
A |
B |
C |
D |
||||||
|
1. nap |
293 |
308 |
323 |
333 |
1257 |
918,8 |
|||
|
2. nap |
298 |
353 |
343 |
363 |
1357 |
2468,8 |
|||
|
3. nap |
280 |
323 |
350 |
368 |
1321 |
4392,8 |
|||
|
4. nap |
288 |
358 |
365 |
345 |
1356 |
3674 |
|||
|
5. nap |
260 |
343 |
340 |
330 |
1273 |
4616,8 |
|||
|
Átlagok |
283,8 |
337 |
344,2 |
347,8 |
|||||
|
Oszlopösszeg |
1419 |
1685 |
1721 |
1739 |
|||||
|
Oszlopnégyzetösszeg |
884,8 |
1770 |
934,8 |
1182,8 |
|||||
A megoldás menete:
A feladat megoldása nagyon egyszerűnek tűnik. Úgy gondolhatjuk, hogy a feladatot meg lehet oldani két külön egyszeres osztályozásra bontva.
Ez azonban nem helyes elgondolás, mert egyszer úgy tekintenénk, mintha az adatok változékonyságát csak az oszlop-hatás és a véletlen okozná, majd másodszor azt feltételeznénk, hogy az adatok változékonyságát csak a sor-hatás és a véletlen okozza. Valójában azonban a sor-hatás és az oszlop-hatás egyidejűleg okoz változékonyságot az adatokban. Ha a két hatást egyidejűleg vesszük figyelembe, a teljes adathalmaz szórásában a véletlennek kisebb lesz a szerepe, és a sor-hatás valamint az oszlophatás a kisebb véletlen-hatásból (kisebb zajból!) jobban ki fog emelkedni, azaz szignifikánsabb lesz. Az érdekesség kedvéért vizsgáljuk meg a helyzetet mind a két módszerrel, azaz két egyszeres osztályozással, és egy kétszeres, kölcsönhatás nélküli osztályozással is!
-
módszer:
-
Kérdés: Van-e különbség a gépek között?
Az egyszeres osztályozás ANOVA táblája
|
A szóródás oka |
Eltérés négyzetösszeg |
Szabadságfok |
Szórásnégyzet |
|
Csoportok közötti eltérés |
Q1 |
k-1 |
(s1)2=Q1/(k-1) |
|
Csoportokon belüli eltérés |
Qe |
N-k |
(se)2=Qe/(N-k) |
|
Total |
Q |
N-1 |
Fszám=(s1)2/(se)2 |
A táblázat alapján Fkrit értéke f1=16 és f2=3 értékek mellett 3,2.
A Fisher próba feltétele, hogy Fszám>Fkrit. Amennyiben ez a feltétel teljesül, az azt jelenti, hogy a szórásnégyzetek szignifikánsan különböznek egymástól.
Esetünkben 15,0251 >3,2 teljesül, tehát szignifikáns különbözést tapasztalhatunk.
-
Kérdés: Van-e különbség a napok között? (Van-e bejáratási jelenség?)
A kísérleti beállítások és a kísérleti eredmények táblázatát átrendezzük az egyszeres osztályozásnak megfelelő alakra:
|
Mérés |
Napok megnevezése |
Sorösszeg |
Sornégyzetösszeg |
|||||||
|
1. nap |
2. nap |
3. nap |
4. nap |
5. nap |
||||||
|
1. gép |
293 |
298 |
280 |
288 |
260 |
1419 |
884,8 |
|||
|
2. gép |
308 |
353 |
323 |
358 |
343 |
1685 |
1770 |
|||
|
3. gép |
323 |
343 |
350 |
365 |
340 |
1721 |
934,8 |
|||
|
4. gép |
333 |
363 |
368 |
345 |
330 |
1739 |
1182,8 |
|||
|
Átlagok |
314,25 |
339,25 |
330,25 |
339 |
318,25 |
|||||
|
Oszlopösszeg |
1257 |
1357 |
1321 |
1356 |
1273 |
|||||
|
Oszlopnégyzetösszeg |
918,8 |
2468,8 |
4392,8 |
3674 |
4616,8 |
|||||
Az egyszeres osztályozás ANOVA táblája:
|
A szóródás oka |
Eltérés négyzetösszeg |
Szabadságfok |
Szórásnégyzet |
|
Csoportok közötti eltérés |
Q1 |
k-1 |
(s1)2=Q1/(k-1) |
|
Csoportokon belüli eltérés |
Qe |
N-k |
(se)2=Qe/(N-k) |
|
Total |
Q |
N-1 |
Fszám=(s1)2/(se)2 |
A Fisher-féle F-próba 5%-os szignifikanciaszinthez tartozó kritikus értékei táblázatos formában fentebb találhatók.
A táblázat alapján Fkrit értéke f1=15 és f2=4 értékek mellett 3,1.
A Fisher próba feltétele, hogy Fszám>Fkrit. Amennyiben ez a feltétel teljesül, az azt jelenti, hogy a szórásnégyzetek szignifikánsan különböznek egymástól.
Esetünkben 1,9968>3,1nem teljesül, tehát szignifikáns különbözést nem tapasztalhatunk a napok között.Nincs bejáratási jelenség.
-
módszer:
Oldjuk meg most a feladatot a kétszeres osztályozás módszerével (tehát mindkét faktor hatásának egyidejű figyelembevételével)!
Feltételezzük, hogy a kereszt-hatás nem számottevő. Ezért nem is végzünk ismételt méréseket, így az egyes cellákban csak 1-1-mérési adat található
A kétszeres osztályozás ANOVA táblája:
|
A szóródás oka |
Eltérés négyzetösszeg |
Szabadságfok |
Négyzetes közép |
|
Oszlop-hatás |
Qc |
c - 1 |
sc2 = Qc / ( c – 1 ) |
|
Sor-hatás |
Qr |
r - 1 |
sr2 = Qr / ( r – 1 ) |
|
Kereszt-hatás |
-- |
-- |
-- |
|
Reziduál |
Qe = -Qr - Qc |
(r-1)(c-1) |
se2 = Qe / (r-1)(c-1) |
|
Teljes |
Q |
rc - 1 |
-- |
A korábban már kiszámolt adatokkal feltöltjük az ANOVA táblát. Az ANOVA tábla kereszt-hatás sora most üresen marad:
|
A szóródás oka |
Eltérés négyzetösszeg |
Szabadságfok |
Négyzetes közép (szórásnégyzet) |
|
Oszlop-hatás (gépek) |
|
4 – 1 = 3 |
sc2=13444,8/3=4481,6 |
|
Sor-hatás (napok) |
|
5 - 1 = 4 |
sr2=2146,2/4=536,6 |
|
Kereszt-hatás |
-- |
-- |
-- |
|
Reziduál |
18217,2 – 13444,8 – 2146,2 = 2626.2 |
(4-1)(5-1) = 12 |
se2=2626.2/12=218.9 |
|
Teljes |
18217,2 |
5*4 – 1 = 19 |
-- |
F-próbával megvizsgáljuk, hogy szignifikáns-e az oszlop-hatás (a gépek közötti különbség)?
A Fisher-féle F-próba 5%-os szignifikancia-szinthez tartozó kritikus értéke a táblázat alapján értéke f1=12 és f2=3 értékek mellett Fkrit = 8,7.
Fszám > Fkrit, tehát a gépek között van szignifikáns különbség.
Megvizsgáljuk azt is, hogy szignifikáns-e a sor-hatás (a napok közötti különbség)?:
A Fisher-féle F-próba 5%-os szignifikancia-szinthez tartozó kritikus értéke a táblázat alapján értéke f1=12 és f2= értékek mellett Fkrit =5,9.
Fszám < Fkrit, tehát a napok között ezzel a módszerrel sem mutatható ki szignifikáns különbség, de látható, hogy most az Fszám közelebb került a kritikus értékhez.
Tehát a gépek között szignifikáns különbséget találtunk, de bejáratási jelenség nem volt tapasztalható.
7.4. Feladat
Szórásanalízis, kétszeres osztályozás kereszthatás vizsgálatával.
Kidolgozta: Urbin Ágnes, PhD ösztöndíjas hallgató
Ellenőrizte: Dr. Wenzel Klára
Egy üzemben ötvözetek edzési tulajdonságait vizsgálják. Keménységet mérnek 4 különböző összetétel alkalmazásával (A, B, C és D). A kísérleteket 3 ötvöző kemencében végzik (1, 2 és 3). Minden kísérletet 2-szer végeztek el azonos körülmények között. Kérdések:
-
Van-e eltérés a kemencék között?
-
Van-e eltérés az ötvözetek között?
-
Van-e kölcsönhatás?
Kísérleti beállítások és a kísérleti eredmények
|
Mérés |
Gép megnevezése |
Sorösszeg |
Sornégyzetösszeg |
|||||
|
1 |
2 |
3 |
||||||
|
A |
18 19 37 |
20 21 41 |
14 17 31 |
109 |
11881 |
|||
|
B |
24 22 46 |
27 30 57 |
20 23 43 |
146 |
21316 |
|||
|
C |
19 21 40 |
20 18 38 |
17 16 33 |
111 |
12321 |
|||
|
D |
16 15 31 |
16 18 34 |
14 12 26 |
91 |
8281 |
|||
|
Oszlopösszeg |
154 |
170 |
133 |
Teljes összeg 457 Teljes összeg négyzete: 208849 |
||||
|
Oszlopnégyzetösszeg |
23716 |
28900 |
17689 |
|||||
A cellán belüli adatok összegét piros színnel jelöltük meg.
A számítások során alkalmazott képletekben az átlagokat az előző táblázatban feltüntetett sor-, oszlop- és cella összegek alapján számoltuk ki.
A sorok közöttii eltérés négyzetösszeg:
Az oszlopok közötti eltérés négyzetösszeg i:
A cellák közötti (kereszthatás) eltérés négyzetösszeg:
A teljes (totál) eltérés négyzetösszeg:
A residuális („maradék” négyzetösszeg:
A számításoknál a Steiner-formulát alkalmaztuk.
A kereszthatást nem kell külön kiszámolni, hanem az eddigiekből adódik, mivel
Q = Qr + Qc + Qrc + Qe
Ezért Qrc = Q – Qr – Qc – Qe
A számítást úgy szokták elvégezni, hogy először a kereszthatást számolják ki. Ha az nem szignifikáns, akkor annak eltérés négyzetösszegét a reziduálhoz adják (mivel véletlenszerű a hatása) és az így kapott új residuálhoz hasonlítják a többi hatást.
A számszerű értékek pedig:
Qr=264,46
Qc=86,08
Qrc=22,92
Qe=25,50
Q=398,96
ANOVA Tábla:
|
A szóródás oka |
Eltérésnégyzetösszeg |
Szabadsági fok |
Négyzetes közép |
|
Sorhatás |
Qr = 264,46 |
fr = 4-1=3 |
sr2 = 88,15 |
|
Oszlophatás |
Qc = 86,08 |
fc = 3-1=2 |
sc2 = 43,04 |
|
Kereszthatás |
Qrc = 22,92 |
frc = (4-1)(3-1)=6 |
src2 = 3,82 |
|
Reziduál |
Qe 25,50 |
fe = Nössz –( 4 * 3)=12 |
se2 = 2,12 |
|
Teljes |
Q = 398,96 |
f = Nössz –1 = 23 |
Van-e kölcsönhatás? (Van-e kereszthatás?)
nincs kereszthatás
Mivel nem mutatható ki kereszthatás, vagyis a cellákon belüli szóródás pusztán a véletlen műve, a kereszthatás eltérés négyzetösszegét hozzá adjuk a reziduális négyzetösszeghez, és így egy új reziduál jön létre:
(Qe)’ =Qe + Qrc = 25,50 + 22,92 = 48,42
(fe)’ = fe + frc = 12 + 6 = 18
(se2) ’ = (Qe)’ / (fe)’ = 48,42/18=2,69
Az új reziduállal újabb F-próbákkal megvizsgáljuk a sor-hatás és az oszlop-hatás szignifikanciáját:
Van-e különbség az ötvözetek között? (Van-e sorhatás?)
van sorhatás
Van-e különbség a kemencék között? (Van-e oszlophatás?)
van oszlophatás
Tehát az ötvözetek és a kemencék is szignifikáns különbségeket mutatnak, de a kölcsönhatás nem szignifikáns .
7.5. Feladat
Faktoriális kísérleti terv, feles replikáció, 3 ismétlés
Kidolgozta: Manhertz Gábor, PhD ösztöndíjas hallgató
Ellenőrizte: Dr. Wenzel Klára
Olyan kísérletet kell tervezni, amelynek alapján új polimer, mégpedig kéntartalmú antioxidáns optimális előállítási feltételei határozhatók meg. Ez az új polimer nagy molekulájú polisztirol és kén reakciójából keletkezik. A feladat olyan stabilizátor előállítása, amelynek adagolása az izotaktikus polipropilénhez megnöveli az indukciós periódust anélkül, hogy a polimer fizikai-mechanikai tulajdonságait rontaná.
|
Faktorok |
Faktorok szintjei |
Variációs intervallum |
||||
|
-1 |
0 |
+1 |
||||
|
– a reakciós közeg hőmérséklete, °C |
200 |
220 |
240 |
20 |
||
|
– a kén adagolása, súlyrész |
3 |
6 |
9 |
3 |
||
|
– a reakcióidő, perc |
40 |
100 |
160 |
60 |
||
|
– antioxidáns adagolása a polipropilénhez, sr |
1 |
2 |
3 |
1 |
||
A megoldás menete:
Négy faktor vizsgálatára először egy négyfaktoros teljes kísérleti terv juthat eszünkbe. Ez 24= 16 kísérletet jelent. Azonban van más lehetőség is: alkalmazhatunk egy háromfaktoros, feles replikációjú kísérleti tervet, így ugyan valamelyik kölcsönhatás vizsgálatáról le kell mondanunk (leginkább a háromszoros kölcsönhatásról, mert ebben már 3 hatás keveredik) de így csak 8 kísérletet kell elvégezni.Ha pedig ezt a 8 kísérletet kétszer végezzük el (16 kísérlet), lehetőség nyílik a kísérleti eredmények megbízhatóságának (az együtthatók szignifikanciájának) vizsgálatára is. Válasszuk ezt az utóbbi lehetőséget!
A kísérleti terv a következő táblázatban látható. Vizsgáljuk meg a terv felépítését:
-
Minden oszlopban ugyanannyi + és – beállítás található; tehát fennáll az szimmetria
-
Bármely két oszlop skaláris szorzatának összege 0, tehát fennáll az ortogonalitás.
-
Van olyan sor (kísérlet), amelyben minden beállítás + és van olyan, amelyben minegyik – szintű. Tehát egy kísérletben eljutunk a kísérleti tartomány egyik szélső (legalsó szintű) sarkától amásik szélsőig (legfelső szintű).
|
x0 |
x1 |
x2 |
x3 |
x4 |
x1x2= =x3x4 |
x1x3= =x2x4 |
x2x3= =x1x4 |
y1 |
y2 |
y3 |
y |
|
|
1 |
+ |
+ |
+ |
- |
- |
+ |
- |
- |
10 |
11 |
9 |
10 |
|
2 |
+ |
- |
- |
- |
- |
+ |
+ |
+ |
9 |
8 |
9 |
8,67 |
|
3 |
+ |
+ |
- |
- |
+ |
- |
- |
+ |
15 |
14 |
16 |
15 |
|
4 |
+ |
- |
+ |
- |
+ |
- |
+ |
- |
25 |
22 |
26 |
17,67 |
|
5 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
20 |
19 |
22 |
20,33 |
|
6 |
+ |
- |
- |
+ |
+ |
+ |
- |
- |
14 |
12 |
16 |
14 |
|
7 |
+ |
+ |
- |
+ |
- |
- |
+ |
- |
5 |
5 |
6 |
5,33 |
|
8 |
+ |
- |
+ |
+ |
- |
- |
- |
+ |
20 |
19 |
21 |
20 |
|
bi |
13,875 |
-1,2 |
3,125 |
1,04 |
-0,625 |
-0,625 |
-0,875 |
2,125 |
Határozzuk meg az egyes faktorokhoz tartozó együtthatókat!
A kiszámított oszlop segítségével (mely a 3 kísérlet átlaga), meghatározható az együtthatók értéke. Ez úgy történik, hogy az egyes együtthatóhoz tartozó oszlopot előjelesen össze kell adni és átlagolni.
Így pl.:
Vizsgálja meg az együtthatók szignifikanciáját!
A szignifikancia vizsgálat elvégzéséhez szüksége van a megbízhatósági intervallum/intervallumok hosszára minden egyes együtthatóra vonatkozóan. Ehhez először a bi regressziós együttható s2{bi}szórásnégyzetét kell meghatározni. Ez a következő képen történik.
meghatározásához a következő módon kell eljárni:
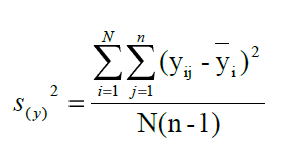
ahol:
-
n– a kísérleti eredmények
-
N– az adat sorszáma
-
j– a csoport sorszáma
-
– egy adott kísérleti elrendezéshez tartozó eredmény
-
– a kísérletek eredményeinek átlaga
A szükséges számítások elvégzése után:
A kapott eredmény segítségével meghatározható
A megbízhatósági intervallum félszélessége úgy határozható meg pl. 0,05-ös szignifikancia szinten, hogy a 0,05-ös szinthez tartozó Student-féle t-próba táblázatból először ki kell keresni a kísérlet szabadságfokaihoz tartozó számértéket.
Mivel a szabadságfokok száma jelenleg 7 (a faktorok száma), így t = 2,365
A megbízhatósági intervallum félszélessége a következő ekvivalens alakban írható fel:
Kiszámítva:
Egy adott együttható akkor szignifikáns, ha az abszolút értéke nagyobb a megbízhatósági intervallum félszélességénél.
|
Sorszám |
bi |
Δbj |
Szignifikáns? |
|
0 |
13,875 |
1,454 |
Igen |
|
1 |
-1,2 |
1,454 |
Nem |
|
2 |
3,125 |
1,454 |
Igen |
|
3 |
1,04 |
1,454 |
Nem |
|
4 |
-0,625 |
1,454 |
Nem |
|
5 |
-0,625 |
1,454 |
Nem |
|
6 |
-0,875 |
1,454 |
Nem |
|
7 |
2,125 |
1,454 |
Igen |
Az iménti táblázat alapján a 2 és a 7 jelű együttható szignifikáns.
Határozza meg, hogy a kísérletek következő sorozatában melyik faktorokat illetve melyik kölcsönhatásokat célszerű vizsgálat tárgyává tenni!
A kísérletek következő sorozatában az előző lépésben meghatározott szignifikáns együtthatókhoz tartozó faktorokat, tehát az x2 faktort és a7 jelű együtthatóhoz tartozó kölcsönhatások közül a szignifikáns x2 faktornak az x3 faktorral való kölcsönhatását célszerű a vizsgálat tárgyává tenni.
7.6. Feladat
Faktoriális kísérleti terv, 2 5-2 replikációjú, 2-szer ismételt faktoriális kísérleti terv
Kidolgozta: Balla Petra, PhD ösztöndíjas hallgató
Ellenőrizte: Dr. Wenzel Klára
Egy vegyi anyag előállítási folyamatának optimalizálására a feladat. Úgy határoztak, hogy a kísérleti tervben az 1. táblázatban feltüntetett 5 faktort variálják.
Optimalizációs paraméterként a kihozatal százalékában kifejezett értékét tekintették.
A kísérlet tervezési mátrixát a 2. táblázat tartalmazza.
|
Faktorok |
Faktorok szintjei |
Variációs intervallum |
||||
|
-1 |
0 |
1 |
||||
|
x1 - a NaOH és az a anyag aránya |
1:01 |
1,25:1 |
1,5:1 |
0,25 |
||
|
x2 - a c és az a anyag aránya |
1:01 |
1,25:1 |
1,5:1 |
0,25 |
||
|
x3 - időtartam, óra |
3 |
4 |
5 |
1 |
||
|
x4 - hőmérséklet, ˚C |
20 |
25 |
30 |
5 |
||
|
x5 - az a anyag betöltésének ideje, perc |
20 |
40 |
60 |
20 |
||
-
táblázat A faktorok szintjei és a variációs intervallumok
|
Kísérleti beállítás sorszáma |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
y1 |
y2 |
|
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
50 |
52,5 |
|
2 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
57,2 |
56,8 |
|
3 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
48,1 |
47,9 |
|
4 |
1 |
1 |
-1 |
1 |
-1 |
1 |
46 |
46,7 |
|
5 |
1 |
-1 |
1 |
1 |
-1 |
1 |
64,8 |
62,9 |
|
6 |
1 |
1 |
-1 |
-1 |
1 |
1 |
45,3 |
44,2 |
|
7 |
1 |
-1 |
1 |
-1 |
1 |
1 |
54,8 |
52,9 |
|
8 |
1 |
1 |
1 |
1 |
1 |
-1 |
53 |
51,9 |
|
bi |
52,1875 |
-2,05 |
4,6 |
0,475 |
-2,425 |
0,0125 |
|
|
Megjegyzés: A kísérletek sorrendjét randomizáltuk, hogy a környezeti hatások változása ne befolyásolja a kísérletek eredményét szignifikáns módon.
Az adott esetben a tervezéshez egy 25 típusú faktoriális kísérlet ¼-esreplikációját használták fel. Ekkor 32 kísérleti beállítás helyett 8 beállítás szükséges. A mátrixot az x4 = x1x2x3, x5 = -x1x2 generáló összefüggések, azaz az 1 = x1x2x3x4 = -x1x2x5 = -x3x4x5 összefoglaló meghatározó kontraszt által adták meg.
Az x5 = -x1x2 generáló összefüggés megválasztásában szerepet játszott az a feltételezés, hogy az x1x3 és x2x3 interakciók jelentősek. Az ilyen 1/4-es replikációból kapható együttes becslések:
b1 → β1 – β25 + β234 -β1345
b2 → β2 – β15 + β134 –β2345
b3 → β3 – β45 + β134 -β1235
b4 → β4 – β35 + β123–β1245
b5 → β5 – β12 + β34 + β12345
b13 → β13 – β24 + β235 -β145
b14 → β14 – β23 - β245 -β135
Kijelöltek egy második kísérleti beállítási sorozatot is arra az esetre, ha az optimális feltételek keresése nem bizonyul hatékonynak. Ezt úgy választották, hogy a hármas szorzatok ellenkező előjelűek legyenek, mint az első egynegyedes replikációhoz tartozók. E második ¼-esreplikáció összefoglaló meghatározó kontrasztja: 1 = x1x2x3x4 = x1x2x5 = x3x4x5.
A kísérleti beállítások és a mérési eredmények alapján:
|
n=2 |
|
N=8 |
|
i=1…8 |
|
j=1…2 |
A két méréssorból kapott értékek átlaga:
|
yátlag |
|
51,25 |
|
57 |
|
48 |
|
46,35 |
|
63,85 |
|
44,75 |
|
53,85 |
|
52,45 |
A mérési eredmények szórásnégyzete:
|
s^2 (y) |
|
3,125 |
|
0,08 |
|
0,02 |
|
0,245 |
|
1,805 |
|
0,605 |
|
1,805 |
|
0,605 |
|
(y1-y2)^2 |
|
6,25 |
|
0,16 |
|
0,04 |
|
0,49 |
|
3,61 |
|
1,21 |
|
3,61 |
|
1,21 |
A szórásnégyzetek átlaga: 1,03625
Az átlagos szórás: 1,01796
A Student-féle t-próba 5%-os szignifikanciaszinthez tartozó kritikus értékek táblázatából a 8 szabadsági fokhoz tartozó kritikus t érték: 2,306
A megbízhatósági intervallum félszélessége:
Δbj = ts(y)/, tehát
Δbj = (2,306*1,01796)/ = 0,8299
Minél szűkebb a megbízhatósági intervallum, annál szignifikánsabb az együttható.
Alapszabály: Ha az együttható abszolút értéke nagyobb, mint a megbízhatósági intervallum félszélessége akkor az együttható szignifikáns.
Ezen szabály alapján könnyen megállapítható a szignifikancia:
|
bi |
b0=52,1875 |
b1=-2,05 |
b2=4,6 |
b3=0,475 |
b4=-2,425 |
b5=0,0125 |
|
Abszolút értékét összehasonlítva Δbj-vel |
kisérleti beállítások középpontja |
szignifikáns |
szignifikáns |
szignifikáns |
szignifikáns |
nem szignifikáns |
7.7. Feladat
Faktoriális kísérleti terv készítése; 1/16 replikáció, két ismétlés
Kidolgozta: Pintér Ádám, PhD ösztöndíjas hallgató
Ellenőrizte: Dr. Wenzel Klára
Egy piperazin származék előállítási folyamatának optimalizálása a feladat. Az alábbi táblázatban közölt két faktornak a termékkihozatalra való hatását tanulmányozzuk. A 27 típusú faktorális kísérlet 1/16 részét használjuk fel. Ez lehetőséget ad arra, hogy a kísérleti beállítások számát 128-ról 8-ra redukáljuk.
|
Faktorok |
Faktorok szintjei |
Variációs intervallum |
||||
|
-1 |
0 |
+1 |
||||
|
x1 - a reakciós masszába az a anyag beöntése előtt bevitt NaOH mennyisége g/mól |
0,0075 |
0,018 |
0,0285 |
0,0105 |
||
|
x2 - pH fenntartásának módja (az oldat fajtája) |
NaOH 18%-os oldata metanolban |
- |
NaOH 4%-os oldata vízben |
- |
||
|
x3 - az a anyag és a NaOH oldat beöntésének időtartama, óra |
3 |
4,5 |
6 |
1,5 |
||
|
x4 - időtartam, óra |
1 |
2 |
3 |
1 |
||
|
x5 - hőmérséklet, °C |
20 |
25 |
30 |
5 |
||
|
x6 - a b anyag és a metanol súlyaránya, g/g |
1:3 |
1:3,5 |
1:4 |
1:0,5 |
||
|
x7 - az a ás b anyag móltörtje |
1:1 |
1:1,1 |
1:1,2 |
1:0,1 |
||
A tervezési mátrixot és a lineáris egyenlet megfelelő együtthatóit a következő táblázat tünteti fel.
|
Kísérleti beállítás sorszáma |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
y1 |
y2 |
|
1 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
19,3 |
18,2 |
|
2 |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
23,8 |
24,3 |
|
3 |
+ |
- |
- |
+ |
+ |
- |
- |
+ |
31,3 |
33,4 |
|
4 |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
12,8 |
12,1 |
|
5 |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
32,0 |
30,7 |
|
6 |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
14,0 |
14,8 |
|
7 |
+ |
+ |
+ |
- |
+ |
- |
- |
- |
25,0 |
23,9 |
|
8 |
+ |
+ |
- |
+ |
- |
+ |
- |
- |
30,5 |
32,0 |
|
bj |
23,5875 |
1,0625 |
-5,8125 |
0,1875 |
3,3125 |
0,0625 |
-1,3125 |
-1,7875 |
|
|
Annak érdekében, hogy eldönthessük, hogy elhanyagolhatunk-e faktorokat, meg kell vizsgálnunk az együtthatók szignifikanciáját. Ezt megtehetjük a Stundent-féle t-próbán alapuló vizsgálattal. A megbízhatósági intevallumok szélessége minden egyes együtthatóra vonatkozóan egyenlő egymással. A számszerű vizsgálathoz szükségünk van a bi regressziós együttható szórásnégyzetre, amelyet az alábbi képlettel határozhatunk meg:
Mivel nekünk két mérési sorozatunk van, y1 és y2, ezért a véletlen hatás meghatározása érdekében 2-2 ismételt kísérleti eredmény szórásnégyzetétt határozzuk meg, majd ezek átlagát vesszük.
Megjegyzés: 2 mérésből alapvetően nem lehet szórást meghatározni, de a szórásanalízisben elfogadott, hogy több adat felhasználása esetén 2-2 adat eltérés négyzetösszegével számolunk.
|
y1 |
y2 |
s2 |
|
19,3 |
18,2 |
0,605 |
|
23,8 |
24,3 |
0,125 |
|
31,3 |
33,4 |
2,205 |
|
12,8 |
12,1 |
0,245 |
|
32,0 |
30,7 |
0,845 |
|
14,0 |
14,8 |
0,32 |
|
25,0 |
23,9 |
0,605 |
|
30,5 |
32,0 |
1,125 |
|
SZÓRÁS-ÁTLAG |
0,7594 |
|
A fentebbi képletet alkalmazva bj szórásnégyzete (N=8):
A megbízhatósági intervallum sugara megszerkeszthető a következő alapján:
,
ahol t a Student-féle próba táblázatából vett értéke. Ez esetünkben, 95%-os szignifikancia szinten: 2.365, ahol a szabadságfokok száma 7, mivel -t is ezzel a szabadságfokkal (n-1) határoztuk meg.
A regressziós együttható szórása a szórásnégyzetének a négyzetgyöke, azaz:
A megbízhatósági intervallum sugara a következő ekvivalens alakban írható fel:
Egy adott együttható akkor szignifikáns, ha abszolút értéke nagyobb a megbízhatósági intervallum sugaránál. Így nincs más dolgunk, mint az egyes együtthatókat megvizsgálni, hogy mely együtthatókra igaz mindez. Amennyiben egy együttható a fentebb levezetett konfidencia intervallum sugaránál nagyobb, akkor szignifikáns, azaz nem hagyhatjuk el a következő kísérletsorozatunkból (és nem vehetünk be például helyette másik faktort), amelyek viszont kisebbek, azokra azt mondhatjuk, hogy jó eséllyel elhagyhatjuk őket, ugyanis hatásuk nem szignifikáns:
|
bj |
23,5875 |
1,0625 |
-5,8125 |
0,1875 |
3,3125 |
0,0625 |
-1,3125 |
-1,7875 |
|
|bj| |
23,5875 |
1,0625 |
5,8125 |
0,1875 |
3,3125 |
0,0625 |
1,3125 |
1,7875 |
|
∆bj |
|
0,728 |
0,728 |
0,728 |
0,728 |
0,728 |
0,728 |
0,728 |
|
SZIGNIFIKÁNS? |
|
IGEN |
IGEN |
NEM |
IGEN |
NEM |
IGEN |
IGEN |
7.8. Feladat
Taguchi kísérleti terv készítése
Kidolgozta: Manhertz Gábor, PhD ösztöndíjas hallgató
Ellenőrizte: Dr. Wenzel Klára
Feladat
Készítsen Taguchi módszerrel kísérlet tervet arra az esetre, ha az A , B, C, D, E, F, G és H faktor hatását kívánjuk megvizsgálni. Ezek közül a C, F, G és H faktor szintjeinek beállítása nagyon költséges, a D és E faktor szintjeinek beállítása meglehetősen költséges, az A faktor szintjeinek beállítása viszonylag egyszerű, és a B faktor szintjeinek beállítása nagyon egyszerű. Érdekesnek tűnik még az AB, BC, BD, BE, BF, BG és BH kölcsönhatás is. Keresse meg a megfelelő lineáris gráfot, készítse el a háromszög-táblázatot és az ortogonális táblázatot!
Megoldás:
A feladatban összesen 8 faktort kell vizsgálni, melyek A, B, C, D, E, F, G és H. Az önálló faktorok vizsgálata mellett továbbá szükséges vizsgálni a B faktor minden más faktorral való kölcsönhatását. Így rendre: AB, BC, BD, BE, BG, BG, és BH. Ezeknek az alapkövetelményeknek az ismeretében kimondható, hogy összesen 15 tényezőt kell vizsgálni.
Taguchi módszere szerint a 15 tényező vizsgálatához egy L16 (215) kísérleti terv szükséges. A „szakácskönyvnek” megfelelően az ortogonális, valamint a kölcsönhatás táblázat a következő:
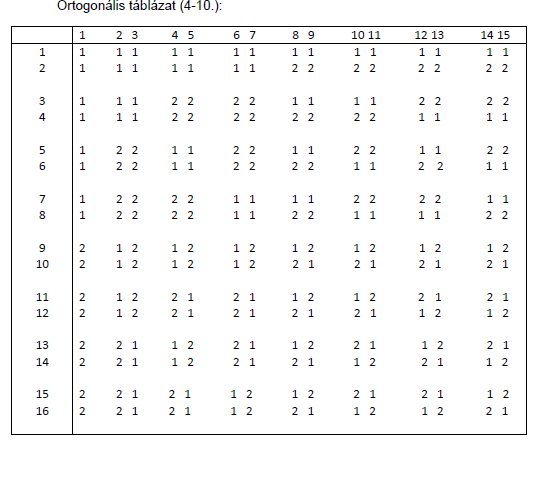
Az ortogonális táblázat

A kölcsönhatás táblázat
Taguchi módszere szerint 8 hatás és 7 kölcsönhatás vizsgálatára az alábbi lineáris gráfok a megfelelőek:
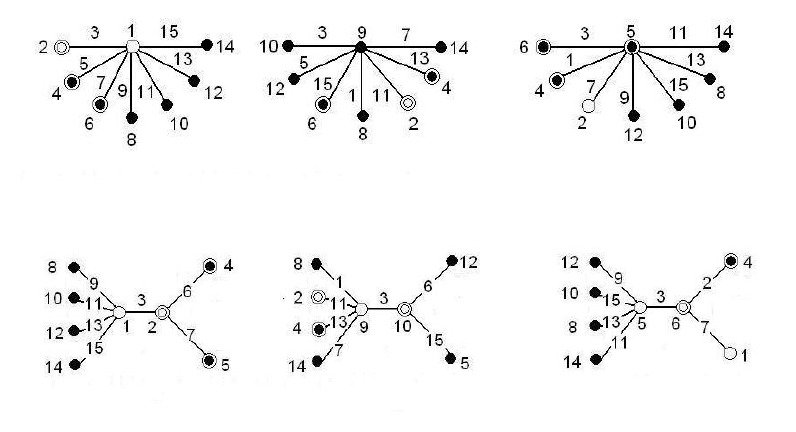
A fentebbi gráfok közül ki kell választani azt a gráfot, mely az adott kísérleti feladathoz illeszkedik. A kiválasztás után a csomópontok és az ágak beazonosíthatóak lesznek az egyes faktorokkal. A megfelelő gráf kiválasztása a faktorok beállítási nehézségei alapján történik. A feladat szerint a C, F, G és H faktor szintjeinek beállítása nagyon költséges, a D és E faktor szintjeinek beállítása meglehetősen költséges, az A faktor szintjeinek beállítása viszonylag egyszerű, és a B faktor szintjeinek beállítása nagyon egyszerű. A gráfokon a beállítási nehézségek a csomópontok jellege alapján azonosítható, így:
-
fekete kör: nagyon költséges (C, F, G, H)
-
fekete kör körül fehér keret: meglehetősen költséges (D, E)
-
fehér kör körül fehér keret: viszonylag egyszerű (A)
-
fehér kör: nagyon egyszerű (B)
Mivel a B faktor kölcsönhatását vizsgáljuk minden másik faktorral, így övé a kitűntetett szerep. A megfogalmazás szerint a faktor beállítása nagyon egyszerű, így olyan gráfot kell keresni, melynek középpontjában csak egy faktor áll és az fehér körrel van jelölve. Ezeknek a feltételeknek csak a felső sor, bal szélső gráfja tesz eleget, így ez a szükséges lineáris gráf a kísérleti tervhez (a többi faktor tulajdonságának megfelelő szimbólumok is megfelelőek).
A gráf kiválasztása után szükséges a számjelölések beazonosítása. Ennek megfelelően a faktorok:
-
1: B faktor
-
2: A faktor
-
3, 6: D és E faktor
-
8, 10, 12, 14: C, F, G és H faktorok
A kölcsönhatások megfeleltetése a csomópontok alapján történik, illetve a közéjük húzott ággal. Ennek megfelelően a kölcsönhatások:
-
3: AB kölcsönhatás
-
5: BD kölcsönhatás
-
7: BE kölcsönhatás
-
9: BC kölcsönhatás
-
11: BF kölcsönhatás
-
13: BG kölcsönhatás
-
15: BH kölcsönhatás
Ellenőrzés képen a beazonosítások összevethetőek az ortogonális táblázattal. Így például BE kölcsönhatásának száma a 7-es, B faktor száma 1, E faktor száma 6. Az ortogonális táblázatban a 6-os jelzésű oszlop és az (1) jelzésű sor metszéspontjában található számértéket kell kikeresni. Ez ebben az esetben a 7-es, amely helyesen a BE kölcsöhatás azonosítója.
7.9. Feladat
Taguchi kísérleti terv készítése
Kidolgozta: Gárdonyi Gábor, PhD ösztöndíjas hallgató
Ellenőrizte: Dr. Wenzel Klára
Egy takarmány gyárban a termék minőségének javítása a cél. A termék minőségét a tápérték, az emészthetőség és az önköltség mutatóiból alkotott cél-függvény alapján 1-től 100-ig terjedő számozással jellemzik. Előzetes gyártási tapasztalatok alapján úgy tűnik, hogy a termék minősége (A faktor) nem azonos a téli és a nyári időszakban. Ezért ezt a faktort a kísérletekre szánt egy éven belül két szinten lehet vizsgálni, és nem lehet váltogatni a szinteket. Két féle gyártási technológiát (B faktor) kell megvizsgálni. A technológia módosítása az egész gépsor átszerelését igényli, ezért ezt a faktort is lehetőleg keveset célszerű módosíttatni. Két gépen folyik a kísérlet (C faktor), és mivel a két gépen a kísérletek alatt is folyamatosan folyik a gyártás, a gépek váltogatása nem megoldható. Két féle utókezelés hatását (D faktor) kell megfigyelni; ennek változtatása viszonylag egyszerűen megoldható. A gyártás végén két féle tartósító adalékot (E faktor) adnak a takarmányhoz. Ennek a váltogatása egyszerű.
Készítsen Taguchi módszerrel kísérlet tervet arra az esetre, ha az A , B, C, D, és E faktor hatását kívánjuk megvizsgálni. Érdekesnek tűnik még az összes kettős kölcsönhatás is. Keresse meg a megfelelő lineáris gráfot, készítse el a háromszög-táblázatot és az ortogonális táblázatot!
A faktorok-szintek beállításának nehézsége:
-
A – nagyon költséges
-
B – nagyon költséges
-
C – meglehetősen költséges
-
D – viszonylag egyszerű
-
E – nagyon egyszerű
Megoldás:
Taguchi módszer alapján feladatunk az La(bc) kísérleti tervhez tartozó ortogonális és kölcsönhatás táblázatok felírása. A feladatban definiált kísérlet esetén
-
a = 16 a kísérletek száma
-
b = 2 a faktorszintek száma
-
c = 15 a vizsgálható hatósok száma
Mivel nincs előzetes információnk arról, hogy vannak-e kölcsönhatások az egyes hatások között, ezért Taguchi szerint a következőképpen ajánlott a kísérleti tervet elkészíteni:
-
5 faktor esetén L16 terv alkalmazása szükséges
-
A főhatások elhelyezése az 1. , 2. , 4. , 8. és 15. oszlopokba
5 faktor és az összes kétszeres kölcsönhatás vizsgálatára a Taguchi szakácskönyv a jegyzet 4.7. ábrájának lineáris gráfjait ajánlja. A faktorok nehézségi szintjeit is figyelembe véve az alábbi lineáris gráfot alkalmazzuk, az ábrán piros betűvel bejelölt faktorok szerint.
A lineáris gráf:
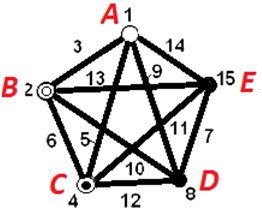
-
– 1. csoport – nagyon könnyű állíthatóság
-
– 2. csoport – viszonylag könnyű állíthatóság
-
– 3. csoport – viszonylag nehéz állíthatóság
-
– 4. csoport – nagyon nehéz állíthatóság
Az L16 (215) kísérleti terv ortogonális táblázata:
|
1 A |
2 B |
3 AB |
4 C |
5 AC |
6 BC |
7 DE |
8 D |
9 AD |
10 BD |
11 CE |
12 CD |
13 BE |
14 AE |
15 E |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
3 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
|
4 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
|
5 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
|
6 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
|
7 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
|
8 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
|
9 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
10 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
|
11 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
|
12 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
|
13 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
|
14 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
|
15 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
|
16 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
1 |
Az ortogonális táblázatba a kölcsönhatásokat a lineáris gráf vagy a háromszög-táblázat alapján lehet beírni.
Ezek után a faktoriális tervek kidolgozásához hasonló módon járunk el. Az ortogonális táblázathoz egy (ismétel kísérletek esetén több) újabb oszlopot csatolunk, és ide írjuk be az egyes sorok beállításaival elvégzett kísérletek eredményét. Majd meghatározzuk a b együtthatókat, és meghatározzuk, hogy ezek közül melyik szignifikáns. Szükség esetén a szignifikáns faktorokkal további kísérleteket végzünk.
Az L16 (215) kísérleti terv kölcsönhatás vagy háromszög táblázata:
|
1 A |
2 B |
3 |
4 C |
5 |
6 |
7 |
8 D |
9 |
10 |
11 |
12 |
13 |
14 |
15 E |
|
(1) |
3 |
2 |
5 |
4 |
7 |
6 |
9 |
8 |
11 |
10 |
13 |
12 |
15 |
14 |
|
(2) |
1 |
6 |
7 |
4 |
5 |
10 |
11 |
8 |
9 |
14 |
15 |
12 |
13 |
|
|
(3) |
7 |
6 |
5 |
4 |
11 |
10 |
9 |
8 |
15 |
14 |
13 |
12 |
||
|
(4) |
1 |
2 |
3 |
12 |
13 |
14 |
15 |
8 |
9 |
10 |
11 |
|||
|
(5) |
3 |
2 |
13 |
12 |
15 |
14 |
9 |
8 |
11 |
10 |
||||
|
(6) |
1 |
14 |
15 |
12 |
13 |
10 |
11 |
8 |
9 |
|||||
|
(7) |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
||||||
|
(8) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||||
|
(9) |
3 |
2 |
5 |
4 |
7 |
6 |
||||||||
|
(10) |
1 |
6 |
7 |
4 |
5 |
|||||||||
|
(11) |
7 |
6 |
5 |
4 |
||||||||||
|
(12) |
1 |
2 |
3 |
|||||||||||
|
(13) |
3 |
2 |
||||||||||||
|
(14) |
1 |