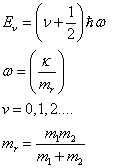1. fejezet - Atomok, molekulák, szilárd testek lehetséges energiaállapotai
A fény és az anyag kölcsönhatásának klasszikus tárgyalása szerint a fény elektromágneses tere az anyag töltött részecskéivel vagy dipóljaival lép kölcsönhatásba, azokat gyorsítja vagy rezgésbe hozza. A gyorsuló illetve rezgő töltések pedig fényt bocsátanak ki.
Az atomok, molekulák és szilárd testek a kvantummechanika segítségével meghatározható energiaállapotokkal rendelkeznek. Fénnyel való kölcsönhatásuk bizonyos esetekben a megengedett állapotok közötti átmenetet eredményezi. Ha a fénykvantum energiája az anyagban egy lehetséges energia-átmenet gerjesztésére elegendő, akkor a fény elnyelődhet. Fordított folyamat - fénykibocsátás - szintén lejátszódhat. Ha T ≠ 0 és az anyag környezetével hőmérsékleti egyensúlyban van, termikus fénykibocsátás történik. A kibocsátott fény energiasűrűségének frekvencia-eloszlását ilyenkor a Planck-törvény írja le.
Fénykibocsátás akkor is lehetséges, ha valamilyen külső energiaforrás segítségével gerjesztjük az anyagot. A külső energiaforrás lehet fényforrás, elektromos kisülés, áram, kémiai reakció, stb. Az íly módon szelektíven gerjesztett anyag által kibocsátott fény frekvencia-eloszlását már nem a Planck-törvény írja le.
Bármely anyag atomokból épül fel. Az atomok előfordulhatnak önállóan, például egy ritka gázban, vagy más atomokkal kölcsönhatásban molekulát, folyadékot vagy szilárd testet hozhatnak létre. Az anyagot alkotó mikrorészecskék a kvantummechanika törvényszerűségeinek megfelelően viselkednek. A mikrorészecskék "mozgásának" leírására, állapotainak meghatározására a kvantummechanika fogalomrendszerét kell használni.
1.1. Atomok lehetséges állapotai
A legegyszerűbb atom a H-atom, mely egy protonból és egy elektronból áll. H-szerű atomoknak nevezik azokat az atomokat, melyek Z protont és csak egy elektront tartalmaznak. Ezek lehetséges energiái:
|
|
(1.1) |
ahol Z a protonszám, n=1, 2, ... pozitív egész szám, az energia értéke pedig eV-ban értendő. Az energia negatív, mert kötött állapotról van szó.
1eV energiára tesz szert egy elektron 1V feszültséggel gyorsítva. Mivel az elektron töltése 1,6·10-19 C, az energia értéke SI egységben 1,6·10-19 J.
Több elektronnal rendelkező atom esetén csak jóval bonyolultabban adhatók meg a lehetséges energiaértékek, de minden atomra jellemző, hogy diszkrét energiaszintekkel rendelkezik, melyek távolsága tipikusan eV-os nagyságrendű.
1eV-os energiájú foton vákuumbeli hullámhosszát megkapjuk, ha a fénysebesség és a Planck-állandó (h=6,63 10-34 Js) értékének szorzatát elosztjuk a J-ban kifejezett energia értékével, vagyis jelen esetben ez megfelel 1,24 µm-nek.
1.2. Molekulaállapotok
Az atomokhoz hasonlóan tárgyalhatók a molekulák is, de mivel ezek több atom együtteséből állnak, figyelembe kell venni a molekula rezgéséből és forgásából eredő hatásokat is.
1.2.1. Rezgési energia
A legegyszerűbb molekula két atomból áll. Ekkor a rezgés potenciális energiája, ha m 1 és m 2 jelöli az atomok tömegét és a kitérés az erővel lineáris és x irányú,
|
|
(1.2) |
alakban írható, ahol κ a rugóállandó. A lehetséges rezgési energiák megegyeznek a kvantummechanika egyik alapproblémájának, a harmonikus oszcillátornak az energiaértékeivel
|
|
(1.3) |
ahol m
r
a redukált tömeg, v a rezgési kvantumszám és ω a sajátfrekvencia. Érdemes megjegyezni, hogy a rezgési energiaszintek egymástól való távolsága mindig 
. Így a κ rugóállandó a redukált tömeg ismeretében a rezgési vonalak távolságából meghatározható. Az oszcillátor legalacsonyabb energiája
|
|
(1.4) |
a szintek távolságának fele és nem 0. Ez az energiaérték az ún. zérusponti energia. 
tipikus értéke molekuláknál 0,05-0,5eV, ami megfelel 2,5-25µm hullámhossznak.
Többatomos molekula esetén többfajta rezgés is lehetséges különböző rugóállandóval.
1.2.2. Forgási energia
Megint a legegyszerűbbet, a kétatomos molekulákat példaként tekintve a forgási energia kvantummechanikai megfelelője felírható a klasszikus forgási energia alapján
|
|
(1.5) |
alakban, ahol I a molekula tehetetlenségi nyomatéka, az I(I+1) pedig az impulzusmomentum lehetséges értékeiből származtatható, vagyis I az impulzusmomentum kvantumszáma. A tipikus energiaértékek 0,001-0,01eV tartományba esnek, ami hullámhosszban megfelel a távoli infravörös (100 µm-1 mm) tartománynak.
1.2.3. A molekula teljes energiája
A molekula teljes energiája az elektron-, a rezgési és a forgásból eredő energiák összege
|
|
(1.6) |
mivel az egyes tagok energiában igen különböző nagyságrendűek, ezért a molekula-átmenetek hullámhosszából következtetni lehet arra, hogy milyen típusú energia-átmenetről van szó.
1.2.4. Festékmolekula
A szerves festékek nagy bonyolult molekulákból állnak, melyek elektronenergiái, rezgési és rotációs szintjei egymásra épülve a nagyon sok, egymáshoz közeli energiaszintből sávokat hoznak létre (1.1. ábra).
1.3. Elektronállapotok szilárd testekben
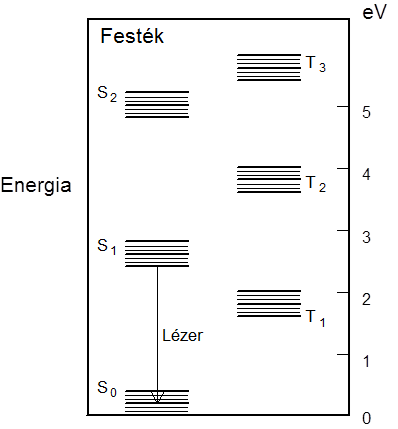
Az atomok és molekulák diszkrét energiáitól eltérően a szilárdtestben az eredeti atomi elektronszintek nagymértékben kiszélesednek. A kiszélesedés az iontörzstől távolodva növekszik. A kiszélesedett, s ezért át is fedő sávok betöltöttségének függvényében nagymértékben változó tulajdonságok miatt három típusú szilárdtestet szokás megkülönböztetni (1.2. ábra): fémet, félvezetőt és szigetelőt.
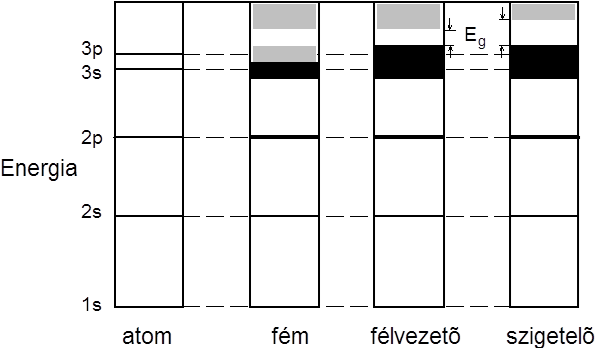
Azok az anyagok, melyekben a legfelső energiasáv csak kis mértékben betöltött, s ezért elektronjaik szinte tetszőlegesen kis energiával gerjeszthetők, a fémek. Azok az anyagok, amelyekben a legfelső energiasáv teljesen betöltött és a következő sáv, mely 3 eV - nál közelebb van, T=0 hőmérsékleten teljesen üres, a félvezetők. Hasonlóan jellemezhetők a szigetelők, csakhogy ezeknél az üres sáv távolsága 3eV-nál messzebb van. A legfelső betöltetlen, vagy részlegesen betöltött sáv a vezetési sáv. A teljesen betöltött legfelső sáv a vegyértéksáv. A kettő távolsága a tiltott sáv, melynek energiaszélességét E g -vel jelölik. g a gap (jelentése rés) angol szó kezdőbetűje.
A különböző típusú szilárdtest anyagok eltérő tulajdonságát jól mutatja vezetőképességük nagymértékű eltérése. A vezetőképesség Ωcm-ben kifejezett tipikus értéke fémekben 106, félvezetőkben 10-6-103 és szigetelőkben 10-12.
Szigetelő típusú szilárdtest-lézer volt az első működő lézer is, a rubinlézer. A rubin krómmal szennyezett alumíniumoxid kristály. A lézerműködés szempontjából érdekes nívói az (1.3. ábra) ábrán láthatók.
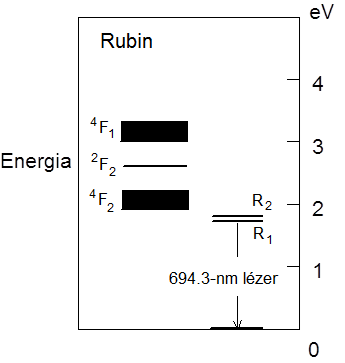
A lézerátmenet a krómion közbülső diszkrét energiaszintjei között történik, míg a szilárd testeket jellemző sávok (az (1.3. ábra) ábrán 4F1 és 4F2) alkalmasak a lézerátmenet szélessávú gerjesztésére.
A két legismertebb félvezető anyag a Si és a GaAs. Tiltott sávjuk szélessége 1,11 eV (Si) és 1,42 eV (GaAs). A sávszélesség értékének alapján a Si látszik könnyebben gerjeszthetőnek. A tiltott sáv környéki lehetséges energiaállapotok részletesebb tanulmányozása alapján belátható, hogy a Si -ban a vezetési sáv és a vegyértéksáv között nem lehetséges foton kibocsátásával vagy elnyelésével kapcsolatos közvetlen átmenet, mivel az impulzus-megmaradás ezekre a folyamatokra nem tud teljesülni. (A Si indirekt sávú, a GaAs pedig direkt sávú félvezető.) Ezért a félvezető lézerek legfontosabb alapanyaga a GaAs és különböző módosulatai, mint pl. GaAlAs, InGaAs, GaAsP, InGaAsP stb.