2. fejezet - Fény és anyag kölcsönhatása (fénykibocsátás, fényelnyelés)
Az elektromágneses térrel való kölcsönhatás következtében egy anyagi részecske, legegyszerűbb esetben egy atom lehetséges energiaszintjei között fénykibocsátásos illetve fényelnyeléses átmenetek fordulhatnak elő. Válasszuk ki egy atomnak két energiaállapotát, E 1 és E 2 -t. Legyen az energiakülönbségnek megfelelően a rezonanciafrekvencia ν 0 , vagyis
|
|
(2.1) |
Három kölcsönhatási folyamat lehetséges: spontán emisszió, abszorpció és indukált emisszió.
2.1. Spontán emisszió
Amikor az atom a magasabb energiájú E 2 állapotból egy ν≈ν 0 frekvenciájú foton kibocsátásával kerül az alacsonyabb energiájú E 1 állapotba, akkor spontán emisszióról beszélünk. A kibocsátott foton frekvenciájának legvalószínűbb értéke a ν 0 frekvencia, de attól eltérő is lehet, mivel az E 1 és E 2 energiaszintek csak a legvalószínűbb energiaértéket adják meg, a nívók nem végtelen keskenyek.
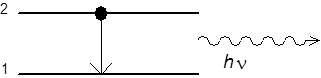
Ha a spontán emisszió valószínűsége egységnyi idő alatt p sp , akkor p sp Δt annak a valószínűsége, hogy a [t, t+Δt] időintervallumban ν frekvenciájú foton kibocsátása történik. Ha N az atomsűrűség (egységnyi térfogatban, dV-ben az atomok száma) a felső E 2 szinten, akkor spontán emisszióval
|
|
(2.2) |
atom fog bomlani egységnyi térfogatban, a gerjesztett atomok számának változása pedig dV-ben
|
|
(2.3) |
A gerjesztett atomok száma exponenciálisan csökken az 1/p sp időállandóval.

2.2. Abszorpció
Abszorpció során az atom egy ν frekvenciájú foton hatására az E 1 állapotból az E 2 állapotba megy át, minek következtében a térben jelen lévő ν frekvenciájú fotonok száma eggyel csökken.
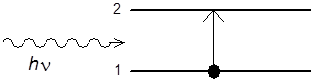
2.3. Indukált emisszió
Az abszorpciós folyamat fordítottja. Egy ν frekvenciájú foton hatására egy ugyanolyan tulajdonságú "hasonmás" foton keletkezik, miközben az atom a magasabb energiájú E 2 állapotból az alacsonyabb energiájú E 1 állapotba kerül. A ”hasonmás” foton ugyanolyan energiájú, irányú, mint a beérkezett foton és az általa leírt elektromágneses hullám polarizációja és fázisa is megegyezik a beérkező foton által képviselt hullám megnevezett tulajdonságaival.
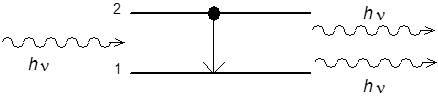
Az indukált emissziós folyamat hozza létre a lézerek "nem közönséges tulajdonságú" fényét!!
Az abszorpció és az indukált emisszió matematikai leírásához szükségünk van egy új fogalom, a fluxussűrűség bevezetéséhez. Tekintsük az atom kölcsönhatását egy csupa ν frekvenciájú fotonokból álló (monokromatikus) nyalábbal! Jellemezzük a fotonnyalábot a ν frekvencián kívül az I intenzitásával. (Az intenzitás az egységnyi felületre beeső fényteljesítmény.) Vezessük be az egységnyi felületre, egységnyi idő alatt beeső fotonszámot, a fluxussűrűséget, mely az intenzitással definíció szerint a következő kapcsolatban van:
|
|
(2.4) |
Az indukált emisszió vagy az abszorpció egységnyi idő alatti valószínűségét, W i -t a következőképpen írhatjuk le:
|
|
(2.5) |
ahol σ(ν) az anyagi részecske kiválasztott átmenetéhez rendelhető, frekvencia-függő, felület dimenziójú mennyiség, a hatáskeresztmetszet. Egységnyi idő alatt annyi indukált emisszió vagy abszorpció játszódik le, ahány fotont „fog be” az anyagi részecske a fotonnyalábból. A hatáskeresztmetszet rezonancia jellegű frekvencia-függvény. Jellemzése lehetséges maximális értékével σ(ν 0 )=σ 0 -lal, félérték-szélességével Δν-vel és a görbe alatti S területtel (2.5. ábra).
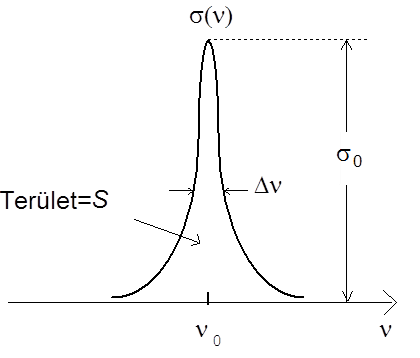
W i annál nagyobb, minél nagyobb a fluxussűrűség és a hatáskeresztmetszet. σ(ν) tehát az atomhoz rendelhető hatásos felület, melyen ha a foton áthalad, biztosan bekövetkezik az indukált emisszió vagy az abszorpció folyamata.
2.4. Homogén és inhomogén rendszerek hatáskeresztmetszete
A frekvenciafüggő hatáskeresztmetszet szabja meg, hogy az anyag kiválasztott átmenete milyen Δν tartományban képes abszorpcióra ill. emisszióra. A különböző anyagformák esetében a frekvenciafüggvény alakja és Δν szélessége változik.
Az anyagi rendszerek a fénnyel való emissziós és abszorpciós kölcsönhatások szempontjából két csoportra oszthatók. Vannak olyan rendszerek, melyeknek a kölcsönhatásban résztvevő atomjai, vagy molekulái mind azonosan viselkednek, ezeket homogén típusú rendszereknek nevezik, és vannak olyanok, melyeknél atom- ill. molekulacsoportok különbözőképpen viselkednek, s így a teljes kölcsönható rendszer csak egy átlagos frekvencia-kiszélesedéssel jellemezhető. Ezek az inhomogén típusú rendszerek.
A homogén rendszerek hatáskeresztmetszetének frekvenciafüggése a Lorentz-függvénnyel adható meg:
|
|
(2.6) |
ahol Δν a maximum felénél a Lorentz-görbe szélességének értéke. Homogén viselkedést eredményez az anyagi rendszerekben:
-
a gerjesztett energiaszintek véges élettartama (a gerjesztés egy idő után „lecseng”, a rendszer visszatér a gerjesztés előtti egyensúlyi állapotába) miatt fellépő kiszélesedés, amit természetes vonalszélességnek neveznek, tipikus nagysága 10-20 MHz;
-
gázokban a nyomás növekedésével gyakoribbá váló ütközés miatti kiszélesedés, tipikus értéke 5-10 MHz / torr (760 torr = 1 atm);
-
kristályokban a hőmérséklet növekedésével egyre effektívebbé váló rezgés.
Az inhomogén rendszerek hatáskeresztmetszetének frekvenciafüggése Gauss-függvénnyel adható meg:
|
|
(2.7) |
ahol M a részecske tömege, c a fénysebesség vákuumban, T az abszolút hőmérséklet, k B a Boltzmann-állandó.
Inhomogén viselkedést eredményez gázokban a mozgó részecskék fényirányú eltérő sebessége (Doppler-hatás), vagy szilárd testekben az adalék eltérő környezete (az adalékatom, vagy –ion átmenete a lézerátmenet). Az inhomogén kiszélesedést is szokás a maximális érték felénél felvett frekvenciakülönbség értékével (félértékszélesség) jellemezni. Számítsuk ki a (2.7) alapján:
|
|
(2.8) |
(2.8) alapján látható, hogy a kiszélesedés fordítottan arányos az átmenet hullámhosszával és a részecskék tömegének négyzetgyökével. Ezért infravörös tartományban és molekulák esetén (pl. CO 2 lézer 10,6 µm-es hullámhosszán) nagyságrendekkel kisebb az inhomogén kiszélesedés mértéke.
2.5. Különböző lézerközegek jellemző kiszélesedései
Elsőnek számítsuk ki a He- Ne lézer leggyakoribb, λ=0,6328µm-es átmenetének (Ne atomok átmenete) inhomogén kiszélesedését. Tételezzük fel, hogy a He-Ne gázkisülésben a kialakuló egyensúlyi hőmérséklet 400 K. További adatok:
|
|
(2.9) |
A (Táblázat 2.1) táblázatban különböző lézerközegek jellemző kiszélesedéseit gyűjtöttük össze.
|
Típus |
Gáz |
Folyadék |
Szilárdtest |
|
|---|---|---|---|---|
|
Homogén |
természetes ütközési kristályráccsal kölcsönh. |
1 kHz - 10 MHz 5 - 10 MHz/torr - |
elhanyagolható 9 THz - |
elhanyagolható - 300 GHz (300K) |
|
Inhomogén |
Doppler lokális tér |
50 MHz – 1 GHz - |
elhanyagolható 15 THz |
- 30 GHz – 15 THz |









