4. fejezet - Passzív optikai rezonátorok
A lézerek létrehozásához nem elegendő csak koherens erősítőt építeni, mert az erősítő működtetéséhez ekkor a belépő fluxussűrűséget valamilyen külső forrásból állandóan biztosítanunk kell. Ehelyett célszerű az erősítőt elhagyó egyszer már felerősödött fényt visszacsatolni a közegbe. Erre a feladatra látszik alkalmasnak a passzív optikai rezonátor, mely reflektáló felületekkel rendelkező üreg. Az üregben az elektromágneses térnek a határfeltételekkel meghatározott állapotai létezhetnek csak, melyeket módusoknak neveznek.
A lézereknél használt rezonátorok az általános üregtől (pl. amit a mikrohullámú technikában is használnak) jelentősen különböznek, mivel 1) általában hiányoznak az üreg oldalsó határoló felületei, vagyis a rezonátorok nyitottak; 2) a rezonátor mérete nagyságrendekkel meghaladja a lézer hullámhosszát. A lézerek hullámhossza u.i tipikusan 0,1 .. 10-20µm, ami rezonátorhossznak túl kicsi lenne a megfelelő erősítés biztosításához.
A nyitottság miatt bármely módusnak a rezonátorban elkerülhetetlenül vesztesége lesz, az energia egy része el fogja hagyni az üreget.
A nyitott rezonátorban csak az optikai tengely közelében koncentrálódó módusoknak lesz elegendően kicsi a vesztesége, a többi igen gyorsan ki fog szóródni. A nyitottság előnyösen használható pl. az aktív anyag oldalirányból való gerjesztésére is (lásd előző fejezet (3.9. ábra) ábra).
Szokás definiálni a rezonátoroknál az ún. jósági tényezőt, mely
|
|
(4.1) |
A jósági tényező a következő alakba írható:
|
|
(4.2) |
ahol Δνr a módusok frekvencia szerinti félértékszélessége a rezonátorban. A frekvencia szerinti kiszélesedés a veszteség miatt lép fel, annál nagyobb, minél nagyobb a veszteség. Így a jósági tényező pedig akkor nagy értékű, ha kicsi a vesztesége a módusnak, mivel Q fordítva arányos Δνr-rel.
4.1. Rezonátortípusok
A legismertebb rezonátortípusokat ismertetjük. A tükrök lehetnek négyszögletesek vagy kerekek, sík vagy rádiuszos tükrök, távolságuk néhány cm-től néhány méter lehet, a tükörátmérő tipikus értéke néhány mm - től néhány cm - ig terjed.
4.1.1. Sík II-os (Fabry-Perot) rezonátor
|
|
Az eredő tér két ellenkező irányban haladó hullám szupepoziciójaként kialakuló állóhullám, melynek hullámhosszát megadja az |
|
|
(4.3) |
ahol n pozitív egész szám. A lehetséges frekvenciák pedig
|
|
(4.4) |
Ha abból indulnánk ki, hogy a módus fennmaradásának szükséges feltétele, hogy egy körüljárás után a fáziskülönbség 0 (vagy 2πn) legyen, ugyanerre az eredményre jutnánk, mert:
|
|
4.1.2. Koncentrikus vagy szférikus rezonátor
|
|
Két ellenkező irányban haladó gömbhullám szuperpoziciója. A rezonáns frekvenciák megegyeznek a Fabry-Perot rezonátoréval. |
4.1.3. Konfokális rezonátor
|
|
Az ábrán a geometriai optikai sugármenetet tüntettük fel. A módusok se nem sík, se nem gömbhullámok lesznek, a rezonáns frekvenciák egyszerű módon nem adhatók meg. |
4.1.4. Sík és gömbtükör kombinációk
|
hemikonfokális
|
hemiszférikus
|
A geometria meghatározza a lehetséges módusok térkitöltését, befolyásolja az erősítés értékét, hatással van a kilépő fény terjedési tulajdonságaira (nyalábátmérő, divergencia).
4.1.5. Általános rezonátor
|
Az általános rezonátor két tetszőleges rádiuszú tükörből áll egymástól L távolságra. Két kategóriája különböztethető meg: vannak stabil és instabil rezonátorok. Instabil egy rezonátor, ha a sugár a tükrök közötti oda-vissza verődésekor a rezonátor tengelyéből kidivergál; pl. |
|
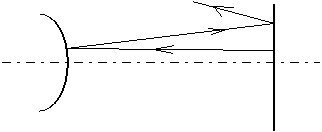
A továbbiakban a stabil rezonátorok két fontos típusával, a sík II-os rezonátorral és a konfokális rezonátorral foglalkozunk. Megmutatjuk, hogy minden stabil, legalább egy rádiuszos tükröt tartalmazó általános rezonátor leírása visszavezethető egy vele ekvivalens konfokális rezonátor leírására.
4.2. Sík II-os rezonátor, frekvenciák közelítő meghatározása
Közelítőleg meghatározzuk a sík II-os rezonátor lehetséges frekvenciáit. Zárt négyzetes hasáb alakú rezonátor esetén (2a a négyzet egy oldala, L a hasáb magassága) az állóhullámú feltételből kiindulva meghatározhatók a lehetséges frekvenciák.
|
|
|
A nyitott rezonátorban csak olyan módusok lehetségesek, melyekre m,l << n, egyébként túl nagy lenne a diffrakciós veszteség. A gyakorlatban m,l értéke ~ 0, ezért jó közelítéssel teljesül a frekvenciára a
|
|
(4.5) |
összefüggés. A zárójelben lévő második tag is elhanyagolhatóan kicsi a gyakorlatban, ezért az egyszerű megfontolásokból nyert (4.4) összefüggés szerint számíthatók a síkpárhuzamos rezonátorban a módusok lehetséges frekvenciái. Két egymás melletti módus frekvenciakülönbsége pedig
|
|
(4.6) |
azaz csak a fénysebesség és a tükrök távolságának a függvénye. Pl. L = 0,5 m esetén
|
|
(4.7) |
azaz tipikusan néhányszor 100 MHz. Ha pl. a frekvencia 5·1014 s-1 (a hullámhossz 0,6 µm) (4.4) alapján n is kiszámítható
|
|
(4.8) |
A módusok téreloszlása a síkpárhuzamos rezonátorban csak numerikusan határozható meg és mint látni fogjuk, a gyakorlatban ez a rezonátorfajta csak ritkán használatos, mert a két síktükör egymástól adott távolságban való párhuzamban tartása gépészetileg nehezen kivitelezhető feladat és kis szöghiba esetén már instabillá válik a rezonátor.
4.3. Konfokális rezonátor
A konfokális rezonátorban a módusok téreloszlása analitikusan is meghatározható. A számítás mellőzésével megadjuk az x és y irányú téreloszlást, U m,l - et a tükrökön:
|
|
(4.9) |
ahol H m és H I m és I - edrendű Hermite-polinomok. A legegyszerűbb esetben, ha m = I = 0, a módusnak megfelelő téreloszlás Gauss - függvény
|
|
(4.10) |
Az amplitúdó 1/e-ad részére esik akár x, akár y irányban, ha
|
|
(4.11) |
w s (s - spot angol szó kezdőbetűjéből) a foltsugár a tükrön.
A transzverzális módusok jelölésére a TEMml használata terjedt el a "transzverzális elektromos és mágneses" elnevezés kezdőbetűkből következően. A (4.2. ábra) ábrán néhány módus jellegzetes intenzitáseloszlását lehet látni.
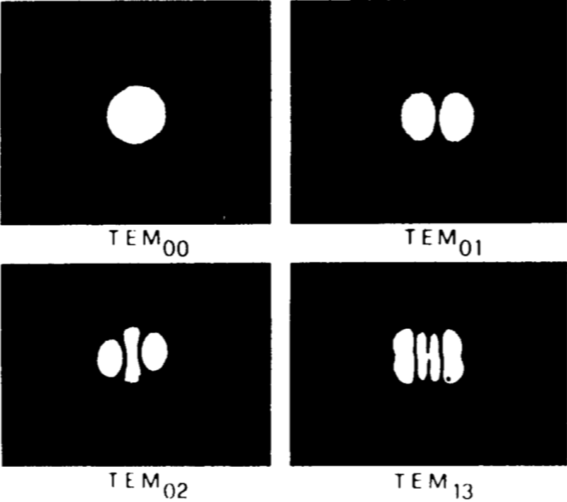
A konfokális rezonátorban az amplitúdó-eloszlás a rezonátor belsejében is bármely helyen felírható. Válasszuk a koordinátarendszer középpontjául a rezonátor közepét. Jelölje w(z) az amplitúdó 1/e - ad részének távolságát az optikai tengelytől. w(z) definíció szerint a nyalábsugár. A rezonátor tengelye mentén, azaz a z távolság függvényében a nyalábsugár
|
|
(4.12) |
alakba írható, ahol w 0 a minimális nyalábsugár, a "nyalábderék" a z= 0 -ban. w 0 éppen (2)1/2 -ed része (4.11) - nek
|
|
(4.13) |
A Gauss - nyaláb leginkább egy gömbhullámhoz hasonlít. Az azonos fázisú felületek közelítőleg gömbfelületek. A fázisfelület görbületi sugara a z tengely mentén
|
|
(4.14) |
alakba írható. A rezonátor közepén és a végtelenben sík a fázisfelület, míg egy tetszőleges helyen (4.14) alapján számítható a görbületi sugár. A tükrökön, azaz a z = L / 2 helyen a görbület éppen megegyezik L - lel, azaz a konfokális geometria miatt a tükör görbületi sugarával. Emiatt, ha az azonos fázisú felületek helyére a rezonátoron belül, a fázisfronti görbületnek megfelelő rádiuszú tükröt helyezünk, a téreloszlás nem fog megváltozni (lásd 4.3. ábra ábra). Elhelyezhetünk egy tükröt az 1' helyre, egyet pedig a 2' helyre, az eredményül kapott rezonátor már nem lesz konfokális rezonátor, mégis ugyanaz marad a foltméret és a téreloszlás. Az egyik tükör, ha a z = 0 helyre tesszük, akár sík is lehet. Ezért elmondható, hogy bármely legfeljebb csak egy sík tükröt tartalmazó általános rezonátorban meghatározható az amplitudóeloszlás egy ekvivalens téreloszlást adó konfokális rezonátor segítségével.
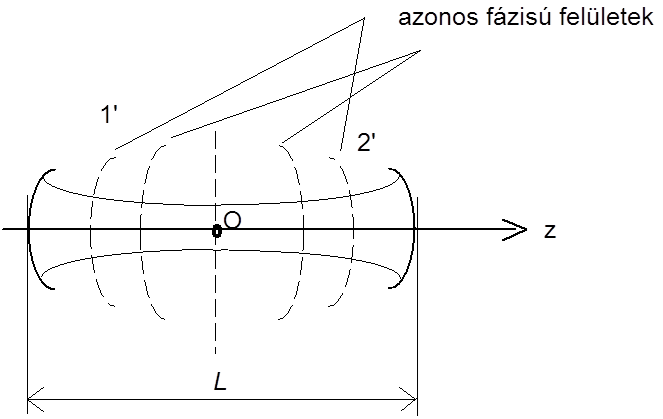
4.4. Általános rezonátor
Az előzőek alapján bármely legalább egy rádiuszos tükröt tartalmazó általános rezonátor tárgyalását a következőképpen végezhetjük.
|
|
Megkeressük az elrendezésnek megfelelő ekvivalens konfokális rezonátort az |
|
|
(4.15) |
egyenletek megoldása alapján. A három egyenlet három ismeretlent (z 1 , z 2 és L e ) tartalmaz. A számítás menete a következő: meg kell határozni pl. R1 távolságát a 0 - tól, ezután pedig az ekvivalens konfokális rezonátor hosszát (L e - t)!
Speciális esetben, pl. szimmetrikus rezonátorra
|
|
||
|
|
(4.16) |
4.5. Stabilitási feltétel
Vezessük be a következő paramétereket
|
|
(4.17) |
Bizonyítás nélkül a rezonátor stabilitásának feltétele a
|
|
(4.18) |
egyenlőtlenség teljesülése (4.4. ábra).
|
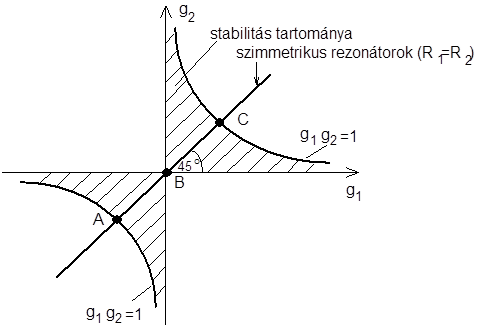 4.4. ábra - A stabil rezonátorok a bevonalkázott területen belül vannak.
|
Három határeset:
|
A.) hátránya, hogy igen kicsi a foltméret a rezonátor közepén, rendkívül érzékeny, ezért ritkán használják; B.) esetén is kicsi a nyalábméret; C.) instabil, de jó térkitöltésű! A leggyakrabban használt rezonátorok két nagy rádiuszú ((2-10) x L), vagy egy sík és egy nagy rádiuszú tükörrel készülnek.
4.6. Gauss-nyaláb terjedése szabad térben
A rezonátorból kilépő TEM00 nyaláb szabad térben való terjedését vizsgáljuk. Ehhez szükséges, hogy w(z) és R(z) kifejezésébe L helyére w 0 - t írjunk.
|
|
(4.19) |
|
|
|
(4.20) |
ahol z a nyaktól mért távolság, R(z) az azonos fázisú pontok görbülete. Adott λ - ra és z - nél w és R csak w 0 - tól függ. A nyalábnyaktól távol
|
|
(4.21) |
w(z) hiperbola, melynek aszimptótája
|
|
(4.22) |
szöget zár be a z tengellyel (4.5. ábra).
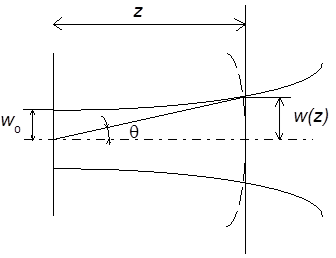
θ a lézernyaláb divergenciája, tipikus értéke gázlézereknél néhány mrad.




































