10. fejezet - Az emberi test adatainak mérése
A test pontjai térbeli helyzetének pontosabb mérésére szolgáló, egyre inkább terjedő eszközök az optikai elveken működő 3D-s letapogató berendezések.
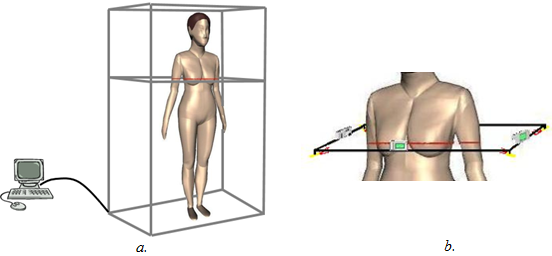
10.1. A 3D-s letapogató berendezés
Az elv az, hogy (10.1. ábra/a ábra) számítógéppel vezérelten mozgatott mérőkeretére fényképezőgépeket és lézer vonalsugárzókat szerelünk. A cél az, hogy a vonalsugárzók által megvilágított testfelületről készített (10.1. ábra/b ábra) képek feldolgozásával megállapítható legyen a testfelület pontjainak térbeli helyzete.
A módszer lényege, hogy a lézer vonalsugárzók a test felületének vízszintes síkokkal képzett metszetét világítják meg. Az így adódó testkontúrt a lézerek síkja felett adott távolságra elhelyezett, a lézerek által kijelölt sík és a test függőleges súlyponti vonala metszéspontjára néző fényképezőgépek rögzítik. A kontúr pontjainak térbeli helyzete a kontúr síkjának magasságából, a fényképek feldolgozásával megállapítható.
10.1.1. A mérőberendezés vezérlése
A berendezés kézzel és soros kommunikációval is vezérelhető. A 9600,N,8,1 formátumban küldött ASC parancsok
|
|
(10.1) |
formátumúak. Az első S karakter a parancs kódja, az xx yy zz üzenet karakterek és a záró 2 byte CC CC egy 16 bites (hexa) checksumma. A készülék
|
|
(10.2) |
üzenettel válaszol.
10.1.2. Kamerák
A bemutatott berendezés Basler SCOUT scA1000-30 1/3" CCD FireWire.B Monochrome Camera ipari video kamerákkal működik (10.2. ábra).
![A Basler kamera [10.1.]](images/image_X_2.jpeg)
10.1.2.1. Az objektívek kiválasztása
Az optikai rendszernek megfelelő minőségű képet kell előállítani a detektoron: látószög, felbontás, kontraszt, geometriai hibák és mélységélesség szempontjából.
10.1.2.1.1. A testszkennerhez alkalmazott kameraobjektív látószöge
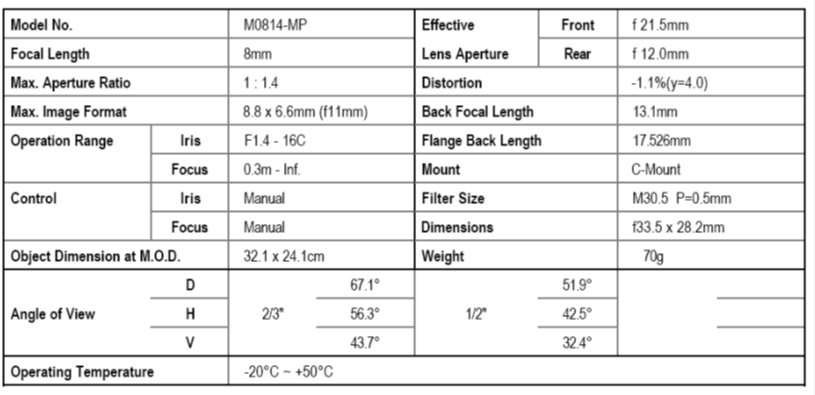
Mivel vertikális irányban az 1400 mm távolságban lévő tárgysík 1000 mm szélességű részét kell leképezni, így az ez irányú látószög hozzávetőlegesen 40 foknak felel meg. Figyelembe véve a kamera detektorméretét (1/3”) az alábbi C-menetes kamera objektívek jöhetnek számításba. Az alkalmazott objektív a Computar M0814-MP2, melynek felépítését és képét az 10.3. ábra mutatja. A paraméterek a (10.4. ábra) ábrán láthatók.
![A Computar objektív [10.2.]](images/image_X_3.png)
10.1.2.1.2. Optikai szűrés
A színszűrők alatt olyan optikai elemeket értünk, amelyek elnyelik a rájuk eső fény egy részét. Az elnyelés illetve áteresztés adott hullámhosszakon, vagyis színeken történik. A szűrők tipikus alkalmazásai, amik itt is fontosak: kontraszt növelése, jel-zaj viszony javítása. Készülhetnek üvegből, folyadékból vagy zselészerű anyagokból, az utóbbiak előnye a rugalmasság. Áteresztőképességük szerint szokták őket osztályozni:
-
rövidhullámhosszú áteresztő (short-wavelength pass),
-
hosszúhullámhosszú áteresztő (long-wavelength pass),
-
sávszűrő (bandstop),
-
sáváteresztő (bandpass, passband),
-
monokromatikus szűrő (monochromatic), stb.
-
stb.
Lézerfény szűréséhez értelemszerűen a monokromatikus szűrő a legalkalmasabb, ami egy nagyon kis sávszélességű sáváteresztő szűrő, de lehet alkalmazni sáváteresztő szűrőt, ha a digitális szűrés megfelelő kompenzációt biztosít. A szűréshez a lézer fényt kiemelő szűrők alkalmaznak.
10.1.3. A lézer vonalsugárzók
Sokféle lézer létezik, de emberek 3D szkennelésének támogatására nem mindegyik alkalmas vagy célszerű. Mivel a berendezés lézersugárzókkal működik. Itt a megfelelő képminőség mellett a szemek védelmére is gondolni kell. A feladatra tökéletesen megfelelnek a kisméretű félvezető lézerek, ugyanis csak „megvilágítás” céljára kerülnek a szerkezetbe, vagyis nem vágásra hegesztésre kell használni őket, így a milliwattos nagyságrendű teljesítmény elegendő. Fontos, hogy minél kisebb veszélyt jelentsenek az emberi szemre, és kis távolságra kell vetíteniük.
A lézerpointerek pontszerű nyalábot bocsátanak ki, a vonalsugárzókból egy síkfelületre vonal vetül. Ahogy már említettem egy egyszerű vonalsugárzó és pointer között az a különbség, hogy a vonalsugárzóban van egy optikai elem, ami vonallá „tágítja” a pontot. Ezeknek a lencséknek van egy FAN szöge, amely azt adja meg, hogy milyen széles a lézercsík. Ugyanazon teljesítményű lézerforrás biztonságosabb, ha nagyobb FAN szögű lencse van előtte.
Az optikai elem optikai és geometriai tulajdonságától függően a lézervonal egyenlő (10.5. ábra), illetve gaussi intenzitásúak lesz (10.6. ábra). Ezeknek a lencséknek van egy FAN szöge, amely azt adja meg, hogy milyen széles a lézercsík. Ugyanazon teljesítményű lézerforrás biztonságosabb, ha nagyobb FAN szögű lencse van előtte.

Zöld lézert választottunk, mert a test felülete ezt jobban reflektálja, mint a pirosat.
10.1.4. A lézeres letapogató berendezés felépítése, működése
A berendezés vezérlését a videó felvételek készítését a megfelelő szintazonosításokkal egyetlen integrált szoftver végzi. Nem elég, hogy párhuzamosan négy kamera felvételét kell rögzíteni, hanem még szinkronizálni is kell a kiemelt képeket. A vezérlő szoftver
GeniCam XML alapú szabvány interface, a Basler FireWire kameráival a kapcsolatot a GeniCam API biztosítja. Ez lehetővé teszi, hogy adott jelre exponáljon a kamera, ezért egy elektronikus érzékelő minden kamerának párhuzamosan, a keret adott magasságpozícióiban adja az expozíciós jelet. A 3D letapogató berendezés részleteit a (10.7. ábra) ábrán látható montázst mutatja.

10.2. A mérések matematikai modellje
A leképezés matematikai modelljét felállíthatjuk a [10.3.] alapján.
10.2.1. Kamera modell
Egy egyszerű, de jó kamera modell a pinhole (tűlyuk) kamera modell. A tűlyuk egy képzeletbeli fal, a közepén egy kisméretű lyukkal. A fal minden fénysugarat blokkol, kivéve azokat, amelyek a tűlyukon keresztül haladnak. Egy igazi tűlyuk kamera igazából nem túl jó, mert a gyors exponálásokhoz nem kap elegendő fényt. Ezért vannak lencsék a szemünkben, és a kamerákban, hogy több fénysugár érkezzen be, mint ami egy kisméretű lyukon keresztül lehetséges. Cserébe a lencsék torzítják a képet. Egy kamera paraméterei két fő csoportba oszthatók:
-
Intrinsic: A kamera belső felépítését leíró paraméterek.
-
Extrinsic: A kamera világbeli helyzetét leíró paraméterek.
10.2.1.1. Intrinsic paraméterek
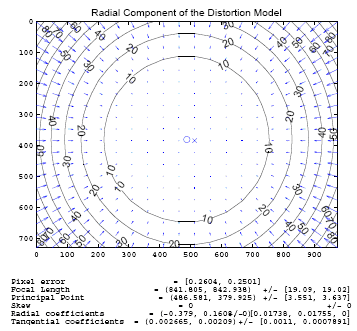
Fókusz távolság: f x , f y A kamera pozíció és a kép távolsága pixelekben kifejezve. Azért van két fókusztávolság, mert a pixelek az olcsóbb kamerákon téglalap alakúak lehetnek a négyzet helyett.
-
Optikai középpont (principle point): c x , c y A kamerában lévő képalkotó chip optikai tengely menti középpontja pixelekben. Ez általában nem a kép középpontja, mert a kamera gyártásakor a chip kicsit arrébb csúszhat.
-
Lencse torzítás: Két fő komponense van:
-
Radiális: k1, k2, k3 Főleg a kép széleihez közel vehető észre, az optikai középpontnál ennek a mértéke 0. Ez okozza a hordó, vagy párna torzítást. Az optikai középpont körüli Taylor sorba fejtett számtani sor első 2, vagy 3 párosadik együtthatójával jellemezhető. A 3. együttható nagy látószögű kamerák esetében érdekes.
-
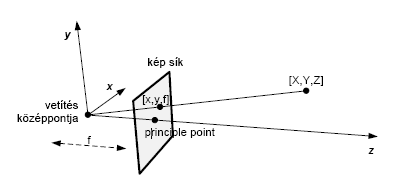
Tangenciális: p0, p1 Az okozza, hogy a gyártás során a lencse nem lesz teljesen párhuzamos a képsíkkal. A középpontos vetítés ezekkel a paraméterekkel a következő módon írható le (x, y a kamera képére vetített pont, X, Y , Z a pont világbeli pozíciója, a kamera az origóban van, és a ~Z tengely irányába néz, 10.8. ábra):

(10.3)
Ugyanez mátrixos formában is felírható, az eredmény homogén koordinátákban lesz:

(10.4)
-
A térbeli pontok a lencse által torzított pozíciói pixel koordinátákban (x, y). Ezeket normalizált kamera koordinátákba (x, y) kell alakítani első lépésként a torzítás kiküszöbölésére. Az x = 0 és y = 0 pont az optikai középpont, és a (10.8. ábra) ábrán a z = f helyett a z = 1 síkon vannak ezek a pontok.
|
|
(10.5) |
A radiális torzítás okozta elmozdulás (10.9. ábra) a következő módon határozható meg (r az optikai középponttól való távolság, azaz 
|
|
(10.6) |
A tangenciális torzítás okozta elmozdulás a következő módon határozható meg:
|
|
(10.7) |
Ezek alapján a pont igazi pozíciója normalizált kamera koordinátákban:
|
|
(10.8) |
10.2.1.2. Extrinsic paraméterek
-
Pozíció: ~t a kamera világbeli pozíciója
-
Orientáció: R a kamera világbeli nézeti iránya. Több fajta módon leírható:
-
Bázis vektorokkal: Ez egy 3 × 3 forgatás mátrix, amely a kamera koordináta-rendszerből a világ koordináta rendszerbe transzformál, azaz a mátrix oszlopai a kamera koordináta rendszer világbeli bázis vektorai.

(10.9)
-
Csavaró-Billento-Forduló forgatással: Bármely orientáció előállítható három egymás utáni forgatással. Az (_, _, ) csavaró-billentő-forduló (roll, pitch, yaw) szögekkel megadott orientációba a következő mátrix visz át:
R = R z (γ)R y (β)R x (α)
Az R x , R y , R z mátrixok az ~x, ~y, ~z tengely körüli forgatások:

(10.10)
Ennek a megadási formának az az előnye, hogy 9 változó helyett 3 változóval ugyanazt le lehet írni.
-
Tengely körüli forgatással: Az orientáció egy tengellyel (~r egység vektor), és a tengely körüli óramutató járásával ellentétes irányú forgatás szögével (_) is megadható. A Rodrigues képlettel lehet mátrixos formára alakítani az így megadott orientációt (I 3 × 3 egység mátrix) [10.4.] :

(10.11)
Tömörebben egy vektorral is megadható az orientáció, ahol a vektor nagysága a forgatás mértéke, a vektor iránya pedig a forgatási tengely. A két extrinsic paraméter leírható együtt egy 3 × 4-es mátrixban:

(10.12)
-
10.2.1.3. Kamera kalibrálás
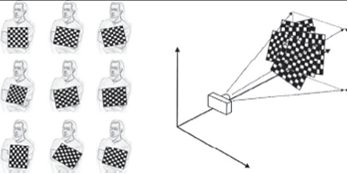
A kalibrálás során az intrinsic és extrinsic paramétereket kell meghatározni. A feladat megoldására a szabadon használható, komoly matematikai hátteret mozgató [10.7.] programkönyvtárak kínálnak függvényeket. Az Intel által fejlesztett nyílt forráskodú OpenCV ehhez tartalmaz függvényeket.
A cvCalibrate2 függvénnyel meg lehet határozni egyszerre az intrinsic, és extrinsic paramétereket. Bemenete egy síkbeli objektum néhány képbeli és világbeli pontja több nézetből (10.10. ábra). A síkbeli objektum egy sakktábla, amelynek belső sarkai megtalálására az OpenCV szintén tartalmaz függvényt. Minden nézetre vissza lehet kapni az extrinsic paramétereket a sakktáblához képest. Mivel a világ origója nem a sakktábla környékén van, ezért a cvFindExtrinsicCameraParams2 függvénnyel a már ismert intrinsic paramétereket felhasználva meghatározható a kamera helye (~t0), és orientációja (amely a Rodrigues képlettel alakítható mátrixszá, R0), és a következő összefüggés világ koordinátákból ( ~ P o ) kamera koordinátákba visz át ( ~ P c ):
|
|
(10.13) |
Ennek azonban fordítottja kell. Mivel az R0 mátrix forgatás mátrix, ezért az inverze a transzponáltja, azaz a kamera bázis vektorai az R0 mátrix sorai. A kamera pozíció pedig:
|
|
(10.14) |
10.2.2. A pont helyének meghatározása
Több módszer is alkalmazható egy pont világbeli pozíciójának meghatározásához.
10.2.2.1. Síkból síkba történő transzformáció
Ha a pontok végig egy síkon vannak, akkor alkalmazható egy 2D-s perspektivikus vetítés, amely a kamera kép 2D-s síkjából a pontok 2D-s síkjába visz át (10.11. ábra). A módszer előnye, hogy elég hozzá egy kamera is, hátránya, hogy a pontok csak egy síkban lehetnek, így a síkok helyzete ismert kell, legyen.
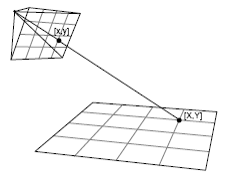
A mérőkeret kameráinak egymáshoz viszonyított helyzete egy mérési sorozatban nem változik. Kameráink lencserendszerén torzítást nem volt tapasztalható, az egyenesek egyenesek maradtak.
10.2.2.2. A perspektivikus leképezés
A (10.1. ábra/b) ábrán látható, hogy a mérőkeret adott pozíciójában a vonalsugárzók a testfelület egy vízszintes síkban fekvő görbéjét világítják meg. A fényképen a síkgörbe pontjai egyértelműen meghatározhatók a képfeldolgozás eszközeivel. A testfelület pontkoordinátáinak méréséhez a fényképfelvételek alapján a pontok eredeti helyzetét kell meghatározni. A fényképezőgépek által megvalósított perspektivikus leképezés a teret síkba vetíti, így a tér megvilágított síkgörbéjének síkját is síkba vetíti – a kamerák szinguláris elhelyezésétől eltekintve – kölcsönösen egyértelmű leképezéssel. A perspektivikus vetítés homogén koordináták használatával homogén lineáris transzformáció [10.5.] . A síkot síkba leképező perspektivikus vetítés síkbeli négyszöget síkbeli négyszögbe transzformál, így a (10.12) mátrixának nyolc független koordinátája van. Ez azt jelenti, ha ismerjük egy négyszög geometriájú test sarokpontjainak koordinátáit a térben, és a sarkok képének helyét a fényképen, akkor erre a nyolc független koordinátára nyolc lineáris egyenlet írható fel, melyek megoldásaként a fényképről a tér kitüntetett síkjára vetítő perspektivikus leképezés meghatározott. Ezt bármely képpontra alkalmazva meghatározható a pont eredeti helye a vonalsugárzók síkjában.
|
|
(10.15) |
Ha a (10.12. ábra) ábrának megfelelően egy négyszög alakú tárgy sarokpontjainak koordinátái  , és a kép sarokpontjának koordinátái
, és a kép sarokpontjának koordinátái  (i=0, 1, 2, 3) akkor a transzformáció mátrixos alakja:
(i=0, 1, 2, 3) akkor a transzformáció mátrixos alakja:
|
|
(10.16) |
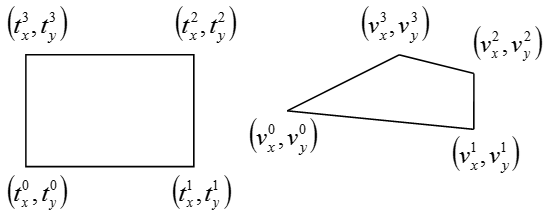
A (10.15) formula szerint felírt (10.16) lineáris egyenletrendszer megoldása éppen a transzformációs mátrix elemeit adja [10.5.] .
|
ahol, i=0, 1, 2, 3 |
(10.17) |
10.2.2.3. A mérőberendezés kalibrációja
Mivel a lézersugárzók és a kamerák egymáshoz viszonyított helyzete nem változik, valamint a pontossági igényeink figyelembevételével a kamerák radiális torzítása elhanyagolhatónak bizonyult, a mérőberendezések kalibrációja elvégezhető. A kalibráció vizsgálatához végül a letapogató minden mérés végén rögzíti egy síkban elhelyezkedő négy led helyzetét. Mivel a ledek képi és valós pozíciója ismert a kalibráció az elvégezhető.
A kalibrációs elv alapján készített mérések megfelelőek, problémát okoz azonban az, hogy a geometria könnyen előforduló, apró változásánál is (valamelyik kamera helyzete megváltozik) újra kell kalibrálni, ami a mérések lebonyolíthatóságát rontja. Ennek kiküszöbölésére szolgál egy sötétre festett kalibráló lap és annak négy sarkába négy kigyújtható led fényforrás (10.13. ábra). Minden méréskor a kamera felvételeinek utolsó frame-je a kalibráló lap kép kigyújtott ledekkel rögzített képeit tartalmazza. A tényleges mérés során a ledek nem világítanak. Így minden méréshez a saját kalibrációját rögzíthetjük és a ledek helyzetéből és képeiből a kalibráció mérésenként automatikusan elkészíthető.

10.3. Az emberi test felületi pontjainak meghatározása
A mérő software két jól elkülönülő részből áll. Az egyik a keret vezérlését, a triggerelt képek feldolgozását és mentését végzi, a másik a kalibrációt és a pontok térbeli helyzetének meghatározását.
A mérésvezérlő program feladata a teljes rendszer vezérlése és a mérési adatok tárolása. A program a felelős a kamerák inicializálásáért, a mozgató rendszer engedélyezéséért, a mozgó rész fel-, le mozgatásáért és a lézerek és ledek ki-, bekapcsolásáért.
Megjeleníthető és menthető a fényességi hisztogramm, beállíthatók az expozíciós idők és a vágási küszöbszintek.
A program képes az előnézeti kép megjelenítésére akár az összes kameraképet mutatva, akár egy kiválasztott kamera képét 1:1 méretben megjelenítve. Megvizsgálhatjuk a kalibrációs pontokat is.
A mérés során egy web kamerával fényképet készítünk, majd elindul a mérés.
A program képes az adatokat további feldolgozásra menteni is az alábbi formátumban
-
frame száma
-
x,y - fehér pixelek koordinátái (és intenzitása)
-
-1,-1 frame vége
-
-1 file vége
A program képes beolvasni az előző fejezetben specifikált mérési eredményt is és azokat akár szintenként megjeleníti (10.14. ábra).
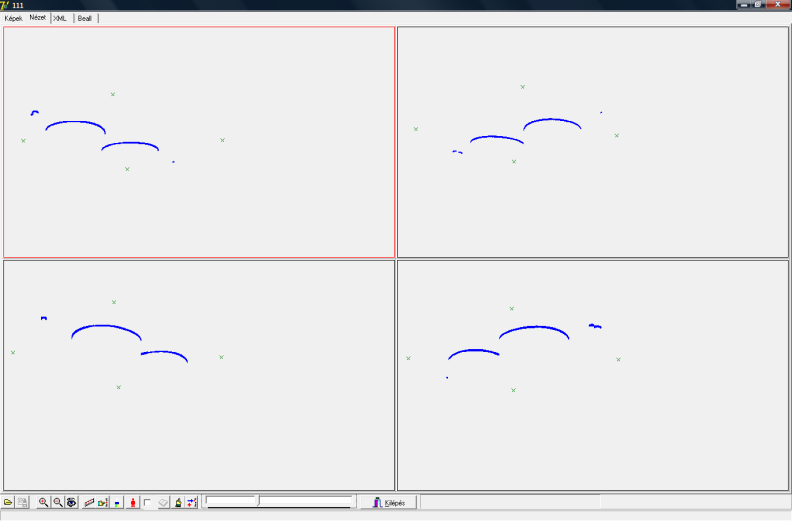
A modellező program feladata az előző fejezetben ismertetett mérésvezérlő program által szolgáltatott eredmények feldolgozása, kalibráció végzése, a pontok térbeli pozícióinak számítása, a pontok térbeli megjelenítése, valamint az eredmények más rendszerekbe való továbbításának biztosítása.
A síkmetszetek pontjai a mérőkeret aktuális magassági adatával kiegészítve, térbeli pontfelhőt eredményeznek.
A fentiek alapján a keretet a mérés nulla szintjét képező dobogótól kezdve meghatározott lépésekkel felfelé mozgatva, a felületi pontok koordinátái szintenként számíthatók. A felületi pontok magassági (z) koordinátáját a keretvezérlés magassági adata szolgáltatja, az x- és y-koordinátákat a képfeldolgozásból határozhatjuk meg. A mozgatási lépések hossza attól függ, hogy a kamerákból mely képeket vesszük ki.
A kalibráció alapján a pontfelhő megjeleníthető szintenként (10.15. ábra), illetve teljes egészében (10.16. ábra).
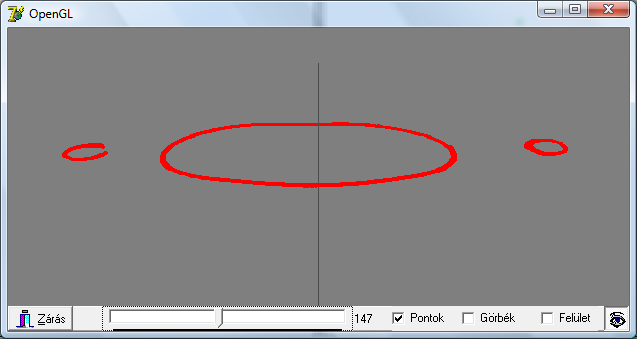

10.3.1. Testrészek keresése
Az emberi test szerkezete olyan, hogy a zárt körvonallal jellemezhető testrészek száma a föld szintjén, a kézfej végénél, a lábtő, a hónalj és a fejtető magasságában ugrásszerűen változik. (10.17. ábra).
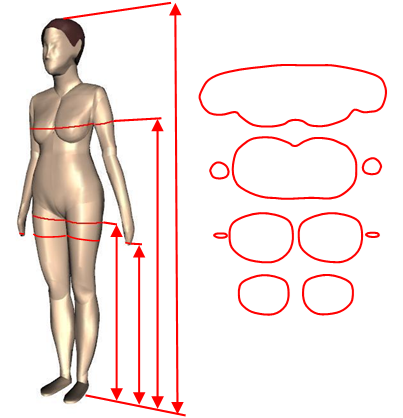
A testrészek automatikus elkülönítéséhez a mérőkeret fényképezőgépei által rögzített pontok adatait használhatjuk. A kalibráció alapján, a meghatározott képpontokból számíthatók a síkmetszetpontok valós x és y koordinátái, amelyek a z koordinátával kiegészítve a térben szolgáltatják a testfelület pontjait. A pontfelhő pontjait szintenként vizsgálhatva, első lépésben meghatározható az adott szinten az összes pont súlypontja, ez a koordináta-rendszer origója. A síkban az x és y koordináta-tengelyek iránya megegyezik a kalibráció során rögzített tengelyekkel. Az adott x koordinátával bíró pontok darabszámára – az x tengelynek a képen látható intervallumát 200 részre osztva – hisztogramot készíthető (10.18. ábra).
A hisztogram nem nulla területei az esetek többségében elkülönülnek egymástól, és csoportokat alkotnak. A 10.18. ábra alapján az alábbi esetekkel találkozhatunk:
-
A lábak környékén két csoportot találunk.
-
A lábtő alatt a lábtőhöz közel a kezek (karok) is csoportot alkotnak, így ott a csoportok száma három, illetve négy, hiszen nem biztos, hogy a karok egyforma hosszúak, illetve a tartás is okozhat eltérést.
-
A lábtő felett a hónaljmagasságig a csoportok száma három.
-
A hónalj felett a csoportok száma egy.
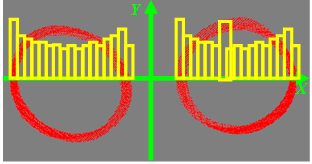
A testrészek elkülönítésére a fenti módszer nem minden esetben használható. Egyrészt a test elfordulhat a kalibrált tengelyekhez képest, másrészt a lábtő, illetve a hónalj környékén a testrészek összeérhetnek. Ezért a kritikus magasságokban meghatározhatóak az adott sík pontjainak súlyponti tehetetlenségi tengelyei, és az így meghatározott koordináta-rendszerben az x-tengely mentén elkészül a tengelytől mért átlagos távolság közelítő lépcsősfüggvénye. (10.19. ábra) A lépcsősfüggvénynek a hónaljak, illetve a lábtő környékén lokális minimuma lesz, melynek alapján a hónaljmagasság a jobb- és a baloldalon, valamint a lábtőmagasság meghatározható.
Az így kialakuló csoportok meghatározzák, hogy mely pontok, mely testrészekhez tartoznak. A 10.20. ábra a test pontjainak testrész szerinti csoportosítását mutatja.

10.3.2. Képfeldolgozás a térben
A csoportosított testpontokon további, képfeldolgozás jellegű tevékenységek végezhetők, hogy a környezetből érkező zavaró fényeffektusokat kiszűrjük.
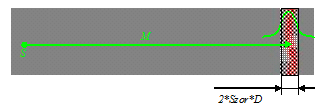
Első lépésben csak azokat a térbeli pontokat vesszük figyelembe, amelyeknek a test tengelyétől (az összes pont függőleges súlyponti tengelye) való távolsága nem haladja meg a 0,75 métert. Erre a mérendő személy beállításakor ügyelni kell.
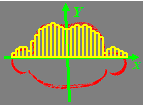
Miután előzőleg már meghatározott az, hogy melyik pont melyik testrészhez tartozik, a térben folytatható a képfeldolgozási tevékenység. Ennek célja a hibás pontok kiszűrése. Minden szinten minden csoportnak meghatározható a súlypontja (S), a pontok súlyponttól számított távolságának várható értékét (M) és szórását (D). A testrészeknél csak azokat a pontokat kell figyelembe venni, amelyeknek az S súlyponttól való távolságuk eltérése az M várható távolságtól nem haladja meg a D szórás megadott többszörösét. A többszöröző érték (szor) a kísérleti számítások alapján testrészenként változtatható. A lábnál, a karnál és a törzsnél kisebb (szor=2), a vállrésznél nagyobb (szor=4). A fej környékén ez az érték kisebb, mint egy (szor=0,8). Ennek oka, hogy a hajszálak szétszórják a sugarakat, ez azonban nem befolyásolja a mérést, hiszen a frizurát nem mérünk (10.21. ábra).
10.3.3. A felületi görbék közelítése
A felvételeken – az alkalmazott felbontás mellett – a megvilágított felületi görbék képének szélessége 6-8 pixel.
A görbe pontjai meghatározhatók lennének képfeldolgozási eszközökkel is, azonban a felületi görbéket trigonometrikus regresszióval, Fourier-sorok szeleteivel közelítetve további szűrés végezhető. A közelítő függvény független változója a ponthoz tartozó φ szög, amely a pont és a ponthalmaz súlypontja által meghatározott egyenes és az x tengely által bezárt szög, közvetlenül számítható a ponthalmaz súlypontjából és az aktuális pontból.
A közelítő függvény tehát a pontok a ponthalmaz súlypontjától mért távolságát (R) a φ szög függvényében határozza meg (10.18). A Fourier-sor első 2*n+1 tagját veszem csak figyelembe. A közelítéskor a „fokszámot” – a Fourier sorból figyelembe vett tagok számát (n) – a különböző testrészek esetén a geometriai jellegzetességek alapján határoztam meg; értéke a láb esetén 6, a törzs esetén 12, a karok esetén 6, a váll részen 12, a nyakon 6 esetében bizonyult a legjobbnak.
|
|
(10.18) |
A kérdéses Fourier-együtthatók meghatározását a legkisebb négyzetek módszerével végzem. Ha az aktuális szinten az N darab mért felületi pont távolsága és szöge (Rk,φk) k=1…n, akkor az ai, bi együtthatók a (10.19) függvény minimumaként adódnak. A minimum meghatározásához egy lineáris egyenletrendszert kell megoldani.
|
|
(10.19) |
A 10.22. ábra a fentiek szerint meghatározott közelítő görbét mutatja a comb egy keresztmetszetében.
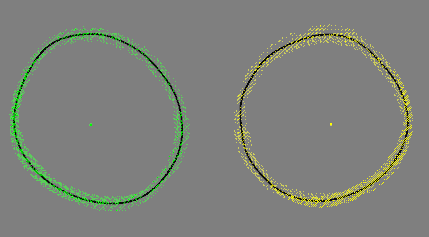
Kérdés, hogy mekkora hibája a 6-8 pixel széles lézervonal regressziós közelítésének.
10.3.4. A modell mozgásának kiszűrése
A test imbolygása és a karok akaratlan lengése azt okozza, hogy a különböző szinteken készített felvételek a testrészeket nem azonos helyzetben rögzítik, azaz a felvételeken a test vízszintes szeletei egymáshoz képest elcsúszott helyzetűek lesznek. Ennek kiküszöbölésére minden testrészen meghatározható az adott szint súlypontja és a szomszédos szintek súlypontjainak átlaga közti T i távolságot (10.20). A szintek közti eltérés szűrhető.
|
|
(10.20) |
A szűrés hatására a mozgásból eredő pontatlanság (10.23. ábra bal oldala) megszűnt, mint ahogyan az a 10.23. ábra ábra jobb oldalán látható. A mérések tapasztalatai azt mutatták, hogy a módszer alkalmas a felvételek hibáinak kiküszöbölésére.
10.3.5. Pontossági analízis
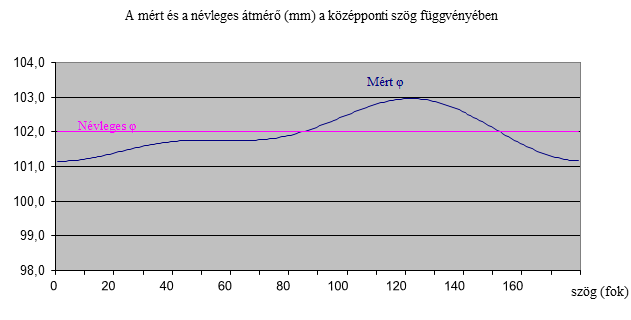
A pontosság megállapítása céljából ismert átmérőjű hengert helyezhető a mérőeszköz különböző pozícióiba. A feldolgozáskor a mért személy lábára jellemzően használt (n=6) közelítés alkalmazható. A henger átmérője 10,2 mm.
A mérés és a közelítés pontosságát egyetlen mérésen belül a középponti szög függvényében 10.24. ábra mutatja.
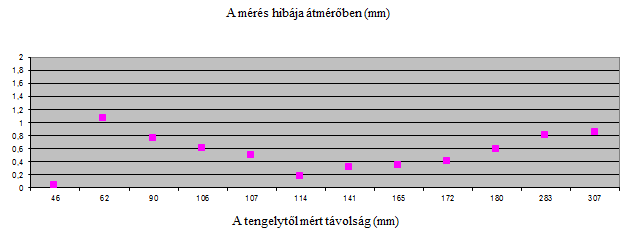
A kalibráló eszköz középpontjától mért távolságot tekintve különböző helyeken ellenőrző mérések eredményekei a (10.25. ábra) ábrán láthatók.
Az ellenőrző mérésekből megállapítható, hogy a választott felbontás mellett, az alkalmazott kalibrációs eljárással a mérések abszolút hibája átmérőben 1 mm alatt marad.
Hivatkozások
[10.1.] „http://www.baslerweb.com,” [Online]. .
[10.2.] www.computar.com. [Online]. .
[10.3.] Differential methods for nonmetric calibration of camera lens distortion.. In Proceedings CVPR. pp. 477–482. 2001.
[10.4.] Computer-Aided Analysis and Optimization of Mechanical Systems Dynamics.. Springer-Verlag.. 1984.
[10.5.] Háromdimenziós grafika, animáció és játékfejlesztés. ComuterBooks. Budapest . 2003.
[10.6.] A Palanar Perspective Image Matching using Point Correspondesand Rectangle-to-Quadrilateral Mapping,. Fifth IEE Southwest Symposium on Image Analysis and Interpretation. 2002.
[10.7.] „http://opencv.willowgarage.com/documentation/camera_calibration_and_3d_reconstruction.html,” [Online].














