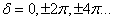9. fejezet - Rugalmassági modulus meghatározása interferometrikus úton

A tizenkilencedik század második felében a fizikusok érdeklődésének középpontjába került az éter elv, a műszaki feltételek és a méréstechnika fejlődése lehetővé tette, hogy a Föld éterbeli mozgásának jellemzőit mérésekkel próbálják meghatározni. Albert Michelson és Edward Morley a mai Case Western Reserve University-n 1887-ben kísérleti elrendezést épített, melynek elsődleges célja volt kimérni a Földnek az éterhez, illetve az abszolút térhez viszonyított sebességét [9.1.] . A kísérlet lelkét a Michelson által szerkesztett és kivitelezett, róla elnevezett Michelson-interferométer adta. A kísérlet maga pedig Michelson–Morley-kísérlet néven vonult be a fizika történetébe. A történethez hozzátartozik, hogy a vizsgálatot először 1881-ben Michelson egyedül végezte el, amit 1887-ben Morley segítségével megismételt.

Egy eredeti elgondolás alapján a Michelsonról elnevezett interferométerben a forrásból kilépő fényt egymásra merőleges nyalábokra osztották egy nyalábosztó segítségével, majd ezeket a sugarakat különböző utakon bejáratva újra egyesítették, interferenciajelenséget hozva létre. A sugárutakban beállított úthosszkülönbség a felfogott interferenciaképben jelent meg. Feltételezték, hogy a Föld éterben végzett mozgása folytán az egymásra merőleges sugarak sebessége különbözik, így az interferométer elforgatásával, az úthosszkülönbségek is megváltoznak, így a felfogott interferenciában a csíkok eltolódását kellet volna megfigyelni, és a változásból akár a Föld éterhez képesti sebességét is kiszámíthatták volna.

Michelson kiváló érzékű kísérleti fizikus volt, javasolt berendezése is erről árulkodik. A mérést terhelő zajok kiiktatása célából az interferométert egy betontömbre helyezte, amely higanyágyon úszott, és a könnyű elforgatást biztosító csapágyazás is biztosítva lett így. Az úthosszakat számtalan tükör és több nyalábosztó beiktatásával növelte meg. A kísérlet eredményeként semmilyen eltolódás sem volt detektálható az interferenciaképben [9.5.] . A kísérlet eredménye az éter létezésének elméletének felülvizsgálatára alapvető hatással volt és komoly lökést adott a speciális relativitáselmélet megfogalmazásának. Maga az elrendezés annyira szellemesnek bizonyult, hogy ma is az egyik legszélesebb körben alkalmazott méréstechnikai interferometrikus elrendezés.

A hullámoptika összefüggéseivel leírható interferencia, mint jelenség már régóta

ismert, fizikai magyarázata kidolgozott. A méréstechnikai alkalmazás szintén komoly hagyományokkal rendelkezik, mint mérési módszer számtalan olyan helyen nyert alkalmazást, ahol a mérendő méretek a fény hullámhosszával vethetők össze [9.7.] , elvárt hogy a mérés gyors és érintésmentes legyen. Az indukált emisszió elvén működő lézer fényforrások újabb lehetőséget kínálnak az interferometria fejlődéséhez és széleskörű elterjedéséhez.

A alábbiakban az interferometria jelenségének hullámoptikai leírását és egy

Michelson interferométert működését tárgyaljuk, valamint egy annak segítségével megvalósítható anyagjellemzőre vonatkozó mérést ismertetünk.

A hullámoptika eszköztárával, a fény hullámtermészetével értelmezhető jelenségeket tárgyaljuk. A fényt periodikus olyan hullámként értelmezzük, melyben egy vagy több fizikai mennyiség időben és térben periodikusan változik. A hullámoptikába tartozó jelenségek nagy részének magyarázatához alkalmazhatók az általános hullámtan fogalmai, törvényszerűségei.

Egy homogén, izotróp és állandó közegben az irányban haladó monokromatikus síkhullám az alábbi egyenlettel írható le:

Ahol:       

Homogén és izotróp közegben:

vákuumban

ahol

A közeg vákuumra vonatkozó törésmutatójára érvényes, hogy

Érvényes továbbá, hogy

Ezek után a következő hozható:

melyben az szorzatot optikai úthossznak nevezzük.

Két vagy több fényhullám együtthaladásakor vagy találkozásakor a fényhullámok szuperpozíciójának elve alapján olyan hullám jön létre, amelynek hullámfüggvénye az egyes hullámfüggvények összege [9.6.] , [9.7.] .

A fény intenzitása, ahogy az egy általános hullám esetében is igaz, arányos az

amplitúdó négyzetével.

Fényinterferencia lép fel két egyenlő frekvenciájú fényhullám találkozásakor, és a fényintenzitásoknak maximuma illetve minimuma van azokon a helyeken, amelyeken a két hullám közötti fáziskülönbség a -nek páros illetve páratlan számú többszöröse.

Tehát maximuma van, ha

és minimuma van, ha

Ha a tér egy adott helyén két interferenciára képes hullám találkozik, akkor a szuperpozíció elve alapján [9.7.] :

Felhasználva a hullámfüggvényt

és

Behelyettesítve

A megfelelő átalakítások után

Ahol

Továbbá

Mindezek alapján

Legyen

Ekkor

Négyzetre emelés, összeadás és egyszerűsítés után

Ahol

Behelyettesítve

Az amplitúdó és az intenzitás közötti arányosság alapján

Ahol

A fáziskülönbség.

Két koherens forrás esetén a két fázisállandó azonos, így

Így a fáziskülönbség időben állandó [9.8.] , [9.9.]

Ahol

Az interferencia komparátor egy Michelson típusú interferométer, mely elsősorban mérőhasábok kalibrációjára szolgál [9.7.] . Az ábrán látható, úgynevezett Kösters-típusú interferencia komparátor spektrál lámpát alkalmaz fényforrásként, melynek spektrumából monokromatikus sávot egy interferenciaszűrő vagy monokromátor választ ki. A referenciatükör mellet a másik tükör szerepét maga a vizsgált mérőhasáb tükröző felülete, illetve egy üveghasáb, melyre a mérendő mérőhasáb van feltapasztva, látja el. Mivel a mérőhasáb hossza a fény hullámhossza közötti kapcsolat miatt az üveghasábról és a mérőhasáb felületéről reflektálódó hullámok nem azonos fázisban interferálnak, az interferencia csíkok nem folytonosak. E csíkok fáziseltolódásából a hullámhossz ismeretében a mérőhasáb mérete számítható.

A koherens fényforrásból (lézer) kilépő fényt egy optikai rendszer – a nyalábtágító távcső – a mérés céljaira alkalmas síkhullámokká alakítja. Az osztótükör (esetleg osztóprizma) a hullámokat osztva, azok egy részét a referenciatükörre, másik részét a rugalmassági modulusérték meghatározására kijelölt rúdra szerelt tükörre irányítja. E tükrökről visszaverődő hullámok az osztóelem túloldalán újra egyesülve interferenciajelenséget hoznak létre, mely megfelelő eszközökkel (kamera, fényképezőgép) rögzíthető.

Ha a vizsgált jelű rudat, mely anyaga rugalmassági modulusának megha­tározása a cél, ismert erőterhelés éri, az deformálódik, lehajlik, s vele együtt fordul a rászerelt tükör is. Ennek következtében, a nyalábosztó elem túloldalán újra egyesülő hullámok egymáshoz képesti szöge módosul úgy, hogy ez arányos a lehajlás szögével.

Mivel a lehajlás szöge, ami az interferenciacsíkokból meghatározható, függ a keresett rugalmassági modulustól, illetve az erőterheléstől, annak helyétől, illetve a rúd másodrendű nyomatékától, amik viszont ismertek, így a rugalmassági modulus könnyen 'meghatározható.

Ha egy külső erő vagy erőpár munkát végez egy tartón, akkor ezt a munkát a külső erők munkájának nevezzük. Ez a munka a tartóban belső energia formájában tárolódik. Ha a rugalmas tartót erőkből és nyomatékú erőpárokból álló egyensúlyi erőrendszer terheli, akkor a test deformálódik, tehát az erők támadáspontja elmozdul, a nyomatékok síkjai elfordulnak. Ha az erő elmozdulás vektora és ennek az erő irányába eső összetevője , akkor az erő munkája

Hasonlóan az nyomatékú erőpár munkája

Az így meghatározható munkák szuperpozíciójával az egész – a tartót terhelő – erőrendszer munkája

A fenti összefüggés természetesen csak akkor érvényes, ha a testre ható külső erőrendszer a terhelés folyamán egyensúlyi rendszert alkot. Ez statikailag határozott tartók esetén érvényesül, s ilyenkor a reakcióerők támadáspontjainak nincs elmozdulása, tehát azok külső munkája nullával egyenlő. Ha az -edik erő nagyságát -vel megváltoztatjuk, akkor a külső erők munkája megváltozik és a erőt tartalmazó rendszer munkája

lesz. Ha a terheletlen tartóra csak a erőt visszük fel, akkor annak munkája

lesz. A tartóra ható terhelések munkája és a erő munkája pedig

Mivel ezen erő támadáspontjának elmozdulása, így

Ebből felírható a Castigliano tétel, mely szerint [9.4.]

illetve hasonló gondolatmenet alapján

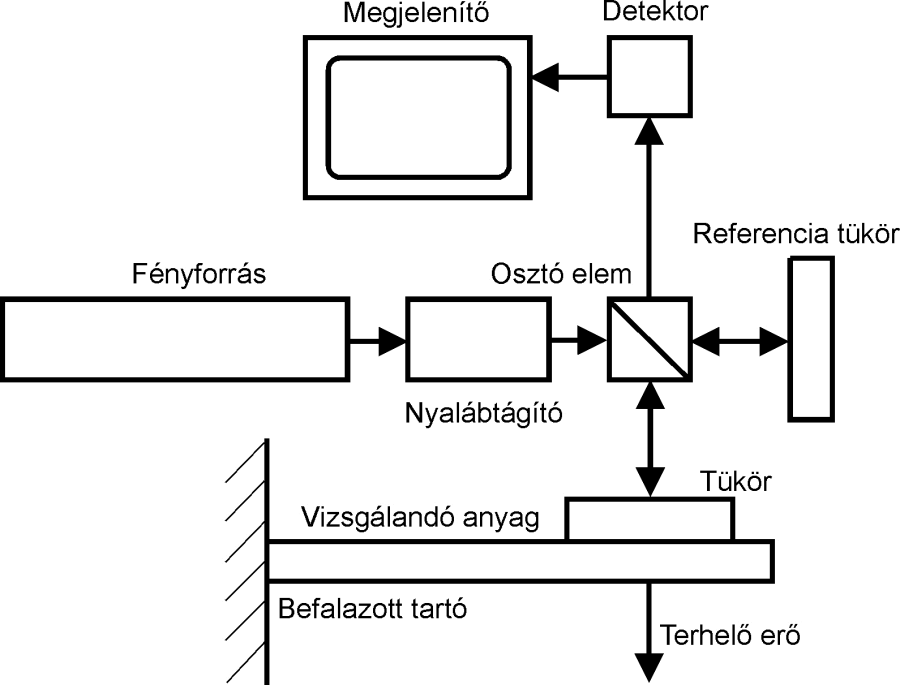
Tekintsük a következő statikailag határozott koncentrált erővel terhelt befalazott tartót.

 

A tartóra ható külső erők munkája

Alkalmazva a fentebb levezetett Castigliano tételt

ahol

és

Behelyettesítve és a műveleteket elvégezve

Ha , akkor

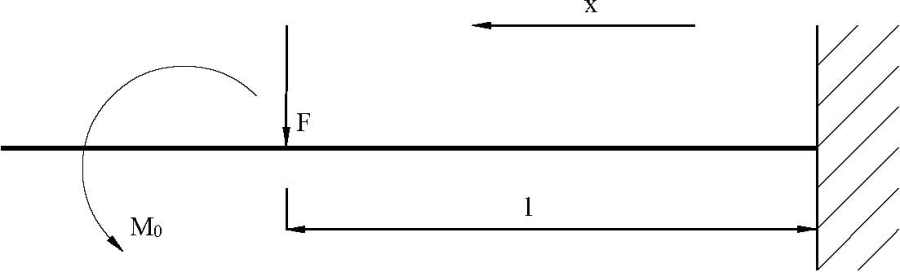
Ha a tartó téglalap keresztmetszetű, akkor a vízszintes tengelyére vett inerciájára érvényes

A Steiner tétel alapján [9.4.]

tehát

A lézeres forrás bekapcsolása, a hullámfront és az interferenciajelenség beállítása után különböző terhelések mellett mérjük a megjelenítőn az interferenciacsíkok paramétereit, például periódushosszukat. Minden egyes terhelési állapothoz tartozó valóságos interferenciacsík mérethez meghatározható a forrás hullámhossza alapján az interferáló hullámfrontok egymáshoz képesti szöge, amiből számítható a tartóra szerelt tükör szöghelyzete is. A különböző terhelési állapotok közötti erőterhelés különbség hatására fellépő tartólehajlás szögkülönbségek arányából a másodrendű nyomaték és a koncentrált erő helye alapján számítható a rugalmassági modulus.