5. fejezet - Lézerműködés feltételei
A lézer egy olyan koherens optikai erősítőből álló oszcillátor, melynek kimenete a bemenetre fázishelyesen van visszacsatolva. A lézerműködést a gerjesztett közeg spontán fénykibocsátása képes beindítani oly módon, hogy a rezonátor tengelye irányában haladó spontán emisszióval kibocsátott fény az erősítő közegen áthaladva felerősödik, majd tükörrel visszatáplálva tovább erősödik a lézerközegben. Ez a folyamat addig tart, amíg az erősítés telítődése megakadályozza a további növekedést és stacionárius működés jön létre. Két feltételnek kell teljesülnie:
-
a közeg erősítésének nagyobbnak kell lenni, mint amekkora a visszacsatoló rendszer vesztesége,
-
a teljes fázistolás egy körüljárásra 2 egészszámszorosa kell legyen (fázishelyes visszacsatolás szükséges).
Ezek a feltételek csak megfelelően gerjesztett közeg és jól kiválasztott visszacsatoló rendszer (optikai rezonátor) esetén teljesíthetőek. Az optikai rezonátor nyitottsága miatt a lehetséges módusok közül csak néhány módus esetén teljesülhet a veszteségre vonatkozó feltétel. Emiatt lehetséges az, hogy a széles sávban erősítésre képes aktív közegben csak keskeny sávú oszcilláció jön létre.
Ha α r az egységnyi hosszra eső veszteségi tényező a rezonátorban, az első feltételnek megfelelően a következő egyenlőségnek kell teljesülnie
|
|
(5.1) |
ahol γ 0 (ν) a közeg egységnyi hosszának erősítése a gerjesztés hatására.
A fázisfeltétel teljesüléséhez a passzív rezonátor és az aktív közeg együttes fázistolása 2 egészszámszorosa kell legyen. A lézermódusok frekvenciái kismértékben eltérnek a passzív rezonátor frekvenciáitól, de az eltérés csak a frekvencia sokadik tizedesjegyében jelentkezik. A gyakorlatban az egyszerű megfontolások alapján felállított (4.4) kifejezés jól használható.
Ha az első feltétel teljesül, akkor beindul a lézeroszcilláció. A lézerfrekvenciák pedig a 2. feltételnek megfelelően alakulnak ki. A fluxussűrűség mindaddig növekedni fog, míg a telítődött erősítés el nem éri a veszteség értékét (5.1. ábra), ami a stacionárius működés feltétele.
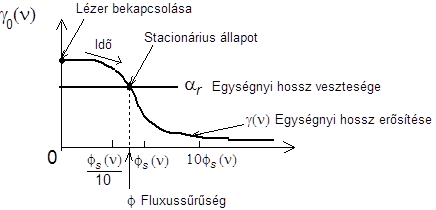
A stacionárius működés feltételéből meghatározható a fluxussűrűség stacionárius értéke, vagy ennek alapján a kimenő teljesítmény.
Ha T az egyik tükör transzmisszióképessége, akkor a kilépő fluxussűrűség, intenzitás illetve teljesítmény
|
|
(5.2) |
ahol A a kilépő tükör felülete.
A transzmisszió nemcsak a fény egy részének kicsatolását eredményezi, hanem növeli a rezonátor veszteségeit is, így meghatározza a stacionárius fluxussűrűség értékét is. Ha nem csatolnánk ki teljesítményt, a belső fluxussűrűség értéke nagyobb lehetne. A növekvő tüköráteresztés egy ideig növekvő teljesítményt eredményez, azután a veszteség növelése miatt a stacionárius működési feltételhez már alacsonyabb fluxussűrűség fog tartozni. Vagyis a transzmisszióképességnek optimuma van.
5.1. A lézerfény sávszélessége
A lézerfény sávszélességét az átmenet és a rezonátormódusok kiszélesedése együttesen befolyásolja. Az erősítésre vonatkozó (4.4) feltétel teljesülése alapján definiálható az a működő sávszélesség (B), melyen belül lehetséges a lézeroszcilláció (5.2. ábra).
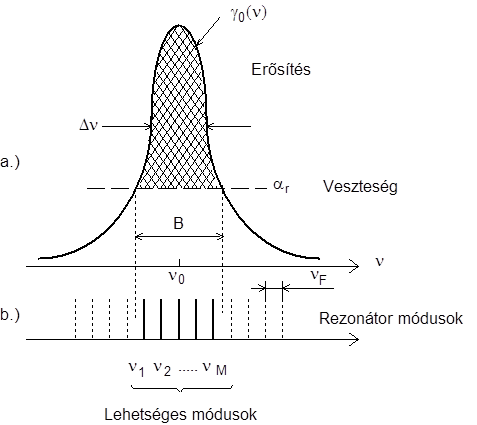
B szélességét az atomi vonalszélesség Δν és a γ 0 (ν) / αr arány határozza meg. A fázisfeltétel teljesülése alapján a lehetséges frekvenciák azok a diszkrét frekvenciák (ν 1 , ν 2 , ν M ) lesznek, melyek a B működő sávszélességen belül esnek, ahol M a lehetséges módusok száma. Közelítőleg meghatározható az
|
|
(5.3) |
összefüggés alapján.
A lehetséges módusok tényleges száma függ a közeg kiszélesedését eredményező hatások fajtájától is. De az általában elmondható, hogy a lézerekben a több módusú oszcilláció az általános. Emiatt a lézerfény sávszélességét a módusok száma és a módusok sávszélessége határozza meg.
5.2. Egyetlen vonalon, egyetlen módusban való működés
A közeg, melyben az inverz populációt létrehoztuk, a legtöbb esetben több átmeneten (vonalon) is alkalmas lézerműködésre. Egy speciális átmenetet (vonalat) úgy lehet kiválasztani, hogy hullámhosszfüggő veszteséget viszünk a rendszerbe, ami lehet:
-
keskeny sávban nagy reflexiójú sokrétegű dielektrikum tükör,
-
szélessávú egyik tükör és rács vagy prizma a másik tükör helyett.
Egyetlen transzverzális módusban való működésről a passzív rezonátoroknál a (4. fejezet) fejezetben már beszéltünk. A módusok diffrakciós vesztesége tetszőlegesen növelhető a rezonátorban megfelelő korlátozó apertúrával, s íly módon elérhető, hogy csak egyetlen módus, célszerűen a TEM00 módus vesztesége legyen az erősítéssel kompenzálható. De ekkor még (4.4) alapján több longitudinális módus is kialakulhat. Lehet L - et olyan kicsire választani, hogy csak egy módus "férjen bele" az erősítési görbébe, de ekkor a rövid hossz az aktív közeg térfogatának a csökkenését is eredményezi, ami korlátozza az elérhető teljesítményt.
Egyetlen longitudinális módusú működés érhető el másképpen pl. egy Fabry - Perot etalonnak a rezonátorba helyezésével (az 5.3. ábra ábra szerint). A Fabryt - Perot etalon lehet egy síkpárhuzamos üveglemez.
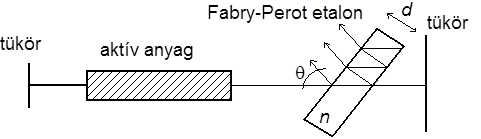
- tól függően a többszörösen reflektált sugarak kiolthatják egymást, vagyis elérhető, hogy a reflexiós veszteség nulla legyen az etalonon. Két ilyen "0" hely távolsága frekvenciában fordítottan arányos az etalon vastagságával, tehát ha d kellően kicsi, az etalon által megengedett működésre képes lehetséges módusok távolsága frekvenciában jóval nagyobb lehet, mint a (4.4) által meghatározott frekvenciakülönbség, s így elérhető, hogy a B sávszélességen belül csak egyetlen longitudinális módus működhessen.
Kérdés, hogy mi határozza meg ebben az esetben a működő módus sávszélességét? A rezonátormódusok kiszélesedése a rezonátor veszteségétől függ, de a módus frekvenciájának stabilitását pl. a rezonátor mechanikai stabilitása nagy mértékben befolyásolja.
U.i. a frekvencia állandóságához szükséges a rezonátorhossz állandó-ságának biztosítása. Ha stabilizálni akarjuk a rezonátor hosszát, pl. igen kis hőtágulású anyagból készítjük, milyen stabilitást érhetünk el? Mivel
|
|
(5.4) |
Vagyis a hosszstabilitásnak a frekvenciastabilitás nagyságrendjébe kell esni. Ez a feltétel még akkor sem teljesíthető, ha különösen alacsony hőtágulású anyagokat választunk a rezonátor építéséhez. Pl. ha a rezonátort különösen alacsony hőtágulási együtthatójú anyagból készítenénk, pl. invarból, aminek a lineáris hőtágulási együtthatója ~ 10-6 / K, a relatív hosszstabilitásra
|
|
(5.5) |
adódna. Feltéve, hogy a hőmérsékletet 0,001 K - re tudjuk tartani, a hossz-, s ezáltal a frekvenciastabilitásra 10-9 adódik.
Ha a hőtágulásból eredő ingadozást meg is szüntettük, még más problémák is maradnak: pl. akusztikus vibráció, törésmutató ingadozás, áram ingadozás (gázlézereknél), stb. Vagyis a gyakorlatban megvalósuló relatív sávszélesség rossabb, mint a hosszstabilitásból becsült érték.
A sávszélesség csökkentésére a hőfok és áramstabilizáláson kívül hatásosabb ú.n. aktív stabilizálási módszer is van.
Egymódusú gázlézerekben állandó gerjesztés mellett az 5.4. ábra ábra szerinti teljesítményspektrum mérhető pl. az rezonátor hosszának finom változta-tásával (λ/2 - n belül ).
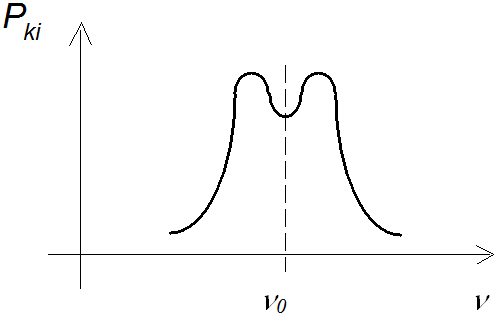
A mozgás miatt általában kétféle atomcsoport vesz részt az indukált emisszió folyamatában, a + v és - v sebességűek. A középfrekvencián viszont csak azonos atomokkal történik a kölcsönhatás oda - vissza is, ezért itt kisebb kimenő teljesítmény adódik.
Stabilizálás lehetséges pl. oly módon, hogy az egyik tükör piezos mozgatásával és visszaszabályozással a teljesítményt állandóan minimumon tartják. Az elérhető stabilitás így 10-9. Még jobb stabilitás érhető el, ha a rezonátorba külön abszorpciós cellát tesznek (aktív stabilizálás), melyben nincs kisülés. A cella az abszorpció telítődése miatt a középfrekvencián egy idő után átlátszó lesz, míg másutt továbbra is elnyel. Fordított Lamb - dip jelenség fog megvalósulni, vagyis a cellával a teljesítmény éppen a közepes hullámhosszon lesz maximális és az elérhető stabilitás 10-12 - 10-13, ami sávszélességben ~100 Hz - nek felel meg.
5.3. A lézerfény koherenciatulajdonságai
Célszerű először tisztázni a koherencia fogalmát.
A hullámfront térbeli koherenciájáról beszélünk, ha tekintjük a hullámfront P 1 és P 2 pontjait, ezen pontokban a téramplitudók E 1 (t), E 2 (t). Ha t = 0-ban ezen pontokban a fáziskülönbség 0 és ez bármely t > 0 - ra megmarad, akkor a két pont között tökéletes térbeli koherencia van. Ha bármely hullámpontbeli pontra ez igaz, akkor a nyaláb térbeli koherenciája tökéletes. Ha csak a P 1 pont véges környezetére igaz, akkor bevezethető a koherencia terület fogalma, s ekkor csak részleges a térbeli koherencia.
A hullámfront időbeli koherenciájáról beszélünk, ha a P - pontban E(t) és E(t+τ) közötti fáziskülönbség bármely t - re állandó bármely τ esetén is. Ha csak esetén teljesül, akkor τ a koherencia idő, illetve τ c c = L c a koherencia hossz. Az időbeli koherencia közvetlenül kapcsolatos a sávszélességgel illetve a monokromatikussággal, mivel
|
|
(5.6) |
A lézerelmélet alapján számolható, hogy az egymódusú, erősen gerjesztett lézerek nyalábja tökéletes térbeli koherenciával rendelkezik.
Az időbeli koherencia a sávszélességtől függ. A legkisebb elérhető sávszélesség a ~ 100 Hz (aktív stabilizálású He - Ne lézer), ekkor
|
|
(5.7) |
Konvencionális fényforrás (pl. Na-lámpa) esetén
|
|
(5.8) |
Laboratóriumi He-Ne lézer, több módusú, nem stabilizált
|
|
(5.9) |
5.4. Impulzusüzemű lézerműködés
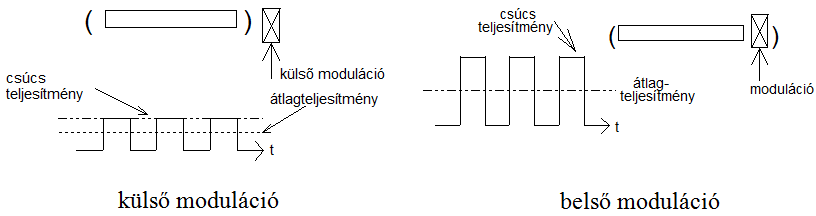
Stacionárius lézerből fényveszteség árán mindig lehet impulzuslézert csinálni külső modulátor vagy kapcsoló segítségével. Gyakran előfordul, hogy laboratóriumban háttérfény melletti mérési feladatnál a jel/zaj viszony növelése érdekében ehhez a módszerhez kell folyamodni. Hatásosabb a belső (rezonátoron belüli) moduláció. Ilyenkor kikapcsolt állapotban az energia betáplálása folyik (akár fény, akár populáció inverzió formájában), ami aztán periodikusan el tud távozni illetve beindulhat a lézeroszcilláció. Ezen az alapon rövid idejű és a stacionárius teljesítményt jóval meghaladó csúcsteljesítményű impulzusokat lehet előállítani. A kétfajta moduláció eltérését jól érzékelteti az 5.5. ábra ábra.
5.4.1. Szokásos módszerek a belső moduláció megvalósítására:
-
erősítés kapcsolása,
-
Q-kapcsolás (vagy rezonátor kiürítése),
-
móduscsatolás.
-
Az elvet az (5.6. ábra) ábrán láthatjuk. Ebben az esetben az inverzió létrehozása impulzusgerjesztéssel történik. Például villanólámpával gerjesztett szilárdtestlézer esetén a bekapcsolt gerjesztések alkalmával egy idő után a rendszer erősítése meghaladja a veszteségeket, s ekkor fényimpulzusok generálódnak. Ez a leggyakrabban használt impulzuselőállítási módszer.
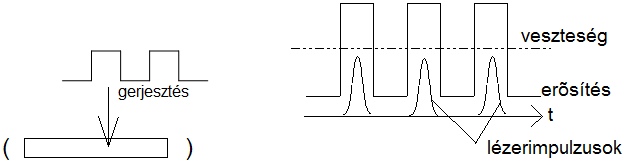 5.6. ábra - Erősítés kapcsolásának elve
5.6. ábra - Erősítés kapcsolásának elve
-
A rezonátor jósági tényezőjének a kapcsolása a veszteségek periódikus változtatásával lehetséges. A megvalósítás vázlata az (5.7. ábra) ábrán látható.
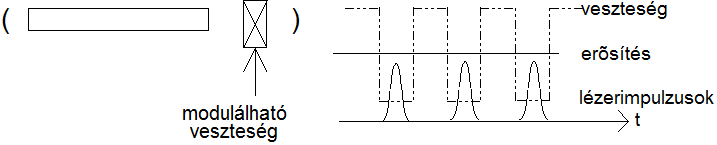 5.7. ábra - A Q-kapcsolás elvi megvalósítása
5.7. ábra - A Q-kapcsolás elvi megvalósítása
A gerjesztés Q-kapcsolásnál folyamatos lehet vagy impulzus módban is történhet. A tipikus impulzushossz néhány ns - tól 10ns nagyságrendű, a tipikus csúcsteljesítmény néhány MW -tól néhányszor 10MW lehet.
A működés szükséges feltétele, hogy az átmenet felső szintjének élettartama viszonylag hosszú legyen (lehetőleg ms nagyságrendű), hogy a gerjesztés alatt még ne csökkenjen az inverziósűrűség. Szilárdtestlézerekben (Nd:YAG, rubin) és CO2 lézer esetén teljesül ez a feltétel.
A gyakorlatban a Q - kapcsoló lehet pl. mechanikusan mozgatott tükör vagy prizma, elektro-optikai kapcsoló, akuszto-optikai kapcsoló vagy valamilyen telítõdõ anyag, pl. szerves festék.
A rezonátor kiürítése (5.8. ábra) a Q kapcsolás fordítottja, mivel kikapcsolt állapotban a fotontér be van zárva a rezonátorba, bekapcsoláskor lehetséges a fotonok eltávozása. Gondoljunk egy vizesvödörre, melybe folyamatosan folyik a víz, aztán egy dugó kihúzásával hirtelen kiürül. A vödör a rezonátor, az állandó vízutánpótlás a folyamatos gerjesztés, a dugó pedig például a lézertükör.
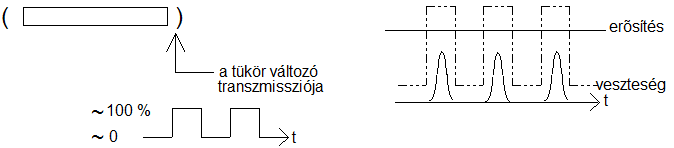 5.8. ábra - A rezonátor kiürítésének elve.
5.8. ábra - A rezonátor kiürítésének elve.
-
Lézermódusok fázisainak csatolása. Minél több a lehetséges módusok száma, annál rövidebb impulzus állítható elő, u.i. az impulzusok szélessége fordítottan arányos B - vel, a működési sávszélességgel. Az elérhető tipikus impulzusparaméterek: ultrarövid impulzushossz (10fs -tól néhányszor 10ps -ig), GW -os csúcsteljesítmény.