6. fejezet - Lézernyaláb optika alapjai
Vissza		Előre

6. fejezet - Lézernyaláb optika alapjai

Tartalom

6.1. Mi a különbség a fénycső és a lézer működése között?
6.2. A konfokális rezonátor
6.3. A lézernyaláb intenzitás eloszlása a nyaláb keresztmetszet irányában
6.4. A lézernyaláb intenzitása a terjedési irány mentén
6.5. A lézer nyaláb módosítása
6.6. A vékony lencse egyenlete Gauss nyalábra
6.7. Kollimált lézernyaláb fókuszálása kis ponttá
6.8. Nyalábnyak újra fókuszálása
6.9. A nyalábnyak relézése
6.10. Gauss nyaláb kollimálás

6.1. Mi a különbség a fénycső és a lézer működése között?

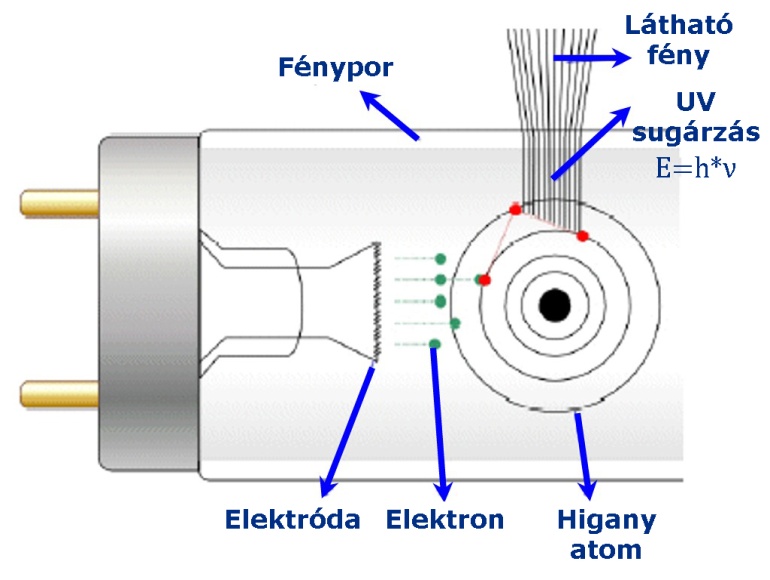
6.1. ábra - A fénycső működési elve

A fénycsőben lévő gázatomok az elektromos térben felgyorsuló elektronok által gerjesztett állapotba kerülnek, majd abból - spontán módon és véletlenszerű időpontban visszatérnek az alapállapotba. Ekkor a magasabb energia nívójú pályára gerjesztéskor került elektronok alapállapotba való visszatérésükkor leadják a két pályához tartozó – gerjesztéskor kapott energiájukat úgy, hogy ez az energia különbség egy foton keletkezését okozza, amely

$Δ E = h υ$

(6.1)

energiával rendelkezik, ahol h a Planck állandó és ʋ a foton frekvenciája. A fény színe a frekvenciától függ, hullámhosszal is jellemezhető a

$c = ν λ$

(6.2)

összefüggés segítségével, ahol a c a vákuumbeli fénysebesség és λ a fény hullámhossza.

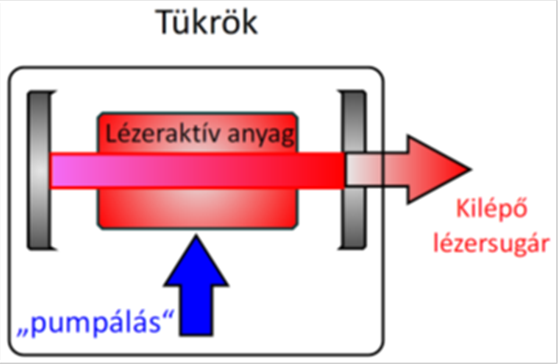
6.2. ábra - A lézer működés vázlata

Lézer esetében a gerjesztés során az atomok a fénycsőhöz hasonlóan gerjesztett állapotba kerülnek – elektronjaik egy magasabb nívójú pályára ugranak fel, majd onnét az alapállapotba visszatérve szintén egy fotont bocsájtanak ki. Csakhogy az alapállapotba történő visszatérés nem véletlenszerűen zajlik le, hanem az ún. indukált emisszió által, ami a rezonátor két tükre között mozgó fotonoknak a gerjesztett atomnál való elhaladásakor jön létre. Az ekkor keletkező foton fázisa lesz az éppen elhaladó foton fázisával, ezért lesz a lézerfény koherens.

A fotonok korábbi gerjesztett atomok mellett elhaladva újabb fotonokat „visznek magukkal”, tehát a folyamat lavinaszerűen erősödik. Ehhez járul hozzá a rezonátor, amelyben a keletkezett fotonok oda - visszaverődés közben sokasodnak – ezt hívjuk fényerősítésnek. A külső energia ahhoz kell, hogy az alapállapotban lévő atomokat állandóan pumpálva gerjesztett állapotba juttassa, vagyis elektronhéjaikat fordított betöltöttségűre változtassa (inverz populáció). A lézer szó jól jellemzi az elmondottakat

	Light
	Amplification by
	Stimulated
	Emmission of
	Radiaton

6.2. A konfokális rezonátor

TEM ₀₀ tulajdonságai

Térerősség a rezonátor tükrén

	$U_{m, l} (x, y) = H_{m} (x) H_{l} (y) e^{- \frac{π}{L λ} (x^{2} + y^{2})}$
	$U_{00} (ρ) = e^{- \frac{π}{L λ} ρ^{2}}$ , ahol x²+y²=ρ²

Ha a exponenciális kifejezés kitevője 1, akkor ρ = w_s, ahol w_s a nyalábsugár a tükrön (itt esik az amplitudó e-ad részére, azaz az intenzitás az e²-ed részére) azaz

$w_{s} = {(\frac{L λ}{π})}^{\frac{1}{2}}$

Térerősség a rezonátoron belül

$w (z) = w_{0} {[1 + {(\frac{2 z}{L})}^{2}]}^{\frac{1}{2}}$

(6.3)

ahol $w_{0} = {(\frac{L λ}{2 π})}^{\frac{1}{2}}$ a nyalábderék, Gauss nyalábnak az a pontja, ahol legkisebb a nyalábsugár.

A TEM00 módus térerőssége és az intenzitása a rezonátorban

$U (ρ, z) = U_{0} (z) e^{- \frac{ρ^{2}}{w^{2} (z)}}$

$I (ρ, z) = U^{2} (ρ, z) = I_{0} (z) e^{- \frac{2 ρ^{2}}{w^{2} (z)}}$

Gauss nyaláb fényteljesítménye

$P = \int_{0}^{\infty} I (ρ, z) 2 π ρ d ρ = = 2 π I_{0} (z) \int_{0}^{\infty} e^{- \frac{2 ρ^{2}}{w^{2} (z)}} ρ d ρ$

$x = \frac{\sqrt{2} ρ}{w}$ és $d x = \frac{\sqrt{2}}{w} d ρ$ jelölésekkel

$P = 2 π I_{0} (z) {(\frac{w (z)}{\sqrt{2}})}^{2} \cdot \int_{0}^{\infty} e^{- x^{2}} x d x$

felhasználva, hogy $\int_{0}^{\infty} x e^{- x^{2}} d x = \frac{1}{2}$

$P (z) = \frac{1}{2} I_{0} (z) w^{2} (z) \cdot π$

azaz az összteljesítményt megkapjuk, ha a csúcsintenzitás felét szorozzuk a nyalábsugárba zárt területtel.

A nyaláb tengelye mentén a csúcsintenzitás az összteljesítményből származtatható

$I_{0} = \frac{2 P}{π w^{2}}$

(6.4)

Véges detektorméret (ρ₀- detektorsugár) esetén a nyaláb teljesítményének hányad része esik a detektorra?

	$P (ρ_{0}) = \int_{0}^{ρ_{0}} I (ρ) 2 π ρ d ρ = ?$
	$\begin{array}{l} \frac{P (ρ_{0})}{P} = \frac{1}{P} \int_{0}^{ρ_{0}} I (ρ) 2 π ρ d ρ = \frac{1}{P} [\int_{0}^{\infty} I (ρ) 2 π ρ d ρ - \int_{ρ_{0}}^{\infty} I (ρ) 2 π ρ d ρ] = \\ = 1 - e^{- \frac{2 ρ_{0}^{2}}{w (z)}} \end{array}$

Ha w(z) = ρ₀_, akkor 1-e^-2=0,86 azaz az adott pontban a Gauss nyaláb összteljesítményének 86 százaléka esik a detektor felületére. Ellenben, ha 1,5w(z)=ρ₀_, akkor 1-e^-2=0,99 azaz az adott pontban a Gauss nyaláb összteljesítményének 99 százaléka esik a detektor felületére.

Fázisfelületek a Gauss nyalábban

Fázisfelületnek a nyaláb azonos fázisú pontjai által meghatározott felületet nevezzük.

A Gauss nyaláb fázisfelületei változó sugarú gömbfelületek.

A fázisfelület sugara szimmetrikus rezonátor esetén:

$R (z) = z [1 + {(\frac{L}{2 z})}^{2}]$

(6.5)

	z=0	R(0)=∞
	z=±L/2	R(±L/2)= ±L
	z=∞	R(∞)=∞

A nyalábsugár ábrázolva a nyaláb tengelye mentén

$R (z) = z + \frac{L^{2}}{4 z}$

(6.6)

A fázisfelületre betehető a felület rádiuszának megfelelő geometriájú tükör anélkül, hogy elrontaná a kialakult eloszlást. Ha a rezonátort az egyik végén sík tükör zárja le, akkor arra a tükörre a nyalábderék esik. Bármely általános rezonátorhoz, ami két gömbtükörből épül fel, megtalálható az ekvivalens konfokális rezonátor, így a nyalábsugár kiszámítható a tükrökön.

Gauss nyaláb áthaladása lencsén

A nyalábsugár a nyaktól z távolságra

$w (z) = w_{0} {[1 + {(\frac{2 z}{L})}^{2}]}^{1 / 2}$

ahol $w_{0} = {(\frac{λ L}{2 π})}^{1 / 2}$ tehát $\frac{L}{2} = \frac{π}{λ} w_{0}^{2} \equiv z_{0}$

ami definíció szerint a Rayleigh távolság vagy fókuszmélység.

A nyalábnyak és a fázisfelület görbületének sugara kifejezve a Rayleigh-távolsággal

	$w (z) = w_{0} {[1 + {(\frac{z}{z_{0}})}^{2}]}^{1 / 2}$	(6.7)
	$R (z) = z {[1 + {(\frac{z_{0}}{z})}^{2}]}^{}$	(6.8)

Gauss nyaláb áthaladása vékonylencsén

A lencse két oldalán a belépő és a kilépő nyalábsugarak (w₁és w₂) megegyeznek, mert a lencse vékony.

$w_{1} = w_{2}$

A fázisfelületek sugarának változását az alábbi összefüggés adja meg, ha a lencse fókusztávolsága f:

$\frac{1}{R_{1}} - \frac{1}{R_{2}} = \frac{1}{f}$

(6.9)

Nyalábderék méretének és helyének meghatározása ismert nyalábsugarú és fázisfelület görbületű Gauss nyalábnál

Ismert R és w

w₀=?

z=?

	$R = z [1 + {(\frac{z_{0}}{z})}^{2}]$ így $z = \frac{R}{[1 + {(\frac{z_{0}}{z})}^{2}]}$
	valamint $w^{2} = w_{0}^{2} [1 + {(\frac{z}{z_{0}})}^{2}]$

Mindkét oldalt beszorozva π/λ-val és kihasználva, hogy a $\frac{w^{2} π}{λ} = z_{0}$ szorozva;

$\frac{π}{λ} w^{2 =} \frac{z_{0}^{2} + z^{2}}{z_{0}^{}}$

kapjuk.

A fenti egyenletből R-re a következőt kapjuk:

$R = \frac{z^{2} + z_{0}^{2}}{z^{}}$ .

Minkét egyenletet z²+z₀²-re kifejezzük

	$\frac{π}{λ} w^{2} z = R z$
	$\frac{z_{0}}{z} = R \frac{λ}{π w^{2}}$

Tehát a nyak távolsága és a nyak mérete kifejezve

	$z = \frac{R}{1 + {(\frac{R λ}{π w^{2}})}^{2}}$	(6.10)
	$w_{0} = \frac{w}{{[1 + {(\frac{π w^{2}}{R λ})}^{2}]}^{1 / 2}}$	(6.11)

Divergencia

Ha a z>>z_0, azaz távol vagyunk a nyaktól

$z_{0} = \frac{π w_{0}^{2}}{λ}$

$w = w_{0} {[1 + {(\frac{z}{z_{0}})}^{2}]}^{1 / 2}$

(6.12)

A zárójelen belül az 1 elhanyagolható ha z>>z₀, így

$w = \frac{w_{0}}{z_{0}} z = w_{0} \frac{λ}{π w_{0}^{2}} z = θ \cdot z$

ahol θ a divergencia félszög és

$θ = \frac{λ}{π w_{0}}$

(6.13)

megállapítható

$θ w_{0} = \frac{λ}{π} = á l l a n d ó$

(6.14)

6.3. A lézernyaláb intenzitás eloszlása a nyaláb keresztmetszet irányában

6.3. ábra - A lézernyaláb intenzitás eloszlása a keresztmetszet irányában

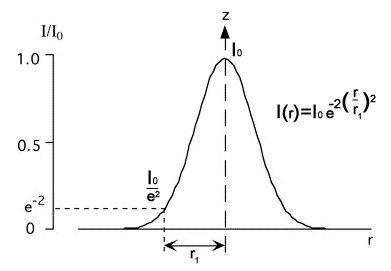
A lézernyaláb a terjedési irányra merőlegesen Gauss függvény szerinti intenzitású.

$I (r) = I_{0} e^{- 2 {(\frac{r}{r_{1}})}^{2}}$

(6.15)

ahol

	$I_{0}$	a nyaláb intenzitása a nyaláb tengelyében
	$r$	a tengelytől valótávolság
	$I (r)$	a nyaláb intenzitása a tengelytől r távolságra
	$r_{1}$	a tengelytől mért azon távolság, amelynél a nyaláb intenzitása a tengelyen lévő intenzitás $e^{2}$ -ed része.

$I (r_{1}) = I_{0} / e^{2}$

(6.16)

$r_{1}$ -et a nyaláb sugarának, kétszeresét pedig $(d_{1} = 2 r_{1})$ a nyaláb átmérőjének nevezzük. $d$ -vel is felírható a nyaláb intenzitás képlete:

$I_{(d)} = I_{0} e^{- 2 {(\frac{d}{d_{1}})}^{2}}$

(6.17)

, ahol $d = 2 r$

6.4. A lézernyaláb intenzitása a terjedési irány mentén

6.4. ábra - A lézernyaláb eloszlása a terjedési irány mentén

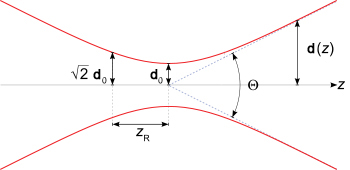
A terjedési irány mentén a lézernyaláb előbb definiált mérete az alábbi összefüggés szerint változik:

$d^{2} (z) = d_{0}^{2} + Θ^{2} z^{2}$

(6.18)

ahol

	$d$	a nyaláb átmérője, amely a $z$ terjedési irány mentén változik
	$d_{0}$	a nyaláb nyak átmérője (beam waist)
	$Θ$	a nyaláb végérintőinek szöge, amelyet a nyaláb divergenciájának nevezünk.

E két nyalábjellemző között egy adott hullámhosszú $(λ)$ lézer esetén az alábbi összefüggés áll fenn:

$d_{0} = \frac{4 λ}{πΘ}$

(6.19)

Az összefüggést átalakítva

$d_{0} Θ = \frac{4 λ}{π}$ = állandó

(6.20)

képlethez jutunk, ami azt jelenti, hogy egy adott lézer nyalábnál a nyaláb nyak és a divergencia fordítottan arányos.

Ebből már most levonható a következtetés a későbbiekben tárgyalandó lézervágásra vonatkozóan: Ha azt szeretnénk, hogy kicsi legyen a nyaláb nyak, akkor azt nagy Θ divergenciájú leképzés során hozhatjuk létre, vagyis nagy átmérőjű és kis fókusztávolságú lencsével, pontosabban kis $f / D$ viszonyú (relatív nyílású) optikával. ( $f$ a lencse fókusztávolsága és $D$ az átmérője.

A (6.4. ábra) ábrán $Z_{R}$ jelenti azt a nyakból való távolságot, amelynél a nyaláb $d (Z_{R})$

6.5. A lézer nyaláb módosítása

A lézerből kilépő nyalábot formálni lehet. A nyaláb áthaladhat lencséken, tükrökön, eközben azonban viselkedése nem követi a geometriai optika törvényeit, mint például a vékonylencse egyenletét:

$\frac{1}{s^{'}} = \frac{1}{s} + \frac{1}{f}$

(6.21)

ahol

	$s$	a tárgy és lencse közötti távolság
	$s^{'}$	a kép és a lencse közötti távolság
	$f$	a lencse fókusztávolsága

és a Newton-formulát sem:

$z z^{'} = - f^{2}$

(6.22)

6.6. A vékony lencse egyenlete Gauss nyalábra

A lencsék nyalábformálását úgy képzelhetjük el, mintha a nyaláb nyak lenne a tárgy, amelyet a lencse egy újabb nyaláb nyakba képezne le, amely képként lenne értelmezhető.

A leképzés során a tárgyoldali nyaláb paraméterek ( $d_{0}, Θ, z_{R}$ ) megváltoznak és létrejönnek a képoldali megfelelőik ( $d_{0}^{'}, Θ', {z'}_{R}$ ).

A Newton-féle (6.22) formulában szereplő tárgy ( $z$ ) és képtávolságok ( $z'$ )

	$- z = s - f$ és
	$z^{'} = s^{'} - f'$ lesznek,

amelyekkel a Gauss nyalábra vonatkozó lencseegyenlet:

$(s - f) (s^{'} - f^{'}) = f^{2} - f_{0}^{2}$

(6.23)

ahol megjelenik az $f_{0}$ , amely a diffrakció jellemzője:

$f_{0}^{2} = z_{R} z_{R}^{'}$

(6.24)

és amely az alábbi módokon számítható ki:

	$f_{0} = \frac{d_{0}^{'}}{Θ}$	(6.25)
	$f_{0} = \frac{d_{0}}{Θ^{'}}$	(6.26)
	$f_{0} = \frac{π d_{0} d_{0}^{'}}{4 λ}$	(6.27)
	$f_{0} = \frac{4 λ}{π Θ Θ^{'}}$	(6.28)

Ha a lineáris nagyítást a nyaláb nyakok méretére (mint az optikai tengelyre merőleges tárgyméretekre) vonatkoztatjuk

$\frac{d_{0}^{'}}{d_{0}}$

és a longitudinális nagyítást a $z$ méretek változására

$\frac{z^{'}}{z} = \frac{s^{'} - f^{'}}{s - f}$

,akkor a két nagyítás ismert viszonya miatt

$\frac{s - f}{s^{'} - f^{'}} = \frac{d_{0}^{2}}{d_{0}^{' 2}}$

(6.29)

írható.

A (6.23) – ből

$s' - f' = \frac{f' - f_{0}^{2}}{s - f}$

Ezt helyettesítsük be a (6.29) – be

$\frac{{(s - f)}^{2}}{f^{2} - f_{0}^{2}} = \frac{d_{0}^{2}}{d_{0}^{' 2}}$

Vegyük figyelembe (6.25) – t:

$\frac{{(s - f)}^{2}}{f^{2} - \frac{d_{0}^{' 2}}{Θ^{2}}} = \frac{d_{0}^{2}}{d_{0}^{' 2}}$

Szorozzuk be a bal oldal nevezőjével!

${(s - f)}^{2} = f^{2} \frac{d_{0}^{2}}{d_{0}^{' 2}} - \frac{d_{0}^{2}}{Θ^{2}}$

Mivel

	$z_{R} = \frac{d_{0}}{Θ}$
	${(s - f)}^{2} = f^{2} \frac{d_{0}^{2}}{d^{' 2}} - z_{R}^{2}$

Végig szorozva $d^{' 2}$ -tel

$d_{0}^{' 2} [{(s - f)}^{2} + z_{R}^{2}] = f^{2} d_{0}^{2}$

(6.30)

adódik.

Ha a tárgy és a képoldali nyaláb nyak átmérők közötti átszámítást tekintjük, akkor ez olyan, mint a lineáris nagyítás.

$d_{0}^{' 2} = \frac{f^{2}}{{(s - f)}^{2} + z_{R}^{2}} d_{0}^{2} = β^{2} d_{0}^{2}$

(6.31)

ahol

$β = \frac{| f |}{\sqrt{{(s - f)}^{2} + z_{R}^{2}}}$

(6.3)

Ez a nagyítás – mint látható – csak axiális értékektől függ ( $z_{R}, f, s - f$ ).

Ha ß értéke ismert, akkor a leképzés utáni nyalábjellemzők kiszámíthatók:

	$d_{0}^{'} = β d_{0}$	(6.33)
	$Θ^{'} = \frac{4 λ}{π d_{0}^{'}} = \frac{4 λ}{π β d_{0}} = \frac{Θ}{β} = \frac{Θ}{β}$	(6.34)
	$z_{R}^{'} = \frac{d_{0}^{'}}{Θ^{'}} = \frac{β d_{0}}{\frac{Θ}{β}} = β^{2} z_{R}$	(6.35)

(6.29) – ből és (6.33) – ből az új nyak helye kifejezhető

$(s' - f) = \frac{d_{0}^{' 2}}{d_{0}^{2}} (s - f) = β^{2} (s - f)$

és innen

$s' = f + \frac{f^{2} (s - f)}{{(s - f)}^{2} + z_{R}^{2}}$

(6.36)

vagy (6.31) segítségével

$s' = f + \frac{f^{2} (s - f)}{{(s - f)}^{2} + z_{R}^{2}}$

(6.37)

6.7. Kollimált lézernyaláb fókuszálása kis ponttá

A lézer alkalmazások gyakori esete a lézerfénnyel történő vágás, fúrás. Ilyenkor nagy felületegységre jutó teljesítményre van szükség, ezért kell kis ponttá leképeznünk a korábbi lézernyakat.

A (6.33) – ből láttuk, hogy

$d_{0}^{'} = β d_{0}$

ami azt jelenti, hogy kis $d_{0}^{'}$ - t kicsi ß – val tudunk előállítani.

A (6.32) – ből viszont látható, hogy ß számlálójában a lencse fókusztávolsága szerepel:

$β = \frac{| f |}{\sqrt{{(s - f)}^{2} + z_{R}^{2}}}$

tehát kis fókusztávolságú lencsét kell választani.

Mivel a nyaláb kollimált, feltételezhető, hogy $s$ és $z_{R} > > f$ ,

ezért (6.32) nevezőjében az $f$ elhanyagolható:

$β = \frac{f}{\sqrt{s^{2} + z_{R}^{2}}}$

(6.38)

Itt két határesetet különböztethetünk meg, a közel tér és a távoltér esetét:

Közel tér esete

$s < < z_{R}$ , vagyis a lencsét a lézerhez egészen közel, a $z_{R}$ tartományhoz elhanyagolható távolságra helyezzük el.

Ekkor

$β = \frac{f}{z_{R}} = \frac{f Θ}{d_{0}}$

(6.39)

és ezzel a nyaláb paraméterek:

	$d_{0}^{'} = β d_{0} = f Θ$	(6.40)
	$Θ' = \frac{Θ}{β} = \frac{Θ d_{0}}{f Θ} = \frac{d_{0}}{f}$	(6.41)
	$z_{R}^{'} = β^{2} z_{R} = \frac{f^{2}}{z_{R}^{2}} z_{R} = \frac{f^{2}}{z_{R}}$	(6.42)

és a kis ponttá fókuszált nyalábnyak lencsétől l mért távolsága a (6.27) – ből:

$s' = f + β^{2} (s - f) \approx f$

(6.43)

Távoltér esete

Tegyük a lencsét távol a lézertől!

Ekkor $s > > z_{R}$ és a (6.38) – ből

$β = \frac{f}{s}$

(6.44)

Ezzel a nyaláb paraméterek:

	$d_{0}^{'} = β d_{0} = \frac{f d_{0}}{s}$	(6.45)
	$Θ' = \frac{Θ}{β} = \frac{s Θ}{f}$	(6.46)

megjegyzendő, hogy a lencsénél a nyaláb átmérője $D = s Θ$ lesz, tehát ettől nagyobb kell legyen a lencse átmérője.

$z_{R}^{'} = β^{2} z_{R} = \frac{f^{2}}{s^{2}} z_{R}$

(6.47)

és a nyaláb nyak helye a (6.37) – ből:

$s' = f + \frac{(s - f) f^{2}}{s^{2}} ≅ f$

(6.48)

Példa a lézernyaláb fókuszálására

Legyen adva egy He - Ne lézer az alábbi adatokkal:

Divergencia: $Θ = 0,8$ mrad

Fókuszáljuk egy $f = 100$ mm fókusztávolságú lencsével.

Kérdés: mekkora lesz a nyalábnyak $d_{0}^{'}$ mérete a fókuszpontban?

A feladatot bontsuk három részre!

$s < < z_{R}$ ez a közel tér esete, amikor a lencsét a lézer közelében helyezzük el.
$s = z_{R}$ amikor a lencsét éppen Rayleigh távolságra helyezzük a lézertől.
$s > > z_{R}$ ez a távoltér esete.

Megoldás:

Először számítsuk ki, mekkora a kiinduló nyalábnyak mérete a lézerben és mekkora a tárgyoldali Rayleigh távolság. Ezek ugyanis a nyaláb jellemzői.

	$d_{0} = \frac{4 λ}{π Θ} = \frac{4 \cdot 633 \cdot 10^{- 6}}{π \cdot 0,8 \cdot 10^{- 3}} = 1 m m$
	$z_{R} = \frac{d_{0}}{Θ} = \frac{1 \cdot 10^{- 3} m}{0,8 \cdot 10^{- 3} r a d} = 1,25 m$

eset

$s < < z_{R}$ tehát $β = \frac{f}{\sqrt{s^{2} + z_{R}^{2}}}$ képletben az $s$ elhanyagolható.

A nyalábnyak mérete a fókuszban:

$d_{0}^{'} = f Θ = 10^{- 1} \cdot 0,8 \cdot 10^{- 3} = 80 μ m$

eset

$s = z_{R}$

A nyalábnyak mérete a fókuszban:

$d_{0}^{'} = \frac{f d_{0}}{\sqrt{{(s - f)}^{2} + z_{R}^{2}}} = \frac{10^{- 1} \cdot 10^{- 3}}{\sqrt{{(1,25 - 0,1)}^{2}}} = 60 μ m$

Megjegyzés:

Érdekes, hogy egy kollimált lézernyalábba tett lencse fókuszában a nyak mérete kisebb, ha távolodik a lencse a lézertől.

eset

$s > > z_{R}$ legyen mondjuk $z_{R} = 12,5 m$

A nyalábnyak mérete a fókuszban:

$d_{0}^{'} = \frac{f d_{0}}{s} = \frac{0,1 \cdot 10^{- 3}}{12,5} = 8 μ m$

Megjegyzések:

Meglepő, hogy távoltérben milyen kicsi lesz a nyak mérete a közel térihez képest.

Tekintettel kell lenni azonban arra, hogy a 12,5 m távolságban a lézernyaláb már jelentősen kitágult, átmérője

$D = Θ s = 0,8 \cdot 12,5 = 10 m m$

ami azt jelenti, hogy legalább ilyen átmérőjű lencsét kell alkalmazni.

6.8. Nyalábnyak újra fókuszálása

Erre az esetre akkor van szükség, ha a nyalábnyak kialakult méretével nem vagyunk elégedettek. Például azt szeretnénk, hogy egy CCD detektor pixeljeit éppen töltse ki a nyalábnyak egy lézer szkenner esetében.

Vagyis a nyalábnyak nagyításáról vagy kicsinyítéséről van szó, ennek érdekében egy újabb lencsével újra kell fókuszálni a nyalábot.

Kiindulásul ki kell először számítanunk a nyalábnyak szükséges nagyításának mértékét (ß)

Mivel $d_{0}^{'} = β d_{0}$

ezért $β = \frac{d_{0}^{'}}{d_{0}}$

A divergencia pedig $Θ' = \frac{Θ}{β}$ és a Rayleigh tartomány $z_{R}^{'} = β^{2} z_{R}$ lesz.

ß definíciójából kiindulva meghatározhatjuk $s$ értékét:

	$β^{2} = \frac{f^{2}}{{(s - f)}^{2} + z_{R}^{2}}$
	${(s - f)}^{2} + z_{R}^{2} = \frac{f^{2}}{β^{2}}$
	${(s - f)}^{2} = \frac{f^{2}}{β^{2}} - z_{R}^{2}$
	$s = f \pm \sqrt{{(\frac{f}{β})}^{2} - z_{R}^{2}} = f \pm \frac{1}{β} \sqrt{f^{2} - f_{0}^{2}}$	(6.49)

Megjegyzés:

Meglepve látjuk, hogy nem mindegy fókusztávolságú lencsét használunk! A négyzetgyök alatt ugyanis nem lehet negatív, ezért

$f \geq f_{0}$ kritérium mondható ki.

Mivel $f_{0} = z_{R} z_{R}^{'}$ , ezért $f^{2} \geq f_{0}^{2} = z_{R} z_{R}^{'}$ kritériumnak megfelelően kell megválasztanunk az alkalmazandó lencsét.

Példa a nyalábnyak újra fókuszálására

He – Ne lézerünk adatai

	$d_{0} = 1 m m$
	$Θ = 0,8 m r a d$
	$z_{R} = 1,25 m$

A nyalábnyak a lézer kilépő ablakának síkjában található az adatlap szerint.

Feladat: csökkentsük a nyalábnyakat $d_{0}^{'} = 184 μ m$ nagyságúra!

Megoldás:

	$β = \frac{d_{0}^{'}}{d_{0}} = \frac{184 μ m}{1 m m} = 0,184$
	$z_{R}^{'} = β^{2} z_{R} = {0,184}^{2} \cdot 1,25 = 42 m m$
	$f_{0}^{2} = z_{R} \cdot z_{R}^{'} = 1250 m m \cdot 42 m m = 52500 m m^{2}$
	$f_{0} = 229,129$

vagyis $f > 230 m m$ feltételt kell a lencse megválasztásánál figyelembe vennünk.

eset

Találtunk egy a kritériumnak megfelelő lencsét a készletünkben $f = 300 m m$ fókusszal. Számítsuk ki, mekkora helyet igényel a nyaláb újrafókuszálás, vagyis milyen távolságra kell tennünk a lencsét az eredeti nyaktól és a lencsétől milyen távolságra jön létre az új nyak?

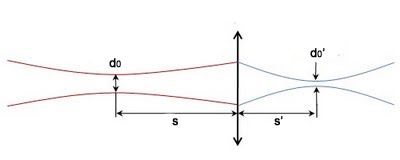6.5. ábra - Lézernyak újra fókuszálása

A (6.49) összefüggésből

$s = f \pm \frac{1}{β} \sqrt{f^{2} - f_{0}^{2}} = 300^{2} \pm \frac{1}{0,184} \cdot \sqrt{300^{2} - 230^{2}} = 1347 m m$

Megjegyzés:

Csak a pozitív előjelnek van értelme, máskülönben $s$ értéke negatív lenne.
Az 1347 mm-es távolság igen nagy egy műszer építésénél, ezért keresni kell egy kisebb fókuszú lencsét!

eset

Találtunk egy $f = 235 m m$ -es lencsét.

Ezzel

$s = 235 + \frac{1}{0,184} \cdot \sqrt{235^{2} - 230^{2}} = 497 m m$

Nézzük, mekkora lenne $s'$ !

A (6.39) – ből

$s' = f + β^{2} (s - f) = 235 + {0,184}^{2} (497235) = 244 m m$

Megjegyzés:

A teljes távolság a lézertől a fókuszig $s + s' = 497 + 244 = 741 m m$ , ami még mindig túl nagy ahhoz, hogy egy asztalon elférő műszerben megfelelő legyen, rendeljünk tehát egy pontosan $f_{0}$ -nak megfelelő $f = 230 m m$ -es lencsét!

eset

$f = f_{0} 230 m m$

Ezzel a gyök alatt zérus lesz és így $s = s^{'} = f = 230 m m$ adódik, vagyis az elérhető legkisebb méret:

$s + s' = 2 f = 460 m m$

6.9. A nyalábnyak relézése

Külön érdemes megvizsgálnunk azt az esetet, amikor nem azzal van dolgunk, hogy a nyalábnyaknak nem megfelelő a mérete, hanem azzal, hogy rossz helyen van a megépítendő műszerünkben, át kellene helyezni máshová anélkül, hogy megváltozna a mérete. Ezt az esetet relézésnek nevezzük, amelyre tehát az jellemző, hogy a nagyítás

$β = \frac{d_{0}^{'}}{d_{0}} = 1$

$β$ definíciójából:

$β^{2} = \frac{f^{2}}{{(s - f)}^{2} + z_{R}^{2}} = 1$

Mivel (6.49) szerint

$s = f \pm \sqrt{\frac{f^{2}}{β^{2}} - z_{R}^{2}}$

, ezért $β = 1$ -gyel

$s = f \pm \sqrt{f^{2} - z_{R}^{2}}$

(6.50)

Megjegyzés:

Nem mindegy tehát itt sem, hogy a lencse fókuszát mekkorára választjuk:

$f \geq z_{R}$ a kritérium!

A fókusz értéket meghatározhatjuk a (6.49) - ből is.

A (6.49) feletti sorból kiindulva és $β = 1$ - et helyettesítve

	$f^{2} = {(s - f)}^{2} + z_{R}^{2} = s^{2} - 2 s f - f^{2} + z_{R}^{2}$
	$s^{2} - 2 s f + z_{R}^{2} = 0$

amelyből $f$ -et kifejezve

$f = \frac{s^{2} + z_{R}^{2}}{2 s}$

(6.51)

A (6.39) – ből pedig

$s' = f + β^{2} (s - f) = f + s - f = s$

A teljes távolságot a két nyak között a (6.50) kifejezés 2-vel való szorzásával kaphatjuk meg:

$s_{12} = s + s' = 2 f \pm 2 \sqrt{f^{2} - z_{R}^{2}}$

(6.52)

A gyök alatti mennyiségek miatt két speciális esetet különböztethetünk meg:

Ha $f > > z_{R}$ , akkor

$s_{12} = 4 f$

Megjegyzés:

Ez az eset megfelel a geometriai optikából ismerteknek, mely szerint ha egy tárgynak egy lencse kétszeres fókuszába helyezünk, akkor a képe szintén a kétszeres fókuszban keletkezik, tehát a tárgy és képe közötti távolság $4 f$ lesz.
Figyelembe kell venni, hogy a keletkező nyaláb erősen divergens lesz.

Legyen $f = z_{R}$ , amikor a gyök alatt zérus adódik!

Ekkor a (6.50) szerint $s = s^{'} = f$ és a (6.52) szerint $s_{12} = 2 f$

Megjegyzés:
1. Ezt az esetet Gauss relézésnek hívjuk.
2. Meglepő ez az eredmény! Ugyanis a geometria optikában a fókuszba helyezett tárgy képe a végtelenben lesz, semmiképpen nem a fókuszban!
  
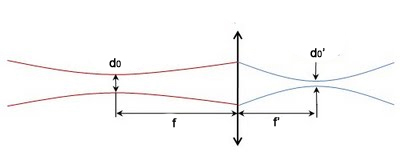  6.6. ábra - A Gauss relézés
3. Ez az eset nem valósítható meg mindig - $z_{R}$ nagysága miatt.

6.10. Gauss nyaláb kollimálás

Mint tudjuk, párhuzamos lézernyaláb nincs. Mit nevezünk akkor kollimátornak? Kétféleképpen fogalmazhatjuk meg, hogy mit szeretnénk:

Legyen a nyaláb Θ divergenciája kicsi vagy egy lencse után.
Legyen a következő lézernyak nagyon távol ( $s'$ ).

1. eset

Mivel $z_{R}^{'} = \frac{d_{0}^{'}}{Θ'}$ , ezért ha azt szeretnénk, hogy Θ’ kicsi legyen, akkor ez egyenértékű azzal, hogy $z_{R}^{'}$ nagy legyen.

Mivel $z_{R}^{'} = β^{2} z_{R}$ maximális, ha $β^{2}$ is az.

Viszont $β$ definíciójából

$β^{2} = \frac{f^{2}}{{(s - f)}^{2} + z_{R}^{2}}$ akkor lesz nagy, ha a nevezőben $s - f = 0$ lesz, vagyis a lencsét úgy helyezzük el, hogy a megelőző nyak a lencse fókuszában legyen.

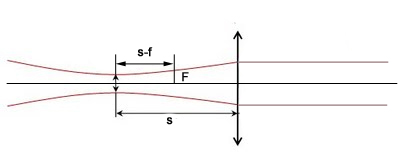6.7. ábra - Vázlat a lézernyaláb kollimálásához

$s - f = 0$ esetében a nagyítás $β^{2} = \frac{f^{2}}{z_{R}^{2}}$ és mivel $z_{R}^{'} = β^{2} z_{R}$

$z_{R}^{'} = \frac{f^{2}}{z_{R}^{2}} z_{R} = \frac{f^{2}}{z_{R}}$

(6.53)

A (6.53) szerint $z_{R}^{'}$ akkor lesz nagy, ha $f$ nagy és $z_{R}$ kicsi.

Hogyan valósítható meg mindkét követelmény?

Úgy valósítható meg, hogy az eredeti nyalábot egy kis fókusztávolságú lencsével leképezzük, (ekkor $z_{R}$ értéke lecsökken), majd egy nagy fókusztávolságú lencsével újra kollimáljuk. Ismerjük fel, hogy ezt a két mozzanatot éppen egy fordított irányban használt Kepler, vagy Galilei-féle távcső valósítja meg!

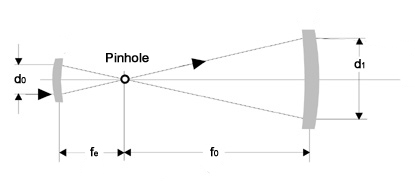6.8. ábra - Fordított Kepler-féle távcső, mint nyalábtágító

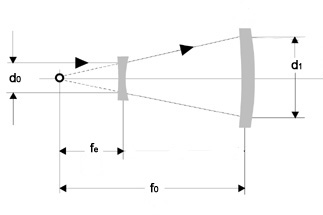6.9. ábra - Fordított Galilei távcső, mint nyalábtágító

Számítsuk ki ezen kettős nyalábformálás paramétereit!

Az okulár lencse kis fókusztávolsága azt jelenti, hogy a lézer közel terében vagyunk.

Ekkor

	$β = \frac{f_{e}}{z_{R}}$
	$d_{0}^{'} = β d_{0} = \frac{f_{e}}{z_{R}} d_{0} = f_{e} Θ$	(6.54)
	$Θ' = \frac{d_{0}}{f_{e}}$
	$z_{R}^{'} = \frac{f_{e}^{2}}{z_{R}}$
	$s' = f_{e}$

Megjegyzés:

A Kepler-féle távcső közös közbenső fókuszpontjába egy tű-lyukat (pin hole) célszerű helyezni, amely előnyösen „térszűri” a nyalábot, hatására a kitágított nyaláb hullámfrontjai kisimulnak és az ernyőn felfogott nyaláb képében nem lesznek zavaró interferencia gyűrűk. Ez különösen holográfiai alkalmazásoknál fontos.

2. eset

Itt az a célkitűzés, hogy $s'$ legyen maximális, vagyis a leképzett nyak a lehető legtávolabb legyen.

Ha a Newton formula szerinti távolságot ( $z$ ) éppen $z_{R}$ -re választjuk, akkor

$s = f + z_{R}$ lesz.

(6.55)

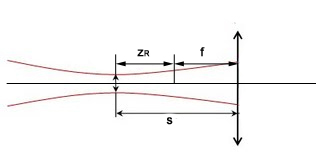6.10. ábra - Vázlat a maximális nyalábnyak távolság levezetéséhez

ß definíciója szerint

$β = \frac{| f |}{\sqrt{{(s - f)}^{2} + z_{R}^{2}}} = \frac{| f |}{\sqrt{z_{R}^{2} + z_{R}^{2}}} = \frac{| f |}{z_{R} \sqrt{2}}$

(6.56 )

Ezzel számítsuk ki $s'$ -t és $z_{R}^{'}$ -t az első lencsére

	$s' = f + β^{2} (s - f) = f + \frac{f^{2}}{2 z_{R}^{2}} z_{R} = f + \frac{f^{2}}{2 z_{R}}$	(6.57)
	$z_{R}^{'} = β z_{R} = \frac{f^{2}}{2 z_{R}^{2}} z_{R} = \frac{f^{2}}{2 z_{R}}$	(6.58)

Megjegyzés:

Ahhoz, hogy $s'$ nagy legyen, $z_{R}$ -nek kicsinek kell lenni.

A második lencsére

$s = f_{o b j} + z_{R}^{'}$

A második lencse nagyítása legyen $β'$

$β' = \frac{f_{o}}{z_{R} \sqrt{2}}$

A második lencse által leképzett új nyakméret $d_{o}^{''}$

$d_{0}^{"} = β' d_{0}^{'} = β' β d_{0} = β " d_{0}$

ahol $β "$ az eredő nagyítás

	$β " = β' β = \frac{f_{o b j}}{z_{R} \sqrt{2}} \cdot \frac{f_{e}}{z_{R}} = \frac{f_{e}}{z_{R}} \cdot \frac{f_{o b j}}{\frac{f_{e}^{2}}{z_{R}} \sqrt{2}}$
	$β " = \frac{f_{o b j}}{f_{e} \sqrt{2}} = \frac{γ}{\sqrt{2}}$

ahol $γ = \frac{f_{o b j}}{f_{e}}$ a távcső szögnagyítása

Megjegyzés:

Mivel $Θ " = \frac{Θ}{β "}$ és $β " = \frac{γ}{\sqrt{2}}$ , így a kollimáltság $\frac{γ}{\sqrt{2}}$ -vel megnő

A Rayleigh tartomány szintén megnő

$z_{R}^{"} = β "^{2} z_{R} = \frac{γ^{2}}{2} z_{R}$

A nyak áthelyeződik:

$s " = f_{o b j} + \frac{γ^{2}}{2} z_{R} = f_{o b j} + z_{R}^{"}$

Mindez az 1. esetben:

	$β " = γ$
	$s " = f_{o b j}$

A nyak az $f_{o b j}$ hátsó fókuszában lesz és a divergencia $\sqrt{2}$ -ed lesz.

Példa a nyalábtágításra

He – Ne lézer

	$d_{0} = 1 m m$
	$Θ = 0,8 m r a d$
	$z_{R} = 1,25 m$
	$γ = 40$ - szeres nagyítású távcső
	$f_{o b j} = 160 m m$
	$f_{e} = 4 m m$

Megoldás

1. eset

	$β " = \frac{f_{o b j}}{f_{e} \sqrt{2}} = \frac{40}{\sqrt{2}} = 28,28$
	$β "^{2} = \frac{40^{2}}{2} = 800$

Az új nyalábjellemzők:

	$d_{0}^{"} = β " d_{0} = 28,28 m m$
	$Θ " = \frac{Θ}{β "} = 28,28 m r a d$ (!)
	$z_{R}^{"} = β "^{2} z_{R} = 1 k m$ (!)

Megjegyzés:

Ezt csak diffrakció limitált esetben lehet elérni.

1. eset

	$β = 40$ $β "^{2} = 1600$
	$d_{0}^{"} = 40 m m$
	$Θ " = 20 m r a d$
	$z_{R}^{"} = 2 k m$

Példa összetett lencsék alkalmazására

Tekintsük a nyalábnyak szűkítő példát!

He – Ne lézer

	$d_{0} = 10 m m$
	$Θ = 0,8 m r a d$
	$z_{R} = 1,25 m$

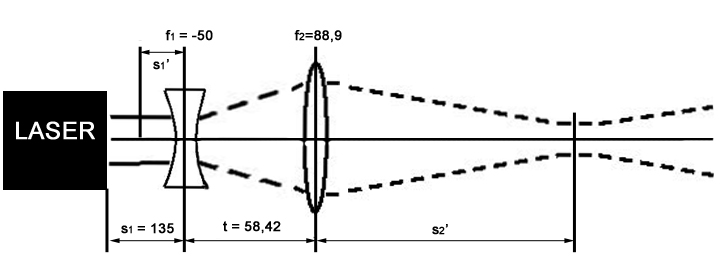
6.11. ábra - Példa összetett lencsék alkalmazására

Az 1. lencsére

	$s_{1} - f_{1} = 185 m m$
	$β = \frac{\| - 50 \|}{\sqrt{185^{2} + 1250^{2}}} = 4 \cdot 10^{- 2}$
	$d_{0}^{'} = 4 \cdot 10^{- 2} \cdot 1 m m = 40 μ m$
	$Θ' = \frac{Θ}{β} = 20 m r a d$
	$z_{R}^{'} = β^{2} z_{R} = 2 m m$
	$s_{1}^{'} = f_{1} + β^{2} (s_{1} - f_{1}) = - 50 + 16 \cdot 10^{- 4} \cdot 185 = - 50 + 0,3 = - 49,7 m m$
	$s_{2} = - t + s_{1}^{'} = - 58,42 + (- 49,7) = - 108,1 m m$

A 2. lencsére

	$f_{2} = 88,9$
	$s_{2} - f_{2} = - 108,1 + 88,9 = - 19,2 m m$
	$β' = \frac{88,9}{\sqrt{{19,2}^{2} + 2^{2}}} = 4,605$
	$d_{0}^{"} = β' d_{0}^{'} = 4,605 \cdot 40 μ m = 184,2 μ m$
	$Θ " = \frac{20 m r a d}{4,605} = 4,34 m r a d$
	$z_{R}^{"} = β' 2 \cdot z_{R}^{'} = 42,4 m m$
	$s_{1}^{'} = f_{2} + β^{' 2} (s_{2} - f) = 88,9 + {4,605}^{2} \cdot 19,2 = 496 m m$

A teljes távolság a lézertől!

$135 + 58,4 + 496 = 689 m m$

Példa tágított lézernyaláb alkalmazására

A Föld - Hold távolság megmérése az Apollo 11 projektben

Holdra szállás: 1969. július 20.

Űrhajósok: Armstrong, Aldrin

100 db sarokprizmát helyeztek el a Holdon a Nyugalom tengerében.

A Lick Obszervatóriumból (University of California at Santa Cruz) 1969. augusztus 1-én rubin lézerrel, Ø 120”-os teleszkóppal Ø 4 m-re tágított lézernyaláb impulzust lőttek a Holdra. Az impulzus 2,58 sec ± 0,1 $μ s$ idő alatt tért vissza.

A visszatért nyaláb 15 km átmérőjű volt.

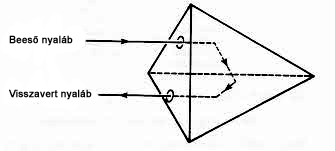
6.12. ábra - Sarokprizmáról a fény önmagával párhuzamosan tér vissza

A futásidővel megmérték a Föld - Hold távolságot a mérés pontosságát az időmérés 0,1 $μ s$ bizonytalansága korlátozta. Ez 6 m-es bizonytalanságot jelzett!

Kevéssel ezután a McDonald Observatóriumban (Texas) 2 ns-os pontosságú mérést hajtottak végre, amely 30 cm-es bizonytalanságot jelentett.

Vissza		Előre
5. fejezet - Lézerműködés feltételei	Főoldal	7. fejezet - A lézerek ipari alkalmazásai