18. fejezet - Szervopneumatikus pozícionáló szabályozásának tervezése és szimulációja

A 13. fejezet fejezetben a pneumatikus munkahenger részletes modelljét bemutatva világossá vált, hogy a rendszer nemlineáris (pl. súrlódás) összefüggései mellett több paramétere sem konstans, azaz változik (pl. kamra kapacitások).  A nehézkes pozícionálhatóság oka a kamrákban levő sűrített levegő összenyomhatóságának és a nemlineáris súrlódásnak együttes jelenléte, mely kihívásra csak kevés, robosztus szabályozást biztosító szabályozási algoritmus alkalmas. Az üzemszerűen optimális beállást biztosító szabályozáshoz a számos, arányait tekintve nagymértékben változó paraméter a rendszer átviteli függvénnyel történő felírását értelmetlenné teszi –ez alól csak az előző fejezetekben bemutatott, minden egyes pontban az ott érvényes paraméterek meghatározásával és linearizálással történő szabályozási paraméterek meghatározásával tehetünk kivételt. Ezzel együtt a paraméterek meghatározása a legtöbb szabályozási algoritmus számára alapvető fontosságú.

Első lépésként az elkészített rendszermodell vizsgálatához az összefüggéseken túlmenően szükség van az egyes együtthatók (súrlódási együtthatók), paraméterek ismeretére, melyek külön, speciálisan az adott paraméter mérésére fókuszálva mérés útján, vagy a valós rendszer működés közben történő vizsgálatával, paraméterbecsléssel állapítható meg. A paraméterek ismeretében szimulációs környezetben is vizsgálható az adott berendezés. Amennyiben a valós rendszer is rendelkezésre áll, és az egyes szabályozási algoritmusok kipróbálása sem a berendezést, sem a környezetet nem veszélyezteti, azon is tesztelhető - a fejezetben bemutatásra kerülő szabályozók összehasonlítása céljából a paraméterek meghatározása ezen utóbbi módon valósult meg.

Egy szabályozást akkor tekintünk hatékonynak, ha az előírt pozícióba minimális túllendüléssel, maradó hiba nélkül gyorsan beáll. Ezen feltételek egymásnak ellentmondóak, ezért mindig meg kell találni a feladathoz legjobban illő kompromisszumot. Bizonyos esetekben a legfontosabb szempont a gyors beállás, és akár a nagy túllendülés is megengedett, ellentétben a gyártásban használt szerszámgépeknél, ahol elsődleges szempont a túllendülés elkerülése. Ahogy említésre került a szabályozási algoritmus eredményét a paraméterek becslésének pontossága nagymértékben befolyásolja. Ez legjobb szándék ellenére sem teljesen pontos, azaz már ebben a lépésben rontunk a szabályozó optimális működéséhez képest. Emellett megemlítendő, hogy nem csak a paraméterek becsléséhez használt mérés útján nyert adatsorok, hanem a szabályozó működése során felhasznált adatok is zajjal terheltek.

Az általánosan használt PID szabályozás a tipikusan paraméterváltozásra érzékeny szabályozók közé tartozik. Ez többek között abban mutatkozik meg, hogy a pozícionálás pontossága nagymértékben függ a mozgatott tömegtől, a dugattyú pozíciójától, de még a tápnyomás változásától is. A digitális technika fejlődésével nemlineáris, adaptív, illetve egyéb robosztus szabályozási algoritmusok is elterjedtek, melyek a szervopneumatikus szabályozásokban is hatékonyan alkalmazhatóak [18.2.] .

Az alábbi ábrákon különböző paraméterű digitális PID szabályozókkal végzett mérések eredményei láthatók, az egyszerű összehasonlíthatóság végett minden paraméterhez kirajzoltatva a pozíciót, a beavatkozó jelet és a hibajelet. A hibajelek kinagyított ábráin jól nyomon követhetőek a beállások pontosságai, a legpontosabbnak vélt görbe értékének feltüntetésével.

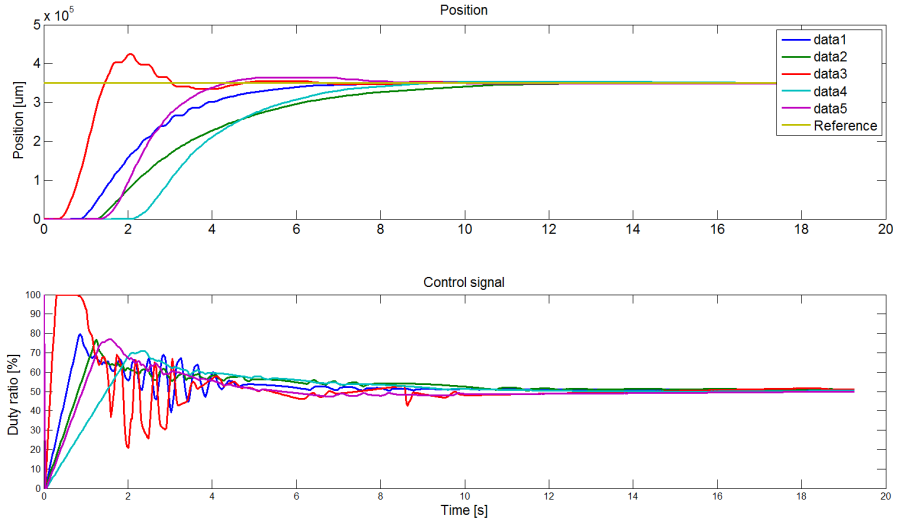
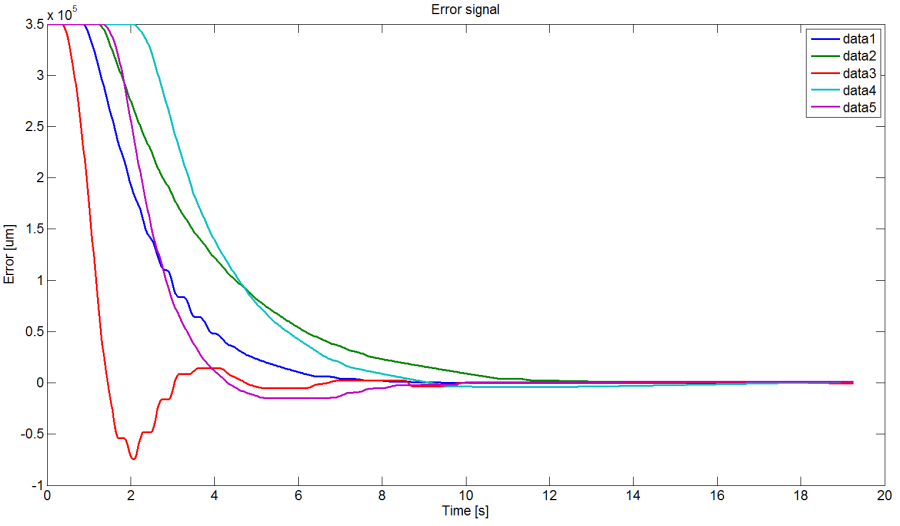
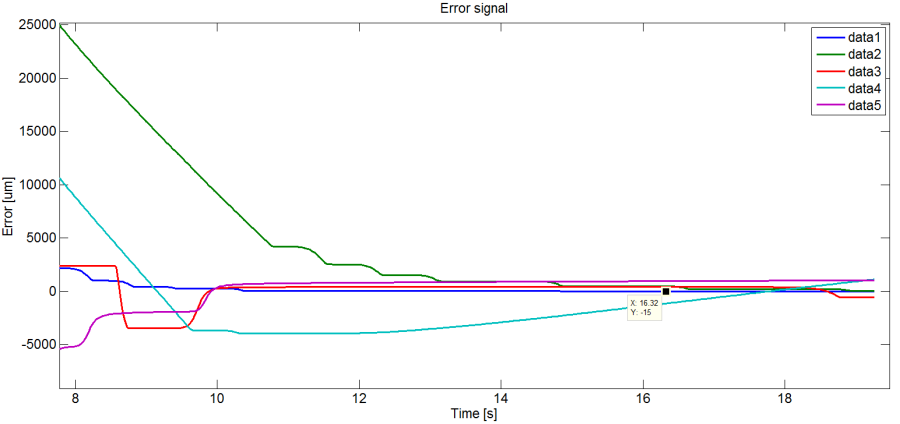
A (18.1. ábra – 18.3. ábra) ábrák eredményét összefoglalva dominánsan kitűnik, hogy az I tag (integráló tag időállandója) növelésével lassul a rendszer és a maradó hiba is lassabban szűnik meg, igaz az aperiodikus jelleg is csökken. A D tag (deriváló tag időállandója) növelésével, ezzel ellentétben, gyorsabb működést érhetünk el. A P (arányos) tag növelésének is gyorsul a beállás, mely továbbá a beállási pontosságot is növeli. Ezzel együtt a szabályozó paraméterei csak szűk tartományban változtathatók, megtalálva a kompromisszumot a fejezetrész elején említett egymásnak ellentmondó szempontokat szem előtt tartva. A további vizsgálat, paraméter változtatások eredményeképpen javul a dinamika, viszont most már szemmel láthatóan megjelenik a Coulomb súrlódás okozta akadozó csúszás hatása is.

 

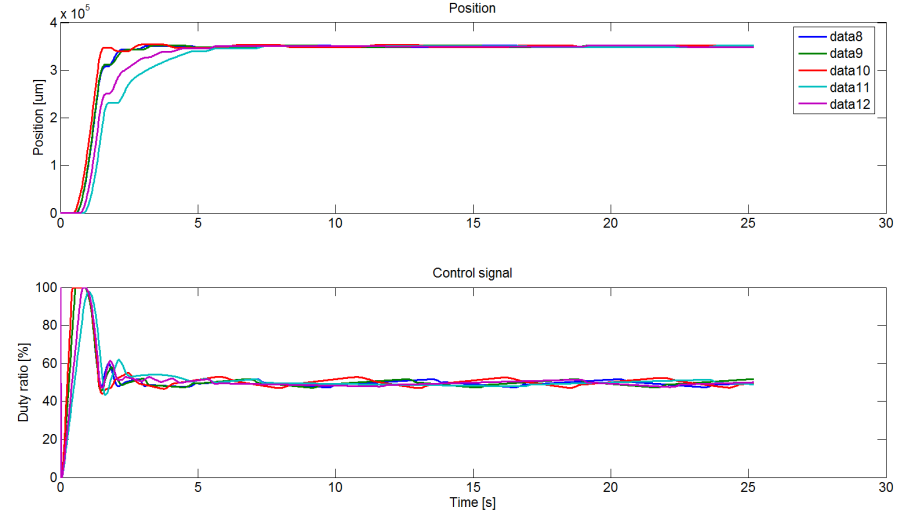
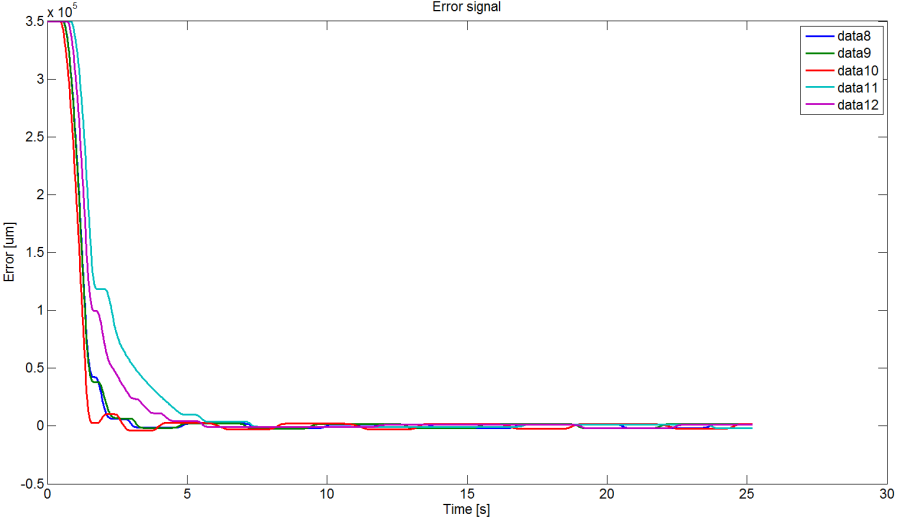
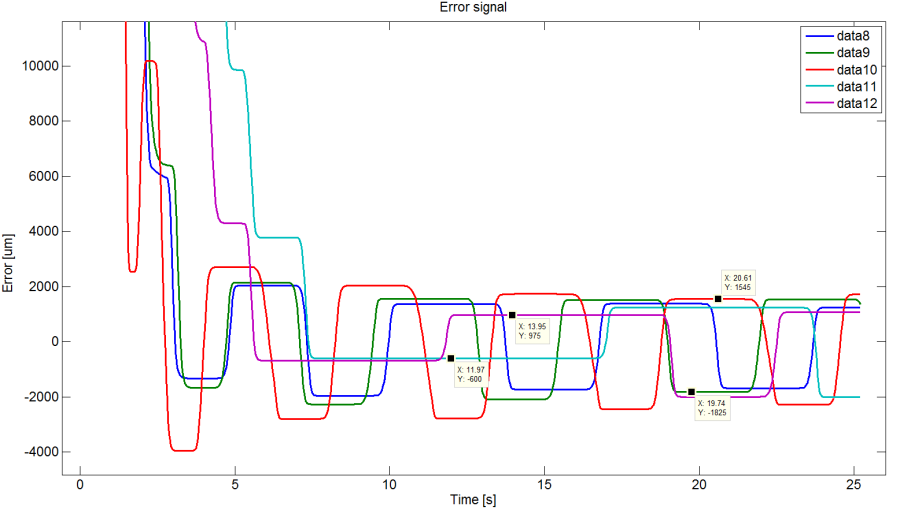
A működés szempontjából optimális eredményeket a (Táblázat 18.2) táblázatban szereplő paraméterekkel lehet elérni, azonban ezeknél a pontos pozícionálás szakaszán az integrátor állandósult hibát eltüntető hatása és a dugattyú betapadása oszcillációhoz vezet. Ez a folyamat úgy értelmezhető, hogy az integrátor a maradó hibát az idő elteltével folyamatosan összegezve -integrálva- növeli a beavatkozó jelet, azaz jelen esetben a kamranyomást. A Coulomb súrlódás miatt a nyomás növekedése nem jár a maradó hiba azonnali csökkenésével, azaz a dugattyú lassú megmozdulásával, hanem az elmozdulás csak akkor következik be, ha a kamrák nyomáskülönbségéből fakadó, dugattyúra ható erő a tapadási súrlódó erő értékénél nagyobb nem lesz. Mivel a haladás során fellépő súrlódó erő a tapadási súrlódó erő értékénél kisebb, ez azzal jár, hogy a dugattyú nem az alapjel által meghatározott pozícióban fog megállni, hanem azon túlszaladva–ezúttal a kívánt pozíciót tekintve azzal ellentétes oldalon- áll meg folyamatos oszcillációt okozva.

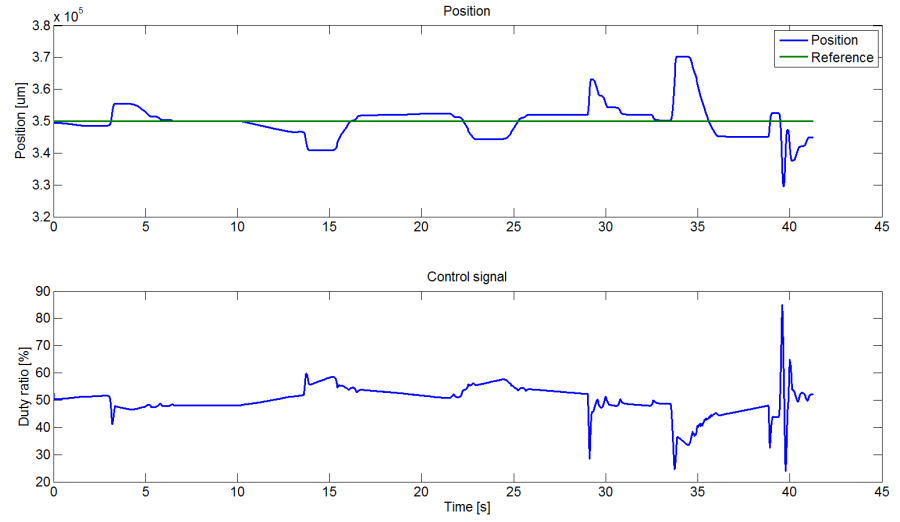
A szabályozások másik fontos paramétere, amivel jellemezhetők, a zavarérzékenységük és a terhelésváltozás kompenzáló képességük. Megvizsgálva a PID szabályozó ezen képességét, az eredmények alapján a változást ugyan képes kompenzálni, azonban ez időbe telik, ami jelentős pozícióból történő kimozdulást is eredményezhet.