4. fejezet - Egyszerű példák hálózati és impedancia módszer alkalmazására
- 4.1. Torziós tengely és tárcsa dinamikai modelljei keresztváltozó forrással
- 4.2. Torziós tengely és tárcsa dinamikai modelljei különböző változatokban
- 4.3. Állapottér modell formáinak létrehozása
- 4.4. Impedancia módszer MK meghatározására
- 4.5. Forrás egyenérték számítása
- 4.6. Szuperpozíció elvének alkalmazása több forrás esetén
- Szakirodalom
A bemutató jellegű feladatokat didaktikai szempontok alapján tettük sorrendbe. Kezdetben, kevésbé összetett példákon a források, a transzformátor típusú átalakító és a rendszám, valamint a lineárisan független egyenletek száma közötti kapcsolatokat szemléltetjük. Ezt követően, vegyes típusú rendszerek vizsgálatát energia átalakító alkalmazásával mutatjuk be. Tekintettel arra, hogy gépészeti alapról indul ki a mechatronika ismeretanyagának elsajátítása, mechanikai forgó rendszerek vizsgálatával kezdjük a módszerek bemutatását. A vizsgált rendszerek természetükből adódóan olyanok, hogy lineáris rendszeregyenlettel írhatók le, de persze ennek nem feltétlenül állandóak az együtthatói. A mechatronikai forgó rendszerek túlnyomó többsége esetében olyan tehetetlenségi nyomatékokat kell modellezni, amelyek kifejezetten kiegyensúlyozottak, ezért értékük forgás közben állandó. Ilyenek a különféle motorok forgórészei, a tengelyek és a tengelyekre szerelt tárcsák, alkatrészek többsége. Az ilyen rendszerek esetében indokolt a hálózati, vagy impedancia módszerek alkalmazása. Ha a torziós rugalmasságok szögfüggését, vagy a csillapítások szögsebesség függését is figyelembe kívánjuk venni, ennek a rendszeregyenlet felírása után nincsen semmi akadálya, a kiindulásként állandónak vett paramétereket helyettesítjük a megfelelő függvénnyel.
Figyelem! A kanonikus változók jelölése a (Táblázat 3.1) táblázatában látható. Minden további fejezetben ezt a jelölési módot alkalmazzuk. Ha mód van rá, akkor kisbetűvel az időbeli változót, nagybetűvel pedig ennek Laplace transzformáltját jelöljük. Vannak természetesen kivételek, ha az adott kis, vagy nagybetű hagyományosan mást szimbolizál. Egy-két példát kiragadva azonnal érthetővé válik a probléma. A mechatronikában a szögsebességet mindkét tartományban nagy omegával (Ω) jelöljük, mert a kis omega (ω) a villamosságtanban és az automatikában a körfrekvenciát jelenti. Továbbá nem jelölhetjük kis m-mel az időfüggő forgatónyomatékot, mert „m” hagyományosan a tömeget jelöli.
4.1. Torziós tengely és tárcsa dinamikai modelljei keresztváltozó forrással
Az első példa igen egyszerű, két tárolós (másodrendű) rendszer. Az irányítástechnikában ezt a tagot PT2-vel jelölik (két tárolós, arányos tag). Ezen a példán ugyanakkor be fogjuk mutatni mindhárom matematikai modellt, az állapottér modell esetében ráadásul kétféle változatot is.
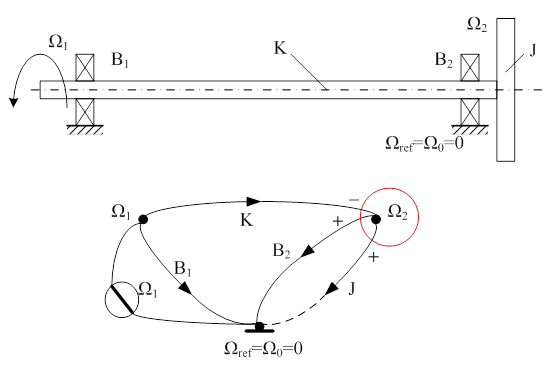
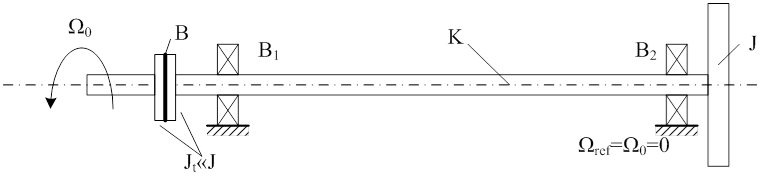
Az ábrán egy viszonylag hosszú, elcsavarodásra képes tengely baloldali végén szögsebesség forrást látunk, amely például egy DC motor és a hozzá kapcsolt nagy módosítású hajtómű kimenetét jelképezheti. A tengely másik végén egy szíjtárcsa látható, amely a továbbiakban a forgó mozgást alakítja át egyenes vonalú mozgássá.
Ezt a váltót még nem vizsgáljuk a példában, erre később kerül sor, mert ebben a fejezetben, egyszerű eseteken (max. másodrendű rendszereken) mutatjuk be és hasonlítjuk össze a módszereket. A tengely forgását két végén gördülőcsapággyal biztosítjuk.
A gráf megszerkesztése a független keresztváltozók (csomópontok) kijelölésével kezdődik. Minthogy az irányított gráf élek mellett az adott elem paramétere van feltüntetve, világos, hogy ez az ábrázolási mód az időtartományban érvényes. Esetünkben 3 ilyen csomópont van, a tengely két csapágyazásánál és a referenciánál, amelynek szögsebesség értéke legyen zérus Ω0=0. A forrás keresztváltozó, ezért az első csomóponthoz rendelt az Ω1 szögsebesség a referenciához viszonyítottan ismert, előírt érték, hiszen ez a hajtómű kimenete. Az Ω1 forrással párhuzamosan kapcsolt B1 csillapítás (csapágy) nem játszik szerepet, mert a keresztváltozó értéke rá van „kényszerítve”. A három csomóponti változó közül csak egyetlen ismeretlen, az Ω2. Ezt az egyenlet szám csökkenést jeleztük a csomóponti és hurok egyenletek számával foglalkozó fejezetben. Nem lehet tehát azt a gráf szabályt a műszaki példákban gondolkodás nélkül alkalmazni, miszerint „a csomópontok száma mínusz egy=lineárisan független csomóponti egyenletek száma”.
Legyen keresett az Ω2 keresztváltozó, azaz a tárcsa szögsebessége. Tehát a fentebb leírtak miatt felírjuk Ω2 csomópontra a csomóponti egyenletet.
Minden csomópontra, illetve szelvényre igaz, hogy az átmenő változók előjelhelyes összege zérus. Az általános átmenő változót célszerűen Φ-vel jelöljük, a példában ez a forgatónyomaték:
Az előjelek „önkényesek”, de a logikát a teljes gráf minden csomópontjára érvényesíteni kell. Azaz, ha a kifelé mutató irányított gráf élek előjelét pozitívnak választottuk, akkor a befelé mutatóké csak negatív lehet. Nincs akadálya annak sem, hogy egy csomópontba csak befelé, vagy csak kifelé mutassanak az irányított élek, de a kész rendszeregyenleten látni fogjuk, hogy az elgondolásunk nem volt helyes. Az irányítottság - a termikus rendszerek esetét kivéve - nem jelenti azt, hogy az átmenő változók csakis a nyíllal kijelölt irányba „folyhatnak” Ellenkezőleg. Az előjelek csak egy pillanatnyi, feltételezett állapotot rögzítenek, és lehetővé teszik az egyenletrendszer felírását.
A csomóponti egyenletbe behelyettesítjük a passzív elemek fizikai egyenleteit:
Ebben az esetben az egyenlet differenciálásával jutunk a rendszeregyenlethez, és Laplace transzformálás után az átviteli függvényhez, miközben „K” leosztásával a másodrendű rendszerekre jellemző alakot igyekszünk létrehozni:
Ha, amint a fejezet elején jeleztük, a paraméterek értékei nem állandóak, akkor a következő lépésben lehetőség nyílik a megfelelő függvények beírására.
Ettől kezdve azonban már csak digitális számítógépes szimuláció révén ismerhetjük meg a kimenőjel időbeli viselkedését.
Laplace transzformálás útján juthatunk az átviteli függvényhez:
Az átviteli függvény előállítása nem öncélú. A hagyományos szabályozókörök stabilitás vizsgálatai (zárt és felnyitott körökre vonatkozóak egyaránt) ezen a rendszeregyenlet formán nyugszanak.
A frekvencia átviteli függvényt (frekvencia menetet) az s=jω helyettesítés után kapjuk:
A függvényből abszolút érték előállítása után a logaritmus képzésével és 20-as faktorral való szorzással előállítható a Bode diagram amplitúdó „menete”, amelynek dimenziója a „dB” (decibel), az Arc képzés révén pedig a fázis „menet”:
Rendszeregyenlet nem csupán a differenciálegyenlet és az átviteli függvény lehet, hanem az állapottér modell is. Ez utóbbi forma – mint tudjuk – a modern szabályozástechnika alapja, és a digitális számítógépes szimulációk forrásnyelve is. Adott rendszer állapottér modellje többféle módon előállítható. Ha az n-ed rendű differenciálegyenletből, vagy az átviteli függvényből indulunk ki, akkor az állapottér modell (ÁTM) kanonikus alakját kapjuk. Ez a forma kedvező, ha az állapotszabályozás stabilitását kell beállítani, ugyanakkor nem feltétlenül vezet olyan ÁTM-hez, amelyben minden állapotjelző valós, és mérhető is. Ebben a mintapéldában ez még nem jelentkezik problémaként, hiszen a két állapotjelző Ω2 és ε2 (szögsebesség és szöggyorsulás). De, gondolatban emeljük csak meg a differenciálegyenlet rendszámát eggyel, és azonnal látni fogjuk, hogy a szöggyorsulás deriváltja már nem valós állapotjelző, és ennek folytán nem is mérhető.
Kanonikus ÁTM alak:
Az állapotjelzők nemzetközileg elfogadott jelölését alkalmazva átalakítjuk a differenciálegyenletet:
Ha „K” és „B” paraméterek nem állandóak, akkor a két elsőrendű differenciálegyenlet (un. Cauchy-féle normál alak) számítógépes szimulációval oldható meg. Ha a paraméterek konstansak, akkor az ÁTM mátrixos alakba írható:
A szokásos jelölésekkel:
Ha az állapottér modellt nem a kanonikus alakban kívánjuk előállítani, akkor a fizikai és mérhető állapotjelzőket, amelyek átmenő, vagy keresztváltozók, az integro-differenciál egyenletből kiindulva kell létrehozni:
A torziós rugómerevséggel rendelkező tengely energia állapotát az MK átmenő változóval, mint állapotjelzővel írjuk le. A tárcsa energia állapotának leírására pedig Ω2 keresztváltozó szolgál. Ezek az állapotjelzők fizikai „tartalommal” bírnak, és mérésük megfelelő szenzorokkal megoldott.
Így tehát egy lehetséges másik ÁTM az alábbi módon definiálható:
Fontos észrevenni, hogy mindkét ÁTM rendszermátrixában a főátló csak zérust, vagy negatív előjelű tagot tartalmaz. Ez egy passzív, nem visszacsatolt rendszer esetében elvárható is, hiszen ez a feltétele a stabilitásnak.
A modellezési módszerek által adható kép akkor válik teljessé, ha ezen a feladaton bemutatjuk az impedancia módszert is. A gráf egyszerűen átalakítható impedancia hálózattá, hiszen a gráfok a hálózatok leírására szolgálnak. Az egyes éleken téglalapok jelképezik az impedanciákat, az idő tartományban szokásos irányított gráf élek helyett. Paraméter helyett minden elemnél már az impedanciát kell feltüntetni, az ábrázolás operátor tartományban történik.
Az ábra baloldalán a rendszer impedancia hálózata látható, amelynél a bemeneti oldalon elhelyezkedő csapágy impedanciáját már figyelmen kívül hagytuk. A jobboldali képen a hálózat már szét van választva passzív és aktív részre. A passzív rész itt két párhuzamos impedancia eredője, mert közös keresztváltozójuk a keresett Ω2.
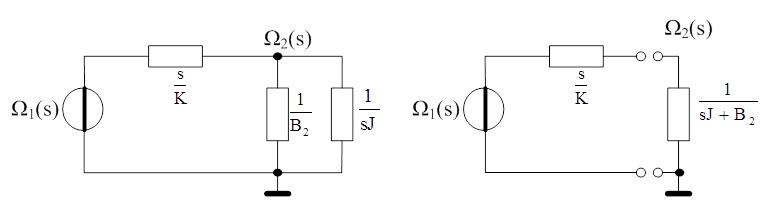
Az aktív rész belső impedanciája s/K, az új forrás változatlanul Ω1, mert terheletlen kapcsokon mérhető keresztváltozó érték (üresjárati) is ez. Keresztváltozó keresett, és keresztváltozó a forrás. Ebben az esetben az átviteli függvényt közvetlenül a keresztváltozó osztó adja:
Az impedancia módszer ebben az esetben - minden kétséget kizáróan - néhány lépésben azonnal eredményhez vezetett. A villamosmérnöki gyakorlatban ezért kedvelt módszer, de, amint látható, eredményesen lehet mechanikai rendszerek, sőt minden technikai rendszer esetében is alkalmazni.
4.2. Torziós tengely és tárcsa dinamikai modelljei különböző változatokban
Az első példában bemutatott, igen egyszerű, két tárolós (másodrendű) rendszert célszerű bemutatási céllal tovább vizsgálni. Elsőként bemutatjuk, hogy elegendő csupán a forrás típusát megváltoztatni, azonnal megváltozik a rendszer és így a gráf is. Legyen a példában a forrás az Mbe forgatónyomaték. A B1 csapágycsillapítás immár nem mellőzhető, hiszen az Ω1 keresztváltozóhoz tartozó csomópontban a nyomatékforrás által szolgáltatott átmenő változó megoszlik két részre: egyrészt arra fordítódik, hogy „leküzdje” a csapágy súrlódó nyomatékát, másrészt továbbhalad a torziós tengelyen a tárcsa felé. Ebből adódóan más lesz a lineárisan független csomóponti egyenletek száma is, mert két „valós” csomópont jön létre.
Tekintettel arra, hogy az előző feladatban a csomóponti módszert már szemléltettük, ebben a feladatban a hurok módszert mutatjuk be, és célszerűen átmenő változóra keressük a rendszeregyenletet. Legyen ez a változó az MK torziós nyomaték, mert erre a változóra később az impedancia módszer alkalmazása eléggé tanulságos lesz.
Az elektrotechnikában újabban, az átmenő változó forrás esetében használatos jelölés mellé egy nyilat tettünk. Ez a nyíl a hagyományos jelölési módnál a forrást jelképező körben helyezkedik el. Átmenő változó forrásokat ésszerűen, minden esetben a rendszer olyan csomópontjai felé kell irányítani, amelyekhez rendelt keresztváltozó nem a referencia. A gráf élek irányítottságán nem változtattunk. A hurok-felvétel „kaszkád”, (egymás után következő) sorrendben történt. Ez egy célszerű forma, mert szabályos lesz az impedancia mátrix, könnyen ellenőrizhető, nincs-e hiba a felírásban.
Nagyon fontos kihangsúlyozni, hogy a gráfon látható hurok kijelölés nem kedvező, ha B1, vagy B2 jelű csillapítók nyomatékát kellene meghatároznunk. Ebben az esetben a keresett változó két nyomaték különbségeként adódik, több a számítási munka. Ahogy korábban már leírtuk, úgy kell kijelölni a hurkokat, hogy azt az elemet, amelyen egy átmenő változót keresünk, csak egy hurok érintsen.
Úgy határozunk, hogy a csomópontokból kifelé irányuló élek legyenek pozitívak. A gráfon látszólag három hurok látható, de az első hurok változója nem ismeretlen, ez a forrás, tehát ide nem írunk fel hurokegyenletet. Annál inkább nem lehetséges ez, mert Mbe ismert, és ez nem keresztváltozó.
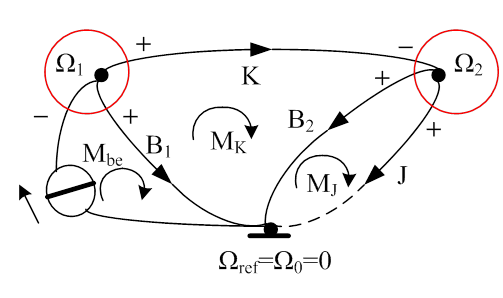
Ismert, hogy egy hurok körüljárása során, az elemeken megjelenő keresztváltozók előjeles összege zérust kell, hogy adjon. Az általános keresztváltozót χ-vel (görög chi) jelöljük.
Ennek megfelelően a két hurokegyenlet az alábbi formában jelenik meg:
Behelyettesítjük a fizikai egyenleteket, és előáll a szimultán differenciálegyenlet rendszer:
Amennyiben az állapottér modellt kell felírni, a legjobb, ha a szimultán differenciálegyenleteket felhasználva vezetjük be az állapotjelzőket. Ezek az energiatárolóknak megfelelően az alábbiak lehetnek:
Tehát a torziós tengelyen fellépő nyomaték és a tárcsa szögsebessége. Az állapottér modellre még visszatérünk, elsőként az átviteli függvényt határozzuk meg.
Ha az átviteli függvény, vagy a differenciálegyenlet meghatározása a cél, akkor a Laplace transzformálást követően, a szimultán differenciálegyenleteket mátrix-vektor egyenletbe foglaljuk össze:
A mátrix minden eleme impedancia, ezért impedancia mátrixnak szokás nevezni. Az egyenlet tulajdonképpen az általánosított Ohm törvény:
A mátrixban szabályosság fedezhető fel, köszönhetően a csomóponti egyenletek célszerű felvételének. A főátló minden eleme pozitív, és egy-egy ismeretlen változót megtestesítő csomópontot érintő impedanciákat foglalja magába. A főátlóra szimmetrikus a mátrix, és elemei negatívak. Az átló elemei azoknak az impedanciáknak felelnek meg, amelyek a hurokváltozóknak megfeleltetett hurkok közös elemei. A jobboldalon jogosan jelenítettünk meg keresztváltozó vektort, ugyanis a Thevenin ekvivalencia szerint az átmenő változó forrás és a mellette párhuzamosan kapcsolt impedancia egyenértéke keresztváltozó forrás lenne:
A következő lépés előtt eldöntjük, hogy mindkét változót (forgatónyomatékokat), vagy csupán az egyiket keressük? Ha mindkettőt, akkor az impedancia mátrixot invertálni kell:
Az inverz mátrix kiszámítása során meg kell határozni az eredeti mátrix adjungáltját és a determinánsát. Ez utóbbi művelet az oka annak, hogy a hálózatelmélet bevezetése során kikötöttük, hogy csak lineárisan független egyenletek írhatóak fel. Ellenkező esetben a determináns zérus lesz. Fokozottan ügyeljünk arra, hogy adjungált mátrix kiszámítása során az aldeterminánsok képzése után még egy sor-oszlop cserét is végre kell hajtani.
Amennyiben csak egy változó, esetünkben a torziós nyomaték MK(s) keresett, célszerű a Cramer-szabályt alkalmazni. A számlálóban a determináns MK-hoz tartozó, első oszlopát kell helyettesíteni az egyenlet jobb oldalán található bemeneti vektorral:
Közös nevezőre hozzuk az átviteli függvény nevezőjét, és az „s” operátortól független kifejezéssel beosztjuk az átviteli függvény számlálóját és nevezőjét is. Érdemes ugyanis az átviteli függvény nevezőjét a szabályozástechnikai gyakorlatban alkalmazott formára alakítani, azaz az átviteli függvény nevezőjében az „s” operátortól független tag legyen =1. Ez a célszerű alak, mert egyszerű az állandósult állapot meghatározása. A Laplace transzformáció idevonatkozó szabálya szerint:
A „szabályos” alak létrehozásához általában be kell osztani a kapott nevező s-től független kifejezésével az átviteli függvény számlálóját és nevezőjét is. Tekintettel arra, hogy az „s” operátor dimenziója [r/s] (radián/secundum), mellette szorzóként kizárólag [s] (secundum=másodperc) dimenziót adó kifejezés állhat, és ebben az értelemben tovább, az operátor hatványainak megfelelően [sn]. A „radián” dimenzió nélküli.
ahol
Minden számításnál, különösképpen a bonyolultabb kifejezések esetében „kötelező” elvégezni ezt a dimenzió vizsgálatot. Hibás eredmény, vagy bármely hibás köztes lépés esetén azonnal láthatóvá válik a hiba, ha a paraméterek dimenzióit SI mértékegységekben behelyettesítjük. Ezt a „normálást” a korábbi átviteli függvényeken is elvégeztük, a fenti eset már kissé bonyolultabb, ezért látványosabb az átalakítás. A forgatónyomatékok között felírt átviteli függvény dimenzió nélküli, hiszen azonos dimenziójú változók között teremt kapcsolatot.
Az átviteli függvényből az is leolvasható, hogy állandósult állapotban, tehát tranziens folyamatok lecsengése után, a csapágyak csillapításának aránya határozza meg a tengelyen megjelenő torziós nyomatékot, ahol természetesen a forrástól távolabbi disszipatív elem a mérvadó.
4.3. Állapottér modell formáinak létrehozása
Az állapottér modell mindkét változatának meghatározása is tanulságos lépéseket tartalmaz. Egyrészt azért, mert a valós állapotjelzőkkel felírt változat eredménye nem egy lépésben adódik a szimultán differenciálegyenlet rendszerből. Másrészt pedig azért, mert az átviteli függvényből, visszavezetéssel adódó un. „normál” állapottér alak előállítása sem egyszerű, hiszen az átviteli függvény számlálójában van „s” operátor.
Nézzük először a valós (kanonikus) állapotjelzőkkel adódó formát, amelyek a feladat bevezetőjében bemutatott módon, az energiatárolóknak megfelelően az alábbiak lehetnek:
A probléma megértése érdekében megismételjük a szimultán differenciálegyenleteket:
Az első egyenletből MK-ra, a másodikból Ω2 -re írjuk fel az elsőrendű differenciálegyenletet. Látható, hogy mindkét egyenletben MJ változót ki kell fejezni a két állapotjelző segítségével, mert ezek „idegen testek” az állapottér modellben. Elsőként a második egyenletből algebrai egyenletet formálunk, és kifejezzük MJ-t úgy, hogy az integrál kifejezést helyettesítjük az eredeti változóval, hiszen az állapotegyenlet integrált nem tartalmazhat. Az integrál minden esetben maga az egyik állapotjelző lesz, azaz kereszt-vagy átmenő változó. Ez a hálózati módszer korábban már jelzett, nagy előnye:
A kapott MJ változót behelyettesítjük az első szimultán differenciálegyenletbe, és rendezzük az MK állapotjelző deriváltjára.
Az állapottér modell második (több ilyen típusú energiatároló esetében i-edik) egyenlete ilyen típusú feladatoknál az integrál kifejezésből (kifejezésekből) adódik.
Mivel MJ változó nem szerepelhet az egyenletben, ezért a korábban már felhasznált összefüggést ismételten alkalmaznunk kell az eliminálására:
Befejezésül felírjuk mátrixos alakban az állapottér modell főegyenletét valós, mérhető állapotjelzőkkel.
Az így kapott változatban nincs szükség segédegyenletre, ha csak az állapotjelzőket tekintjük kimeneteknek.
Nem így az átviteli függvényből visszavezethető forma esetében. Itt két probléma jelentkezik. Az első az, hogy az egyik állapotjelző fiktív változó, azaz nem fizikai mennyiség lesz. A második pedig az, hogy az átviteli függvényből felírt, Laplace transzformált egyenlet jobb oldalán a visszatranszformálás után a bemenőjel deriváltját kapjuk. Ezt azért kell kerülni, mert nem minden jeltípus deriváltja állítható elő nehézségek nélkül, márpedig az állapottér modellnek általános érvényűnek kell lennie. A gerjesztés (bemenet) deriváltként nem maradhat a modellben.
ahol helyettesítést alkalmaztunk.
Nem folytatjuk az inverz Laplace transzformációval, mert látható, hogy az eredmény zsákutcához vezetne. Jobb oldalon ugyanis idő tartományban megjelenne a gerjesztés deriváltja.
Helyette formális átalakítást végzünk el az átviteli függvényen, olyat, amely eredményeként egy, az új állapotjelzőket, valamint a kimenetet adó részt szét lehet választani szorzat formájában. Két átviteli függvényt kapunk, amelyek közül a második nyilvánvalóan nem „igazi” átviteli függvény, hiszen a számlálóban az operátor fokszáma magasabb, mint a nevezőben. E problémától a cél érdekében ezúttal eltekintünk:
Az első átviteli függvényből az állapottér modell főegyenlete, míg a másodikból a kimeneti, vagy segédegyenlet adódik.
Az átviteli függvényeket egyenlet formájára rendezzük, majd beszorzás után végrehajtjuk az inverz Laplace transzformálást:
Bevezetjük a „mesterséges” állapotjelzőket, feltételezve, hogy a deriváltak léteznek:
Megjegyezzük, hogy a „valóságban” x1=MK, és x2=dMK/dt, és ez utóbbi nem mérhető fizikai mennyiség. Ezért a jelző: „mesterséges”. Ez a függvény célszerűen numerikus úton (az esetleges hibákat tudomásul véve) közelíthető. Ugyanakkor arra is felhívtuk korábban a figyelmet, hogy az állapottér modell „normál” alakjának felhasználásával, sokkal egyszerűbb az állapotszabályozás stabilitásának beállítása, számítása.
Általános formában a nevezőben „an”, a számlálóban „bm” együtthatókat alkalmazunk:
A második átviteli függvényből az állapottér modell kimeneti egyenlete lesz, a keresett mennyiséget egy kimenet (x2) formájában kapjuk:
Mátrixos alakban felírva:
A főegyenletnek fent látható formáját nevezi a szakirodalom „normál” alaknak, és mint jeleztük, alkalmazása az állapotszabályozások esetében célszerű.
Az állapottér modell főegyenletének homogén megoldását a későbbiekben bemutatjuk két változatban, a fenti példához hasonló feladaton. A megoldáshoz azért választunk újabb feladatot, hogy a modellezés gyakorlására is lehetőség legyen.
A feladat megoldása a passzív rész meghatározása miatt impedancia módszerrel is igen tanulságos.
4.4. Impedancia módszer MK meghatározására
A következő ábrán a feladat impedancia hálózatát látjuk. Első lépésben ki kell jelölnünk a keresett változót, jelen esetben ez az összehasonlítás kedvéért ugyancsak az MK torziós nyomaték lesz. Az impedancia hálózatot a keresett változónak alárendelve választjuk passzív és aktív részre. Vigyázni kell, mert a passzív rész nem csupán a tengely rugómerevségéből számított impedancia, hanem mindazon elemek, amelyek a szétválasztás után keletkezett kapcsok felől nézve „látszik”. Így tehát a rugómerevség impedanciájával sorosan kapcsolva figyelembe kell venni egy további eredő impedanciát is. Ez a tárcsa tehetetlenségi nyomatéka és a vele párhuzamosan kapcsolt csillapítás (csapágysúrlódás modellezése) impedanciáinak eredője.
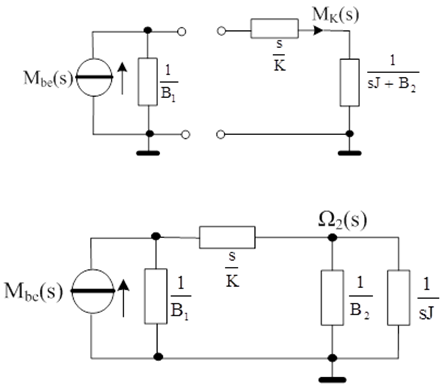
Az aktív rész egyszerű Norton alak.
A terhelő impedancia ismeretében, az átmenő változó osztó („áramosztó”) segítségével közvetlenül felírható a keresett MK(s)/Mbe(s) átviteli függvény.
Az irányítástechnikában szokásos átalakítás után természetesen ugyanazt az átviteli függvényt kaptuk, amelyet a mátrix-vektor egyenletek kifejtésével:
4.5. Forrás egyenérték számítása
Ha az átmenő változó forrással gerjesztett forgó mechanikai rendszert annyiban módosítjuk, hogy az Ω2(s)/Mbe(s) átviteli függvényt keressük, akkor be tudjuk mutatni a forrás egyenérték számítást is.
Majd ezt követően, az eredeti forgó mechanikai rendszerbe beépítünk egy csúszó tengelykapcsolót, és az így átalakított rendszeren bemutatjuk az aktív rész új forrás értékének meghatározását, ami figyelemre méltó lépéseket tartalmaz.
Ha Ω2 keresztváltozó keresett Mbe átmenő változó forrás hatására, akkor az osztó szabályok közvetlenül nem alkalmazhatóak. Ebben az esetben keresztváltozó osztó felírása lenne a legegyszerűbb forma. Ehhez át kell alakítanunk az aktív részt. Azt kell megvizsgálni, hogy mi az adott aktív rész Thevenin ekvivalense. A passzív rész a tárcsa és a csapágy impedanciájának párhuzamos kapcsolása.
A következő ábrán, bal oldalon látható az aktív rész, amelynek egyenértékű kapcsolását keressük. Az új, keresztváltozó forrás értéke az aktív rész terheletlen kapcsain (üresjárat) megjelenő keresztváltozó érték. Ebben az esetben az s/K impedancia nem játszik szerepet, mert terheletlenül nincsen elcsavarodás, így nincs torziós nyomaték, és nincs a két tengelyvég között szögsebesség különbség sem. Analógiaként képzeljünk el egy áramforrást, amellyel párhuzamosan egy ellenállás van kacsolva, és ehhez egy olyan induktivitás csatlakozik, amelynek egyik vége szabad. Áram nem folyik, így feszültségesés sem jöhet létre.
Az ekvivalens forrás értéke Ohm törvényével adódik:
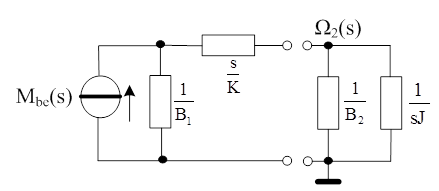
Az ekvivalens, új keresztváltozó forrás belső ellenállását kell következő lépésben meghatároznunk. Ezt a belső ellenállást az aktív rész kapcsai felől „benézve” kell kiszámítani. Tekintettel arra, hogy az átmenő változó forrás saját belső ellenállása elméletben végtelen nagy, szakadással helyettesítjük. Az ekvivalens forrás belső impedanciája ennél fogva a két impedancia soros eredője:
A keresett átviteli függvény keresztváltozó osztó segítségével most már megadható:
Az átviteli függvény azt mutatja, hogy stacionárius állapotban, tehát bekapcsolással járó tranziens folyamat lezajlása után a szögsebességet a két csapágy fogja „beállítani”.
Annak bemutatására, hogy az aktív rész új forrása azonos típusú források esetében is igényelhet egy-két számítási lépést, átalakítottuk a vizsgált rendszert. A tengelyt baloldalon meghosszabbítottuk, és az ismeretek egyidejű bővítése céljából beiktattunk egy elhanyagolható tehetetlenségi nyomatékkal (csak a példában, és nem a valóságban) rendelkező, szabályozható csúszással rendelkező tengelykapcsolót. Ez a különleges tengelykapcsoló csökkenteni képes a motor által okozott torziós lengéseket a hajtóművön, de a forgatónyomatékot maradéktalanul átviszi, hiszen látjuk, hogy a gráfban nincsen elágazás. Ilyen típusú hidrodinamikus tengelykapcsoló például a „Föttinger Kupplung”, amely szabályozható csúszást képes biztosítani. Ilyen jellegű tengelykapcsolókról a Braess és Seiffert [4.1.] gépjárművek konstrukciós kérdéseivel foglalkozó művében olvashatunk bővebben.
A szabályozható csúszást a „B” csillapítási tényezővel modellezzük.
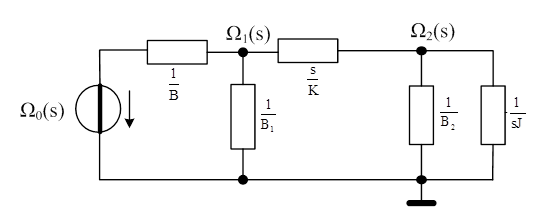
A következő ábra az impedancia hálózatot mutatja. A passzív rész a keresett keresztváltozóhoz tartozó két párhuzamos impedancia eredője (tárcsa és B2-es jelű csapágy).
Az átviteli függvény keresztváltozó osztóval adható meg, persze, ehhez ki kell számítani Zb és ΩF(s) értékét. A keresett átviteli függvény:
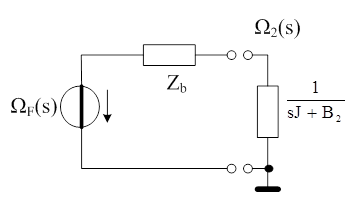
Az aktív rész új ΩF(s) forrása természetesen nem egyezik meg az eredeti kapcsolás Ω0(s) forrásával. Terheletlen állapotban a tengely nem tud megcsavarodni, szögsebesség különbség nem jön létre a két vége között, így nem vesszük figyelembe a számításnál. Az új keresztváltozó forrás ezért egy keresztváltozó osztóval adható meg:
Az új aktív rész belső ellenállását a szabad kapcsok „felől” a hálózatba „tekintve” számítjuk ki, miközben tudjuk, hogy Ω0(s) saját belső ellenállása zérushoz tart, ezért rövidzárként helyettesíthető:
Behelyettesítve a keresztváltozó osztó képletébe, az alábbi formát kapjuk:
Végül a szabályozástechnikai átviteli függvényformára törekedve alakítjuk át a törtet:
Könnyen leolvasható az átviteli függvényből az a műszaki szempontból természetes állapot, hogy amennyiben elhanyagolható mértékű a tengelykapcsoló csúszása, akkor állandósult állapotban a tengely végén lévő tárcsa szögsebessége megegyezik a forrás (bemenet) szögsebességével.
4.6. Szuperpozíció elvének alkalmazása több forrás esetén
Már említettük, hogy az impedanciákkal való számolás közepesen bonyolult rendszerekig meggyorsíthatja az eredményhez jutást. Az eddigiekben több esetet megvizsgáltunk, egyedül a szuperpozíció szabályának alkalmazása hiányzik.
A bemutatás érdekében az eredeti faladatot annyiban módosítottuk, hogy a tárcsához fékező nyomatékot rendeltünk hozzá, „-Mt” formában. A negatív előjel arra utal, hogy nem hajtó, hanem fékező nyomatékról van szó. A következő ábrákon látjuk a modellt, és az impedancia hálózatot.
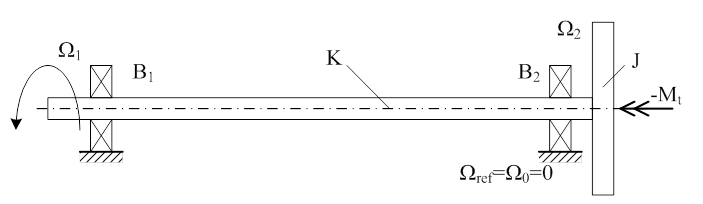
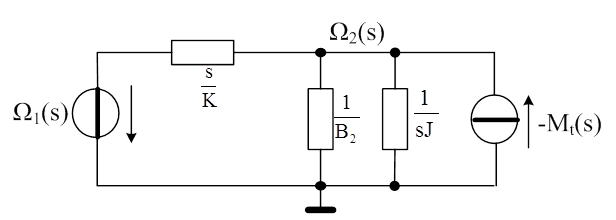
A passzív rész továbbra is a tárcsa tehetetlenségi nyomatéka és a csapágysúrlódás alapján adódó, párhuzamos impedanciák eredője, ezeken, együttesen lép fel a keresett, keresztváltozó kimenet. Természetes, hogy egyrészt a baloldali keresztváltozó forrás értékével, másrészt a fékezőnyomatékkal állítható be a keresett tárcsa-szögsebesség.
A szuperpozíció elve szerint minden forrás hatását külön-külön vizsgáljuk a kérdéses impedancián (eredőn), majd a hatásokat előjel-helyesen összegezzük. Eközben a nem „aktív” forrásra úgy tekintünk, mintha annak saját belső ellenállását „látnánk”. Az Ω1(s) forrás felől nézve a –Mt(s) nyomatékforrás szakadásnak „látszik”, míg a fékező nyomatékforrás felől vizsgálva az Ω1(s) forrás rövidzárként viselkedik.
A hálózatot ennek megfelelően kell „átrajzolni”. Az átviteli függvény felírásához az egyik esetben keresztváltozó osztóra lesz szükség, míg a másik forrás felől „nézve” elegendő egy eredő impedancia számítás és egy Ohm-törvény alkalmazása.

A szuperpozíció elve két forrás esetén a matematika nyelvén megfogalmazva:
A nyomatékforrás felől nézve a következő eredő impedancia látható:
Végül a keresett változó az Ohm törvény alkalmazásával:
Teljesen nyilvánvaló, hogy a két átviteli függvény nevezője nem térhet el egymástól, hiszen ez az adott rendszer dinamikáját meghatározó karakterisztikus polinom. A számláló már más eset, ott az adott gerjesztés (bemenet) hatása figyelhető meg. Ha például adott kezdeti szögsebességgel forog a tárcsa, nincsen Ω1 bemeneti szögsebesség, és a rendszer túlcsillapított, akkor a tárcsa szögsebessége állandó fékezőnyomaték rákapcsolása esetén –lengés nélkül - exponenciális függvényt követve csökken zérusra.
Összefoglalva az előbbieket látjuk, hogy több forrás esetében, a keresett kimenetre, minden forrás hatását külön-külön kell egy-egy átviteli függvénnyel leírni:
Az analízis módszereinek bemutatása után sor kerülhet majd a mechatronikában leggyakrabban előforduló szabályozott szakaszok, illetve szabályozóköri komponensek matematikai modelljeinek bemutatására.
Szakirodalom
[4.1.] Handbuch Kraftfahrzeugtechnik. Vieweg+Teubner Verlag. Wiesbaden . 2011.