3. fejezet - A hálózati módszerek eszköztára
A hálózati módszerek alkalmazásához szükséges ismereteket négy csoportba foglalhatjuk össze:
-
A változók származtatása és definiálása.
-
A passzív elemkészlet koncentrált paraméterű modellezéshez.
-
A források típusainak definiálása.
-
Az energia-átalakítók rendszerezése
3.1. A változók definiálása
A változók származtatását az előző fejezetben mutattuk be, amikor a hálózati módszerek energetikai hátterét taglaltuk. Ezek szerint az intenzív mennyiségeket keresztváltozónak, az extenzív mennyiségek áramát pedig átmenő változónak tekintjük.
A keresztváltozókat és az átmenő változókat több külföldi és hazai szakirodalomban kiemelten kezelik. Fodor György a Lineáris rendszerek analízise című munkájában [3.1.] ezeket a mennyiségeket egyenesen „kanonikus változóknak” nevezi.
3.2. Passzív elemkészlet
3.2.1. Összefoglaló elemtáblázat
A passzív elemkészletet leíró fizikai egyenleteket táblázatosan foglaltuk össze, és célszerűségből megjelenítettük az egyes elemek impedanciáit is. A hálózati módszer alkalmazása szempontjából különösen fontosak azok az összefüggések, amelyek egy-egy passzív elemen, energia-átalakítón a kereszt- és átmenő változók közötti kapcsolatot írják le. Ezek az egyenletek a mechatronika szakon tanulók számára nem jelentenek újdonságot, legfeljebb ezek rendszerezése.
Az impedancia módszer alkalmazása – amely ugyancsak hálózatelméleti alapokon nyugszik – a fentieken túlmenően öt fontos ismeretet feltételez. Az impedancia módszerrel a későbbiekben részletesen foglalkozunk, de a következő táblázatban, amelyben a kereszt- és átmenő változók közötti kapcsolatokat mutatjuk be, a teljesség kedvéért megjelenítjük az egyes passzív elemek impedanciáit is.
Az impedanciával (komplex ellenállás), és reciprok értékével az admittanciával (komplex vezetőképesség) előzetesen annyit kell tudni, hogy a táblázatban látható impedanciákat a fizikai egyenletek definíció szerinti Laplace transzformálása révén kapjuk. Az impedancia az „s” operátor függvénye, definíciója szerint:
Tekintettel arra, hogy s=jω, a leírás olyan rendszerekre alkalmazható, amelyek gerjesztései és válaszjelei Fourier analizálhatóak, azaz harmonikus függvényekkel felépíthetők, csak állandó együtthatókkal rendelkeznek, és lineárisak.
|
Rendszer típus |
Energiatárolás keresztváltozóval |
Energiatárolás átmenő változóval |
Disszipatív elemek |
||||
|---|---|---|---|---|---|---|---|
|
Fizikai egyenlet |
Impedancia |
Fizikai egyenlet |
Impedancia |
Fizikai egyenlet |
Impedancia |
||
|
Mechanikai transzlációs |
|||||||
|
Mechanikai rotációs |
|||||||
|
Villamos |
R |
||||||
|
Fluid |
Folyadékos |
||||||
|
Akusztikai |
|||||||
|
Pneumatikus |
nincs |
nincs |
|||||
|
Termikus |
nincs |
nincs |
|||||
A fenti táblázattal kapcsolatban több fontos megjegyzésre, magyarázatra van szükség:
A mechanikai transzlációs és rotációs rendszerek esetében a keresztváltozók indexében látható „R” betű arra utal, hogy ezek az energia-tárolók keresztváltozói csak a referenciára vonatkoztathatók. Az elemtáblázatban, az akusztikai energiatárolók esetében látható csillagozott jelölés arra utal, hogy az akusztika tudományterületén más fajta elnevezések szokásosak.
Az elemtáblázattal kapcsolatos további magyarázatok az itt következő alfejezetekben találhatók meg.
3.2.2. Mechanikai és villamos rendszerek energiatárolói
A három rendszertípust együtt tárgyaljuk. Három típusról lesz szó, mert a mechanikai egyenes vonalú mozgást végző rendszert el kell választani a forgómozgást végző rendszerektől. Sem a paraméterek, sem pedig a változók nem azonosak. Azt, hogy a két rendszer között merev test esetében jól leírható a kapcsolat, tudjuk. A kapcsolat leírásához ebben az esetben váltókat alkalmazunk. A váltók az energia átalakítók között vannak részletesen ismertetve.
-
Tömeg („tehetetlenség”)
A tömeg a keresztváltozóval (sebesség) tárol energiát . A tömeg esetében a kereszt- és átmenő változó közötti fizikai kapcsolatot a Newton második törvényéből
származtatjuk úgy, hogy a gyorsulás helyére a sebesség deriváltja kerül. Azt, hogy a tömeg a nehézségi erőtérben mozog, a gráf technika segítségével is kifejezzük, mert a tömeg gráf éle kizárólag a referenciához irányítható, és az él alsó felét szaggatott vonallal szokás jelölni. Ez látható például az 5.1. ábra ábrán.
-
Tehetetlenségi nyomaték (forgó mozgást végző merev test forgási tehetetlensége)
A mechatronikában a keresztváltozóval energiát tároló elemeket túlnyomórészt a forgó gépalkatrészek képezik. A tehetetlenségi nyomaték a szögsebességgel tárol energiát. Ezek állandó paraméter értéket képviselnek J=konst, mert a gépalkatrészek kiegyensúlyozására igen nagy gondot fordítanak. Newton törvénye rögzített tengely körül forgó merev testre is kiterjeszthető:
A szöggyorsulás helyére ugyancsak a keresztváltozó, a szögsebesség deriváltja kerül a hálózatelmélet szellemében. Az energia módszernél már jeleztük, hogy azon mechatronikai feladatok esetében, amelyek jellegzetesen nemlineáris rendszerek (pl. fordított inga, segway stb.), a matematikai modell felírásához a hálózati módszer nem alkalmazható. Ugyanakkor állandó „J” paraméterek esetében a hálózati módszer célravezetőbb, mint az energia módszer.
-
Rugómerevség (transzlációs)
A transzlációs mechanikai rendszerekben azon részegységeket, alkatrészeket modellezünk rugómerevségként, amelyek a rugalmas alakváltozás tartományában ér erőterhelés, és az erő-elmozdulás összefüggés lineáris összefüggéssel leírható (Hook-törvény). A „rugómerevség” modell-elemmel nem csak laprugót, vagy tekercsrugót, hanem gépelemeket is modellezünk, hiszen rögzítő csavarok, csapágyak, keretszerkezetek is lehetnek rugómerevségek a modellünkben. A rugalmas elem az átmenő változóval, az erővel tárol energiát. A rugalmas elem alakváltozása nem keresztváltozó, ezért a Hook-féle egyenletben az alakváltozást az alakváltozási sebesség integráltjával helyettesítjük:
Fontos a modellezésben tehát tudni azt, hogy a „rugómerevség” alatt nem csak lemez, vagy tekercsrugó rugómerevségét kell elképzelni. A rugalmas elem lehet fém, és lehet polimer alkatrész is, sőt mágneses és pneumatikus „rugó” is van. Minden esetben elengedhetetlen tudni, hogy a valóságban nem létezik „ideális” rugalmasság, csak az un. Kelvin modell által leírt forma, azaz a rugóval párhuzamosan megjelenik a veszteség is, nincs olyan rugalmas fém, amelynek alakváltozása során ne lépne fel a kristály deformációból származó belső veszteség. A polimerek esetében a precíz modell ennél még sokkal bonyolultabb.
-
Torziós rugómerevség
A transzlációs rugómerevség analógiáját látjuk a torziós rugómerevségben. A torziós rugó ugyancsak az átmenő változóval, a forgatónyomatékkal tárol energiát. Most ugyancsak ne korlátozzuk magunkat a „spirálrugó” modellezésére, habár a nemzetközi szakirodalom a jelölésre éppen egy spirálrugót szokott alkalmazni. Mechatronikai rendszereinkben csaknem minden forgó tengely torziós rugómerevséggel modellezhető, még precízebb a modellünk, ha vele párhuzamosan megjelenik a veszteség (belső csillapítás) is. A fizikai egyenlet a transzlációs analógiája, mert a torziós elem két vége közötti relatív elcsavarodás helyett a szögsebesség (keresztváltozó) integráltja jelenik meg:
-
Villamos kapacitás
A villamos rendszerekben a kondenzátor tárol energiát a keresztváltozóval. Ez első pillanatban furcsának tűnhet, hiszen köztudott, hogy a kondenzátor elektromos töltések tárolására alkalmas. Ha azonban deriváljuk az alap fizikai egyenletet, azonnal világossá válik, hogy a töltés deriváltjaként megjelenő villamos áram révén kapcsolatot tudunk teremteni kereszt és átmenő változók között:
A „kondenzátor” modell-elem alatt nem csak a kereskedelmi termékeket kell érteni. Látni fogjuk, hogy egy piezokerámia lapka is kondenzátorként viselkedik, mert a lapka két ellentétes felületén kialakított „töltésgyűjtő” fémréteg között szigetelőanyag – a piezokerámia - helyezkedik el.
-
Induktivitás
A villamos rendszerekben az induktivitás (vezető tekercs) az a technikai elem, amely az átmenő változóval, az árammal tárol energiát. Ha a kereszt és átmenő változók között keressük a kapcsolatot, akkor a fizikai egyenletből kell kiindulni. A nyugalmi indukció (önindukció) azt jelenti, hogy a vezető (tekercs) és a mágneses tér nem mozognak egymáshoz képest (vö. mozgási indukció). A jelenséget sokan ismerik a villanykapcsolók érintkezőjének „beégése” formájában, ha a terhelések között sok az induktív jellegű. Az áram megszakítása ugyanis olyan feszültséget indukál, amely a Lenz törvény értelmében a folyamatot továbbra is fenntartani igyekszik. Az indukált feszültség mind a bekapcsolás, mind pedig a kikapcsolás során létrejön. Ez az indukált feszültség károsítja az egyenáramú gépek (villanymotorok) kommutátorait és keféit, hiszen forgás közben sorozatos a kefék és az egyes kommutátor szegmensek közötti megszakítás és érintkezés. Ez a feszültség hozza létre a jól ismert és jól látható „kefeszikrázást”.
Az árammal átjárt vezető körül, illetve a tekercs belsejében és körülötte mágneses erőtér alakul ki (H). Az „l” hosszúságú és „N” menetszámú tekercs „H” mágneses erőtere, amelyet az „I” tekercsáram hoz létre, kellően hosszú tekercs közepén közelítőleg az alábbi módon számítható:
A mágneses erőtér és a mágneses indukció „B” közötti kapcsolatot az egyik Maxwell-egyenlet írja le. A mágneses fluxus „ΦB” az „A” felületet metsző indukcióvonalak számával fejezhető ki.
Ha az áram időben változik, akkor ez a változás a „ΦB” mágneses fluxus időbeli változását vonja maga után, ami a vezető (tekercs) két végpontja között villamos feszültség formájában jelentkezik.
Az anyagi (mágneses) és geometriai jellemzőket csoportosítva kapjuk a tekercs „L” öninduktivitását, és ennek felhasználásával a kereszt és átmenő változó közötti kapcsolatot:
Vigyázat, mert az öninduktivitás fentebb látható képlete egy adott tekercs elrendezésre érvényes. A mechatronikai feladatokban minden esetben meg kell határozni az adott konfiguráció öninduktivitását és a szimulációkhoz ki kell számítani a konkrét értéket. Egyszerűsíti a helyzetet, ha az induktivitás egy szervomotor induktivitása, mert ezt az értéket a katalógusok közlik, a meghatározásával nem kell bajlódni.
3.2.3. Disszipatív elemek modellezésének problémái
A „b” és „B” csillapítási tényezők csak durva közelítéssel álladó értékek. A hálózati módszerekkel felírt állandóegyütthatós rendszeregyenletekben – ha indokolt – helyettesíteni kell a „b” és „B” csillapítási együtthatókat leíró függvényekkel. A mechatronika mechanikai rendszereiben leggyakrabban a Coulomb és a Stribeck effektust is magába foglaló, ugyanakkor a nagyobb sebességnél (fordulatszámnál) viszkózus jellegű közelítő összefüggést alkalmazzák.
A legfontosabb az, hogy mindenki, aki modellezéssel foglalkozni kezd, tudatosítsa magában, hogy a mechanikai disszipatív elemek, a súrlódási együtthatóként definiált paraméterek, a villamos ellenállással nem analóg paraméterek! A mechanikai csillapítási tényező a villamos vezetőképességgel analóg, és éppen ezért egy mechanikai rendszer időállandóit egészen más módon kell szemlélni, mint egy villamos rendszerét. Látni fogjuk a hajtóművel foglalkozó fejezetben, hogy a terheletlen DC motor mechanikai időállandója nagyobb, mint a hajtóművel egybeépített motoré. Ebből nem szabad azt a hibás következtetést levonni, hogy a nagyobb mechanikai időállandójú motor dinamikai szempontból rosszabb. Éppen ellenkezőleg! A T=J/B időállandó képlet miatt érthető, hogy kisebb súrlódású rendszer időállandója nagyobb lesz. Egy „felpörgetett”, mozgási energiát tároló, forgó tárcsa (tehetetlenségi nyomaték) annál hosszabb ideig képes mozgásban maradni, minél kisebb a csapágyainak súrlódása. A kérdés gyakorlati oldalával a 4. fejezet fejezetben is foglalkozunk.
Az áttekintés érdekében bemutatunk néhány mechanikai súrlódási modellt, amelyeken kívül továbbiak is vannak, pl. Dahl-modell [3.3.], Lu Gre-modell [3.4.] stb. Általános érvényű nincsen, esetenként kell megvizsgálni ezek érvényességét, és a választott modellt méréstechnikai úton lehetőleg ellenőrizni kell.
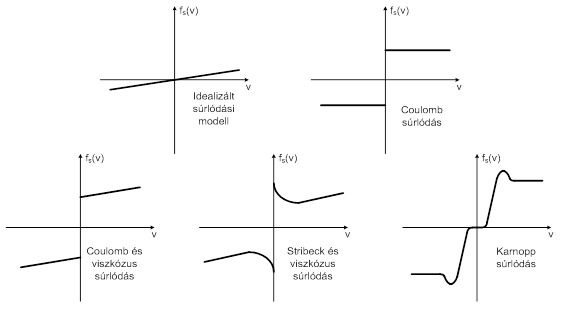
A fluid rendszereken belül, a folyadékos rendszerekben, „RF”, „RA”, és „RP” többnyire nemlineáris elemek, de lehetnek lineárisak is (lamináris súrlódási viszonyok, Poiseuille-féle áramlás esetén, Re<2300). RF a folyadék-ellenállást, RA az akusztikai ellenállást és RP a pneumatikus ellenállást jelöli.
A képletben látható jelölések magyarázatát lejjebb találjuk.
Minden olyan fluid áramlási ellenállás, amelyben megjelenik az áramló közeg sebességének négyzete, felírható más formában is. A nem lineáris ellenállás képletében a sebesség helyére – a felület figyelembe vételével a térfogatáram írható. A térfogatáram négyzetét bontva az egyiket az ellenállás definíciója szerint a p/qv =RF(qv) összefüggésben használjuk fel, míg a másikat abszolút értékével magában az ellenállás képletben vesszük figyelembe. Erre látunk a következőkben néhány példát:
Kilépési (belépési) veszteség (ellenállás):
Súrlódási veszteség (ellenállás):
Csőidomdarabok okozta veszteség (ellenállás):
A fenti képletekben az alábbi jelöléseket alkalmaztuk:
|
ρ |
: folyadék sűrűség |
|
|
η |
: dinamikai viszkozitási tényező |
|
|
l |
: csőhosszúság |
|
|
λ S |
: csősúrlódási tényező |
|
|
ξ ID |
: veszteségi tényező (értéke méréssel határozható meg, gyakoribb formák táblázatban találhatók) |
|
|
d |
: csőátmérő |
Az akusztikai fluid alrendszerben is létezik ellenállás típusú disszipatív elem, ez az akusztikai ellenállás. Feladata hangelnyelő rendszerekben az, hogy a levegőrészecskék mozgási energiáját hővé alakítsa. Ezért az akusztikai ellenállás általában olyan szerkezet, amelyben porózus fedőanyag alatt laza szerkezetű kőzetgyapotot, vagy üveggyapotot találunk. Nem csak a laza szerkezetű, szálas anyagok, de a rések és kör keresztmetszetű nyílások is akusztikai ellenállást jelentenek. A nyílások felülethez viszonyított arányát külön tényezőkkel veszik figyelembe. Az akusztikai ellenállás paramétere az alábbiak szerint számítható:
A képletben „Ξ” a hosszra vonatkoztatott áramlási ellenállást jelöli, értékét méréssel határozzák meg.
A pneumatikus ellenállásnak, szakszóval „fojtásnak” fontos szerepe van az időzítésekben. Ezért azon túlmenően, hogy a pneumatikus rendszerekben is előfordulnak olyan ellenállások, amelyek szűkületek és idomok miatt okoznak nyomásveszteséget - hasonlóan a folyadékos rendszereknél bemutatott formában - léteznek szabályozható pneumatikus ellenállások, fojtások is.
3.2.4. Folyadékos rendszerek energiatárolói
-
Nyitott tartály folyadék kapacitása
A nyitott folyadéktartály fenéknyomása a referenciaként választott (pl.: külső nyomás) értékéhez viszonyítottan az alábbi képlettel számítható.
Töltés és ürítés esetében a tartály térfogatárama a folyadékfelszín felületének figyelembe vételével – amennyiben ez állandó érték – a folyadékoszlop magasságának változásával van kapcsolatban:
Ha a folyadékoszlop magasságváltozásának segítségével a két egyenletet összekapcsoljuk, akkor a folyadék kapacitás meghatározásához szükséges összefüggéshez jutunk:
A képletben a p1R nyomás az adott referenciához viszonyított fenéknyomás:
-
Csővezetékben áramló folyadék „induktivitása”(Folyadék tehetetlenség)
Régebbi rendszertechnikai irodalmakban ez a paraméter „folyadék inertivitásként” szerepel. Az energia tárolás a csővezetékben áramló közeg révén jön létre. A súrlódási jelenségektől eltekintünk, mert ezeket a disszipatív elemekkel modellezzük. Ebben az esetben egy kicsiny dV=Adx térfogatrészbe foglalt folyadék tömegre ható gyorsító erő a dx csőszakaszban fellépő dp nyomáskülönbségre vezethető vissza. Miután a súrlódó erőt kivettük a vizsgálatból, a nyomásból származó erő és a gyorsító erő tartanak egyensúlyt:
Állandó csőkeresztmetszet mellett a dV térfogatrész folyadék tömegére az alábbi összefüggést írjuk, és az „A” keresztmetszetre rendezzük:
Az erőegyensúly képletébe behelyettesítjük a keresztmetszetre kapott összefüggést:
Az erőegyensúlyban a tömeg nem játszik szerepet, csak a közeg sűrűsége:
A térfogatáram definíciója állandó csőkeresztmetszetet feltételezve:
A fenti egyenletből a térfogatáram időbeli változása állandó csővezeték keresztmetszet esetében:
A csővezeték dx hosszdarabján létrejövő dp nyomáskülönbség a behelyettesítés után:
Az „l” hosszúságú csővezeték két vége között (1 és 2 számmal jelölt pontban) létrejövő nyomáskülönbséget integrálással nyerjük:
Az egyenletben a folyadék „induktivitás” számítására az
összefüggés használható. Az elnevezés azért indokolt, mert a térfogatáram időbeli megváltozásából származó nyomáskülönbség egyenlete tagról-tagra (teljes) analógiát mutat a villamos induktivitásra érvényes összefüggéssel.
3.2.5. Akusztikai rendszerek energiatárolói
Az akusztikai rendszerek modellezése esetében tudnunk kell, hogy a folyamatokat leíró összefüggések bonyolultabbak. Egyrészt azért, mert koncentrált paraméterű modellezésnél tekintettel kell lenni arra, hogy a vizsgált frekvenciákon az adott rendszer geometriai méretei és a hullámhossz negyede miként viszonyulnak egymáshoz, ha üregekben és hosszabb nyílásokban vizsgáljuk az akusztikai jelenségeket, mert a hang szabad térben másként terjed. Már önmagában az is nagy különbség, hogy az akusztikai térfogatáram kör, vagy téglalap keresztmetszetű „csővezetékekben” jön létre, mert mindkettő másként viselkedik.
Zárt terekben, amelyek méretei sehol nem haladják meg a λ/4 értéket, a folyadékos rendszerekhez hasonló energiatároló elemeket találunk, a keresztváltozó a nyomás, az átmenő változó a térfogatáram. Szabad és fél-szabad akusztikai terekben ilyen elemek nincsenek, a keresztváltozó ugyancsak a nyomás, de az átmenő változó az „A” felület hiányában a részecske (pl.: levegő, víz stb.) „v” sebessége. Ez a sebesség nem összetévesztendő a hullámterjedés sebességével. A szabad tér (levegő) is rendelkezik impedanciával, de ezt hullámimpedanciának nevezzük, és értéke
ahol clev a hangterjedés sebessége meghatározott nyomású és páratartalmú levegőben. A két akusztikai „tér” egymáshoz illesztése azért különösen fontos, mert a hangtechnikai eszközök többsége (hangszóró, mikrofon stb.) úgy van felépítve, hogy ezekben kisebb csatornák és üregek mellett megjelennek olyan membrán felületek, amelyek a szabad, vagy fél-szabad akusztikai térrel kerülnek kapcsolatba. A szerkezet geometriai méretei és a hullámhossz viszonya különösen a nagyobb frekvenciákra készülő hangtompítók tervezése esetében játszanak szerepet. A kiáramló gázok útjába semmiféle akadály nem tehető, ugyanakkor lehetőség van a kiáramló gázok csővezetékére megfelelően méretezett akusztikai rezonátorokat (csőcsonkokhoz kapcsolódó üregek különféle méretekben) csatlakoztatni, és így egy kívánt frekvencia tartományban „hullámszűrőket” létrehozni. Hullámszűrőről azért lehet beszélni, mert a csillapítani kívánt hang frekvenciatartományához tartozó hullámhosszak negyedei rövidebbek, mint a hangtompító geometriai méretei. A téma a gépészetben és a mechatronikában a zajcsökkentés miatt kiemelkedő fontosságú, ezért javasoljuk az ide vonatkozó szakirodalmak részletes tanulmányozását.
Tehát az akusztikai rendszerekre is kiterjeszthető a folyadékos rendszerek elemkészlete, ha az adott rendszer geometriai méretei minden irányban kisebbek, mint a hullámhossz negyede. Ebben az esetben ugyanis még nem beszélhetünk a rendszeren belül hullámterjedésről.
-
Üreg akusztikai kapacitása *C A (akusztikai „rugalmasság”)
Akusztikai rendszerekben keresztváltozóval, azaz a nyomással az üreg tárol energiát, miután összenyomható közegről van szó. Az akusztikai szakirodalomban az üreg nem kapacitásként, hanem mint „akusztikai rugalmasság” jelenik meg. Az elnevezés teljesen indokolt, hiszen a gázok összenyomhatósága miatt egy üreg – főként, ha a nyílására egy dugattyút képzelünk – „légrugóként” viselkedik. A pneumatikus rendszerekre is igaz ez, a mintafeladatok bemutatása során a légrugóra külön hangsúlyt fektetünk. Az üreg mechanikai „rugalmasságának” az oka egyértelmű, ha a zárt üreghez egy rövid csőszakaszon gördülő membránnal (nincs mechanikai súrlódás a dugattyú és a csőfal között) dugattyút csatlakoztatunk. A rendszer egy fordító váltót képez (girátor), ahol az eltérő típusú rendszerek (mechanikai-pneumatikus) eltérő típusú változóit köti össze az átalakító állandója:
A fordító váltó többek között ellentétes típusúra „váltja” az energiatárolókat is: Az akusztikai kapacitás mechanikai oldalon rugalmasságként jelenik meg.
Az akusztikai kapacitás (rugalmasság) paraméterének kiszámításához egy nyílással ellátott zárt üregből indulunk ki. Feltételezzük, hogy az üreg falain keresztül nem megy végbe hőcsere, miután az akusztikai folyamatok (rezgések) gyorsak.
Ismert, hogy ilyen esetekben
ahol „κ” az adiabatikus exponens. Az akusztikai üregben kis nyomásváltozások és kis térfogatváltozások jellemzőek. Azt keressük a variációszámítással, hogy a két mennyiség változása miként függ össze? Ehhez deriváljuk a kiinduló egyenletet:
A levegő nyugalmi nyomása p0=105 N/m2, az üreg nyugalmi térfogata „V0” és levegő esetében κ=1,4.
A dinamikai modellezéshez a nyomás és a térfogat időbeli változására van szükségünk:
Végül olyan összefüggést kapunk az átmenő és a keresztváltozó között az akusztikai kapacitásra, amely alakjában a folyadékos rendszerrel analóg, de a kapacitás, mint paraméter igen eltérő. Tudott, hogy kifelé áramlás esetén csökken, ellentétes irányban pedig nő az üreg nyomása a környezethez képest, ezért az előző egyenlet átrendezése után az előjelet már nem tüntetjük fel:
-
Akusztikai induktivitás *L A (akusztikai „tömeg”)
Akusztikai rendszerekben a térfogatáram is képes energiát tárolni, akár csak a folyadékos rendszerek esetében láttuk. Az akusztikában a nyomás ingadozása jellemzően az atmoszférikus nyomás tartományában marad, nem úgy, mint a pneumatikus rendszerek esetében, ezért a kétféle energiatároló között lengés lehetséges. Az akusztikai induktivitás paraméterét hasonló módon számítjuk, amint a folyadékos rendszerekben, ezért csak az összefüggéseket mutatjuk be:
Ugyanakkor meg kell jegyezni, hogy kis „l” értékre, azaz, ha például egy vékony lemezben található nyílásról van szó, az akusztikai induktivitás értékére irreálisan kis érték adódna. Ilyen esetben szokás egy nyílás-korrektúrát figyelembe venni, mert a részecskék egy hányada a nyílás mindkét oldalán együtt mozog a nyílásban található levegővel:
A korrektúra tapasztalati értékei függenek a nyílás formájától.
Kör keresztmetszetű nyílás esetén:
Téglalap keresztmetszetű nyílás esetén, ha „b” a nyílás szélessége:
3.2.6. Pneumatikus rendszerek energiatárolója
A pneumatikus elemek a mechatronika igen fontos építőkövei, a fluid rendszerek alrendszerét képezik. Tárgyalásukra azért kerül sor az folyadékos és akusztikai rendszereket követően, mert a pneumatikában csak kétféle elem fordul elő, és ezek lényegében már le vannak írva a megelőző rendszerek tárgyalása során.
A pneumatikában csak ellenállás és kapacitás létezik, hiszen a csővezetékekben a tápnyomás lehetetlenné teszi a hosszabb csőbe zárt levegő lengését. A pneumatikus rendszerben nem a szabad levegő nyomása körüli, kismértékű ingadozások jellemzőek, amint az akusztikai rendszerekben láttuk.
A linearizált pneumatikus kapacitás levezetését nem mutatjuk be külön, mert az megegyezik az akusztikai kapacitással (üreg). A lineáris kapacitás alatt azt értjük, hogy a „V0” nyugalmi térfogat esetében a legtöbb esetben átlagos üregmérettel számolunk, amelynél a dugattyú két véghelyzete közötti különbség felét vesszük figyelembe. A munkahenger mozgása során ugyanis változik a térfogat, és ez nemlineáris kapacitást eredményez. Nagypontosságú szervopneumatikus szabályozások esetében ezt a nemlinearitást figyelembe veszik, és ennek következtében, természetesen, állapottérrel modellezik a pneumatikus rendszert.
3.3. Ideális források
Az ideális források elengedhetetlenül fontosak a hálózati módszerek tárgyalásához, hiszen ezek adják a rendszerek gerjesztéseinek túlnyomó többségét.
Három forrás típust különböztetünk meg:
-
Átmenő változó forrás
-
Keresztváltozó forrás
-
Vezérelt forrás
A forrásokat azért nevezzük ideálisnak, mert közös jellemzőjük, hogy ésszerű terhelések mellett megtartják előírt értéküket.
-
Átmenő változó forrás
Ez a forrás típus az adott rendszertől függően lehet erő, forgatónyomaték, áram, térfogatáram, vagy hőáram. A belső ellenállása ideálisan végtelenül nagy, ezért a hálózatban szakadásként jelenik meg. Valós ellenállását egy vele párhuzamosan kötött ellenállással jelenítik meg. Általában összetett rendszer, amelyet külső energiaforrás táplál. A legjobban érthető gépészeti (hidraulikai) megfelelője a fogaskerék szivattyú. A folyadék (térfogat) kiszorítással működő forrás valós belső ellenállást mutat a hálózat felől nézve. Van valós vesztesége (ellenállása), az un. résveszteség, az a térfogatáram-hányad, amely a fogak és a ház tömítetlenségein visszaáramlik. Az újabb ábrázolásokon jelképe egy kör, benne vízszintes vastagított vonal utal a szakadásra.
-
Keresztváltozó forrás
Az előző pontban látható sorrendben ez a forrás típus lehet sebesség, szögsebesség, feszültség, nyomás, vagy hőmérséklet. Belső ellenállása ideálisan zérus, ezért a hálózatban rövidzárként jelenik meg. Valós ellenállását egy vele sorosan kötött ellenállással jelenítik meg. Általában összetett rendszer, amelyet külső energiaforrás táplál. A legjobban elképzelhető gépészeti megfelelője a centrifugál szivattyú. Más, szemléletes gyakorlati példa az akkumulátor. Terheletlen (üresjárati) kapocsfeszültsége nagyobb, mint a terhelt állapotban mérhető feszültség, hiszen a zárt áramkörben folyó áram miatt a belső ellenálláson is esik feszültség. Jó állapotú akkumulátornál ez az ellenállás kis értékű, jól példázza az ideális forrás esetét. Újabb ábrázolásokon a jelképe egy kör, benne függőleges vastagított vonallal, ami a hálózat ellenállás nélküli folytatására utal.
-
Források egyenértékűsége (átszámítások)
Legfőképpen az impedancia módszer alkalmazása során kínál előnyöket a két forrás típus közötti átszámítás lehetősége. Amint látni fogjuk, az impedancia módszer lényege, hogy minden egyes forrást tekintve a rendszert aktív és passzív részre lehet szétválasztani. Erről a módszer bemutatása során még részletesen lesz szó. A módszer végeredményeként általában keresztváltozó, vagy átmenő változó osztó alakhoz jutunk. Ha a forrás és a keresett mennyiség eltérő típusúak, akkor szükség lehet az átszámításra. Az ideális átmenő változó forrást, és a vele párhuzamosan kapcsolt ellenállást „Norton” alaknak, míg az ideális keresztváltozó forrást és a vele sorba kapcsolt ellenállást „Thevenin” alaknak nevezi a szakirodalom. A Norton alak üresjárati keresztváltozója az egyenértékű Thevenin alak forrás értékének felel meg. Ez a maximális keresztváltozó érték, amit az adott forrás szolgáltatni képes, és ezt az Ohm törvény alkalmazásával határozzuk meg. A Thevenin alakot „rövidre” zárva, az Ohm törvény alkalmazásával megkapjuk a forrásból kivehető maximális átmenő változó értékét, ez lesz az egyenértékű Norton alak forrás értéke.
-
Vezérelt források
Működésükhöz segédenergiára (tápfeszültség, tápnyomás stb.) van szükség. Ideális esetben a kimenet nincs visszahatással a bemenetre. A bemeneti mennyiséggel vezérlik a kimenő mennyiség értékét. Jelképi ábrázolása két gráf élet mutat, amelyek közül a kimeneti oldalon található egy forrást jelképez, amelyhez a bemeneti oldal élétől szaggatott gráf él vezet. A gráf él irányítása a bemenet felől a kimenet felé mutat. Ilyen vezérelt forrás látható például a (14.8. ábra) ábrán. Három egyszerű példa jól mutatja működésüket, és jelentőségüket a mechatronikában. Egyik legegyszerűbb vezérelt forrás a tranzisztor. Egy kollektor ellenálláson keresztül tápfeszültségre kapcsolva tranzisztort, a bázis-emitter feszültséggel (bemenő jel) vezérelhető a kollektor-emitter áram, vagy ennek folytán a kimenő feszültség. Összetettebb eszköz a műveleti erősítő. A differencia feszültséggel (szimmetrikus bemenőjel) vezéreljük az erősítő aszimmetrikus kimenő feszültségét. A szimmetrikus feszültség azt jelenti, hogy a földponthoz képest a bemenetnek két bemeneti pontja van, míg a kimeneti pontot egyedül a földponthoz viszonyítjuk. Az erősítőn belül visszahatás nincsen. A nyílt hurkú erősítés elméletben végtelen nagy, az erősítőt külső, negatív visszacsatolással lehet stabil működésűvé tenni. A zárt hurkú erősítés értéke jellemzően 105 körül van. Az erősítők feszültség-illesztése érdekében (a kimenő jelszint továbbítása minél kisebb hibával) az erősítő bemenő ellenállása nagy (MΩ…GΩ nagyságrendű), míg a kimenő ellenállás relatív kis értékű (30…70 Ω). A pneumatikus rendszerek esetében, fix tápnyomás mellett, gyakran szabályozzák egy fojtószelep segítségével a rendszerbe beáramoltatott levegő mennyiségét (térfogatáram). Ebben az esetben mechanikai elmozdulás (szelepház és működtető relatív elmozdulása) segítségével vezérlik a pneumatikus oldal átmenő változó forrását.
3.4. Energia átalakítók
Az alábbiakban az energia átalakítókkal kapcsolatos, legfontosabb általános tudnivalókat foglaltuk össze. Az energia átalakítók konkrét elemzését az egyes példáknál találjuk meg (szenzorok, aktuátorok, mozgás átalakítók).
Az energia átalakítók elengedhetetlenül fontosak a komplex mechatronikai rendszerek leírásához, mert ezek teszik lehetővé a különböző rendszerrészek közötti folyamatok modellezését. Régebbi szakirodalmak ezeket az eszközöket az „elektromechanikus” rendszerek között tárgyalták, de ez természetesen erős szűkítés, mert minden, korábban felsorolt technikai rendszertípus között megtalálhatjuk az ideális és a valós energia átalakítás lehetőségeit.
Az ideális energia átalakító veszteségmentes, a bemeneti és kimeneti teljesítmények megegyeznek, a hatásfok 100%. Teljesen egyértelmű, hogy a valóságban ilyen eszközök nem léteznek. Minden energia átalakító tartalmaz, vagy tartalmazhat energia tárolókat és disszipatív elemeket. Sok esetben ezek az elemek az átalakító működéséhez elengedhetetlen alkatelemek. Fontos ugyanakkor kiemelni, hogy modellezésük során az energia átalakítást minden esetben egyetlen paraméterrel, dimenzióval rendelkező együtthatóval, vagy puszta számmal jellemezzük. Az átalakító részét képező minden passzív elemet a hálózat többi passzív elemével együtt vesszük figyelembe. Az energia átalakítás mindig kétirányú, de a fizikai jelenséget leíró törvény nem feltétlenül azonos, jó példa erre az elektrodinamikus átalakító.
Az energia átalakítók alapvetően négypólusok. Ennek ellenére lehetséges, hogy a bemeneti és kimeneti oldalnak van közös keresztváltozója (pl.: közös földpont), és ezzel az átalakító lényegében „hárompólussá” alakul. Jelölésük a gráf technikában két gráf él, az alacsonyabb keresztváltozó felé irányítottan, és a két élet szaggatott vonallal megadott ellipszis, vagy fektetett nyolcas köti össze. A kapcsolatot jelképező szaggatott vonal fölé (alá) szokás írni az átalakítót jellemző paramétert. Impedancia módszer esetében szabályos négypólust kell rajzolni, a „dobozba” (téglalappal jelzett átviteli tag) vagy az átalakító két egyenletét, vagy csak a paramétert szokás beírni. Az átmenő változók mindkét oldalon a tagba befelé mutatnak.
Három típus különböztethető meg:
-
Transzformátorok
A transzformátorok azonos típusú rendszerek azonos típusú változóinak kapcsolatát írják le. Ebbe a csoportba tartozik a villamos transzformátor, a gépészetben a hajtómű, az egy-és kétkarú emelő kis elfordulások esetében, vagy a differencia-dugattyú. Jelölésük gráf esetében a két élet összekötő fektetett ellipszis. Ezt láthatjuk a (7.7. ábra) ábrán. Impedancia hálózatban négypólusként jelenik meg, az átmenő változók mindkét oldalon befelé mutatnak. Tekintettel a definícióra a transzformátorokat jellemző paraméter dimenzió nélküli, gondoljunk a villamos transzformátor primer-szekunder tekercsei menetszámainak arányára, vagy a hajtómű módosítására.
-
Váltók
A váltók a mechatronikai rendszerek jellegzetes átalakítói, mert a vegyes rendszerek hálózati módszerekkel való tárgyalását teszik lehetővé. Eltérő típusú rendszerek azonos típusú változóinak kapcsolatát írják le. Ebbe a csoportba tartoznak az elektrodinamikus átalakítók, a fogaskerék-fogasléc kapcsolat, a vonóelemes mozgás-átalakítók minden formája, a menetes orsós, napjainkban legfőképpen a golyósorsós mozgás-átalakítók. Jelölésük gráf esetében a két élet összekötő, szaggatott vonalú fektetett ellipszis, hasonlóan a transzformátorokhoz, felette (alatta) a váltót jellemző paraméterrel. Ezt a (6.15. ábra) ábrán láthatjuk. Impedancia hálózatban négypólusként jelenik meg, az átmenő változók mindkét oldalon befelé mutatnak. A definícióból következik, hogy a váltókat jellemző paraméter dimenzióval rendelkezik, hiszen eltérő a két oldalon elhelyezkedő rendszerrész típusa.
-
Fordító váltók
A fordító váltók a mechatronikai rendszerek másik fontos, és jellegzetes átalakítóinak csoportját képezik. Eltérő típusú rendszerek eltérő típusú változói között teremtenek kapcsolatot. Ilyen átalakítók a hidraulikus és pneumatikus munkahengerek, és ennek segítségével írható le a piezoelektromos energia átalakítás. Jelölésük gráf esetében a két élet összekötő, szaggatott vonalú fektetett nyolcas, felette (alatta) a váltót jellemző paraméterrel. Ilyen gráf ábrázolást látunk a (6.1. ábra) ábrán. A paraméter itt is rendelkezik dimenzióval, hiszen eltérő típusú fizikai rendszerekről van szó. Impedancia hálózatban a fordító váltó is négypólusként jelenik meg, az átmenő változók mindkét oldalon befelé mutatnak. A „blokkba” vagy az átalakító két egyenletét, vagy a paramétert szokták beleírni.
Együtt van tehát minden olyan eszköz, amely a mechatronikai – jellemzően vegyes típusú – rendszerek hálózati és impedancia módszerrel történő, egyszerű leírásához szükséges: A változók, a passzív elemkészlet, a források és az energia átalakítók.
3.5. A hálózati és impedancia módszer alkalmazásának szabályai
A 4. fejezetben néhány egyszerű feladaton mutatjuk be a hálózati és impedancia módszerek alkalmazását. Ezt követően a legfontosabb mechatronikai aktuátorok, szenzorok és mozgás átalakítók dinamikai elemzésére kerül sor külön fejezetekben. Az építőelemek bemutatását komplex mechatronikai, szabályozott rendszerek tervezése és szimulációja követi.
A fejezetben igyekeztünk tömören összefoglalni azokat az ismereteket, amelyekre a módszerek sikeres alkalmazása érdekében szükség van.
3.5.1. Melyik változót milyen módszerrel keressük?
A keresett változó típusa, és az alkalmazandó módszer összefüggenek. Ha eldöntöttük, hogy a vizsgált rendszer lineáris, tehát hálózati (impedancia) módszerrel modellezhető, akkor a következő kérdés minden modellezésénél az, hogy mi a keresett „kimeneti” változó? A célszerűen (ésszerűen) alkalmazott módszer kiválasztását ennek a kérdésnek kell alávetni.
Hálózati módszer esetében, ha egy keresztváltozó keresett, akkor célszerű csomóponti módszert alkalmazni, míg ha átmenő változó, akkor a hurok módszert. Impedancia módszer esetében az a kérdés, hogy a keresett változó milyen impedancián, vagy impedanciák eredőjén jelenik meg? Ha keresztváltozót keresünk, akkor az átalakítások során célszerűen keresztváltozó osztóhoz, míg egy keresett átmenő változó esetén átmenő változó osztóhoz törekszünk eljutni. Ezeknél egyszerűbb forma nem létezik.
Hálózati módszerek esetében a lineárisan független egyenletek száma azért lényeges kérdés, mert több ismeretlen változó esetében nyilvánvalóan integro-differenciál, ritkábban differenciál egyenletrendszerhez jutunk. Lineáris esetben a továbblépés úgy lehetséges, ha az egyenletrendszert Laplace transzformáljuk. A matematikában szokásos még a differenciáloperátor bevezetése is, de a mérnöki gyakorlatban a Laplace operátor alkalmazása célravezetőbb, hiszen sok esetben, végső soron majd a frekvencia átviteli függvény meghatározása lesz a cél. A Laplace operátor kínálja ezt a lehetőséget s=jω helyettesítéssel (hiszen definíciója szerint s=jω). Ha az egyenletek nem függetlenek egymástól, akkor az egyenletrendszerből felírt mátrix-vektor egyenlet mátrixa (elemei jellegre impedanciák, admittanciák, vagy vegyes típusúak) szinguláris lesz, és nem invertálható. Ennek folytán a keresett változó(k)ra nem lehet felírni a rendszeregyenletet.
A lineárisan független egyenletek száma és a rendszer rendszáma között nincs összefüggés, ezt gyakran eltévesztik. A rendszám a független energiatárolók számával egyezik meg. A független jelző kiemelt fontosságú. Az energiatárolók „szimpla” összeszámolása ugyanis nem elegendő, mert a források típusa, elhelyezkedése és az energia átalakítók határozzák meg a független tárolók számát. Ennek bemutatására a későbbiekben látunk még feladatokat.
3.5.2. Hálózati módszerek
Lineárisan független csomóponti egyenletek száma
Elméletben a struktúra gráf alapján meghatározható csomópontok (szelvények) száma alapján lehet eldönteni a lineárisan független csomóponti egyenletek számát. A témával részletesen foglalkozik például a [2.4.] szakirodalom, itt csupán a gyakorlati alkalmazás néhány problémájára hívjuk fel a figyelmet. Az egyenletek száma a gráf fa elemszámával egyezik meg. Köznapi nyelven fogalmazva „cs-1”, a csomópontok száma mínusz 1, hiszen a gráf fa csomópontjainak száma mindig eggyel kevesebb, mint az elemszáma, mert egy elemhez két végpont, azaz csomópont tartozik. Ez azonban csak elméletben, elméleti gráfokra igaz, mert technikai rendszerek esetében figyelembe kell venni, hogy a csomópontok közül nem mindegyik „valódi” csomópont. Lehetséges egy szelvénybe két, vagy több csomópontot is belefoglalni, de nem célszerű műszaki rendszerek esetében. A gyakorlatban az sem mindegy, hogy melyik csomópontokat jelöljük ki. Az a célszerű, ha az ismeretlen keresztváltozókhoz tartozó csomópontokra írjuk fel a csomóponti egyenleteket.
Lineárisan független hurokegyenletek száma
Elméletben a struktúra gráf alapján meghatározható gráf pótfa elemeinek száma alapján lehet eldönteni a lineárisan független hurokegyenletek számát. A pótfa a fa kijelölése után visszamaradó elemekből áll össze. Ez azonban szintén csak elméletben igaz, mert technikai rendszerek esetében a források és átalakítók ebbe keményen beleszólnak. Célszerűbb a kérdést úgy megfogalmazni, hogy a lineárisan független hurokegyenletek száma megegyezik a független hurkok számával. A dolog igen egyszerű, mert mindazon hurkok függetlenek egymástól, amelyek legalább egyetlen elemükben különböznek egymástól. A hurkokat egy technikai gráfban – elméletileg - természetesen többféle módon fel lehet venni. A gyakorlat szempontjából az a helyes, ha a vizsgált elemen keresett átmenő változó egyetlen hurokváltozóval azonos. Ellenkező esetben két, vagy több hurokváltozó összegeként (különbségeként) adódik a keresett mennyiség. Másként fogalmazva: szomszédos hurkok rendelkeznek egy, vagy több közös elemmel. A hurkokat és ezzel a hurokváltozókat célszerű úgy kijelölni, hogy a vizsgált elem ne legyen közös.
3.5.3. Impedancia módszer
A módszer bemutatása a 4. fejezetben, gyakorlati példákon történik, itt csak a módszer eszköztárát foglaljuk össze.
Aktív-passzív részre történő szétválasztás
Az impedancia módszer esetében is első lépés a keresett mennyiség kijelölése. Ha ez keresztváltozó, és több párhuzamos, vagy soros impedancia eredőjeként jelenik meg, akkor az impedanciák eredője lesz a hálózat „passzív” része, vagy más néven „terhelés”. A keresett keresztváltozó természetesen megjelenhet egyetlen impedancián is, ebben az esetben ez az impedancia önmagában lesz a passzív „rész”. Ha a keresett mennyiség átmenő változó, akkor ebben az esetben is óvatosan kell eljárni. Lehetséges, hogy az adott átmenő változó nem csak egyetlen impedancián, hanem a vizsgált tagon, és az utána következő impedanciák eredőjén, együttesen lép fel. Az így kijelölt impedancia, vagy az impedanciák eredője képezi a passzív rendszert, ennek értékét a szétválasztáskor létrejövő kapcsok felől „betekintve” kell kiszámítani. Körülbelül úgy kell eljárni, mintha az aktív rész helyébe „képzelnénk magunkat”, és a „terhelés” irányába néznénk.
Minkét verzióra érvényes, hogy a visszamaradó impedanciák és források alkotják az un. „aktív” részt. Vigyázni kell azonban arra, hogy az aktív részt képező új forrás nem minden esetben azonos az eredeti forrással! Ha a szabad kapcsokra egy eredeti keresztváltozó-forrás csak keresztváltozó osztón keresztül jut el, akkor ezt figyelembe kell venni az új aktív forrás meghatározásakor! Hasonlóképpen kell eljárni az esetleges új átmenő forrás kiszámítása során is. Az aktív rész eredő belső impedanciáját a szabad kapcsok felől nézve kell számítani.
Szuperpozíció szabálya
Lineáris rendszerben, több forrás (mindegy, milyen típusúak) esetében nehézkessé teheti a módszer alkalmazását, hogy a szuperpozíció szabálya alapján minden egyes forrás hatását külön-külön kell vizsgálni a keresett passzív részen, majd a hatásokat előjelhelyesen összegezni kell. Egy adott forrás a többi forrást úgy „látja”, mint annak belső ellenállását. A kiválasztott forrás felől nézve a hálózatban rövidzárral helyettesítjük a keresztváltozó forrásokat, és szakadással az átmenő változókat. Ezek után összevonjuk az aktív rész impedanciáit, és kiszámítjuk az aktív rész belső impedanciáját. Ha a forrás átszámítására is szükség van, akkor ezt is el kell végezni.
Források átszámítása
A Norton alak Thevenin formába, illetve fordított irányban átszámítható, úgy, ahogy ezt a források bemutatásával foglalkozó fejezetben bemutattuk.
Különböző típusú rendszerek impedanciáinak egymásba való átszámítása
A vegyes rendszerek tárgyalását rendkívüli módon leegyszerűsíti az, hogy a különböző típusú rendszerek impedanciái az energia átalakító(k) paraméterének felhasználásával átszámíthatóak egymásba. Ilyen esetek főként az aktuátorok és aktív szenzorok dinamikai modelljeinek meghatározása során fordulnak elő. Ha ez az egyenértékűség nem volna érvényes, akkor az impedancia hálózatok egyszerűsítése vegyes rendszerek esetében nem lenne lehetséges. A gyakorlottság és a keresett változó típusa dönti el, hogy egy háromféle típusú alrendszert tartalmazó rendszer melyikében végezzük el a számításokat és az összevonásokat. Egy elektrodinamikus nyomásszenzor (dinamikus mikrofon) háromféle alrendszerből áll össze: akusztikai, mechanikai és villamos. Tekintettel arra, hogy a kimenőjel villamos mennyiség, a szakirodalomban azt látjuk, hogy a két másik rendszer impedanciáit egyenértékű villamos impedanciákká számítják át. Az átszámításhoz szükség van az átalakítók mindkét egyenletére.
Az átszámítást látni fogjuk a 6. fejezetben, a szenzorok és az aktuátorok modellezése során, de érdemes ezen a helyen összefoglalva is bemutatni az impedanciák egyenértékűségét. A következőkben egymás után bemutatjuk a váltó, a transzformátor és a fordító váltó esetében alkalmazott átszámításokat.
Elsőként nézzünk egy váltót, legyen ez az elektrodinamikus átalakító. Kiindulás minden esetben az átalakító két egyenlete. Jelen esetben az egyik egyenlet a Lorentz erőn, a másik az indukciós törvényen alapul, az igen részletes levezetést a 6.3. fejezetben találjuk. Ebben az esetben (ez nem általános) két külön fizikai törvény írja le a két irányban érvényes összefüggéseket.
Az „nv” váltó paraméter a DC motor esetében maga a gépállandó, vagy nyomatékállandó lesz, jele KM, más váltóknál esetleg geometriai paraméter, például a golyósorsós mozgásátalakító esetében h/2п, ahol „h” a menetemelkedés.
Az átmenő változókra felírt egyenletben zárójelbe került az előjel, mert az impedancia egyenérték kiszámítása során ennek nincs jelentősége.
Ha a két egyenletet elosztjuk egymással, akkor az admittanciák között kapunk összefüggést:
azaz mindkét oldalon admittanciákat látunk. Ezek reciprok értéke az impedancia, az átszámítás tehát elvégezhető.
Fontos kiemelni, hogy az átalakító paraméterének négyzete - dimenzióját tekintve - összetett! Az átalakító paramétere csak számértékét tekintve azonos a két egyenletben! Látható, hogy dimenziójuknak különbözniük kell. Az elektrodinamikus váltó (forgó mozgás) esetében az átmenő változók közötti paraméter dimenziója mNm/A, esetleg Nm/A, a keresztváltozók közötti paraméteré pedig Vs/rad.
Hasonló módon kell eljárni az átalakítók egyenleteinek felhasználásával a transzformátorok és a fordító váltók esetében is.
A hajtómű transzformátor típusú átalakító, amelynek az egyenletei a következőek. Az 1-es index a bemeneti (behajtás), a 2-es a kimeneti oldalt (kihajtás) jelöli:
A két egyenletet elosztjuk egymással:
Látható, hogy mindkét oldalon azonos rendszertípushoz tartozó impedanciák szerepelnek:
ahol nT=i, a módosítás. A mechatronikában lassító, nyomatéknövelő hajtóműveket alkalmazunk, tehát i>1. Az impedanciák közötti átszámítás az alapja a géptervezésben alkalmazott „redukálásnak”. A redukálás azt jelenti, hogy a bemeneti és kimeneti oldal tehetetlenségi nyomatékait nem lehet algebrai úton összegezni. Attól függően, hogy melyik oldalról vizsgáljuk a rendszert, a tehetetlenségi nyomatékokat a módosítás négyzetével, vagy annak reciprokával kell súlyozni az összegezés során. A kihajtó oldalra redukálva a behajtó oldal tehetetlenségi nyomatékát, látjuk, hogy azt i2-tel kell szorozni:
Ha a behajtás, tehát a motor felől nézzük a rendszert, akkor a kihajtó oldal tehetetlenségi nyomatékát (esetleg több eredőjét) i2-tel osztva kell a behajtó oldali értékhez, például „n” db bemenő oldali tehetetlenségi nyomaték összegéhez hozzáadni:
Az átszámítás, redukció gyakorlati alkalmazására a későbbi tervezési feladatokban visszatérünk még (golyósorsós szakasz, fogazott szíjas szakasz méretezése, motorválasztás).
A fordító váltók esete kissé bonyolultabb, a dualógia (duálisan analóg rendszerek) miatt. Az energiatárolók ellentétes típusra váltanak, mert ellenkező esetben az „s” operátortól való függés benne maradna az átszámítás képletében. A források típusa is ellentétesre vált, és megváltozik a kapcsolás jellege is. Sorosan kapcsolt impedanciákból párhuzamosan kapcsoltak, és párhuzamosan kapcsoltakból soros kapcsolásúak lesznek.
Példaként a közismert hidraulikus/pneumatikus munkahengert vizsgáljuk. A negatív előjel nem minden fordító váltó esetében jelenik meg, ebben az esetben arra utal, hogy az „A” dugattyú felület normál vektora és az „F” erő ellentétes irányúak. Az impedancia átszámításnál az előjelnek nincs szerepe, ugyanúgy, mint a transzformátor és a váltó esetében láttuk.
Osztjuk a két egyenletet egymással (figyelmen kívül hagyva az előjelet), és látjuk, hogy közvetlen módon impedanciákhoz admittanciák tartoznak:
Olyan impedanciákat és admittanciákat kell tehát egymáshoz rendelni, amelyek esetében az „s” operátor kiegyszerűsíthető:
A gyakorlati tapasztalatot igazolja, hogy a pneumatikus kapacitás (összenyomható közeggel töltött üreg) mechanikai szempontból rugalmasságnak „érződik”, a rugómerevség értéke az üreg kapacitásából számítható:
ahol p0 a külső nyomás, V0 az üreg (dugattyú) kiinduló térfogata, κ az adiabatikus kitevő.
A további ismereteket az adott rendszerek vizsgálatánál mutatjuk be.
Osztó szabályok alkalmazása az átviteli függvény felírásához
Az impedancia módszer tulajdonképpen „rajzos”, egyszerűsítő módszer. A végső alakig több lépésben kell átalakítani a kapcsolást, amíg végül a legegyszerűbb alakhoz jutunk.
Az aktív és passzív részre szétválasztott rendszer összevonások utáni kapcsolása alapján az átviteli függvény közvetlen felírására a következő lehetőségek vannak:
-
Keresztváltozó osztó, ha a mind a keresett mennyiség, mind pedig a forrás keresztváltozó.
-
Átmenő változó osztó, ha a keresett mennyiség és a forrás átmenő változó.
-
Ohm törvény, ha a két változó különböző.
Szakirodalom
[3.1.] Lineáris rendszerek analízise. Műszaki Könyvkiadó. Budapest . 1967.
[3.2.] Grundlagen der technischen Akustik. Akademische Verlagsgesellschaft. Leipzig . 1968.
[3.3.] A Solid Friction Model. The Aerospace Corporation. Technical Report. 1968.
[3.4.] Revisiting the LuGre Model. IEEE Control Systems Magazine. 2008.