14. fejezet - Aktív rezgéscsillapító szakaszának modelljei és a szabályozások tervezése
- 14.1. A rezgéscsillapítás „referencia problémája” és átviteli függvényei
- 14.2. A szemiaktív pneumatikus rezgéscsillapító
- 14.3. Aktív mechatronikai rezgéscsillapító szakaszának tervezése
- 14.4. A dinamikus erő kompenzátor uk(t) bemenő jelének meghatározása
- 14.5. A kompenzáló hatás igazolása kísérleti modellen végzett mérésekkel
- 14.6. Aktív rezgéscsillapító 3D modellje és szabályozása
- Szakirodalom
Az ultraprecíziós technológiákra jellemzők a rezgésekre különösen érzékeny mérő és gyártó berendezések. Az „ultraprecíziós” jelzővel ellátott technológiák valójában gyűjtő fogalmat takarnak, mert ezek közé tartoznak napjaink vezető technológiái. Ilyenek a mikroelektronika gyártóeszközei, MEMS: Micro Electro Mechanical Systems gyártóeszközei, MEOMS: Micro Electro Optical Mechanical Systems gyártóeszközei, a litográfiás technika eszközei, a gépipar ultraprecíziós CNC esztergagépei és köszörűgépei, a két-és háromkoordinátás mérőgépek, stb. Mindezen berendezések megfelelő működésének komoly környezeti feltételrendszere van. Ezek közül csak néhányat említünk, ilyen a levegőtisztaság (fokozatai: 10, 100, 1000, 10 000 nanométer méretű, lebegő szennyező részecske a munkatér 1m3 –ében), a levegő páratartalma, légnyomás, környezeti rezgések.
Az ultraprecíziós technológiákhoz igényelt rezgéscsillapítás tervezése során nem lehet abból a feltételezésből kiindulni, hogy egy épületszerkezet, például födém, jobb esetben „ház a házban” kivitelezésben megépített laboratóriumban a földszint, vagy alagsor padlózata nyugalomban lenne. Nincs nyugalomban, és a födémet, vagy a padlózatot semmi esetre nem lehet vref=0 referencia sebességként értelmezni. Az ultraprecíziós technológiák világában nincsen olyan fix pont, amelyhez képest megengedett lenne a mozgások viszonyítása. Mivel ilyen fix pont nincsen, ezért célszerűbb a mechanika keresztváltozóját, a sebességet alkalmazni, és az adott tér minden pontjának sebességét abszolútnak tekinteni. Abszolútnak, mert minden pont a nehézségi erőtérben mozog, és a vonatkoztatás is ennek megfelelően történik, tehát a Föld „középpontjának” sebességét tekintjük zérusnak (esetünkben a bolygónk Naprendszerhez viszonyított mozgása irreleváns), és erre vonatkoztatjuk minden rezgő pont, test sebességét. Sokan megszokták, hogy egyszerűbb rezgéstani feladatok esetében a környezet, padlózat, stb. sebessége a vref=0 vonatkoztatási pont. Ez a szemlélet a vizsgált ultrapracíziós rendszerek esetében alkalmatlan a rezgéscsillapítási feladat megoldására.
A továbbiakban néhány fontos gondolat a rezgéscsillapítással kapcsolatos „aktív” és „passzív” jelzőkről. Az akusztika és a rezgéstan egyik ipari szempontból kiemelten fontos szakterületén, a zaj-és rezgéscsökkentésben, korábban más volt a két jelző értelmezése. A két jelzőt még napjainkban is nem rendszertechnikai szemlélettel alkalmazzák, amely szerint aktív az a rendszer, amelyik szabályozással rendelkezik, és segédenergia igénybevételével a megváltozott feltételekhez alkalmazkodni képes, valamint passzív az, amelyben nincsen segédenergia, kizárólag passzív rendszertani elemekből épül fel. A zaj-és rezgésvédelemben, a szakterület céljainak megfelelően, aktív a zaj-és rezgéscsillapítás akkor, ha a zaj-és rezgésforrás által kibocsátott energia csökkentését tűzi ki célul, és passzív akkor, ha a rezgésforráshoz és környezetéhez nem nyúlunk hozzá (technikailag kivitelezhetetlen, túl költséges, stb.) hanem a zajoktól és rezgésektől megvédeni kívánt egységet látjuk el „passzív” védelemmel.
Esetünkben tehát nem a zaj-és rezgésvédelem osztályozását, hanem a rendszertani értelmezést alkalmazzuk. Aktív az a rezgéscsillapítás, amelyben egy (több) szabályozás segítségével mintegy „ellene hatunk” a zavaró tényezőknek (pl.: padlózat rezgése), külső energia bevitelével kompenzáljuk ezeket. Passzív a rezgéscsillapítás akkor, ha az csupán arra korlátozódik, hogy passzív szűrőként bizonyos gerjesztő hatásokat (padlórezgés, erőhatások csillapítson). Ebben a fejezetben lesz még említés „szemi”(fél)aktív rendszerről is. Ez azt jelenti, hogy van ugyan a rezgéscsillapító berendezésben szabályozókör, de az csak bizonyos típusú gerjesztések, változások kompenzálására alkalmas. Hogy ne maradjon homályban az ilyen típusú eszközök mibenléte, jelezzük, hogy a méréstechnikában és optikában elterjedten alkalmazott, pneumatikus szabályozással ellátott rezgéscsillapító asztalok mindegyike szemiaktív, mert csak az asztalra ható erők kompenzálására alkalmas. Ha megváltozik a mérő-vagy gyártóberendezés elrendezése, és ennek következtében a súlypont, akkor a súlypontváltozás következtében megbillent asztallap eredeti (vízszintes) helyzetét a pneumatikus szabályozás kiegyenlíti. A padlózat felől érkező rezgések szempontjából ezek a rendszerek passzív csillapítóként, aluláteresztő szűrőként működnek.
A következő ábrákon szemiaktív pneumatikus rezgéscsillapító rendszer részeit (a többcélú asztalt és a különféle magasságú szabályozott pneumatikus lábazatokat), valamint egy jellegzetes interferometrikus elrendezést láthatunk.

A tématerület régóta igen terjedelmes szakirodalommal rendelkezik, ennek még a tömör összefoglalására sem vállalkozhatunk, mert a jegyzet célja a modellezés és tervezés. A aktív rezgéscsillapítás ugyanakkor egy igen jellegzetes mechatronikai feladat, a szerző PhD dolgozatának témája volt a 90-es évek elején, ld.: A. Huba: Mechatronischer Schwingungsisolator für die Ultrapräzisionstechnik, 1994. [14.1.]. Helyszűke miatt, a rezgéscsillapítással foglalkozó munkák közül csak egyetlen, gyűjtő jellegű könyv két kiadását említjük: C. M. Harris, Ch. E. Crede: Shock and Vibration Handbook, 1976. [14.2.], és az új ismeretekkel bővített, hatodik kiadás: Harris’ Shock and Vibration Handbook, 2009. [14.3.].
14.1. A rezgéscsillapítás „referencia problémája” és átviteli függvényei
A bevezető után néhány egyszerű és általánosan alkalmazott modell segítségével igyekszünk bemutatni a legfontosabb problémát, ami a referencia megválasztásával függ össze. Láttuk, hogy kis amplitúdójú, de káros és csillapítandó környezeti rezgések esetében nincs mód „fix”, azaz nyugalomban lévő pont kijelölésére, mert rezeg az épület, és un. hajlító hullámok formájában „mozog” a padlózat is.
Egy általános ultraprecíziós berendezésre az alábbi ábrán megjelölt gerjesztések hatnak. Erő (átmenő változó forrás) típusú gerjesztések a berendezésben található rezgésforrások (motorok, stb. technológiai és inerciaerői), amelyek közvetlenül és áttételesen hathatnak, és a kezelő személyek (robotok) által végrehajtott beavatkozások. Sebesség típusú (keresztváltozó forrás) a padlózat „le nem fogható” rezgése.
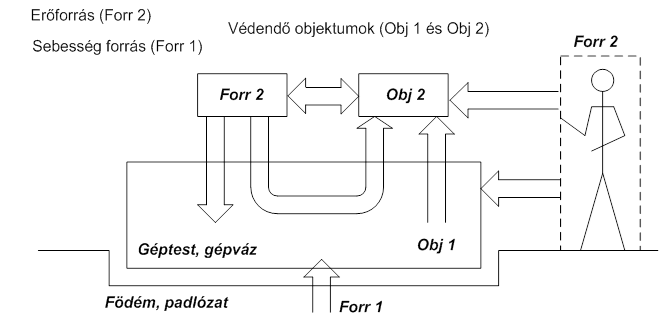
A (14.1. ábra) ábrát alapul véve nézzük meg a rezgéscsillapítás legegyszerűbb modelljeit, kizárólag a függőleges irányú mozgásokat vizsgálva. Tekintettel arra, hogy a szemiaktív rezgéscsillapítók a padlózat (födém) felől jövő sebesség gerjesztések tekintetében lényegében pontosan ugyanolyan frekvencia átviteli tulajdonsággal rendelkeznek, mint a passzív társaik, közös ábrán lehet őket ábrázolni. A szemiaktív rezgéscsillapítók „aktivitása” az asztalra ható erők kompenzálására vonatkozik.
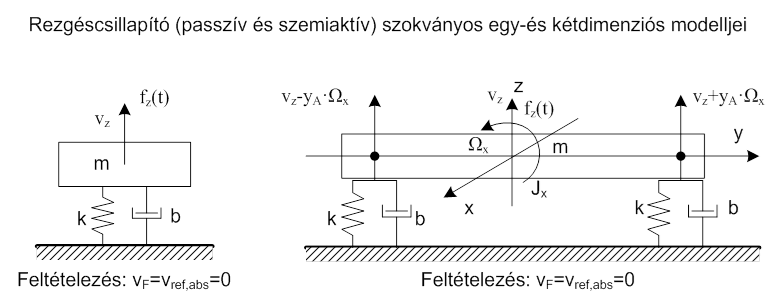
Látjuk, hogy a modellekben a padlózat mozgását nem vették figyelembe, feltételezték, hogy a padlózat sebessége zérus, és megegyezik az abszolút vonatkoztatási sebességgel.
Ebben az esetben csak az erő lehet ésszerű gerjesztő forrás. A tömegre ható sebesség gerjesztés azt jelenti, hogy a tömeg-rugó-csillapítás párhuzamos rendszeren „előírjuk” sebességet, amely persze nem más, mint a tömeg sebessége. Ennél fogva nincs megoldandó differenciálegyenlet, mert a három elemmel a keresztváltozó forrás párhuzamosan van kapcsolva.
A baloldali modell esetén, ha a gerjesztő erő a tömeg súlypontjára hat, az átviteli függvény az Ohm törvény segítségével, egyszerűen megadható. A jobboldali modell esetében az erő már a súlyponttól eltérő helyen is hathat, ezt megfelelő erőkarral kell figyelembe venni. Jelenlegi vizsgálódásaik szempontjából azonban ez az utóbbi modell nem fontos, tehát nem részletezzük. A későbbiekben lesz olyan rezgéscsillapító asztal modell, ahol az „x” és „y” tengelyek körüli forgásokat is figyelembe vesszük.
|
|
(14.1) |
Az átviteli függvényből látjuk, hogy DT2 tagról van szó, amely sávszűrőként működik, tehát bizonyos frekvencia tartományban sajnos átengedi az erőgerjesztéseket.
Nézzük, milyen átviteli tulajdonságokat mutat egy valódi, a padlózat sebességét is figyelembe vevő modell.
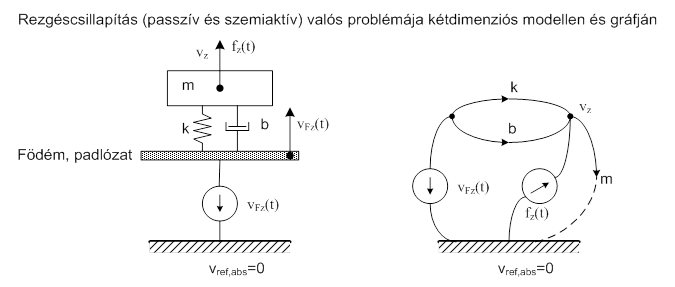
A (14.4. ábra) ábrán látható gráf az egyszerű, veszteséges rugalmassággal alátámasztott rezgéscsillapítót és a szemiaktív pneumatikus rendszert is egyaránt modellezi. Ez utóbbi esetében előfordul, hogy a lábazatban egy helyett két pneumatikus kamra (mint légrugó) van, de ez a frekvenciameneten lényegileg nem változtat. A födém alacsony frekvenciás rezgései akadály nélkül átjutnak a védett objektumra (asztalra).
Az ultraprecíziós (UP) rezgéscsillapítás esetében tehát különösen fontos megakadályozni a födém sebesség átvitelét az asztalra. A legegyszerűbb, ha az átviteli függvények felírásához ismét az impedancia módszert alkalmazzuk. Az átviteli függvény egy egyszerű keresztváltozó osztó, hiszen VA (az asztal függőleges sebessége) a kimenet és VF (a födém/padlózat függőleges sebessége) a bemenet. A sebességeket abszolút értelemben használjuk, vonatkoztatás a nehézségi erőtér vref=0 idealizált pontja.
|
|
(14.2) |
Szokásos alakban:
|
|
(14.3) |
A passzív és a szemiaktív rezgés csillapító tehát nyilvánvalóan nem képes csökkenteni alacsony frekvenciákon a födém felől érkező rezgéseket. Az átviteli függvény számlálójából látjuk, hogy ez a csillapító hatás csak az ωs1=k/b körfrekvencia felett következik be.
A fent leírt dinamikus viselkedést visszaigazolják a következőkben bemutatott frekvenciamenetek, amelyeket műszaki adatlapokból „ollóztunk” ki. A leírást azért mutatjuk be változtatás nélkül, hogy az aluláteresztő szűrő jelleggel kapcsolatos megállapításaink alátámasztást nyerjenek.
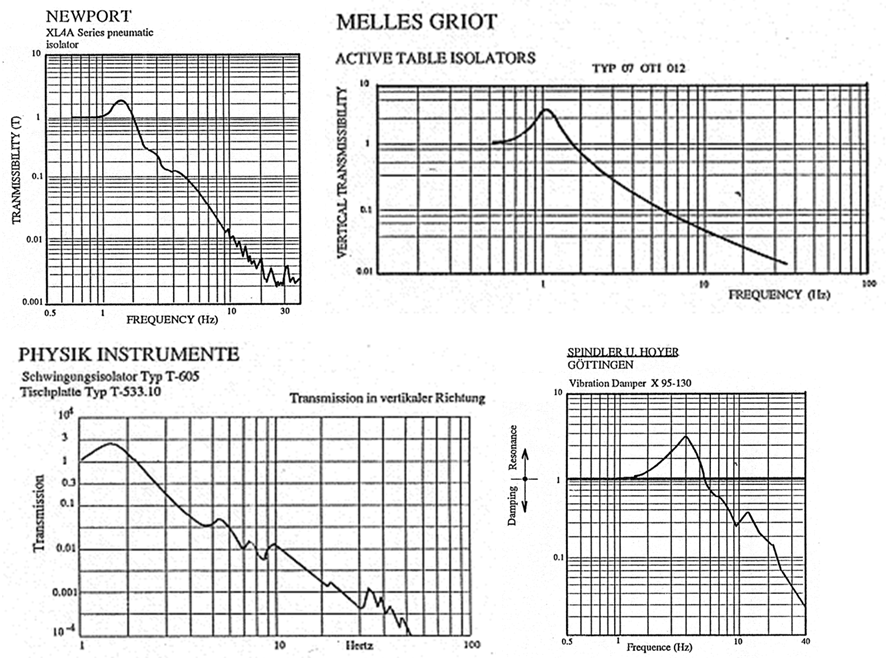
Ugyanezek a passzív és szemiaktív rendszerek azonban szerencsésebb működést mutatnak az asztalra ható erőkre vonatkozóan. Ennek igazolására felírjuk az erő-átviteli függvényét is. Erő bemenetre a három impedancia ugyanúgy párhuzamosan kapcsoltnak „látszik”, mint a 14.1. egyenletben bemutatott rendszernél, mert a vF forrást rövidre kell zárnunk (szuperpozíció):
|
|
(14.4) |
Látható, hogy a rezgéscsillapító erre a bemenetre sávszűrőként működik, azaz az áteresztő sávon kívül mind az alacsony, mind pedig a nagyobb körfrekvenciák tartományában megfelelően csillapít.
14.2. A szemiaktív pneumatikus rezgéscsillapító
Az előző, 14.1. szakasz fejezetben olvashattuk, hogy a szemiaktív pneumatikus rezgéscsillapító tulajdonképpen a passzív rezgéscsillapítóhoz hasonló frekvencia átviteli tulajdonságokat mutat. Hatalmas előnye ugyanakkor, hogy a statikus deflexió (összenyomódás), ami a passzív gumi, vagy fémrugók esetében elkerülhetetlen, ennek a rendszernek az esetében pneumatikus szabályozással kiegyenlíthető. Jeleztük, hogy a lábazatokban egy, vagy két pneumatikus üreg (kamra) van, lényegét tekintve tehát ez a rendszer nem más, mint egy (veszteséges) légrugóval ellátott, tömeg-rugó rezgő rendszer. A két kamra és a közöttük lévő fojtószelep csupán kis mértékben változtatja a frekvenciamenet meredekségét. A szabályozás itt arra szolgál, hogy az asztal előre beállított helyzetét az asztalra ható erőterhelések hatására megtartsa. Rendszerint 3 lábazat a 4 közül pneumatikus szabályozással rendelkezik, a negyedik láb légrugójában un. referencia nyomást és magasságot állítanak be. Három láb alkalmazása csak kisebb rendszereknél jön szóba, mert négy láb esetén, az asztal síkjában, csaknem tetszőleges pontokon terhelhető.
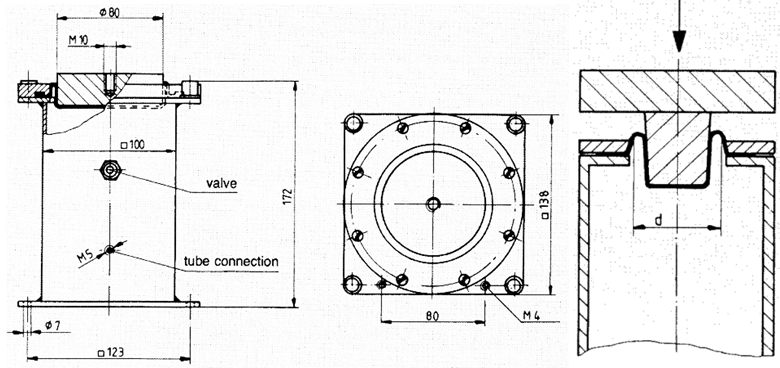
Nézzük a klasszikus pneumatikus szemiaktív rezgéscsillapító „lelkét” képező lábazatot, a légrugót. A következő ábrán, a baloldali képen egy pneumatikus lábazat műszaki rajza látható, és mellette jobboldalon külön megjelenítettük a gördülő membránt. Ez a gépelem a légrugó esetében kiemelkedően fontos szerepet játszik. Feladata a tömítés olyan módon, hogy a tömeget (asztalt) hordozó dugattyú és a lábazat fala között minél elhanyagolhatóbb legyen a súrlódásos kapcsolat. A gördülő membrán egy hálós merevítésű, de igen rugalmas műgumi kompozit, rugómerevsége gyakorlatilag szinte alig érzékelhető. Önmagában tehát képtelen lenne a tömeget megtartani, felfújás nélküli állapotban a dugattyú felső pereme nyugszik a lábazat felső karimáján, a jobboldali képen látjuk. Baloldali műszaki rajzon ábrázolt lábazat dugattyúja is rendelkezik karimával, amit az a félnézet-félmetszet képen látható.
A műszaki rajz alapján elkészítettük egy kétkamrás lábazat működési vázlatát és struktúra gráfját, ez a következő ábrákon látható. A lábazat a vF abszolút függőleges sebességgel mozgó padlózaton áll. A rezgésvédett asztal tömegét a dugattyúra helyezett „m” jelzi. A pneumatikus szabályozás alapjele az asztal és a padlózat (lábazat) között beállított távolság. A szabályozás értéktartó, mert amint az asztal és a padlózat (lábazat) közötti relatív távolság megváltozik, a szelep vagy táplevegőt enged a felső kamrába, vagy lefúj. A működési vázlaton a pneumatikus szelepet rácsozott négyszög jelzi, és felette látható a rugós visszatérítésű szelepműködtető csap, a végén görgővel. A függőleges szelepmozgató csapot egy változtatható karhosszúságú egykarú emelő nyomja a szelepházba, vagy éppen kifelé engedi mozogni. A szelep karakterisztikájával a későbbiekben foglalkozunk majd, a vázlaton látható szelepfüggvény bővebb magyarázatot igényel. A kar-arány és a szelep karakterisztika adja az arányos szabályozó „Ac” arányos tényezőjét.
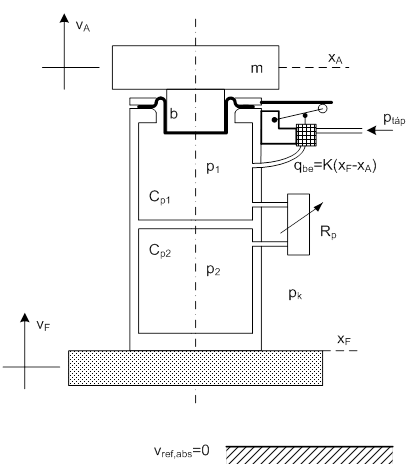
A szerkezeti (és működési) működési vázlat az ultraprecíziós technikában döntő szerepet játszó födém (padlózat) rezgés vFz(t) asztalra történő átvitelét mutatja. A vázlat alapján szerkesztettük meg a struktúra gráfot, és a teljesség kedvéért feltüntettük az fz(t) asztalra ható erőgerjesztést is.
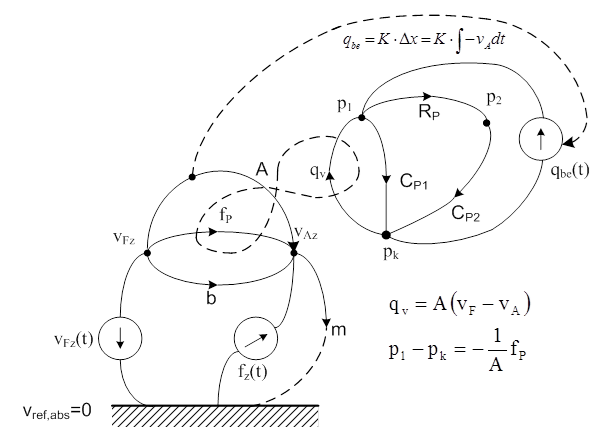
Az ábrán látható gráf tartalmazza a szakaszt és az arányos szabályozás szabályozó körét is. A szakasz mechanikai részében „b” csillapítási tényező alakjában foglaltuk össze a mechanikai veszteségeket. A mechanikai részt fordító váltó kapcsolja „A” állandóval a pneumatikus rész felső kamrájához. A födém kis amplitúdójú rezgései a szelep karakterisztikában nem játszanak szerepet, ezért jeleztük Δx helyén a –vA asztal sebesség integrálját, mint a szelep nyitásáért felelős mennyiséget. A szelep ugyanis úgy működik, mint egy vezérelt átmenő változó forrás. Az állandó ptáp tápnyomás az állítható fojtású szelepen keresztül juttatja a kamrába a qbe térfogatáramot, attól függően, hogy a Δx relatív elmozdulás mekkora.
Nézzük tehát a szabályozható állású fojtószelep működését és karakterisztikáját.
Szelepműködés általános leírása
A szelep működtetése a födém (lábazat) és az asztal relatív mozgásán alapszik. Azt feltételezzük, hogy a födém elmozdulás amplitúdója összemérhető az asztaléval. Valójában egy igen extrém (lehetetlen) esetet tükrözne, ami az UP rezgéscsillapítás esetében nem érvényes. A szemiaktív rezgéscsillapítók azonban nem is arra a célra készülnek, hogy a födém mozgását az asztal irányában csillapítsák. A táplevegő nyomásával ugyanis az asztal megkívánt szintjét/magasságát (vízszintes helyzet) lehet szabályozni, ha pl. terhelés-áthelyezés miatt megváltozna. A födémrezgések amplitúdója normális esetben (gondosan tervezett épület, ház a házban elrendezés, stb.) nem haladja meg a 0.1 mm-t. A pneumatikus szelep ugyanakkor még Δx=1 mm relatív elmozdulásra sem tud nyitni.
Az általános leírásból a valós UP rezgéscsillapító esete azonban levezethető.
Ugyanakkor lehetséges a rendszer más célú felhasználása is, olyan esetekre, ahol az xF(t) elmozdulások amplitúdója lényegesen nagyobb, és összemérhető az xA(t) elmozdulások amplitúdójával, ilyen a járművek esete.
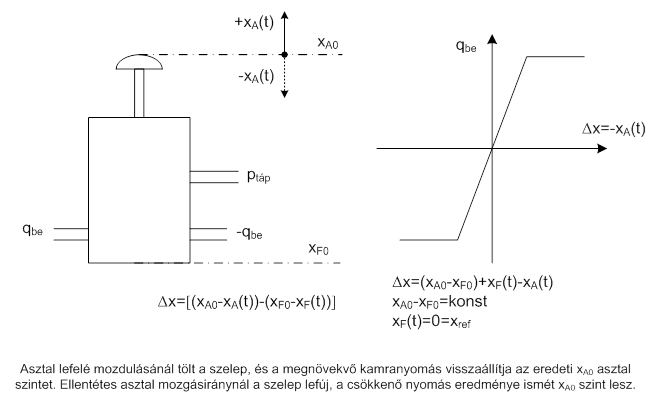
Az ábra baloldalán látható a töltőszelep sematikus képe. A szeleprúd „Δx” relatív elmozdulása nyitja, vagy zárja a szelepet, amelynek a szokásosnál „lomhább” a karakterisztikája. (Normál gyártmányoknál ugyanis egy küszöbértéknyi Δx elmozdulásra azonnal teljes mértékben tölt, vagy lefúj a szelep, ilyen eszközök érzékeny szabályozásra nem alkalmasak.)
A szelep karakterisztika megállapításához szükség van néhány megállapodásra.
Az asztal xA0 és a födém xF0 függőleges helyzetét (lábanként külön-külön) egy elméleti xref szinthez mérjük. A függőlegesen felfelé irányuló elmozdulás pozitív, az ellentétes negatív előjelet kap.
A konstrukcióból eredően xA0–xref > xF0–xref . Felírható ennek alapján a szelepet működtető Δx relatív elmozdulás az általános esetre:
Természetes, hogy minden alkalmazásra xA0-xF0=konst lesz, ezért a „változásban” nem játszik szerepet. Így egyszerűbben írható fel a relatív elmozdulás:
Végül a szelep karakterisztika általános esetre az alábbi lesz:
Szelepműködés UP rezgéscsillapítóra vonatkozó leírása
Az általános leírásnál már láttuk, hogy a pneumatikus szint-szabályozás az asztal beállított szintjének megtartását célozza, nagyobb mértékű változások esetén. Jeleztük azt is, hogy az UP rezgéscsillapítás esetében a vF(t) födémrezgések amplitúdói nem képesek nyitni a szelepet. Ezért tehát az aktív rezgéscsillapítás esetében a pneumatikus szabályozást figyelmen kívül hagyjuk, a láb kamráját passzív légrugóként modellezzük. A kamra p1 belső nyomása csak a dugattyú kis amplitúdójú rezgéseinek hatására változik (ld.: pneumatikus fordító váltó egyenleteinek levezetését).
Ezért tehát jogosan írhatjuk erre a technikai szerkezetre, hogy vF(t)=0, amiből a módosult szelep-karakterisztika adódik:
Ha tehát az asztal lapját nagyobb erővel lefelé nyomjuk, azaz Δx=-(-xA) lesz, „életre kel” a pneumatikus szabályozás, nyit a szelep, és a megnövekvő belső nyomás visszaállítja az asztal eredeti helyzetébe.
A fordító váltó egyenletei
Tanulságos a gráfban látható fordító váltó egyenleteinek felírása is. Ebben az esetben nem lehet meggondolás nélkül alkalmazni a munkahengerek, vagy egy referenciához kötött házú légrugó összefüggéseit, mert a vizsgált rendszerben függőleges irányban vF(t) sebességgel mozog a födém és vA(t) sebességgel az asztal is. Ellentétben ugyanis a pneumatikus szabályozással, a fordító váltó működésében már nem lehet figyelmen kívül hagyni a födémrezgéseket! Itt a lábazat (kamrafal) és a dugattyú közötti relatív elmozdulás sebessége a pneumatikus rendszerben történő energiatárolás (ti.: légrugó) leírásához elengedhetetlen.

A (14.10. ábra) ábrán látható működési modell alapján elkészítettünk egy táblázatot, amelyben a fordító váltó pneumatikus és mechanikai oldala közötti összefüggéseket foglaltuk össze. Ennek a táblázatnak az alapján könnyen megfogalmazhatóak a keresett átalakító egyenletek.
|
Δv A |
Δv F |
arány |
virtuális töltés: +qv virtuális lefújás: -qv |
|
↑ + |
↓ - |
-q v |
|
|
↑ + |
↑ + |
-q v |
|
|
↑ + |
↑ + |
+q v |
|
|
↓ - |
↓ - |
+q v |
|
|
↓ - |
↓ - |
-q v |
|
|
↓ - |
↑ + |
+q v |
A táblázat alapján megszülethet a következtetés, az asztal és födémsebességek és a virtuális térfogatáram közötti összefüggés, mint az átalakító egyik egyenlete:
|
(14.5) |
Az átalakító másik egyenletének felírása nem követel ekkora körültekintést, mert az előjelek a felület normálisa és az erő iránya révén adottak.
Végül tehát nézzük a légrugó, mint pneumatikus váltó egyenleteit arra az esetre, ha a henger fala nem referenciához rögzített:
|
(14.6) |
Ezek után a (14.8. ábra) ábrán látható gráf alapján már nincs akadálya a csomóponti egyenletek felírásának. Azért választjuk ezt a módszert, mert a későbbiekben, az aktív szabályozás tervezésének során szükség lesz az itt megalkotott állapottér modellre, amelyet természetesen kiegészítünk majd az aktív erőforráshoz tartozó elemekkel.
Helyettesítsük be a fizikai és az átalakító egyenleteket, miközben szem előtt tartjuk a korábban leírtakat. A pneumatikus szabályozás szempontjából tehát vF(t) padlózat sebességet zérusnak vesszük, az energiatárolás (fordító váltó) esetében nem.
Átrendezés után kapjuk a szemiaktív pneumatikus rezgéscsillapító állapottér modelljét:
Az állapottér modell alapján megszerkesztjük a szemiaktív pneumatikus szabályozás jelfolyam gráfját, mert ezen az úton lehet a leggyorsabban és szemléletesen felírni az átviteli függvényeket. A jelfolyam gráfban az állapotjelzők deriváltjaihoz tartózó csomópontokat a Laplace-operátorral való szorzással jelöltük. A szerkesztési szabályokról Csáki: Szabályozások dinamikája [14.4.] című munkájának 1.4. fejezetében:
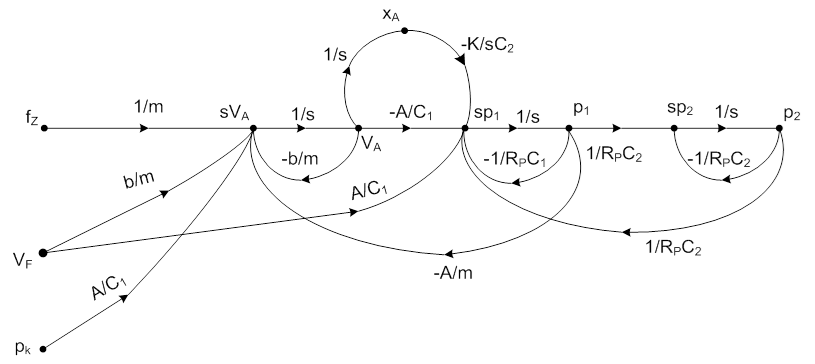
A számításokat helyhiány miatt nem lépésenként mutatjuk meg, hanem igyekszünk azokat a pontokat felvázolni, amelyek segítségével az olvasó könnyen rekonstruálhatja a műveleteket.
A jelfolyam gráf tehát egy szabályozókör matematikai modellje, amelyben két, elemben kapcsolt (összefüggő) hurok található, leszámítva az állapotjelzők eredeti függvényét visszacsatoló kisebb hurkokat. A két kapcsolt hurok a visszacsatolásokról ismerhető fel. Az egyik hurok visszacsatoló ágában (-A/m), a másikéban (1/RpC2) művelet szerepel az éleken. Ezért a zárt kör átviteli függvényének nevezőjében nem szerepel majd a két hurok vegyes szorzata, csupán a két hurokátviteli függvény GH1 és GH2.
A Ger eredő átviteli függvény azon átviteli operációk eredője, amelyek az adott kimenetet és bemenetet „egyenes” úton összekötik, azaz a hurkok hatását itt nem kell figyelembe venni.
A fentiek könnyebb megértéséhez emlékeztetőül álljon itt a jelfolyam gráfok szabályaira vonatkozó néhány fontosabb összefüggés:
Átviteli függvény független hurkok esetén:
|
|
Átviteli függvény elemben, vagy csomópontban kapcsolt hurkok esetén. Ez az eset fordul elő a vizsgált rendszerben:
|
|
A rezgéscsillapító esetében az elvi összefüggés tehát az alábbi:
A számítási lépések jól követhetők, ha először a két hurokátviteli függvényt írjuk fel:
Továbbá
A következő lépésben összeadjuk a két hurokátviteli függvényt:
A továbblépés csak akkor megengedett, ha elvégeztük a dimenzióellenőrzést, és mindent rendben találtunk. A zárt szabályozási kör karakterisztikus polinomja a GH1+GH2 eredő átviteli függvény nevezőjének és számlálójának összege.
A méretek, a helyigény miatt, a karakterisztikus polinom általános alakját írjuk fel, és az együtthatókat külön adjuk meg:
A kifejezések bonyolultak, ezért elvégeztünk egy ismételt dimenzió ellenőrzést, ezúttal azt vizsgáltuk, hogy az a4/a0…a1/a0 együttható osztások eredményeként valóban s4…s (másodperc hatványai) dimenziókat kapunk-e. Az eredmény jó, tehát van értelme a továbblépésnek.
Amikor az előre vivő átvitelt felírjuk, nem szabad elfeledkeznünk a két hurok összegének nevezőjéről, mert ez volt az „emeletes” tört nevezője, midőn a K(s) polinomot létrehoztuk.
Az alábbi kifejezéssel ugyanis a Ger(s) átvitelt szorozni kell!
Nézzük a jelfolyam gráf alapján a VA(s)/FZ(s) átviteli függvényt, azaz az asztalra ható zavaró erőhatás kompenzálását:
A zárt kör átviteli függvénye erre a bemenetre és kimenetre, azaz az erőátvitelre, vagy csillapításra:
Az átviteli függvény azonnal mutatja, hogy a passzív rezgéscsillapítóhoz képest nem sok változás történt. A szemiaktív pneumatikus rezgéscsillapító is sávszűrőként működik az erő bemenetre, csupán a Bode diagram meredeksége változott, hiszen a rendszer negyedrendű lett a másodrendű helyett, bár a számlálóban lévő zárójeles kifejezések rontják a szűrő-karakterisztika meredekségét.
Ha a szabályozott szemiaktív rendszer födém sebesség átvitelét nézzük, akkor első lépésben le kell szögezni, hogy az így vizsgált rendszernek nincsen köze a valóságos ultrapracíziós technikákhoz. Mindazonáltal jeleztük korábban, hogy elképzelhető egy olyan rendszer, amelyben hasonló pneumatikus szabályozással, de nagyságrendekkel nagyobb vF gerjesztő amplitúdóval dolgozunk. Ilyen rezgéscsillapítók már az 1980-as években készültek pl. a holdjárművekben történő alkalmazásra, de nem voltak publikusak. Érdekességük, hogy a talaj egyenetlenségét a jármű elé pozícionált lézersugár segítségével, mintegy „előre” mérték. Ha a feladatot általánosítjuk, akkor az eddig látott módszerrel, a jelfolyam gráf alapján levezethető ez az átviteli függvény is. A levezetést nem visszük végig, csak az eredményt mutatjuk be. Gyakorlás céljából az ellenőrzést az olvasóra bízzuk. Az átviteli függvény számlálójában ismét meg fog jelenni a kiemelhető „s” operátor, azaz a rendszer erre a gerjesztésre is sávszűrőként fog működni. Ennek oka a pneumatikus szabályozóban lévő integrálás, amelynek során a vA jelből a szelepkonstrukció xA elmozdulást hoz létre. Az átviteli függvényből kiolvashatjuk, hogy a rendszer normális működésének feltétele, hogy a mechanikai csillapítás nagyobb legyen, mint a fojtószelep ellenállásából számított egyenértékű csillapítás. Magyarra fordítva: Ilyen típusú rezgéscsillapító esetében teljesen felesleges a két kamra (és közöttük a fojtás) alkalmazása, a tervező ilyesmivel csak a saját baját szaporítaná.
Az ultraprecíziós technikák szempontjából sokkal fontosabb annak vizsgálata, hogy a szemiaktív pneumatikus rezgéscsillapító milyen körülmények között képes a padlózat (födém) alacsonyfrekvenciás rezgéseit csillapítani. Mielőtt felírjuk a sebesség átvitel függvényét, fontolóra kell venni minden valóságos feltételt.
A jelfolyam gráf ebben az esetben módosul, ki kell kapcsolnunk a pneumatikus szabályozókört, mert korábban már hosszan értekeztünk arról, hogy a kis amplitúdójú födémrezgések nem képesek működésbe hozni a szelepet. A sebesség átvitel tekintetében a szemiaktív pneumatikus rezgéscsillapító tehát passzív rendszerként működik, amely természetesen másodrendűnél magasabb rendszámú.
Nézzük tehát a módosított jelfolyam gráfot, a kikapcsolt szabályozással:
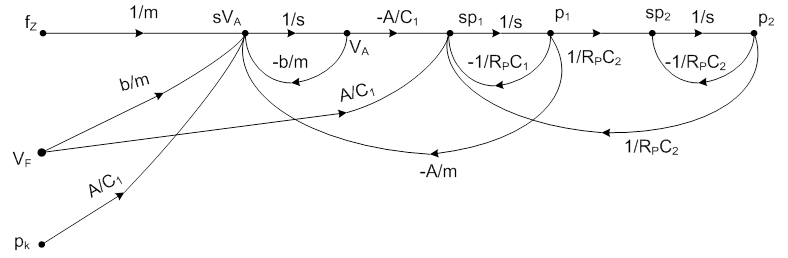
Megváltoznak természetesen a GH1 és GH2 hurkok:
A két hurok összegének kiszámítása szükséges a karakterisztikus polinom meghatározásához:
A fenti törtfüggvény számlálójának és nevezőjének összege lesz a keresett átviteli függvény karakterisztikus polinomja. Tekintettel arra, hogy az összefüggés terjedelmes, az együtthatókat ismét külön tüntetjük fel. Tekintettel arra, hogy elmarad a szabályozásból az integráló jelleg, a rendszer csak harmadrendű lesz.
ahol
A dimenzió ellenőrzés elvégzése után továbblépünk és a jelfolyam gráf alapján felírjuk a keresett átviteli függvény előre vivő ágát, de nem szabad elfeledkezni az átviteli függvény nevezőjében létrehozott közös nevezővel való szorzásról sem, hiszen „emeletes” törttel van dolgunk:
Tekintettel arra, hogy a két kamra közötti pneumatikus fojtásból kiszámított egyenértékű csillapítás sokkal nagyobb, mint a gördülő membrán csekély csillapítása bP>>b, a fenti képletben a legelső tagot elhagyjuk. A két sebesség ezután ellenfázisú lesz (negatív előjel).
Ilyen feltételek mellett a keresett átviteli függvény az alábbi formát nyeri:
A dimenzióellenőrzést sikeresen végrehajtottuk. Ezt követően sajnos megállapítható, hogy matematikai úton is igazolást nyert a feltételezés: A szemiaktív pneumatikus rezgéscsillapító a kis amplitúdójú födémrezgésekre nem aktiválja a szelepet, és ennek folytán a rendszer a passzív rezgéscsillapítókhoz hasonló módon aluláteresztő szűrőként működik, azaz az alacsony frekvenciás rezgéseket csillapítás nélkül átengedi az asztalra.
A megoldás tehát egy aktív rendszer kidolgozása, amely esetében a födém sebesség folyamatos mérése mellett lehetséges a rendszerbe szabályozott erő érintésmentes bevitele. Amikor a födém felfelé mozdul, az erőhatásnak az asztalt lefelé, a födém irányába kell húznia, és fordítva. Ezek a dinamikus erők természetesen lényegesen kisebbek, mint azok a statikus erők, amelyeket a pneumatikus szabályozókör segítségével kompenzálunk (asztal szintszabályozása).
Kérdés tehát, hogy mi lehet az az erő generátor, amely megfelelő függvénnyel megfogalmazott parancs alapján, érintésmentesen erőt képes vinni a rendszerbe?
14.3. Aktív mechatronikai rezgéscsillapító szakaszának tervezése
Az előző fejezet végén feltett kérdésre adunk választ, amikor aktív mechatronikai rendszer tervezését tűzzük ki célul. A módszeres tervezéshez ismét vissza kell nyúlnunk arra a jelfolyam gráfra, amely a légrugós mechanikai rezgéscsillapítót ábrázolta, de annyit módosítunk, hogy a számítások egyszerűbbé tételére a két pneumatikus kamrát egyesítjük. Ez a gyakorlatban a fojtószelep kinyitásával történik. A két kamra egyesítése a frekvenciamenetben a görbe meredekségének csökkenését eredményezi, mert a rendszám csökken, a meredekség -40 dB/dekád helyett -20 dB/dekád lesz.
Az egykamrás pneumatikus, szemiaktív rezgéscsillapító struktúra gráfját a módosítás után kapjuk. Az elképzelésünket „belefogalmaztuk” a gráfba, a födém (padlózat) és az asztal közé kapcsolt kompenzáló erőforrás fkomp formájában. Ebben az esetben tehát nem a szokványos modellezési utat járjuk, ami lényegében analízis, hanem szintetizálni kívánunk egy új rendszert.
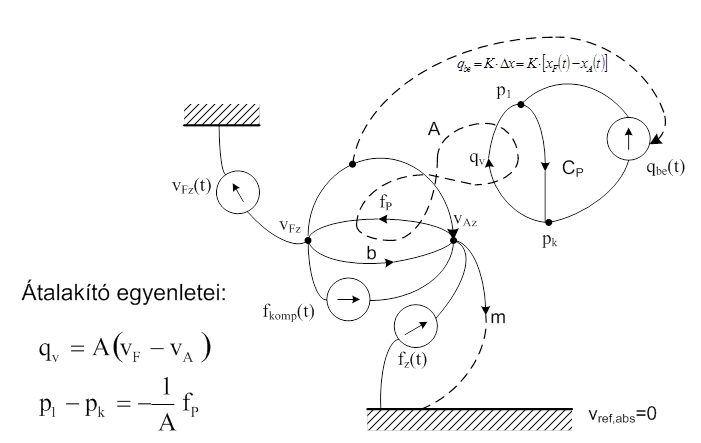
A gráfon látható elképzelést működési modell, pontosabban szabályozástechnikai tömbvázlattal kombinált formában is megrajzolhatjuk, ezt mutatja a következő ábra. A képen két szabályozó rendszert látunk. A baloldali az ismert, és korábban részletesen levezetett szemiaktív pneumatikus, értéktartó szintszabályozást ábrázolja úgy, hogy lényegében a légrugó rugómerevségét változtatjuk. A baloldali szabályozókör tehát a (nagy) statikus erők (terhelés) kompenzálására alkalmas. A jobboldali már egy új szabályozókör, amelyik a dinamikus erők kompenzálását lenne hivatva elvégezni.
A mechanikai referencia problémát figyelembe véve ennek a szabályozásnak a megtervezése nem egyszerű feladat. Látjuk a struktúra gráfon, hogy a nehézségi erőtér erre a célra nem használható ki, a szabályozott erőgenerátort fizikailag csak a födém (padlózat) és a védett tömeg közé lehet kapcsolni. Jelen ismereteink szerint érintésmentesen csak villamos (elektromechanikus) úton lehet a szerkezet adott két pontja közé erőt bevinni. Az elektrosztatikus út a rendszer méreteit és az egyéb körülményeket figyelembe véve ezúttal nem jöhet szóba. Így nem marad más, mint az elektrodinamikus elv, amely a rendszerhez adaptálva csak úgy képzelhető el, hogy a permanens mágneses mezőt szolgáltató állandó mágnes (esetleg gerjesztett elektromágnes) a tömege miatt a padlózaton kerül elhelyezésre, és a mágneskör légrésében érintésmentesen lineáris mozgást végző un. merülő tekercs az asztal aljára van erősítve.
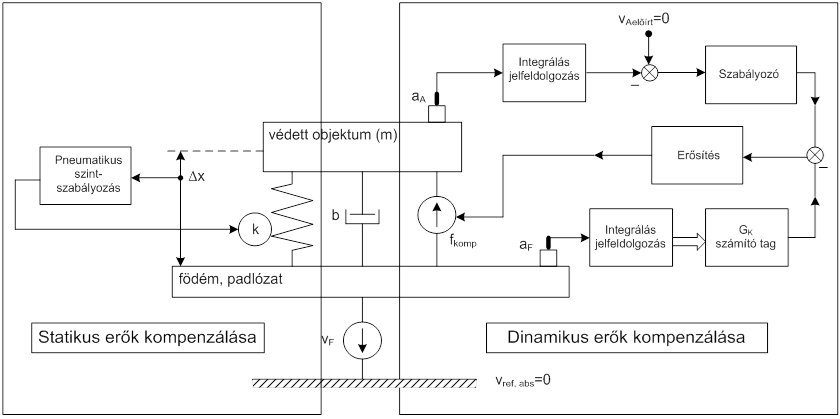
További igen fontos kérdés, hogy mi legyen az alapjel? Már leírtuk, hogy „panta rei”, azaz minden mozgásban van, tehát a szint (magasság), azaz az elmozdulás, illetve szint nem lehet fix érték. Az asztal gyorsulása sem lehet alapjel, mert aA(t)=0 esetében az állandó sebesség lehetséges, és ez nem kívánatos. Hála a rendszertechnika változóinak (kanonikus változók) éppen az asztal vA(t) sebessége az, amelyik alapjelként felhasználható. Gondot csak az egyenes vonalú mozgás „abszolút” sebességének mérése jelent, erről a későbbiekben még lesz szó. Az abszolút jelző, arra utal, hogy a mérés során a sebességet a nehézségi erőtér vonatkoztatási rendszeréhez viszonyítottan kell értelmezni. Ilyen eszközök a szeizmikus (elektrodinamikus) sebességérzékelők.
A jobboldali szabályozókör szabályozója PD jellegű, hogy a lineáris motor L/R időállandója által okozott törést kompenzálni lehessen. Ezzel a körrel a továbbiakban nem foglalkozunk, legyen elég annyi, hogy a szabályozó paramétereit a szakasz konkrét paramétereinek ismeretében számítottuk ki, és állítottuk be a 35° körüli fázistartalékot.
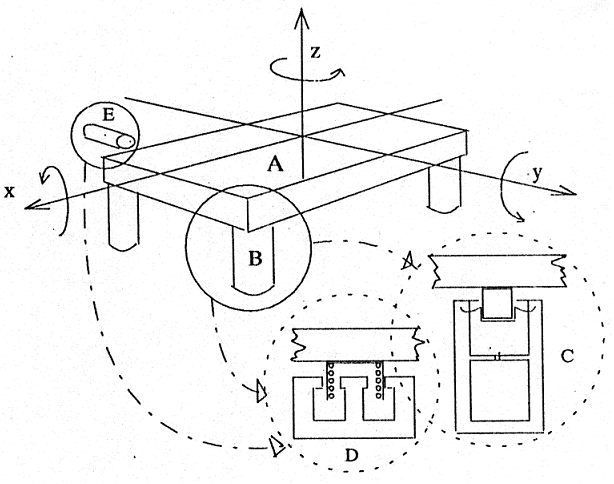
Az új, aktív rendszer felépítésének vázlatát a következő ábra mutatja.
A 3D vázlaton „A” jelöli az asztal lapját, „B” a négy alátámasztás, amelyekből három kettős rendszerből áll, a „C” pneumatikus (egy, vagy kétkamrás) láb pneumatikus szintszabályozással a statikus erők kompenzálására, és „D” az elektrodinamikus lineáris motor a dinamikus erők kompenzálására, ez mind a négy lábazatnál van. A „B” alátámasztások közül egy passzív, csupán a kívánt asztal-szint beállítására szolgál. Az „E” jelű elektrodinamikus erő-kompenzátorra csak akkor van szükség, ha a pneumatikus lábak gördülő membránjai nem tudnak megfelelően működni, a dugattyúk nem állnak a láb tengelyében, és a „z” tengely körüli gerjesztő nyomatékokat más módon nem lehet kompenzálni.
A leírtaknak megfelelően kiegészítjük a struktúra gráfot a lineáris motor elektromechanikus váltójával. A váltó egyenleteinek meghatározása nem automatikus, hiszen a mechanikai rendszer két pontja egymáshoz képest relatív mozgást végez. Ezért az elektrodinamikus váltó egyenleteinek meghatározására külön gondot fordítunk.
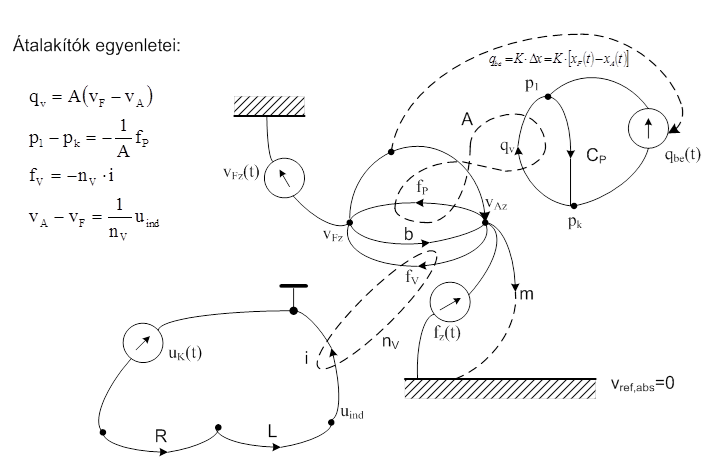
A struktúra gráfon látszik, hogy a villamos rendszer referenciája „lebeg”, nincs sem a padlózathoz, sem a tömeghez kötve, és ez az elektrodinamikus erő-becsatolás nagy előnye. A szabályozásokat a következők során szétválasztjuk. A következő ábrákon és a levezetéseken a pneumatikus szintszabályozás már nem fog megjelenni, mert az a nagy, statikus erők kompenzálását szolgálja. Figyelmünket a dinamikus erők kompenzálására fogjuk koncentrálni, ezek igen kis amplitúdójú rezgésekkel kapcsolatosak.
Elsőként meg kell határozni az elektrodinamikus váltó egyenleteit.
A merülő tekercs árama által átjárt vezetődarab, és a mágneses indukció hatására keletkező Lorentz erő iránya közötti kapcsolat nem jelent gondot. A relatív mozgás miatt nem ilyen egyszerű az indukált feszültség előjelének meghatározása. A mozgó alkatrészek egymáshoz való viszonyát és a légrésben mozgó tekercsben indukálódó feszültség előjelét gondos elemzés alapján kell leírni. Ezt segíti a következő ábra, amelyen a tekercs egy darabját megvastagított vonal jelöli. A vezető darab +vA és –vA sebességgel mozoghat a mágneses mezőhöz képest merőlegesen, miközben a mágneses mezőnek a sebessége +vF és –vF lehet. Ezeket a sebességeket abszolút értelemben kell venni, a vonatkoztatás, akárcsak a mechanikában, a vref=0.
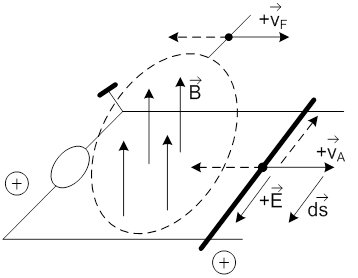
Az alábbi táblázatban, az első két oszlopban úgy jelöltük a tekercs és a mágneses mező (padlózathoz kötött) sebességeit, mintha azok egy abszolút referencia ponthoz képest mozognának.
|
Δv A tekercs |
Δv F mágn. indukció |
arány |
||
|
↑ + |
↓ - |
+ |
+ |
|
|
↑ + |
↑ + |
+ |
+ |
|
|
↑ + |
↑ + |
- |
- |
|
|
↓ - |
↓ - |
- |
- |
|
|
↓ - |
↓ - |
+ |
+ |
|
|
↓ - |
↑ + |
- |
- |
A táblázat alapján felírható a keresztváltozók közötti váltó egyenlet, tehát a feszültség előjele és a két mechanikai pont egymáshoz viszonyított mozgása tehát egyenlet formájában rendelkezésre áll.
A váltó átmenő változók közötti egyenlete:
14.4. A dinamikus erő kompenzátor uk(t) bemenő jelének meghatározása
Célunk, hogy a lineáris motorral kiegészített mechanikus-pneumatikus rendszer matematikai modellje alapján meghatározzuk azt az uk(t), illetve Uk(s) bemenő függvényt, amellyel a lineáris motor a dinamikus erő kompenzációt a lehető legtökéletesebben képes megvalósítani. A háromféle matematikai modell közül a legsokoldalúbban az állapottér modell használható.
A struktúra gráf alapján, az állapottér modell megalkotásához, a villamos részre hurokegyenletet, a mechanikai és a pneumatikus részekre pedig célszerűen csomóponti egyenleteket írunk fel, és ahogy már jeleztük, a statikus erők pneumatikus szintszabályozását nem tárgyaljuk újra, azt a szemiaktív rezgéscsillapítóval foglalkozó fejezetben már megtettük.
Emlékeztetünk arra, hogy a modellezés módszereivel foglalkozó fejezetben megmutattuk azt, hogy energia átalakítókat tartalmazó rendszerekben (kizárólag ezeknél) lehetséges a hurok és csomóponti módszer vegyes alkalmazása, ha az így kapott modell egyszerűbben kezelhető. Az elektrodinamikus váltó és a pneumatikus fordító váltó egyenletei nélkül a fenti három egyenlet nem kapcsolható össze.
A fizikai egyenletek behelyettesítése után rendezzük az egyenleteket az állapotjelzők deriváltjára:
A teljesség kedvéért felírjuk az állapottér modellt mátrixos formában is, de nem ezt az alakot használjuk az átviteli függvények felírására, mert a mátrixos számítás körülményes és nem szemléletes.
Az állapottér modell mátrixos alakban:
Az eredeti célunkhoz a jelfolyam gráf által kínált rajzos, és könnyen áttekinthető úton juthatunk el a legkönnyebben, ezért az állapottér modellt jelfolyam gráfon ábrázoljuk. További előny a dimenziók és előjelek ellenőrzésének egyserűsége a jelfolyam gráfon.
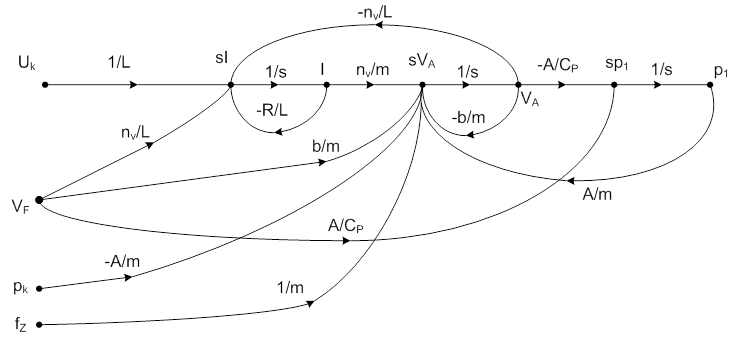
A gráfon baloldalra csoportosítottuk a gerjesztéseket. Következetesen operátor tartományban ábrázoltuk az állapottér modellt, ezért az integrátorok bemenetén az állapotjelzők „s” operátorral való szorzatát tüntettük fel. Ha lehetséges, akkor a nagybetű a változó Laplace transzformáltjára utal. A nyomás esetében pl. ezt nem lehet alkalmazni. A bemenetek közül, a dinamikus erőkompenzáció szempontjából számunkra a VF és az Uk igazán fontosak. A pk külső nyomást feltüntettük, de ennek változása valós esetben nem befolyásolja a rendszert, mert az ultraprecíziós technikában, laboratóriumi körülmények között, biztosítani kell az állandó és előírt légnyomást, páratartalmat és légnedvességet. Azokat a dinamikus gerjesztő erőket, amelyek nem a födém (padlózat) rezgése révén ébrednek az asztalon, fz jelöli, és ezek kompenzálását külön meg fogjuk vizsgálni.
A probléma megoldása szempontjából kulcsfontosságú az, hogy a jelfolyamon a VF gerjesztés (padlózat rezgés) fizikai adottságok miatt három úton hat az asztal VA sebességére, amelyet elképzelésünk szerint ideálisan zérusra szeretnénk csökkenteni. A három út az elektromechanikus (nV/L), a mechanikus (b/m) és a mechanikus-pneumatikus (A/CP). Tekintettel a kiinduláskor rögzített elvre, miszerint Vref ≠ VF, tehát a VF sebességgel kötelesek vagyunk számolni, nem marad más, mint a jelfolyam gráf segítségével és VF figyelembe vételével új utat keresni. Ennek az új útnak a meghatározása a szerző PhD disszertációjának egyik sarkalatos tézise volt.
A jelfolyam gráf mintegy „felkínálja” a megoldást. Ha VF kiküszöbölhetetlen, akkor nem tehetünk mást, mint minél pontosabban mérjük az értékét. Keresünk egy olyan átviteli tagot, amelynek bemenetére ezt a VF zavaró jelet rákapcsolva olyan Uk villamos kimenő jelet kapunk, amely a lineáris motort (megfelelő kompenzációval) működtetni képes.
Átviteli függvényekkel leírva a kompenzáció az alábbi módon valósítható meg.
Kitűzött célunk az alapjelnek megfelelően: VA=0
Mik ezek az átviteli függvények?
|
GF=VA/VF |
Sebesség átviteli függvény a födém és asztal között (fizikai „adottság”) |
|
|
GU=VA/Uk |
A lineáris motor kapocsfeszültsége és az asztal sebessége közötti átvitel |
|
|
GK=VA/Uk |
A keresett kompenzáló tag átviteli függvénye |
Ha létezik, tehát műszaki szempontból realizálható a GK átviteli tag, akkor VF precíz mérése révén el tudjuk érni, hogy az asztal a födém rezgései ellenére nyugalomban maradjon, azaz VA=0 legyen. Természetesen vF(t) méréséről van szó, de az operátor térben történő tárgyalás miatt nem „ugrálhatunk” ide-oda.
A keresett GK átviteli taggal kiegészítettük az alább látható jelfolyam gráfot. A szükséges matematikai modell meghatározásának lépései a gráf segítségével jobban követhetőek.
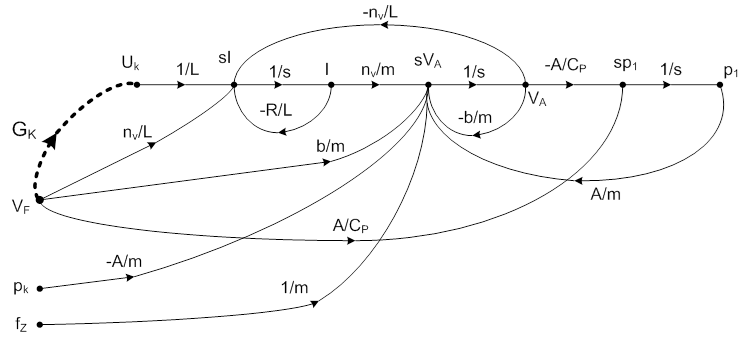
A cél tehát, hogy VA=0 legyen. VA-hoz „szerencsére” két út vezet, a természetes átvitel, azaz GF=VA/VF továbbá a kompenzációs céllal megtervezett GK-n és GU-n keresztül ugyanezen két jel között.
A gráfban két, elemben kapcsolt (összefüggő) hurok ismerhető fel, ezért az átviteli függvény nevezőjében a csak két függő hurokátviteli függvény összege szerepel, vegyes tag nincsen:
A VF természetes átvitele három rendszertípuson keresztül valósul meg. Ez három fizikai út az átviteli függvény számlálójában három átvitel összegeként jelenik meg. Érdemes, és tanulságos a jelfolyamon követni ezt.
Tudjuk az impedancia egyenérték átszámítás révén, hogy:
azaz a légrugó rugómerevsége. Behelyettesítve pneumatikus rugómerevséget, egyszerűbbé válik a dimenzió ellenőrzés:
Végül a kP egyenértékű rugómerevség kiszámításához hasonlóan a villamos ellenállás egyenértékű bR mechanikai csillapítását is meghatározhatjuk, és ezzel egyszerűbb alakú lesz az átviteli függvény, és egyszerűbb a dimenzió ellenőrzés is. Íme, tehát a sebesség átvitel a födém és az asztal között. Amint várható volt, az aluláteresztő szűrő jelleg változatlanul megmutatkozik.
Nézzük ezek után, hogy a lineáris motor kapcsai felől miként írható fel az átvitel. Az átvitel Uk kapocsfeszültség bemenettel azt jelenti, hogy érintésmentes a kompenzáló erő bevitele a rendszerbe elektromechanikus úton.
A két hurokátviteli függvény természetesen változatlan:
A dimenzió ellenőrzés a normált alak felhasználásával hajtható egyszerűen végre:
Természetes, fizikai adottság az asztal VA sebessége, ami a födém felőli VF gerjesztésre jön létre, ezt a GF(s) átviteli függvénnyel írtuk le. Ugyanakkor beiktattunk a rendszerbe egy olyan erőgenerátort, ami érintésmentesen (súrlódásmentesen) képes kompenzáló erőt bevinni a rendszerbe, ez az elektrodinamikus, lineáris, merülő tekercses motor. A motor kapocsfeszültsége felől is kaptunk VA-ra egy átviteli függvényt, ez a GU(s).
Célunk, hogy találjunk egy olyan GK(s) kompenzáló átviteli függvényt, amellyel GU(s)-t beszorozva, VF felől a két út algebrai összege zérust ad. Ebben az esetben az asztal a referenciához képest nyugalomban lesz VA=0.
Levezettük, hogy keresnünk kell egy olyan GK átviteli tagot, amelyre igaz, hogy:
Elvégezzük GK kiszámításához a két átviteli függvény osztását. Ez egyszerű művelet, mert mindkét átviteli függvény nevezője szükségszerűen azonos, így csupán a számlálókkal kell foglalkozni. (Azonos rendszer két különböző változója között írtuk fel az átviteli függvényeket, tehát a nevező, a karakterisztikus polinom nem változhat.)
Dimenzióellenőrzést végzünk, és megállapítjuk, hogy a kapott komplex függvény dimenziója helyes, azaz GK(s)[Vs/m].
Látjuk tehát, hogy létezik olyan sorosan kapcsolt kompenzáló átviteli függvény, amely biztosítja, hogy bármilyen VF gerjesztésre a VA=0 előírás megvalósulhasson.
A keresett kompenzáló tag a gyakorlatban három párhuzamosan kapcsolt, és fázist forgató tagot jelent (negatív előjel):
A deriváló tagot kiegészítettük az elengedhetetlen nevezővel, ahol természetesen törekszünk a T→0 feltétel teljesítésére. Ettől kezdve azonban a kompenzáló tag mind digitális algoritmussal, mind analóg kapcsolással megvalósítható. A három párhuzamosan kapcsolt tagot valós PID szabályozónak tekinthetjük.
Méréstechnikai szempontokat is figyelembe véve el kell gondolkodni azon, hogy adott feltételek között hogyan lehet a födém sebességének mérését egyszerűen, de kis hibával megoldani. Három változatot vizsgálunk meg:
-
Mérjük a födém abszolút sebességét, és a jel deriválását, valamint integrálását rábízzuk a GK átviteli függvény által kijelölt algoritmusra. Van olyan eszköz, amely a födém (talaj) abszolút sebességét méri alacsony frekvenciás tartományban, csak kissé robosztus, még a hordozható verziója is. (A MEMS eszközök a kérdéses alacsony frekvenciás tartományban nem mindig alkalmazhatók.) A szeizmikus abszolút sebességmérőt a földrengésvizsgálat céljaira alkalmazzák. A mérőberendezés működésének elve elektrodinamikus. Egy extrém lágy rugón felfüggesztett tekercs mozog függőlegesen a talajon (padlózaton) elhelyezett műszerházhoz képest. A műszerházban egy „edény-mágnes” van rögzítve, ennek légrésében mozog a rugalmasan felfüggesztett tekercs. Persze ahhoz, hogy a talaj sebességével mozgó mágneskör, követve a talaj mozgását, el tudjon mozdulni a felfüggesztett tekercshez képest, és így a sebességkülönbséggel arányos villamos feszültség jöjjön létre, nem csak „lágy” felfüggesztés, hanem az alacsony frekvenciás mérési tartományra való hangolás miatt nagy rezgő (lengő) tömeg (tekercs-hordozó) is szükséges. Nyilvánvaló, hogy ilyen eszközt finommechanikai konstrukciós ismeretek nélkül építeni nem lehet, mert a nagy tömeg a lágy rugót lehetetlen mértékig megnyújtaná. Ezt a problémát kiküszöbölve, a szeizmikus abszolút sebességmérőben keresztcsuklós csapágyazással, egy kar végére függesztik fel a szeizmikus tömeget, a kart pedig tengelyvonalában szabályozható rugóerővel feszítik a csapágyazás irányában a műszerházhoz.
-
Mérjük az abszolút gyorsulást. Erre a célra - az adott alacsony frekvenciás tartományban - különlegesen alkalmas eszköz a szeizmikus induktív gyorsulásérzékelő. A piezoelektromos gyorsulásérzékelő ebben a frekvencia tartományban nem alkalmazható. A (idő tartományban) mért aF jel egyszeres integrálásával az abszolút sebességet (vF), kétszeres integrálással pedig az abszolút elmozdulást (xF) lehet előállítani. A GK kompenzáló tag átviteli függvényének bemenete az abszolút sebesség, így csupán egyetlen integrátorra van szükség.
-
Abszolút elmozdulás érzékelő „direktben” a gyakorlatban nem megvalósítható, mert a födém (talaj) mikro rezgései áttevődnek a falakra is. Nincs olyan referencia (viszonyítási) pont, amely „teljesen” nyugalomban lenne. Az „abszolút” elmozdulás mérésének gondolatát el kell vetni.
Az alfejezet címében megfogalmazott feladat teljesült, tudjuk, hogy a lineáris motor kapocsfeszültségét milyen átviteli tag segítségével lehet előállítani.
Befejezésül bemutatjuk a teljes rendszer szabályozástechnikai tömbvázlatát. A „teljes” rendszer alatt az un. aktív „egylábat” értjük, azaz az asztallap nem végez kismértékű forgó mozgásokat sem.
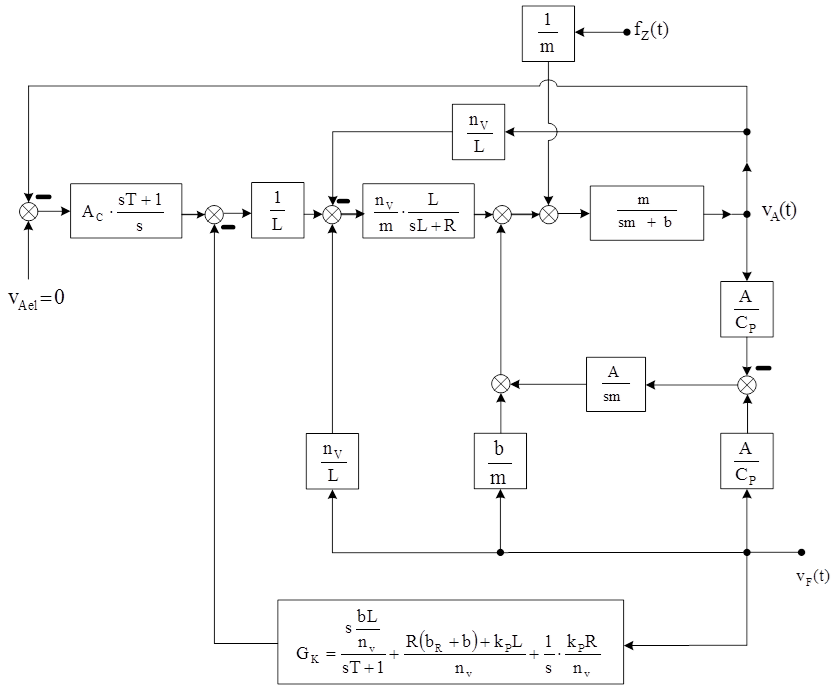
14.5. A kompenzáló hatás igazolása kísérleti modellen végzett mérésekkel
Az eddigi elméleti vizsgálatokat olyan modelleken végeztük, amelyek esetében nem vizsgáltuk a rezgéscsillapító rendszerek 3D viselkedését, úgy tekintettük, mintha a födém és az asztal kizárólag függőleges mozgásokat végezne. Ha feltételeztünk is az asztal esetében térbeli kiterjedést, a modelljeink megalkotásakor nem vettük figyelembe az asztal súlypontján átmenő x és y tengelyek körüli forgást. Bár a rezgéscsillapítók több lábon állnak, az eddigi modellek esetében az asztal minden pontja azonos sebességgel mozgott függőleges irányban.
Ez az egyszerűsítés az átviteli függvények (szemiaktív és passzív rendszerek sebesség és erő átvitelei) egyszerűbb kezelhetőségét és a kompenzáló tag meghatározását szolgálta.
A kompenzáló tag matematikai modelljének meghatározása után bemutatunk néhány kísérleti eredményt, amelyek laboratóriumi körülmények között születtek, és amelyek során ugyancsak kizárólag a függőleges mozgásokat vizsgáltuk, forgás nélkül.
Annak érdekében, hogy a jelenségek méréstechnikai feldolgozása egyszerűbb legyen, építettünk egy olyan rázóasztalt, amely a födém függőleges mozgását volt képes felnagyítva utánozni, 0.01…30 Hz tartományban, diszkrét szinusz sebesség gerjesztések formájában. A födémet reprezentáló síklapon állítottuk fel az aktív rezgéscsillapítót, amely már nem modell, hanem egy olyan rendszer, amelyet kisebb mikroszkópok rezgéscsillapítására szokás alkalmazni. Az asztal három, szabályozott pneumatikus lábon állt, síkja vízszintes volt, és az asztal lapja alatt, annak súlyvonalában rögzítettük az asztalhoz a lineáris motor tekercsét. A motor állandó mágnes-köre a födém-modellhez volt rögzítve, a légrésben a tekercs nem súrlódott. A kompenzáló tagot egy elektronikus kapcsolóval a szabályozókörtől le lehetett választani, illetve visszakapcsolni. A födém és az asztal sebességét integrálással állítottuk elő, egy-egy induktív gyorsulásérzékelő jeleit felhasználva. Ellenőrzésképpen a födém-imitáción elhelyeztünk egy hordozható szeizmikus sebességmérőt is. Az integrálással nyert sebesség jelek és a direktben mért sebesség egyezősége megfelelő volt.
A levezetéseink eredményeit igazolták azok a mérések, amelyek a kompenzáló tag bekapcsolása nélkül születtek, és amelyek közül négy jellegzetes példa a (14.21. ábra) ábrán látható.
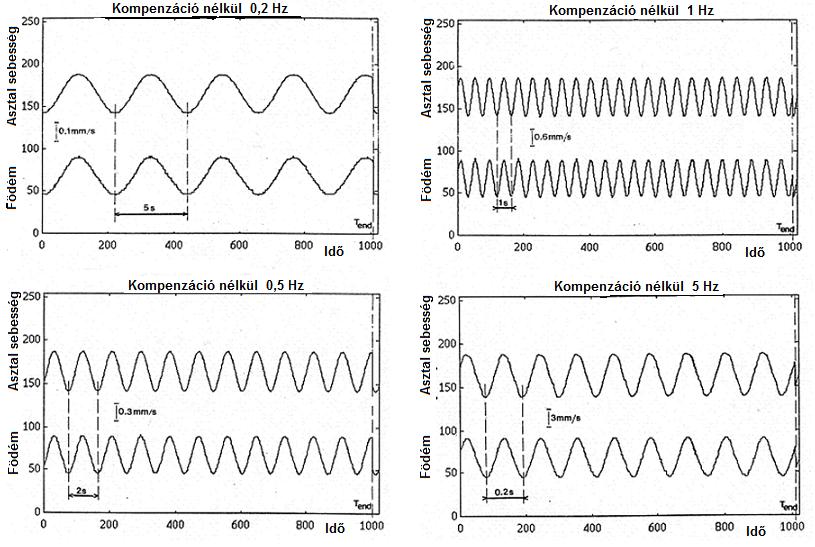
Látjuk a (14.21. ábra) ábrán, hogy a födém és az asztal sebessége, a kompenzációs tag működtetése nélkül, a négy kiválasztott alacsony frekvencián azonos. A szemiaktív pneumatikus rezgéscsillapító rendszer szelepei a födém kis rezgés amplitúdóinak hatására nem nyitnak, a rendszer passzív rezgéscsillapítóként, aluláteresztő szűrőként működik, pontosan úgy, ahogy a fejezetben bemutatott négy gyártmány adatlapjain látható frekvenciamenet mutatja.
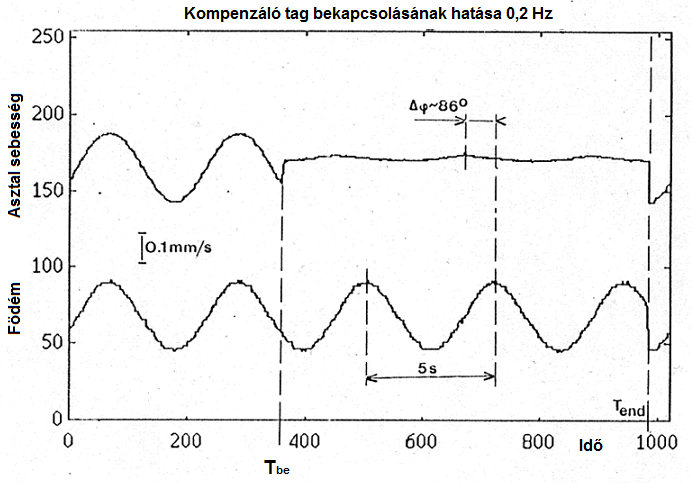
A (14.22. ábra) ábrán folyamatában mutatjuk be azt, hogy mit eredményez 0.2 Hz-es födémgerjesztésnél, ha Tbe időpillanatban bekapcsoljuk a kompenzáló tagot. Az asztal födémet követő harmonikus mozgása csaknem teljesen megszűnik, és amit látunk, az tulajdonképpen egy 40 dB-lel kisebb sebesség amplitúdó, némi fázistolással. Azt, hogy az asztal mozgása teljes mértékben megálljon, az adott kísérleti berendezés, a kompenzáló tag függvényének közelítő jellege, a gyorsulás jelek integrálása és a mérési zajok miatt nem várhatjuk. Ugyanakkor kétséget kizáróan igazolást nyert, hogy a kidolgozott kompenzáció elve működik.
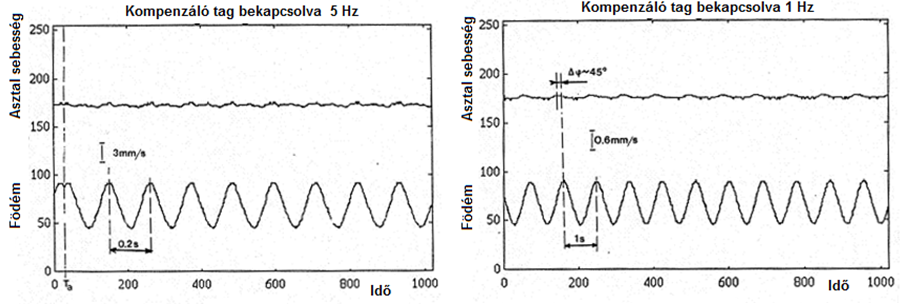
A bekapcsolási folyamat mellett, a (14.23. ábra) ábrán az aktív rezgéscsillapító működése látható, két jellegzetesen alacsony frekvencián, amelyek az épületrezgésekre jellemzőek. A kompenzáló hatás mérésekkel egyértelműen beigazolódott.
A modellkísérletek után, amelyeket kisebb méretű berendezésen végeztünk, érdemes kiterjeszteni a vizsgálódást nagyobb szerkezetekre, amelyek esetében már nem feltételezhető, hogy az asztal minden pontjának függőleges sebessége azonos, és az sem, hogy az asztal lábazatok alatti födém is azonos frekvenciával és fázisban rezeg.
14.6. Aktív rezgéscsillapító 3D modellje és szabályozása
Lássuk tehát, miben változik a modell, ha a védendő objektum (asztal) térbeli kiterjedései – főként az x-y síkban - nagyobbak. Az aktív rezgéscsillapító négy lábazaton áll, amelyek a statikus erőkompenzációt pneumatikus értéktartó szabályozókörrel biztosítják. A négy láb közül három szabályozott, a negyedik csak a kívánt szint beállítására szolgál. Ugyanakkor minden láb mellett találunk egy-egy lineáris motort, amelyek a födém felől érkező sebesség gerjesztések hatásának kompenzálását szolgálják. A rendszer matematikai modelljének megalkotásához szükség van a következő ábrán látható vázlatra. A vázlaton csupán a modellhez szükséges mozgásokat és a változók közötti kapcsolatokat tüntettük fel. A lábazatok belső felépítése pontosan megegyezik a 14.2. szakasz fejezetben látható egy-és kétkamrás pneumatikus lábakéval, ezért azok nem szerepelnek a vázlaton.
Az ilyen jellegű rezgéscsillapító asztalok forgása a „z” tengely körül nem lehetséges, ha a gördülő membránok szakszerűen vannak szerelve. Az „x” és „y” tengelyek körüli, kismértékű forgás teljesen normális, hiszen egy ilyen asztal méretei 2m x 1.5m-nél kezdődnek. Anyaguk gránit, vagy gyakrabban könnyűszerkezetes konstrukció, amelynek alsó és felső lapjai között függőleges elrendezésű méhsejt-merevítés található.
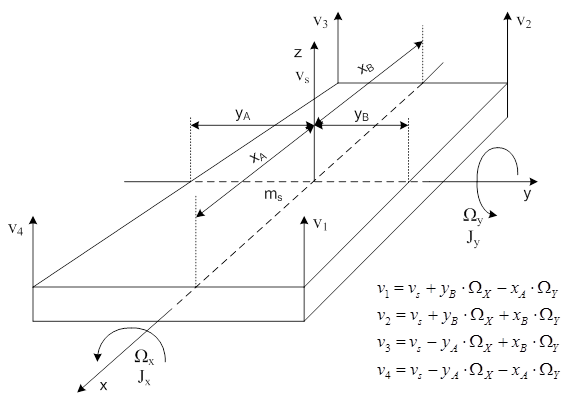
Amint a vázlaton látható, feltételeztük, hogy a födém a négy lábazat alatt nem azonos amplitúdóval és frekvenciával rezeg, ugyanakkor az asztallap sarkainak sebessége a merev mechanikai rendszer miatt természetesen meghatározott. Az asztal sarkok sebességei, amelyek nem állapotjelzők, hanem kiadódó értékek, a vázlat jobb alsó részén láthatóak. A merev asztallap súlypontjának vs függőleges sebessége és a súlyponton átmenő „x” és „y” tengely körüli forgások szögsebességei lesznek az állapotjelzők.
A csupán függőleges mozgást végző rezgéscsillapító gráfjának felhasználásával megszerkeszthető az a struktúra gráf, amelyik már a lehetséges térbeli mozgások figyelembevételére is alkalmas. Ezt a gráfot látjuk a következő ábrán. A részletek ismétlődése miatt választottuk ezt a térbeli elrendezést. A három szemiaktív és egy passzív pneumatikus láb a négy sarokban, középen a tömeg mozgása, alatta és felette a tengelyek körüli forgás miatti tehetetlenségi nyomatékok.
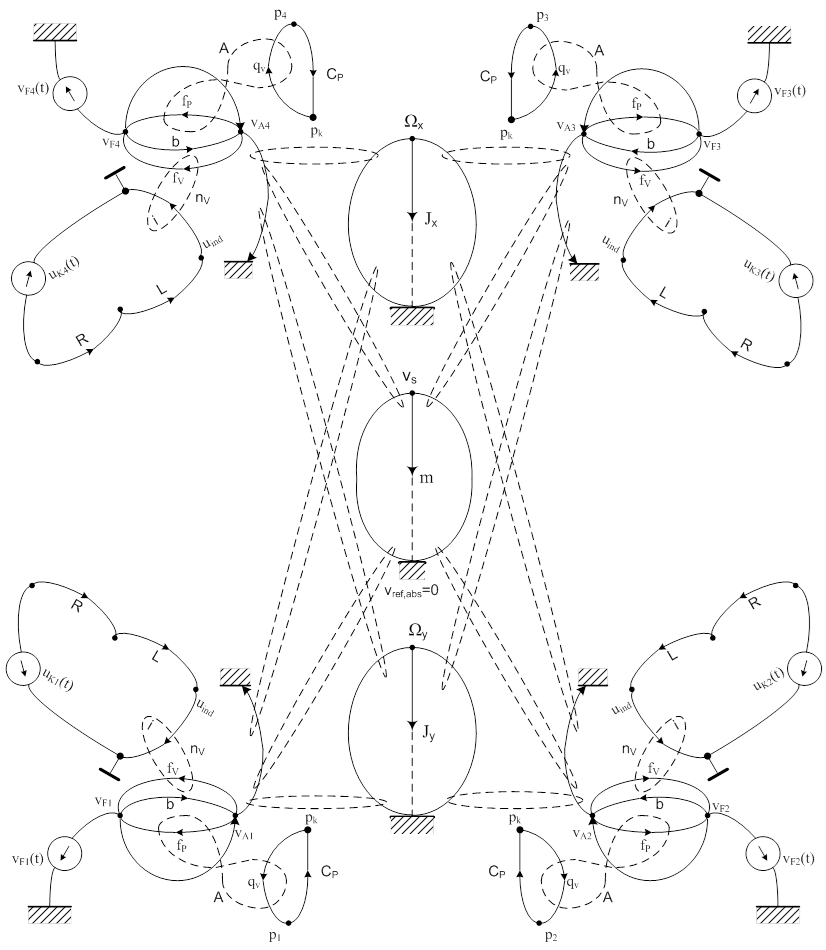
Az áttekinthetőség kedvéért a mechanikai váltók és transzformátorok (egyenes és forgó mozgások közötti kapcsolatok) állandóit nem rajzoltuk a gráfba. A kapcsolódást jelentő egyenletek egy csoportját (keresztváltozók közötti kapcsolatok) a 3D vázlat alsó részén láthatjuk. Ugyancsak nem tüntettük fel a négy kompenzáló tagot és a szabályozás többi elemét sem, a gráf csak a szakasz matematikai modelljének felírására szolgál.
A matematikai modell csak állapottér lehet, mert a paraméterek és állapotjelzők nagy száma miatt más modell kezelhetetlen lenne. Állapottér mellet szól az is, hogy a továbbiakban szimulációk segítségével kívánjuk bemutatni azt az összetett mozgást, amelyet az aktív rezgéscsillapítású asztal a térben végez.
Mielőtt felírnánk az állapotegyenleteket, definiálnunk kell az állapotjelzőket. A súlypont sebességét, a két tengely körüli szögsebességeket már említettük. További állapotjelzők a négy lineáris motor tekercs árama, és az egykamrás légrugós lábakban uralkodó belső nyomás. A vizsgálatot ebben a jegyzetben kétkamrás lábazatokra kiterjeszteni terjedelmi korlátok miatt lehetetlen.
A 11 állapotjelző tehát a következő:
A terjedelmi korlátok miatt, az eddigiektől eltérő módon nem írjuk fel a gráf alapján a hurok és csomóponti egyenleteket, csak a számítások eredményét adjuk meg. Ezek az rendszermátrixból és az átalakítók egyenleteinek alkalmazásával rekonstruálhatóak.
Az rendszermátrix elemeinél látható, hogy feltételeztük a következőket:
Mind a négy láb CP pneumatikus kapacitása azonos, azonosak a lineáris motorok nV állandói és R, L paraméterei.
A 3D vázlaton láthatók az asztalra vonatkozó xA, xB, yA, és yB távolságok, illetve kararányok.
A bemeneti és kimeneti mátrixokat nem mutatjuk be, a méretek hasonlóak, bár az oszlopok száma kevesebb. Bárki számára belátható az rendszermátrix szemlélése alapján, hogy ilyen rendszám mellett a „kézi” megoldás reménytelen vállalkozás, de egyben értelmetlen is.
Pontosan azért mutatjuk az olvasónak ezt az összetett mechatronikai rendszert, hogy érzékeltessük a digitális számítógépes szimulációban rejlő nagy lehetőségeket.
A következő ábrákon a szimulációs eredményeket láthatjuk. Tekintettel arra, hogy az ábraszövegek idegen nyelvűek, az alábbi magyarázatot adjuk:
|
PLOT 1…8 |
Görbék sorszáma |
|
|
ECKE 1…8 |
Asztallap sarkainak sebessége, a 3D vázlat sorrendjének megfelelően |
|
|
FUBOD 1…8 |
A födém lábazatok alatti sebessége |
A szimulációkat SI mértékegységekkel végeztük és az eredményeit természetesen SI mértékegységben (m/s) mutatjuk be.
A szimulációs eredmények bemutatása előtt természetesen leszögezzük, hogy a szimulációk során nem csak harmonikus gerjesztésekkel dolgoztunk, hanem nagy súlyt fektettünk a különböző sávszélességű, alacsony frekvenciás zajok hatásának vizsgálatára is. Ezek eredményeit terjedelmi korlátok miatt nem áll módunkban közölni.
Az első ábrán azt a szimuláltuk, hogy a négy lábazat közül három alatt a födém nyugalomban van, a negyedik alatt a födém sebességének amplitúdója kb. 2.5·10-2 m/s és a szinuszos rezgés frekvenciája 2 Hz. Az ábrafelirat szerint a kompenzáló tagok nincsenek bekapcsolva (ohne Rechnerglied: számító-kompenzáló tag nélkül) és látjuk, hogy az asztallap négy sarka nagyjából ugyanakkora sebesség amplitúdóval mozog, mint a födém. A görbék sejtetik, hogy igen bonyolult térbeli mozgásról van szó.
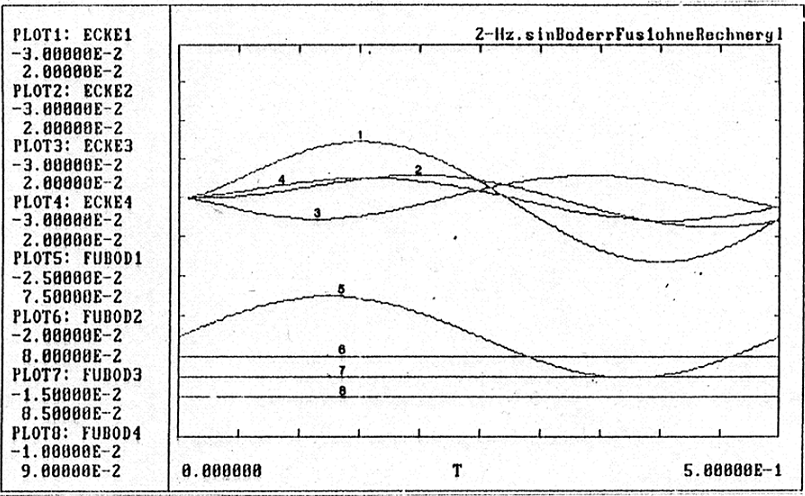
Nézzük, mit eredményez a szimuláció, ha a szabályozás mellett bekapcsoljuk a kompenzáló tagokat is.
Ezekből a szimulációs eredményekből mutatunk be egyet.
A szimulációban alkalmazott födémgerjesztések célzottan eltérő frekvenciájúak minden láb alatt azért, hogy a szimulációban rejlő lehetőségeket vizsgálhassuk. A korábbi amplitúdóval, de ezúttal minden láb alatt más-más szinuszos frekvencián (0.5, 1, 2, és 4 Hz) gerjesztjük az aktív rezgéscsillapítót. És bár az 1…4 görbéken az asztal sarkainak szeszélyes mozgásait látjuk, a kompenzáció hatása tökéletes, mert az is látható, hogy 4 nagyságrend különbség van a födém sebességek amplitúdói (10-2 m/s=10 mm/s) és az asztal sarkok sebesség amplitúdói (3…5 μm/s !!!) között.
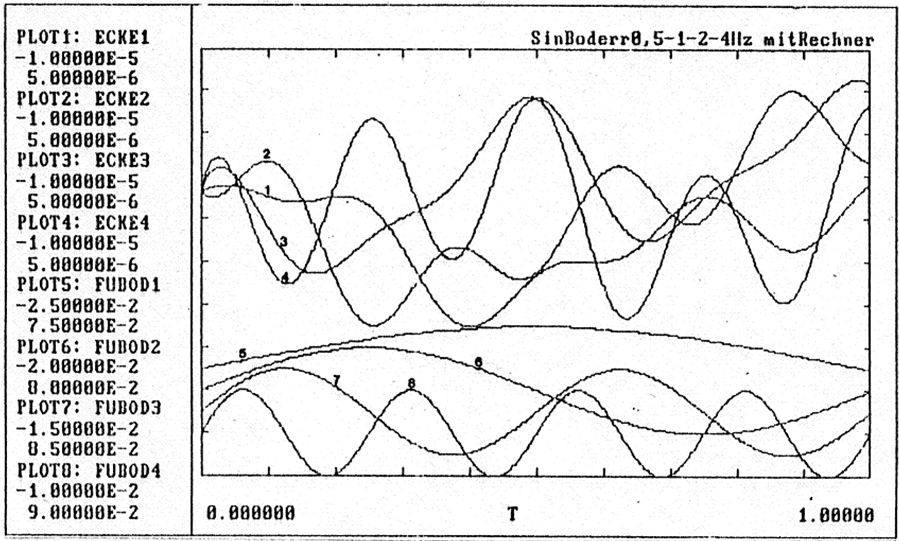
A mechatronikai aktív rezgéscsillapító hosszúra nyúlt tárgyalását befejezzük azzal a meggyőződéssel, hogy ez a fejezet jó összefoglaló példája a módszeres mechatronikai tervezésnek.
Íme, az aktív rezgéscsillapító, mint a mechatronika komplex rendszereinek egyik jellegzetes példája áll előttünk. A mechatronika definíciója akár ennek a példának a tanulmányozása után is megszülethetett volna. A definíció sarkalatos pontja ugyanis kimondja, hogy a mechatronikai az a berendezés, amelyben az elektronika/elektrotechnika, a gépészet és az informatika „szinergikus” egymásra hatása megnyilvánul. A hangsúly a szinergián van, amely kifejezés „egymást segítő”, „egymást kiegészítő” kifejezésekkel adható vissza magyar nyelven. A mechatronikai aktív rezgéscsillapítású asztal magasságának beállítása fém, vagy polimer rugóval nem megoldható. Meg kell jelenjen a szabályozható pneumatikus rendszer, a légrugó, hiszen szükség van a nagy statikus terhelések, erők szabályozható kompenzálására. Persze tudjuk, hogy a pneumatika is a gépészet szakterületéhez tartozik, de azért ez a terület mégsem a klasszikus műszaki mechanika világa. Ezt a statikus feladatot elektromechanikusan megoldani értelmetlen vállalkozás volna, hiszen esetenként 400…1000 kg tömeg elektrosztatikus, vagy elektrodinamikus „lebegtetetéséhez” aránytalanul nagy villamos energiára lenne szükség. Az áram által okozott hőterhelés azután éppen annak az ultraprecízós feladatnak a megoldását tenné lehetetlenné, amelynek a rezgésvédelmére az egész rendszert létrehoztuk. A födémrezgések okozta dinamikus erők, hiszen itt alacsony frekvenciákról és kis amplitúdójú sebességekről van szó, már könnyebben kompenzálhatók elektrodinamikus úton. A villamos megoldás azért is „kellemes”, mert a lineáris motor kapcsainak egyike sem kötött a mechanikai referenciához. Villamos oldalról a „beavatkozás” érintésmentes lehet, ha megfelelő aktuátort találunk. Informatika és szabályozástechnika nélkül a lineáris motor kapcsaira nem tudnánk eljuttatni azt a villamos jelet, amely a dinamikus erők megfelelő fázisban történő kompenzálását biztosítja.
A mai időkben, a műszaki életben, a hagyományokhoz való olyan típusú ragaszkodás, amely azt eredményezi, hogy szakemberek egy terület „felsőbbrendűségét”, vagy kizárólagosságát hirdetik, nem csak idejét múlt hozzáállás, hanem egyenesen veszélyezteti a tudományos haladást.
Az „egykerekezés”, mint cirkuszi mutatvány évszázadok óta ismert. Az instabil mechanikai rendszert a nyeregben ülő, gyakorlott ember „szenzorai” (belső fülhöz tartozó körkörös ívjárat), szabályozó rendszere (központi idegrendszere) és „aktuátorai” (izmai) stabilizálják. A mechatronikai segway attól mechatronikai, hogy az érzékelés, szabályozás és beavatkozás feladatát az elektromechanika és az elektronika vette át. Az alap rendszer ettől még egy instabil mechanikai (gépészeti) rendszer marad. A mechatronika a nemzetközi tapasztalatok szerint csak olyan szakemberek által művelhető hatékonyan, akik tisztában vannak azzal, hogy a mechatronikai rendszerek alapvetően gépészeti rendszerek. Az első mechatronikai szakkönyveket is végzett, elsődlegesen gépész, vagy villamosmérnökök számára írták [1.1.]. A mechatronikai mérnökök olyan szakemberek, akik birtokában vannak a műszaki mechanika, a gépszerkezettan, a konstrukció, a CAD, a végeselemes modellezés és az anyagtudomány nélkülözhetetlen ismereteinek, de „közös” nyelvet képesek beszélni a villamosmérnökökkel és az informatikusokkal, feladatokat tudnak megfogalmazni és az eredményt szakszerűen ellenőrizni. Képesek esetenként maguk is egyszerűbb villamos, vagy informatikai problémák megoldására.
Szakirodalom
[14.1.] Mechatronischer Schwingungsisolator für die Ultrapräzisionstechnik Dissertation. Technische Universität Ilmenau. 1994.
[14.2.] Shock and Vibration Handbook. McGraw-Hill. 1976.
[14.3.] Harris’Shock and Vibration Handbook. McGraw-Hill Handbooks. 2009.
[14.4.] Szabályozások dinamikája. Akadémiai Kiadó. Budapest . 1974.