15. fejezet - CD-fej fókusztávolság szabályozásának tervezése és szimulációja
A CD-fej (optikai egység, angolul Optical Pick Up, röviden OPU) igazi mechatronikai szerkezetnek tekinthető, mechanikai, villamos és optikai részegységek együttese beépített szabályozóval. A CD fej speciális kialakítású rugós vezeték rendszere a hengerlencse több irányú mozgatását teszi lehetővé a hozzá csatlakoztatott lineáris merülő tekercses motorok segítségével. Ebben a fejezetben a hengerlencse és a CD lemez közötti – precízen tartandó – fókusztávolságot mint szabályozott jellemzőt fogjuk vizsgálni.
Először összefoglaljuk röviden a fókuszáló rendszer, mint szakasz 6.4. szakasz fejezetben bemutatott dinamikus modelljét, majd ezt követően helyzetszabályozást tervezünk a megkövetelt pontosságú beállításhoz.
A CD lemez 120 mm átmérőjű, 1,2 mm vastag, fröccs-sajtolással előállított műanyag (polikarbonát, PVS vagy akril) alapú korong. Az átmérőre megengedett eltérés legfeljebb 0,5 mm, vastagságban legfeljebb 0,01 mm. Az excentricitás megengedett legnagyobb értéke 50 µm.
Az adatok belülről induló spirálon tárolódnak, a spirál két szomszédos (azonos sugárra eső) szakasza egymástól 1,6 μm távolságra esik. A bináris 0 és 1 értékeknek a bevonatrétegben kiemelkedések (bordák) és mélyedések (angol elnevezéssel pit) felelnek meg. Az információt hordozó pitek hosszúsága eltérő.
A lemez lejátszásakor a spirális sávra fókuszált lézersugár a lemez hátoldalán lévő rétegről verődik vissza. A bordákról sokkal több fény verődik vissza, mint a mélyedésekből. (A pitek kialakítása olyan, hogy az aljukról és tetejükről visszaverődő nyalábok egymást kioltó interferenciája miatt gyakorlatilag nincs visszaverődés.)
A CD lemezeknél az adatokat tartalmazó szektorok fizikai hosszúsága állandó. A lemez forgási sebessége éppen ezért nem állandó, különben a spirál olvasófejhez viszonyított sebessége a sugár mentén eltérő lenne. A fej és a lemez egymáshoz viszonyított állandó sebességét, az állandó lineáris sebességet (CLV, Constant Linear Velocity) úgy biztosítják, hogy változtatják a forgási sebességet annak függvényében, hogy a lemez melyik részét kell éppen olvasni. A spirális sáv minden pontján állandó letapogatási sebességet biztosító fordulatszám-szabályozást szokták állandó kerületi sebességű szabályozásnak is nevezni.
A letapogató rendszer mozgatását lineáris motorral biztosítják. A lézerdiódát a kibocsátott fényt irányító, polarizáló, tükröző, felfogó elemekkel együtt egy egységbe, az optikai fejbe szerelik. Ennek része a fókuszálást biztosító lencsét mozgató két-tengelyű (optikai tengely irányú és sávra merőleges) elem, amelynek egyik tengely menti elmozdulása a fókuszt szabályozza, a másik a pit-sávon való haladást biztosítja.
A lemez deformációja (vetemedése) miatt bekövetkező fókusztávolság változás dinamikus után-állítása és az excentricitásból származó sávkövetési hibák elhárítása elengedhetetlen a pontos olvasáshoz.
A fej mindkét tengelye mentén szükséges a szabályozás. A lencsét mozgató rendszerben lévő négy csuklós mechanizmus mozgását (Lorentz-erő segítségével) lineáris motor biztosítja. A homogén mágneses mezőt két mágnes hozza létre. A fejben lévő két egymásra merőleges tekercs vége a mágneses mezőben van. A tekercsen átfolyó áram hatására a Lorentz-törvény értelmében erő hat a tekercsekre és így a fejre. A csuklók lehetővé teszik a mozgást, miközben megőrzik a síkok párhuzamosságát.
15.1. Matematikai modell előállítása
A CD-fej egyszerűsített modelljében a villamos részt egy soros RL-körrel adhatjuk meg, a mechanikai rész pedig egy tömeg-rugó-csillapítás rendszer. A villamos és mechanikai rendszer kapcsolatát a lineáris motor, mint elektromechanikai energiaátalakító (váltó) biztosítja.
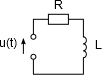
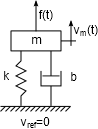
Az összekapcsolt rendszer modelljét struktúragráffal szemléltethetjük.
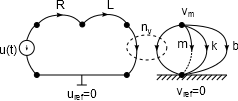
A váltó típusú energiaátalakító egyenletei:
|
|
(15.1) |
|
|
|
(15.2) |
ahol f [N] az erő, i [A] a villamos áram, v [m/s] a sebesség, u [V] a feszültség és nv [N/A=Vs/m] az energiaátalakító állandója.
A villamos rész egyenleteit a hurokmódszerrel írjuk fel
|
|
(15.3) |
A megfelelő feszültségeket a fizikai összefüggésekből kifejezve és az u(t) gerjesztést az egyenlet jobb oldalára rendezve
|
|
(15.4) |
A kapott egyenletet Laplace-transzformáljuk (zérus kezdeti érték feltételezésével).
|
|
(15.5) |
A mechanikai rész egyenletét csomóponti módszerrel írjuk fel
|
|
(15.6) |
A megfelelő erőket a fizikai összefüggésekből fejezzük ki (a tömeg vm sebességét v-vel jelölve a továbbiakban)
|
|
(15.7) |
A kapott egyenletet Laplace-transzformáljuk (zérus kezdeti érték feltételezésével).
|
|
(15.8) |
Az i áramot és a v sebességet választva állapotváltozóknak a rendszer mátrixos alakú állapotegyenlete
|
|
(15.9) |
A sebesség Laplace-transzformáltját, mint a feszültség Laplace-transzformáltjnak függvényét a fenti egyenletrendszerből fejezhetjük ki
|
|
(15.10) |
Először a törtet tüntetjük el a nevezőből, majd felbontjuk a zárójelet
|
|
(15.11) |
Az időállandós alakhoz átrendezve
|
|
(15.12) |
A G(s) átviteli függvény definíció szerint a kimenő jel Laplace-transzformáltjának és a bemenő jel Laplace-transzformáltjának hányadosa. Esetünkben a bemenő jel az U(s) feszültség, a kimenő jel a CD-fej függőleges elmozdulása, jele X(s)
|
|
(15.13) |
Mivel kimenetként a V(s) sebesség áll rendelkezésünkre, alkalmaznunk kell a sebesség és elmozdulás közötti (időtartományban deriválással adott) összefüggést.
|
|
(15.14) |
A feszültség és elmozdulás közötti átviteli függvény így
|
|
(15.15) |
Általános alakba átírva arányos harmadrendű rendszert azonosíthatunk
|
|
(15.16) |
A rendszer valóban harmadrendű, hiszen három független energiatárolója van:
-
a villamos oldalon az L [H] induktivitás
-
a mechanikai oldalon az m [kg] tömeg és a k [Ns/m] rugó
Részben saját mérések alapján, részben katalógusból választott adatokkal pontosan számíthatjuk az átviteli függvény együtthatóit.
|
Elektromechanikai energiaátalakító (váltó) |
nv = 0,0515 Vs/m |
|
Induktivitás |
L = 0,00039 Vs/A |
|
A CD-fej tömege |
m = 1,82 g |
|
Rugómerevség |
k = 25,7 N/m |
|
Csillapítási tényező |
b = 0,032 Ns/m |
|
Ellenállás |
R = 7 Ω |
15.2. A szakasz szimulációs modellje
A National Instruments cég LabVIEW (Laboratory Virtual Instrumentation Engineering Workbench) szoftvercsomagja (http://www.ni.com/labview/) 2009-es verziójában, a Control Design and Simulation Module (http://www.ni.com/labview/cd-sim/) elemkészletével készült az átviteli függvény szoftveres leképezése. A LabVIEW és a kiegészítő használatában a [15.1.], [15.2.], [15.3.] hivatalos források mellett szintén találhatunk interneten hozzáférhető segédanyagokat és mintapéldákat.
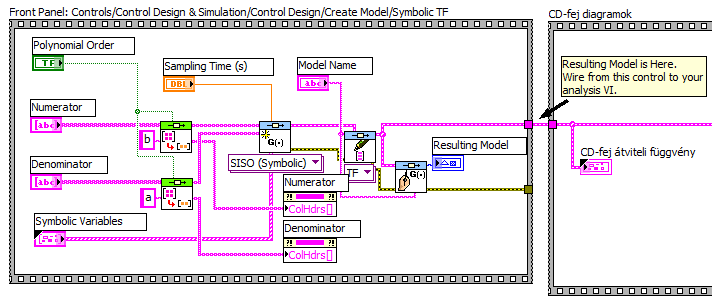
A paraméteres átviteli függvény a VI előlapján (Front Panel) a Controls/Control Design & Simulation/Control Design/Create Model paletta útvonalon elérhető Symbolic TF blokkal készült. Az alábbi ábra bal oldalán látható a program által létrehozott elemkészlet, a sárga nyíltól jobbra eső „CD-fej átviteli függvény” kijelző (Indicator) a programozási felületen (blokkdiagramon, Block Diagram) elkészült keret kimenetén a „Resulting Model is Here. Wire from this control to your analysis VI.” címkéjű kiemeneten Create Indicator paranccsal létrehozott gyári átviteli függvény (transfer function, TF) modellstruktúra.
A szimbolikus megadású átviteli függvény bemenet (Control) elemei:
-
Model Name (string): ide írhatjuk a modell nevét, esetünkben ez CD-fej
-
Sampling Time (s): mintavételes rendszernél itt lehet beállítani a másodpercben mért mintavételi időt. Példánkban folytonos rendszerrel dolgozunk, ezért marad az eredetileg felkínált 0 s mintavételi idő beállítás.
-
Polynomial order: a kiválasztott Descending (Mathscript) állapotban az átviteli függvény számláló és nevező polinomjában szereplő együtthatókat az s Laplace-operátor csökkenő hatványai szerint rendezzük, ahogy a levezetett matematikai modellben. A számításokban a másik lehetőségnek – Ascending (LabVIEW) – megfelelően, vagyis s emelkedő hatványai szerint rendezett együtthatókat találunk. Utóbbi alakban jelenik meg a „CD-fej átviteli függvény” nevű TF típusú modell a kép jobb oldalán.
-
Numerator: a számláló polinom együtthatóit adhatjuk meg paraméteres alakban ebben a Table Control (szöveges táblázat, vagyis string típusú elemek két dimenziós tömbje) adattípusú elemben. Egyetlen, b0-lal jelölt konstanst kell megadnunk, a levezetett matematikai modellben szereplő változónevekkel. A táblázat első sorában szerepelnek a b0, b1, b2, … általános paraméter nevek, számozásuk megegyezik a megfelelő s hatvány kitevőjével (a Descending értékűnek választott Polynomial Order miatt).
-
Denominator: a nevező polinom megadására szolgáló, előzőhöz hasonló felépítésű elem. A harmadrendű rendszer nevezőjében a0, a1, a2 és a3 általános paramétert adunk meg, a levezetett átviteli függvényben szereplő formulákkal.
-
Symbolic Variables: ez a beépített típusdefiníció (TypeDef) egy dimenziós tömbbe rendezve tartalmazza a tetszőleges sorrendben megadott, a számlálóban és nevezőben használt változókat. A változó neve (Name) string típusú, értéke (Value) double típusú (64 biten ábrázolt, 15 jegyes pontosságú) valós szám. A Name-Value párok cluster adattípusba vannak összefogva. A változó-érték párok sorrendje tetszőleges.
-
Resulting Model: kép (picture) típusú kijelző, a VI futtatása után itt jelenik meg a matematikai modell, jelen esetben a változók behelyettesítésével meghatározott numerikus átviteli függvény „szépírással” (azaz a kézíráshoz hasonló tört formában).
A számításokhoz használt átviteli függvény adattípusú elem az említett „CD-fej átviteli függvény” kijelzőn látható. Az adattípus két (további változókat tartalmazó) elemből álló cluster. A „properties” tartalmazza a kijelzőn látható „Model Name” és „Sampling Time” változók értékét. A „transfer function(s)” akár több bemenetű-több kimenetű (Multiple Input, Multiple Output, MIMO) lineáris rendszerek átviteli függvényeinek számláló és nevező polinom együtthatóit is tartalmazhatja. Egy átviteli függvény egy clustert foglal el, ahol a Numerator és Denominator double típusú számokból álló vektorok a számláló és a nevező polinom együtthatóit tartalmazzák, növekvő s hatványok szerint (azaz Ascending (LabVIEW) beállításnak megfelelően, szemben a szimbolikus megadásnál választott Descending (Mathscript) csökkenő hatvány szerint rendezett együtthatókkal).
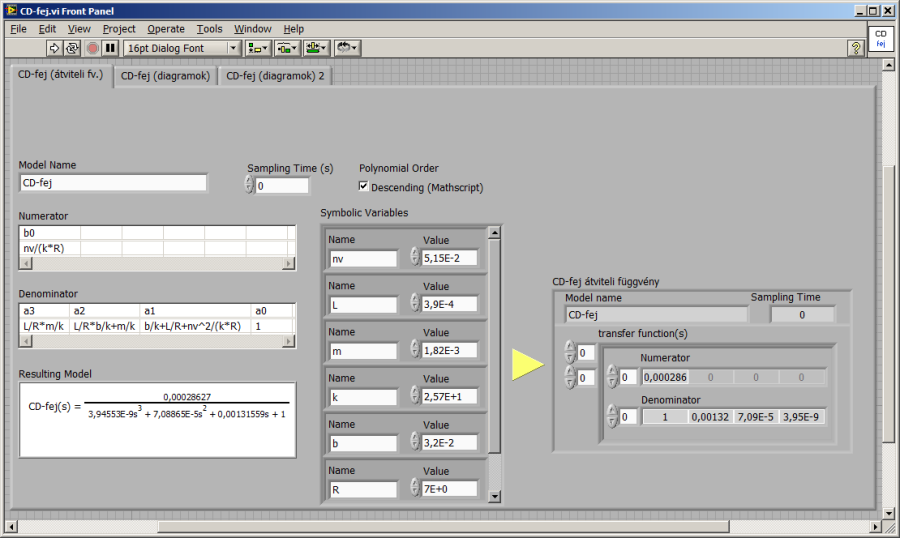
A következő ábra bal oldalán látható keretet (Sequence struktúrát) az előlapi, Controls/Control Design & Simulation/Control Design/Create Model paletta útvonalon elérhető Symbolic TF blokk választása hozta létre, megkímélve a felhasználót a számításokban használt formátumú átviteli függvény adattípus „saját erejű” előállításától (vagyis a szükséges LabVIEW programrészlet „megírásától”).
Az alábbiakban látható – „CD-fej diagramok” címkéjű, szintén Sequence struktúrába foglalt – programrészlet az átviteli függvénnyel adott rendszer jellegzetes idő- és frekvenciatartománybeli diagramjait és az átviteli függvény gyökeloszlását ábrázolja. A VI-ok a Control Design & Simulation/Control Design paletta útvonalon érhetők el, az alpaletták neve és az illető VI neve az alábbiakban szerepel, az ábrának megfelelően a blokkokat balról, majd fentről lefelé sorolva:
-
Dynamic Characteristics/CD Damping Ratio and Natural Frequency.vi: a pólusok jellemzőit számszerűen megadó blokk, kimenetei (egydimenziós double elemű tömb formában) a csillapítási tényezők (Damping Ratios) és sajátfrekvenciák (Natural Frequencies), valamint a pólusok (Poles) egydimenziós komplex (complex double, CDB) tömbként
-
Time Response/CD Step Response.vi: átmeneti függvény
-
Frequency Response/CD Bode.vi: Bode-diagrampár (amplitúdó és fázis)
-
Frequency Response/CD Nyquist.vi: Nyqusit-diagram (helygörbe), alapértelmezés szerint a (-∞,∞) (kör)frekvenciatartományban, ezt bírálja felül a bekötött „Frequency Range” cluster konstansban 0-ra átírt „Initial frequency” változó, így a [0, ∞) körfrekvencia (rad/s) tartományban rajzolunk (az alapértelmezett frekvenciát a -1 jelzi)
-
Dynamic Characteristics/CD Pole-Zero Map.vi: pólus-zérus eloszlás a komplex számsíkon
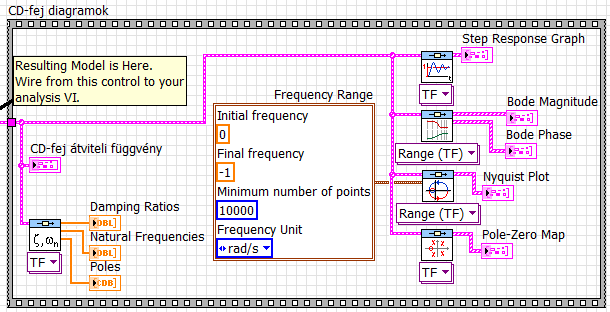
Az előlapi grafikus kijelzőket legegyszerűbben a fent felsorolt négy rajzoló VI megfelelő kimenetére jobb egérgombbal kattintva a „Create Indicator” menüvel készíthetjük el. Az egyes grafikus kijelzőket természetesen igény szerint módosíthatjuk, a példában láthatókon a vonalvastagságot növeltük. A kijelzők neve a program által adott, persze igény esetén ezt is változtathatjuk.
Valamennyi szimuláció SI mértékegységekkel történt. A soron következő, „.vi” fájlokkal megjelenített diagramokon az alábbi SI prefixum jelöléseket látjuk:
u: mikro; n: nano; m: mili
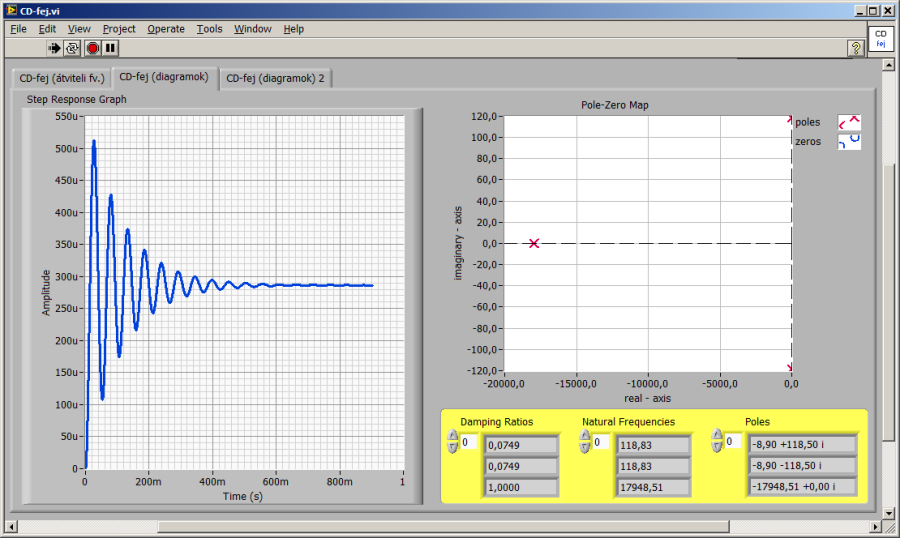
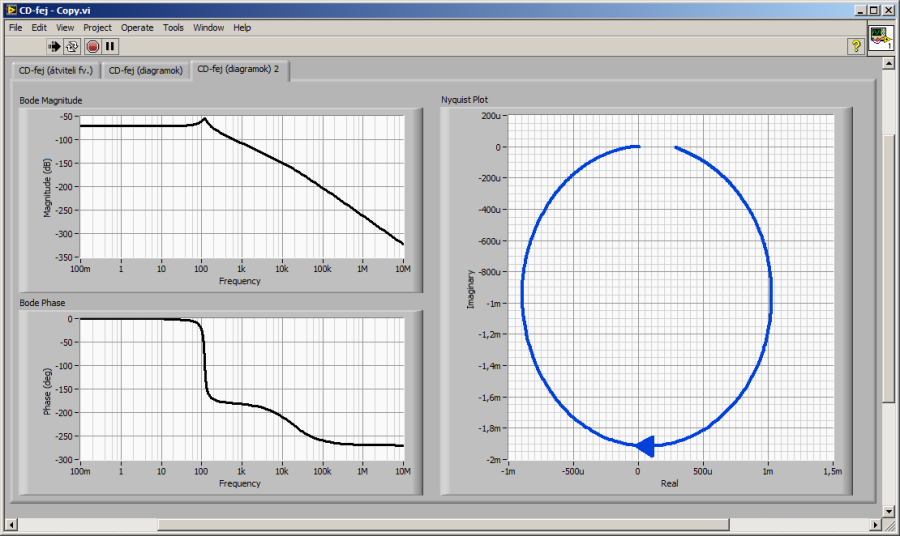
Az eredmények alapján felvetődik, hogy a legtávolabbi pólus elhanyagolásával vizsgáljuk a rendszert.
15.3. A modell egyszerűsítése a számított eredmények alapján
A konkrét paraméterek behelyettesítésével felírt átviteli függvény nevezőjének és a paraméteresen adott általános elsőrendű tag és másodrendű tag soros kapcsolásával előállított átviteli függvény nevezőjének egyenlővé tételével és az s hatványokra vonatkozó három egyenlet megoldásával kapjuk az elsőrendű tag T időállandóját, valamint a másodrendű tag ξ csillapítási tényezőjét és T0 időállandó jellegű paraméterét.
Az egyenletrendszer megoldásához a GNU GPL licenc által szabályozott hozzáférésű Maxima (http://maxima.sourceforge.net/) számítógépes algebra rendszert (a wxMaxima grafikus felületet) használjuk a COMA, COntrol engineering with MAxima (http://www.austromath.at/daten/maxima/zusatz/) kiegészítővel. A Maxima rendszer hivatalos dokumentációja [16.4.] mellett az interneten igen sok oktatóanyag és mintapélda található. A COMA (COntrol engineering with MAxima) szabályozástechnikai számításokat megkönnyítő kiegészítő [15.4.] angol és [15.5.] német leírása mellett mintapéldákat is letölthetünk.
A wxMaxima munkafüzetben szereplő számítások és az egyenletrendszer megoldásai az alábbi táblázatban szerepelnek.
Az elhanyagoláshoz szükséges wxMaxima számítások:

Az egyetlen szóba jövő megoldás az utolsó a listában (csupán itt szerepel három valós érték), ahonnan látszik, hogy T két nagyságrenddel kisebb T0-nál, tehát valóban elhanyagolhatjuk:
-
T = 5,571493182021775e-5
-
T0 = 8,4152416857412e-3
-
ξ = 0,074856931881115
A wxMaxima munkafüzet folytatásában szerepel az eredeti és az elhanyagolással számított átmeneti függvény összehasonlítása. Az átmeneti függvényt az átviteli függvény és az egységugrás gerjesztés Laplace-transzformáltjának szorzatából a COMA csomagban lévő numerikus inverz Laplace-transzformációval (nilt) határozzuk meg. és ábrázoljuk. A diagramról kiderül, hogy valóban igen kicsi az eredeti és az elhanyagolással előállított matematikai modell közötti eltérés.
Az eredeti és az elhanyagolással kapott rendszer átmeneti függvényének összehasonlítása wxMaxima+COMA felhasználásával:
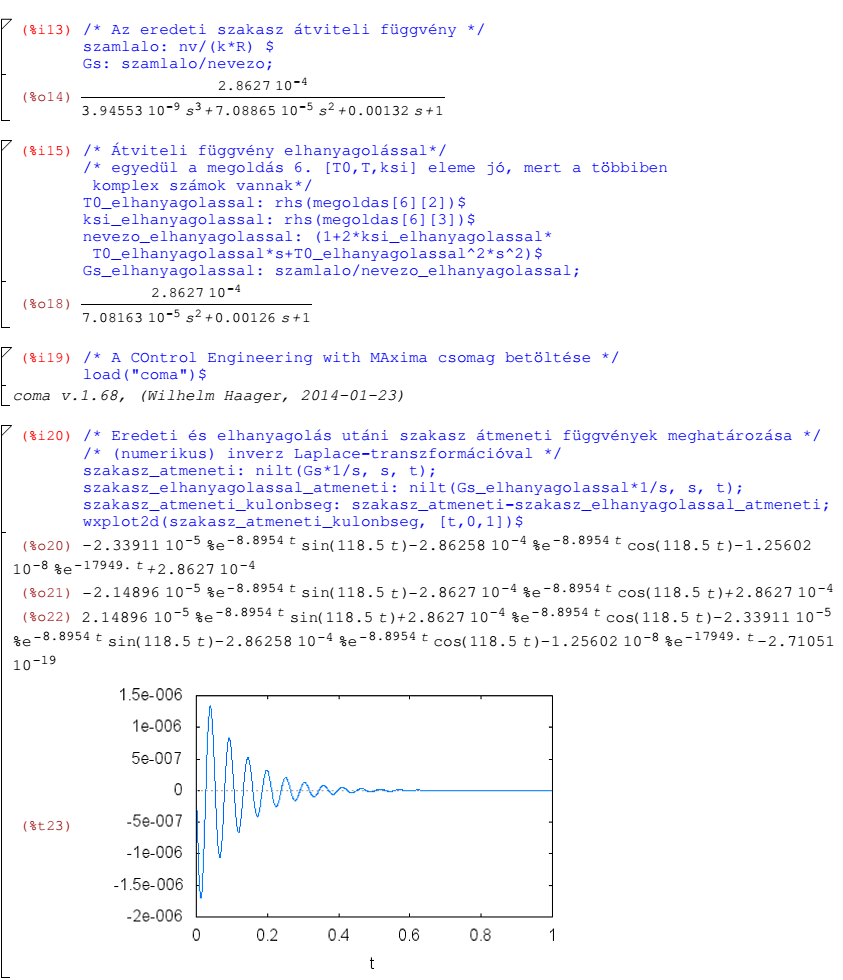
Az alábbiakban az eredeti harmadrendű és az elhanyagolás utáni másodrendű (lengő) rendszer LabVIEW-ban készített megfelelő ábrái szerepelnek.
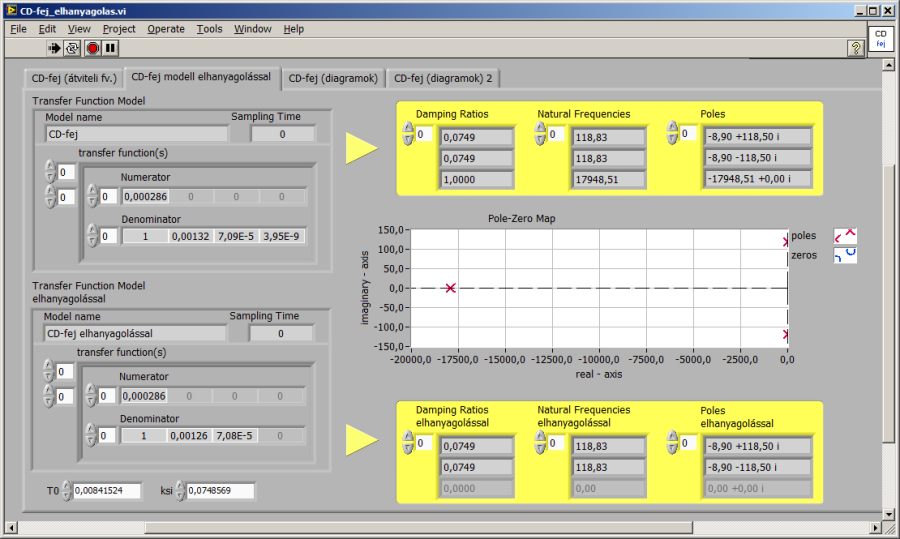
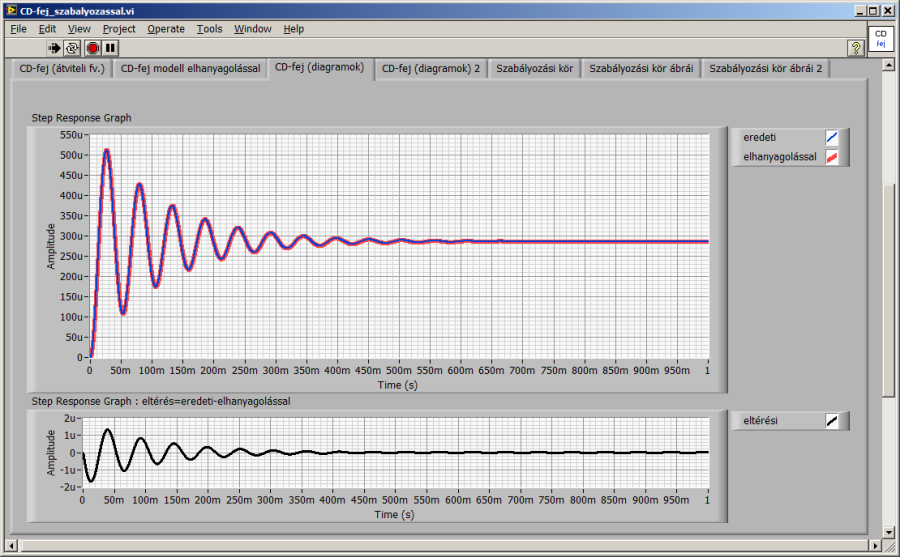
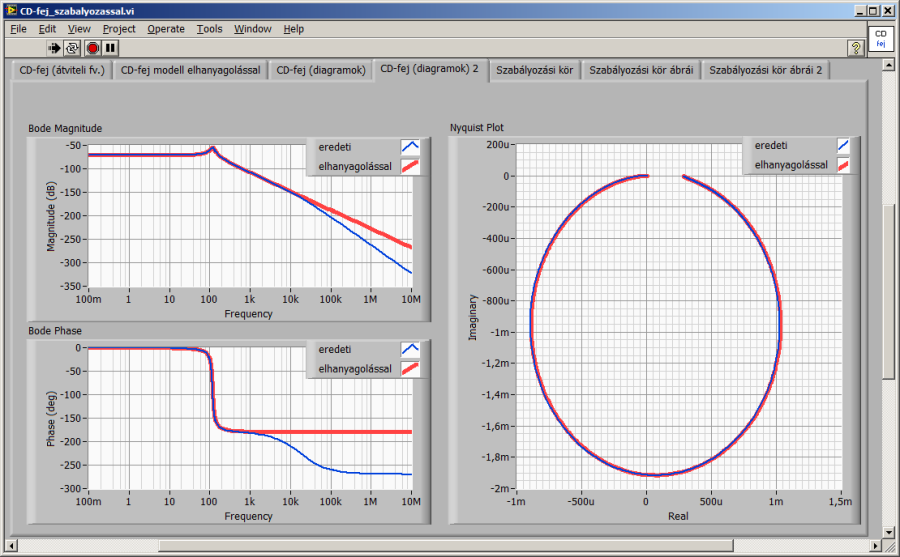
15.4. Szabályozás tervezése
A 6.4. szakasz fejezetből megismertük a szakasz matematikai modelljét, és láttuk a 15.1. szakasz fejezet végén a paraméterek kiindulási értékeit. Meggyőződtünk arról, hogy a szabályozókör tervezéséhez elegendő a szakasz másodrendű modelljét használni.
Kizárólag oktatási céllal, és nem „próbálgatással” megmutatjuk először azt, hogy a legegyszerűbb szabályozó, a P-tag nem elegendő a zárt kör optimálisnak tartott dinamikának beállításához beállításához. Ez az optimális viselkedés a legrövidebb beállási idő mellett, a legkisebb túllendülést jelenti. A tervezés folyamatában a szimulációs lépések ugyancsak oktatási céllal vannak részletezve.
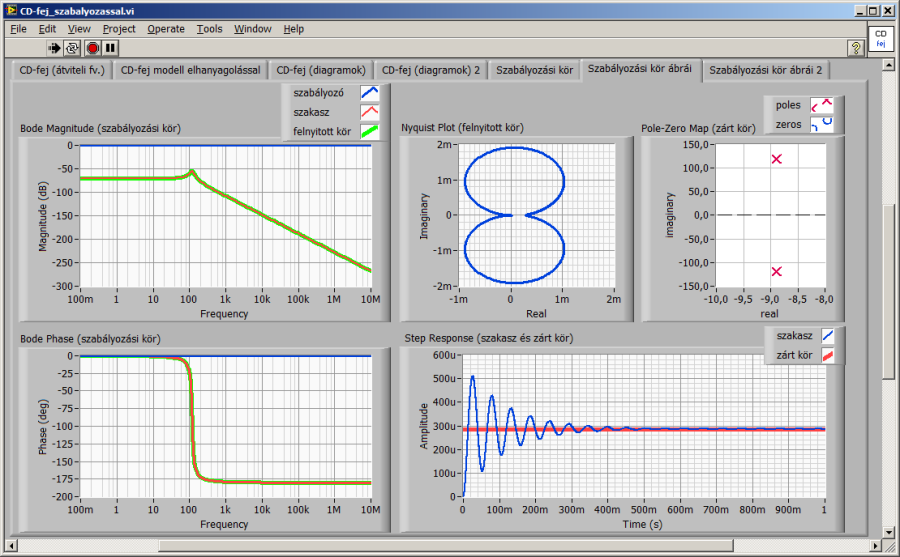
A szakasz átmeneti függvényből és a pólus-zérus térképből jól látszik, hogy a szakasz dinamikai tulajdonságai az elvárt stabilitású, gyorsaságú és pontosságú működést önmagában nem biztosítják. A gyors és előírt pontosságú pozícionáláshoz szükséges dinamikai tulajdonságoknak nem felel meg az átmeneti függvényen látható nagymértékű túllendülés és az ezt követő viszonylag lassan csillapodó lengés. A csillapítás kicsi ugyan, de óriási előny, hogy a rugalmas egyenes vezeték kizárólag a Kelvin-modellnek megfelelő belső csillapítással rendelkezik, semmiféle gördülő, vagy csúszó mechanikai vezeték nem okoz problémát a maradó hiba formájában. Ehhez, a kis csillapítású szakaszhoz mindenképpen szükséges a szabályozás, hogy az előírt dinamikai tulajdonságokat be lehessen állítani.
Először szabályozó nélkül (tulajdonképpen egységnyi átviteli tényezőjű P-szabályozóval), a szabályozási kör visszacsatoló ágában szintén egységnyi átviteli tulajdonságot feltételezve vizsgáljuk az egyszerűsített másodrendű rendszert.
A visszacsatoló ágban lévő egységnyi átvitel megfelelően közelíti az egyébként szabályozási körökben használatos érzékelő és jelátalakító dinamikai tulajdonságait.
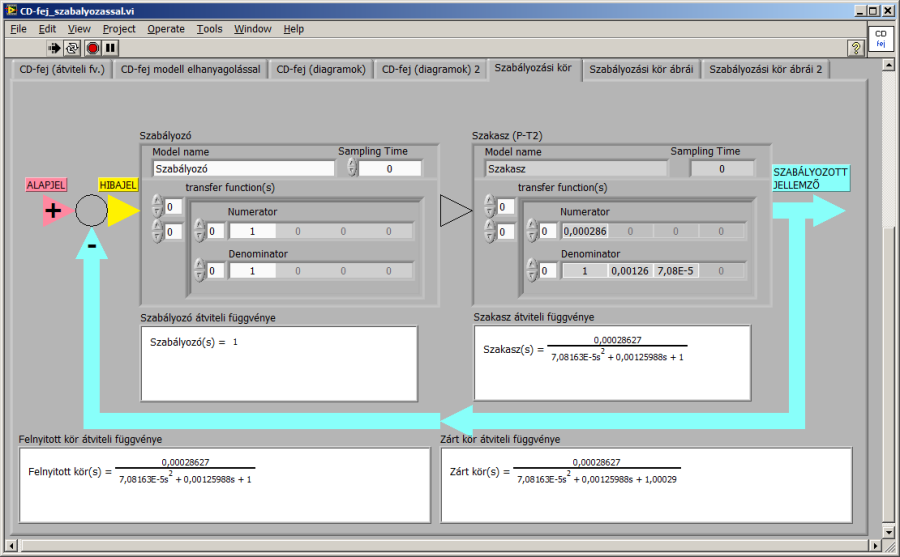
A felnyitott és a zárt kör eredő átviteli függvényének előállításához (kör) a CD Series.vi és a CD Feedback.vi nevű, Control Design & Simulation/Control Design/Model Interconnection paletta útvonalon elérhető blokkokat használhatjuk.
A fenti ábrán jól látszik, hogy az egységnyi arányos szabályozással a felnyitott kör (ebben az esetben a szakasz) és a zárt kör átviteli tulajdonságai gyakorlatilag azonosak. Ezt a wxMaxima+COMA munkafüzet számításai is alátámasztják.
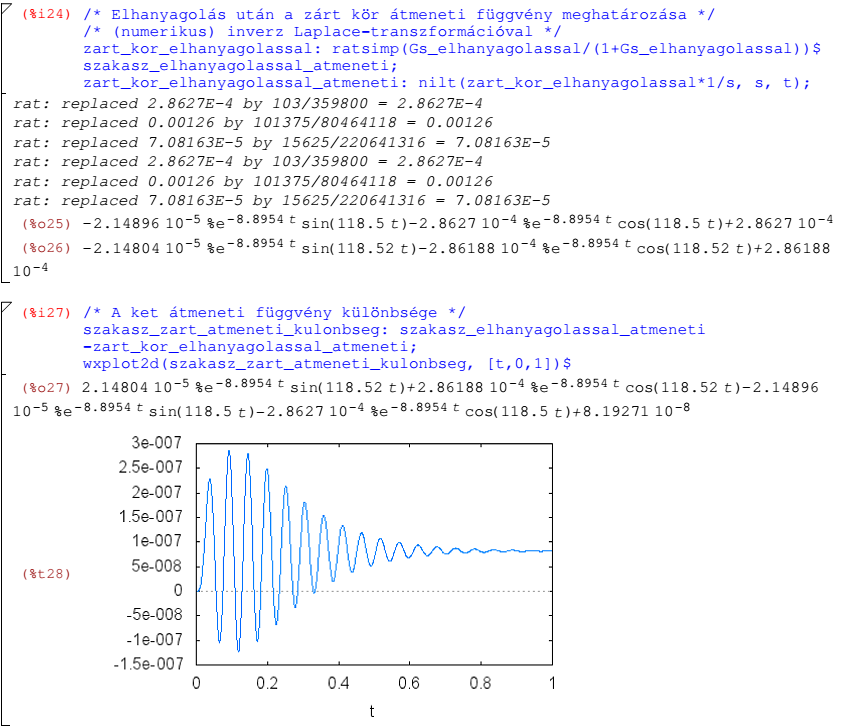
Az elhanyagolással kapott szakasz mint felnyitott kör és az ebből származó zárt szabályozási kör átmeneti függvényének összehasonlítása wxMaxima+COMA felhasználásával:
A fentiek alapján mindenképpen el kell helyeznünk egy megfelelően választott struktúrájú és paraméterezésű szabályozót az előírt dinamikai tulajdonságok biztosításához.
A szabályozó tervezésénél, ha az adott szakasz paraméterei lehetővé teszik, választhatunk úgy PID-jellegű struktúrát, hogy a szabályozó átviteli függvényének számlálója egyezzen meg a szakasz átviteli függvényének nevezőjével. Így megteremtjük a lehetőséget a szakasz „kellemetlen tulajdonságú” pólusainak áthelyezésére, megőrizve a (zárt szabályozási) rendszer másodrendű jellegét.
Ez a PID-jellegű struktúra valós pólusú szakaszok esetén nevezhető kettős töréspontáthelyező algoritmusnak. A szakasz két töréspontját (pólusát) a szabályozó két (a TA és TC jellemzővel adott) zérusa kompenzálja, az előírt dinamikai tulajdonságokat biztosító felnyitott szabályozási körbeli gyököket pedig a szabályozó (TB és TD időállandónak megfelelő) zérusai adják. Az AC erősítési tényezővel biztosíthatjuk az integráló tulajdonságot nem tartalmazó felnyitott körű szabályozás megfelelően kicsi állandósult hibáját (azaz előírt pontosságát).
|
|
(15.17) |
Esetünkben olyan pólus áthelyező struktúrára van szükség, amivel a szakasz alulcsillapított (konjugált komplex gyökpárral adott) pólusait közömbösítjük.
|
|
(15.18) |
A zárt kör előírt dinamikai tulajdonságainak biztosításához, vagyis az aperiodikus átmeneti függvényhez szükséges mértékű fázistartalékhoz, a gyors beálláshoz tartozó nagy vágási körfrekvenciához és a pontossághoz tartozó elegendően kicsi maradó hibát biztosító kisfrekvenciás erősítéshez kell méreteznünk a választott szabályozó struktúra paramétereit. A szimuláció ismételt futtatásával, különböző paraméter beállításokkal elérhetjük az igényeinknek megfelelő zárt kör dinamikát.
Az alábbiakban a szakasz pólusait kiejtő, egyébként nem megvalósítható – de számításokban szerencsére kezelhető – szabályozó struktúrával kezdjük a vizsgálódást.
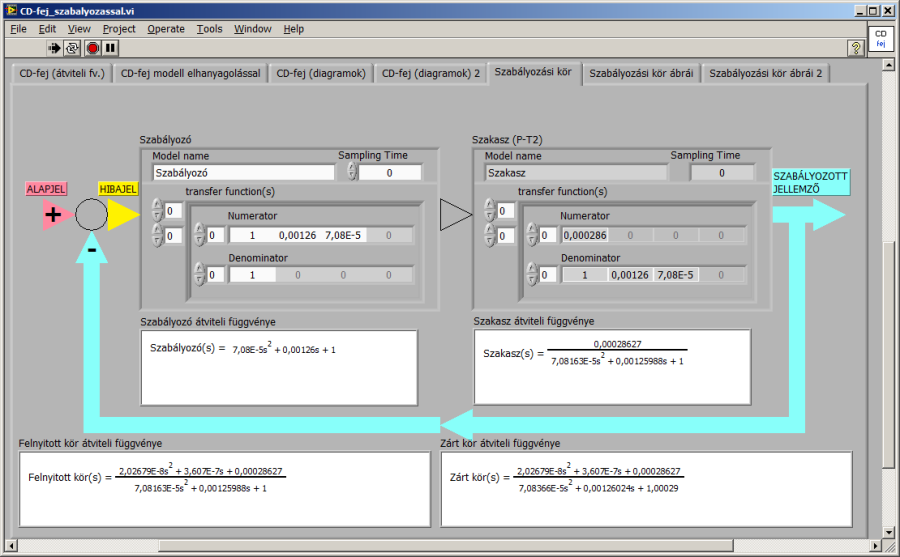
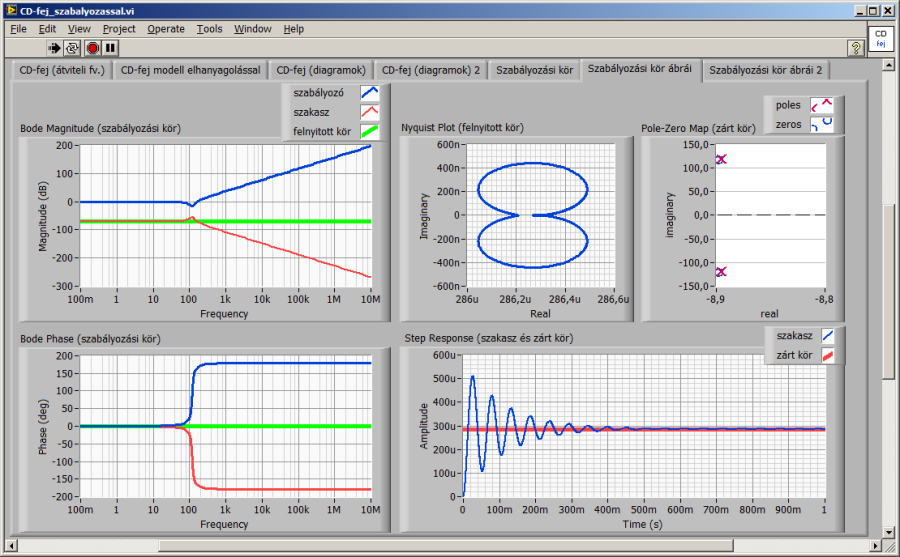
A szabályozó megvalósíthatóságához elengedhetetlen, hogy átviteli függvényében a számláló polinom fokszáma ne legyen alacsonyabb a nevező polinom fokszámánál. Ha az előző ábrákon látható módon a szabályozó zérusaival semlegesítjük a szakasz pólusait,
a szabályozó pólusaival definiálhatjuk a felnyitott kör és természetesen ezen keresztül a zárt rendszer pólusait.
Az alábbi ábrákon szereplő megoldással például minimális túllendülésű zárt kör választ állíthatunk elő.
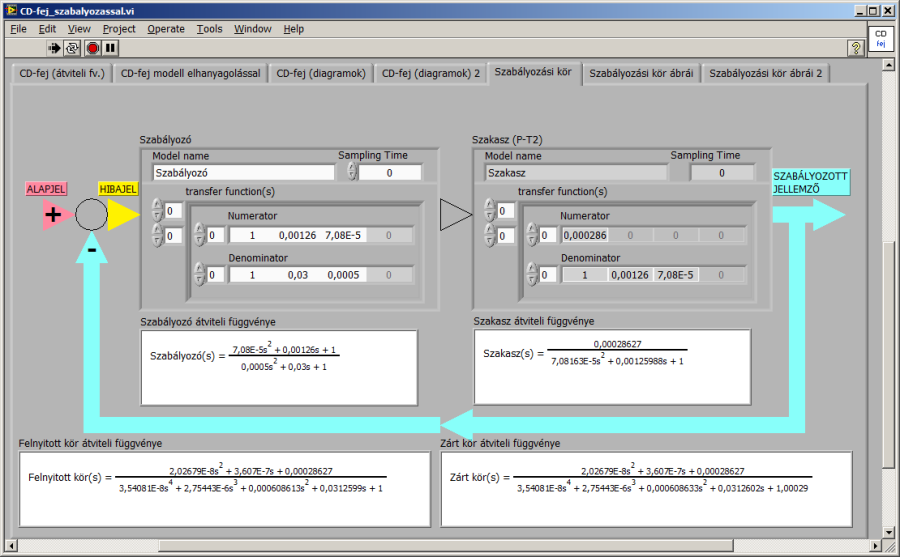
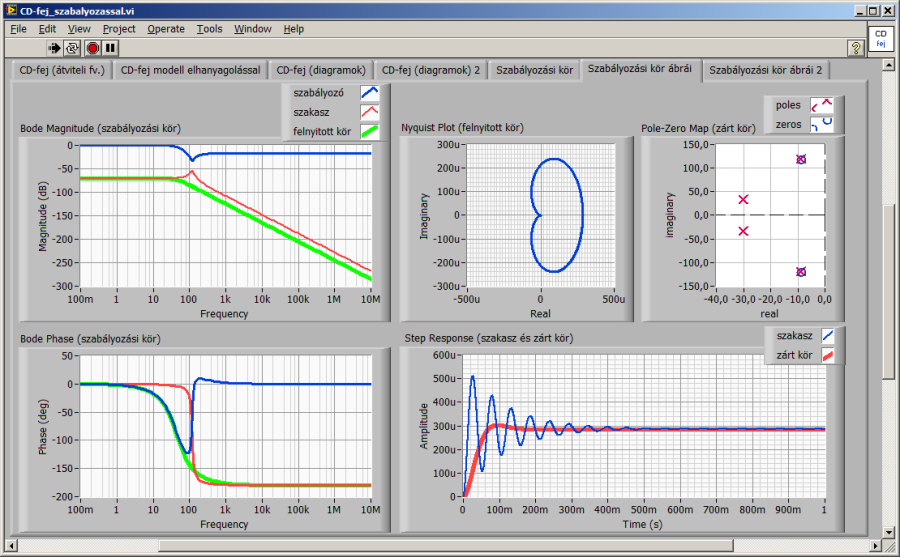
A szabályozástechnikában megismert különböző PID-jellegű struktúrák közül választva és a szabályozó paramétereit folyamatosan változtatva a szimulációs program segítségével úgy alakíthatjuk a zárt kör válaszát, hogy a célul kitűzött dinamikai sajátságokat elérjük. Ismert a szabályozástechnikából, hogy ezek a sajátságok a zárt kör domináns póluspárjára vonatkozóan a ξ≈0.7 csillapítási számmal biztosíthatóak. Így adódik a legkisebb túllendülés, a legrövidebb beállási idő és a PID szabályozás integrátorának köszönhetően a zérus maradó hiba.
Szakirodalom
[15.1.] LabVIEW 2009 Help http://www.ni.com/pdf/manuals/371361f.zip.
[15.2.] LabVIEW Control Design User Manual, June 2009 http://www.ni.com/pdf/manuals/371057g.pdf.
[15.3.] LabVIEW 2009 Control Design and Simulation Module Help http://www.ni.com/pdf/manuals/371894d.zip.
[15.4.] Maxima, a Computer Algebra System: Documentation http://maxima.sourceforge.net/documentation.html.
[15.5.] COMA, Control Engineering with Maxima és Regelungstechnik mit Maxima http://www.austromath.at/daten/maxima/zusatz/Control_Engineering_with_Maxima.pdf.