13. fejezet - Szervopneumatikus rendszer szakaszának modellje
Vissza		Előre

13. fejezet - Szervopneumatikus rendszer szakaszának modellje

Tartalom

13.1. A munkahenger modellezési problémái

A 6.2. szakasz fejezetben a pneumatikus munkahenger modelljének egyszerűsített változata már bemutatásra került, amely modell elsősorban a fordító váltó típusú rendszerek modellezésének bemutatását tartotta szem előtt. A valós rendszer működését pontosabb közelítéssel leíró összefüggések ettől természetesen részben eltérnek, hiszen más célból kerültek megfogalmazásra, felírásra. A pneumatikus munkahengerekkel felépített rendszerre jellemző nehéz pozícionálhatóság több tényező eredménye, amelyek a hatékony működtetés szempontjából nem elhanyagolhatóak. A modellezés során mechatronikai szemszögből több rendszertípust (mechanikai egyenes vonalú, fluid, villamos, termikus) egy berendezésen belül egyszerre alkalmazunk, mely a műszaki ismereteink alapján megalapozott elhanyagolásokkal együtt is összetett rendszerleírást eredményez. A szervopneumatikus rendszer modelljéhez alapvetően két úton is eljuthatunk. Az egyik, a 6.2. szakasz fejezetben bemutatott út, amikor a rendszert eleve átgondoltan linearizált energiatárolókból és disszipatív elemekből építjük fel. A másik úton a mechanika, termodinamika, áramlástan alapösszefüggéseit felhasználó egyenletrendszerből kiindulva jutunk el a rendszer matematikai modelljének felírásáig, bemutatva az egyes összefüggések nemlineáris jellegét.

13.2. A szervopneumatikus pozícionáló rendszer bemutatása

A szabályozott szakasz bármely dugattyúrudas, vagy dugattyúrúd nélküli hengerre érvényes, amelyekbe a beáramló tömegáram szabályozását proporcionális szervo szelepek végzik. A szervopneumatikus pozícionálás elvi felépítését az alábbi ábra szemlélteti.

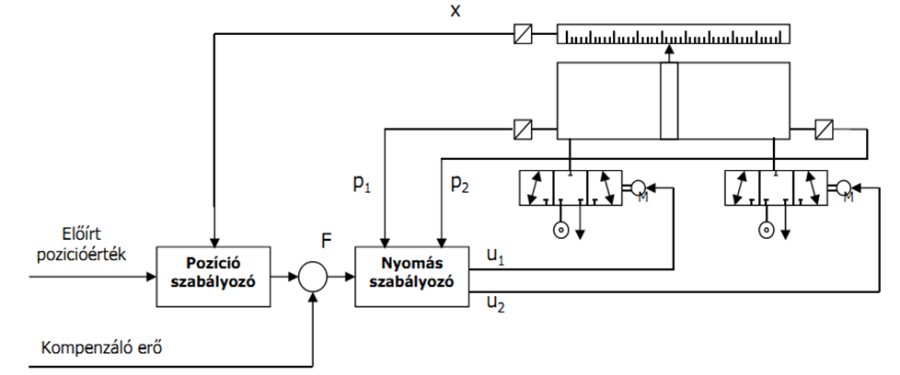
13.1. ábra - A rendszer felépítése a figyelembe vett fizikai jellemzőkkel

A modellezés szempontjából elsődleges fontosságú a szabályozott szakasz, amibe jelenleg a beavatkozó szervet is (jelen esetben a szelepet) beleértjük. A rendszerben a szelepek feszültségének állításával befolyásoljuk a szervoszelepeken átáramló levegő mennyiségét. A munkahengerbe áramló levegő hatására a munkahenger kamrái között nyomáskülönbség jön létre, mely a munkahenger dugattyújára erőt fejt ki. Amennyiben a nyomáskülönbségből fakadó erő a súrlódás leküzdéséhez elegendő, a dugattyú elmozdul. A modell felírása során kapcsolatot kívánunk teremteni a szelepet vezérlő feszültség (u) és a munkahenger dugattyújának elmozdulása (x) között.

13.3. A munkahenger, mint szakasz modellje

A szervopneumatikus rendszerek döntő többségében a munkavégző elem egy dugattyúrúd nélküli munkahenger, melynek felépítése az alábbi ábrán látható. Ez a típus modellezés szempontjából a dugattyúrudas kivitelű munkahengerekhez képest éppen a dugattyúrúd hiánya miatt előnyös, hiszen ebben az esetben a dugattyú kamranyomásokkal terhelt keresztmetszete mindkét oldalt azonos nagyságú.

13.2. ábra - Dugattyúrúd nélküli munkahenger felépítése [13.4.]

A munkahengert két változó térfogatú kamraként modellezzük, melynek elmozduló falait a dugattyú egy-egy oldala alkotja. A rendszer leírásához meg kell határoznunk az összefüggéseket a dugattyú mozgása, a kamrákban lévő levegő állapotváltozói, és a kamrákba beáramló levegő tömegáramai közt.

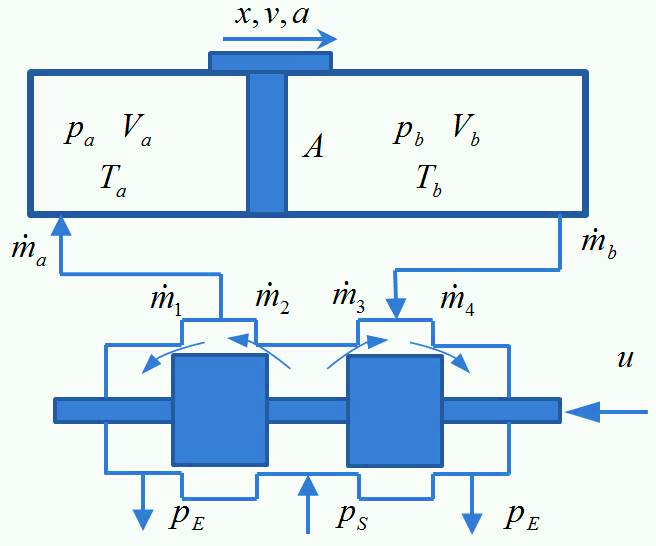
13.3. ábra - A rendszer felépítése a figyelembe vett fizikai jellemzőkkel

A pneumatikus rendszer modellezése során szereplő fizikai mennyiségek:

x	[m]	pozíció
v	[m/s]	sebesség
a	[m/s²]	gyorsulás
l	[m]	munkahenger lökethossz
m	[kg]	mozgatott tömeg
F	[N]	erő
p	[Pa]	nyomás
k	[N/m]	rugómerevség
T	[K]	hőmérséklet
A	[m²]	dugattyú keresztmetszet
A _sz	[m²]	szelep átömlési keresztmetszet
${\dot{m}}_{a}$	[kg/s]	tömegáram
Q	[J]	közölt hőmennyiség
W _f,1→2	[J]	térfogati munka
ρ	[kg/m³]	sűrűség
v _g	[m/s]	gáz áramlási sebesség
c	[J/(kg*K)]	fajlagos hőkapacitás
κ	[-]	adiabatikus kitevő
R	[J/(mol*K)]	specifikus gázállandó
$\dot{V}$	[m³/s]	térfogatáram
α	[-]	átömlési tényező
Ψ	[-]	tömegáram paraméter
u	[V]	feszültség

13.3.1. A munkahenger mozgásegyenlete

Elsőként írjuk fel a mozgásegyenletet a dugattyúra, mely az erők egyensúlyi egyenletének felírásával történik. A felíráshoz valamely irány pozitív előjelű kijelölése szükséges, azaz példának okáért a jobbra haladó mozgásirány legyen pozitív előjellel jelölve. Ez akkor teljesül, ha az „a” oldali kamranyomás a „b” oldali kamranyomásnál legalább annyival nagyobb erőt fejt ki a dugattyúra amekkora a súrlódás leküzdéséhez szükséges. Az ezen felüli erőkülönbség a dugattyú –és a mozgatott tömeg- gyorsítására fordítódik.

$m_{d} \cdot \ddot{x} = F_{a} - F_{b} - F_{s}$

(13.1)

A dugattyú a illetve b oldalán levő nyomásból származó dugattyúra ható erő F_a és F_b:

	$F_{a} = A \cdot p_{a}$	(13.2)
	$F_{b} = A \cdot p_{b}$	(13.3)

a dugattyú sűrített levegővel érintkező felülete az a illetve b kamrarészben, p_a, és p_b a kamrákban uralkodó nyomás.

A rendszer dinamikus viselkedését a súrlódás, különösen a közeg –sűrített levegő- összenyomhatósága miatt, nagymértékben befolyásolja. A súrlódás leírására az egyszerűbb esetekben a kvázi statikus súrlódási modellek alkalmazhatóak, amikor is a mozgás iránya gyakran változik, a dugattyú mozgásának sebessége pedig nem túl nagy. A modellek közül az egyik legegyszerűbb a Coulomb súrlódás, mely két szilárd test között lép fel és egy konstans nagyságú, a mozgás irányával ellentétes irányba ható erővel írható le. Fontos megjegyezni, hogy míg a mechanikai rendszerek nagy részében a Coulomb súrlódás a felületek közötti normálerő és a köztük jelentkező súrlódási együtthatóból az $F_{C} = μ_{d i n} F_{N}$ összefüggéssel felírható, addig a pneumatikus rendszereknél a súrlódást jelentős részben a dugattyú tömítésének hengercsőbe feszülése okozza, mely az összeszerelés pillanatától jellemzi a munkahengert. Ez ahhoz vezet, hogy a súrlódás Coulomb összetevője (F_C) az imént említett összefüggéssel nem számítható. A súrlódás leírását tovább nehezíti, hogy a legtöbb munkahengerben ajakos tömítés található, melyeknél - a tömítés alakja miatt- a kamrában uralkodó nyomás az ajakos részt a hengercsőnek feszíti, így egy nyomástól is függő súrlódási erőt okoz. Ha utóbbitól eltekintünk a Coulomb súrlódás összefüggése:

$F_{s} = s i g n (\dot{x}) \cdot F_{C}$

(13.4)

A jelenség egy másik megközelítése a viszkózus súrlódás, mely főként a folyadékokra jellemző, az anyag belső súrlódását írja le. A viszkózus súrlódási erő egyenesen arányos a mozgás sebességével, iránya azzal ellentétes:

$F_{s} = b \cdot \dot{x}$

(13.5)

ahol b a folyadékra jellemző csillapítási tényező.

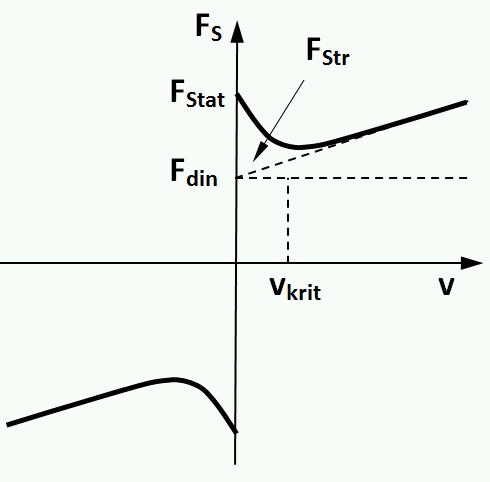
Az említett két súrlódási modell eredője még mindig nem ad pontos közelítést a nulla körüli sebességek esetében, arra jó közelítéssel a Stribeck-féle modell alkalmazható, melyet a következő egyenlet ír le:

$F_{S t r} (\dot{x}, \ddot{x}) = {\begin{matrix} s i g n (\dot{x}) \cdot F_{s t a t} \cdot {(\frac{| \dot{x} | - {\dot{x}}_{k r i t}}{{\dot{x}}_{k r i t}})}^{4} h a \begin{matrix} (| \dot{x} | \leq {\dot{x}}_{k r i t}) \land \\ (s i g n (\dot{x}) = s i g n (\ddot{x})) \end{matrix} \\ 0 e g y é b e s e t b e n \end{matrix}$

(13.6)

ahol Fstat a tapadási súrlódási, vagy álló helyzetben fellépő maximális súrlódási erő. ${\dot{x}}_{k r i t}$ az a kritikus sebesség, mely alatt az akadó csúszás jelensége figyelhető meg. Ezt legegyszerűbben úgy képzelhetjük el, mintha egy rugó segítségével mozgatnánk a testet: ha elkezdjük húzni a rugót állandó sebességgel, a test nem mozdul, amíg a rugón keresztül átadódó erő el nem éri az F_stat-ot, eközben a rugó nyúlik. Amikor átlépjük a maximális súrlódási erőt, akkor mivel a csúszási súrlódási együttható kisebb, mint a tapadási, nagyobb sebességgel indul el a test, mint amivel a rugót húzzuk, így elkezdi behozni lemaradását, kvázi utoléri azt. A rugó megnyúlása, ezáltal a rugón keresztül átadódó erő csökken, aminek következtében a test újra megáll, és a jelenség kezdődik elölről. Ezt a jelenséget hívják akadozó-csúszási súrlódásnak (stick-slip). Az akadozó csúszás kevésbé érvényesül, ha nagyobb sebességgel mozgatjuk a testet, illetve egy kritikus sebesség ( ${\dot{x}}_{k r i t}$ ) felett a hatása elhanyagolható. Ezt a tendenciát írja le a fenti Stribeck-féle modell. A határsebességet az alábbi képlet írja le:

${\dot{x}}_{k r i t} = F_{N} \frac{(μ_{s t a t} - μ_{d i n})}{\sqrt{k \cdot m}} = \frac{F_{s t a t} - F_{d i n}}{\sqrt{k \cdot m}}$

(13.7)

Ahol k a mozgatott rendszer rugóállandója, m a tömege. F_N a felületeket összeszorító normál erő, mely egy állandónak tekinthető a dugattyúhoz csatolt rendszer tömegét és az összeszerelés szorító erejét leíró erőből, és egy változó, a munkahenger kamrájában lévő nyomástól (mely a dugattyún lévő tömítőgyűrűt a kamra oldalához szorítja), a kamrában lévő hőmérséklettől, és emiatt (a dugattyú sokáig egy helyben áll akkor letapad) időtől függő erőből áll.

13.4. ábra - Stribeck súrlódási modell - súrlódó erő a sebesség függvényében

13.3.2. Kamrák nyomás viszonyainak vizsgálata a munkahengerben [13.1.], [13.2.], [13.6.]

A munkahengert, két változó térfogatú kamraként modellezzük. A modellezés szempontjából a kamrák nyomásának az idő függvényében leírt változása lényeges. A folyamatok végiggondolásával belátható, hogy egy kamrában a nyomás változását az alábbi módokon következhet be:

a kamra térfogata változik (dugattyú elmozdul)
a kamrában található anyagmennyiség változik (a kamrába sűrített levegőt juttatunk, vagy engedünk ki)
a kamra falán keresztül a kamrában található gáz és a környezet között hőcsere megy végbe (a termikus folyamat időállandója az előző két változáshoz képest nagyobb - hatását lényegesen lassabban fejti ki-, így -a modellezést némileg egyszerűsítve- ezzel a továbbiakban nem számolunk, azaz adiabatikus folyamatot feltételezünk).

A fejezetrészben az említett folyamatok részletes leírására kerül sor.

A nemlineáris modellel kapcsolatban az alábbi kikötéseket, egyszerűsítéseket tesszük meg:

A kamrában adiabatikus folyamatok mennek végbe, így a hőátadást a kamrák és a környezet között elhanyagoljuk,

A kamrában lévő gáz ideális,
A kialakuló áramlások egy dimenziósak,
stacionáriusak.

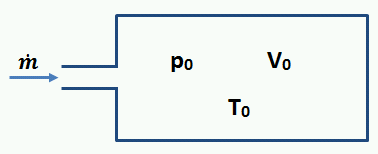
13.5. ábra - Pneumatikus tartály (kapacitás), állapotváltozókkal

A gáz állapotváltozóinak meghatározásához, alábbi egyenleteket használjuk fel. Mivel a leírás a szakirodalomban több helyen részletes bemutatásra kerül, itt csak az egyenletek rövid magyarázattal kerülnek bemutatásra:

Állapotegyenlet (itt m a gáz tömegét jelöli):

	$p \cdot V = m \cdot R \cdot T$	(13.8)
	$\frac{p}{ρ} = R \cdot T$	(13.9)

Termodinamika I. Főtétele zárt rendszer esetén, ahol Q a közölt hőmennyiség; W_f a térfogati munka:

$0 = Q_{1 \to 2} + W_{f,1 \to 2}$

(13.10)

Ahol $d Q = c \cdot m \cdot d T$ ; $c = {\begin{matrix} c_{p} f a j h ő i z o b á r á l l a p o t v á l t o z á s e s e t é n \\ c_{v} f a j h ő i z o c h o r á l l a p o t v á l t o z á s e s e t é n \end{matrix}$ ,

melyre érvényes: $δ W_{f} = V d p$

A specifikus gázállandó:

$R = c_{p} - c_{v}$

(13.11)

Az adiabatikus kitevő:

$κ = \frac{c_{p}}{c_{v}}$

(13.12)

A kamrában lévő levegő nyomásviszonyait, a nyomást leíró függvény változásának vizsgálatával érthetjük meg:

$\frac{\partial p (m (t), V (t), T (t))}{\partial t} = \frac{\partial p}{\partial T} \cdot \dot{T} + \frac{\partial p}{\partial V} \cdot \dot{V} + \frac{\partial p}{\partial m} \cdot \dot{m}$

(13.13)

Az egyes tagok vizsgálatára a következő fejezetrészben kerül sor.

13.3.2.1. A nyomás változása hőmérsékletváltozás hatására

$\frac{\partial p}{\partial T} \cdot \dot{T} = {\dot{p}}_{T}$

A nyomás megváltozását írja le a hőmérsékletváltozás hatására, miközben a térfogat és a gáz tömege állandó. A térfogat és a tömeg állandóságából következik, hogy hőmérsékletváltozás csak hőközlés útján jöhet létre. Mivel adiabatikus folyamatváltozást tételeztünk fel, ettől a tagtól, ahogy a bevezetőben már említésre került, a továbbiakban eltekintünk.

13.3.2.2. A nyomás változása a térfogatváltozás hatására

$\frac{\partial p}{\partial V} \cdot \dot{V} = {\dot{p}}_{V}$

Írja le a nyomás megváltozását a térfogatváltozás hatására, miközben a kamrában lévő hőmérséklet és a gáz tömege állandó. A térfogat megváltozását, a munkahenger dugattyújának elmozdulása okozza. A dugattyú munkáját felírva a rendszerre (mely a tömeg állandóságából következően zártnak tekinthető), az energiaegyenlet (13.10) (izochor folyamatváltozás esetében):

$m \cdot c_{v} \cdot d T = - p \cdot d V$

(13.14)

Felhasználva az ideális gáz állapotegyenletét (13.8) és a szorzatfüggvények deriváltjára vonatkozó szabályt:

$c_{v} \cdot d (\frac{p \cdot V}{R}) = \frac{c_{v}}{R} \cdot (p \cdot d V + V \cdot d p) = - p \cdot d V$

(13.15)

Rendezve, és behelyettesítve az izochor és izobár fajhők közti összefüggést (13.12) az alábbi alakot kapjuk:

$c_{v} \cdot V \cdot d p = - c_{p} \cdot p \cdot d V$

(13.16)

Az adiabatikus kitevőre vonatkozó összefüggést (13.12) behelyettesítve:

$V \cdot d p = - κ \cdot p \cdot d V$

(13.17)

Ez alapján a nyomás megváltozása:

${\dot{p}}_{V} = - \frac{κ}{V} \cdot p \cdot \dot{V}$

(13.18)

13.3.2.3. A nyomás változása az anyagmennyiség változásának hatására

$\frac{\partial p}{\partial m} \dot{m} = {\dot{p}}_{m}$

A gáz nyomásának megváltozását írja le a tömeg változásának hatására, miközben a kamra térfogata, és a gáz hőmérséklete állandó. Mivel a kamra térfogata állandó, a tömegváltozás a sűrűség megváltozását eredményezi:

$d m = V \cdot d ρ$

(13.19)

mivel V állandó, így:

$\frac{\partial p}{\partial m} = \frac{d p}{d ρ} \cdot \frac{1}{V}$

(13.20)

Az állapotegyenletből (13.13) kifejezve p-t, behelyettesítve az adiabatikus állapotváltozásra vonatkozó egyenletbe, megkapjuk a nyomás változását a sűrűség függvényében:

$p (ρ) = \frac{p_{0}}{ρ_{0}^{κ}} \cdot ρ^{κ}$

(13.21)

Ezt a sűrűség szerint deriválva:

$\frac{d p}{d ρ} = κ \cdot \frac{p_{0}}{ρ_{0}^{κ}} \cdot \frac{ρ^{κ}}{ρ}$

(13.22)

A (13.21) egyenletet (13.22)-be helyettesítve:

$\frac{d p}{d ρ} = κ \cdot \frac{p}{ρ}$

(13.23)

A gáztörvényt (13.9) behelyettesítve kapjuk:

$\frac{d p}{d ρ} = κ \cdot R \cdot T$

(13.24)

Tehát a nyomás megváltozása a tömegváltozás hatására:

${\dot{p}}_{m} = \frac{\dot{m}}{V} \cdot κ \cdot R \cdot T$

(13.25)

(13.18) és (13.25) felhasználásával a nyomás változása a munkahengerben:

$\dot{p} = {\dot{p}}_{m} + {\dot{p}}_{V} = \frac{κ}{V} \cdot R \cdot T \cdot \dot{m} - \frac{κ}{V} \cdot p \cdot \dot{V}$

(13.26)

Felhasználható, hogy a térfogatváltozás a dugattyú mozgásából adódik (a henger keresztmetszete nem változik):

$\dot{V} = A \cdot \dot{x}$

(13.27)

Behelyettesítve (13.26)-ba:

$\dot{p} \cdot V = κ \cdot (R \cdot T \cdot \dot{m} - A \dot{\cdot x \cdot} p)$

(13.28)

Az összefüggések levezetése után most már figyelembe vehető, hogy a dugattyú jobbra történő elmozdulása - a feltételezett pozitív irányt szem előtt tartva - a bal oldali kamra térfogatának növelésével, míg a jobb oldalinak csökkenésével jár. Az összefüggésben V_0a és V_0b a két kamra holtterének térfogatát, illetve l a munkahenger lökethosszát jelöli.

	$V_{a} = V_{0 a} + A \cdot x$	(13.29)
	$V_{b} = V_{0 b} + A \cdot (l - x)$	(13.30)

Ugyan általában a gáz az egyik kamrába befelé, míg a másikból kifelé áramlik, ez csak a szelepmodell során lesz figyelembe véve. Itt mindkét kamra töltését leíró egyenlet látható. A munkahenger bal oldali kamrájára:

$\dot{p_{a}} \cdot (V_{0 a} + A \cdot x) = κ \cdot (R \cdot T_{a} \cdot {\dot{m}}_{a} - A \cdot \dot{x} \cdot p_{a})$

(13.31)

A jobb oldali kamrájára:

${\dot{p}}_{b} \cdot (V_{0 b} + A \cdot (l - x)) = κ \cdot (R \cdot T_{b} \cdot {\dot{m}}_{b} + A \cdot \dot{x} \cdot p_{b})$

(13.32)

13.3.3. A nyomáskülönbség hatására fellépő tömegáramok meghatározása [13.3.]

A munkahenger modelljének leírásához meg kell határoznunk az egyes kamrákba be, illetve kiáramló levegő tömegáramát, mely a szelep viselkedése leírásához döntő fontosságú. A rendszer viselkedésére tett kikötések a kamrák nyomásviszonyait vizsgáló fejezetben leírtakkal azonosak. A felíráshoz a továbbiakban felhasználjuk:

a gázok áramlásának leírására a Bernoulli egyenletet:

$\frac{v_{2}^{2} - v_{1}^{2}}{2} = - \int_{p_{1}}^{p_{2}} \frac{d p}{ρ (p)}$

(13.33)

valamint az adiabatikus állapotváltozásra vonatkozó egyenletet:

$\frac{T_{2}}{T_{1}} = {(\frac{p_{2}}{p_{1}})}^{\frac{κ - 1}{κ}}$

(13.34)

A tömegáram meghatározásához először a Bernoulli egyenletet (13.33) az áramvonal mentén a kamrából kiáramló gázra kell felírni, feltételezve, hogy a kamrában lévő gáz kvázistatikus állapotban van, így annak sebessége zérus.

$\frac{v^{2}}{2} = - \int_{p_{1}}^{p_{2}} \frac{d p}{ρ (p)}$

(13.35)

Az 1-es indexszel a kamrában lévő állapotokat, 2-es indexszel a kiáramló gáz állapotváltozóit jelöljük. Az állapotegyenletből (13.9) kifejezve p-t, behelyettesítve az adiabatikus állapotváltozásra vonatkozó egyenletbe (13.34), megkapjuk a sűrűség változását a nyomás függvényében:

$ρ (p) = \frac{ρ_{0}}{p_{0}^{\frac{1}{κ}}} p^{\frac{1}{κ}}$

(13.36)

ahol p₀ a légköri nyomás, illetve ρ₀ a légköri nyomáson a levegő sűrűsége. (13.36)–t behelyettesítve (13.35)-be, majd elvégezve az integrálást:

$\frac{v^{2}}{2} = - \frac{κ}{κ - 1} \frac{p_{1}^{\frac{1}{κ}}}{ρ_{1}} {[p^{1 - \frac{1}{κ}}]}_{p_{1}}^{p_{2}}$

(13.37)

A behelyettesítéseket elvégezve, egyszerűsítve, kifejezve v-t megkapjuk a kamrából kiáramló gáz átlagsebességét:

$v = \sqrt{\frac{2 \cdot κ}{κ - 1} \cdot \frac{p_{1}}{ρ_{1}} \cdot (1 - {(\frac{p_{2}}{p_{1}})}^{\frac{κ - 1}{κ}})}$

(13.38)

Feltételezve, hogy a kiáramló gáz sűrűsége a kiáramlási pontnál időben állandó (stacionárius az áramlás), a tömegáram számítására az alábbi (13.40) összefüggést használhatjuk, valamint, hogy a térfogatáram kiszámítására (13.39) összefüggés érvényes:

	$\dot{V} = A_{s z} \cdot v$	(13.39)
	$\dot{m} = A_{s z} \cdot v \cdot ρ$	(13.40)
	$\dot{m} = A_{s z} \cdot ρ_{2} \cdot \sqrt{\frac{2 \cdot κ}{κ - 1} \cdot \frac{p_{1}}{ρ_{1}} \cdot (1 - {(\frac{p_{2}}{p_{1}})}^{\frac{κ - 1}{κ}})}$	(13.41)

A sűrűségváltozásra vonatkozóan (13.36)–t behelyettesítve a kifejezést alakítsuk át az alábbi formára:

$\dot{m} = A_{s z} \cdot \sqrt{\frac{κ}{κ - 1} \cdot {(\frac{p_{2}}{p_{1}})}^{\frac{2}{κ}} \cdot (1 - {(\frac{p_{2}}{p_{1}})}^{\frac{κ - 1}{κ}}) \cdot} \sqrt{2 ρ_{1} \cdot p_{1}}$

(13.42)

Az összefüggést megvizsgálva a szakirodalom a (13.42) összefüggés első gyökjel alatti részét tömegáram paraméternek nevezi, melyet a továbbiakban Ψ-vel jelöljük

$Ψ = \sqrt{\frac{κ}{κ - 1} \cdot {(\frac{p_{2}}{p_{1}})}^{\frac{2}{κ}} \cdot (1 - {(\frac{p_{2}}{p_{1}})}^{\frac{κ - 1}{κ}})}$

(13.43)

Ψ –t p₂/p₁ nyomásviszony függvényében ábrázolva, ahol p₂ a kilépő oldali illetve p₁ a belépő oldali nyomásértéket jelöli.:

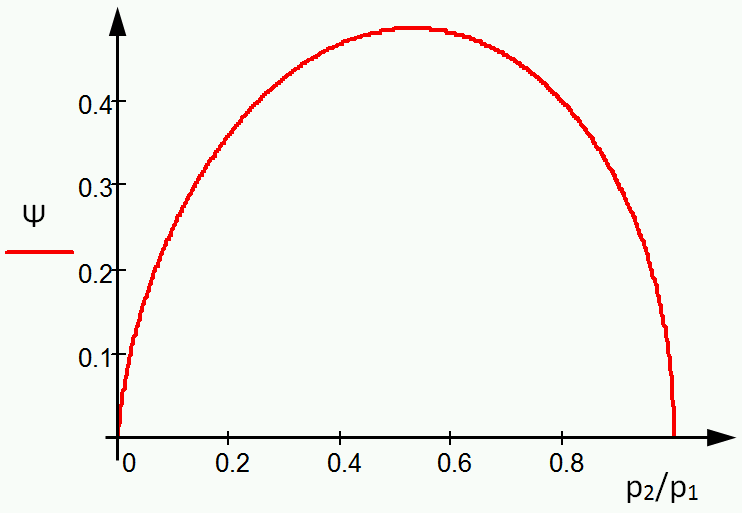
Átömlési tényező Ψ(f),f=p2/p1 ; (κ=1.4) esetén

13.6. ábra - Átömlési tényező Ψ(f),f=p₂/p₁ ; (κ=1.4) esetén

Amint azt láthatjuk, a függvénynek maximuma van. A szélsőérték meghatározásához írjuk fel a függvény deriváltját, majd az alábbi egyenletet megoldva:

	$\frac{dΨ (\frac{p_{2}}{p_{1}})}{d (\frac{p_{2}}{p_{1}})} = 0$	(13.44
	${(\frac{p_{2}}{p_{1}})}^{\frac{1}{κ} + 1} (\frac{1 + κ}{2} - {(\frac{p_{2}}{p_{1}})}^{\frac{1}{κ} - 1}) \frac{1}{\frac{p_{2}}{p_{1}} (1 - κ) \cdot \sqrt{\frac{κ}{κ - 1} \cdot ({(\frac{p_{2}}{p_{1}})}^{\frac{2}{κ}} - {(\frac{p_{2}}{p_{1}})}^{\frac{1 + κ}{κ}})}} = 0$ )

Az egyenletnek csak a középső tényezője lehet zérus, melyből:

${(\frac{p_{2}}{p_{1}})}^{\frac{1 - κ}{κ}} = \frac{1 + κ}{2}$

(13.45)

Tehát a kritikus nyomásviszony, ideális kétatomos gáz (κ=1.4) esetén

${(\frac{p_{2}}{p_{1}})}_{k r i t i k} = {(\frac{2}{κ + 1})}^{\frac{κ}{κ - 1}} = 0.5283$

(13.46)

A kritikus nyomás kialakulásának megértéséhez vizsgáljuk meg a kiáramló gáz sebességét a kritikus nyomásnál, (13.38)-ba behelyettesítve a (13.9) gáztörvényt:

$v = \sqrt{\frac{2 \cdot κ}{κ - 1} \cdot R \cdot T_{1} \cdot (1 - {(\frac{2}{κ + 1})}^{\frac{κ}{(κ - 1)} \cdot \frac{(κ - 1)}{κ}})}$

(13.47)

A kilépő gáz hőmérsékletét megkapjuk, ha az adiabatikus állapotváltozásra vonatkozó (13.34) összefüggésbe behelyettesítjük a kritikus nyomás (13.46) értékét.

$T_{1} = \frac{κ + 1}{2} \cdot T_{2}$

(13.48)

Ezt (13.48) behelyettesítve a sebességképletbe (13.47) azt kapjuk, hogy a kiáramlási sebesség megegyezik a gázban a hang adott hőmérsékletre vonatkozó terjedési sebességével.

$v = \sqrt{\frac{2 \cdot κ}{κ - 1} \cdot R \cdot \frac{κ + 1}{2} \cdot T_{2} \cdot \frac{κ - 1}{κ + 1}} = \sqrt{κ \cdot R \cdot T_{2}} \cdot c_{v} \cdot p \cdot d V = - c_{p} \cdot p \cdot d V$

(13.49)

Ahogy elkezdjük növelni a nyomást a tartályban (vagy a külső nyomást csökkenteni), a nyomáskülönbség által áramlás alakul ki, melynek sebessége a nyomásviszonyoktól függ. A kritikus nyomásviszonyt elérve azt tapasztaljuk, hogy a kiáramlási sebesség és a kilépő gáz állapotváltozói nem változnak. Ezt azzal magyarázhatjuk, hogy a gázokban a nyomásváltozás nyomáshullámként jön létre, mely nyomáshullám terjedési sebessége éppen a hangsebességgel egyenlő, így ha a kilépő gáz sebessége eléri a hangsebességet, a nyomásváltozás nem képes átlépni a kiáramlási keresztmetszetet, a nyomásviszony változása tehát nem tudja módosítani a nyomásmegoszlást a kamra és a kilépési pont között.

Tehát a kritikus nyomásviszony fölött az a tömegáram paraméter állandó marad. A számítások egyszerűsítése végett a paramétert a különböző szakirodalmakban alkalmazott alábbi közelítő függvénnyel közelítjük:

$Ψ^{'} (\frac{p_{2}}{p_{1}}) = Ψ_{0} \cdot \sqrt{1 - {(\frac{\frac{p_{2}}{p_{1}} - p_{k r i t}}{1 - p_{k r i t}})}^{2}}$

(13.50)

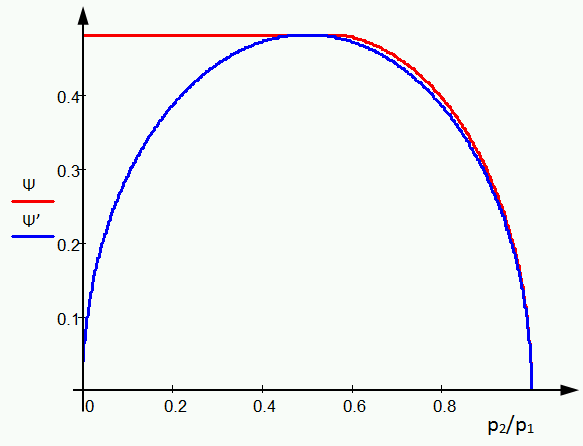
13.7. ábra - Valós átömlési tényező Ψ, és a közelítő függvénye Ψ’; p_krit =0,5; κ=1,4

A tömegáram alakulása a munkahenger kamráinál:

$\dot{m} = A_{s z} \cdot \sqrt{2 \cdot ρ_{1} \cdot p_{1}} \cdot Ψ (\frac{p_{2}}{p_{1}})$

(13.51)

A sűrűségtől való függés, a gáztörvény (13.9) felhasználásával megszüntethető:

$\dot{m} = A_{s z} \cdot p_{1} \cdot \sqrt{\frac{2}{R \cdot T_{1}} \cdot} Ψ (\frac{p_{2}}{p_{1}})$

(13.52)

A tömegáramok számításánál a veszteségek (súrlódás, hő) és az áramlási keresztmetszet geometriai sajátosságai következtében korrekciós együtthatót kell alkalmazzunk, mely α átömlési tényezővel kerül számításra. Ez a korrekciós együttható empirikus módon, az alábbi összefüggés érvényességét szem előtt tartva kerül meghatározásra, melyre a szakirodalomban [13.5.] találunk mérési eljárást, becsült értékeket

$\dot{m} = α \cdot A_{s z} \cdot p_{1} \cdot \sqrt{\frac{2}{R \cdot T_{1}}} \cdot Ψ (\frac{p_{2}}{p_{1}})$

(13.53)

13.3.4. A szervoszelep modellje

Az alkalmazások jelentős részében egy szervoszelep a tolattyú fordítása, vagy lineáris mozdítása révén szabályozza a munkahenger kamráiba beáramló, illetve az onnan kiáramló tömegáramokat. A szelep a bemenő feszültség alapján változtatja a tolattyú szöghelyzetét vagy pozícióját, mely a szelep átömlési keresztmetszetére van hatással. A tömegáramokat az átömlési keresztmetszetek változása, és a szelep egyes kamráiban uralkodó nyomások befolyásolják. A szelep modelljét az alábbi ábra segítségével érthetjük meg jobban.

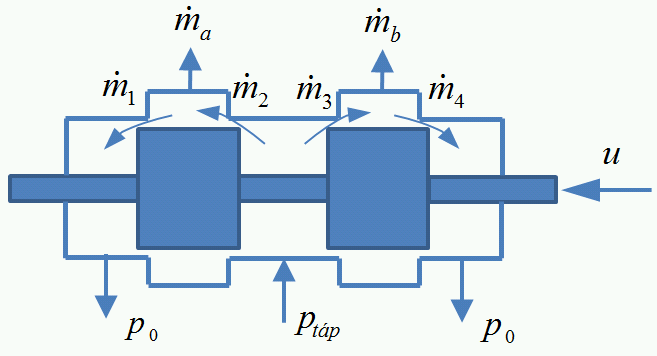
13.8. ábra - Szelep modell, tömegáramokkal

A szelep alsó középső csatlakozójához kötjük a tápnyomást (továbbiakban p_táp, a másik két alsó csatlakozó a leszellőzést biztosítja. A rendszerből távozó levegő nyomását p₀-val jelöljük.

A munkahenger levegőellátását a szelep a tápnyomáson keresztül a felső csatlakozókon biztosítja. Az ábrának megfelelően mind a két kamra esetében a kamrát töltő tömegáram ( ${\dot{m}}_{a}$ és ${\dot{m}}_{b}$ ) pozitív. Ugyan fizikai értelemben az ábrán látható szelepkonstrukció esetében ez, hogy egyszerre töltsük mindkét kamrát, nem lehetséges, azonban a tolattyú elmozdulásának megfelelő nyitási keresztmetszetek miatt ${\dot{m}}_{1} \dots {\dot{m}}_{4}$ tömegáramok értékei az egyik kamra tömegáramra negatív előjelet eredményeznek, melyet az alábbi összefüggések írnak le:

	${\dot{m}}_{a} = {\dot{m}}_{2} - {\dot{m}}_{1}$	(13.54)
	${\dot{m}}_{b} = {\dot{m}}_{3} - {\dot{m}}_{4}$	(13.55)

A tömegáramok számítása az előző fejezetrészben tárgyalt módon a tartályból való kiáramlás képletével történik. Miszerint:

	${\dot{m}}_{1} = α_{1} \cdot A_{s z 1} \cdot p_{a} \cdot \sqrt{\frac{2}{R \cdot T_{a}} \cdot} Ψ (\frac{p_{0}}{p_{a}})$	(13.56)
	${\dot{m}}_{2} = α_{2} \cdot A_{s z 2} \cdot p_{t á p} \cdot \sqrt{\frac{2}{R \cdot T_{0}}} \cdot Ψ (\frac{p_{a}}{p_{t á p}})$	(13.57)
	${\dot{m}}_{3} = α_{3} \cdot A_{s z 3} \cdot p_{t á p} \cdot \sqrt{\frac{2}{R \cdot T_{R}}} \cdot Ψ (\frac{p_{a}}{p_{t á p}})$	(13.58)
	${\dot{m}}_{4} = α_{4} \cdot A_{s z 4} \cdot p_{b} \cdot \sqrt{\frac{2}{R \cdot T_{0}}} \cdot Ψ (\frac{p_{a}}{p_{t á p}})$	(13.59)

A szelep tolattyúja másodrendű csillapított rendszerként működik, ahol a rendszer energiatárolóit a tolattyú tehetetlensége, valamint a súrlódásból és kamranyomás ellenállásából adódó csillapítás alkotja.

Matematikailag az alábbi differenciálegyenlettel írható fel, ahol x_sz a tolattyú elmozdulása, a F_sz szelep tekercse által a tolattyúra kifejtett erő, mely a szervo-szelepet szabályozó feszültségtől u függ:

${\ddot{x}}_{s z} + 2 \cdot ζ \cdot ω \cdot {\dot{x}}_{s z} + ω^{2} \cdot x_{s z} = k_{s z} \cdot ω^{2} \cdot F_{s z}$

(13.60)

ahol ω a rendszer körfrekvenciája ξ a csillapítás foka.

A _szi szelep geometriai kialakításától függően feltételezzük, hogy a szelep csatlakozójának átömlési keresztmetszete közelítően egyenesen arányos a tolattyú elmozdulásával x_sz.

13.4. A szervopneumatikus rendszer állapottér modellje

Az alábbi fejezetrészekben levezetett összefüggések numerikus szimulációval minden további nélkül használhatóak, a munkahenger dugattyújának pozíciója a szelep működtetésének függvényében meghatározható. A rendszer modellezésének szempontjából legfontosabb összefüggések a mozgásegyenlet (13.1) valóságos működést minél jobban megközelítő súrlódási modellel felírt összefüggése, illetve a kamrák nyomásának kialakulása (13.31) (13.32). Amennyiben munkaponti linearizálást használunk, illetve élünk néhány egyszerűsítési lehetőséggel, a rendszer működését leíró legfontosabb négy állapotjelzőhöz köthető modellt kapunk (az állapottér modell részletesebb leírás az 1. fejezet és 5. fejezet fejezetekben található). A mozgásegyenlet ezúttal csak viszkózus súrlódást figyelembe véve:

$m \cdot \frac{d v}{d t} - p_{a} \cdot A + p_{b} \cdot A + b \cdot v = 0$

(13.61)

A nyomás kialakulást leíró egyenletek amennyiben a kamrák holtterétől eltekintünk:

	$\dot{p_{a}} = - \frac{κ \cdot A \cdot p_{a}}{A \cdot x} \cdot \dot{x} + \frac{κ \cdot R \cdot T_{a}}{A \cdot x} \cdot \dot{m_{a}}$	(13.62)
	$\dot{p_{b}} = - \frac{κ \cdot A \cdot p_{b}}{A \cdot (l - x)} \cdot \dot{x} + \frac{κ \cdot R \cdot T_{b}}{A \cdot (l - x)} \cdot \dot{m_{b}}$	(13.63)

Az utóbbi egyenletekből (13.61), (13.62) és (13.63) Látszik, hogy az állapotjelzők (a rendszer működését leíró energiatárolók töltöttségi állapotát leíró állapotjelzők) vektora, kiegészítve a pozícióval a következő:

$\underline{x} = [\begin{matrix} \begin{matrix} x \\ v \end{matrix} \\ \begin{matrix} p_{a} \\ p_{b} \end{matrix} \end{matrix}]$

(13.64)

Az állapottér modell főegyenlete:

$\dot{\underline{x}} = [\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & - \frac{b}{m} & \frac{A}{m} & - \frac{A}{m} \\ 0 & A_{32} & 0 & 0 \\ 0 & A_{42} & 0 & 0 \end{matrix}] \underline{x} + [\begin{matrix} 0 & 0 \\ 0 & 0 \\ B_{31} & 0 \\ 0 & B_{42} \end{matrix}] [\begin{matrix} \dot{m_{a}} \\ \dot{m_{b}} \end{matrix}]$

(13.65)

ahol a nyomás kialakulását leíró összefüggések nem csak egy változótól függenek, ezért kezelésük a hagyományos módon nem lehetséges. Így a rendszermátrixban jelölt összefüggések:

	$A_{32} = - \frac{κ \cdot A \cdot p_{a}}{A \cdot x} = - \frac{κ \cdot p_{a}}{x}$	(13.66)
	$A_{42} = - \frac{κ \cdot p_{b}}{l - x}$	(13.67)

a bemeneti mátrix esetében:

	$B_{31} = \frac{κ \cdot R \cdot T_{a}}{A \cdot x}$	(13.68)
	$B_{42} = \frac{κ \cdot R \cdot T_{b}}{A \cdot (l - x)}$	(13.69)

Az állapottér modell segédegyenletével határozható meg a keresett változó, esetünkben a pozíció értéke. Ez közvetlenül a kimeneti mátrix egyszerű felírásából kaphat, hiszen a pozíció az egyik állapotjelző is:

$\underline{y} = [\begin{matrix} \begin{matrix} 1 \\ 0 \end{matrix} \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix}] \underline{x} + [\begin{matrix} \begin{matrix} 0 \\ 0 \end{matrix} \\ \begin{matrix} 0 \\ 0 \end{matrix} \end{matrix}] \underline{u}$

Fontos kihangsúlyozni, hogy ez a felírás csak minden egyes pontban linearizált esetre igaz, továbbá jelen állapottér modell a szelep működését leíró nyitási keresztmetszet, illetve áramlási karakterisztikáit nem tartalmazza! Ezzel együtt látható, hogy a működés szempontjából legfontosabb összefüggés a mozgásegyenlet. A nyomások kialakulását leíró összefüggésekkel jelen a felírás csak becslést ad a dugattyú mozgására.

A rendszer működésének valósághű modellezésére, a fejezetben leírtaknak megfelelően, csak teljes körűen megalkotott, és a valós paraméterek (súrlódási együttható, nemlineáris karakterisztikák) identifikációval történő meghatározása után nyílik lehetőség.

Szakirodalom

[13.1.] Lajos, Tamás. Az áramlástan alapjai. Budapest . 1992.

[13.2.] Oswatitsch, K.. Grundlagen der Gasdynamik. Springer-Verlag. 1976.

[13.3.] Grollius, Horst-W. Grundlagen der Pneumatik. Carl Hanser Verlag. 2012.

[13.4.] Modular Pneumatic Linear Drive Systems catalouge. Hoerbiger-Origa.

[13.5.] Szente, Viktor. Pneumatikus teljesítmény-átviteli rendszerek áramlástani jellemzői Ph. D. értekezés. Budapest. 2008.

[13.6.] Murrenhoff, Hubertus. Grundlagen der Fluidtechnik: Teil 2: Pneumatik. Shaker Verlag. 2006.

Vissza		Előre
12. fejezet - Fogazott szíjas lineáris mozgató, mint szakasz méretezése	Főoldal	14. fejezet - Aktív rezgéscsillapító szakaszának modelljei és a szabályozások tervezése