12. fejezet - Fogazott szíjas lineáris mozgató, mint szakasz méretezése
A fogazott szíjas átalakító annyira alapvető rendszer a mechatronikában, hogy a vonóelemes szakaszok közül csak ezzel foglalkozunk részletesen. Az ilyen típusú átalakítót tartalmazó szabályozott szakaszt is nagy körültekintéssel kell tervezni, mint a pontossági, mind pedig a dinamikai követelmények miatt.
A fogazott szíjas átalakító tervezésének és méretezésének legfontosabb szempontjait részben Dr.-Ing. Thomas Nagel a BME MOGI Tanszéken több szemeszterben tartott vendégelőadásainak anyagára támaszkodva foglaltuk össze, de a modellezés szempontjai szerint kiegészítettük azt. A szerző az említett oktatóval együtt fejlesztett és rendszeresen cserélt oktatási anyagokat. Dr. Nagel hosszabb idő óta, minden év szeptemberében, Drezdában, nagy érdeklődés mellet szervezi meg a fogazott szíjas hajtásokkal foglalkozó fontos szakmai konferenciát, amelyen német gyártók mellett valamennyi mértékadó európai gyártó cég képviselői megjelennek. A fogazott szíjas hajtásokkal kapcsolatos kutatásainak eredményeit Dr. Nagel a „Zahnriemengetriebe” címmel, [10.1.] 2008-ban megjelent munkájában foglalta össze.
12.1. A fogazott szíjas lineáris mozgatók felépítése
A fogazott szíjas lineáris mozgatók több változatban készülnek, amint a következő ábrán látható:
![Fogazott szíjas lineáris mozgatók legismertebb elrendezései [10.1.]](images/image_XII_1.png)
A fogazott szíjas átalakítót a gépészet, járműipar és a mechatronika, ezen belül különösen a robottechnika és elektronikai szerelő automaták területén egyre kiterjedtebben alkalmazzák, köszönhetően azoknak a fejlesztési eredményeknek, amelyek főként a 2000. év után lettek átültetve az ipari gyakorlatba. A legfontosabb irány jelenleg az élettartam és a megbízhatóság növelése, ami különösen a járműipar számára kulcsfontosságú. A következő táblázatban rövid, szemelvényes áttekintést adunk a fogazott szíjas átalakító alkalmazási területeiről, ötletadás céljából.
A fogazott szíjas lineáris mozgató rendszerint két egységből áll, egy motor és hajtómű egységből és a fogazott szíjas mozgás-átalakítóból, ahogy a következő ábra mutatja:
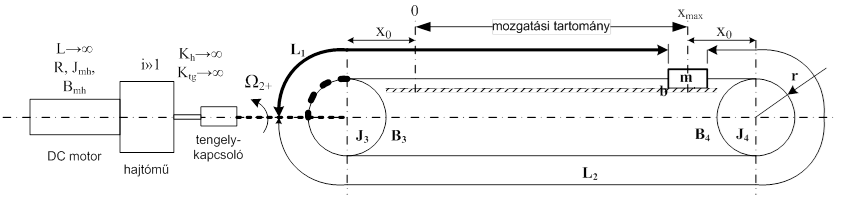
Azokat a jelöléseket, hogy Kh→∞ és Ktg→∞ a fogazott szíjas átalakító rugómerevségéhez viszonyítva kell értelmezni. A hajtómű eredő rugómerevsége és a tengelykapcsoló rugómerevsége ezek szerint lényegesen nagyobb, mint a fogazott szíjé. Dinamikai szempontból a rendszert külön, a 12.5. szakasz fejezetben vizsgáljuk részletesen, annak függvényében, hogy a motor-hajtómű egység visszahatásmentesen szétválasztja két soros tagra a rendszert, vagy a teljes struktúra csak egyetlen, összefüggő rendszerként modellezhető.
Tervezési szempontból a fogazott szíjas pozícionáló (lineáris mozgató) dinamikai és pontossági szempontból legfontosabb része a fogazott szíj.
A különféle, jelenleg kereskedelemben kapható fogprofilokról ugyancsak közlünk tájékoztatást.
|
Fogosztás [mm] |
~2 |
~5 |
~10 |
~20 |
|
|---|---|---|---|---|---|
|
Példák szabványos profilokra |
Átlagos trapézprofil |
T2; T5; MXL; |
T5; XL |
T10; AT10; L; H |
T20; AT20; XH |
|
Nagyteljesítményű profilok 1. |
HTD3M; S2M; S3M |
HTD5M; S5M |
HTD8M; S8; S8M |
HTD14M; HTD20M; S14M |
|
|
Nagyteljesítményű profilok 2. |
AT3 |
AT5 |
AT10 |
AT20 |
|
|
Nagyteljesítményű profilok 3. |
GT3M; RPP3 |
GT5M; RPP5 |
GT8M; RPP8 |
GT14M; RPP14 |
|
|
Hajtókerék fordulatszám [1/min] |
<40 000 |
<40 000 |
<15 000 |
<6 000 |
|
|
Szíjsebesség [m/s] |
<80 |
<80 |
<60 |
<40 |
|
|
Tárcsa minimális fogszáma |
>10 |
>10 |
>12 |
>15 |
|
|
Átvihető teljesítmény [W] |
<1 |
<5 |
<60 |
<220 |
|
|
Alkalmazás |
Miniatűr hajtások Nyomtatók Plotterek Vezérlőművek Háztartási gépek |
Pozícionálók Szerszámgépek Robotok Textilgépek Háztartási gépek |
Pozícionálók Építőgépek Szivattyúk, sűrítők Robotok Faipari gépek |
Építőipari gépek Malmok Fafeldolgozó gépek Nehézgépek |
|
Szakmai körökben ismert, hogy néhány kifejezetten nagy teljesítményre kialakított fogprofiltól eltekintve, nem a fogprofil, hanem a fogtávolság és a szíj szélessége mérvadó az átvihető teljesítmény tekintetében. Újabban nem csak nyomatékátvitel a fogazott szíj feladata, hanem a lineáris mozgatókban a pozícionálás. Amíg a merevítő szálak rendszere és a szíj anyaga nem volt a maihoz hasonló, ilyen precíziós feladatok céljára fogazott szíjat nem alkalmaztak. Ma már egy plotter, egy nyomtató, tömegcikk, és az ár alacsony szinten tartása érdekében elképzelhetetlen fogazott szíjak alkalmazása nélkül.
A fenti táblázat első sorában megjelennek a szabványos fogprofilok. A könnyebb áttekinthetőség érdekében, a következőkben nézzünk néhányat ezek közül:
A fogazott szíjas hajtást a speciális tulajdonságai miatt egyebek mellett, tervezni kell élettartamra és pozícionálási pontosságra is.
12.2. Fogazott szíj méretezésének lépései
A napjainkban kínált fogazott szíj gyártmányok esetében a tervezőnek bizonyos mértékig meg van kötve a keze. A korlátozás legfőbb okai a kereskedelemben kínált szíjak anyaga, a fogprofil, a fogosztás és a szíjhossz. Amint a későbbiekben látni fogjuk, például a szíj rugómerevségének beállítására egyedül a szélesség ad bizonyos mozgásteret.
A fenti áttekintő táblázatban látjuk, hogy milyen teljesítmény igényre milyen fogprofil és fogosztás ajánlott. A gyártók ismertetői természetesen ennél az áttekintésnél lényegesen bővebbek, ez a táblázat csak az összehasonlítás kedvéért készült.
A tervező számára nyolc pontban összefoglaltuk a fogazott szíjas hajtás tervezési lépéseit. Természetesen lehetséges ezektől eltérni, de nem ajánlott.
-
Fogazott szíj anyagának kiválasztása a működési feltételek figyelembe vételével
-
Fogazás profil kiválasztása (profiltól függő tulajdonságok, ár, beszerezhetőség)
-
Fogtávolság meghatározása a teljesítmény átvitel függvényében
-
A hajtás geometriájának meghatározása (fogszámok, tengelytávolságok, hajlítási ívek, szükséges szíjhosszúság)
-
A kínálati szíjhosszúság ellenőrzése (katalógusok)
-
A hajtás geometriájának átszámítása, a gyártott szíjhosszak figyelembevételével
-
A szükséges szíjszélesség kiszámítása
-
A legközelebb eső standard szélességű és hosszúságú szíj kiválasztása
A tervezés tehát többszörös iterációs folyamat, és feltételezi a tervező rugalmas hozzáállását, mind az elrendezés, mind a szíjhossz és a tárcsaátmérők tekintetében. A tárcsák átmérője és szélessége sem tetszőlegesen választható jellemző, e tekintetben is igazodni kell a kínálathoz. A megfelelő szíj kiválasztásában hathatós segítséget nyújt a Drezdai Műszaki Egyetem Finommechanikai és Elektronikai Design Tanszéke (Technische Universität Dresden, Institut für Feinwerktechnik und Elektronik Design) által kidolgozott programcsomag. E program tanuló verziója az Interneten ingyenesen elérhető, tervezéssel foglalkozó cégek részére pedig természetesen bővebb verziókat is kínálnak, német és angol nyelvű utasításokkal. A tervező program a www.eassistant.eu honlapon érhető el. A következő képpel a program ügyes használhatóságát akartuk alátámasztani. Amint látható, a fogazott szíjas hajtás 2D-s modellje a koordinátarendszer segítségével méretarányosan elkészíthető. A programban beállítható a tervező által elképzelt teljesítmény igény és a fogprofil, a rendszer megadja az alkalmas szíj típusát, a fogtávolságot. Az elképzelt elrendezéshez megadja a legközelebbi gyártott szíjhosszat. Be kell állítani a fogazott tárcsák fogszámát, és kiadódnak a hatásos tárcsa átmérők. A program ügyel arra, hogy adott anyagú, fogprofilú és fogtávolságú szíjhoz milyen átmérőjű fogazott tárcsa rendelhető. A szíjak élettartamát nagymértékben csökkentheti az, ha a szíj merevségéhez viszonyítottan kis tárcsaátmérő miatt csökken a hajlítási sugár, és ezzel nő a szíj hajlító igénybevétele.
![Korszerű program fogazott szíjas mozgatás tervezéséhez [12.1.]](images/image_XII_4.png)
A csapágyak méretezéséhez szükség van az előfeszítő erő figyelembe vételére. A fogazott szíjas mozgatás minőségének egyik – sok esetben döntő – kritériuma a szíjfeszesség beállítása. A következőkben készítettünk egy összeállítást, amelyből kitűnik, hogy ez a kérdés igen ellentmondásos.
Előfeszítő erő beállítása
|
Előfeszítő erő kicsi |
Előfeszítő erő nagy |
|---|---|
|
Szíjfog átugorhat egy tárcsafogat |
Zajemisszió növekedése |
|
Élettartam csökkenés a tárcsa- és szíjfogak közötti súrlódások növekedése miatt |
Élettartam csökkenés a túlzott húzó igénybevétel, a szíj túlfeszítése miatt, |
|
Zajemisszió növekedése |
Növekvő csapágyterhelés |
|
Csökkenő pozícionálási pontosság |
Élettartam csökkenés a megnövelt hajlító igénybevétel miatt |
|
De: Csökkenő csapágyterhelés |
De: Nincs fogátugrás |
A szíj és fogazott tárcsa közötti kapcsolatot igen jól szemlélteti a következő két kép, amely Dr. T. Nagel előadási anyagából származik. A baloldali kép egy „laza” szíjat mutat, az előfeszítő erő az előírásosnak a fele. A jobboldali képen egy 50%-kal túlfeszített szíj kapcsolódását látjuk. Amíg a laza szíj a kapcsolódás és elválás során ismétlődő dörzshatások az élettartam csökkenéséhez vezethet, és rontja a pozícionálási pontosságot, addig a túlzottan feszes állapot a szíjfogak deformációját, és a csapágyak túlterhelését eredményezi. A szíjfogak deformációja ugyancsak pozícionálási hibaként jelentkezik.
![Az előfeszítés hatása a fogazott tárcsánál [10.1.]](images/image_XII_5.png)
A szíj feszessége nem csak a fogak deformációján keresztül befolyásolja a rendszer pozícionálási pontosságát, hanem a szíj és a fogazott tárcsa közötti kapcsolódás ívével, a szíj tárcsára való felfekvésével is. Ugyancsak Dr. T. Nagel anyagából származik az a diagram, amelyet a 10.4. szakasz fejezetben találunk, és amely az előfeszítő erő és a terhelés nagyságának függvényében mutatja felfekvési ív és az ideális felfekvési rádiusz közötti eltéréssel összefüggésben lévő pozícionálási hiba nagyságát.
12.3. A motor kiválasztása
A lineáris mozgatóhoz szükséges motor és hajtómű egység kiválasztásához a golyósorsóhoz hasonlóan szükség van a rendszer gráfjára, vagy impedancia hálózatára annak érdekében, hogy a szükséges teljesítményt és fordulatszámot megállapíthassuk.
A gráfon a motor-hajtómű egység és a fogazott szíjas mozgató külön van választva, ami azt jelenti, hogy a hajtómű módosítása elegendően nagy a visszahatás mentesség biztosítására. A motorteljesítmény megállapításához valójában mindegy, hogy van-e visszahatás, mert a szükséges mértékű tartalékok biztosítására a teljes rendszer motor „felől” nézett eredő tehetetlenségi nyomatékára szükség van.
A méretezéshez szükséges mennyiségek jelölését és mértékegységüket az alábbiakban adjuk meg:
|
m |
[kg] |
mozgatott tömeg |
|
|
b |
[Ns/m] |
egyenes vezeték csillapítási tényezője |
|
|
i |
hajtómű módosítása (i˃1: lassítás) |
||
|
r |
[mm] |
a tárcsák sugara (pozícionálónál mindkét sugár azonos értékű) |
|
|
ke |
[N/m] |
a fogazott szíj eredő rugómerevsége |
|
|
F |
[N] |
előtoló erő (tervezett, igényelt) |
|
|
Fs |
[N] |
egyenes vezetéken fellépő súrlódási erő |
|
|
Fa |
[N] |
gyorsító erő |
|
|
M0 |
[Nm] |
üresjárati nyomaték |
|
|
MT1 |
[Nm] |
terhelő nyomaték állandó sebességű emelésnél (függőleges elrendezésnél) |
|
|
MT2 |
[Nm] |
terhelő nyomaték állandó sebességű süllyedésnél (függőleges elrendezésnél) |
|
|
MS |
[Nm] |
a teljes rendszer eredő súrlódási nyomatéka (számítást ld. külön) |
|
|
MSH |
[Nm] |
hajtómű eredő súrlódó nyomatéka |
|
|
MM |
[Nm] |
motor hajtó (villamos) nyomatéka |
|
|
MTa |
[Nm] |
terhelő nyomaték gyorsításnál |
|
|
Ma |
[Nm] |
gyorsító nyomaték |
|
|
MMa |
[Nm] |
motor hajtónyomaték gyorsításnál |
|
|
Jm |
[kgm2] |
motor forgórész tehetetlenségi nyomatéka |
|
|
Jmr |
[kgm2] |
a mozgatott tömeg átszámított tehetetlenségi nyomatéka |
|
|
J |
[kgm2] |
tehetetlenségi nyomaték |
|
|
J0,1 |
[kgm2] |
hajtómű bemeneti és kimeneti oldali tehetetlenségi nyomatéka |
|
|
B1,2 |
[Nms/r] |
hajtómű bemeneti és kimeneti oldali csillapítási tényezői |
|
|
J1,2 |
[kgm2] |
hajtó és hajtott tárcsák tehetetlenségi nyomatéka |
|
|
Pm |
[W] |
motor teljesítmény konstans sebességnél |
|
|
Pma |
[W] |
motor teljesítmény gyorsításnál |
|
|
sa |
[mm] |
gyorsítási úthossz |
|
|
ta |
[s] |
gyorsítási idő |
|
|
v |
[m/s] |
mozgatás sebessége, azaz az asztal előírt végsebessége |
|
|
nM |
[1/min] |
motor fordulatszám |
|
|
η |
hajtómű hatásfoka (katalógus) |
||
|
η1 |
fogazott szíjas átalakító hatásfoka emelésnél |
||
|
η2 |
fogazott szíjas átalakító hatásfoka süllyedésnél |
A motor szükséges nyomatékának meghatározása állandó fordulatszám esetén
A motor hajtónyomatékának meghatározásához az alábbi összetevők szükségesek. Ha a vonóelemes pozícionálót függőleges helyzetben is üzemeltetni kell, akkor figyelembe kell venni, hogy süllyesztésnél az MT2 nyomaték negatív, akkor a motort fékezni kell, ezért jelenik meg az összefüggésben külön összetevőként.
A képletekben felismerhető a vonóelemes átalakító „r” átalakítási tényezője, valamint a hajtómű „i” módosítása. Az ezres osztó azért szerepel, mert a fogazott tárcsa sugarát mm-ben adjuk meg.
Állandó sebesség mellett (stacionárius állapot) a motor teljesítménye:
A modellezés során keresztváltozóként „Ω” szögsebességet használunk, de a motor katalógusokban „n” fordulatszám szerepel. Ezért szükséges az átszámítás.
Motorválasztás szempontjából érdekes lehet stacionárius állapotban vonóelemes átalakítóval mozgatott tömeg (asztal) előírt „v” végsebessége, és az ehhez szükséges motor fordulatszám is:
A motor szögsebességére állandósult állapotban, illetve, ha a hajtómű rugómerevsége nagy, felírható, hogy
Ezt az összefüggést a későbbiekben is felhasználjuk.
A mozgatott tömeg a hajtómű kimeneti oldalán van, ezért kell a módosítást figyelembe venni. A vonóelemes átalakító „r” átalakítási tényezője a transzlációs sebesség átszámításához szükséges, a 103 szorzó pedig azért jelenik meg, mert „r” mm-ben, „v” pedig m/s dimenzióban lesz megadva.
A motor szükséges nyomatékának meghatározása gyorsítás esetén
A motorral szemben támasztott összes nyomaték igény, amely gyorsítás esetén felléphet, az alábbi összetevőkből adódik:
A számításhoz felhasználjuk az előzőekben meghatározott M0 üresjárati nyomatékot. Ebben már benne foglaltatik az egyenes vezetékeken fellépő súrlódó erő, de a képletben nem feledkeztünk el a csapágyazások súrlódási nyomatékáról sem.
Következő lépésben a gyorsítandó rendszerre ható MTa terhelő nyomatékot kell meghatározni, amelyben az előtolás szükséges (tervezett, előírt) erőértékét és a tervezett gyorsító erőt kell figyelembe venni:
A nyomaték, amely a teljes vonóelemes pozícionáló rendszer eredő tehetetlenségi nyomatékát gyorsítja, kétféle módon határozható meg. Egyrészt az előírt gyorsítási úthossz és a gyorsításhoz szükséges idő segítségével, másrészt a motor fordulatszámának felhasználásával, ha a névleges fordulatszámra kívánunk gyorsítani.
Ha a terhelési oldalon, tehát a hajtómű kimeneti oldalán előírt az asztal gyorsítási úthossza és az ehhez szükséges idő, akkor az alábbi összefüggések írható fel, ΩM=Ω1 feltételezéssel:
Ahol „J” a motor oldalára redukált eredő és egyenértékű tehetetlenségi nyomaték, „Ω1” a hajtómű bemenő szögsebessége, ami azonos a motor szögsebességével. Mindkét esetben figyelembe kell venni a motorhoz csatlakoztatott hajtómű hatásfokát is.
Észre kell venni azt is, hogy a „Nm” dimenzió helyes, annak ellenére, hogy a gyorsítási úthosszat „mm”-ben adjuk meg. Ezt kompenzálja a hajtó (hajtott) tárcsa „r” sugara, amely ugyancsak „mm”-ben lesz behelyettesítve. Ettől kezdve csak az sa/r arány számít.
Ha a motor szögsebessége helyére a hajtómű kimeneti oldali „Ω2” szögsebességét helyettesítjük, majd ezt a szögsebességet a golyósorsó (váltó) átalakítási tényezőjével sebességgé számítjuk át, akkor alábbi összefüggés már a gyorsítási úthossz és a gyorsítási idő függvényében szolgáltatja a szükséges nyomaték értékét.
A gyorsítás után elért motor fordulatszám, ha a hajtómű kimeneti oldalán elért úthosszat vesszük alapul, egy hosszabb átszámítás után adódik:
Ha viszont a motor teljes „kivezérlési” tartománya érdekes, tehát zérus fordulatszámról a lehető legnagyobb értékig, a névleges fordulatszámig kívánjuk gyorsítani a motort az adott terhelésekkel, akkor a következő összefüggést kell alkalmazni:
A képletekben előforduló „J” eredő tehetetlenségi nyomaték összetevői a modell gráfja segítségével érthetők meg.

Az eredő tehetetlenségi nyomatékot a motor „felől nézve” kell meghatározni, hiszen a motor kiválasztásáról van szó. Így az eredőben a motor saját tehetetlenségi nyomatéka és a hajtómű bemeneti oldali tehetetlenségi nyomatéka összeadható, de a hajtómű kimeneti oldalán szereplő tehetetlenségeket már csak a redukálás szabályai szerint adhatjuk ezekhez hozzá, nem beszélve arról, hogy az egyenes vonalon mozgatott tömeg tehetetlenségi nyomaték egyenértékét a golyósorsó átalakítási tényezőjének felhasználásával kell meghatározni.
Az átszámítás (és a redukció) elméleti hátterét a modellezés alapelveivel foglalkozó fejezetben találhatjuk meg.
Hátra van még a szükséges motorteljesítmény meghatározása.
Ezt egyrészt hagyományos módon adhatjuk meg, ha előírt a fogazott szíjjal mozgatott tömeg (asztal) „v” végsebessége, és az ehhez a sebességhez kiszámított motor fordulatszám:
A motorteljesítmény meghatározásánál figyelembe vettük a súrlódásokból eredő veszteségeket, ld.: FS és MS a megfelelő képletekben.
A súrlódási nyomatékokat (erőket) vagy tapasztalati adatok segítségével becsülhetjük, vagy mérésekkel határozzuk meg. Ha szükség van az eredő veszteség különálló becslésére is, akkor azt az alábbi formula segítségével lehet megtenni:
Az összefüggésben „B” a motor „felől” látható eredő súrlódási tényező. Kiszámítása a tehetetlenségi nyomatékhoz hasonlóan, összevonással és redukálással történik:
A fenti képletben látható csillapítási tényezők megtalálhatók a gráfban. Az egyenes vezetéken mozgatott tömeg lineáris csapágyazásaiból eredő csillapítási tényező „b” jelölést kapott.
12.4. Fogazott szíjas pozícionálás pontossága
Amint a golyósorsós mozgatók esetében az eredő rugalmasság és a súrlódások befolyásolják a pozícionálási pontosságot, úgy a fogazott szíjas átalakító esetében is fel kell térképeznünk, hogy melyik tényező milyen mértékben van hatással a pontosságra.
Első lépésben definiáljuk a pozícionálás hibáit, és azokat a jellemzőket, amelyeket a méréselmélet és a valószínűségszámítás segítségével lehet meghatározni. A számításokhoz szükséges adatokhoz alapvetően egy elkészült pozícionáló rendszer méréstechnikai vizsgálatával juthatunk. Ugyanakkor táblázatos formában összefoglaltuk a pozícionálási hiba forrásait, hogy a tervezés és méretezés fázisában is mód nyíljon ezek figyelembe vételére.
|
Hiba ok |
Jellemző |
Az eltérés számításához szükséges adatok, ismeretek |
Eltérés |
|---|---|---|---|
|
Terhelt szíjág nyúlása Δxsz |
Szíjág merevség Szíjág merevség ingadozás |
Specifikus szíjág-merevség ks Szíjág hossza L1,2 és szélessége h |
|
|
Fogrugalmasság okozta deformáció a kapcsolódási íven ΔxF |
Kapcsolódási ív eredő fogrugalmassága Fogosztás eltérés esetén a szíj radiális irányú rugómerevsége |
Specifikus fogmerevség kSF Aktív szíjfogak száma zK Szíj szélesség h Szíjág merevség Tárcsa és szíj fogosztása közötti eltérés |
|
|
Áttétel ingadozásából származó hiba ΔxfR Tárcsa excentricitásból eredő hiba Δxex |
Fogazott kerék sugarának ingadozása A feszített szíj osztásának ingadozása |
Fogazott kerék alakhibája fR1, fR2 körfutási hibák Csapágyazás hibája Excentricitás |
A táblázatban alkalmazott jelölések magyarázata a következő:
|
kFS |
[N/mm2] |
Specifikus fogmerevség (egy fogra), N/mm a szíjszélesség 1 milliméterére vonatkoztatva |
|
|
kS |
[N/mm2] |
Specifikus szíjmerevség, N/mm a szíjszélesség 1 milliméterére vonatkoztatva |
|
|
z |
Tárcsa fogszáma |
||
|
d |
[mm] |
Tárcsa átmérője |
|
|
zK |
Szíj tárcsával kapcsolódó fogainak száma |
||
|
p |
[mm] |
Szíj névleges fogtávolsága |
|
|
pF |
[mm] |
Feszített szíj nyújtott fogtávolsága |
|
|
Fsz |
[N] |
Szíjágban ébredő erő |
|
|
h |
[mm] |
Szíj szélessége |
|
|
Lk |
[mm] |
Kapcsolódó (fogakkal) szíjhossz |
|
|
fR |
[mm] |
Tárcsa sugarának hibája |
|
|
e |
Tárcsa excentricitása |
||
|
x |
[mm] |
Mozgatási hossz |
|
|
φ |
[°] |
A tárcsa szögelfordulása |
|
ΔLmax=0,2 mm/m, értéke függ a gyártmánytól és a szíjfeszítéstől |
![A szíj fogazott kerékre való felfekvéséből származó hiba [10.1]](images/image_XII_7.png)
Az áttétel hibája is kiszámítható, ez egyenes vonalú (transzlációs) hiba formájában jelenik meg. A feszített fogazott szíjas átalakító ΔxP szíjfeszítés miatti hosszváltozás tűrése lineáris mozgatás és ΔpF értékkel megnyújtott fogosztás esetén:
A szíjág megnyúlása ismert ΔFSZ nagyságú szíjfeszítő erő esetén:
A táblázatban összefoglalt pozícionálási hibaokozók között a második sorban szerepel a húzott fogazott szíj tárcsán való felfekvésének ideális helyzettől való eltérése. A következő ábrán gyakorlati mérési adatokat láthatunk, amely a különböző terhelési százalékok függvényében a szíj sugárirányú helyzete és az ideális felfekvési sugár közötti hibát szemlélteti.
A pozícionálás maximális abszolút hibája [12.2.]
A maximális abszolút hiba a legkedvezőtlenebb esetet felételezi, amikor is minden rész-hiba abszolút értékét összeadjuk. Kétségtelen tény, hogy ezek a hibák egyszerre jelennek meg a pozícionálás során, de mértékük ingadozhat. Olyan eset, amelynél minden rész-hiba maximuma lép fel, igen csekély valószínűséggel fordul elő a műszaki gyakorlatban, ezért a méréstechnikában, hasonló esetekben, inkább a súlyozott szórásnégyzetek összegéből származó eredő szórással szokás jellemezni a bizonytalanságot. A pozícionálás statisztikai jellemzőit külön összefoglalva bemutatjuk.
Az eredő abszolút (maximális) hiba a következő tényezőkből tevődik össze:
ahol:
|
Δxsz |
Szíjág nyúlása (terheléstől függő) |
|
|
ΔxF |
Eredő fogrugalmasság miatti alakváltozás a kapcsolódási íven (terheléstől függő) |
|
|
ΔxP |
Szíjfeszítés miatti hosszváltozás tűrése (feszítőerőtől függő) |
|
|
ΔxSP |
Szíj fogosztásának hibája (katalógus adat) |
|
|
ΔxfR |
Fogazott tárcsa sugarának hibája |
|
|
Δxex |
Fogazott tárcsa excentricitása |
A pozícionálás bizonytalanságának meghatározása
A pozícionálási bizonytalanságot mindenképpen csak empirikus (gyakorlati mérési adatokra alapozva) úton lehet becsülni.
Két út lehetséges:
-
Régebbi adatok, tapasztalatok felhasználásával („B”-típusú méréstechnikai becslés)
-
Mérési adatok felhasználásával („A”-típusú méréstechnikai becslés)
A valószínűségszámításból tudjuk, hogy a véletlen változó „várható értéke” μ (ahol μ=E(x)) és a „szórásnégyzete” (varianciája) σ2, (ahol σ2=D2(x)) nem függvényei az x valószínűségi változónak, hanem „x” eloszlásának tulajdonságait kifejező un. „funkcionálok”. E(x) az „x” valószínűségi változó eloszlásának elhelyezkedésére jellemző, és D2(x) a szóródás (vagy koncentráció) mértékszáma. Tehát „μ” és „σ” elméleti értékek, a gyakorlatban „μ” várható érték helyett átlagérték, és „σ” szórás helyett „s” tapasztalati szórás, vagy s* korrigált tapasztalati szórás meghatározására van lehetőség. A korrigált tapasztalati szórás kiszámításánál – jellemzően 30-nál kevesebb mérési adat esetében - figyelembe vesszük a szabadságfok csökkenését. Szeretnénk hangsúlyozni, hogy a mérnöki gyakorlatban sem ajánlatos keverni a várható értéket az átlaggal és a szórást a tapasztalati szórással. Ezzel kapcsolatban látszik, hogy „pongyolaság” az ismétlőképesség tartományának emlegetése „six sigma” elnevezéssel, mert ehhez pontosan ismerni kellene a valószínűségi változó eloszlásfüggvényét (Normál, Student), vagy legalább 100 mérési adat kellene, hogy rendelkezésre álljon. Helyesebb lenne tehát a „6s*”, vagy „6s” megnevezés.
Egy adott pozíció közelítése történhet „alulról”, azaz alacsonyabb értékek felől, és „felülről”. A következő ábrán szemléltetjük a pozícionálás hibáit és a pozícionálás bizonytalanságát.
A pozícionálási eltérés és az irányváltás hibája az „xe” elméleti, vagy előírt pozícióhoz viszonyítottan jelentkezik. A pozícionálási eltérés az „xe” és a valós alulról történő közelítés átlaga valamint a valós felülről történő közelítés átlaga és „xe” közötti különbség. Az irányváltás hibája a és átlagértékek közötti különbség. A pozícionálás teljes bizonytalansági tartománya az adatok normál eloszlása esetében és 99.73% konfidencia szinten .
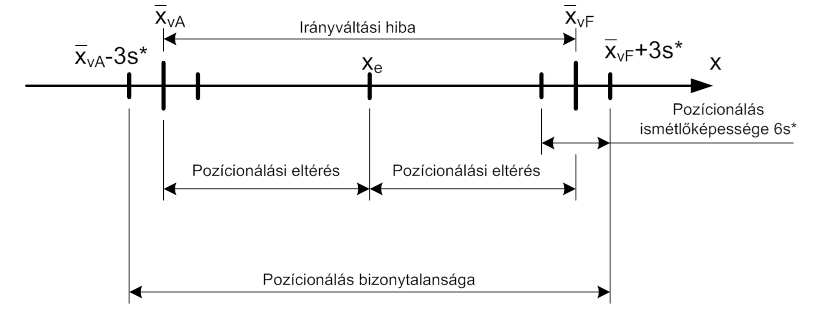
Az előző ábrán megadott jellemzőket összefoglaltuk táblázatosan is, megadva az egyes jellemzők kiszámításának módját is.
|
Ismérv |
Közelítés felülről |
Közelítés alulról |
|---|---|---|
|
Pozícionálási hiba (véletlen hiba) |
||
|
Pozícionálási hiba átlaga |
||
|
Korrigált tapasztalati szórás |
||
|
Pozícionálás ismétlőképessége (P=99,73 %) |
PF=6sF* |
PA=6sA* |
|
Irányváltási hiba |
||
|
Pozicionálás bizonytalansági tartománya |
||
12.5. A szakasz állandó együtthatós, lineáris matematikai modellje
A 12.1. szakasz fejezetben már volt arról szó, hogy a fogazott szíjas lineáris mozgató rendszerint két egységből áll, egy motor és hajtómű egységből és a fogazott szíjas mozgás-átalakítóból. Ennek megfelelően járunk el a fogazott szíjas szakasz lineáris matematikai modelljeinek megalkotása során.
Attól függően, hogy a méretektől és az erőhatásoktól függően, a hajtómű esetében számolnunk kell-e a valós modellel, és figyelembe kell-e vennünk a motor induktivitását, többféle változattal dolgozhatunk, hasonlóan a golyósorsós szakaszhoz.
Egyszerűsíti a feladatot, hogy a 10.5. szakasz fejezetben bemutattuk a vonóelemes lineáris mozgató átviteli függvényének levezetését impedancia módszerrel, amely lineáris, állandó paraméterű modellezés esetében másodrendűnek adódott. Az egyszerű szabályozás megtervezéséhez, ha a szakasz a hajtómű kimenetén szétválasztható, elegendő az átviteli függvények ismerete. Pozíciószabályozás esetén a kimenet természetesen nem a sebesség, hanem az elmozdulás „Xm” lesz, tehát a következő átviteli függvényhez egy integrátort sorosan még hozzá kell kapcsolni.
Fogazott szíjas lineáris mozgatóra, az egyszerűsített és linearizált esetre a katalógusok az eredő rugómerevséget a következőképpen határozzák meg:
Ahol
|
k SP |
[N/mm] |
a fogazott szíj specifikus rugómerevsége, annak egy milliméter szélességére vonatkoztatva |
|
|
h |
[mm] |
vonóelem szélessége |
|
|
L 1 |
[mm] |
húzott (terhelt) ág hossza |
|
|
L 2 |
[mm] |
terheletlen ág hossza |
Elsőrendű motor és hajtómű egység és fogazott szíjas mozgató
Ennek a modellnek az a feltétele, hogy a hajtómű módosítása elegendően nagy legyen a szétválasztáshoz. Ha ez a feltétel teljesül, akkor a szakasz átviteli függvénye a motor-hajtómű egység és a fogazott szíjas lineáris mozgató sorosan kapcsolt két átviteli függvényéből adódik:
Az így meghatározott átviteli függvény egy negyedrendű arányos átviteli tagot reprezentál, a szabályozástechnikában szokásos alak az alábbi:
ahol
Harmadrendű motor és hajtómű egységgel kombinált fogazott szíjas mozgató
A szakasz eredő átviteli függvényében G2(s) változatlan az első modellhez képest, hiszen igazoltuk, hogy az állandó együtthatós, lineáris mozgató átviteli függvényének rendszáma kettő. Ezért a szakasz átviteli függvénye a második változatban a következő lesz:
TS és ξS az elsőrendű változatnak megfelelő értékek, az „ai” együtthatókba foglalt paramétereket a 8.1. szakasz fejezet végén találjuk, de a könnyebb érthetőség kedvéért „importáltuk”:
A szakasz hatodrendű lesz, látjuk, hogy As az első változathoz viszonyítva csak „alakra” módosult, mert az első változatban Be csillapítási tényező alatt mást értettünk. Emlékeztetőül megjelenítjük az első változat eredő csillapítási tényezőjét és eredő tehetetlenségi nyomatékát:
Ha most a második változat eredő csillapítását kibontjuk, és összevetjük a fent látható első változattal, meggyőződhetünk, hogy nincsen változás, mert a csillapítási tényezőkön és elhelyezkedésükön nem változtatunk:
A szakasz átviteli függvényét célszerű a fenti formában meghagyni, ha a szabályozókör tervezését Bode diagramokkal végezzük.
Negyedrendű motor és hajtómű egység fogazott szíjas lineáris mozgatóval
A szakasz eredő átviteli függvénye felírásához G1 kiegészül a változatlan G2-vel, és végső soron két szorzatra bontható hetedrendű rendszert kapunk:
TS és ξS az elsőrendű változatnak megfelelő értékek, az „ai” együtthatókba foglalt paramétereket a 8.1. szakasz fejezet végén találjuk, de a könnyebb érthetőség kedvéért „importáltuk”:
Ha a G1 átviteli függvény rész együtthatói a tervezési követelmények miatt kötöttek, akkor érdemes a rendelkezésre álló adatok behelyettesítésével a paraméteres formáról áttérni a konkrét szám-együtthatós alakra.
A nevező összeszorzása most sem célszerű, de ha olyan számítógépes szimulációs program áll rendelkezésre, amely n-edrendű átviteli függvény Bode diagramjának megszerkesztésére alkalmas, akkor az összeszorzást érdemes programmal (konvolúció utasítással) elvégeztetni.
12.6. A szakasz nemlineáris állapottér modellje
Láttuk a 10.5. szakasz fejezetben, hogy a vonóelemes átalakító, a mechatronikában döntően a fogazott szíjas lineáris mozgató struktúra gráfja a linearizálást megelőzően összetett, és látszólag három rugómerevség ágat tartalmaz, de valójában kettő az, amelyek a mozgatott tömeghez kapcsolódik. Az egyik ág a terhelt (húzott) ág, a másik a terheletlen, de forgásiránytól függően ez is változik. A három gráf-él azért látszólagos, mert az egyik ág közvetlenül, a másik pedig a visszatérítő tárcsán keresztül csatlakozik a tömeghez. Az ágak rugómerevsége változó nagyságú, mert a tömeg pozíciójától függően változik a terhelt (húzott) és terheletlen szíjágak hossza. A rugómerevségük értéke függ a mozgatott tömeg pozíciójától, és függ a mozgatás irányától is. Ezek a nemlineáris rugómerevségek eredő rugómerevségek, hiszen láttuk a 12.4. szakasz fejezetben, hogy a szíj rugalmasságán kívül a kapcsolódási ív rugalmassága és a fogak eredő rugalmassága sem elhanyagolható. A terhelés, illetve az előfeszítés tulajdonképpen az eredő karakterisztikán jelöl ki egy „kezdeti” munkapontot.
A soron következő vizsgálódásainkban arra szeretnénk választ kapni, hogy leíró függvényekkel milyen pontossággal közelíthető a valós helyzet.
Megjegyezzük, hogy a vizsgálódásaink során csak a szíjágak rugómerevségét vesszük figyelembe, az előfeszítéstől és a terheléstől függő a fogrugalmasságot és a kapcsolódási ív rugalmasságát nem.
Fentebb említettük, hogy a mozgatott tömeghez két szíjág csatlakozik. Elsőként a húzott (terhelt) ág rugómerevségével foglalkozunk, és ezt követően megvizsgáljuk, hogy az adott terhelt ághosszhoz milyen terheletlen szíjág tartozik. A nemlineáris rugómerevséget a két rugómerevség párhuzamos eredője (összege) adja. A rugómerevségek leíró függvényeihez szükséges értékek kiszámításához elegendő az adott mozgatási irányban a két véghelyzetet vizsgálni, a mindenkori pozícióhoz tartozó szíj rugómerevség képlete ismert.
Kétszer két ábrából álló ábrasor következik. Az első kettő azt a szíjmerevség változást szemlélteti, amikor a tömeget xmax pozícióból, a forgató tárcsa pozitív forgásiránya mellett, az x0 pozícióba mozgatjuk. A harmadik és negyedik ábra azt mutatja, hogy megfordul a hajtótárcsa forgásiránya, és ennek következtében a tömeget az x0 pozícióból az xmax pozícióba mozgatjuk. Az ábrasor végén bemutatjuk, hogy egy konkrét fogazott szíj típus, adott mozgatási hossz, specifikus rugómerevség, stb. esetében milyen értékhatárok között változik a húzott ág rugómerevsége.
A húzott ágak rugómerevsége mellett számolni kell a terheletlen ág rugómerevségével is, hiszen többször hangsúlyoztuk, hogy a tömeg két ágon keresztül kapcsolódik a hajtótárcsához. A következő táblázatban az összetartozó (párhuzamosan kapcsolt) terhelt és terheletlen ághosszakat foglaltuk össze. Az ághosszakkal a szíj rugómerevségek összefüggenek, ezt az indexeléssel jelezzük. Az egyes összetevőket a kétszer két ábrából álló ábrasorról olvashatjuk le.
A lineáris modellhez hasonlóan úgy tekintjük, hogy a tömeghez a tömeg-középpontban csatlakoztattuk a szíjvégeket.
|
Húzó (terhelt szíjág) hossza és rugómerevsége |
Terheletlen szíjág hossza és rugómerevsége |
||
|---|---|---|---|
|
Lt1=xmozg+x0+rπ/2 |
k1 |
L4= x0+2(rπ/2) + 2x0+xmozg+rπ/2 |
k4 |
|
Lt2= x0+rπ/2 |
k2 |
L3=xmozg+x0+2(rπ/2)+2x0+ xmozg+ rπ/2 |
k3 |
|
Lt3=xmozg+x0+2(rπ/2)+2x0+ xmozg+ rπ/2 |
k3 |
L2= x0+rπ/2 |
k2 |
|
Lt4= x0+2(rπ/2) + 2x0+xmozg+rπ/2 |
k4 |
L1=xmozg+x0+rπ/2 |
k1 |
A fenti táblázatban, és a következőkben az alábbi jelöléseket alkalmaztuk. Az összetartozó terhelt és terheletlen szíjágak hossza természetesen állandó.
|
Lt1…t4 |
Adott tömeg-pozícióhoz tartozó húzó (terhelt) ághossz |
|
|
L1…4 |
Terheletlen ághossz |
|
|
k1…4 |
Rugómerevségek (terhelt és terheletlen ágak) |
|
|
Lh |
A húzott szíjág abszolút hosszúsága |
|
|
kh1…h4 |
Abszolút rugómerevségek (terhelt és terheletlen ágak) |
|
|
r |
Fogazott tárcsa sugara |
A négy ábra az általános szerkezeti modellt jeleníti meg. Egy valóságos szerkezetnél Lt1…4 úgy is adódhat, hogy a szíjvégek nem a tömeg-középpontba vannak csatlakoztatva. Az egyszerűség kedvéért, a 12.5. szakasz fejezet elején jelzett módon úgy vesszük, mintha esetünkben Lt1…4 a tömegközéppontig terjedne, hiszen nem ismert a konkrét tömeg mérete.
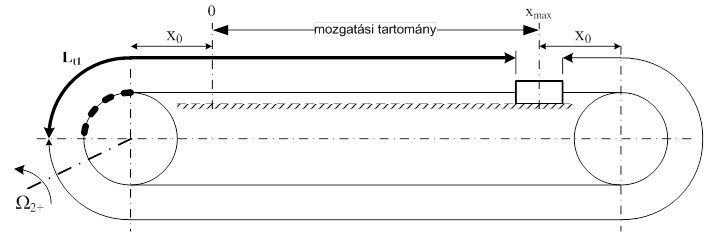
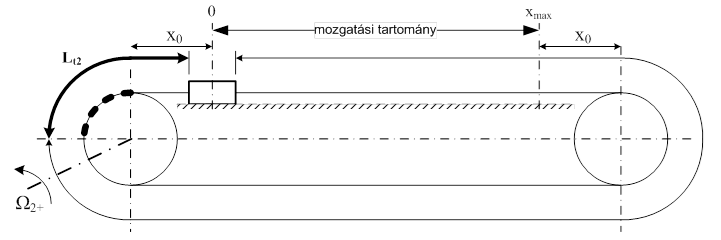
Az első két ábra alapján az alábbi megállapításokat tehetjük.
Hajtótárcsa matematikai pozitív forgásirányban:
A húzott ág rugómerevségének megállapításához figyelembe vett szíjhosszakat vastagabb méretvonallal jelöltük. Vigyázat, ezek a vastag vonalak méretvonalak, a hosszúság megadásához a szíj és a fogazott tárcsa valódi ívhosszát kell alapul venni. A fogazott szíjnak van egy x0 hosszúságú darabja, amely a fogazott kerék negyed körívéhez illeszkedő szíjhosszhoz hozzáadódva azt a minimális szíjhosszat adja, amely ebben a mozgatási irányban a maximális rugómerevséget eredményezi. Az ábrákon nem foglalkoztunk a mozgatott tömeg méreteivel, ami a szíj „holt” szakaszának hosszát természetesen befolyásolja, hanem az x0 távolságot a tömegközéppontig mértük. A fogazott szíjakat részletesen tárgyaló 10.5. szakasz fejezetben látjuk, hogy a szíj eredő rugalmasságához a mozgató fogazott tárcsa kapcsolódási ívének negyedében jelentkező fogrugalmasságot kell hozzávenni. Ugyanebben a mozgatási irányban az előbbi két hosszúsághoz hozzáadva az xmax teljes mozgatási hosszat megkapjuk ennek az iránynak a minimális rugómerevségét. Az Lt2 hosszúsághoz tartozó, terhelt rugómerevség (húzott ág) a két irányban működtetett rendszer legnagyobb rugómerevsége, ennél kisebb az Lt1 hosszhoz rendelt, terhelt ág rugómerevsége.
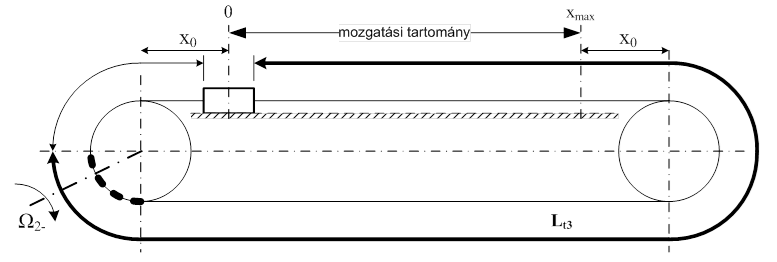
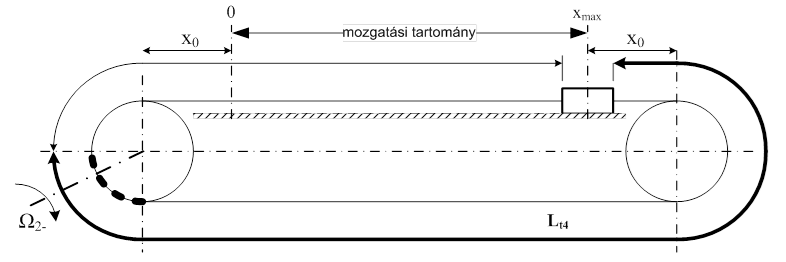
Hajtótárcsa matematikai negatív forgásirányban:
A húzó (terhelt) ág hosszabb ebben a forgásirányban, amint azt a következő két ábrán láthatjuk. A terhelt ág rugómerevségei ennek megfelelően ebben a mozgatási irányban kisebbek lesznek, a minimális értéke az Lt3 hosszúságnál van, tehát éppen akkor, amikor a hajtó tárcsa a tömeget a vezetéken visszafelé kezdi mozgatni. A szíj rövidülésével nő a rugómerevség, de ez a változás nem olyan mértékű, mint a matematikai pozitív forgásirányú tárcsa esetében volt.
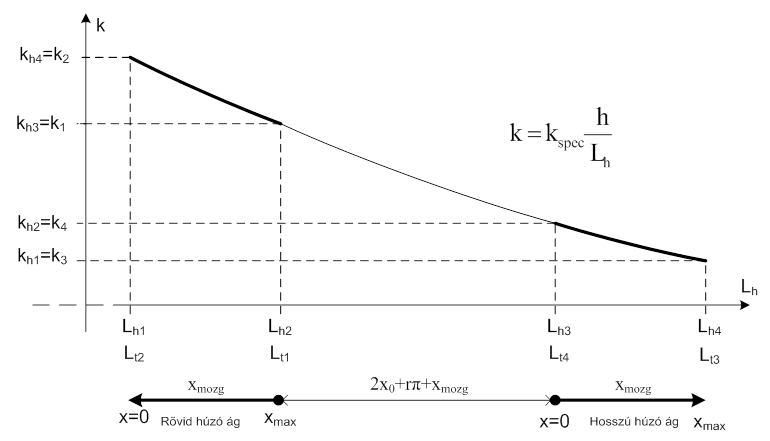
Foglaljuk össze a négy ábra alapján szerzett ismereteinket, és ábrázoljuk a terhelt ág rugómerevségeit a szíj hosszúságának függvényében. Ismert, hogy a szíjágak rugómerevsége fordítottan arányos a szíj hosszával. A fogazott szíj rugómerevsége folytonos függvény, de a lineáris mozgató két mozgási irányának esetében ebből a függvényből csak meghatározott két tartományt használunk fel. A következő diagramon alul látjuk azt is, hogy az adott szíjhosszakkal miként függ össze a tömeg mozgatásának iránya.
A terhelt (húzott) szíj rugómerevségének változása jobban érzékelhető, ha az értékeket egy, a szerszámgépiparban, robottechnikában használatos fogazott szíj típus esetére megvizsgáljuk.
A példaként választott szíj adatai:
|
Fogtávolság |
p=5 mm |
|
|
Szíj szélesség |
b=10 mm |
|
|
Tárcsák fogszáma |
z=28 |
|
|
Tárcsa sugara |
r=22.3 mm (kiadódó méret: ) |
|
|
Specifikus rugómerevség |
ksp=7,7·103 N/mm a szíj szélességének 1 mm-rére és a szíj 1 mm hosszúságára (Mulco katalógusból) |
|
|
„Holt szakasz” |
x0=25 mm |
|
|
Mozgatási tartomány |
800 mm |
Ezeknek az adatoknak az alapján meghatározhatóak a húzott (terhelt) és terheletlen ághosszak és a rugómerevségek. A 10.5. szakasz fejezetben bemutatott végeselemes szimulációs eredmény alapján úgy tekintjük, hogy a hajtó tárcsán felfekvő szíjhossznak csupán egy része van húzásra fokozottan igénybe véve. Módosítás nélküli vonóelemes mozgató esetében ez szíjhossz a fogazott tárcsa negyed körívén fekszik fel, a szíj belépésétől a rendszer hossztengelyéig. A többi szíjméret a négy ábráról közvetlenül leolvasható.
|
L2 |
L1 |
L4 |
L3 |
|
|
L [mm] |
600 |
860 |
980 |
1780 |
|
k [N/mm] |
1,28·102 |
0,9·102 |
0,78·102 |
0,43·102 |
A rugómerevség változását bemutató diagramon is látható, hogy a merevség a szíj hosszával fordítottan arányos. Ennek következménye, hogy a rövid szíjhosszakkal történő működtetési tartományban a két véghelyzet között nagyobb a különbség, mint a nagyobb szíjhosszak esetében.
A következő feladatunk a négy tömeg-pozícióhoz tartozó eredő rugómerevségek meghatározása. Ehhez felhasználjuk a terhelt és terheletlen szíjágak rugómerevségeinek táblázatát.
|
Hajtótárcsa forgásiránya |
Tömeg pozíciója |
Terhelt ághosszúság |
Terhelt ág rugómerevsége |
Terheletlen ághosszúság |
Terheletlen ág rugómerevsége |
Eredő rugómerevség |
|---|---|---|---|---|---|---|
|
+ |
xmax |
Lt1 |
k1 |
L4 |
k4 |
k1+k4 |
|
+ |
x0 |
Lt2 |
k2 |
L3 |
k3 |
k2+k3 |
|
- |
x0 |
Lt3 |
k3 |
L2 |
k2 |
k2+k3 |
|
- |
xmax |
Lt4 |
k4 |
L4 |
k1 |
k1+k4 |
A táblázat az eddigi megfontolásaink összefoglalásának tekinthető, és segítségével meghatározható az a leíró függvény, amely a nemlineáris rendszermodell megalkotásához elengedhetetlen. Azt kell ugyanis függvény formájában megadnunk, hogy a mozgatott tömeg „x” pozíciója miként befolyásolja a fogazott szíj eredő rugómerevségét. A táblázat alapján az alábbi grafikus függvénykapcsolat feltételezhető:
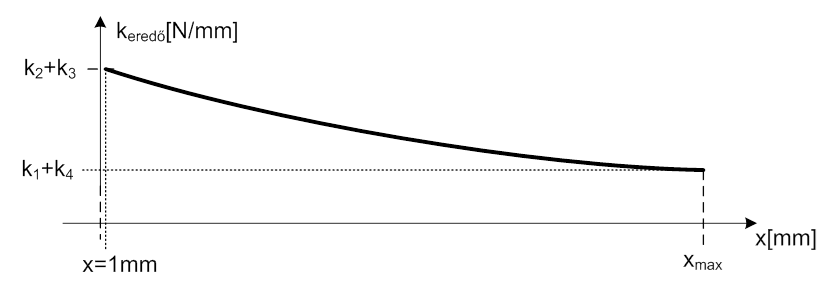
Az adott elrendezésnél, tehát a lineáris mozgatónál az xmax-hoz tartozó k1+k4=ke eredő rugómerevség a minimális értéket éri el. Ez egybecseng azzal a megállapítással, amit csaknem minden gyártó számítási útmutatójában fellelhetünk: A szíjágak eredő rugómerevsége akkor éri el a minimális értékét, ha a húzott (terhelt) és terheletlen ág hossza megegyezik. A korábbi ábráinkról leolvasható, hogy a példaként bemutatott rendszerben, az óramutató járásával megegyező hajtótárcsa forgásirány esetében, tömeg xmax pozíciójában lesz a két szíjág hossza a közel azonos. Megjegyezzük, hogy a példában vizsgált, egyszerű elrendezés esetében a két szíjág hossza a tömeg semmilyen pozíciójában nem lehet teljesen azonos, de ez más térbeli elrendezésnél nyílván előfordulhat.
Nagyobb szíjhosszak esetében a helytől és tárcsa forgásiránytól függő rugómerevség értékek egymáshoz képesti különbsége már nem elhanyagolható.
Konkrét alkalmazási példa esetében az eredő rugómerevség maximális és minimális értéke kiszámítható. A két szélsőérték között 1/x jelleggel változik a függvény, hiszen tudjuk, hogy a rugómerevség és a szíjhossz fordítottan arányosak, de természetesen az x=0 mm nem értelmezett. Helyette, például az x=1 mm = 10-3 m értékhez rendelhetjük hozzá a k2+k3=ke eredő rugómerevséget. A keresett függvénykapcsolat tehát:
A „K” állandót következőképpen határozhatjuk meg:
A tömeg pozíciója és a rugómerevség értéke közötti függvénykapcsolat ismeretében megalkotható a szakasz nemlineáris állapottér modellje.
Joggal feltételezhetjük, hogy a hajtómű rugómerevsége lényegesen nagyobb, mint a fogazott szíjas lineáris mozgatóé. Ezért tehát a motor és hajtómű egység elsőrendű változatát alkalmazzuk. A vonóelemes átalakító gráfját látjuk a következő ábrán. A korábbi gyakorlatnak megfelelően a transzlációs elemekhez redukáljuk az Ω2 szögsebességű két forgó mechanikai elemet, és képezzük az eredőket. A rugómerevség ke eredőjének meghatározását, valamint a leíró függvényt e fejezet korábbi részeiben találjuk.
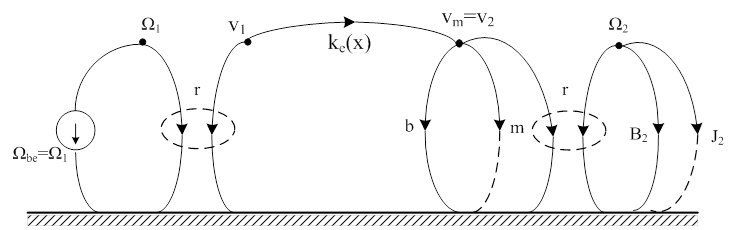
A gráf elemeinek értelmezéséhez az alábbiakat tudjuk:
ahol .
Felírjuk a vm keresztváltozóval jelzett csomópontra a csomóponti egyenletet, majd elsőrendű differenciálegyenlet rendszerré alakítjuk a vonóelemes átalakító modelljét.
A teljes szakasz nemlineáris állapottér modellje a fentiekkel:
A modell használhatóságát valós műszaki adatokkal érdemes ellenőrizni. E fejezetben, a számításokhoz korábban már alkalmaztunk valós adatokat a fogazott szíjra, hajtótárcsára, mozgatási hosszra, stb., ezért a szimulációhoz ismételten ezeket az adatokat használjuk fel.
A nemlineáris szíj rugómerevség kiszámításához táblázatban közöltük a tömeg pozíciójától és a forgásiránytól függő értékeket, és ezeket használjuk továbbra is megtartva a mozgatási hosszat 800 mm-ben.
|
ki |
k2 |
k1 |
k4 |
k3 |
|
k [N/mm] |
1,28·102 |
0,9·102 |
0,78·102 |
0,43·102 |
k2+k3=1,71 102 N/mm=1,71 105 N/m
k1+k4=1,68 102 N/mm=1,68 105 N/m
A szíj nemlineáris rugókarakterisztikájának egyenlete a korábban bemutatott számítási mód szerint:
A lineáris mozgató tervezéséhez szükséges legfontosabb adatokat „importáltuk” a fejezet korábbi részéből. A szimulációhoz szükséges adatokat SI egységekben helyettesítettük be, ez a legcélszerűbb eljárás. A lineáris mozgató felbontása várhatóan 0,1 mm, azaz 10-4 m lesz, ezért az eredmények megjelenítésénél alkalmasan kell majd megválasztani a léptéket.
|
Fogtávolság |
p=5 mm |
|
|
Szíj szélesség |
h=10 mm |
|
|
Tárcsák fogszáma |
z=28 |
|
|
Tárcsa sugara |
r=22.3 mm=2.23·10-2 m (kiadódó méret: ) |
|
|
Specifikus rugómerevség |
ksp=7,7·103 N/mm a szíj szélességének 1 mm-rére és a szíj 1 mm hosszúságára (Mulco) |
|
|
„Holt szakasz” |
x0=25 mm |
|
|
Mozgatási tartomány |
800 mm |
|
|
Mozgatott tömeg |
2 kg |
|
|
Súrlódásból adódó csillapítási tényező |
5·10-2 Ns/m (tapasztalati érték) |
|
|
Motor-hajtómű időállandó Tmh |
0,020 s |
|
|
Motor nyomatékállandója KM |
50 mNm/A= 5·10-2 Nm/A |
|
|
Motor csillapítási tényezője Bm |
10-3 Nms/r |
|
|
Motor armatúra ellenállása R |
15 Ω |
|
|
Hajtómű módosítása i |
500 |
|
|
Motor-hajtómű Amh arányos |
5,71·10-3 rad/Vs |
A nemlineáris állapottér modell feltételezett paraméterekkel:
Az állapottér modell időállandói között a legkisebb a harmadik egyenlet második együtthatójában található, értéke 7,44·10-6 s=7,44 μs. Ez a szimulációk során megköveteli a ΔT=5·10-7…10-6 s körüli, de lehetőleg e tartománynál kisebb iterációs lépésközt, ami a számítási időt jelentősen megnövelheti, bár a modell legkisebb és legnagyobb időállandói között 106 a szorzó, és ez s digitális szimulációk esetében nem jelent még gondot.
Szakirodalom
[12.1.] www.eassistant.eu. GWJ Technology GmbH. Braunschweig .
[12.2.] Kleiner Wissenspeicher Zahnriemengetriebe. IFWT TU Dresden. 2000.