11. fejezet - Golyósorsós pozicionáló szakasz tervezése
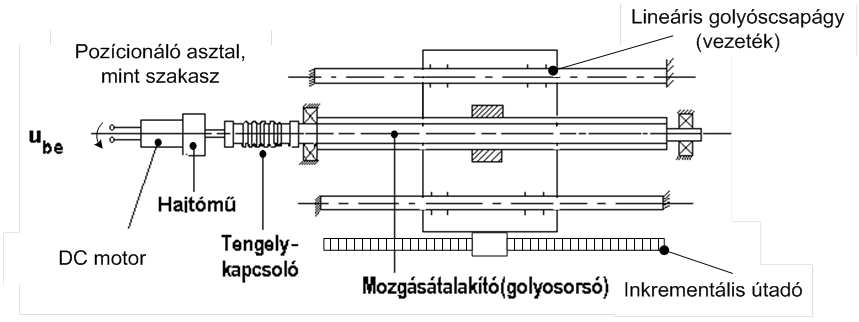
A golyósorsós mozgásátalakítóval megvalósított pozicionáló szabályozott szakaszának leggyakrabban megvalósított formáját mutatja a következő ábra. Ezt az elrendezést a három koordinátának megfelelően egymásra építve is szokás alkalmazni („huckepack” elrendezés, kombinált rendszer), figyelembe véve természetesen a terhelést, amely egy-egy irányú mozgás megvalósítása révén az alsóbbakra átadódik. Ha a rendszer függőleges helyzetű, akkor a méretezésénél külön figyelembe kell venni az emelésnél és süllyesztésnél fellépő mennyiségeket.
A példánkban egy irány dinamikai szempontból történő méretezését mutatjuk be, ami a megfelelő motor kiválasztását és a szakasz elvárt dinamikai jellemzőit foglalja magába. A géptervezés szempontjából történő méretezés további feladatokat ró a tervezőre. Ilyenek az átlagos (közepes) fordulatszám és az axiális terhelés közötti összefüggés, az anya előfeszítettsége és a terhelés közötti kapcsolat, az anya és az orsó névleges élettartama, a kritikus fordulatszám meghatározása, és az orsóra ható megengedett hajlító erő kiszámítása. Konstrukciós szempontból fontos, hogy a gyártási pontatlanságok ismeretében legyenek jusztírozási (finombeállítási) lehetőségek is a vezetékek keretbe történő rögzítésénél, és a golyósorsó önbeálló csapágyazással legyen ellátva. Ezen a helyen érdemes megemlíteni, hogy a PI (Waldbronn) cég már 1992-ben utólagos jusztírozási lehetőségek nélkül, igen magas színvonalú gyártóberendezésekkel készítette precíziós pozícionáló asztalait, többek között az ábrán látható elrendezésben is, „nulla” tűréssel. Ez természetesen csak „céges szleng”, nulla tűréssel nem lehet gyártani, viszont a valóságban a tűrés olyan szigorú, hogy a pozícionálási bizonytalanságnak csupán tört részét képezi.
Ha nem is a fejezetben látható részletességgel, de bizonyos gyártók adnak számítási segédleteket a termékeikhez. Ilyen példát találhatunk a golyósorsós lineáris szán tervezéséhez a www.boschrexroth.com honlapon [11.1.], pl.: a Linearschlitten, Berechnung (számítási segédlet) oldalon. Az ilyen részletességű ismertetés azonban az internetes katalógusokban csak elvétve fordul elő. A géptervező mechatronikai mérnök figyelmébe segédletként M. Weck: Werkzeugmaschinen Bd.3. [11.2.] 1995-ben megjelent kötetét ajánljuk.
11.1. A motor és hajtómű kiválasztása
A következő lépésekben tehát a motor kiválasztásához elengedhetetlen számításokat mutatjuk be, amelyek megértéséhez szükségesek a 9. fejezet fejezetben, a golyósorsós mozgásátalakító általános modellezésénél bemutatott összefüggések.
A méretezés során rendszeresen előforduló mennyiségek jelölését és mértékegységüket az alábbiakban adjuk meg:
|
d1 |
[mm] |
orsó külső átmérője |
|
|
d2 |
[mm] |
orsó magátmérője |
|
|
h |
[mm] |
orsó menetemelkedése |
|
|
l |
[mm] |
az orsó szabad (működő) hossza |
|
|
m |
[kg] |
mozgatott tömeg |
|
|
i |
hajtómű módosítása (i˃1: lassítás) |
||
|
F |
[N] |
előtoló erő (tervezett, igényelt) |
|
|
Ff |
[N] |
előfeszítési erő (kettős anyánál) |
|
|
Fs |
[N] |
egyenes vezetéken fellépő súrlódási erő |
|
|
Fa |
[N] |
gyorsító erő |
|
|
M0 |
[Nm] |
üresjárati nyomaték |
|
|
MT1 |
[Nm] |
terhelő nyomaték állandó sebességű emelésnél |
|
|
MT2 |
[Nm] |
terhelő nyomaték állandó sebességű süllyedésnél |
|
|
MM |
[Nm] |
motor hajtó (villamos) nyomatéka |
|
|
MTa |
[Nm] |
terhelő nyomaték gyorsításnál |
|
|
Ma |
[Nm] |
gyorsító nyomaték |
|
|
MMa |
[Nm] |
motor hajtónyomaték gyorsításnál |
|
|
MS |
[Nm] |
orsó csapágyazások eredő súrlódó nyomatéka, a „többi súrlódás” M0-ban |
|
|
MSH |
[Nm] |
hajtómű eredő súrlódó nyomatéka |
|
|
Jm |
[kgm2] |
motor forgórész tehetetlenségi nyomatéka |
|
|
Jo |
[kgm2] |
orsó tehetetlenségi nyomatéka |
|
|
Jmr |
[kgm2] |
a mozgatott tömeg átszámított tehetetlenségi nyomatéka |
|
|
J |
[kgm2] |
tehetetlenségi nyomaték |
|
|
J1,2 |
[kgm2] |
hajtómű bemeneti és kimeneti oldali tehetetlenségi nyomatéka |
|
|
B1,2 |
[Nms/r] |
hajtómű bemeneti és kimeneti oldali csillapítási tényezői |
|
|
Pm |
[W] |
motor teljesítmény konstans sebességnél |
|
|
Pma |
[W] |
motor teljesítmény gyorsításnál |
|
|
sa |
[mm] |
gyorsítási úthossz |
|
|
ta |
[s] |
gyorsítási idő |
|
|
v |
[m/s] |
előtolás sebessége, azaz az asztal előírt végsebessége |
|
|
nM |
[1/min] |
motor fordulatszám |
|
|
η |
hajtómű hatásfoka |
||
|
η1 |
golyósorsós átalakító hatásfoka emelésnél |
||
|
η2 |
golyósorsós átalakító hatásfoka süllyedésnél |
||
|
c |
előfeszítési együttható (0,1…0,19) az anyánál fellépő súrlódó erő számításához |
A motor szükséges nyomatékának meghatározása állandó fordulatszám esetén
Ez a méretezés viszonylag egyszerű. A motor hajtónyomatékának meghatározásához az alábbi összetevők szükségesek. Ha a pozícionáló függőleges helyzetben is működtetve lesz, akkor süllyesztésnél az MT2 nyomaték negatív, akkor a motort fékezni kell, ezért jelenik meg az összefüggésben külön összetevőként.
A képletekben felismerhető a golyósorsó h/2π átalakítási tényezője, valamint a hajtómű „i” módosítása. Az ezres osztó azért szerepel, mert az orsó menetemelkedését a katalógusok mm-ben adják meg.
Állandó sebesség mellett (stacionárius állapot) a motor teljesítménye:
A modellezés során keresztváltozóként „Ω” szögsebességet használunk, de a katalógusokban „n” fordulatszám szerepel. Ezért szükséges az átszámítás.
Motorválasztás szempontjából érdekes lehet stacionárius állapotban az asztal előírt „v” végsebessége, és az ehhez szükséges motor fordulatszám is:
A motor szögsebességére állandósult állapotban, illetve, ha a hajtómű rugómerevsége nagy, felírható, hogy
Ezt az összefüggést a későbbiekben is felhasználjuk.
Az asztal a hajtómű kimeneti oldalán van, ezért kell a módosítást figyelembe venni. A golyósorsó (váltó) átalakítási tényezője a transzlációs sebesség átszámításához szükséges, a 103 szorzó pedig azért jelenik meg, mert „h” mm-ben, „v” pedig m/s dimenzióban lesz megadva.
A motor szükséges nyomatékának meghatározása gyorsítás esetén
A motorral szemben támasztott összes nyomaték igény, amely gyorsítás esetén felléphet, az alábbi összetevőkből adódik:
A számításhoz felhasználjuk az előzőekben meghatározott M0 üresjárati nyomatékot. Ebben már benne foglaltatik az egyenes vezetékeken fellépő súrlódó erő, de a képletben nem feledkeztünk el az orsó csapágyainak MS súrlódási nyomatékáról sem.
Következő lépésben a gyorsítandó rendszerre ható MTa terhelő nyomatékot kell meghatározni, amelyben az előtolás szükséges (tervezett, előírt) erőértékét és a tervezett gyorsító erőt kell figyelembe venni:
A nyomaték, amely a teljes pozícionáló rendszer eredő tehetetlenségi nyomatékát gyorsítja, kétféle módon határozható meg. Egyrészt az előírt gyorsítási úthossz és a gyorsításhoz szükséges idő segítségével, másrészt a motor fordulatszámának felhasználásával, ha a névleges fordulatszámra kívánunk gyorsítani.
Ha a terhelési oldalon, tehát a hajtómű kimeneti oldalán előírt az asztal gyorsítási úthossza és az ehhez szükséges idő, akkor az alábbi összefüggések írható fel, ΩM=Ω1 feltételezéssel:
Ahol „J” a motor oldalára redukált eredő és egyenértékű tehetetlenségi nyomaték, „Ω1” a hajtómű bemenő szögsebessége, ami azonos a motor szögsebességével. Mindkét esetben figyelembe kell venni a motorhoz csatlakoztatott hajtómű hatásfokát is.
Észre kell venni azt is, hogy a „Nm” dimenzió helyes, annak ellenére, hogy a gyorsítási úthosszat „mm”-ben adjuk meg. Ezt kompenzálja a menetemelkedés, amely ugyancsak „mm”-ben lesz behelyettesítve. Ettől kezdve csak az sa/h arány számít.
Ha a motor szögsebessége helyére a hajtómű kimeneti oldali „Ω2” szögsebességét helyettesítjük, majd ezt a szögsebességet a golyósorsó (váltó) átalakítási tényezőjével sebességgé számítjuk át, akkor alábbi összefüggés már a gyorsítási úthossz és a gyorsítási idő függvényében szolgáltatja a szükséges nyomaték értékét.
A gyorsítás után elért motor fordulatszám, ha a hajtómű kimeneti oldalán elért úthosszat vesszük alapul, egy hosszabb átszámítás után adódik:
Ha viszont a motor teljes „kivezérlési” tartománya érdekes, tehát zérus fordulatszámról a lehető legnagyobb értékig, a névleges fordulatszámig kívánjuk gyorsítani a motort az adott terhelésekkel, akkor a következő összefüggést kell alkalmazni:
A képletekben előforduló „J” eredő tehetetlenségi nyomaték összetevői a modell gráfja segítségével érthetők meg.
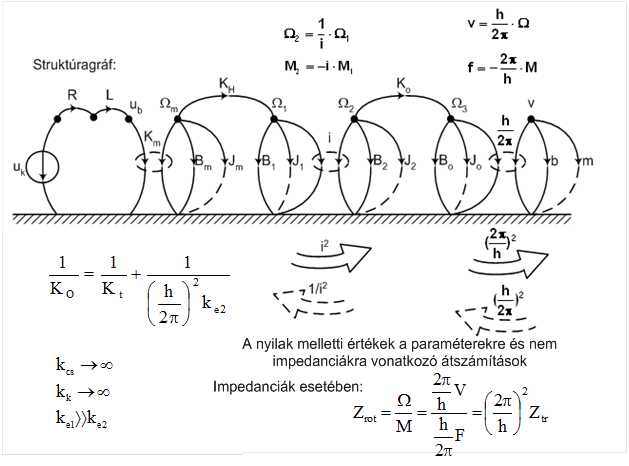
Az eredő tehetetlenségi nyomatékot a motor „felől nézve” kell meghatározni, hiszen a motor kiválasztásáról van szó. Így az eredőben a motor saját tehetetlenségi nyomatéka és a hajtómű bemeneti oldali tehetetlenségi nyomatéka összeadható, de a hajtómű kimeneti oldalán szereplő tehetetlenségeket már csak a redukálás szabályai szerint adhatjuk ezekhez hozzá, nem beszélve arról, hogy az egyenes vonalon mozgatott tömeg tehetetlenségi nyomaték egyenértékét a golyósorsó átalakítási tényezőjének felhasználásával kell meghatározni.
Az előző ábrán a redukció (átszámítás) irányokat és értékeket feltüntettük. Az átszámítás elméleti hátterét a modellezés alapelveivel foglalkozó fejezetben találhatjuk meg.
Hátra van még a szükséges motorteljesítmény meghatározása.
Ezt egyrészt hagyományos módon adhatjuk meg, ha előírt a mozgatott tömeg (asztal) „v” végsebessége, és az ehhez a sebességhez kiszámított motor fordulatszám:
A motorteljesítmény meghatározásánál figyelembe vettük a súrlódásokból eredő veszteségeket, ld.: FS és MS a megfelelő képletekben.
A súrlódási nyomatékokat (erőket) vagy tapasztalati adatok segítségével becsülhetjük, vagy mérésekkel határozzuk meg. Ha szükség van az eredő veszteség különálló becslésére is, akkor azt az alábbi formula segítségével lehet megtenni:
Az összefüggésben „B” a motor „felől” látható eredő súrlódási tényező. Kiszámítása a tehetetlenségi nyomatékhoz hasonlóan, redukálással történik:
A fenti képletben látható csillapítási tényezők megtalálhatók a gráfban. Az orsó csapágyazásaiból eredő csillapítási tényező BO jelölést kapott.
11.2. Golyósorsós szakaszok matematikai modelljei
A megfelelő teljesítményű és fordulatszámú motor, valamint a hajtómű kiválasztása után megalkotható a teljes szakasz dinamikai (matematikai) modellje.
Ez a modell első közelítésben állandó paramétereket alkalmaz, tehát nem veszi figyelembe azt, hogy az orsó rugómerevsége függ a mozgatott tömeg orsóhoz képesti helyzetétől, és azt sem, hogy a súrlódások nem függetlenek a sebességtől és a szögsebességtől.
Ezt a linearizált rendszert látjuk a 11.2. ábra gráfján.
A tervezés második lépésében meghatározzuk a golyósorsós rész átviteli függvényét. Kiindulásként ismét a teljes rendszert tekintjük. Az impedancia hálózatban a legáltalánosabb rendszert rajzoltuk meg, mert a leegyszerűsítés után akkor is ugyanazt a kapcsolást kapjuk, ha figyelembe vesszük a csapágyazások és a keret rugómerevségét, és akkor is, ha nem, de természetesen az eredő paraméter értékek eltérőek. Ennek igazolását a 9. fejezet fejezetben találjuk. Természetes, hogy a belső impedanciák eltérőek, mert az ezeket alkotó impedanciák is eltérnek. Ezt a tervezésnél figyelembe kell majd venni, mert más rezonancia frekvencia és más csillapítási fok adódik.
A két soros eredő impedancia két-két soros rugómerevségből származik. A „ke1” a keret és a csapágy soros eredője, „ke2” pedig az orsó effektív és az anya rugómerevségének ugyancsak soros eredői.
Megjegyezzük, hogy a 9. fejezet fejezetben leírtaknak megfelelően a „ke1” rugómerevséget csak különleges esetekben célszerű figyelembe venni, akkor, ha a keret és a csapágyak rugómerevsége a rezonancia frekvenciát lényegesen befolyásolja. A mintaszámításban ezt a rugómerevséget is szerepeltettük, hiszen a modell struktúráját nem befolyásolja.
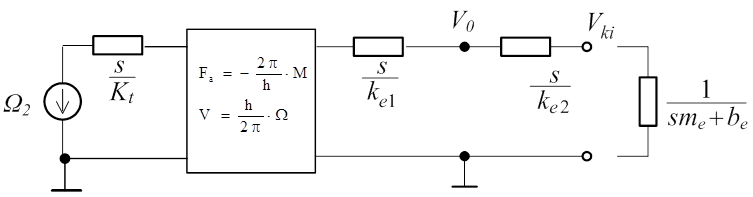
A baloldali forgó mechanikai építőelemeket átszámítjuk a jobboldalra, mert a kimenő mennyiség a sebesség, a golyósorsó által mozgatott asztal (tömeg) szögsebessége. Az átszámított forrás a következő képletben látható, ez a hajtómű kimenetére számított egyenértékű „sebesség”, a golyósorsó átalakítási tényezőjének ismeretében:
A tengelykapcsoló impedanciájának átszámítása ugyancsak a redukcióként ismeretes módszerrel történik. Ennek módszere a modellezéssel foglalkozó bevezető fejezetekben megtalálható.
Az átszámítás után kapott kapcsolás egyszerűbb. A következő feladat a Vki változóhoz tartozó „passzív” rész leválasztása, és a forrásból, valamint a visszamaradó impedanciákból egy Thevenin kapcsolás létrehozása. Ezt követően átviteli függvény gyanánt már csak a keresztváltozó osztót kell felírni. Már jeleztük, hogy az osztó formája nem változik akkor, ha a referenciához kötött eredő impedanciát kiiktatjuk, csak az un. belső impedancia számítása történik más módon.
Ha a csapágy és a keret rugalmasságát is figyelembe kívánjuk venni a tervezésnél, akkor a szabad kapcsok „felől” látható Zb belső impedancia az alábbi lesz:
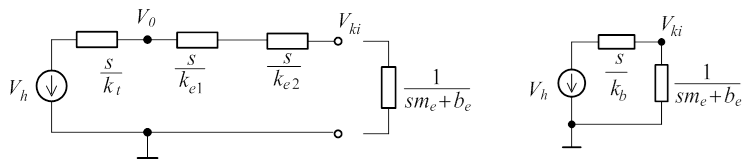
Az átviteli függvény ismét egy keresztváltozó osztóval határozható meg:
Az eredeti bemenet a hajtómű kimeneti oldali szögsebessége, ezért ennek behelyettesítésével kapjuk a keresett átviteli függvényt, ha a kimenet az anya (asztal) sebessége:
Ha a kimenet az asztal pozíciója, akkor az átviteli függvény nevezőjében megjelenik az „s” operátor szorzóként:
Elsőrendű motor és hajtómű egységgel
A szakasz átviteli függvénye a motor-hajtómű egység és a golyósorsós átalakító sorosan kapcsolt két átviteli függvényéből adódik:
Az így meghatározott átviteli függvény egy negyedrendű arányos tagot reprezentál, a szabályozástechnikában szokásos alak az alábbi:
A 16. fejezet fejezetben ezt a szakasz átviteli függvényt használjuk fel a szabályozás tervezéséhez.
Harmadrendű motor és hajtómű egységgel
A szakasz eredő átviteli függvényében G2(s) változatlan az első modellhez képest, hiszen igazoltuk, hogy golyósorsós átalakító átviteli függvényének rendszáma kettő, függetlenül a figyelembe veendő rugómerevségektől. Így azután a második változatban a szakasz átviteli függvénye kompakt alakban az alábbi lesz:
A szakasz tehát hatodrendű, látjuk, hogy As az első változathoz viszonyítva csak „alakra” módosult, mert az első változatban Be csillapítási tényező alatt mást értettünk. Emlékeztetőül megjelenítjük az első változat eredő csillapítási tényezőjét és eredő tehetetlenségi nyomatékát:
Ha most a második változat eredő csillapítását kibontjuk, és összevetjük a fent látható első változattal, meggyőződhetünk, hogy nincsen változás:
Nem is lehet változás, mert a csillapítási tényezőkön és elhelyezkedésükön nem változtatunk.
Érdemes a szabályozókör tervezéséhez a szakasz átviteli függvényét a fentebb látható formában meghagyni, hiszen könnyebb a szabályozó illesztése.
Negyedrendű motor és hajtómű egységgel
A szakasz eredő átviteli függvénye felírásához G1 kiegészül a változatlan G2-vel, és végső soron két szorzatra bontható hetedrendű (!) rendszert kapunk:
Ha a G1 rész együtthatói a tervezési követelmények miatt kötöttek, akkor érdemes a rendelkezésre álló adatok behelyettesítésével a paraméteres formáról áttérni a konkrét szám-együtthatós alakra.
A nevező összeszorzása most sem célszerű, de ha olyan számítógépes szimulációs program áll rendelkezésre, amely n-edrendű átviteli függvény Bode diagramjának megszerkesztésére alkalmas, akkor az összeszorzást érdemes programmal elvégeztetni.
Szakirodalom
[11.1.] www.boschrexroth.com pl.: Linearscklitten, Berechnung (golyósorsós szán, számítások).
[11.2.] Werkzeugmaschinen Bd.3. VDI Verlag. Düsseldorf . 1995.