1. fejezet - A modellezés szerepe a mechatronikai tervezésben
Vissza		Előre

1. fejezet - A modellezés szerepe a mechatronikai tervezésben

Tartalom

Ismereteink és eszközeink jelenlegi szintjén, a mechatronikában, a leggyakrabban modellezés két típusát alkalmazzuk. A hangsúly a „jelenlegi” kifejezésen van, hiszen az ismeretanyag dinamikusan fejlődik.

A modellezés egyik típusa a gépészet alrendszereinek numerikus modellezése a szilárdsági és dinamikai számításokban, az áramlások, a termikus, valamint a csatolt rendszerek numerikus vizsgálatában. Ezekben a modellezési folyamtokban az adott struktúrából indulunk ki, ez például a vizsgált szerkezet 2D-s, vagy 3D-s CAD modellje lehet.

A modellezések másik körébe a szabályozott, komplex rendszerek dinamikai modellezése, vagy részrendszerek dinamikai szimulációja tartozik. A dinamikai szimuláció esetében – speciális kivételektől eltekintve – az adott rendszer (részrendszer) matematikai, tehát absztrakt modelljéből indulunk ki. Azért jeleztük, hogy kivételek is lehetnek, mert több olyan dinamikus szimulációs program is létezik, amely az alkalmazó számára kész „tömbként” kínálja a mechanikai, villamos stb. rendszerelemeket. Az ilyen jellegű kínálat a 80-as évek közepétől erőteljesen növekszik, de meg kell jegyezni, hogy olyan, általánosan érvényes „blokkorientált” programcsalád egyelőre még nem létezik, amelyik minden felmerülő dinamikai szimulációs problémára maradéktalanul kielégítő megoldást kínálna.

Két okból tartjuk célszerűnek, hogy részletesebben foglalkozzunk a dinamikai modellezés hagyományos eszközeivel:

Oktatási anyagról lévén szó, fontos, hogy a dinamikai modellezés fizikai-matematikai hátterével megismertessük a hallgatóságot. A probléma ugyanis ahhoz hasonlatos, amit a VEM (VégesElem Módszer) modellezésből ismerünk. Mert hiába a legjobb VEM szoftver, ha a felhasználó nincs tisztában a műszaki mechanika összefüggéseivel. Egyrészt például képtelen helyes módon megadni a peremfeltételeket, a kényszereket, másrészt nem áll módjában ellenőrizni, hogy a kapott eredmény reális-e?
A dinamikai modellezés alapvető eszköztárával azért szükséges foglalkozni, hogy ennek ismeretében nem konvencionális feladatokat is képesek legyünk megoldani.

A mechatronikai tervezés során nem lehet vita tárgya az, hogy a szabályozott szakasz (vagy egyszerűen csak „szakasz”) valamilyen formájú matematikai modelljéből kell kiindulnunk. Ez a modell lehet adott (ezt tapasztaljuk igen sok szabályozástechnikai tankönyv esetében), de a műszaki életben, az esetek többségében a szakasz matematikai modellje nem, vagy csak részben áll rendelkezésre.

A 14. fejezet fejezet, az aktív rezgéscsillapító szabályozásának tervezése a legjobb példa, amelyen a mechatronika szinergiája bemutatható. Ide, a bevezetésbe kívánkozik a 14. fejezet fejezet befejezésében található konklúzió egy része, ezért azt most idézzük:

„…Az alap rendszer ettől még egy instabil mechanikai (gépészeti) rendszer marad. A mechatronika a nemzetközi tapasztalatok szerint csak olyan szakemberek által művelhető hatékonyan, akik tisztában vannak azzal, hogy a mechatronikai rendszerek alapvetően gépészeti rendszerek. Olyan szakemberek által, akik birtokában vannak a műszaki mechanika, a gépszerkezettan, a konstrukció, a CAD, a végeselemes modellezés és az anyagtudomány nélkülözhetetlen ismereteinek, de „közös” nyelvet képesek beszélni a villamosmérnökökkel és az informatikusokkal, feladatokat tudnak megfogalmazni és az eredményt szakszerűen ellenőrizni. Képesek esetenként maguk is egyszerűbb villamos, vagy informatikai problémák megoldására.”

1.1. A matematikai modellek formái és alkalmazásuk

A fejezet elején a rendszertechnika témaköréből röviden megemlítjük azokat az ismereteket, amelyek a tervezéshez szükségesek. A rendszertechnika témában elmélyülni szándékozók részére ajánljuk Korondi P. „Rendszertechnika” című elektronikus jegyzetét [2.4.].

A mechatronikai tervezésben a dinamikus rendszerek háromféle matematikai modellje használatos:

Differenciálegyenlet
Átviteli függvény
Állapottér modell

A három modell nem egyenértékű sem a valóság közelítése, sem a felhasználhatóság tekintetében. A legfontosabb ismereteket táblázatban foglaltuk össze.

1.1. táblázat - A matematikai modellek összefoglalása

Magyarázat:

állandó ¹ : A táblázat első oszlopában az szerepel, hogy a differenciálegyenlet kerülő úton is felírható, az impedancia módszer alkalmazásával, hiszen a Laplace transzformáció alkalmazásával „kitérőt” teszünk az operátor tartományba. Ez esetben, miután „visszatértünk az idő tartományba, lehetséges az együtthatók helyére változó paramétereket is beírni, és ezzel változó paraméterű differenciálegyenlet előállítani. Ilyen példák lehetnek mechanikai rendszerek esetében a változó rugómerevség és a speciális függvényekkel leírható csillapítási tényező, vagy áramlásos rendszerek esetében bizonyos áramlási ellenállások. Az átviteli függvény esetében ilyen megjelenítés természetesen nem lehetséges.

Az Táblázat 1.1 baloldali, első oszlopában n-ed rendű differenciálegyenlet látható, ami alatt konkrétan egyváltozós differenciálegyenletet értünk. A modellben egy kimeneti változó (x_ki) és egy bemeneti változó (x_be) szerepel. A lineáris differenciálegyenlet, annak homogén, és bizonyos partikuláris megoldása igen lényeges a szabályozások dinamikai minőségi követelményeinek tervezése, beállítása során. Ilyen időbeli minőségi jellemzők a „lappangási idő”, a „felfutási idő”, a „beállási idő”, a „túllendülés” és a „maradó szabályozási eltérés” (hiba). A gépészet sok területén (műszaki mechanika, áramlástan, hőtan) az állapottér módszer mellett a legtöbbet alkalmazott matematikai modell-forma. Az egyszerűbb szakasz-modellek lineáris differenciálegyenletekkel leírhatók, ezért a szabályozástechnikai szakirodalomban ennek a modell-formának kiemelt szerep jut. A rendszer időbeli viselkedését írhatjuk le a segítségével. Ha egy rendszer „n” db. független energiatárolót tartalmaz, akkor a differenciálegyenlet rendszáma „n” lesz. A homogén differenciálegyenlet megoldása műszaki felfogásban a magára hagyott, gerjesztetlen rendszer viselkedését írja le, általános alakban. Konkrét függvényhez természetesen csak a kezdeti feltételek megadásával juthatunk. A villamosmérnöki/szabályozástechnikai gyakorlatban ezt speciális „válaszfüggvényként” interpretálják, amennyiben a differenciálegyenlet lineáris és állandó együtthatós. Ez a függvény a rendszer impulzus bemenőjelre (Dirac-impulzus) adott általános válasza, mostanában használatos nevén „impulzusválasz”, régebbi irodalomban ez súlyfüggvényként szerepel. A mérnöki gyakorlatban, az általános bemenőjelre adott rendszerválaszt nem szokás idő tartományban, a súlyfüggvény és a konvolúciós integrál segítségével meghatározni, hanem az operátor térben, az átviteli függvény alkalmazásával. Mivel az operátor térben a konvolúciós integrál megfelelője bemenőjel Laplace transzformáltjának és az átviteli függvénynek szorzata, ugyanakkor a Dirac-impulzus Laplace transzformáltja =1, az impulzus választ legegyszerűbben az átviteli függvény inverz Laplace transzformálása révén kapjuk meg. A villamosmérnöki gyakorlatban (a gépészeti, áramlásos stb. rendszerektől eltérően) azok a passzív hálózatok, amelyek R-L-C elemeket tartalmaznak, többségükben állandó együtthatós és lineáris differenciálegyenletekkel írhatók le. Ez az oka annak, hogy előszeretettel alkalmazzák ezen a tudományterületen a Laplace transzformációt differenciálegyenletek megoldására. Ez természetesen nem jelenti azt, hogy minden villamos rendszer lineáris. Jól illusztrál egy a gyakorlatban nagy szerepet játszó nemlineáris elektromechanikus rendszert az elektromágneses csapágyazás.

A gépészet területén gyakran tapasztaljuk, hogy a nemlineáris differenciálegyenlettel leírt rendszer vizsgálata során un. munkaponti linearizálást végeznek el annak érdekében, hogy analitikus úton zárt alakú megoldáshoz juthassanak. Ezért, amint látni fogjuk, az 1970-es évektől egyre elterjedtebben alkalmazzák gépészeti dinamikai problémák leírásához hálózati módszert, ezen belül az impedancia módszert. Ha ugyanis tudjuk előre, hogy analitikus úton fogjuk keresni a megoldást, és linearizáljuk a differenciálegyenletet, akkor sokkal célravezetőbb már a folyamat elején egy jelentősen leegyszerűsített, lineáris hálózattal leírható modellből kiindulva megtenni ezt.

Egy adott rendszer differenciálegyenletéhez energia módszerrel, hálózati módszerrel, vagy közvetett módon az impedancia módszerrel juthatunk el.

Az átviteli függvény a Laplace transzformáció egyik szabályával függ össze, és, amint az előbbiekben láttuk, és alkalmazása az időtartománybeli konvolúciós integrált helyettesíti. Csak lineáris rendszer-modellekre alkalmazható. Definíciója szerint a kimenőjel és bemenőjel Laplace transzformáltjának hányadosa zérus kezdeti feltételekkel. Átviteli függvényt csak egyetlen bemenőjel és egyetlen kimenőjel között írhatunk fel. Több forrást, gerjesztést tartalmazó rendszer esetén a szuperpozíció szabályát alkalmazhatjuk. Több gerjesztés és több válasz között pedig az átviteli mátrix segítségével lehet a kapcsolatokat megjeleníteni. Az átviteli függvény az „s” Laplace operátor racionális törtfüggvénye, hiszen az „s” operátor fokszáma a számlálóban nem lehet magasabb, mint a nevezőben. A nevezőben az „s” operátor fokszáma „n”, ha a rendszerben található független energiatárolók száma „n”. A tört számlálója és nevezője egy-egy polinom. A nevezőt „karakterisztikus polinomnak” nevezik, tekintettel arra, hogy a nevező együtthatói a lineáris, állandó együtthatós, közönséges homogén differenciálegyenlet együtthatóinak felelnek meg. A homogén differenciálegyenlet, különböző kombinációkban, hiánytalanul tartalmazza a vizsgált rendszer valamennyi paraméterét, tehát jogos a karakterisztikus polinom elnevezés. Az együtthatók alapján előállított megoldás jellemzi a rendszer dinamikáját, megadja a „karakterét”. Mivel az átviteli függvény polinomokat tartalmaz, kizárt a nemlineáris rendszerek leírásának lehetősége, hacsak előzetesen linearizálás nem történt. A táblázat alatti magyarázatban leírtuk, hogy a változó paraméterekkel leírható lineáris rendszerek esetében is lehetséges első lépésben átviteli függvényt impedancia módszerrel előállítani, majd időtartományba „visszatérve” a kérdéses együtthatók esetében az álladókat megfelelő függvénnyel helyettesíteni.

Az átviteli függvény alkalmazása a szabályozástechnikában igen széleskörű és alapvető. A hagyományos szabályozókörök leírásához alkalmazott tömbvázlatok „dobozaiban” átviteli függvények szerepelnek. Innen egy lépés, és az s=jω helyettesítés révén eljutunk a frekvencia átviteli függvényhez (és a Bode diagramhoz), vagy a komplex síkon történő ábrázolás révén a Nyquist diagramhoz. Ezekkel lehetővé válik a hagyományos szabályozókörök stabilitásának vizsgálata számítással és méréssel egyaránt. A méréses utat külön szeretnénk hangsúlyozni, mert a zárt kör karakterisztikus polinomjából induló stabilitás vizsgálatok számításos eljárások. A stabilitás a minőségi követelmények második „köre”. A szabályozás dinamikai minőségi követelményeiről a differenciálegyenlet címszó alatt beszéltünk. Mind a Bode, mind pedig a Nyquist diagram, valamint az ezekhez kapcsolódó módszerek lényegében azt szemléltetik, hogy a zárt szabályozási kör nevezője semmilyen, a rendszer működése szempontjából lényeges (releváns) körfrekvencia esetében sem adhat zérus értéket. Elméletben természetesen a körfrekvencia tartomány megfogalmazása más módon történik: 0≤ω<∞. A zárt kör átviteli függvénye a szokásos felírási módon:

$W (s) = \frac{X_{S} (s)}{X_{A} (s)} = \frac{G_{C} (s) G_{S} (s)}{1 + G (s)}$

ahol G(s) a felnyitott kör átviteli függvénye, azaz a hurokátviteli függvény, a számlálóban a szabályozó és a szakasz átviteli függvényeinek szorzata található. A „kanonikus” szabályozókör tömbvázlatát a „Bevezetőben” találjuk a (2. ábra) ábrán.

Így tehát kérdéses nevezőt az s=jω helyettesítés után zérussal egyenlővé téve megkapjuk azt a kritikus körfrekvenciát, amely esetében a szabályozókör a stabilitás határára kerül. Ebben az esetben a harmonikus ellenőrző jel és az ugyancsak harmonikus alapjel amplitúdói megegyeznek, a két jel közötti fáziskülönbség pedig ±π, azaz ±180°.

$\begin{array}{l} 1 + G (j ω) = 0 \\ G (j ω) = - 1 \\ | G (ω) | = \frac{| X_{E} (ω) |}{| X_{A} (ω) |} = 1 \\ A r c t g {G (ω)} = ϕ_{E} (ω) - ϕ_{A} (ω) = ϕ (ω) = \pm π \end{array}$

Érdemes egy gondolati kísérlet végezni. Válasszuk le a különbségképző bemenetéről a negatívan visszacsatolt ellenőrző jelet! Legyen az alapjel speciális, mégpedig a kritikus körfrekvenciájú harmonikus jel, amelyet egyetlen periódus elteltével lekapcsolunk! A kritikus körfrekvencián azt tapasztaljuk, hogy ez az alapjel végighaladva a hurkon, ±π fázistolással, és azonos amplitúdóval, ellenőrző jelként megjelenik. Biztosak lehetünk abban, hogy a kör újbóli zárása után oszcilláció, azaz csillapítatlan lengés jön létre, mert a fázisában ±π szöggel eltolt jel a negatív visszacsatolás után éppen ellenfázisba kerül. Ez pedig nem más, mint az eredeti alapjel, tehát a kör alapjel nélkül is „működik”. Az oszcillációt természetesen a szabályozókörbe becsatolt energia tartja fenn.

Megjegyezzük még, hogy a vizsgálatokat azért végezzük harmonikus jelekkel, mert minden műszaki szempontból szóba jöhető periodikus és bizonyos feltételek mellett a nem periodikus jelek is, harmonikus összetevőkre bonthatóak a Fourier transzformáció segítségével. (Megjegyezzük, hogy Fourier sora csak periodikus függvényeknek van). A témáról részletesen Fodor György [3.1.] és Korondi Péter [2.4.] munkájában olvashatunk. Így tehát, ha ismerjük a harmonikus jelek átviteli karakterisztikáját, akkor elvben bármilyen jel átvitele meghatározható.

Az állapottér modell, más néven az állapotegyenletek a fizikai-technikai rendszerek legátfogóbb leírását teszik lehetővé, mind idő, mind pedig operátor (körfrekvencia) tartományban. A modern szabályozások (állapotszabályozás, állapot-megfigyelés, adaptív szabályozás) leírásához kifejlesztett modell-forma. Ezen túlmenően minden, jelenleg ismert digitális számítógépes szimulációs program kiinduló pontja.

Felépítését tekintve ez a matematikai modell a differenciálegyenlet Cauchy-féle normál alakja. Lényeges, hogy „n” db. független energiatárolót tartalmazó rendszer esetében „n” db. elsőrendű differenciálegyenletből épül fel. Ezek a differenciálegyenletek lehetnek lineárisak és nemlineárisak is, állandó és változó együtthatósak.

Ha a rendszer lineáris (linearizálható) és a paraméterek invariánsak (állandók), akkor az állapottér modell felírható mátrix-vektor egyenletrendszer formájában is. Az első egyenlet a főegyenlet, a második a segéd, vagy kimeneti egyenlet.

$\begin{array}{l} \underline{\dot{x}} = \underline{\underline{A}} \cdot \underline{x} + \underline{\underline{B}} \cdot \underline{u} \\ \underline{y} = \underline{\underline{C}} \cdot \underline{x} + \underline{\underline{D}} \cdot \underline{u} \end{array}$

A főegyenletben az $\underline{\underline{A}}$ mátrix a „rendszermátrix”, hiszen elemei különböző kombinációkban a rendszer minden paraméterét tartalmazzák. A $\underline{\underline{B}}$ neve „bemeneti mátrix”, a gerjesztések ezen keresztül hatnak az állapotjelzők időbeli megváltozására. A segédegyenletben a $\underline{\underline{C}}$ a „kimeneti mátrix” és $\underline{\underline{D}}$ a „segédmátrix”. A homogén differenciálegyenlet ebben az esetben is a gerjesztetlen rendszert jelenti. A megoldást idő tartományban az $e^{\underline{\underline{A}} \cdot t}$ exponenciális mátrix Taylor sorfejtésével, vagy operátor tartományban a $\det [s \underline{\underline{E}} - \underline{\underline{A}}] = 0$ karakterisztikus egyenlet gyökeinek meghatározásával kapjuk.

1.2. A modellalkotás folyamata

Bevezetőben le kell szögezni, hogy ismereteink és eszközeink végessége miatt a technikai (és egyéb) rendszerek tökéletes, hiba nélküli leírására vállalkozni illuzórikus lenne. A műszaki rendszerekre ható tényezők elvben „végtelen” nagy száma és a rendszeren belüli összetett kölcsönhatások miatt többnyire „zárt rendszerek” vizsgálatára szorítkozunk. Az un. zárt rendszer határainak kijelölése komoly tárgyi tudást és igen nagy szakmai tapasztalatot feltételez. A mechatronika természetesen az irányítástechnikához (szabályozástechnika és vezérléstechnika) áll a legközelebb, de a problémákat jellemzően nem villamosmérnöki szemlélettel közelíti, hanem a teljes műszaki rendszert egészében vizsgálja. A mechatronikai tervező mérnöknek kellő mélységben ismernie kell a műszaki mechanika, az elektrotechnika az áramlástan és a hőtan tudományterületeket. Felületes ismeretek nem elegendőek. Ezen túlmenően, felhasználói szinten, járatosnak kell lennie az analóg és digitális elektronikában, és az informatikai eszközök kínálatában. Ez utóbbi körébe tartoznak többek között a végeselem (VEM) szimulációs programok, a CAD/CAM rendszerek, a matematikai és dinamikai szimulációs programok, az optikai képfeldolgozásra alkalmas programok, a mikrokontroller és PLC ismeretek. Jól érzékelteti ezt W. Roddeck az Einführung in die Mechatronik című, végzett gépész-és villamosmérnökök számára írt könyvében [1.1.].

A mechatronikai gyakorlatban igen ritka, hogy a szabályozás tervezésénél „adott matematikai modellből” indulunk ki. A matematikai modell általában nem ismert, nem adott, ezt első lépésben a mechatronikai mérnöknek kell létrehoznia, esetenként más szakterületek szakembereinek bevonásával.

A mechatronikai rendszerek minden ismert esetben összetett, esetenként többszörösen összetett rendszerek. A nemzetközi tapasztalatok mennyisége 1984-tól kezdődően, azaz a „mechatronika” szakkifejezés védettségének 15 éves elmúlását követően, a mechatronika szakterületen lavinaszerűen bővül. Jelen pillanatban szinte meg sem jósolható, hogy mely újabb tudományterületeken fog a mechatronikai szemlélet tért hódítani. Egykor a fényképező és videó rendszerekből kiindulva, a gépészet valamennyi területén gyorsan megjelent, és jelenleg, - néhány jellegzetes területet kiemelve - a szórakoztató elektronikától kezdve az építőiparon, a közlekedésen, a mezőgazdaságon át az orvostechnikáig mindenütt jelen van. Az utóbbi években, az intelligens anyagok és szerkezetek kutatásának hatására már nem is mechatronikáról, hanem „adaptronikáról” beszélünk.

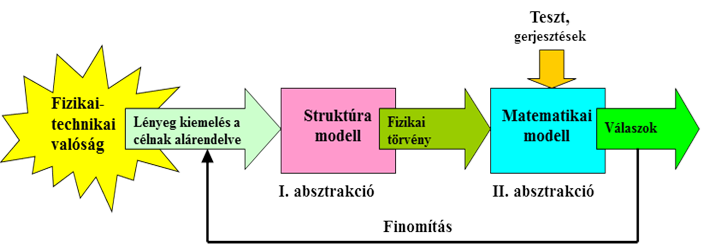
1.1. ábra - A modellezés folyamat ábrája

A modellezés folyamat ábráján minden lényeges mozzanat látható. A bonyolult fizikai-technikai rendszerből két absztrakciós fokozaton áthaladva jutunk el a rendszer matematikai modelljéhez. A fentiekben ismertettük, hogy a vizsgált rendszer a maga teljességében és összes kölcsönhatásait figyelembe véve nem írható le, de erre a műszaki feladatok megoldása során nem is lenne szükség.

Első lépésben meghatározzuk a rendszerhatárokat, és ezt követően un. egyszerű, vagy komplex zárt rendszerről beszélünk. Tulajdonképpen lényegkiemelés történik, az adott modellezési célnak alárendelve. Ebben a fázisban kell eldönteni, hogy szükséges-e elosztott paraméterekkel és parciális differenciálegyenletekkel modellezni, vagy elegendő a megkívánt pontosság betartásához a koncentrált paraméterű modell. Például egy villamos vezető darabot, a jelek jellemző frekvenciájától függően modellezhetünk „R” ohmos ellenállásként, de megjeleníthetjük tápvonalként, négypólusok láncolataként is, amely „Z(ω) hullámimpedanciával rendelkezik. A gerjesztés módjától és frekvenciájától függően jelek (változók) frekvenciájától (hullámhosszától) függően egy lemez, vagy rúd alakú alkatrész modellezhető a mechanikában egyetlen tömegként. Ugyanezt az alkatrészt lehet veszteséges rugalmasságokkal összekötött, parciális tömegrészekből álló, elosztott paraméterű rendszerként is modellezni, amelyek több „módusa” (rezonancia frekvenciája) van. Itt kell eldönteni, hogy milyen, más típusú rendszerekkel való kölcsönhatásokat kell figyelembe venni. Például egy villanymotor modellezése esetében elegendő az elektromechanikus modellt vizsgálni, vagy ki kell egészíteni egy hőtechnikai modellel is. Napjaink gazdaságközpontú gondolkodása igen sok esetben nem teszi lehetővé az aprólékos, részletekbe menő modellek megalkotását, igyekezni kell a „megrendelő” igényeit az elengedhetetlenül szükséges tudományos alapossággal kielégíteni.

Erről a témáról a 19. fejezet fejezetben bővebben is olvashatunk, ahol a módszeres tervezés lépéseit mutatja be a szerző.

Ebben a lépésben kell eldöntenünk, hogy nem lineáris módon, illetve lineáris modellel, állandó, vagy változó paraméterekkel, esetleg mindkettővel, vegyesen írjuk le a zárt rendszert. A mechanikai részrendszerek egyik alapvető problémáját okozza például a különböző súrlódások modellezése. Sokféle közelítés létezik, de az igényes minőségű szimuláció elengedhetetlen részét képezi az adott rendszeren történő mérés, és a keresett leíró függvény kísérleti meghatározása. A súrlódást modellezhetjük „b” csillapítási tényezővel, egy állandóval, ilyen a „Newton-i”, lamináris súrlódási modell, de a Coulomb súrlódás, vagy a Striebeck-effektus precíz leírása már körülményesebb. A súrlódó erő függhet a sebesség mellett, a hőmérséklettől, a hőmérséklet befolyásolja a súrlódási együttható értékét, és sok egyéb hatást ismerünk a tribológiából b(v,µ,T,…). Látható, hogy egy hőmérséklettől függő villamos vezetőképesség (ellenállás reciproka), amely egyenes analógiája a csillapítási tényezőnek, kevesebb gondot okozhat a modellalkotásnál.

A modellezési lehetőségek áttekintését – a teljesség igénye nélkül - segíti az alábbi táblázat:

1.2. táblázat - A dinamikai modellek áttekintő táblázata

Modell jelleg Paraméter típus	Lineáris	Nemlineáris
Koncentrált, állandó paraméterű	$m \ddot{x} + k x = 0$	$Θ_{a} \ddot{ϕ} = M - m g l \sin (ϕ)$
Koncentrált, változó paraméterű	$m \ddot{x} + b (v) \cdot \dot{x} + k (x) \cdot x = 0$	$Θ_{a} (ϕ) \cdot \ddot{ϕ} = M - m g l (ϕ) \cdot \sin (ϕ)$
Elosztott paraméterű	kontinuumok, tápvonalak	a „valóság” közelítésének iránya

1.3. Technikai rendszerjellemzők a matematikai modellekben

Az áttekinthetőség érdekében a bevezetőben, a fejezetben szereplő technikai rendszerjellemzőket külön felsoroljuk.

Elsőrendű rendszerek jellemzői:

Időállandó
Letörési körfrekvencia
Arányos tényező
Csillapítási kitevő

Rezgő rendszerek jellemzői:

Arányos tényező
Periódusidő
Csillapítási fok
Csillapítási kitevő
Csillapítatlan rendszer rezonancia körfrekvenciája
Csillapított rendszer rezonancia körfrekvenciája
Karakterisztikus polinom

A témával kapcsolatosan igen sok szakirodalommal, és többféle megközelítésben találkozhatunk. A mechatronika személetéhez igen közel áll H. Lutz és W. Wendt Taschenbuch der Regelungstechnik c. műve [1.2.], amely a modellezésre építve mutatja be a hagyományos és modern szabályozástechnika legfontosabb ismereteit.

1.3.1. Elsőrendű lineáris rendszerek jellemzői

Az elsőrendű lineáris rendszer időállandója a homogén differenciálegyenlet megoldásában jelenik meg. A levezetést az 5. fejezet fejezetben találjuk, itt csak az eredményt használjuk fel a fontos kapcsolódások bemutatására. Az időállandó összefügg a csillapítási kitevővel.

$x (t) = e^{- a t} = e^{- \frac{t}{T}} = e^{- σ t}$

A megoldásban az „a” paraméter általános jelölés. A műszaki gyakorlatban a másik kettőnek van jelentősége. A „T” az időállandó, „σ=1/T” pedig a csillapítási kitevő (csillapítási exponens).

Ha van kezdeti (esetleg kiindulási) érték, és nincs gerjesztés, akkor az általános alak által kínált görbesereg helyére egy függvény lép lecsengő folyamatnál:

$x (t) = x (0^{+}) e^{- \frac{t}{T}} = x (0^{+}) e^{- σ t}$

Technikai rendszereinkben nem minden esetben áll rendelkezésre a t=0⁺ időpillanathoz (jobboldali, un. kezdeti érték) tartozó érték, erről az 5. fejezet fejezetben egy gyakorlati példa kapcsán esik szó. A megoldás könnyen előállítható, ha a kiindulási érték és a kezdeti érték megegyeznek. Ez a feltétel technikai rendszerek esetében gyakran teljesül, mert a bekapcsolás időpillanatában az energiatároló lehet felöltött állapotban, és a feltöltöttséget jelző változó ilyen esetben nem zérus értékről indul.

Különleges gerjesztések esetében, ilyenek a Dirac impulzus és az ugrás függvény, újabban használt nevén „step function”. Ilyen gerjesztések esetében a számításokhoz különleges megfontolások szükségesek, ez a rendszertechnika egyik fontos területe.

A megoldás mutatja, hogy t=0⁺ és az időállandó között eltelő időben a megoldás függvény az x(0⁺) kezdeti értékről éppen annak e-ad részére csökken, majd újabb időállandónyi idő elteltével ugyancsak az előzőleg kapott érték e-ad részére:

$x (0^{+}) \cdot e^{- 1} = \frac{1}{e} x (0^{+}) \approx 0.368 \cdot x (0^{+})$

Az időállandó tehát az elsőrendű rendszer viselkedését leíró egyik fontos jellemző. Szerepe az operátor, vagy körfrekvencia tartományba is „átnyúlik”, hiszen irányítástechnikából ismeretes, hogy az időállandó reciproka a letörési körfrekvencia. Az irányítástechnikai gyakorlatban szokás az elsőrendű rendszerek Bode diagramjait egyenes szakaszokkal közelíteni. A közelítő függvényen az amplitúdó átvitel logaritmusának húsz-szorosa (dB) a körfrekvencia értékéig állandó (un. arányos átviteli sáv), ettől kezdődően -20 dB/dekád meredekséggel bír. Ismeretes az is, hogy a letörési körfrekvenciánál az átvitel pontos értéke ~3 dB-lel kisebb, mint az arányos átviteli sávban mutatott érték. A ~3 dB méréstechnikai szemszögből már tekintélyes hibát jelent, mert ez a kimeneti jelszint ~30 %-os csökkenését jelenti a bemenetihez viszonyítva.

Az előzőekben említett arányos átviteli sáv fontos jellemzője az „A” arányos tényező. Ez az állandó a differenciálegyenlet „jobb” oldalán látható, az átviteli függvénynek pedig a számlálóját képezi:

$\begin{array}{l} T \dot{x} (t) + x (t) = A u (t) \\ \frac{X (s)}{U (s)} = \frac{A}{s T + 1} \end{array}$

Az „A” tényezőt erősítési tényezőnek is nevezik, ami nem egészen tükrözi a valóságot, mert erősítésről rendszertechnikai szempontból akkor beszélünk, ha a rendszerbe kívülről energiát viszünk be, és valóban erősítjük a bemenő jelet, A>1. Ugyanakkor passzív elsőrendű rendszernek is lehet arányos tényezője, csak jellegzetesen A≤1 értékkel.

A modellezési és tervezési gyakorlatban előfordul, hogy elhamarkodott és hibás következtetéseket vonnak le csupán azért, mert a villamos és a mechanikai rendszerek közötti analógiákat hibásan alkalmazzák.

A jelenség bemutatására a „kifutási” görbék és a mechanikai időállandók kérdését elemezzük.

A hajtóművel foglalkozó fejezetben részletesen bemutatjuk, hogy a valós hajtómű lényegében a következő ábrán látható fontos elemeket tartalmazza: K_H eredő rugómerevség, J₁ és J₂ bemenő és kimenő oldali tehetetlenségi nyomatékok, valamint ugyanezen oldalakhoz tartozó csillapítási tényezők, amelyek a fogsúrlódással és a csapágysúrlódásokkal vannak kapcsolatban.

Ezen a helyen a mechanikai és a villamos időállandó közötti különbség, és nem a hajtómű modelljének bemutatása a cél, ezért a hajtómű gráfjában látható elemeket itt nem részletezzük. A hajtómű részletes modelljeit a 7. fejezet fejezetben találjuk meg.

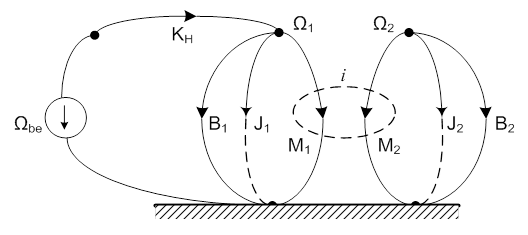
1.2. ábra - Hajtómű egyszerűsített gráf-modellje

Ha a kifutási próba vizsgálatánál eltekintünk a rugalmasságtól, ami teljesen indokolt, továbbá meghatározott M_be0 bemenő nyomatékkal „pörgetjük fel” a hajtóművet, akkor a gráf módosul. A bemenő oldali elemeket redukáljuk a kimenő oldaliakhoz, és az M_be0 nyomaték helyett értelemszerűen M_be=i·M_be0 forrásérték fog megjelenni.

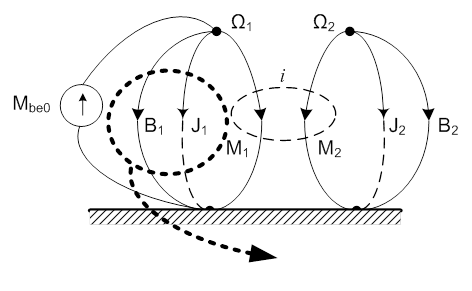
1.3. ábra - A bemeneti oldali paraméterek redukciója

A keresztváltozó forrás „megtartásának” nem lenne értelme, mert ebben az esetben nincs rendszeregyenlet, a párhuzamos elemekre „rákényszerítjük” a szögsebesség forrás értékét.

A redukció után kapott értékek esetében – a megkülönböztetés érdekében - eltekintünk az indexektől.

$\begin{array}{l} J = J_{2} + i^{2} J_{1} \\ B = B_{2} + i^{2} B_{1} \\ M_{b e} = i \cdot M_{b e 0} \end{array}$

A következő ábra már a hajtómű egyszerűsödött gráfját mutatja arra az esetre, ha az eredő rugómerevség kellően nagy ahhoz, hogy az eredő tehetetlenségi nyomatékkal ne tudjon lengő rendszert képezni. A mikromotorokhoz kapcsolt hajtóművek esetében gyakorlatilag ez a helyzet. A gráf alapján felírt csomóponti egyenletből kapott rendszeregyenlet az alábbi:

$\begin{array}{l} M {}_{B}+ M_{J} = M_{b e} \\ B Ω + J \frac{d Ω}{d t} = M_{b e} \\ \frac{J}{B} \frac{d Ω}{d t} + Ω = \frac{1}{B} M_{b e} \end{array}$

Az átviteli függvényt a Laplace transzformálás után kapjuk:

$G (s) = \frac{Ω (s)}{M_{b e} (s)} = \frac{\frac{1}{B}}{s \frac{J}{B} + 1} = \frac{\frac{1}{B}}{s T + 1}$

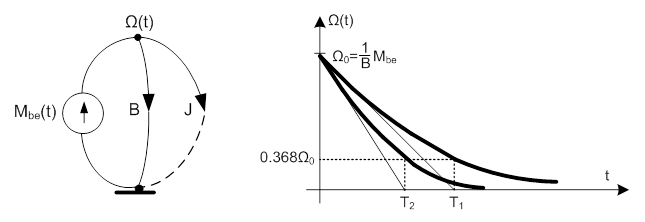
1.4. ábra - Hajtómű és motorral kapcsolt hajtómű „kifutási görbéi”

A gráf mellett a magára hagyott rendszer válaszait láthatjuk, Ω₀ kiindulási érték, és T=J/B időállandó mellett. A vizsgálatunk során T₁ az „induló” időállandó, ez a terheletlenül járó DC motor kifutási görbéjéhez van rendelve. A következő lépésben csatlakoztattuk a motorhoz a hajtóművet, és a T₂ időállandóval jellemzett kifutási görbét kaptuk. Látható, hogy a második esetben, a csekély mértékben megnövekedett az eredő tehetetlenségi nyomaték (J), és jelentősen megnőtt az eredő csillapítási tényező (B) kisebb időállandót eredményezett, a kimenő tengely forgása hamarabb áll le.

A mérésekkel kapott kifutási görbéket a hajtóművel foglalkozó fejezetben is megtaláljuk, de a könnyebb megértés kedvéért itt is szerepeltetjük.

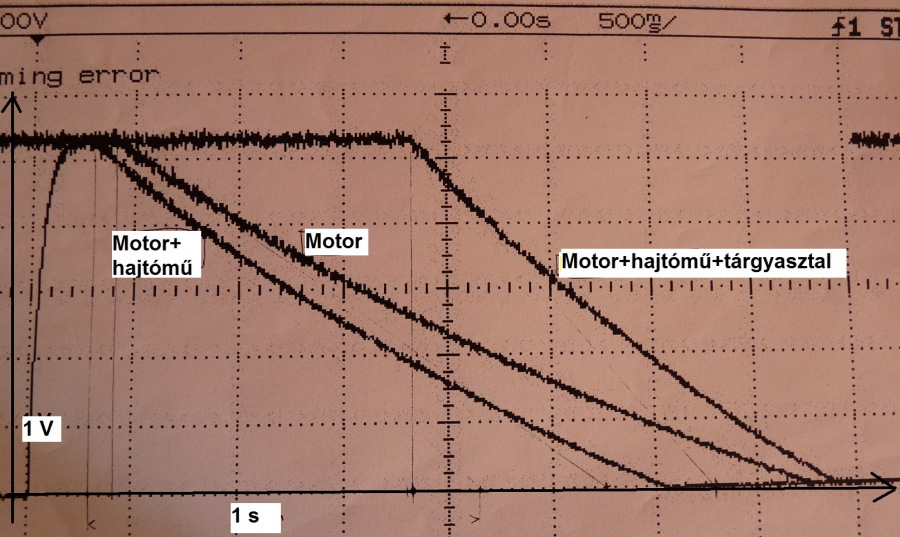
1.5. ábra - Méréssel kapott kifutási görbék

Nyilvánvaló, hogy dinamikai szempontból nem a kisebb időállandójú mechanikai rendszer „jobb”. Ennek belátásához jobban szemügyre kell venni az átviteli függvény számlálóját! A fejezet címében nem véletlenül szerepel hangsúlyosan az „arányos tényező”. Azok az elsőrendű rendszerek, amelyek számlálójában az arányossági tényező egyenlő eggyel, valóban megítélhetők dinamikai szempontból pusztán az időállandóik alapján.

De vigyázat, ez a vizsgált mechanikai rendszer nem ilyen!

A különbség érzékeltetésére bemutatjuk azt a forgó mechanikai rendszert, amelynek átviteli függvényében az arányos tényező értéke egy. A mechanikai rendszer eléggé „iskolás” jellegű, mert ehhez hasonlót a gépészetben nem gyakran lehet találni. Ugyanakkor a mellette látható, és vele strukturálisan analóg (felépítésében hasonló) villamos analóg kapcsolás egy rendszeresen alkalmazott, passzív aluláteresztő szűrőt ábrázol. Meg kell jegyezni még, hogy vannak olyan egyszerű, valós termikus, fluid (akusztikai, pneumatikus és nyitott tartályú hidraulikus) rendszerek, amelyeket ugyanilyen kapcsolás ír le, gondoljunk a termoelektromos hőmérőre, vagy egy fojtáson keresztül töltött tartályra. Az alább bemutatott gépészeti modell csak akkor tekinthető ezekkel analógnak, ha a csapágy súrlódása elhanyagolható, és a tengelykapcsolónál csekély a slip (csúszás).

Megtévesztő lehet az is, hogy az ábrán látható két rendszernek a kifutási görbéhez hasonló az impulzus válaszuk (súlyfüggvényük). Ebben nincsen semmi csodálatos, hiszen a keresztváltozó forrás, és a mellette szereplő impedancia (Thevenin alak) átszámítható egyenértékű Norton alakká, és akkor újra visszakapjuk a kiindulásként látott párhuzamos elemekből és átmenő változó forrásból álló gráfot.

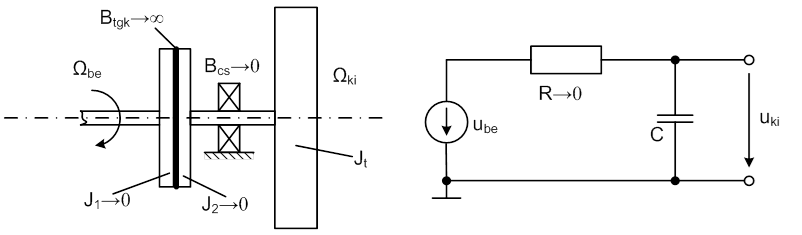
1.6. ábra - Analóg mechanikai és villamos egytárolós arányos rendszerek

Nézzük egymás mellett a két rendszer matematikai modelljeit, ti: átviteli függvényeit, amelyeket az impedancia módszerrel, keresztváltozó osztó alkalmazásával írtunk fel:

$\begin{matrix} \begin{array}{l} \frac{Ω_{k i} (s)}{Ω_{b e} (s)} = \frac{\frac{1}{s J}}{\frac{1}{B_{t g k}} + \frac{1}{s J}} = \frac{1}{s \frac{J}{B_{t g k}} + 1} \\ \frac{U_{k i} (s)}{U_{b e} (s)} = \frac{\frac{1}{s C}}{R + \frac{1}{s C}} = \frac{1}{s R C + 1} \end{array} & i l l e t v e \end{matrix}$

Ha az ábrán jelölt módon „kimerevítjük” a tengelykapcsolót, azaz B_tgk→∞, akkor az a villamos rendszerben az R→0 módosításnak felel meg, tekintettel arra, hogy B_tgk nem az ellenállással, hanem a vezetőképességgel analóg. Ha a jelölt módosításokat elvégezzük, akkor az átvitel a körfrekvenciától függetlenül 1:1 lesz, a harmonikus kimenő és bemenő jelek amplitúdói megegyeznek, fázistolás nincsen.

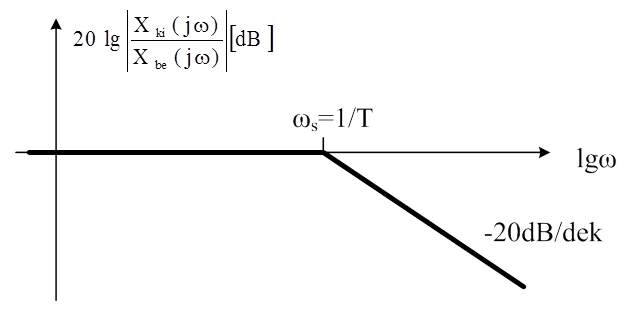
Mindkét átviteli függvény számlálójában „egy” szerepel, a mechanikai és a villamos időállandó „egyedül” fogja „minősíteni” az aluláteresztő szűrőket. Kis időállandóhoz nagy letörési körfrekvencia, és fordítva lesz rendelve, amint az alábbi Bode diagramon láthatjuk. Az arányos átvitel (kör)frekvencia sávjában a számláló értéke miatt természetesen zérus decibelt találunk.

Már az előzőekben is hangsúlyoztuk, hogy a gyakorlatban előforduló forgó mechanikai rendszerek nem azonosak a most bemutatott „iskolapéldákkal”.

A valós hajtóművek dinamikus viselkedése más, és ez az átviteli függvény számlálójának figyelembe vételével válik világossá.

Érthetővé válik a különbség, ha nem csak a kifutási görbe alakját, hanem a rendszer átmeneti függvényét és a Bode diagramot tesszük vizsgálat tárgyává.

1.7. ábra - Egytárolós arányos (PT1) tag amplitúdó menete A=1 esetén

A DC mikromotor és a valós, de rugalmasság nélküli hajtómű átmeneti függvényei a (1.8. ábra) ábrán láthatók. A DC mikromotor méréssel kapott kifutási görbéjén nem láttunk lengéshajlamra utaló jeleket. Ez azért van, mert a kisebb méretű motorok nyugalmi induktivitása (L) meglehetősen kicsi, a súrlódásos veszteségek finommechanikai szerkezetekben dominánsak, a mikromotort a gyártók is elsőrendű (egy energiatárolós) rendszernek tekintik. Így tehát a méréssel kapott kifutási diagramok is két egytárolós rendszert mutatnak.

A DC motorral foglalkozó fejezetben látni fogjuk, hogy a DC motor átviteli függvénye a kapocsfeszültség, mint bemenet, és a szögsebesség, mint kimenet között alakra megegyezik a nyomaték bemenettel gerjesztett hajtómű átviteli függvényével, ha a DC motor nyugalmi induktivitása elhanyagolhatóan kicsi. A levezetést az említett fejezetben találjuk, itt az összehasonlítás miatt csak az eredményt mutatjuk be:

$\frac{Ω (s)}{U_{b e} (s)} = \frac{\frac{K_{M}}{R B + K_{M}^{2}}}{s \cdot \frac{R J}{R B + K_{M}^{2}} + 1} = \frac{A}{s T + 1}$ ,

ha L→0.

A következő ábrán olyan egytárolós arányos tagok átmeneti függvényeit látjuk, amelyek számlálójában az arányos tényező nem egységnyi, hanem jellemző a rendszerre.

Ilyen a fejezet elején említett motor, valamint a motorral egybeépített hajtómű átviteli függvénye is. A levezetést nem ismételjük, csak az eredményt:

$\frac{Ω (s)}{M_{b e} (s)} = \frac{\frac{1}{B}}{s \frac{J}{B} + 1} = \frac{A}{s T + 1}$

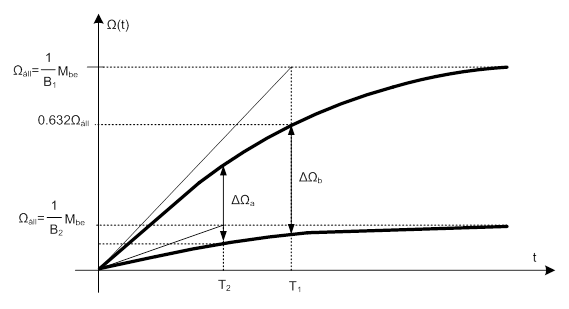
Ha a fenti átviteli függvénnyel jellemzett rendszerre ugrás-szerű nyomatékváltozást adunk, vagy a DC motor egyszerűsített átviteli függvényére ugrás-szerű feszültség változást kapcsolunk, egységugrás bemenőjel formájában, akkor a válaszként kapott szögsebesség (fordulatszám) az alábbi diagramon látható módon fog változni (átmeneti függvény, step response). Tegyük fel, hogy az időállandókat a kifutási görbék segítségével állapítottuk meg. Az önálló motor időállandója T₁, míg a hajtóművel egybeépítetté T₂. Amint a fenti magyarázatból tudjuk, T₁>T₂.

A két átmeneti függvény szemléletes formában ad választ az eredetileg feltett kérdésre: Jellemezheti-e egy elsőrendű mechanikai rendszer dinamikai tulajdonságait az időállandó önmagában? Látszik, hogy nem, hiszen a nagyobb időállandójú motor ugyanakkora bemenő nyomatékra minden időpillanatban nagyobb szögsebességgel válaszol, nem beszélve az állandósult állapotbeli szögsebességről, amelyet egyértelműen a csillapítási tényező – azaz a súrlódás(ok) – határoz(nak) meg.

1.8. ábra - Átmeneti függvények összehasonlítása

A körfrekvenciától való függés is hasonló következtetést sugall. Ha a Bode diagramot vizsgáljuk, akkor látható, hogy a letörési körfrekvencia (ω_s=1/T) nem minden esetben perdöntő, hiszen a nagyobb arányos érték (az átviteli függvény számlálója) nagyobb átviteli tényezőt eredményez, még a kisebb időállandójú mechanikai rendszer törési körfrekvenciáján is. Annak ellenére, hogy ezen a szakaszon a nagyobb időállandójú rendszer diagramja már a „leszálló” ágban van.

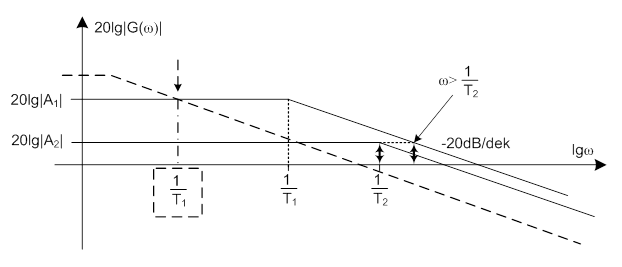
1.9. ábra - Az amplitúdó menetek összehasonlítása

Mindezt arra az esetre feltételeztük, ha a két időállandó nem különbözik egymástól nagyságrendileg, és T₁ a nagyobb. Ha a Bode diagramon szaggatott vonallal jelölt szélsőséges eset fordulna elő, azaz T₁ már nagyságrendekkel nagyobb lenne, mint T₂, akkor az előbbi fejtegetés a (kör)frekvencia tartományban természetesen nem áll meg.

Az idő tartományban, az átmeneti függvényre továbbra is az vonatkozik, hogy azonos értékű gerjesztésre a nagyobb időállandójú mechanikai rendszer kimenőjelének értéke lesz a nagyobb.

1.3.2. Rezgő rendszerek jellemzői

Rezgő, alacsonyabb frekvencia tartományban lengő technikai rendszerek alatt olyan rendszereket értünk, amelyekben minimálisan két olyan energiatároló található, amelyek egymáshoz képest ±180° fázistolással tárolják az energiát. Azért nem írunk „eltérő” típusú tárolót, mert ez nem általánosan érvényes. Ha ugyanis a rendszer két eltérő típusú fizikai rendszerből áll, és a részrendszereket fordított váltó köti össze (pl. piezoelektromos átalakító), továbbá mindkét részrendszerben van egy-egy eltérő típusú energiatároló, akkor a fordító váltó tulajdonságai miatt nem jöhet létre rezgés (lengés). Ugyanis a fordító váltó által azonos oldalra átszámított energiatároló típusa szerint pont az ellentettjére vált, így azonos oldalon két azonos típusú energiatároló lesz, ezek pedig nem képesek lengésre. Ennek a gyakorlati levezetését láthatjuk a 6.1. szakasz fejezetben.

Azért szerepel a bevezető sorban a „minimálisan” kifejezés, mert természetesen lehet kettőnél több energiatároló is, de mindenképpen páros számú, és párosával eltérő típusú.

A legáltalánosabb eset a másodrendű rezgő (lengő) rendszer. A modelljeink között, az egyszerű, energiaátalakítót nem tartalmazó, másodrendű technikai rendszerek két rendszertípus kivételével előfordulhatnak. Ez a két rendszer típus a termikus és a pneumatikus rendszer, amelyekben csak kapacitív tárolók vannak, ennél fogva rezgés (lengés) nincs.

A másodrendű, lineáris rezgő rendszer általános modellje idő és operátor tartományban:

$\begin{array}{l} T^{2} \ddot{x} + 2 ξ T \dot{x} + x = A u (t) \\ \frac{X (s)}{U (s)} = \frac{A}{s^{2} T^{2} + 2 ξ T s + 1} \end{array}$

E formák közül valamelyik – több technikai rendszer modellezésének eredményeként – a jegyzet több fejezetében is előfordul.

A két matematikai modell „direktben” több fontos technikai jellemzőt tartalmaz, továbbiak pedig a felhasználásukkal levezethetőek:

	T	másodrendű rendszer időállandója, T=1/α, ahol α a csillapítatlan rendszer rezonancia körfrekvenciája
	ξ	csillapítás foka, csillapítási szám (dimenzió nélküli, mechanikus rendszereknél a Lehr csillapítás, jelölése: D)
	A	arányos tényező

A fenti jellemzőkből levezethető továbbá a

	T_p	lengési periódusidő, és
	ω_r	csillapított rendszer rezonancia körfrekvenciája

Gyakran nem világos a tervezők előtt, hogy miért a fentebb megadott matematikai modell-formát alkalmazzák a szabályozástechnikában és a mechatronikában. Érdemes ezért az összefüggéseket röviden összefoglalni.

A matematikában egy másodrendű állandó együtthatós lineáris differenciálegyenlet megoldásához homogén algebrai egyenletté átalakítják át a differenciálegyenletet (karakterisztikus egyenlet), bevezetve a „λ” sajátértékeket, majd megkeresik λ megoldásait:

$\begin{array}{l} T^{2} \ddot{x} + 2 ξ T \dot{x} + x = A u (t) \\ T^{2} λ^{2} + 2 ξ T λ + 1 = 0 \end{array}$

A másodfokú egyenletből kapott megoldásokat exponenciális függvény kitevőjében látjuk viszont. Általános alakban (kezdeti érték nélkül) a homogén egyenlet megoldása az alábbi formákat öltheti:

$\begin{array}{l} \begin{matrix} x (t) = C_{1} e^{σ_{1} t} + C_{2} e^{σ_{2} t} & h a & λ_{1} = σ_{1} & λ_{2} = σ_{2} \end{matrix} \\ \begin{matrix} x (t) = C t e^{σ t} & h a & λ_{12} = σ \end{matrix} \\ \begin{matrix} x (t) = C \sin ω_{r} t & h a & λ_{12} = \pm j ω_{r} \end{matrix} \\ \begin{matrix} x (t) = C e^{σ t} \sin ω_{r} t & h a & λ_{12} = σ \pm j ω_{r} \end{matrix} \end{array}$

A fent bemutatott változatok általános formák, egyelőre nem kötjük ezeket valós technikai rendszerekhez, ezért nem tettünk előjelet a megoldások valós része (σ) elé.

A formával kapcsolatosan feltett kérdésre azonban egyúttal itt a válasz is, a gyökoldó képlet formájában:

$λ_{12} = - \frac{2 ξ T}{2 T^{2}} \pm \sqrt{{(\frac{ξ}{T})}^{2} - \frac{1}{T^{2}}} = - \frac{ξ}{T} \pm \frac{1}{T} \sqrt{ξ^{2} - 1}$

A gyökoldó képlet elemzésére most nem térünk ki, sem az előjelre, sem pedig a gyök alatti kifejezésben ξ nagyságára.

A rendszermodellezésben, a Laplace transzformáció bevezetésével, a sajátérték helyét „elfoglalja” az „s” komplex operátor. Az időtartománybeli megoldásokat az inverz Laplace transzformáció segítségével kapjuk, és ez a művelet az átviteli függvény nevezőjéből (karakterisztikus polinom) képzett egyenlet gyökeinek keresésével indul. A karakterisztikus polinomot egyenlővé téve zérussal, az alábbi formát és megoldásokat nyerjük:

$\begin{array}{l} \frac{X (s)}{U (s)} = \frac{A}{s^{2} T^{2} + 2 ξ T s + 1} \\ K (s) = s^{2} T^{2} + 2 ξ T s + 1 = 0 \\ s_{12} = - \frac{2 ξ T}{2 T^{2}} \pm \sqrt{{(\frac{ξ}{T})}^{2} - \frac{1}{T^{2}}} = - \frac{ξ}{T} \pm \frac{1}{T} \sqrt{ξ^{2} - 1} \end{array}$

Mechatronikai rendszerek esetében érdemes a gyököket részletesebben megvizsgálni, mert fontos összefüggéseket látunk az irányítástechnikával.

$\begin{array}{l} \begin{matrix} 1 & x (t) = C_{1} e^{σ_{1} t} + C_{2} e^{σ_{2} t} & h a & s_{1} = σ_{1} & s_{2} = σ_{2} \end{matrix} . \\ \begin{matrix} 2 & x (t) = C_{1} e^{- σ_{1} t} + C_{2} e^{- σ_{2} t} & h a & s_{1} = - σ_{1} & s_{2} = - σ_{2} \end{matrix} \\ \begin{matrix} 3 & x (t) = C t e^{σ t} & h a & s_{12} = σ \end{matrix} \\ \begin{matrix} 4 & x (t) = C t e^{- σ t} & h a & s_{12} = - σ \end{matrix} \\ \begin{matrix} 5 & x (t) = C \sin ω_{r} t & h a & s_{12} = \pm j ω_{r} \end{matrix} \\ \begin{matrix} 6 & x (t) = C e^{σ t} \sin ω_{r} t & h a & s_{12} = σ \pm j ω_{r} \end{matrix} \\ \begin{matrix} 7 & x (t) = C e^{- σ t} \sin ω_{r} t & h a & s_{12} = - σ \pm j ω_{r} \end{matrix} \end{array}$

Passzív másodrendű rendszer esetében, a valós rész előjele a megoldásokban kizárólag negatív lehet.

Ugyanakkor, ha pl. egy zárt szabályozókör átviteli függvényének karakterisztikus polinomjára, és az abból képezett karakterisztikus egyenletre gondolunk, akkor előfordulhat pozitív előjelű valós rész, de nem minden következmény nélkül.

Ha ábrázoljuk a számmal megjelölt gyököket az operátor komplex síkján, akkor a probléma azonnal világossá válik:

Stabil rendszer kizárólag az lehet, amelynek gyökei negatív előjelű valós résszel rendelkeznek. Ez ugyanis az időtartományban negatív kitevőjű exponenciális függvénynek felel meg, ilyenek a 2, 4 és 7 számmal jelölt függvények. A fenti ábrán háttérszínnel jelöltük az instabil rendszert képviselő megoldásokhoz tartozó, „jobboldali” félsíkot, amelybe beletartozik a képzetes tengely is. A színezett mező jobboldali sarkain jelöltük, hogy a kiterjedés csak baloldalon van korlátozva. Azt, hogy a félsík a gyakorlatban átterjed a baloldalra is, a képzetes tengely baloldalán egy „biztonsági” sávval, jelöltük. A gyakorlat számára ugyanis ezen a sávon belül még ugyancsak kritikus egy rendszer viselkedése, mert túlzottan kicsi a csillapítása.

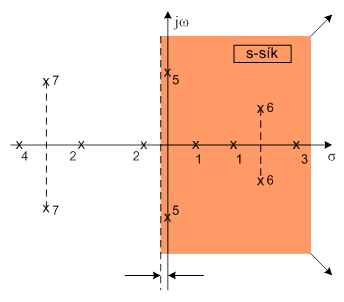
1.10. ábra - A karakterisztikus polinom gyökeinek ábrázolása az s-síkon

Nézzük ezek után, miként befolyásolja a megoldásokat ξ értékének nagysága. A gyakorlatban a következő eseteket vizsgáljuk:

ξ>1 Túlcsillapított rendszer

$x (t) = C_{1} e^{- σ_{1} t} + C_{2} e^{- σ_{2} t}$

két negatív valós megoldás van, 2-es számmal jelölve:

$\begin{matrix} s_{1} = - \frac{1}{T_{1}} = - σ_{1} & é s & s_{2} = - \frac{1}{T_{2}} = - σ_{2} \end{matrix}$

ξ=1 Kritikus csillapítás

$x (t) = C t e^{- σ t}$

kettős negatív valós megoldás, 4-es számmal jelölve

$s_{12} = - \frac{1}{T_{12}} = - σ_{12}$

ξ<1 Alulcsillapított rendszer

$x (t) = C e^{- σ t} \sin ω_{r} t$

konjugált komplex gyökök, 7-es számmal jelölve

Ehhez a megoldáshoz a következőket kell hozzáfűzni:

A megoldás alakja: $s_{12} = - σ \pm j ω_{r}$ , amelyet az exponenciális függvénybe behelyettesítve az Euler összefüggések alapján az alábbi formát kapjuk:

$e^{- (σ \pm j ω_{r}) t} = e^{- σ t} \cdot e^{\mp j ω_{r} t} = e^{- σ t} (\cos ω_{r} t + j \sin ω_{r} t)$

Ezt a komplex függvényt csak a térben, időfüggő vektorként lehet elképzelni. Az idő tengely mentén előrehaladva, forog a vektor, miközben exponenciálisan csökken a vektor abszolút értéke. A gyakorlatban ennél a megoldásnál vagy a valós, vagy a képzetes részt szokták megadni. A 7-es számmal jelölt megoldás esetünkben a komplex részt testesíti meg.

A fejezet elején két olyan jellemzőt soroltunk fel, amelyeket származtatás, levezetés révén kaphatunk, ezek a T_p lengési periódusidő, és ω_r a csillapított rendszer rezonancia körfrekvenciája. Ez a két jellemző az alulcsillapított rendszerhez tartozik, azaz ξ<1.

Nézzük a gyökök megoldásfüggvényét erre az esetre:

$s_{12} = {- \frac{ξ}{T} \pm \frac{1}{T} \sqrt{ξ^{2} - 1} |}_{ξ 〈 1} = - \frac{ξ}{T} \pm \frac{1}{T} \sqrt{- (1 - ξ^{2})} = - \frac{ξ}{T} \pm \frac{1}{T} \sqrt{- 1} \sqrt{(1 - ξ^{2})} = \frac{ξ}{T} \pm \frac{1}{T} j \sqrt{(1 - ξ^{2})}$

Látható, hogy

$\begin{matrix} σ = \frac{ξ}{T} & é s & ω_{r} = \frac{\sqrt{1 - ξ^{2}}}{T} \end{matrix} = α \sqrt{1 - ξ^{2}}$

A fenti képlet azt jelenti, hogy ω_r=α csak zérus csillapítási szám mellett lehetséges. Minden valós, csillapított rendszernek a csillapítatlanhoz képest alacsonyabb a rezonancia körfrekvenciája.

Ezen a helyen fontos megjegyezni, hogy a mechatronikában és irányítástechnikában a másodrendű rezgő rendszer Bode diagramjának rajzolásakor világosan meg kell különböztetni a három esetet. Gyakran előfordul, hogy Bode diagramként csak a ξ>1 értékhez tartozó görbét rajzolják fel, két törésponttal, egyenesekkel közelítve, ami nem mindig helyes. A paraméterek becslése, tapasztalatok, vagy mérési eredmények alapján a diagramot a megfelelő formában kell ábrázolni. Megjegyezzük, hogy a ξ=1 előfordulása valós technikai rendszerben igen ritka.

A csillapított rendszer lengési periódusideje és a másodrendű rendszer időállandója közötti kapcsolat is felírható:

$T_{P} = \frac{2 π}{ω_{r}} = \frac{2 π}{α \sqrt{1 - ξ^{2}}} = \frac{2 π \cdot T}{\sqrt{1 - ξ^{2}}}$

Szakirodalom

[1.1.] Roddeck, W.. Einführung in die Mechatronik. Teubner Verlag. Stuttgart . 1997.

[1.2.] Lutz, H. és Wendt, W.. Taschenbuch der Regelungstechnik. Wissenschaftlicher Verl. Harry Deutch. Frankfurt a.M . 2003.

Vissza		Előre
Bevezető a Mechatronikai rendszerek tervezése című jegyzethez	Főoldal	2. fejezet - A mechatronikai modellezés eszköztára