Bevezető a Mechatronikai rendszerek tervezése című jegyzethez
A „Mechatronikai rendszerek tervezése” című elektronikus jegyzet írói nem vállalkozhattak arra, hogy a mechatronika szerteágazó szakterületének egészét bemutassák. A cím arra utal, hogy a tervezés első, és éppen ezért kritikus, döntő szakaszában folyó munkához szándékozunk módszereket adni és bemutatni, valamint egymással összehasonlítani.
A jegyzet természetesen tartalmaz néhány teljes tervezési folyamatot komplex mechatronikai rendszerekre is – ilyen a mechatronikus rezgéscsillapító – de döntően a szabályozott szakasz, az aktuátorok és a szenzorok modellezése és tervezése a tárgya.
A jegyzet tehát nem szabályozástechnikai, hanem mechatronikai, és ezért bizonyos fokú szabályozástechnikai ismereteket feltételez az olvasótól. A szabályozott szakaszok célorientált modelljének megalkotása a mechatronikai tervezés döntő fázisa. A szerzők feltételezik, hogy az olvasó jártas az alapvető szabályozástechnikai ismeretek terén, ismeri a kaszkád kanonikus szabályozásokat, az analóg és diszkrét szabályozók tervezését és a szabályozókörök behangolását. Ismeri az állapotszabályozás analóg és diszkrét formáját. A szerzők ismételten hangsúlyozni kívánják, hogy a jegyzetük nem irányítástechnikai oktatóanyag, erre a célra számos tankönyv, monográfia, jegyzet áll rendelkezésre.
Az olvasó előtt bizonyára ismeretes, hogy az irányítástechnikai szakirodalomban igen gyakran találhatók olyan szófordulatok, miszerint „adott egy szakasz átviteli függvénye”, vagy „adott a szakasz állapotegyenlete”. Ezt követően indul a szabályozás tervezése. Ez nem is lehet másként, hiszen e munkák nem a szakaszok tervezésével, modellezéssel, hanem a szabályozásokkal foglalkoznak. Szerzőik feltételezik, hogy az olvasók a mechanikai, hőtani, elektrotechnikai stb. szakismereteik alapján képesek megalkotni bármilyen műszaki rendszer éppen aktuális matematikai modelljét. E jegyzet ebben kíván segíteni, és célja az, hogy az olvasó képes legyen összetett mechatronikai szabályozott szakaszok tervezésére és modellezésére önállóan is. Legyen tisztában azzal, hogy az előbb említett munkákban szereplő szakasz modelleket (átviteli függvények, állapottér modellek) miként lehet a célkitűzéseknek megfelelő pontossággal megalkotni.
Az olvasó legyen tisztában azzal, hogy minden modellezési folyamat többé-kevésbé tökéletlen eredményt szolgáltat. Ugyanakkor a befektetett modellezési munkának azonban mindig arányban kell lennie a célkitűzéssel. Túlzott részletességgel, vagy felületesen és elnagyoltan megalkotott modell egyaránt hibás eredményhez vezethet.
A következőkben néhány gondolatot átveszünk a Méréselmélet című TÁMOP jegyzetből, amelynek egyik szerzője, Huba A. azonos e mechatronikai jegyzet egyik írójával. A munka minőségét illetően ugyanis, a modellezés a méréstechnikában is kifejezetten döntő fázis, tehát célszerű a bevezetőben az ott leírtakra az olvasó figyelmét felhívni.
A modern rendszerszemlélet kialakulásával összefüggésben, az 1960-as évektől kezdődően, alig találunk olyan mértékadó méréselméleti, vagy rendszertechnikai és irányításelméleti szakirodalmat, amelyben a megismerési tevékenység középpontjában ne a modellalkotás állana. A mérés és modellezés elválaszthatatlanságának két fejezetet szenteltek a szerzők az idézett munkában. A modellezés fontosságát jelzi, hogy a metrológiában (méréstudomány) már magának a mérésnek is legalább négy modellje ismert és használatos, amelyekkel magát a mérési tevékenységet kísérlik meg leírni.
A „mi megközelítésünk” – tekintettel arra, hogy a szerzők mérnökök, valamint a jegyzet mérnökhallgatók számára készült, természetesen alapvetően mérnöki. A mérnökök vagy kutató tevékenységet végeznek, vagy az ipari termelésben vesznek részt, termékeket és gyártórendszereket terveznek, és a termelést irányítják. A mérés négy modellje közül az egyik az un. „folyamat modell”, a legszemléletesebben mutatja be azt, hogy a mérnöki tevékenység, különösképpen pedig a mérés, tudományos síkon a bennünket körülvevő „világ megismerésére” szolgál, ipari szinten pedig a minőségbiztosítás elengedhetetlen eszköze.
A modellezés és a mérés elválaszthatatlanok, mert a megalkotott modell minőségének ellenőrzése mindenképpen méréssel kell, hogy történjen, kivételes esetekben elégedhetünk csak meg a szimulációval.
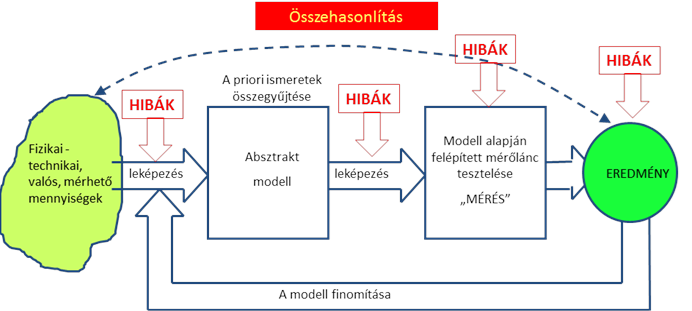
A modellezés folyamatát bemutató ábrával – módosított formában – találkozunk még a modellezéssel foglalkozó fejezetben is, a kettőt együtt érdemes átgondolni.
A fenti ábrán a modellezni kívánt rendszert, a rendszer működését leíró mennyiségek halmazát, továbbá a lánc végén megjelenő eredményt eltérő színnel és formával jelöltük. Ezzel kívánjuk kifejezésre juttatni, hogy a fizikai technikai valóság teljes körű megismerése legfeljebb elméletben lehetséges, hiszen belátható, hogy a jellemzőkre és a mérési-megismerési tevékenységre ható, és azokat befolyásoló tényezők száma végtelenül nagy. Valamennyi befolyásoló tényező gyakorlati megismerésére nincsenek eszközeink, de nem is lenne gazdaságilag indokolható minden hatótényező figyelembe vétele. Ezért minden eredmény leegyszerűsített, és valamilyen „pontossági szintű” – helyesebben hibákkal terhelt – modellje a valóságnak.
Érdemes kiemelni azt is, hogy az ábrán a hibák eredete is nyomon követhető.
A bennünket körülvevő világ mérnöki szempontból megismerni kívánt töredék részét, a jelenségek közötti kapcsolatokat modellek segítségével kíséreljük meg leírni. A modellek nagyvonalakban három kategóriába sorolhatók: fizikai, esetleg kémiai modellek, funkcionális modellek és matematikai (absztrakt) modellek.
A műszaki életben manapság használatos modellezési alapokat 1975-ben megjelent, „General Systems Theory. Matematical Foundation.” (Academic Press, New York, 1975.) művükben M. D. Mesarovic és Y. Takahara fektették le.
A fizikai modellek általános alkalmazása főként régebbi időkben volt elterjedt, ugyanakkor még ma is nélkülözhetetlenek az áramlástechnikai vizsgálatok esetében a kicsinyített, hasonlóság alapján megalkotott modellek. Ugyanakkor összetett mechanikai lengő rendszerek dinamikai vizsgálatának céljából már csak elvétve találkozhatunk analóg villamos áramkörökkel, hiszen a szilárdsági és dinamikai analízis területén szinte egyeduralkodóvá vált a végeselem módszer.
A funkcionális modellek mind a mai napig általánosan elterjedtek a mechanikában, valamint a mérés- és szabályozástechnikában. Ebben az esetben a vizsgálat alá vett rendszert felépítő elemeket idealizált szerepük alapján jelenítjük meg. Minden, alapozó mérnöki ismeretekkel rendelkező szakember tudja, hogy egy rugalmas szerkezeti elem sokféleképpen írható le, de a az ideálist leginkább közelítő változat az, ha helyette egy rugót jelenítünk meg. Azonban sem a fémek, sem a műanyagok viselkedésének pontosabb leírása nem lehetséges egy ilyen módon. Fémeket minimálisan egy rugó és egy csillapítás párhuzamos kapcsolásával szokás modellezni (Kelvin-modell), de relaxációt és kúszást mutató, nemlineáris tulajdonságú elasztomerek esetében – bizonyos követelmények mellett – még ez a forma sem lenne elegendő.
A matematikai modellek absztrakciós lépések eredményeként jönnek létre. Ezeknek napjainkban kiemelt szerepük van, ami a számítástechnika fejlettségének köszönhető. A vizsgált rendszerekben a mérhető és nem mérhető mennyiségeket változók formájában jelenítjük meg, a rendszerre jellemző műszaki tulajdonságokat paraméterek (ezek állandóak és változóak lehetnek) formájában írjuk le. Tudjuk alapozó ismereteink alapján, hogy időben változó mennyiségek villamos jellé történő átalakítása és mérése nélkül bármely mechatronikai rendszer elképzelhetetlen, ezért a méréstechnika kiemelt fontossággal bír a mechatronikában.
A mechatronikai rendszerek megtervezéséhez elengedhetetlen a négy matematikai modell-típus ismerete.
Ezek
-
a differenciálegyenlet (idő tartomány, dinamika, jelkövetés vizsgálata)
-
az átviteli függvény (operátor, vagy frekvencia tartomány, stabilitás vizsgálata)
-
az állapottér modell (idő és operátor tartomány)
-
és speciális esetekben a logikai függvények.
Mihez szükségesek ezek a modellek?
A válasz egyszerű. Ahhoz, hogy a szabályozott szakasz kimenőjele(i) az előírt módon viselkedjenek, a tervezés első lépésében meg kell ismerni a szakasz dinamikai tulajdonságait. A szabályozókör többi tagját ennek adottságaihoz kell illeszteni. A szakaszok nehezen, legalább is nem minden esetben tipizálhatóak, de ugyanakkor kereskedelmi forgalomban kaphatóak a szabályozókör egyéb tagjai, így a mérést végző visszacsatoló tagok és a szabályozók. Gyakran találkozunk hazai és külföldi szabályozástechnikai szakirodalomban azzal, hogy a szerző ismertnek feltételezi a szakasz modelljét, és a szabályozás tervezését valamelyik matematikai modellformából „indítja”. Következő, és hasonló fordulatokat olvashatunk: „Ismert a szabályozott szakasz átviteli függvénye”. Vagy: „Adott a szakasz állapottér modellje”. A jegyzettel ahhoz szeretnénk segítséget nyújtani, hogy „váratlan”, a szokványos modellekkel le nem írható vegyes, komplex rendszerekkel való találkozás esetében is rendelkezzen az olvasó elegendő „munícióval” az adekvát matematikai modell megalkotásához.
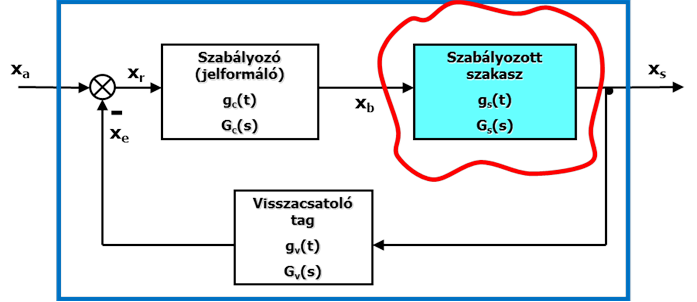
A témához csak két „rajzos” kiegészítést fűzünk. Az egyiken a hagyományos szabályozókört, a másikon az állapotszabályozás egyszerű formáját látjuk. Minkét esetben körvonalaztuk azt a részt, amely rész dinamikai viselkedésének ismerete a kör megtervezésének elengedhetetlen feltétele.
A „tervezés” alatt optimális dinamikával és pontossággal, valamint stabilan működő szabályozókör tervezését értjük.
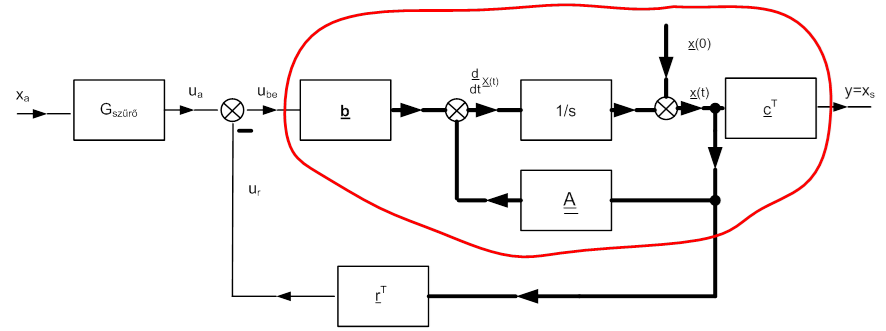
A (3. ábra) ábrán vastagított vonallal a jel-vektorok haladásának irányát jelöltük. Ebben az állapotszabályozásban egy alapjel és egy szabályozott jel van.
Ismeretes talán az is, hogy „mechatronikai rendszerek” alatt nem csak komplett szabályozásokat értünk, hanem a szabályozások egyes „építőköveit”, így az aktuátorokat és a szenzorokat is. Ezért ebben a jegyzetben az aktuátorok és szenzorok dinamikai modelljeivel és tervezésükkel foglalkozó fejezetek megelőzik a jellegzetes szakaszok tervezésével foglalkozó fejezeteket. A szabályozások tervezése és szimulációja sorrendben ezeket követi. A jegyzetet a mechatronika tervezési módszertanával foglalkozó, összefoglaló jellegű fejezet zárja.
Bizonyos mértékű gyakorlati tapasztalattal rendelkezők számára nem szükséges bizonygatnunk, hogy a modell soha nem képes a valóságot teljes komplexitásában leírni. Mindig annak egy részét, vagy bizonyos aspektusait ragadjuk ki, esetenként leegyszerűsítjük a valóságot. A jelenségekről alkotott fizikai elképzeléseink korlátozottak, sok a bizonytalansági forrás. A modell mindig célorientált. Bonyolultságát a megoldandó feladat jellege, a műszaki feltételek, az ésszerűség és gyakran az anyagi lehetőségek korlátozhatják. A mérnöki gyakorlatban a modellek a kutatást, a tervezést és az elemzést segítik, és ide sorolhatók a szabályozott szakaszok leírásához alkalmazott modellek is.
A modellezés során gyakran körül kell határolni a valós rendszernek azt a részét, amellyel az adott feladat megoldása érdekében foglalkoznunk kell. Ez a rész általában un. „zárt rendszert” képez, és ez a modellezési problémáink első forrása. A valóságban a műszaki rendszerek nem zártak, a környezettel és más rendszerekkel kölcsönhatásban állnak. Ezeket a hatásokat bizonyos mértékben természetesen figyelembe lehet, és kell is venni, de a teljesség igénye nélkül. A modellalkotónak tudnia kell azt is, hogy a zárt és nyitott rendszer fogalmát a különböző szakterületek részben eltérően értelmezik, így például a hőtan és a villamosságtan.
A méréstechnikában például egy modell megalkotásához a vizsgálat kezdetén rendelkezésre álló ismeretek összességét „à priori” ismereteknek nevezik. A modellezési és mérési munka végeztével ismereteink jelentősen bővülnek, és ezek következtében immár „à posteriori” információkkal is rendelkezünk. Az à priori ismeretek meghatározóak a modell minősége szempontjából, mert meghatározzák a modell típusát, bonyolultságát, a megkívánt pontosságot, és a költségeket, és ezek következtében magát a mérési eljárást és a mérés kivitelezését is. A korábban ismertetett modellformákra közösen vonatkozik, hogy szükséges egy struktúra és szükségesek hozzá paraméterek. E tekintetben mindegy ugyanis, hogy fizikai, funkcionális, vagy matematikai modellről van szó.
A legnagyobb probléma az, hogy az à priori ismeretek gyakran nem elegendőek a struktúra kiválasztására. Ebben még igen nagy a szerepe a mérnöki tapasztalatnak, a próbáknak és az un. mérnöki intuíciónak. A paraméterek becslésére és identifikációjára már objektívnek tekinthető módszerek állnak rendelkezésre.
A döntően, vagy kizárólagosan à priori ismeretekre támaszkodó modellalkotást „deduktív” szemléletnek, míg az à posteriori ismeretekkel, tehát kísérleti, mérési adatokkal operáló megközelítést „induktív” módszernek nevezik. A rendszertechnikában ez utóbbi módszert méréssel történő identifikációnak nevezik. Normál mérnöki gyakorlatban elvétve alkalmazzák kizárólagosan csak az egyik változatot, mindkettőre szükség van.
A jegyzetben terjedelmi okok miatt nem szerepelnek adaptív mechatronikai berendezések példái, bár ezek a korszerű mechatronikai rendszerekhez hozzátartoznak. Tekintettel azonban arra, hogy modellek az adaptív rendszerek elengedhetetlen részét képezik, a szerzők remélik, hogy a modern szabályozástechnikai irodalomban fellelhető modellek megértéséhez és esetleges adaptációjához is segítséget fog tudni nyújtani a jegyzet.
|
A szerzők |