17. fejezet - Vonóelemes pozícionáló szabályozásának tervezése és szimulációja
Vissza		Előre

17. fejezet - Vonóelemes pozícionáló szabályozásának tervezése és szimulációja

Tartalom

A 10. fejezet fejezetben szereplő vonóelemes mozgásátalakító matematikai modell struktúrájának előállítására mutatunk egyet a lehetséges módszerek közül.

A matematikai modell (átviteli függvény) paraméterezéséhez katalógusból válogatott adatokat használunk.

A matematikai modellel adott rendszer dinamikai (idő- és frekvenciatartománybeli) vizsgálata után szabályozót tervezünk, az ilyen jellegű valóságos rendszerekkel szemben támasztott irányítási célok figyelembe vételével. Elsődleges elvárás természetesen a stabilitás, mégpedig aperiodikus viselkedéssel, túllendülések nélküli, gyors és pontos (hibamentes) alapjel követéssel.

A megoldásban bemutatunk az egyszerűsített linearizált vonóelemes átalakító mellett egy a valóságot jobban tükröző nemlineáris struktúrát. A linearizált modellhez „hagyományos” (PID struktúrájú), a nemlineárishoz pedig állapotvisszacsatolásos szabályozást tervezünk.

17.1. Matematikai modell előállítása

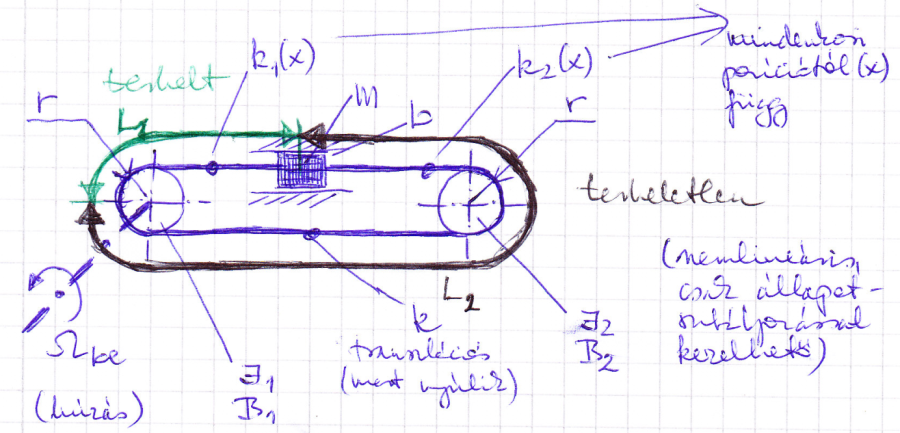
17.1. ábra - A rendszer felépítése a figyelembe vett fizikai jellemzőkkel

A rendszer működését ábrázoló „műszaki vázlat” alapján elkészíthetjük a struktúragráfot. A DC-motorból, hajtóműből, rugalmas tengelykapcsolóból, valamint a vonóelemes mozgatóból (két tárcsa, szíj és mozgatott tömeg) álló rendszer struktúragráfja az alábbi ábrán látható.

17.2. ábra - A rendszer vázlata alapján készített struktúragráf

Az ábrákon (és a további modellekben) szereplő fizikai mennyiségek:

u	[V]	feszültség
R	[Ω]	ellenállás
L	[H=Vs/A]	induktivitás
n_v1=K_M	[Nm/A=Vs/rad]]	az elektrodinamikai energiaátalakító (váltó) ún. motorállandója
Ω	[rad/s]	szögsebesség (m index a motorra, 0 a hajtómű kimenetére, 1 index a motorral hajtott (r [m] sugarú) szíjtárcsára, 2 index a vonóelemmel mozgatott (szintén r [m] sugarú) szíjtárcsára vonatkozik)
J	[kg m²]	tehetetlenségi nyomaték (a szögsebességhez hasonló indexeléssel)
B	[Ns/rad]	transzlációs mechanikai rendszerben értelmezett csillapítási tényező (a szögsebességhez és a tehetetlenségi nyomatékhoz hasonló indexeléssel)
n_t = i		a hajtómű mint energiaátalakító (transzformátor) állandója (módosítás)
K_t	[Nm/rad]	a tengelykapcsoló torziós rugómerevsége
n_v2=r	[m]	a forgó és haladó mozgás közötti energiaátalakító (váltó) állandója, a szíjtárcsa sugara
m	[kg]	a szíjjal mozgatott tömeg
b	[Ns/m]
k	[N/m]	a szíj alsó részében a megnyúlás miatt értelmezhető transzlációs rugómerevség
k₁	[N/m]	a vonóelem (bordásszíj) húzott ágában értelmezett, az elmozdulástól függő transzlációs rugómerevség
k₂	[N/m]	a vonóelem (bordásszíj) húzott ágában értelmezett, az elmozdulástól függő transzlációs rugómerevség
n_v3=1/r	[1/m]	a haladó és forgó mozgás közötti energiaátalakító (váltó) állandója
L₁	[m]	a terhelt szíjhossz
L₂	[m]	a terheletlen szíjhossz

Ugyan már a vázlatban is alkalmaztunk elhanyagolásokat (például a tengelykapcsolóban fellépő súrlódási veszteséget elhanyagoljuk, B_H → 0), de modellünk még mindig igen összetett. Az energiatárolók száma a struktúragráf alapján, egyelőre összevonások nélkül: egy villamos (L), egy torziós rugalmas (K), négy torziós tehetetlenség (J), egy transzlációs mechanikai (m), valamint három transzlációs rugalmas (k). Utóbbiak közül kettő nemlineárisként modellezett. Összesen tíz energiatárolót számolhatunk össze, így gyakorlatilag analitikus módszerekkel kezelhetetlen magasabb rendű rendszermodellt kapunk.

17.2. Egyszerűsített modell

Az összevonható mennyiségek és az egyes részegységek sajátságai figyelembe vételével egyszerűsíthetjük a gráfot.

a DC motor induktivitása mint energiatároló a rendszerben lévő többi tárolóhoz képest gyors dinamikájú (nagyságrendekkel kisebb időállandójú), ezért elhanyagoljuk
a transzlációs rugalmasságokat a 10. fejezet fejezetben ismertetett egyszerűsítéssel linearizáljuk és összevonjuk

$k_{e} = k_{s p} \cdot h \cdot \frac{L_{1} + L_{2}}{L_{1} \cdot L_{2}} = k_{s p} \cdot h \cdot (\frac{1}{L_{1}} + \frac{1}{L_{2}})$

(17.1)

ahol k_SP [N/mm] a vonóelem (szíj) egy milliméter szélességére vonatkoztatott specifikus rugómerevség, h [mm] a vonóelem szélessége, L₁ [mm] a húzott (terhelt) ág hossza, L₂ [mm] a terheletlen ág hossza

17.3. ábra - Az első egyszerűsítés eredménye: induktivitás elhanyagolása és transzlációs rugalmasság összevonása

További egyszerűsítést tesz lehetővé a megfelelően kicsi tehetetlenségű nyomatékú szíjtárcsák választása, így a 2 indexű szíjtárcsát elhagyhatjuk a gráfból. Hasonló megfontolás alapján a hajtott (1 indexű) szíjtárcsát szintén elhanyagolhatjuk.

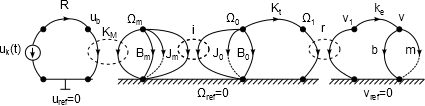
17.4. ábra - Második egyszerűsítés: a kis tehetetlenségi nyomatékú szíjtárcsák elhagyása

A következő lépésben transzlációssá alakítjuk a motort követő rotációs mechanikai részrendszert, így a struktúragráf a DC-motor és hajtómű egységre (hajtó részrendszer) és a transzlációs mechanikai rendszerként modellezett vonóelemes egységre (hajtott részrendszer) választható szét, amennyiben a hajtómű módosítása kellően nagy.

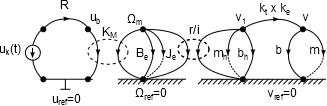
17.5. ábra - Motor-hajtómű egység és vonóelemes mozgatás részrendszere

17.2.1. A hajtó részrendszer modellje

A motor-hajtómű egység működését hálózati módszerrel írjuk fel, ehhez az időtartománybeli jeleket átírjuk Laplace-operátoros tartományba.

Az elektrodinamikai energiaátalakító (váltó) egyenletei

	$Ω_{m} (s) = \frac{1}{K_{M}} \cdot U_{0} (s)$	(17.2)
	$M_{v} (s) = - K_{M} \cdot I_{a} (s)$	(17.3)

A villamos részre felírható hurokegyenlet

$- u_{k} (t) + u_{R} + u_{0} = 0$

(17.4)

Az ellenállásra eső feszültség egyenletét és a megfelelő (indukált feszültség – szögsebesség kapcsolatot megadó) váltóegyenletet behelyettesítve

$- u_{k} (t) + i \cdot R + K_{M} \cdot Ω_{m} = 0$

(17.5)

A forgó mechanikai részre csomóponti egyenletet írunk fel, ahol M_v a másik váltóegyenlettel meghatározott „villamos” nyomaték, M_t a terhelésből származó nyomaték

$M_{v} + M_{B} + M_{J} + M_{t} = 0$

(17.6)

Behelyettesítve

$- K_{M} \cdot i + B_{e} \cdot Ω_{m} + J_{e} \cdot \frac{d Ω_{m}}{d t} = - M_{t}$

(17.7)

Laplace-transzformálva

$\begin{array}{l} i (s) \cdot R + K_{M} \cdot Ω_{m} (s) = u_{k} (s) \\ - K_{M} \cdot i (s) + B_{e} \cdot Ω_{m} (s) + s \cdot J_{e} \cdot Ω_{m} (s) = - M_{t} (s) \end{array}$

(17.8)

Mátrixegyenletként felírva

$[\begin{matrix} R & K_{M} \\ - K_{M} & (B_{e} + s \cdot J_{e}) \end{matrix}] [\begin{matrix} i (s) \\ Ω_{m} (s) \end{matrix}] = [\begin{matrix} u_{k} (s) \\ - M_{t} (s) \end{matrix}]$

(17.9)

Mivel a rendszer visszahatásmentes, M_t=0. Ezt szem előtt tartva például Cramer-szabállyal fejezhetjük ki Ω_m értékét, majd a körfrekvencia és feszültség között felírható átviteli függvényt

$Ω_{m} (s) = \frac{| \begin{matrix} R & u_{k} (s) \\ - K_{M} & 0 \end{matrix} |}{| \begin{matrix} R & K_{M} \\ - K_{M} & (B_{e} + s \cdot J_{e}) \end{matrix} |} = \frac{u_{k} (s) \cdot K_{M}}{R \cdot (B_{e} + s \cdot J_{e}) + K_{M}^{2}}$

(17.10)

A motor-hajtómű rendszer átviteli függvénye

$G_{h a j t ó, Ω} (s) = \frac{Ω_{m} (s)}{u_{k} (s)} = \frac{K_{M}}{R \cdot (B_{e} + s \cdot J_{e}) + K_{M}^{2}} = \frac{\frac{K_{M}}{R \cdot B_{e} + K_{M}^{2}}}{s \cdot \frac{R \cdot J_{e}}{R \cdot B_{e} + K_{M}^{2}} + 1}$

(17.11)

A szögsebesség és sebesség közötti kapcsolat

$Ω_{m} (s) = \frac{i}{r} \cdot v_{1} (s)$

(17.12)

A vonóelemes mozgató hajtott szíjtárcsájára értelmezett transzlációs sebesség és a motorra kapcsolt feszültség közötti átviteli függvény egytárolós arányos jellegű

$G_{h a j t ó} (s) = \frac{v_{1} (s)}{u_{k} (s)} = \frac{\frac{K_{M} \cdot r}{i \cdot (R \cdot B_{e} + K_{M}^{2})}}{s \cdot \frac{R \cdot J_{e}}{R \cdot B_{e} + K_{M}^{2}} + 1} = \frac{A}{s T_{1} + 1}$

(17.13)

A hajtó részrendszerre vonatkozó katalógusadatok és az azokból számított, a szimulációs modellhez szükséges erősítési tényező és időállandó

17.1. táblázat - A hajtó részrendszer átviteli függvény számításához használt értékek

Elektromechanikus energiaátalakító (váltó) állandója	K_M = 8,64⋅10^-3 (N⋅m)/A
Motor ellenállása	R = 24 Ω
Hajtómű módosítása	i = 76
A motor és hajtómű tehetetlenségi nyomatéka	J_e = 5,9⋅10^-8 kg⋅m²
A motor és hajtómű csillapítási tényezője	B_e = 1,1⋅10^-6 (N⋅m⋅s)/rad
A szíjtárcsa sugara	r = 4,82⋅10^-3 m

	$A = \frac{K_{M} \cdot r}{i \cdot (R \cdot B_{e} + K_{M}^{2})} = 5,423 \cdot 10^{- 3}$
	$T_{1} = \frac{R \cdot J_{e}}{R \cdot B_{e} + K_{M}^{2}} = 1,401 \cdot 10^{- 2}$
	$G_{h a j t ó} (s) = \frac{v_{1} (s)}{u_{k} (s)} = \frac{\frac{K_{M} \cdot r}{i \cdot (R \cdot B_{e} + K_{M}^{2})}}{s \cdot \frac{R \cdot J_{e}}{R \cdot B_{e} + K_{M}^{2}} + 1} = \frac{A}{s T_{1} + 1} = \frac{5,423 \cdot 10^{- 3}}{1,401 \cdot 10^{- 2} \cdot s + 1}$	(17.14)

17.2.2. A hajtott részrendszer modellje

A hajtott részrendszer modellezése során a hajtó rendszert keresztváltozó (sebesség) forrással helyettesítjük, ezért az azzal párhuzamosan kapcsolt rotációsból transzlációsba redukált tömeget és csillapítást elhagyhatjuk, mert erre a két elemre rákényszerítjük a forrás előírt értékét.

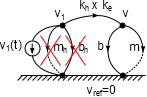
17.6. ábra - A hajtott részrendszer, a hajtó részrendszert sebesség-forrással helyettesítve

A sorba kapcsolt forgóból transzlációsba redukált tengelykapcsoló és az egyszerűsített vonóelem rugalmasság eredőjét jelöljük k_r-rel. A sorosan kapcsolt rugók eredőjét reciprokok összegével számíthatjuk, jelen esetben két rugó eredőjénél az „x”-el jelölt „replusz” módszerrel számíthatjuk

$k_{r} = k_{t} \times k_{e} = \frac{k_{t} k_{e}}{k_{t} + k_{e}} = \frac{K_{t}}{r^{2}} \times k_{e} = \frac{\frac{K_{t}}{r^{2}} k_{e}}{\frac{K_{t}}{r^{2}} + k_{e}}$

(17.15)

Csomóponti egyenletet felírva határozzuk meg az átviteli függvényt

$- f_{k} + f_{m} + f_{b} = 0$

(17.16)

Kifejtve

$- k_{r} \int (v_{1} - v) d t + m \frac{d v}{d t} + b \cdot v (t) = 0$

(17.17)

Laplace-transzformálva és átrendezve

$\frac{k_{r}}{s} \cdot v (s) + m \cdot s \cdot v (s) + b \cdot v (s) = \frac{k_{r}}{s} \cdot v_{1} (s)$

(17.18)

A hajtott rendszer másodrendű, átviteli függvénye

$G_{h a j t o t t} (s) = \frac{v (s)}{v_{1} (s)} = \frac{\frac{k_{r}}{s}}{\frac{k_{r}}{s} + m \cdot s + b} = \frac{k_{r}}{m \cdot s^{2} + b \cdot s + k_{r}} = \frac{1}{\frac{m}{k_{r}} \cdot s^{2} + \frac{b}{k_{r}} \cdot s + 1}$

(17.19)

A hajtott részrendszerre vonatkozó katalógusadatok és az azokból számított, a szimulációs modellhez szükséges erősítési tényező és időállandó

17.2. táblázat - A hajtott részrendszer átviteli függvény számításához használt értékek

A terhelt szíjhossz	L₁ = 0,15 m
A terheletlen szíjhossz	L₂ = 3⋅L₁+2⋅r⋅π = 0,48 m
A szíj szélessége	h = 6 mm
A szíj specifikus rugómerevsége	k_sp = 9155 N/mm
A szíjtárcsa sugara	r = 4,82⋅10^-3 m
A tengelykapcsoló torziós rugómerevsége	K_t = 23 (N⋅cm)/rad
A mozgatott tömeg	m = 0,1 kg
A mozgatott tömeghez kapcsolt csillapítás	b = 5⋅10^-3 (N⋅s)/m

	$k_{e} = k_{s p} \cdot h \cdot \frac{L_{1} + L_{2}}{L_{1} \cdot L_{2}} = 4,80638 \cdot 10^{5} \frac{N}{m}$
	$k_{r} = k_{h} \times k_{e} = \frac{K_{t}}{r^{2}} \times k_{e} = 9,7 \cdot 10^{3} \frac{N}{m}$
	$A = 1$
	$T = \sqrt{\frac{m}{k_{r}}} = 3,21 \cdot 10^{- 3}$
	$ξ = \frac{b}{k_{r} \cdot 2 \cdot \sqrt{\frac{m}{k_{r}}}} = 8,027 \cdot 10^{- 5}$
	$G_{h a j t o t t} (s) = \frac{v (s)}{v_{1} (s)} = \frac{1}{\frac{m}{k_{r}} \cdot s^{2} + \frac{b}{k_{r}} \cdot s + 1} = \frac{1}{s^{2} T^{2} + 2 ξ T s + 1}$	(17.20)

A modellben szándékosan választottunk a fogazott szíj esetében olyan valósághoz közeli értékű rugómerevséget, ami az adott mozgatott tömeggel jól érzékelhető rezonanciát eredményez. A szabályozás egyik célja éppen ennek a rezonancia-hajlamnak a megszűntetése.

17.2.3. A teljes rendszer átviteli függvénye

A rendszer átviteli függvénye a hajtó és a hajtott részrendszer soros eredője kiegészítve egy integrátorral, hiszen eddig a mozgatott rendszer sebességével számoltunk, de valójában az elmozdulásra vagyunk kíváncsiak, pozíciószabályozásról lévén szó.

$G (s) = \frac{x (s)}{u_{k} (s)} = G_{h a j t ó} (s) \cdot G_{h a j t o t t} (s) = \frac{v_{1} (s)}{u_{k} (s)} \cdot \frac{v (s)}{v_{1} (s)} \cdot \frac{1}{s} = \frac{A}{s T_{1} + 1} \cdot \frac{1}{s^{2} T^{2} + 2 ξ T s + 1} \cdot \frac{1}{s}$

(17.21)

A LabVIEW 2009-ben készített szimulációs modellhez ismét a paraméteres átviteli függvény megadást választjuk. Az átviteli függvény együtthatók esetenként igen bonyolult összefüggését nem kézzel, hanem a Maxima programmal számoljuk. A Maxima által „számított” kifejezéseket egyszerűen kijelölve, majd a vágólapra másolva a LabVIEW megfelelő mezőibe illeszthető kifejezéseket kapunk, ahogyan ez az alábbi ábrán is látható (itt a Jegyzettömb programba illesztettük a másolt wxMaxima eredményeket). A pi kifejezést helyettesítjük π=3,14159265359 tetszőleges pontosságú értékével.

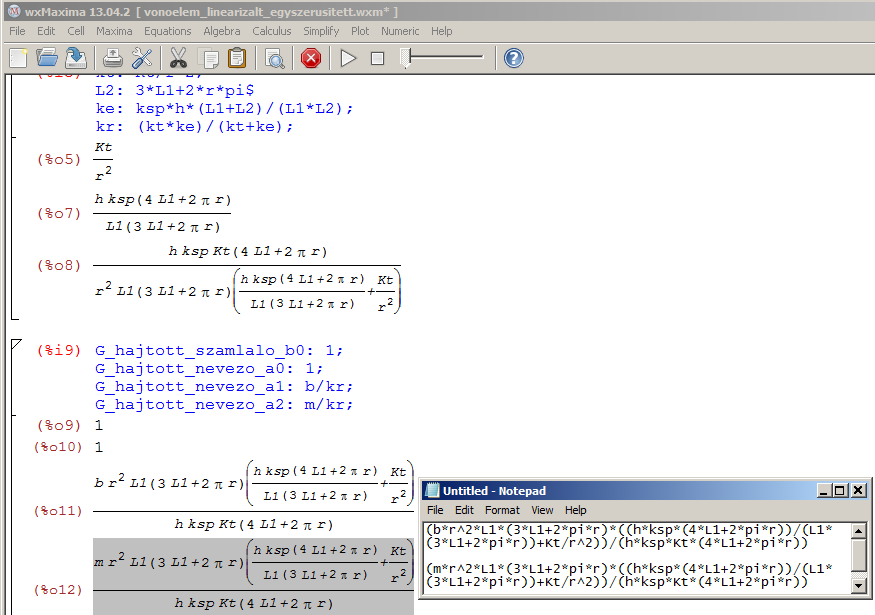
17.7. ábra - Az átviteli függvény együttható formulákat „számító” wxMaxima programrészlet és a Jegyzettömbbe másolt paraméteres összefüggések

A képleteket és a paraméterek értékét bemásolva LabVIEW programunkba megkapjuk a szabályozó tervezéséhez szükséges szakasz átviteli függvényt. Célszerű a sebesség-pozíció konverzióhoz szükséges integrálást egyelőre kihagyni az átviteli függvényből. LabVIEW-ban egyszerűen ábrázolhatjuk a jellegzetes időtartománybeli válaszokat (a súlyfüggvényt és az átmeneti függvényt), a pólus-zérus térképet és a pólusok értékét, valamint frekvenciatartománybeli jellemző diagramokat (Bode és Nyquist).

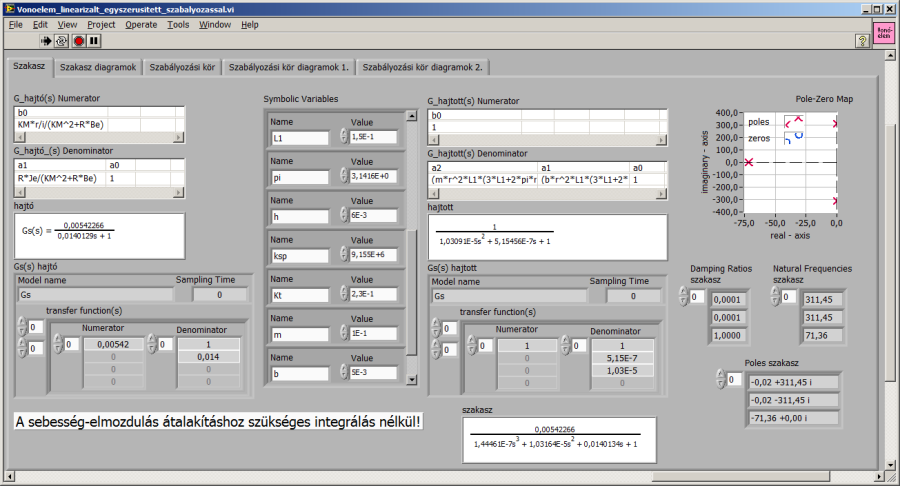
17.8. ábra - LabVIEW-ban számított átviteli függvény, integrálás nélkül, valamint a pólus-zérus térkép a pólusok adataival

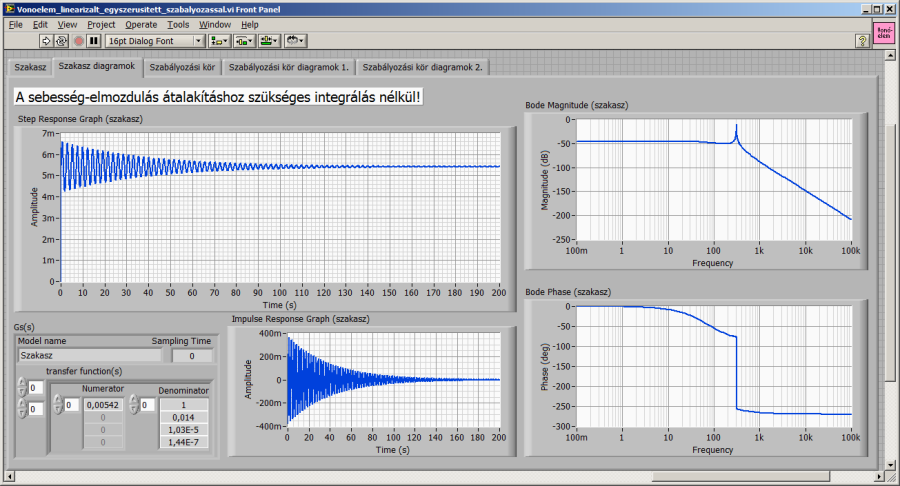
17.9. ábra - Szakasz átmeneti függvénye és súlyfüggvénye, Bode- és Nyquist diagramja

Az átmeneti függvényből és a póluseloszlásból egyértelműen látszik, hogy a harmadrendű rendszer erősen lengő, a feladatnak nem felel meg dinamikai viselkedése (ld. fentebb). Vonóelemes mozgatásnál aperiodikus, gyors és pontos beállást várunk.

17.2.4. Szabályozó tervezés

Először megvizsgáljuk a – most már integráló tulajdonsággal kiegészített – szakasz viselkedését a negatív visszacsatolású „szabályozási” körben, szabályozó nélkül.

17.10. ábra - Szakasz a negatív visszacsatolású szabályozási körben egyelőre szabályozó nélkül

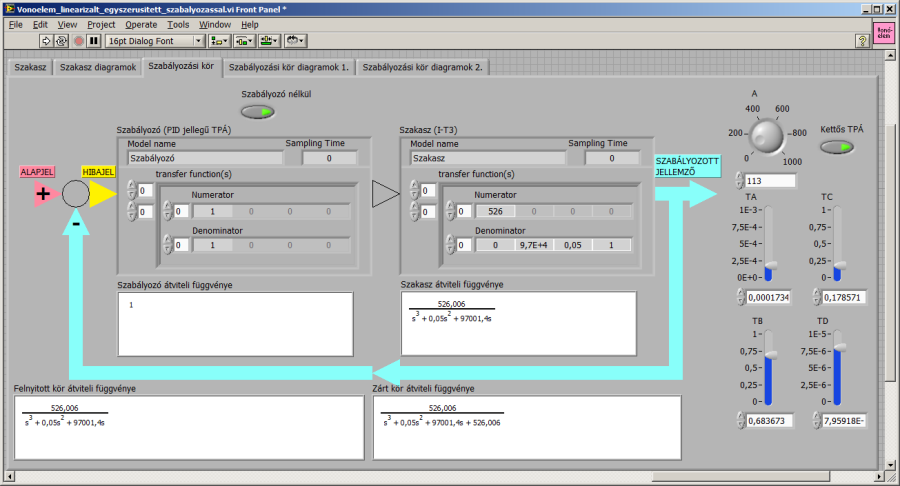
Ha a szabályozót elhagyjuk (egységnyi átviteli tulajdonsággal helyettesítjük), a szakasz és a felnyitott kör átviteli függvénye megegyezik, így egybeesik Bode diagramjuk is.

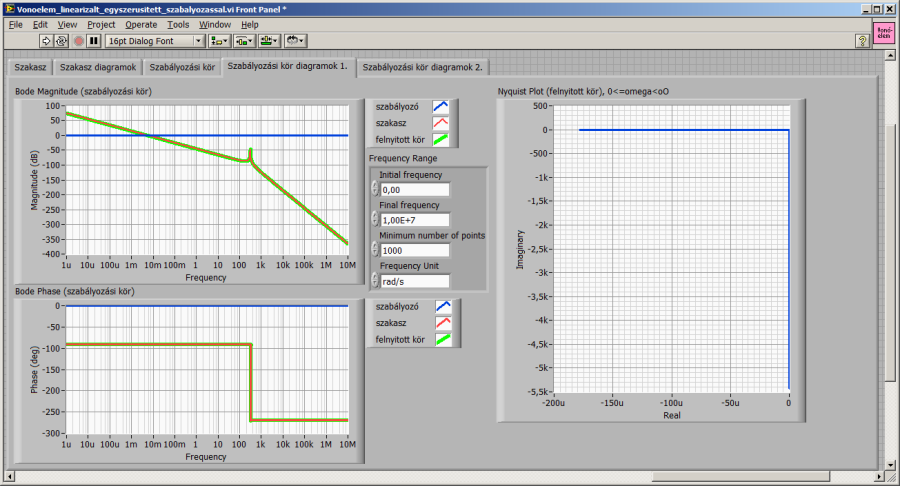
17.11. ábra - Szakasz a negatív visszacsatolású szabályozási körben egyelőre szabályozó nélkül, frekvenciatartománybeli diagramok

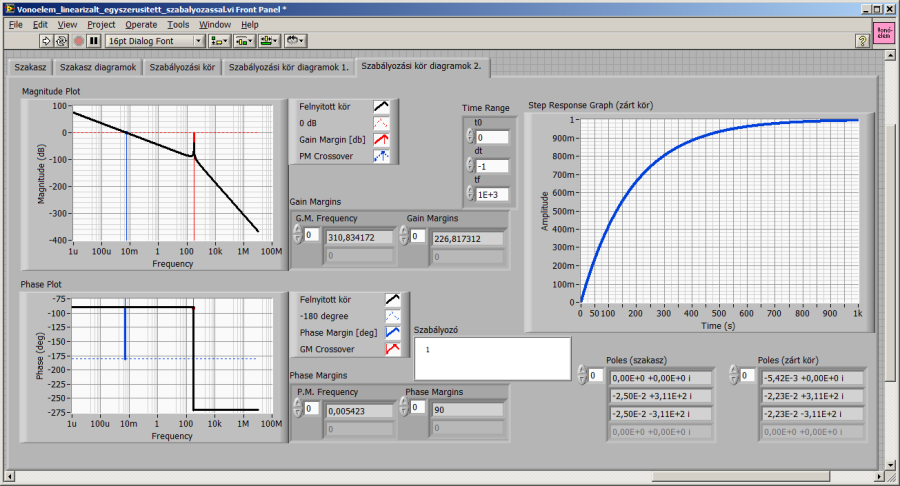
17.12. ábra - Tartalékok a szabályozási körben, valamint a zárt kör átmeneti függvénye egységnyi arányos szabályozóval

Már a fázistartalék értéke alapján is sejthetjük, az átmeneti függvény pedig bizonyítja, hogy az erősen lengő szakaszt aperiodikus beállásúra változtatta a negatív visszacsatolás, azonban a „szabályozott” rendszer igencsak lelassult. A (17.9. ábra) ábrán a szakasz átmeneti függvénye 320 időegységnél „fejeződik be”, a LabVIEW CD Step response.vi automatikusan állította be az ábrázolás határát. Ugyanezzel a megoldással az egységnyi arányos szabályozóval kiegészített szakasz átmeneti függvényét kb. 1500 időegységig ábrázolja a program (17.12. ábra).

Célszerű soros integráló hatás nélküli PID-jellegű szabályozó struktúrát választani, hiszen az a szakaszban már van. Így a szakasz másodrendű lengő részében (a stabilitás szempontjából meghatározó domináns póluspárnál) helyezzük el a pólusokat áthelyező szabályozót.

A választott PID-jellegű struktúra a kettős töréspontáthelyező algoritmus. A szakasz két töréspontját (pólusát) a szabályozó két (a T_A és T_C időállandónak megfelelő) zérusa kompenzálja, az előírt dinamikai tulajdonságokat biztosító felnyitott szabályozási körbeli gyököket pedig a szabályozó (T_B és T_D időállandónak megfelelő) zérusai adják. Az A_c erősítési tényezővel biztosíthatjuk, hogy a vágási körfrekvencia az előírt stabilitási és gyorsasági feltételeket biztosítsa. A szakaszban lévő integráló tulajdonság miatt az ugrásszerű alapjelet a szabályozás mindenképpen hiba nélkül követi.

$G_{c} (s) = A_{c} \cdot \frac{1 + T_{A} \cdot s}{1 + T_{B} \cdot s} \cdot \frac{1 + T_{C} \cdot s}{1 + T_{D} \cdot s}$

(17.22)

A szakasz (egyszerűsített) átviteli függvény egy elsőrendű és egy lengő másodrendű, valamint a sebesség-pozíció átalakítás miatti integráló tag soros eredőjeként felírva

$G_{s} (s) = \frac{A_{s}}{(1 + T_{1} \cdot s) \cdot (1 + 2 ξ T s + T^{2} \cdot s^{2})} \cdot \frac{1}{s}$

(17.23)

Az alábbiakban a szabályozó egy lehetséges beállítását látjuk. A zárt kör aperiodikus jellegű, zérus maradó hibát eredményező átmeneti függvénye a szabályozó nélküli állapotnál jelentősen gyorsabb.

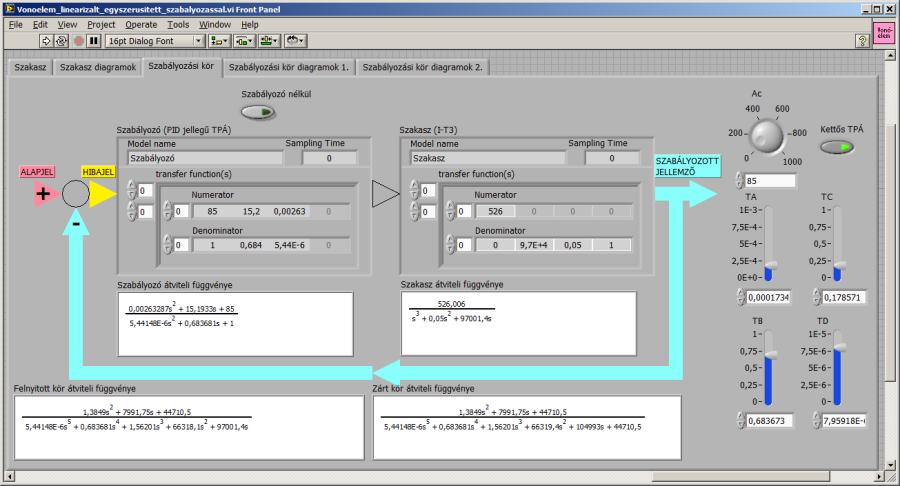
17.13. ábra - A szabályozó egy lehetséges – szükség szerint tovább hangolható – beállítása

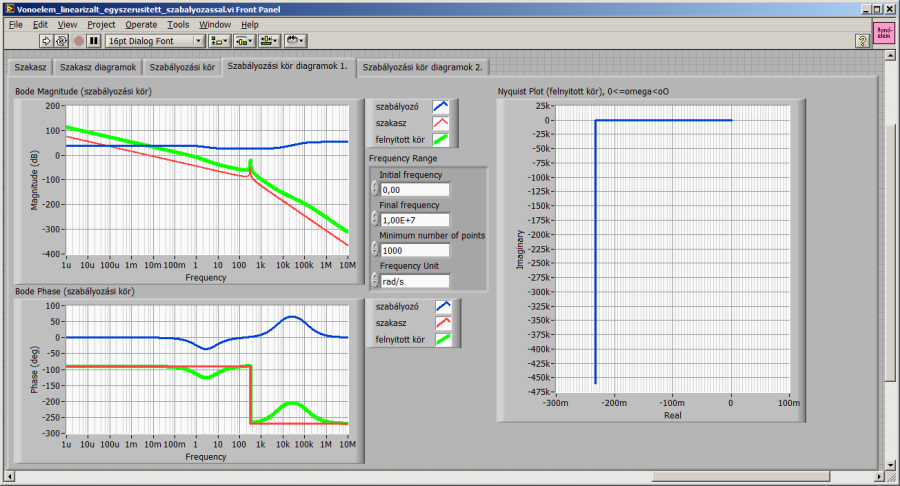
17.14. ábra - A szabályozó egy lehetséges – szükség szerint tovább hangolható – beállításából számított frekvenciatartománybeli diagramok

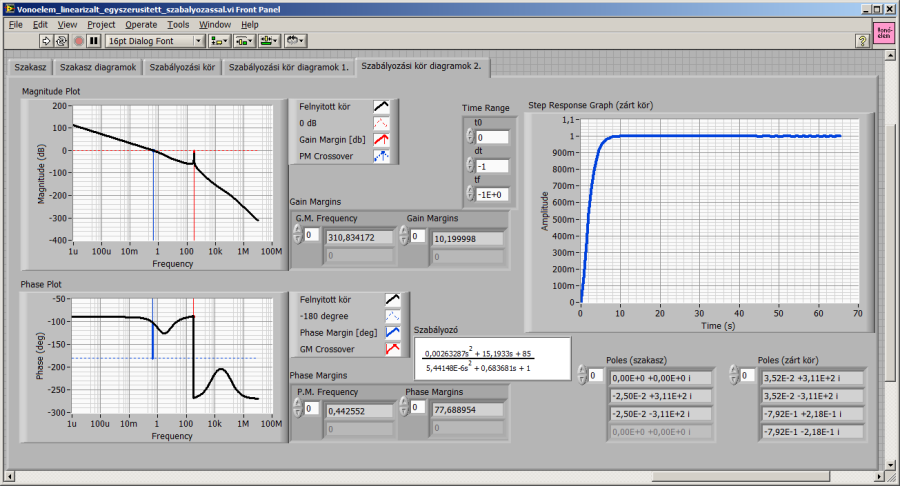
A szabályozó egy lehetséges – szükség szerint tovább hangolható – beállításából számított és ábrázolt tartalékok, valamint a zárt kör átmeneti függvénye

17.15. ábra - A szabályozó egy lehetséges – szükség szerint tovább hangolható – beállításából számított és ábrázolt tartalékok, valamint a zárt kör átmeneti függvénye

Az igényeknek megfelelően tovább változtathatjuk a szabályozó öt paraméterét, természetesen a szabályozáselméletben megismert elveket szem előtt tartva.

17.3. Teljes nemlineáris modell

A szíj pozíciótól függő rugalmasságát a 12. fejezet fejezetben ismertetett elvek alapján vesszük figyelembe. A megfelelően átalakított struktúragráf az alábbiakban látható.

17.16. ábra - A pozíciótól függő rugalmasságot tartalmazó struktúragráf

A korábbi megfontolásokhoz hasonlóan állítjuk elő – továbbra is visszahatásmentes hajtóművet feltételezve – a motor-hajtómű („mh”) részrendszer modelljét. Most nem a hajtott tárcsa v₁ kerületi sebessége és a motorra kapcsolt u_k feszültség közötti átviteli függvényt írjuk fel, a transzlációs v₁ sebesség helyett az Ω₁ szögsebességet használjuk.

$G_{m h} (s) = \frac{Ω_{1} (s)}{u_{k} (s)} = \frac{1}{r} \cdot \frac{v_{1} (s)}{u_{k} (s)} = \frac{1}{r} \cdot \frac{\frac{K_{M} \cdot i \cdot r}{R \cdot B_{e} + K_{M}^{2}}}{s \cdot \frac{R \cdot J_{e}}{R \cdot B_{e} + K_{M}^{2}} + 1} = \frac{\frac{K_{M} \cdot i}{R \cdot B_{e} + K_{M}^{2}}}{s \cdot \frac{R \cdot J_{e}}{R \cdot B_{e} + K_{M}^{2}} + 1} = \frac{A_{m h}}{T_{m h} \cdot s + 1}$

(17.24)

A hajtott tárcsa szögsebességét, tehetetlenségi nyomatékát és torziós csillapítását szintén a korábbi megfontolások alapján a transzlációs rendszerbe redukáljuk. Ezzel az igen egyszerűsített struktúragráf az alábbiak szerint alakul.

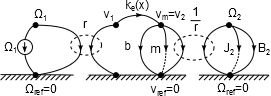
17.17. ábra - A pozíciótól függő rugalmasságot tartalmazó struktúragráf, a hajtó részrendszert szögsebesség forrással helyettesítve

Mivel vizsgálatunkban nem a „2” indexű tárcsa szögsebességére vagyunk kíváncsiak, hanem a mozgatott tömeg v_m sebességére, a forgó rendszert a már ismert elvek alapján redukáljuk. Így be kell vezetnünk az m_e eredő tömeget és a b_e eredő csillapítást az alábbiak szerint

$\begin{array}{l} m_{e} = m + \frac{J_{2}}{r^{2}} \\ b_{e} = b + \frac{B_{2}}{r^{2}} \end{array}$

(17.25)

Ha elhanyagolható a tárcsa tehetetlenségi nyomatéka és csillapítása, az eredő tömeg a mozgatott tömeggel, az eredő csillapítás pedig a mozgatott tömeg súrlódásából adódó csillapítással egyezik meg.

A pozíciótól függő rugalmasság összefüggése a 12. fejezet fejezetben szereplő megfontolások alapján, x_max-al jelölve a teljes mozgatási hosszat, x_m-mel a tömeg méterben mért pozícióját

$\begin{array}{l} k_{e} (x_{m}) = \frac{K}{x_{m} + 0,001} \\ ahol K = x_{\max} \cdot (k_{1} + k_{4}) \end{array}$

(17.26)

17.3.1. A nemlineáris állapottér modell előállítása

A redukált tömeggel és csillapítással felrajzolt struktúragráf és a motor-hajtómű részrendszer átviteli függvénye alapján felírhatjuk a rendszer állapottér modelljét.

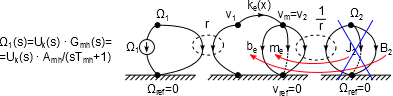
17.18. ábra - A pozíciótól függő rugalmasságot tartalmazó redukált struktúragráf az állapottér modell felírásához

A v_m csomópontra

$- f_{k} (x) + f_{b} + f_{m} = 0$

(17.27)

Az egyes erők

$\begin{array}{l} f_{k} (x) = k_{e} (x_{m}) \cdot \int (v_{1} - v_{m}) d t \\ f_{b} = b_{e} \cdot v_{m} \\ f_{m} = m_{e} \cdot \frac{d v_{m}}{d t} \end{array}$

(17.28)

A hajtott tárcsa szögsebességére és kerületi sebességére vonatkozó összefüggés

$v_{1} = r \cdot Ω_{1}$

(17.29)

A motor-hajtómű rendszer átviteli függvényéből felírt differenciálegyenlet

$T_{m h} \cdot \frac{d Ω_{1}}{d t} + Ω_{1} = A_{m h} \cdot u_{k}$

(17.30)

A mozgatott tömeg pozíciója sebességével kifejezve

$x_{m} = \int v_{m} d t$

(17.31)

Válasszuk az állapotváltozók vektorát az alábbiak szerint

$\underline{x} = {[\begin{matrix} Ω_{1} & v_{m} & f_{k} (x_{m}) & x_{m} \end{matrix}]}^{T}$

(17.32)

Az állapottér modell főegyenlete

$\underline{\dot{x}} = [\begin{matrix} {\dot{Ω}}_{1} \\ {\dot{v}}_{m} \\ {\dot{f}}_{k} (x_{m}) \\ {\dot{x}}_{m} \end{matrix}] = [\begin{matrix} - \frac{1}{T_{m h}} & 0 & 0 & 0 \\ 0 & - \frac{b_{e}}{m_{e}} & \frac{1}{m_{e}} & 0 \\ r \cdot k_{e} (x_{m}) & - k_{e} (x_{m}) & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} (x_{m}) \\ x_{m} \end{matrix}] + [\begin{matrix} \frac{A_{m h}}{T_{m h}} \\ 0 \\ 0 \\ 0 \end{matrix}] \cdot u_{k}$

(17.33)

Az állapottér modell segédegyenletéből csak a tömeg elmozdulására vonatkozó részre van szükségünk

$x_{m} = [\begin{matrix} 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} (x_{m}) \\ x_{m} \end{matrix}] + 0 \cdot u_{k}$

(17.34)

A 12. fejezet fejezetben szereplő adatokkal számíthatjuk az állapottér modell főegyenletében lévő rendszermátrixot és bemeneti vektort.

17.3. táblázat - A hajtó részrendszer átviteli függvény számításához használt értékek (a 12. fejezetből)

Elektromechanikus energiaátalakító (váltó) állandója	K_M = 5·10^-2 (N⋅m)/A
Motor ellenállása	R = 15 Ω
Motor induktivitása elhanyagolható	L → 0
Hajtómű módosítása	i = 1500
A motor és hajtómű tehetetlenségi nyomatéka	J_e = 2,33⋅10^-5 kg⋅m²
A motor és hajtómű csillapítási tényezője	B_e = 10^-3 (N⋅m⋅s)/rad
A tengelykapcsoló torziós rugómerevsége elhanyagolható	K_t → ∞
A motor-hajtómű részrendszer számított erősítési tényezője	A_mh = 5,71·10^-3 rad/(V⋅s)
A motor-hajtómű részrendszer számított időállandója	T_mh = 0,020 s

Az erősítési tényező képlete

$A_{m h} [\frac{r}{V s}] = \frac{1}{i} \cdot \frac{K_{M}}{R \cdot B_{M} + K_{M}^{2}} = \frac{5 \cdot 10^{- 2}}{15 \cdot 10^{2} \cdot (15 \cdot 10^{- 3} + 2,5 \cdot 10^{- 3})} = \frac{5 \cdot 10^{- 2}}{26,25} = 1,90 \cdot 10^{- 3}$

(17.35)

Az időállandó képlete

$T_{m h} [s] = \frac{R \cdot J_{e}}{R \cdot B_{e} + K_{M}^{2}} = \frac{15 \cdot 2,33 \cdot 10^{- 5}}{15 \cdot 10^{- 3} + 2,5 \cdot 10^{- 3}} = \frac{8,85 \cdot 10^{- 7}}{1,75 \cdot 10^{- 2}} = 2 \cdot 10^{- 2}$

(17.36)

A hajtott részrendszer táblázatos adatai között feltüntetjük a négy jellegzetes hosszúságot (a terheletlen ághosszakat) és a hozzájuk tartozó rugómerevséget, valamint a pozíciótól függő rugómerevség összefüggésében szereplő K-val jelölt erő dimenziójú mennyiséget.

17.4. táblázat - A hajtott részrendszer átviteli függvény számításához használt értékek (a 12. fejezetből)

A tárcsák fogszáma	z = 28
A tárcsák fogtávolsága	p = 5 mm
A tárcsák sugara a zp=2rπ kifejezésből	r = zp/(2rπ) = 22,28 mm
„Holt” szakasz	x₀=25 mm
Mozgatási tartomány	x_max=800 mm
A szíj szélessége	h = 10 mm
A szíj specifikus rugómerevsége (a szíj szélesség 1 mm-ére és a szíj 1 mm hosszára)	k_sp = 7,7·10³ N/mm
A szíjtárcsa sugara	r = 4,82⋅10^-3 m
A tengelykapcsoló torziós rugómerevsége elhanyagolható	K_t → ∞
A mozgatott tömeg	m = 2 kg
Súrlódásból adódó csillapítási tényező (tapasztalati érték)	b = 5⋅10^-2 (N⋅s)/m
L ₁ = x _max + x ₀ + r·π/2	L₁ = 860 mm
L ₂ = x ₀ + rπ/2	L₂ = 600 mm
L ₃ = x _max + x ₀ + 2(r·π/2) + 2·x₀ + x_mozg + r·π/2	L₃ = 1780 mm
L ₄ = x ₀ + 2(r·π/2) + 2x₀ + x_max + r·π/2	L₄ = 980 mm
k ₁ = k _sp ·h·L ₁	k₁ = 90 N/mm
k ₂ = k _sp ·h·L ₂	k₂ = 128 N/mm
k ₃ = k _sp ·h·L ₃	k₃ = 43 N/mm
k ₄ = k _sp ·h·L ₄	k₄ = 78 N/mm
K= x _max / (k ₁ + k ₄ )	K = 1,344·10⁵ N

A fenti adatokkal a nemlineáris állapottér modell egyenletei

$\begin{array}{l} \underline{\dot{x}} = [\begin{matrix} {\dot{Ω}}_{1} \\ {\dot{v}}_{m} \\ {\dot{f}}_{k} (x_{m}) \\ {\dot{x}}_{m} \end{matrix}] = [\begin{matrix} - 50 & 0 & 0 & 0 \\ 0 & - 0,025 & 5 & 0 \\ 0,02228 \cdot k_{e} (x_{m}) & - k_{e} (x_{m}) & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} (x_{m}) \\ x_{m} \end{matrix}] + [\begin{matrix} 0,2857 \\ 0 \\ 0 \\ 0 \end{matrix}] \cdot u_{k} \\ x_{m} = [\begin{matrix} 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} (x_{m}) \\ x_{m} \end{matrix}] + 0 \cdot u \end{array}$

(17.37)

17.3.2. A linearizált állapottér modellel adott rendszer vizsgálata

Először a linearizált, pozíciótól nem függő rugómerevségű modellt elemezzük és tervezünk hozzá állapotvisszacsatolásos szabályozót. A linearizált rugómerevséget az L₁ és L₄ ághosszal számoljuk

$k_{e} [\frac{N}{m}] = k_{s p} \cdot h \cdot (\frac{L_{1} + L_{4}}{L_{1} \cdot L_{4}}) = 1,68 \cdot 10^{5}$

(17.38)

Ezzel a linearizált állapottér modell

$\begin{array}{l} \underline{\dot{x}} = [\begin{matrix} {\dot{Ω}}_{1} \\ {\dot{v}}_{m} \\ {\dot{f}}_{k} \\ {\dot{x}}_{m} \end{matrix}] = [\begin{matrix} - 50 & 0 & 0 & 0 \\ 0 & - 0,025 & 5 & 0 \\ 3745,93 & -168106,31 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} \\ x_{m} \end{matrix}] + [\begin{matrix} 0,2857 \\ 0 \\ 0 \\ 0 \end{matrix}] \cdot u_{k} \\ x_{m} = [\begin{matrix} 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} \\ x_{m} \end{matrix}] + 0 \cdot u \end{array}$

(17.39)

A LabVIEW-beli számítást megkönnyíti, ha a sebesség-pozíció miatt szükséges integrálást nem vonjuk be az állapottér modellbe. Mivel a szabályozandó rendszer integráló háromtárolós jellegű, a három tárolónak megfelelő pólusok áthelyezésével foglalkozunk. Az ezt biztosító állapotvisszacsatolásos kompenzációban így csak a három negatív valós részű pólussal (egy valós és egy konjugált komplex gyökpár) foglalkozunk. Az integráló hatásnak megfelelő nulla értékű pólust nem helyezzük át. Emiatt az állapottér modell kimenete a v_m sebesség, amit sorba kapcsolva egy (egységnyi integrálási idejű) integráló taggal ugyanazt az eredményt kapjuk, mintha az integrálást bevonnánk az állapottér modellbe.

$\begin{array}{l} \underline{\dot{x}} = [\begin{matrix} {\dot{Ω}}_{1} \\ {\dot{v}}_{m} \\ {\dot{f}}_{k} \end{matrix}] = [\begin{matrix} - 50 & 0 & 0 \\ 0 & - 0,025 & 5 \\ 3745,93 & -168106,31 & 0 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} \end{matrix}] + [\begin{matrix} 0,2857 \\ 0 \\ 0 \end{matrix}] \cdot u_{k} \\ v_{m} = [\begin{matrix} 0 & 1 & 0 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} \end{matrix}] + 0 \cdot u \end{array}$

(17.40)

Az integrálás nélküli szakasz jellegzetességeit szintén a National Instruments LabVIEW 2009 és a Control Design and Simulation Module segítségével elemezzük.

Először meghatározzuk a szakasz pólusait és ábrázoljuk komplex számsíkbeli elhelyezkedésüket, valamint meghatározzuk a szakasz átmeneti függvényét. Az átmeneti függvény erősen lengő tulajdonságú, ami vonóelemes pozícionálásnál elfogadhatatlan.

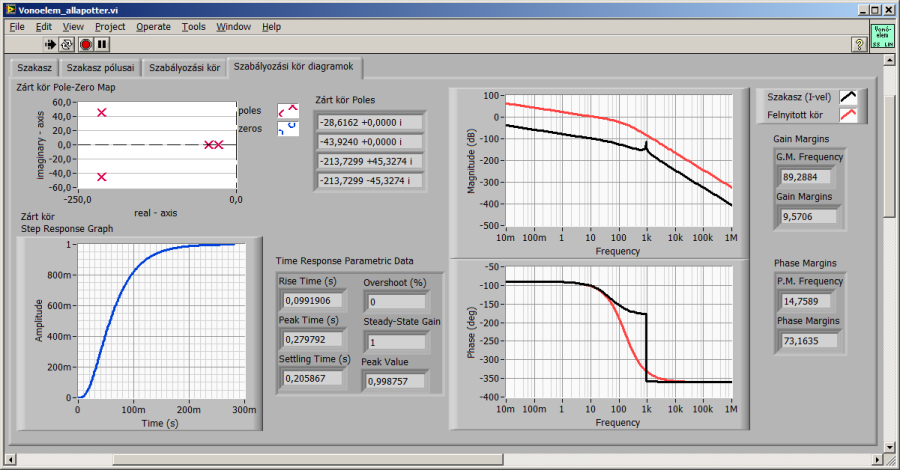
Az integráló tulajdonsággal kiegészített harmadrendű szakaszmodellt felnyitott szabályozási körként kezelve előállítjuk a (szabályozó nélkül vagy egységnyi arányos szabályozóval ellátott) zárt szabályozási kör átmeneti függvényét és pólustérképét. A zárt kör ugyan aperiodikus jellegű és az integráló hatás miatt maradó hiba nélkül követi az egységugrás alapjelet, viszont meglehetősen lassú. (Az automatikusan skálázott átmeneti függvényt a szakasz esetén hozzávetőleg 700, a zárt körnél pedig 70k=70000 időegységig ábrázolja) a program.)

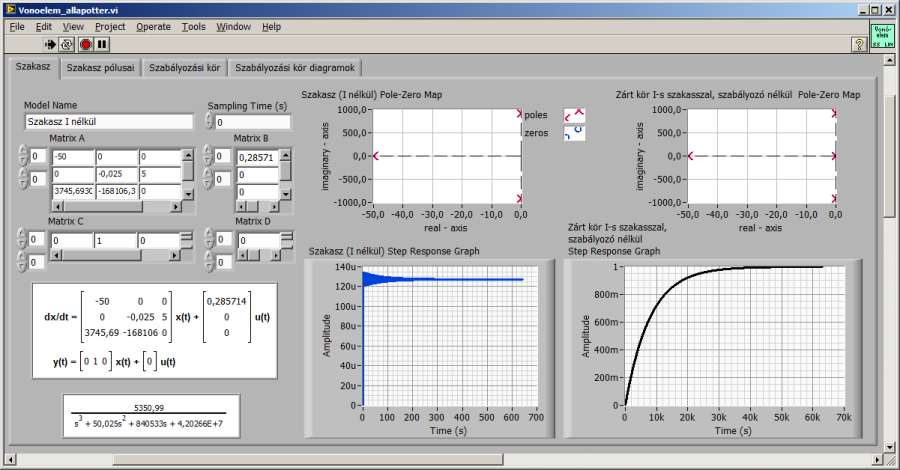
17.19. ábra - Az integrálás nélküli, linearizált állapottér modellel adott szakasz vizsgálata

A LabVIEW program következő – Szakasz pólusai – lapján a vízszintes és függőleges csúszkákkal (vagy digitális kijelzőjükbe közvetlenül beírva a választott értéket) állíthatjuk be a szakasz kívánt pólusait. Kiszámítjuk az eredeti és a megadott pólusokhoz tartozó, egységnyi erősítésűként kezelt átviteli függvényeket és ábrázoljuk egységugrás gerjesztésre adott válaszukat, valamint Bode diagramjukat.

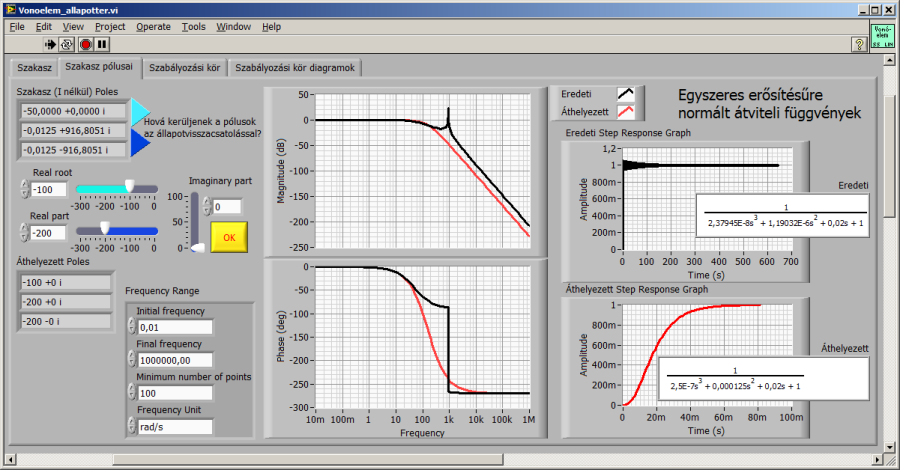
17.20. ábra - Az integrálás nélküli, linearizált állapottér modell eredeti pólusai és a kívánt póluseloszlás

Az új pólusokat megfelelően megválasztva eltüntethetjük a lengő jelleget és gyorsíthatjuk a rendszert. Természetesen a szabályozási körben a sebességből pozícióra áttérést biztosító integrálást is figyelembe vesszük majd.

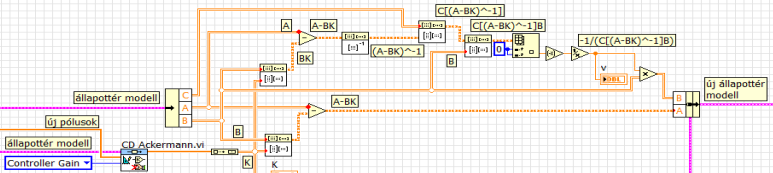
A választott pólusokat biztosító állapotvisszacsatolás K-val jelölt mátrixát a Control Design csomag CD Ackermann.vi blokkjával határozzuk meg. Az Ackermann-képletet alkalmazó számítás bemenete az eredeti (harmadrendű) állapottér modell és a választott pólusok vektora, kimenete pedig az állapotvisszacsatolás mátrixa. Az alábbi ábrán igencsak vázlatos az állapotvisszacsatolás ábrázolása, a pontos összefüggéshez a szakasz általános állapottér modelljét használjuk (ahol a bemenet közvetlenül nem hat a kimenetre).

$\begin{array}{l} \underline{\dot{x}} = \underline{\underline{A}} \cdot \underline{x} + \underline{\underline{B}} \cdot \underline{u} \\ \underline{y} = \underline{\underline{C}} \cdot \underline{x} \end{array}$

(17.41)

17.21. ábra - Az integrálás nélküli, linearizált állapottér modellel adott szakasz vizsgálata

A pólusáthelyezést biztosító állapotvisszacsatolás a v szorzótényező és a K visszacsatoló mátrix segítségével írható fel.

$\begin{array}{l} \underline{\dot{x}} = \underline{\underline{A}} \underline{x} + \underline{\underline{B}} (v \underline{u} - \underline{\underline{K}} \underline{x}) = (\underline{\underline{A}} - \underline{\underline{B}} \underline{\underline{K}}) \underline{x} + v \underline{\underline{B}} \underline{u} = (\underline{\underline{A}} - \underline{\underline{B}} \underline{\underline{K}}) \underline{x} + \frac{- 1}{\underline{\underline{C}} {(\underline{\underline{A}} - \underline{\underline{B}} \underline{\underline{K}})}^{- 1} \underline{\underline{B}}} \underline{\underline{B}} \underline{u} \\ \underline{y} = \underline{\underline{C}} \cdot \underline{x} \end{array}$

(17.42)

17.22. ábra - Az állapotvisszacsatolás paramétereit számító LabVIEW programrészlet

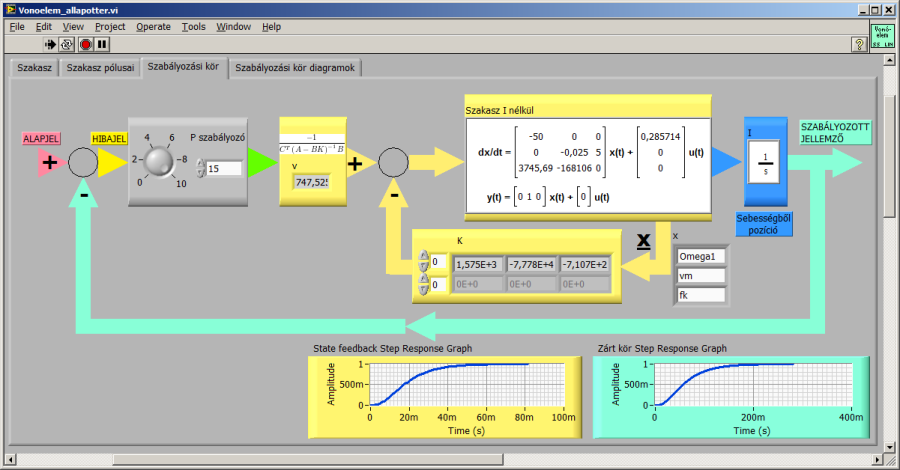
A pólusáthelyezéssel kapott harmadrendű tagot kiegészítjük a sebesség-pozíció konverzió integráló hatásával és egy arányos szabályozót is beiktatunk a körbe, hogy kevesebb „próbálgatással”, gyorsabban kapjunk megfelelő viselkedésű zárt kört. A P-szabályozó létjogosultságát alátámasztja, hogy az integráló tag egységnyi integrálási ideje a zárt kör dinamikai tulajdonságait számunkra kedvezőtlenül befolyásolja, a szabályozó erősítését tulajdonképpen az integrálási idő reciprokának tekinthetjük és ezzel a felnyitott kör Bode-diagramon jól követhető jellegét igényeink szerint alakíthatjuk. Természetesen az állapotvisszacsatolás egyedül is elegendő a szakasztulajdonságok hasonló zárt kör viselkedést eredményező befolyásolására, de komolyabb „fejben számolást” igényel a pólusok eloszlása és az igen könnyen kezelhető szemléletes Bode-diagram kapcsolatának feltérképezése .

A szakasz állapotvisszacsatolásával (és az arányos szabályozóval) megfelelő viselkedésű zárt kört érhetünk el.

A zárt kör átmeneti függvénye és pólustérképe a felnyitott kör (és a kompenzálatlan IT3 szakasz) Bode diagramjával, valamint a tartalékokkal

17.23. ábra - A zárt kör átmeneti függvénye és pólustérképe a felnyitott kör (és a kompenzálatlan IT3 szakasz) Bode diagramjával, valamint a tartalékokkal

A Control & Simulation Loop struktúrában elhelyezett egységugrás jelgenerátorból, arányos szabályozóból, állapottér modellből és a különbségképzővel megvalósított egységnyi negatív visszacsatolásból álló hatásvázlatként adott modellünket szimulációs időlépésenként számítja a LabVIEW a választott differenciálegyenlet megoldóval (példánkban a Runge-Kutta 23-al).

A megoldás – ahogy az alábbi ábrán is látható – a Matlab Simulink nevű, valamint a Scilab Xcos grafikus modellezőjéhez hasonlít.

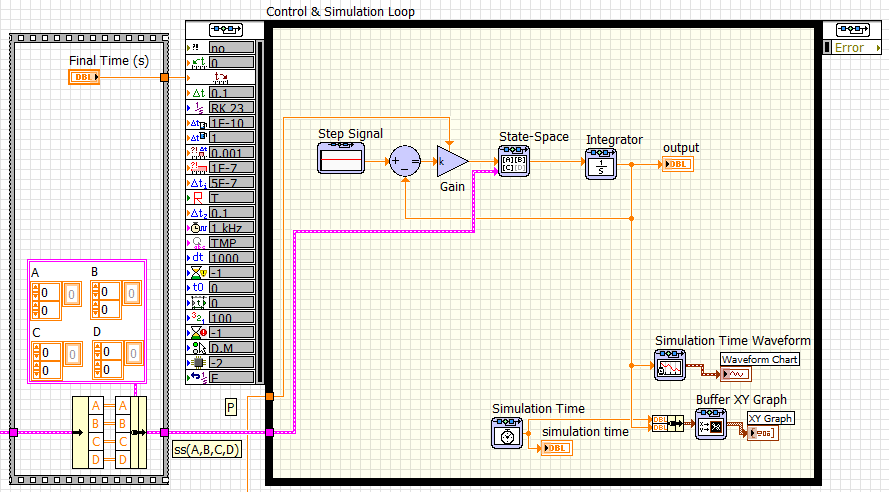
17.24. ábra - A zárt kör átmeneti függvényét számító „blokkdiagram” vagy hatásvázlat a Control & Simulation Loop felhasználásával

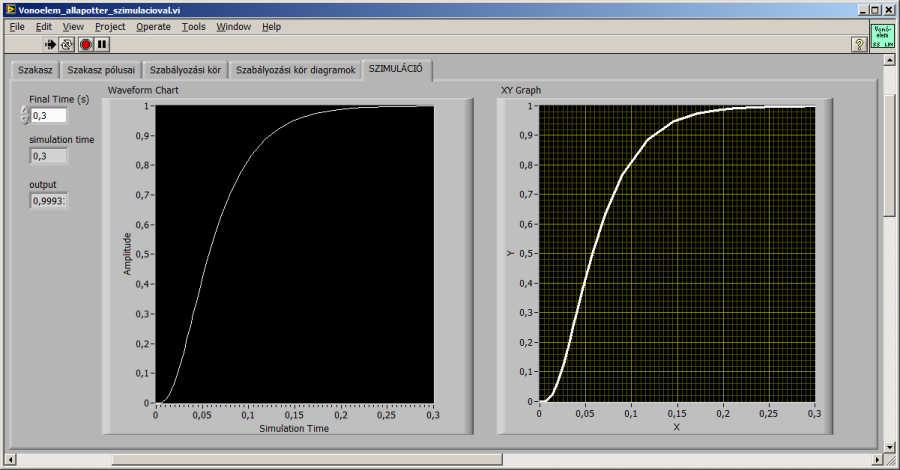
A LabVIEW-beli grafikus rendszermodell eredményei a megszokott módon XY grafikonban és az időlépésenként frissített Waveform Chart (hullámforma diagram) kijelzőn egyaránt ábrázolhatók.

17.25. ábra - A zárt kör átmeneti függvénye a Control & Simulation Loop felhasználásával

17.3.3. A nemlineáris állapottér modellel adott rendszer vizsgálata

A korábbi megfontolásoknak megfelelően a nemlineáris állapottér modellből elhagyjuk az x_m elmozdulásra, mint állapotváltozóra vonatkozó egyenleteket.

$\begin{array}{l} \underline{\dot{x}} = [\begin{matrix} {\dot{Ω}}_{1} \\ {\dot{v}}_{m} \\ {\dot{f}}_{k} (x_{m}) \end{matrix}] = [\begin{matrix} - 50 & 0 & 0 \\ 0 & - 0,025 & 5 \\ 0,02228 \cdot k_{e} (x_{m}) & - k_{e} (x_{m}) & 0 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} (x_{m}) \end{matrix}] + [\begin{matrix} 0,2857 \\ 0 \\ 0 \end{matrix}] \cdot u_{k} \\ v_{m} = [\begin{matrix} 0 & 1 & 0 \end{matrix}] [\begin{matrix} Ω_{1} \\ v_{m} \\ f_{k} \end{matrix}] + 0 \cdot u \end{array}$

(17.43)

Az állapottér modell kimenetének választott v_m elmozdulás integrálásával állítjuk elő az elmozdulást és ezt használjuk fel a rendszermátrix harmadik sorában szereplő elmozdulástól függő rugómerevség számításához. A korábban levezetett összefüggések alapján helyettesítve a rugómerevség kifejezését az állapottér modell mátrixai, pontosabban az (x_m méterben adott elmozdulástól függő) A mátrix, a b oszlopvektor, a c sorvektor és a d skalár az alábbiak.

$\begin{array}{l} A = [\begin{matrix} - 50 & 0 & 0 \\ 0 & - 0,025 & 5 \\ \frac{2996,5545}{x_{m} + 0,001} & \frac{- 134485,04983}{x_{m} + 0,001} & 0 \end{matrix}] \\ B = b = [\begin{matrix} 0,2857 \\ 0 \\ 0 \end{matrix}] \\ C = c = [\begin{matrix} 0 & 1 & 0 \end{matrix}] \\ D = d = 0 \end{array}$

(17.44)

A szimuláció kezdetén az A mátrixba az x_m=0 m kiindulási pozíciónak megfelelő értékeket helyettesítjük.

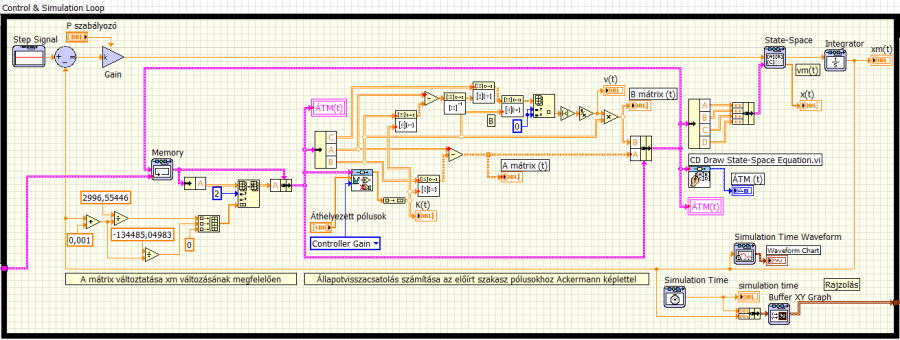
Az előzőleg bemutatott Control & Simulation Loop struktúrában készített lineáris állapottér modellel adott szakaszú szabályozási kör szimulációs modelljéhez hasonlóan vizsgáljuk a nemlineáris rendszert is. Különbséget jelent, hogy minden szimulációs időlépésben kiszámítjuk a rendszermátrix értékét az x_m elmozdulás pillanatnyi értékének felhasználásával. Az így kialakult – A mátrixában változtatott – állapottér modellből és a szakasz előírt pólusaiból az Ackermann-formulával számoljuk az állapotvisszacsatolás A és B mátrixot módosító K mátrixát és v skalárját. A minden szimulációs lépésben kétszeresen módosított állapottér modell négy mátrixát vezetjük be a State-Space szimulációs blokkba. A blokk skalár kimenetét (a mozgatott tömeg v_m sebességét) integrálva kapjuk a tömeg rendszermátrixot befolyásoló x_m elmozdulását.

Az elmozdulás visszacsatolásánál nem keletezik algebrai hurok, mert szimulációs blokkal számított jel visszavezetéséről van szó. (Az algebrai hurok azt jelenti, hogy egy változó értékének kiszámításához magát a változót használjuk fel).

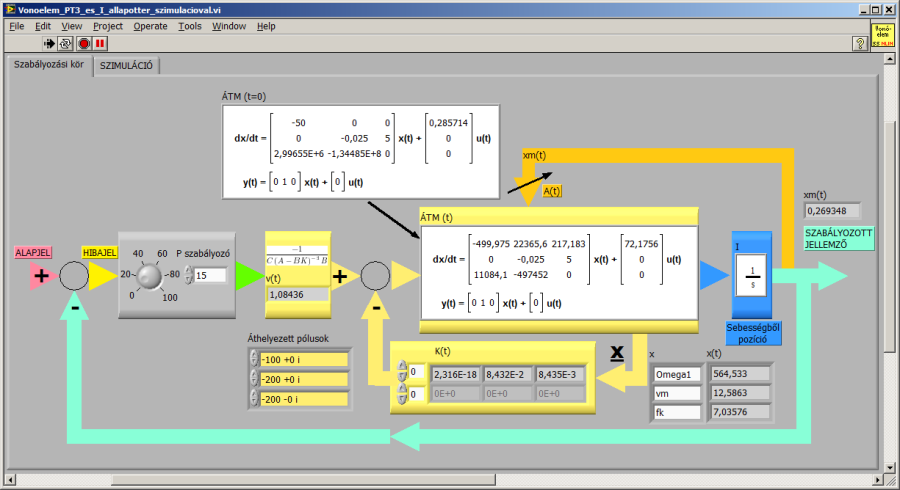
Az ÁTM(t) állapottér modell (rózsaszín, cluster adattípusú) változóba folyamatosan kiírjuk a mátrixok pillanatnyi értékét és ezt az azonos nevű (kék színű, picture típusú) kijelzőben is „kirajzoltatjuk”. Az ÁTM(t) cluster előző szimulációs lépésbeli értékére szükségünk van az A mátrix x_m-től függő módosításához, megtartva a másik három mátrix (B, C és D) értékét. Amennyiben közvetlenül visszavezetnénk az Ackermann összefüggéssel módosított állapottér modellt az A mátrix újraszámításába, algebrai hurok miatt nem működne a programunk. Ennek kiküszöbölésére a Memory blokkot kell használnunk, mert ezzel egy szimulációs időlépéssel korábbi értéket használhatunk az azonos időpillanatbeli helyett a nem szimulációs blokkokal végzett számításban.

A szimuláció körülményei, a modellben használt paraméterek, a szakasz előírt pólusai, a P-szabályozó erősítése és a szimuláció időtartama megegyezik a lineáris rendszer vizsgálatánál szereplőkkel. Mindkét modell megoldására a Runge-Kutta 23 differenciálegyenlet megoldót használjuk.

17.26. ábra - A nemlineáris szakasz állapottér modellel adott szabályozási kör szimulációs modellje

Az elmozdulás időbeli alakulását a szimuláció futása során Waveform Chart kijelzőn folyamatosan követhetjük. Az XY Graphi kijelzőn a futás közben gyűjtött időpont-jelérték párokat ábrázoljuk, miután a Control & Simulation Loop futása befejeződött.

A nemlineáris rendszer eredményeit a lineáris modell eredményeivel az onnan idemásolt, szintén XY Graph-ra rajzolt elmozdulás átmeneti függvény segítségével hasonlíthatjuk össze. Az ábrák alapján kiderül, hogy a linearizált modell meglehetősen jól közelíti a nemlineárist. Az XY Graph kijelzőkön ábrázolt adatokra 16-odfokú polinomot fektetve és azonos időpontokra számítva a polinomiálisan közelített átmeneti függvényeket 0,02 maximális eltérést tapasztalunk a két – 0 és 1 közötti értékeket felveő – átmeneti függvény között a tranziens tartományban.

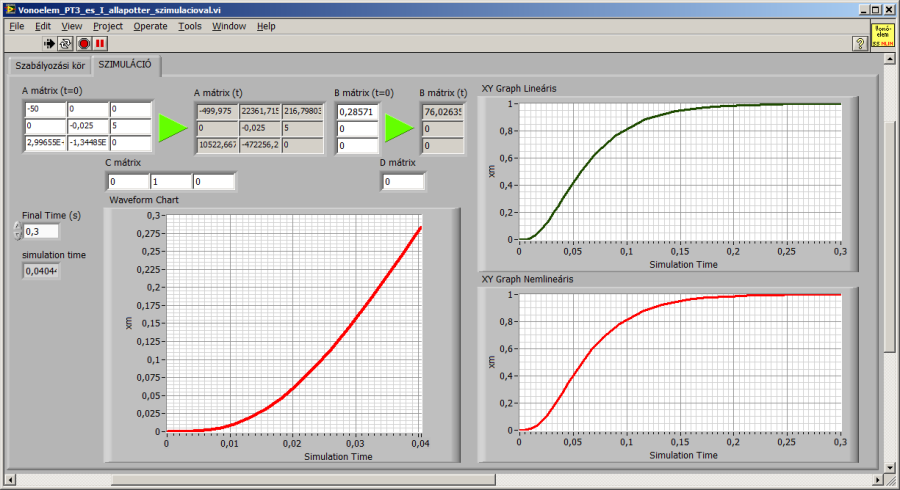
17.27. ábra - A nemlineáris szimuláció futás közbeni pillanatfelvétele a korábbi (azonos körülmények közötti) futtatás XY Graph eredményével

Szintén futás közben követhetjük az állapottér modell alakulását a szabályozási kör sematikus ábráján. A kiindulási állapottér modellel összehasonlíthatjuk az A és B mátrix folyamatosan változó pillanatnyi értékét, valamint követhetjük a három állapotváltozó és az elmozdulás alakulását, nemkülönben az állapotvisszacsatolás K és v paramétereit.

17.28. ábra - Az állapottér modell, az állapotváltozók, a kimenő jel és az állapotvisszacsatolás paramétereinek időbeli alakulása

Szakirodalom

[17.1.] LabVIEW 2009 Help http://www.ni.com/pdf/manuals/371361f.zip.

[17.2.] LabVIEW Control Design User Manual, June 2009 http://www.ni.com/pdf/manuals/371057g.pdf.

[17.3.] LabVIEW 2009 Control Design and Simulation Module Help http://www.ni.com/pdf/manuals/371894d.zip.

[17.4.] Maxima, a Computer Algebra System: Documentation http://maxima.sourceforge.net/documentation.html.

[17.5.] Haager, Wilhelm. COMA, Control Engineering with Maxima és Regelungstechnik mit Maxima http://www.austromath.at/daten/maxima/zusatz/Control_Engineering_with_Maxima.pdf.

[17.6.] Dutton, Ken, Thompson, Steve, és Barraclough, Bill. The art of control engineering. Addison-Wesley. 1997. ISBN 0-201-17545-2.

Vissza		Előre
16. fejezet - Golyósorsós pozícionáló szabályozásának tervezése és szimulációja	Főoldal	18. fejezet - Szervopneumatikus pozícionáló szabályozásának tervezése és szimulációja