2. fejezet - Mérés-és műszertechnika
- 2.1. SI rendszer
- 2.2. SI alapmennyiségek és származtatott mennyiségek.
- 2.3. Metrológiai definíciók
- 2.4. Fontosabb műszertechnikai alapfogalmak
- 2.5. Statikus és dinamikus kalibrálás
- 2.6. Regresszió
- 2.7. Korreláció
- 2.8. Mérés egyenlete, közvetlen és közvetett mérés
- 2.9. Az eredmény szokásos alakja
- Irodalmak
2.1. SI rendszer
A CIPM (Nemzetközi Méteregyezmény) tagországaiban törvénnyel szabályozott módon kötelező az SI (Système International d’Unités) alapegységek és alap mértékegységek használata. Az egyezményt 1971-ben a General Conference on Weight and Measures (Általános Súly-és Mértékügyi Értekezlet) kötötték. Meghatározott feltételek mellett más, törvényes egységek és mértékegységek is alkalmazhatóak, tekintettel a kereskedelemre, és egyéb, fontos területekre. Magyarországon - a korábbi évek rendeleti szabályozása helyett - 1991-ben lépett hatályba a Mérésügyi Törvény (1991. évi XLV. törv.)
2.2. SI alapmennyiségek és származtatott mennyiségek.
Minden méréstechnikával és méréselmélettel foglalkozó szakembernek tisztában kell lennie a törvényes egységekkel és mértékegységekkel, és igen hasznos egy áttekintés a származtatott mennyiségekről is. Ezért a következőkben bemutatjuk ezeket, valamint közöljük az alapegységek jelenleg érvényes definícióit is, rövidített formában.
|
Alapmennyiség |
Jelölés |
Alapegység |
|---|---|---|
|
Hosszúság |
l |
méter (m) |
|
Tömeg |
m |
kilogramm (kg) |
|
Idő |
t |
másodperc (s) |
|
Áram |
I |
amper (A) |
|
Termodinamikai hőmérséklet |
T |
kelvin (K) |
|
Anyagmennyiség |
n |
mol (mol) |
|
Fényerősség |
IV |
kandela (cd) |
|
1 m |
A fény által vákuumban 1/299 792 458 s idő alatt megtett út. |
|
1 kg |
1889 óta Sèvres-ben őrzött platinum-iridium henger, mint a kilogramm nemzetközi ősetalonja, (az egyetlen prototípus alapú alapetalon!) |
|
1 s |
Az alapállapotú cézium-133 atom két hiperfinom energiaszintje közötti átmenetnek megfelelő sugárzás 9 192 631 770 periódusának időtartama. |
|
1 A |
1 A konstans áram folyik két párhuzamos, végtelen hosszú, egymástól 1 m távolságban lévő, elhanyagolható keresztmetszetű vezetőben, ha közöttük vákuumban, méterenként 2x10-7 N erő mérhető. |
|
1 K |
A víz hármaspontja termodinamikai hőmérsékletének 1/273.16-szorosa. |
|
1 mol |
Egy rendszer anyagának azon mennyisége, amely ugyanannyi elemi egységet tartalmaz, ahány atom van a 12-es tömegszámú szén 0,012 kg-jában. |
|
1 cd |
Olyan fényforrás fényerőssége adott irányban, amely 540×1012 Hz frekvenciájú monokromatikus sugárzást bocsát ki, és sugárerőssége ebben az irányban 1/683 W/steradian. |
|
Származtatott mennyiség |
Elnevezés |
Jel |
Más SI egységgel kifejezve |
SI alap-egységgel kifejezve |
|---|---|---|---|---|
|
Síkszög |
radian (a) |
rad |
- |
m·m-1 = 1 (b) |
|
Térszög |
steradian (a) |
sr (c) |
- |
m2·m-2 = 1 (b) |
|
Frekvencia |
hertz |
Hz |
- |
s-1 |
|
Erő |
newton |
N |
- |
m·kg·s-2 |
|
Nyomás, Mechanikai feszültség |
pascal |
Pa |
N/m2 |
m-1·kg·s-2 |
|
Energia, Munka, Hőmennyiség |
joule |
J |
N·m |
m2·kg·s-2 |
|
Teljesítmény, Sugárteljesítmény |
watt |
W |
J/s |
m2·kg·s-3 |
|
Elektromos töltés |
coulomb |
C |
- |
s·A |
|
Elektromos feszültség |
volt |
V |
W/A |
m2·kg·s-3·A-1 |
|
Kapacitás |
farad |
F |
C/V |
m-2·kg-1·s4·A2 |
|
Elektromos ellenállás |
ohm |
V/A |
m2·kg·s-3·A-2 |
|
|
Elektromos vezetőképesség |
siemens |
S |
A/V |
m-2·kg-1·s3·A2 |
|
Mágneses fluxus |
weber |
Wb |
V·s |
m2·kg·s-2·A-1 |
|
Mágneses fluxussűrűség |
tesla |
T |
Wb/m2 |
kg·s-2·A-1 |
|
Induktivitás |
henry |
H |
Wb/A |
m2·kg·s-2·A-2 |
|
Celsius hőmérséklet |
degree Celsius (e) |
°C |
- |
K |
|
Fényáram |
lumen |
lm |
cd·sr (c) |
m2·m-2·cd = cd |
|
Megvilágítás |
lux |
lx |
lm/m2 |
m2·m-4·cd = m-2·cd |
|
Aktivitás (Nukleáris) |
becquerel |
Bq |
- |
s-1 |
|
Elnyelt sugárdózis |
gray |
Gy |
J/kg |
m2·s-2 |
|
Ekvivalens sugárdózis(d) Dózisegyenérték |
sievert |
Sv |
J/kg |
m2·s-2 |
Magyarázat a származtatott mennyiségek táblázatában alkalmazott jelölésekhez:
(a)A radián és a steradián két jellemző kifejezés arra az esetre, amikor eltérő természetű származtatott mennyiségeknek azonos a dimenziója, pontosabban nincs dimenziója. Egy radián az a szög, amely alatt a sugárral megegyező nagyságú ívhossz a középpontból látszik. Másképp a radián a sugárnyi hosszúságú ívhosszhoz tartozó középponti szög 57.2958°. Egy szteradián az a középponti szög, amely a gömbsugár négyzetével egyenlő területű gömbfelületrészhez tartozik.
(b) A gyakorlatban a „rad” és „sr” mértékegységek használatosak, annak ellenére, hogy a definícióból mindkét esetben "1" adódna.
(c) A fotometriában a mértékegység neve steradian, jele „sr”.
(d) Más mennyiségek „sieverts”-ben kifejezve: személyi dózis, effektív dózis, irányított ekvivalens dózis
(e) A Celsius hőmérséklet egysége a Celsius fok, jele °C. A Celsius hőmérséklet „t” numerikus értéke Celsius fokban kifejezve: t/°C = T/K - 273.15. Megjegyzés: Az összefüggésben 273,15 K a víz olvadási hőmérséklete, ami nem azonos a víz-hármaspont 273,16 K hőmérsékletével. Az egyszázados eltérés oka, hogy a zárt víz-hármaspontban a három halmazállapot együtt van jelen, szemben a nyílt edényben olvadó jég két halmazállapotával.
2.3. Metrológiai definíciók
A metrológia legfontosabb meghatározásait a NAT (Nemzeti Akkreditáló Testület) NAR-EA-4/02. jelű anyaga [2.1.] alapján, az alábbiakban gyűjtöttük össze:
-
Alapmennyiség
Megállapodásszerűen, egy adott rendszerben egymástól függetlennek tekintett mennyiségek
-
Származtatott mennyiség
Alapmennyiségek függvényeként definiált mennyiségek
-
Mértékegység
Ugyanolyan fajtájú, más mennyiség nagyságának kifejezésére definiált konkrét mennyiség
-
Egységrendszer
Az alap és származtatott egységek összessége
-
Koherens egység
Alapegységek hatványainak szorzataként kifejezhető egység, az arányossági tényező: 1 (egy)
-
Inkoherens egység
Mint előbb, de az arányossági tényező nem 1 (egy)
-
Etalon
Mérték, mérőeszköz, anyagminta, vagy mérőrendszer, amelynek az a rendeltetése, hogy egy mennyiség egységét, illetve egy, vagy több ismert értékét definiálja, megvalósítsa, fenntartsa, vagy reprodukálja és referenciaként szolgáljon.
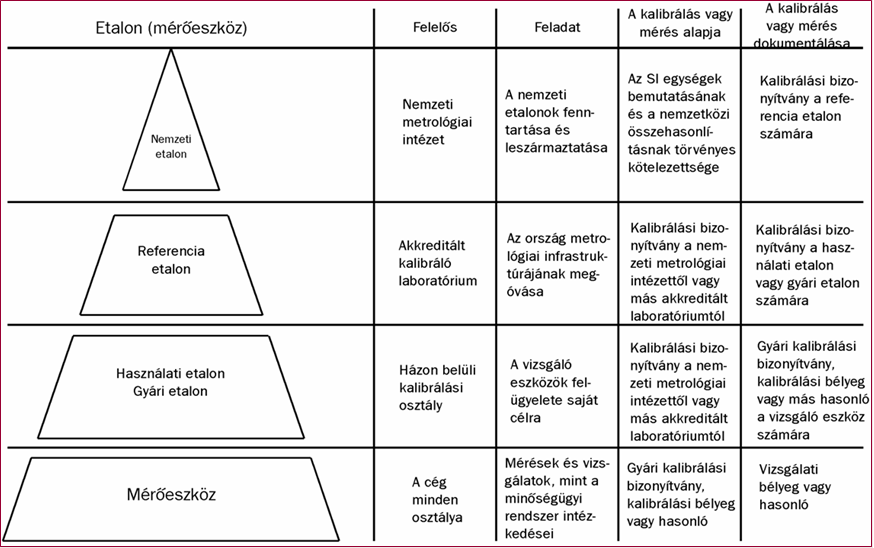 2.1. ábra - Az etalonok hierarchiája
2.1. ábra - Az etalonok hierarchiája
-
Visszavezethetőség
Egy mérés eredményének, vagy etalon értéknek az a tulajdonsága, hogy ismert bizonytalanságú összehasonlítások láncolatán keresztül kapcsolódik megadott referenciákhoz, általános nemzeti (ld. ehhez a magyarázatot a (2.5. szakasz) fejezetben), vagy nemzetközi etalonhoz. A visszavezetési láncban a kevésbé pontos etalonok felől haladunk a pontosabbak felé.
-
Leszármaztathatóság
A visszavezetéssel ellentétes műveletsor.
-
Etalonok csoportosítása
-
Jogi státuszuk szerint:
Nemzetközi etalon
Megállapodás alapján elfogadott etalon
Nemzeti etalon
Adott országban választott viszonyítási alap
Referencia etalon
Adott szervezet legpontosabb etalonja
Használati etalon
Mérőeszközök ellenőrzésére rendszeresen használt etalon
-
Metrológiai státuszuk szerint:
Elsődleges etalon
Nem lehet más etalonból leszármaztatni
Másodlagos etalon
Leszármaztatott etalon
-
Jellegük szerint:
Egyedi etalon
Etalon műszer, mérték, anyagminta
Etalon csoport
Pl.: Súlysorozat, mérőhasáb készlet
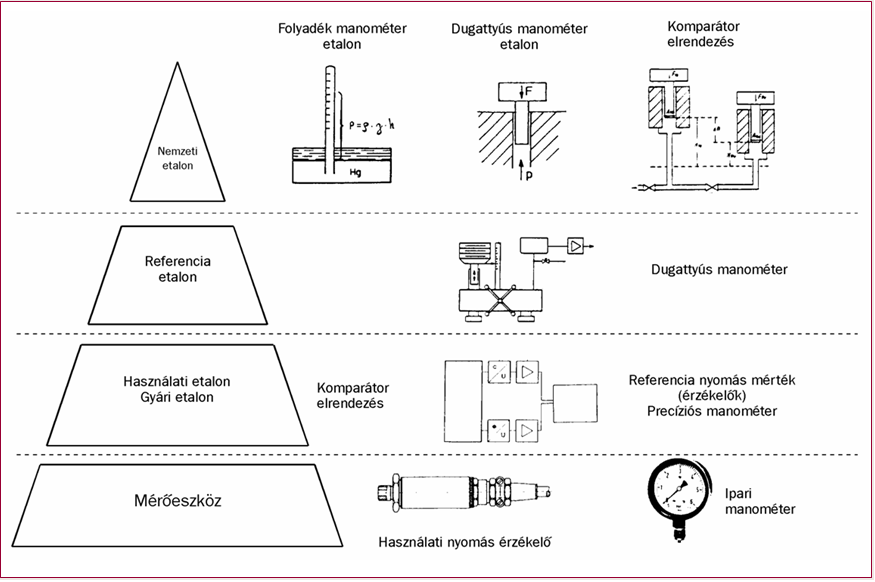 2.2. ábra - Példák a nyomás etalonok megvalósítására
2.2. ábra - Példák a nyomás etalonok megvalósítására
-
-
Illeszkedés
Összefügg a műszertechnikai alapfogalmak között szereplő reprodukálhatósággal és ismételhetőséggel (ld.: ott). Az illeszkedés azt jelenti, hogy különböző helyen és időben végzett mérések eredményei egymással összevethetőek.
-
Joghatással járó mérések
Az ilyen típusú méréseket csak hitelesített mérőeszközökkel lehet elvégezni. Ebbe a körbe a következő tevékenységek tartoznak:
Jogi érdekeket érintő mérések
Minőség tanúsítást célzó mérések
Hatósági bizonyítás céljából végzett mérések
Ellenszolgáltatás mértékének megállapítása (kereskedelmi mérések)
Életvédelem, egészségügy, környezet-és vagyonvédelem területén végzett mérések
-
Hitelesítés
Közigazgatási eljárás. Annak elbírálása, hogy a mérőeszköz megfelel-e a vele szemben támasztott mérésügyi előírásoknak.
-
Kalibrálás
Metrológiai tevékenység. Azon műveletek összessége, amelyekkel meghatáro-zott feltételek mellett megállapítható az összefüggés egy mérőeszköz, vagy egy mérőrendszer értékmutatása, illetve egy mértéknek vagy anyagmintának tulajdonított érték és a mérendő mennyiség etalonnal reprodukált megfelelő értéke között.
-
Valódi érték
Egy adott konkrét mennyiség definíciójának megfelelő érték, amelyet csak „tökéletes” méréssel lehetne meghatározni.
Sajnos, kevés ilyen érték jeleníthető meg. Példaként a Nemzetközi Kilogramm Prototípusát, a víz hármaspontjának hőmérsékletét (273,16 K), a fény vákuumbeli sebességét (299 792 458 m/s), vagy a háromszög szögeinek összegét lehetne felhozni.
-
Helyes érték
Valamely konkrét mennyiségnek tulajdonított, gyakran megegyezés alapján elfogadott olyan érték, amely az adott célnak megfelelő bizonytalanságú. Egy referencia etalon által megvalósított mennyiségnek tulajdonított érték az adott helyen a mennyiség konvencionális helyes értékének tekinthető.
-
Abszolút hiba
Elméletileg ez a mért és a valódi érték közötti különbség. A gyakorlatban a valódi érték helyére a helyes érték kerül.
-
Relatív hiba
Elméletben az abszolút hiba osztva a valódi értékkel. Miután azonban az utóbbit nem ismerjük, helyére osztóként a helyes érték kerül.
-
Redukált hiba
Az abszolút hiba osztva a terjedelemmel, azaz a legnagyobb és legkisebb mért érték közötti különbséggel.
2.4. Fontosabb műszertechnikai alapfogalmak
A mérési adatok kiértékelését természetesen megelőzi az adatok felvétele és rendszerezése. Ehhez mérőeszközök, műszerek, mérőberendezések szükségesek, így a mérés- és a műszertechnika elválaszthatatlanok. Mindenekelőtt tehát tisztázni kell néhány igen fontos műszertechnikai fogalmat.
-
Osztálypontosság
Más néven „Pontossági osztály”, a mérőeszköz hibájának, pontosságának egyik elterjedt megadási módja (ld.: 3. fejezet fejezet, Mérési hibák). Meghatározása szerint az abszolút hiba osztva a mérőeszköz maximális értékmutatásával (végkitérésének értékével), százalékban kifejezve.
-
Mérési tartomány
A mérendő mennyiség azon halmaza, amelyre a mérőműszer hibája a megadott határok között marad.
-
Felbontás
A kijelzőn biztonságosan megjeleníthető értékek közül a legkisebb. A felbontás mindig nagyobb tartományt kell, hogy jelentsen, mint a feloldás, jellemzően a felbontás a feloldás 3-5-szöröse. Ha ez nem teljesül, akkor a kijelzett legkisebb érték „eltűnik” a feloldásból származó bizonytalanságban.
-
Feloldás, érzékenységi küszöb
A bemenet lassú és egyenletes változtatása mellett az a legnagyobb tartomány, amelyben nem tapasztalható értékelhető műszerválasz (kimenet). A nullpont környezetében ezt a jellemzőt érzékenységi küszöb kifejezéssel jelöljük. A feloldás a teljes mérési tartományban változó lehet, de mindig a legnagyobb értéket kell a felbontás meghatározásához figyelembe venni.
-
Műszerállandó
Az a tényező, amellyel a műszeren kijelzett értéket szoroznunk kell, hogy a mérendő fizikai mennyiséget megkapjuk.
-
Érzékenység
A műszer kimenőjele és bemenőjele változásának hányadosa.
-
Érzéketlenségi sáv
Az a maximális tartomány, amelyben a bemenőjel mindkét irányú változása nem hoz létre kimenőjelet a műszeren.
-
Ismétlőképesség
Azonos mérési eljárással (fizikai elv és módszer), azonos mérőeszközökkel, azonos körülmények között, ugyanazon mérőszemély(ek) által elvégzett két mérés közötti eltérés nagysága. Iparvállalatoknál ez a jellemző igen kiemelkedő fontosságú lehet, bizonyos méréseket csak olyan személyre bíznak, akinél az ismétlőképesség egy megadott határon belül marad.
-
Reprodukálhatóság
Azonos mérési eljárással (fizikai elv és módszer), eltérő mérőeszközökkel és eltérő körülmények mellett, más mérőszemély által elvégzett mérés és az eredeti mérés közötti különbség.
-
Stabilitás
A mérőműszer azon tulajdonsága, amely hosszabb időre alkalmassá teszi az eszközt a metrológiai jellemzőinek megőrzésére.
-
Drift
A mérőműszer metrológiai jellemzőinek lassú időbeli változása. Oka lehet termikus, mechanikai, stb. hatás.
-
Pontosság
A méréstechnikában ritkábban használt jellemző. Lényegében azt fejezi ki, hogy a mérőeszköz milyen eltéréssel képes a mérendő mennyiség valós értékét megjeleníteni.
-
Átviteli függvény
Dinamikus rendszerek, így műszerek és mérőrendszerek modellezésére alkalmas matematikai összefüggés. Definíciója szerint harmonikus kimenő és bemenő jelek Laplace transzformáltjainak hányadosa. Csak lineáris és állandó együtthatójú rendszerek viselkedésének leírására alkalmas, ennek ellenére széleskörűen alkalmazzák a mérés- és irányítástechnikában. Minden technikai jel harmonikus összetevőkre bontható, ez a téma a frekvencia analízissel foglalkozó, (6. fejezet) fejezetben van kibontva. Az átviteli függvény a rendszer differenciálegyenletével és állapottér modelljével „rokon”, mert előbbiből Laplace transzformálással, a másodikból pedig mátrix műveletekkel származtatható. A Laplace operátort helyettesítve annak jelentésével, azaz az „s=jω” kifejezéssel, kapjuk a rendszer körfrekvenciától függő, un. átviteli tulajdonságait leíró „frekvencia átviteli függvényt”. Ezt a méréstechnikában Bode-diagramon szokás ábrázolni, amelynek két része van: Az egyik a bemenő és kimenő jel amplitúdó arányát mutatja decibelben (dB), a másik a két jel közötti fáziskülönbséget. Ha a bemenő és kimenő jelek fizikai dimenziói nem azonosak, akkor egy célszerűen választott alacsony körfrekvencián számított (mért) átviteli értékhez „normálják” (viszonyítják) a különféle körfrekvenciákon meghatározott értékeket, így „dimenziótlanítva” az arányt.
-
Átviteli tényező
Az átviteli függvény abszolút értéke (harmonikus kimenőjel és bemenőjel amplitúdóinak aránya) valamely körfrekvencián.
-
Időállandó
Adott műszer egyik fontos dinamikai jellemzője. Első és másodrendű (vagy ilyen rendszámú átviteli tagokra bontható) műszer (mérőrendszer) esetében van szerepe. Elsőrendű rendszer esetében a kimenőjel időbeli lefutásáról és a reciprok értéke az arányos amplitúdó átvitel frekvenciatartományáról ad információt. Időtartományban az ugrásszerű bemenő mennyiségre adott műszer válasz csak késleltetve jelenik meg. Egy elsőrendű műszer (egyetlen) energiatárolójának feltöltődése miatt, a kijelzett érték az időállandóval egyező időpillanatban az állandósult műszerválasz értékének csupán 63,2%-a lesz. Ezért ajánlatos a műszert az időállandó (3-5)-szörösének eltelte után leolvasni. A másodrendű műszer két (független) energiatárolót tartalmaz. Alulcsillapított másodrendű rendszer esetében az időállandó reciprok értéke a csillapítatlan rezonancia frekvencia négyzetgyöke. Túlcsillapított másodrendű rendszer két soros elsőrendű átviteli tag eredőjével írható le, ennek folytán két időállandó jelenik meg. A kritikus csillapítás esetén az időállandók azonosak.
-
Letörési körfrekvencia
Elsőrendű műszer időállandójának reciprok értéke. Az amplitúdó átvitel ezen a körfrekvencián méréstechnikai szempontból már elfogadhatatlan, mert a kimenőjel amplitúdója csupán közel 70%-a a bemenőjel amplitúdójának.
-
Felső határ(kör)frekvencia
A méréstechnikában szokásos 1%-os amplitúdó átviteli hiba a felső határ(kör)frekvenciánál jelenik meg, és ez a körfrekvencia lényegesen alacsonyabb érték, a letörési körfrekvenciának ≈0.14-szerese.
-
Csillapítási fok
Másodrendű rendszer dinamikai tulajdonságaira jellemző szám, amelytől lengő (rezgő) rendszer esetén, rezonancia frekvencián az amplitúdó nagyítás függ.
-
Rezonancia körfrekvencia (csillapított rendszeré)
Az a körfrekvencia, amelynél másodrendű rendszer esetében maximális az amplitúdó nagyítás. Kisebb érték, mint a csillapítatlan másodrendű rendszer rezonancia körfrekvenciája, amely az időállandó reciprok értéke (ld.: Időállandó).
-
Beállási idő
Első és másodrendű műszerek (rendszerek) esetében azon időtartam, amely addig telik el, amíg az ugrásszerű bemenőjelre adott válaszfüggvény az állandósult állapotbeli értékhez viszonyított ±5%-os sávban vesz fel értékeket, és ezt a sávot a kimenőjel már nem hagyja el.
-
Fázistolás
A harmonikus kimenőjel fázisából kivonva a harmonikus bemenőjel fázisa.
2.5. Statikus és dinamikus kalibrálás
A méréstechnikában alapszabály, hogy „ne higgyünk vakon” a mérőberendezések által kijelzett értékekben. A kalibrálás metrológiai definíciója a 2.3. szakasz fejezetben található meg. A témához szorosan kötődik két másik fogalom is, a leszármaztathatóság és a visszavezethetőség.
Tekintettel arra, hogy kalibrálást szinte minden méréstechnikához kapcsolódó munkahelyen végeznek, ez az egyik legáltalánosabb és legfontosabb metrológiai feladat, hiszen a konkrét mérési feladat végrehajtása előtt kalibrálnunk kell, ha
-
ismeretlen mérőeszközt veszünk használatba,
-
elkallódtak a műszer(ek) adatlapjai,
-
régebben volt használatban egy alkalmazni kívánt műszer,
-
saját tervezésű mérőeszközt készítettünk, vagy
-
megterveztünk és összeállítottunk egy mérőláncot.
A fenti néhány kiragadott példa csak szemléltetésül szolgál, ennél sokkal szélesebb ez a terület. Ha a munkaeszköz jellegű mérőműszert kalibrálunk, akkor a használati etalonokkal kell ezeket összehasonlítani, mert a visszavezetési láncban a kevésbé pontos etalonok felől haladunk a pontosabbak felé. A visszavezethetőség metrológiai szabálya általánosságban megköveteli, hogy használati mérőeszközünk ismert bizonytalanságú összehasonlítások láncolatán keresztül kapcsolódjon a nemzeti etalonhoz.
A referencia etalonokat rendszerint az adott ország nemzeti metrológiai laboratóriumában (NMI) kalibráltatják a nemzeti etalonok segítségével. Ezeknek a nemzeti etalonoknak és az adott NMI által kiadott kalibrálási bizonyítványoknak kölcsönös elismerése kötelező, ha az adott ország aláírója az 1998-as CIPM-MRA–nak, vagyis a CIPM Kölcsönös Elismerési Megállapodásának.
A használati etalon ellenőrzése olyan referencia etalon (műszer) segítségével történjen, amelyet a legjobbnak tekintünk az adott mérőlaborban. A használati etalonok referencia etalonnal való összevetésének időtervét az adott szervezet (üzem) metrológiai szabályzata írja elő. Ha nem vagyunk meggyőződve a referencia etalon megbízhatóságáról, akkor helyi, vagy országos mérésügyi szervezethez célszerű fordulni.
Kétféle kalibrálás történhet, statikus és dinamikus, azonban a dinamikus esetében is első lépcső a statikus kalibrálás. A statikus kalibrálás célja főként a műszer karakterisztikájának ellenőrzése, de fontos más metrológia jellemzők vizsgálata is. Ennek során célszerűen választott lépcsőzéssel a vizsgált műszer teljes mérési tartományában összehasonlítjuk a kijelzett értéket a referenciaként használt etalon értékmutatásával. A leolvasás csak a műszer állandósult állapotában történhet. Annak eldöntése, hogy a kalibrálási lépcsők mekkorák legyenek, vagy műszerkönyvek, előírások segítenek eligazodni, vagy a tapasztalatunkra kell hagyatkozni. Fontos a feloldást (érzékenységi küszöböt) több tartományban ellenőrizve meggyőződni arról, hogy a felbontás (legkisebb kijelzett érték) megfelelő-e? A (2.4. szakasz) fejezetben felsorolt műszerjellemzők közül szükség szerint kell továbbiakat kiválasztani.
A dinamikus kalibrálás különösen fontos, ha időben változó mennyiségek mérésére szolgál a vizsgált műszer, vagy mérőrendszer. A dinamikus kalibrálás célja annak eldöntése, hogy a mérőeszköz rendszáma, időállandói, beállási ideje, frekvencia menete, alsó és felső határfrekvenciája, rezonancia frekvenciája, stb. valóban egyeznek-e a feltételezett értékekkel, illetve ezek egyeznek-e az adatlapon megadott értékekkel?
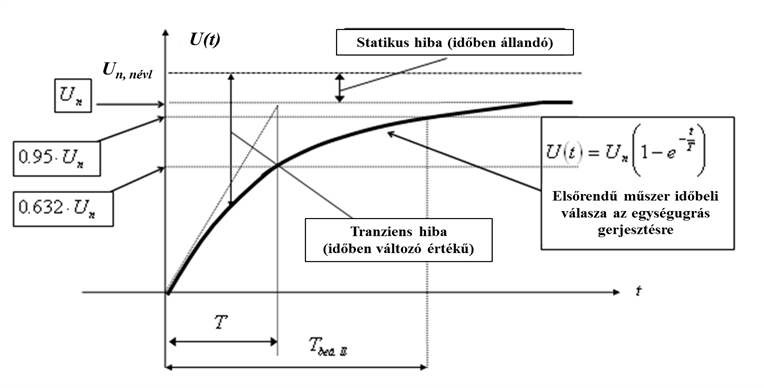
Ismeretes, hogy az elsőrendű rendszer (műszer) egy energiatárolót tartalmaz. Tudjuk, hogy a rendszámot az adott rendszer független energiatárolóinak száma határozza meg.
Az elsőrendű rendszer dinamikus viselkedését leíró differenciálegyenlet általános alakjában megjelenik két olyan fontos műszertechnikai jellemző, amelyek metrológiai szempontból is fontosak, ez a „T” időállandó és az „A” érzékenység (erősítés). A műszer időtartománybeli matematikai modellje az alábbi:
|
|
(2.1) |
A (2.3. ábra) ábrán az x KI kimenőjelet U(t) villamos feszültségként értelmeztük.
A differenciálegyenlet Laplace transzformálása és megfelelő átrendezése után kapjuk az átviteli függvényt. Az átviteli függvényben s=jω helyettesítéssel kapjuk azt a körfrekvenciától függő formát, amely segítségével a Bode diagram megszerkeszthető:
|
|
(2.2) |
|
|
|
(2.3) |
|
|
|
(2.4) |
|
|
|
(2.5) |
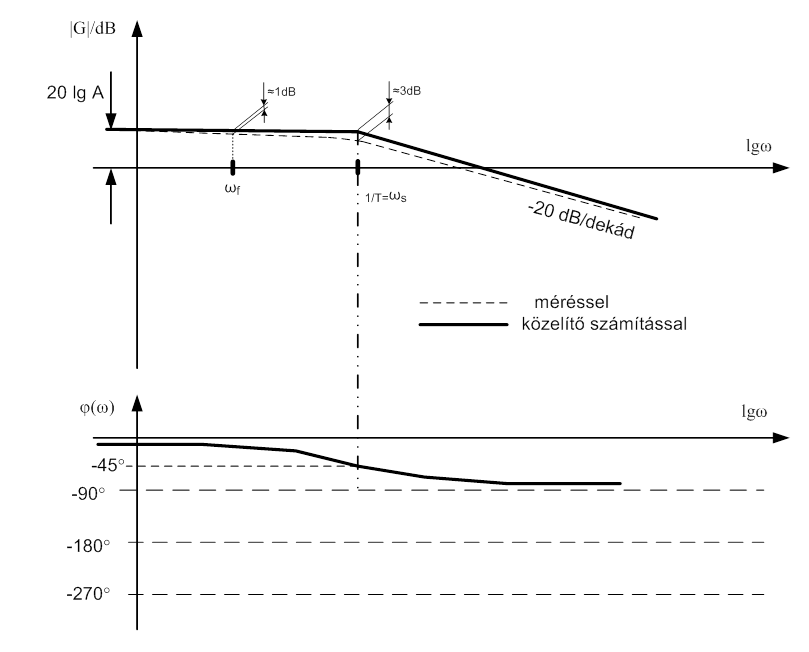
A (2.4. szakasz) fejezetben ismertetett műszertechnikai metrológiai jellemzők felismerhetőek a két ábrán.
2.6. Regresszió
A regresszió alkalmazásával az ismert etalon értékek és a vizsgált műszer által jelzett értékek közötti kapcsolatot szándékozunk kimutatni. A legismertebb forma a lineáris regresszió, amelynek esetében az etalon értékek és a vizsgált műszer által mutatott értékek között lineáris kapcsolatot feltételezünk. A kapcsolatot egy egyenes egyenletének formájában adjuk meg, és ehhez szükség van a regressziós egyenes „m” meredekségére és a „b” nullpont-hibára.
Két változatot kell megkülönböztetnünk. Az egyik esetben az etalon bizonytalansága kisebb, mint a vizsgált műszeré. Az etalon beállított „xi” értékei jelentik a független változót, megadható az ehhez az értékhez tartozó „δi” hiba és alkalmazható a legkisebb négyzetek módszere. A másik esetben – és ez gyakran előfordul a gépészeti méréstechnikában – az etalon és a vizsgált műszer bizonytalansága összemérhető, hasonló. Ilyenkor nem lehet a legkisebb négyzetek módszerét alkalmazni, helyette a „Wald-módszer” nyújt lehetőséget a regressziós egyenes két paraméterének meghatározására. (Wald Ábrahám a XX. sz. elején a kolozsvári Ferenc József Tudományegyetem matematika tanára volt.)
Amennyiben tehát az etalon kisebb bizonytalanságú, pontosabb, mint a vizsgált műszer, a két paraméter meghatározására alkalmazható a Gauss által javasolt „legkisebb négyzetek módszere”. Ilyen típusú kalibrálási feladat például egy olyan finomtapintó ellenőrzése, amelyik 1 μm felbontással rendelkezik, és etalonként mérőhasáb készletet alkalmazunk.
A (2.5. ábra) ábrán látható egy lineáris regresszió, ahol xBE=x és xKI=y:
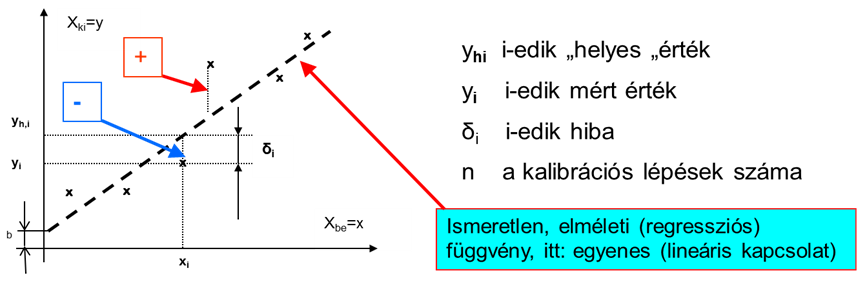
Az ábrán látható eltérések négyzetösszegének minimumát keressük. A pontpárok ismeretében a regressziós egyenes „m” meredekségét és a „b” nullpont-hibát szélsőérték-kereséssel határozhatjuk meg.
|
|
(2.6) |
Az összefüggést „m” és „b” szerint külön-külön parciálisan deriváljuk, és egyenlővé tesszük zérussal.
|
|
(2.7) |
Olyan egyenletrendszert kapunk, amelyik kétszer „n” db egyenletből áll:
|
|
(2.8) |
|
|
|
(2.9) |
A második „csoportból”, azaz egyenletrendszerből „b” azonnal kifejezhető, és meghatározásához már csak az átlagokat kell kiszámítani:
|
|
(2.10) |
|
|
|
(2.11) |
A továbbiakban „m” meghatározása a feladat. Az első egyenletrendszerbe behelyettesítjük a „b”-re kapott eredményt:
|
|
(2.12) |
|
|
|
(2.13) |
|
|
|
(2.14) |
Végül a fenti egyenletből „m”-re rendezve kapjuk az első eredményt, ami ebben a formájában algoritmizálásra egyelőre nem alkalmas.
|
|
(2.15) |
A számláló azonban tovább alakítható:
|
|
(2.16) |
Végül olyan alakhoz jutunk, amely már algoritmizálásra is alkalmas.
|
|
(2.17) |
A nevezőt is át kell formálni. A következő egyenlet már több lépés eredményét mutatja. Ha az egyenlet jobb oldalán elvégezzük a kijelölt műveletet, akkor belátható, hogy az összefüggés helyes.
|
|
(2.18) |
Így mind a számlálóban, mind a nevezőben olyan formákhoz jutottunk, amelyek áttekinthető és jól alkalmazható számítási módot kínálnak a regressziós egyenes meredekségének meghatározására:
|
|
(2.19) |
Az előzőekben bemutatott számítási módszer csak akkor alkalmazható, ha az etalon bizonytalansága kisebb, mint a vizsgált eszközé.
A Wald-módszer viszont segít abban az esetben, ha mind az etalonként alkalmazott eszközt, mind pedig a vizsgált műszert normális eloszlású, véletlen hiba terheli.
Az eljárás lépései a következőek:
-
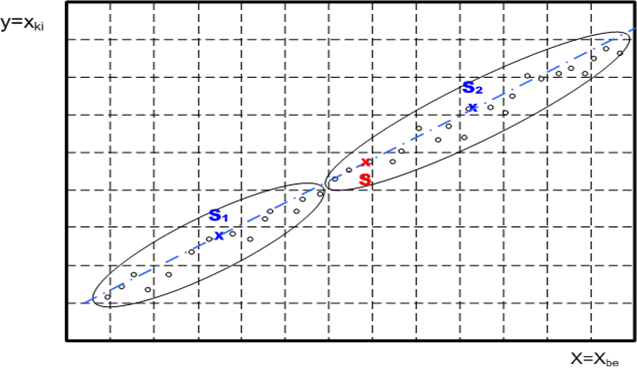
Az értékpárokat nagyság szerint sorba rendezzük. Lehetőleg a mérési tartomány két végének környezetében végezzünk méréseket. A halmazt két részre osztjuk, és mindkét részhalmaz súlypontját képezzük.
-
A két súlypontot (S1, S2) összekötve a regressziós egyenes meredekségét kapjuk.
-
A teljes halmaz „S” súlypontjának kiszámítása után a 2. pontban meghatározott meredekséggel húzunk egyenest az „S” súlyponton keresztül.
A különbségtétel kedvéért a meredekséget „α” és a nullpont-hibát „β” szimbólummal jelöljük.
A két részhalmaz súlypontjának meghatározása a következők szerint történik:
|
|
(2.20) |
Az átlagok segítségével már kijelölhető a meredekség:
|
|
(2.21) |
Végül meg kell határoznunk a nullpont-hibát, az egyenes és a függőleges tengely metszéspontját. Most valamennyi értékpár felhasználásával kiszámítjuk a teljes ponthalmaz súlypontját, és az így kapott átlagértékkel a keresett metszéspontot:
|
|
(2.22) |
|
|
|
(2.23) |
A Wald-módszerrel meghatározott regressziós egyenes egyenletének paramétereivel kapjuk a végeredményt:
|
|
(2.24) |
A regresszió analízis természetesen a fentiekben bemutatottaknál lényegesen szélesebb körű. Ebben a fejezetben csak a méréstechnikában legfontosabb ismeretekre szorítkoztunk.
2.7. Korreláció
Az ipari gyakorlatban sokszor elengedhetetlenül fontos a mérési adatok közötti lineáris kapcsolat objektív kimutatása, a matematika eszköztárának igénybevételével. Gyakori feladat annak eldöntése, hogy két, különböző mérési sorozatból származó mintasokaság, azaz adathalmaz között van-e lineáris összefüggés? A függőség mértékének meghatározása a korrelációszámítással történik.
Ilyen gyakorlati feladat lehet a gépészetben például annak eldöntése, hogy egy tengely vállbeszúrásának megadott erőhatással történő körkörös zömítése (görgőzés) és a görgőzés eredményeként létrejövő alakváltozás között van-e összefüggés? Összefügg-e továbbá a görgőzés (zömítés) mélysége a tengely szilárdságának növekedésével?
A módszer alapja a vektorszámítás. Két vektor között egy pozitív, vagy negatív előjelű szorzó, azaz konstans, akkor teremt kapcsolatot, ha a vektorok között bezárt szög 0°, vagy 180°. Ha két vektor egymáshoz képest 90°-ot zár be, akkor nincsen közöttük egy konstanssal kifejezhető lineáris kapcsolat.
A vektorokra érvényes szabály kiterjeszthető a mérési adatok halmazára is, ha a mért értékek és a várható érték közötti különbségeket egy n-dimenziós vektor elemeinek tekintjük.
A vektor-térben ugyanis egyszerűbb a korreláció (kapcsolat) értelmezése.
Ha ugyanis a két vektor egymással φ szöget zár be, akkor a szög értékével kifejezhető minden lényeges összefüggés:
-
φ=90º, akkor nincs a ponthalmazok között lineáris függés
-
φ=0º, akkor van lineáris összefüggés, a két n-dimenziós vektor között konstans szorzóval kifejezhető a kapcsolat: y=ax
-
φ=180º, akkor a két n-dimenziós vektor között negatív konstans szorzóval kifejezhető lineáris kapcsolat van: y= - ax, a két vektor ellentétesen korrelált
-
φ≈0º, ill. φ≈180º akkor lehet lineáris a kapcsolat, de van egy korrekciós tag is, amelyet „e” szimbólummal jelölünk: y= ax + e, ahol |e|→0
A korrelációs tényező számításhoz szükséges összefüggéshez a következő megfontolások alapján jutunk.
A két vektor közötti hajlásszög cosinus-a -1 és +1 között mozoghat, ezt nevezzük „r” korrelációs tényezőnek (faktornak).
|
|
(2.25) |
Behelyettesítve az előző képletbe a kijelölt matematikai műveleteknek megfelelő alakokat, és figyelembe véve azt, hogy a gyakorlatban a mért adatok felhasználásával nem a korrelációs tényezőt, hanem a tapasztalati korrelációs tényezőt tudjuk csak meghatározni, a következő formát kapjuk:
|
|
(2.26) |
Látható, hogy az egyenlőtlenségből eltűnt az egyenlőség jel, hiszen az elméleti értéket empirikus adatokból nem lehet meghatározni. További átformálások „kínálják” magukat, amelyek révén a számításhoz lényegesen egyszerűbb alakhoz jutunk:
|
|
(2.27) |
A tapasztalati korrelációs tényező kiszámítására alkalmas célszerű alakban a két mérési adathalmaz abszolút hibái mellett a tapasztalati szórások szerepelnek. Ez előnyös, mert ezekre az adatokra, paraméterekre a statisztikai feldolgozás során más célból is szükség van.
|
|
(2.28) |
Végül fontos megjegyezni, hogy a műszaki gyakorlatban csak akkor feltételezzük a lineáris kapcsolatot, ha az empirikus korrelációs tényező értéke 0,7 felett van, de sok esetben már csak a 0,8 feletti értékek elfogadhatóak. A statisztikai szakirodalomban megtalálható „Pearson-táblázatok” a konfidenciaszint és a minta elemszámának függvényében adják meg azt a tapasztalati korrelációs tényezőt, amely mellett a kapcsolat hipotézise elfogadható. E táblázatok azonban nem a műszaki területek sajátosságait veszik alapul, és ezért a gépészetben ajánlatos a fent jelzett szigorúbb vizsgálat.
2.8. Mérés egyenlete, közvetlen és közvetett mérés
Mielőtt az eredmény szokásos alakjait tárgyalnánk – erre a következő, (2.9. szakasz) fejezetben kerül sor - emlékeztetnünk kell arra, hogy a mérési eredményt nem mindig egyetlen ismeretlen mennyiség mérésével kapjuk. A mérési feladatok tekintélyes része olyan, hogy az eredmény többféle mennyiség méréséből származó adat felhasználásával határozható meg. Ezt a szakirodalom közvetett mérésnek nevezi.
Az eredményt egyenlet formájában megadott matematikai modell reprezentálja. Az eredmény általános egyenletében a nagybetűk a valódi értékeket reprezentálják. Az „A” indexű tagok a mérendő bemenő mennyiségeket, míg a „B” indexűek a különböző tényezőket jelentik.
|
|
(2.29) |
Méréseink eredményeként ezt az elméleti „Y” kimenetet becsüljük az „y” átlagértékével:
|
|
(2.30) |
Egy ilyen matematikai modellnek lehet ismert fizikai törvényszerűség az alapja, de ezek mellett, számos esetben, tapasztalati úton nyert összefüggések is megjelenhetnek, mint eredményképlet. Fizikai törvényen alapszik például egy kör keresztmetszetű villamos vezető fajlagos ellenállásának meghatározása:
|
|
(2.31) |
Az ismert képletben négyféle mennyiség mérése szükséges az eredmény meghatározásához. Ha az „ℓ” hosszúságú, „d” átmérőjű vezető két vége közötti villamos feszültség „U” és ennek hatására „I” áram folyik a vezetőben, akkor a fajlagos ellenállás „ρ” meghatározható. Az eredmény egyenletben nem szerepeltettük a korrekciókat (rendszeres hibák) és az eredő mérési bizonytalanságot. Ezekkel külön alfejezetben foglalkozunk.
Egy mérőhasáb hosszának meghatározása a mérőhasábok kalibrálása során interferométerben, optikai úton történik. Az eredmény megadásához alkalmazott eredményegyenletben, a fizikai törvényszerűségeken (pl.: hő okozta alakváltozás hatása) kívül egyéb empirikus ismereteket is felhasználnak:
|
|
(2.32) |
Az eredményképletben a jelölések az alábbiak:
|
l: |
a hasáb hossza 20 °C hőmérsékletre vonatkoztatva |
|
|
q: |
a végzett mérések száma |
|
|
λ i: |
az egyes mérésekhez használt fény névleges hullámhossza |
|
|
n i: |
a levegő egyes mérésekhez kiszámolt törésmutatójának az értéke |
|
|
K i: |
a hasáb hosszon a fény fél hullámhossz számának egészrésze |
|
|
F i: |
a hasáb hosszon a fény fél hullámhossz számának törtrésze |
|
|
α: |
a hasáb lineáris hőtágulási együtthatója |
|
|
ΔT i: |
a hasáb hőmérsékletének 20 °C – tól való eltérése az egyes mérések alkalmával |
A fizikai törvényszerűségeken alapuló összefüggés tartalmaz ezeken felül hétféle Δℓ k tapasztalati korrekciót (ezek ismert, rendszeres hibák), továbbá megjelenik az „U” kiterjesztett mérési bizonytalanság is.
Közvetett mérés esetében tehát ismernünk kell az eredmény egyenletét (matematikai modellt), azaz a matematikai függvényt az eredmény kiszámítására. A szakirodalom helyenként „modellfüggvénynek ” nevezi az eredmény egyenletét, egyébként nagyon helyesen, hiszen a mérés valójában modellalkotási folyamat , ahogy azt a (3. fejezet) fejezetben bemutatjuk.
2.9. Az eredmény szokásos alakja
A mérendő mennyiségek a mérés tárgyát képező tényleges mennyiségek, általában az egyetlen Y mérendő vagy kimenő mennyiség több (i=1,2,…n) Xi bemeneti mennyiség függvénye az Y=f(X1, X2, … Xn) összefüggésnek megfelelően.
A soron következő összefüggések a NAT (Nemzeti Akkreditációs Testület) hivatalos kiadványában megtalálhatóak [2.1.] .
A mérési eljárást és a kiértékelési módszert az „f” modell-függvény képviseli. Az esetek többségében ez egy analitikus kifejezés, de lehet ilyen összefüggések csoportja is, amely a rendszeres hatásokra alkalmazott korrekciós tagokat és korrekciós tényezőket tartalmaz, és ezért olyan összetettebb kapcsolatra vezet, amely egyértelműen nem írható le egyetlen függvénnyel. Lehet továbbá, hogy kísérleti úton vagy csak számítási algoritmusként van meghatározva, vagy „f” lehet mindezek kombinációja is.
A mérendő mennyiség egy becslése az y-nal jelölt kimeneti becslés, amit a modellfüggvényből kapunk, ha az Xi bemeneti mennyiséget az xi bemeneti becsléssel helyettesítjük:
|
|
(2.33) |
A becslésre felírt összefüggésben kétféle bemeneti mennyiséget látunk. Az egyik típus a bemeneti mennyiségek a modell szempontjából fontos összes hatásnak megfelelően korrigált legjobb becslései, ezeknél „A” betűvel való jelölés látható az indexekben. A másik típus azon korrekciók csoportja, amelyeket önálló bemenő mennyiségként veszünk figyelembe, itt „B” betűt látunk az indexekben.
Tehát értékük és bizonytalanságuk meghatározásának módjától függően az Xi bemeneti mennyiségek két csoportra oszthatók:
-
Azokra a mennyiségekre, amelyek értékét és a hozzájuk tartotó bizonytalanságot közvetlenül az adott mérésből határozták meg. Ezek az értékek származhatnak például egyetlen leolvasásból, ismételt leolvasásokból vagy tapasztalaton alapuló döntésekből. Tartalmazhatják az eszközök leolvasási korrekcióit, a befolyásoló mennyiségek miatti korrekciókat, amilyen például a környezeti hőmérséklet, légnyomás, nedvességtartalom.
-
Azokra a mennyiségekre, amelyek becslései és a hozzájuk tartozó bizonytalanságok az adott mérés esetén külső forrásból származnak. Ilyen mennyiségek a kalibrált etalonok vagy a tanúsított anyagminták értékei, vagy a kézikönyvekből származó adatok.
Az előírások a bizonytalanságokat annak megfelelően, hogy a modellfüggvényben szereplő egyes mennyiségek melyik csoporthoz tartoznak, „A” és „B” típusba sorolják.
Ha alaposan megvizsgáljuk az „Y” kimeneti mennyiség becslésére felírt fenti összefüggést, akkor látható, hogy a mérési eredményben szereplő „mérőszám” alapvetően három tagból tevődik össze, amelyek a következőek:
-
Helyes érték, azaz a valódi érték legjobb becslése a modellfüggvény szerint kiszámított átlaggal (egy bemeneti mennyiség esetében egyszerűen a mért adatok átlagával)
-
Korrekciók, azaz a rendszeres hibák előjeles eredője, jele H
A két fenti érték az eredményben különbség formájában jelenik meg. Elkülönítésük csak akkor lehetséges, ha ismerjük az átlagot, vagy a korrekciók eredőjét.
-
(Kiterjesztett) bizonytalanság, azaz a konfidencia szinthez tartozó faktorral és a tapasztalati szórással számított konfidencia intervallum, jele U.
Szembetűnő, hogy a mérőszám 2/3 részben hibákkal kapcsolatos adatokat tartalmaz.
Ez is alátámasztja azt, amit a hibákkal kapcsolatos fejezetben jeleztünk, miszerint jogosan merül fel az igény a mérési hibák okozóinak megismerésére, és a véletlen hibák minél határozottabb visszaszorítására.
A korrekciókról fentebb már írtunk, az „U” kiterjesztett mérési bizonytalanság értelmezése az European Cooperation for Accreditation of Laboratories” útmutatója (Mérésügyi Közlemények XXXIX./3. 1998.) [2.2.] alapján történik.
-
Ha ismert az eredmény egyenlete (modell-függvény), tehát közvetett mérésről van szó, és adott az eredmény egyenlete, akkor az „u” eredő bizonytalanság meghatározásánál – a bemeneti mennyiségek mért adatainak becslése (átlagok: xAi) és korrigált tapasztalati szórásaik mellett - meg kell határozni az un. ci súlyfaktorokat is. A súlyfaktorok az eredmény egyenlet (modell-függvény) bemeneti mennyiségek szerinti parciális deriválásával állíthatók elő, ezt a közvetett mérés modellfüggvénye kapcsán már láttuk. Az így kapott (eredő) bizonytalanság „A” típusú.
-
Az eredmény egyenletben lehetnek olyan bemeneti mennyiségek is (xBj), amelyeknek a bizonytalansága a „B” típusba sorolható. Ezekre a bemenő mennyiségekre is meg kell állapítani súlyfaktorokat, ezeknél cj jelölést alkalmaztunk. Előfordulhatnak olyan további bizonytalanságok is, amelyek a bemenő mennyiségek mellett származhatnak a mérési eljárásból (fizikai elv és módszer), továbbá a mérés kivitelezéséből is. (Pl.: az ismétlőképesség bizonytalansága).
-
A gyakorlatban alkalmazott méréstechnikai előírásokban „k” faktor értéke 95%-os valószínűségi szint mellett ≈2, ha labormérésekről és ipari mérésekről van szó, és a mintasokaság eloszlását Gauss-eloszlásnak feltételezzük. Megjegyezzük azonban, hogy a faktor értéke – 120 mérési adat esetében - Student-eloszlást feltételezve, 95%-os valószínűségi szinten 1.98, normál eloszlás esetében pedig - a mérések számától függetlenül - 1,96 lenne. Látható, hogy kerekítéssel ezek az értékek is kellően reprezentálva vannak az előírásokban található k=2 esetén.
2.9.1. A mérés „A” típusú (eredő) bizonytalanságának megadása
A variancia, és az abból számított szórás elméleti érték, az eloszlást jellemző un. funkcionál. A variancia a véges számú mérések alapján a gyakorlatban nem meghatározható, ehhez ugyanis az eloszlás sűrűségfüggvényének pontos ismerete szükséges. Helyette a tapasztalati szórást, esetleg a korrigált tapasztalati szórást, és az átlag szórását tudjuk a mérési adatokból meghatározni.
A méréstechnikai szakirodalomban látható képletek és kifejezések gyakran nem tesznek különbséget sem a fogalmak jelölésénél, sem azok megnevezésénél. Ezért készítettünk a (2.3. szakasz) és (2.4. szakasz) fejezetben egy metrológiai-műszertechnikai fogalmi összefoglalót. A legfontosabb valószínűség számítási összefüggések pedig a (3. fejezet) fejezetben találhatók.
Ennek ellenére ezen a helyen is fontosnak tartjuk az első előfordulásuk, felhasználásuk alkalmával rögzíteni a következő fontos fogalmakat:
-
Elméleti középérték, várható érték: Jelölése: μ, vagy ξ.
-
Átlag: A minta középértéke. Empirikus, tapasztalati átlag. A várható érték, azaz elméleti középérték, vagy első centrális momentum legjobb becslése. Az empirikus eloszlás elhelyezkedését mutatja. Jelölése: x, vagy y felülvonás.
-
Szórás: Elméleti érték, a második momentum, más néven a variancia pozitív négyzetgyöke. Jelölése: σ. A variancia a szóródás (koncentráció) mértékszáma.
-
Tapasztalati szórás: A szórás torzított becslése, kiszámítása az átlagtól való eltérések négyzetösszegéből történik úgy, hogy azt „n”-nel osztjuk, majd a kapott értékből négyzetgyököt vonunk. Jelölése: s
-
Korrigált tapasztalati szórás: Az előzőhöz hasonló módon számítjuk, de az osztás „n-1”-gyel történik, mert az átlag felhasználása miatt csökken a szabadságfok. Jelölése: s*
Látható, hogy helyes, ha az elméleti jellemzőket (funkcionálok) görög betűvel, és az empirikus úton kapottakat latin betűkkel jelöljük, így az elnevezések és a számítási módok nem keverednek.
Az „A” típusú bizonytalanság ismert modellfüggvényt felhasználva, egymástól független bemenő mennyiségek esetében, amelyek valószínűségi változók, a következő képlettel határozható meg:
|
|
(2.34) |
Látható, hogy a képletben következetesen az átlagok korrigált tapasztalati szórásával, mint az elméleti szórás torzítatlan becslésével számoltunk. Az összefüggés hátterében az eredő variancia számításának módja áll.
2.9.2. A mérés „B” típusú bizonytalanságának megadása
A „B” típusú bizonytalanságok megadása már nehezebb, és mérési munkában való komolyabb jártasságot, műszerismeretet, stb. feltételez. Ebben a formában ugyanis lehetőség van minden olyan tényező figyelembe vételére, amely az adott ismereti szinten számba vehető. Elsődlegesen az eredmény egyenletben (modell-függvény) szereplő olyan bemeneti mennyiségek bizonytalanságát kell megbecsülni, amelyek esetében nem meghatározható a tapasztalati szórás. Ezeken felül figyelembe lehet venni további bizonytalanságokat is.
Az „uj” bizonytalanságokat a következő módon lehet becsülni:
-
A korábbi mérések adataiból,
-
Az anyagok és eszközök tulajdonságainak ismeretéből, az ezekre vonatkozó tapasztalatokból,
-
A kalibrálási és egyéb bizonyítványokban megadott adatokból,
-
A kézikönyv/műszerkönyv adatokhoz tartozó bizonytalanságokból,
-
A mérés körülményeiből,
-
A mérést végző személy ismétlőképessége alapján, stb.
A „B” típusú bizonytalanságok eredője, ha ezek a bizonytalanságok egymástól független véletlen mennyiségek, a következő módon számítható:
|
|
(2.35) |
A szakirodalomban a jelölésre szándékos az „u” betű alkalmazása, hiszen itt bizonytalanságról (uncertainty) van szó.
Irodalmak
[2.1.] A mérési bizonytalanság meghatározása kalibrálásnál. Nemzeti Akkreditáló Testület, NAR-EA-4/02. sz. kiadvány . 2003.
[2.2.] Mérésügyi Közlemények XXXIX/3. Nemzeti Akkreditáló Testület. 1998.