7. fejezet - Spektrum analízis a méréstechnikában
7.1. Analóg frekvenciaanalízis
Ebben a fejezetben az ábra és képanyagok tekintetében a Brüel és Kjaer műszergyártó cég által forgalmazott analizátorokat és tartozékaikat felhasználó műszaki szakemberek részére készült kézikönyvre támaszkodtunk: R. B. Randall: Application of B&K Equipment to Frequency Analysis, 1977. [6.3.] . (A „B & K” cég napjainkban már mintegy 70 éves múltra tekinthet vissza, és vezető a hang-és rezgésmérés mérőeszközeinek gyártásában. Korszerű gyártmányai mellett, a felhasználókat tudományos igényességgel elkészített segédletekkel is támogatja.)
Villamos jelek frekvencia spektrumának meghatározása „klasszikus” analóg formában úgy történik, hogy az analizálni kívánt jelet különböző középfrekvenciájú analóg szűrőkön, vagy egyetlen, de középfrekvenciáját adott (vizsgált) frekvencia tartományban folyamatosan változtatni képes szűrőn bocsátják át, miközben mérik a jel teljesítményét (amplitúdóját).
Egy rögzített középfrekvenciájú szűrő válasza a bemenő jelre a bemenő jel és a szűrő (mint átviteli tag) súlyfüggvényének konvoluciója, amint az a rendszertechnikából ismert. Ennek az időtartománybeli folyamatnak, a Laplace transzformációs szabályok szerint, az operátor térben két komplex függvény szorzata felel meg, nevezetesen a bemenőjel Laplace transzformáltjának és a szűrő-súlyfüggvény Laplace transzformáltjának szorzata. A „frekvencia térben” ezért úgy tekinthetjük, hogy a szűrőn átengedett jel amplitúdó spektruma két individuális jel amplitúdó spektrumának szorzata. Amennyiben a bemenő jel és a szűrő teljesítmény spektruma adott, akkor a kimenő jel a két teljesítmény spektrum szorzata lesz, amint a következő ábrán szemléltetjük.
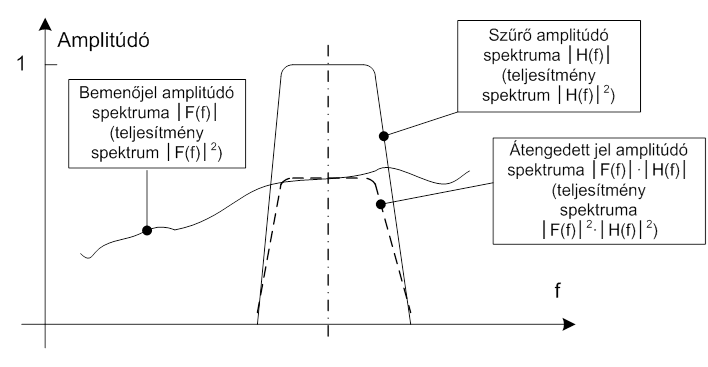
Ugyanakkor a bemenő jel összetevőinek fázisát is befolyásolja a szűrő, ennek azonban nincsen hatása a jel teljesítményére, és a méréstechnikában a fázishelyzetet - kivételektől eltekintve - a nem is szokás ábrázolni.
7.1.1. Analóg szűrők jellemzői
A 7.2. ábra ábra egy egyszerű analóg szűrő tömbvázlatát mutatja.

A vizsgált jel teljes spektrumát csak úgy kaphatjuk meg, ha a szűrő középfrekvenciát léptetjük, esetleg célszerűen választott sebességgel „csúsztatjuk” a kérdéses frekvencia tartományban. A léptetés, illetve csúsztatás sebességét a tömbvázlatban látható átviteli tagok jelet késleltető tulajdonságai határozzák meg. Éppen ezért az analizálás helyessége érdekében részletesen meg kell vizsgálnunk az átviteli tagok dinamikai tulajdonságait, mert ezek hatása döntő az eredményre.
7.1.1.1. Szűrők és szűrő átviteli karakterisztikák
Alapvetően meg kell különböztetni konstans abszolút sávszélességű és konstans relatív (százalékos) sávszélességű szűrőket. A konstans relatív sávszélességet mindig a hangolható középfrekvencia bizonyos meghatározott százalékában kapjuk. A (7.2. ábra) ábrán, összehasonlítás céljából, a kétféle sávszélességet lineáris és logaritmikus frekvencia tengely mentén ábrázoltuk, mert így világítható meg legjobban a két szűrő típus, és az ábrázolás közötti különbség. Az esetlegesen zavaró arányeltolódások logaritmikus lépték és konstans relatív sávszélesség alkalmazása esetében szűnnek meg. A logaritmikus lépték egyben az ábrázolható frekvencia tartomány nagyságát is megnöveli.
A konstans sávszélesség nagyjából egységes felbontást biztosít a lineáris frekvencia skálán, ami akkor előnyös, ha a harmonikus komponensek egyforma felbontását és elkülöníthetőségét kell biztosítani. Megjegyezzük, hogy a régi analóg regisztrálók és megjelenítők sajátosságai miatt, lineáris skála esetében, a lineáris frekvencia skála erősen korlátozta a vizsgált frekvenciatartomány nagyságát. A korszerű, digitális adatrögzítés ezt a problémát kiküszöbölte, mert a tárolt adatokból a tetszőlegesen választott frekvencia tartomány kiemelhető. Ha viszont a spektrumot ki kell nyomtatnunk, akkor a probléma természetesen továbbra is fennáll, és ilyen esetben lineárisan legfeljebb két-három frekvencia dekádot szoktak megjeleníteni.
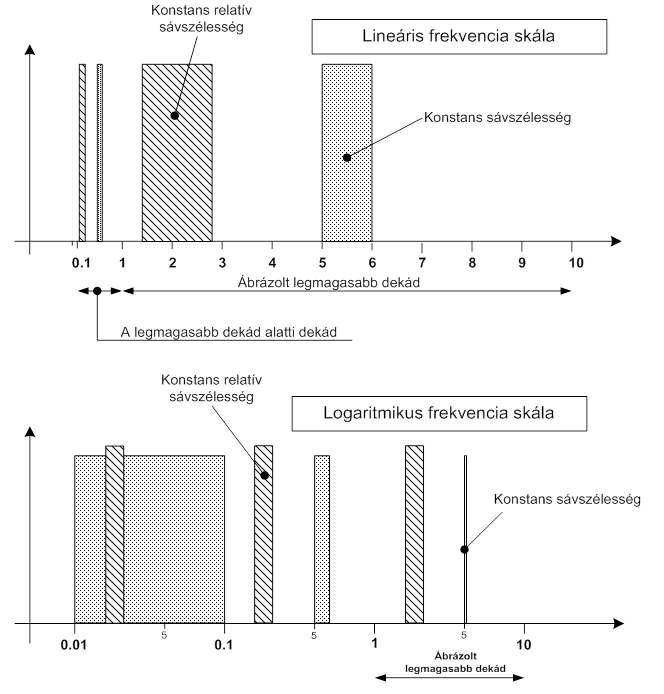
A konstans relatív sávszélesség egyenletes felbontást eredményez a logaritmikus frekvencia skálán, és ezért a nyomtatott protokollok esetében (pl. műszer kalibrálás) egy nagyobb frekvencia tartomány megjelenítése sem okoz gondot. A konstans relatív sávszélesség másik előnye az, hogy a jósági tényezővel (Q) közvetlen kapcsolatban áll. A Q faktor a rezonancia csúcsok nagyságát (magasságát) jellemzi. Ezért olyan spektrumok elemzése során, amelyeknél várhatóan számos rezonancia csúcs fog megjelenni, és ezek kiértékelése fontos a feladat szempontjából, célszerű konstans relatív sávszélességű analízist végezni. Természetesen olyan sávszélességgel kell analizálni, amely kisebb, mint a legkeskenyebb rezonancia csúcs szélessége.
Más okok is a logaritmikus frekvencia skála alkalmazása mellett szólnak:
-
Bizonyos összefüggések jobban érzékeltethetők log-log léptékű skálán, ilyen például a vizsgált átviteli tag (műszer, mérőlánc) integráló jellege, amely ilyen léptékezés mellett egy -20 dB/dekád meredekségű egyenest eredményez.
-
Több soros tag eredő frekvencia átvitele egyszerűen meghatározható.
Megkülönböztetett figyelmet érdemel a konstans relatív sávszélességű szűrők két csoportja, mert ezeket az akusztika és a rezgésvizsgálat területén rendszeresen alkalmazzák, ezek az oktáv- és tercszűrők. Az oktávszűrő esetében a szűrő áteresztő sávjának felső határfrekvenciája kétszerese az alsó határfrekvenciának, ami relatív sávszélességként 70.7 %-ot eredményez. Ez az alábbiak szerint adódik:
|
|
(7.1) |
A sávközép frekvencia a felső és alsó határfrekvencia mértani közepe:
|
|
(7.2) |
Az abszolút sávszélesség megegyezik az alsó határfrekvenciával:
|
|
(7.3) |
A relatív sávszélesség a fentiek felhasználásával:
|
|
(7.4) |
A sávközép frekvenciákat nemzetközi szabványokban rögzítették, valamint azt, hogy a referencia középfrekvencia 1000 Hz legyen.
Látható, hogy ilyen módon három frekvencia dekáddal és ezeken belül 10 oktáv sávval az akusztikában fontos frekvenciasáv lefedhető (itt: 22.5 Hz – 22.5 kHz). Az 1000 Hz-es referenciát viszonyításul véve 22.5 Hz a legalacsonyabb alsó határfrekvencia, és ennek a legalsó oktávsávnak 31.5 Hz a középfrekvenciája. A legfelső (legmagasabb) oktávsáv felső határfrekvenciája 22.5 kHz és 16 kHz a középfrekvenciája.
A szűrés finomítható a terc sávok létrehozásával, amelynek során minden oktávsávban három aláosztott, un. terc sávot képeznek, az alábbi formula szerint:
|
|
(7.5) |
A tercsávok középfrekvenciáját az oktávokhoz hasonlóan ugyancsak a geometriai középérték segítségével határozzuk meg.
|
|
(7.6) |
A (7.9. ábra) ábrán látható módon, egy frekvencia dekádban 10 terc sáv kap helyet, mert:
|
|
(7.7) |
A relatív sávszélesség pedig a következők szerint állapítható meg:
|
|
(7.8) |
7.1.1.2. Szűrő karakterisztikák a gyakorlatban
A gyakorlatban megépíthető szűrők karakterisztikái sajnos eltérnek az ideálistól.
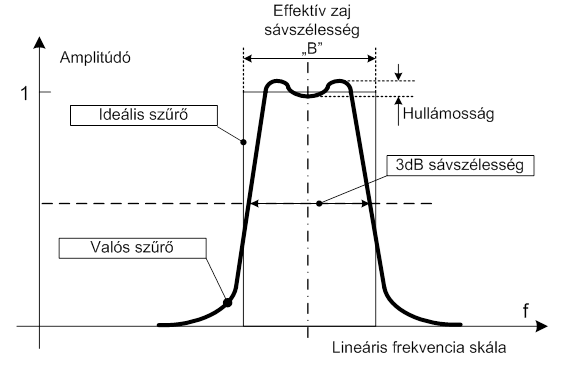
Ha az áteresztő sávban látható „hullámosságot” elfogadható határok között lehet tartani, akkor a gyakorlati szűrő a szelektivitásával és a sávszélességével jellemezhető.
Bevezetőben meg kell említeni a szűrők Beff „effektív zaj sávszélességét” is. Az effektív zaj sávszélességet úgy számítják ki, hogy a valós szűrő karakterisztikája és a frekvencia tengely által bezárt terület értékét (a karakterisztika integrálja a frekvencia szerint) osztják a referencia szinttel. Az effektív zaj sávszélesség másként fogalmazva az a frekvenciasáv, amely egy olyan ideális szűrőhöz tartozik, amely az ideális fehér zajból ugyanakkora teljesítményt enged át, mint az azonos referencia szinttel rendelkező valós szűrő. Ennek a jellemzőnek fontos szerepe van a véges idejű jelminták analízise során. A véges „T” idejű jelmintához (valós méréstechnikai helyzet) tartozó effektív zaj sávszélesség az alábbi szerint állapítható meg:
|
|
(7.9) |
Egy másik sávszélességet is szokás a szűrőkkel kapcsolatban emlegetni, ez pedig a 3 dB sávszélesség. Ez a sávszélesség ahhoz a teljesítmény szinthez tartozik, amely 3 dB értékkel van a szűrő átengedő sávjának csúcsértéke alatt. Tekintettel arra, hogy ennek értéke igen közel van az effektív zaj sávszélességhez, és könnyebben mérhető is, a gyakorlatban előszeretettel alkalmazzák ezt az értéket a szűrő jellemzőjeként. Csak igen gyenge szelektivitással rendelkező szűrők esetében van a két érték között szignifikáns eltérés.
A sávszélesség arról ad információt, hogy a szűrő mennyire képes szeparálni az egyes frekvencia komponenseket, megközelítőleg azonos szinten.
A szelektivitás azt írja le, hogy a szűrő mennyire képes szeparálni a komponenseket eltérő szinteken. A szelektivitást az „alaktényezővel” szokás jellemezni. Rendeljük egyszerűség kedvéért a szűrő átengedési sávjának maximumához a 0 dB értéket (1:1 átvitel). Az alaktényezőt általában, mint a szűrő -60 dB átviteli szintjéhez tartozó sávszélességének és a 3 dB sávszélességének arányát szokták definiálni. Ha a szűrő dinamikája kisebb, mint 60 dB (1000-szeres szorzó), akkor az alaktényező meghatározásához a -40 dB szinthez tartozó sávot alkalmazzák.
|
|
(7.10) |
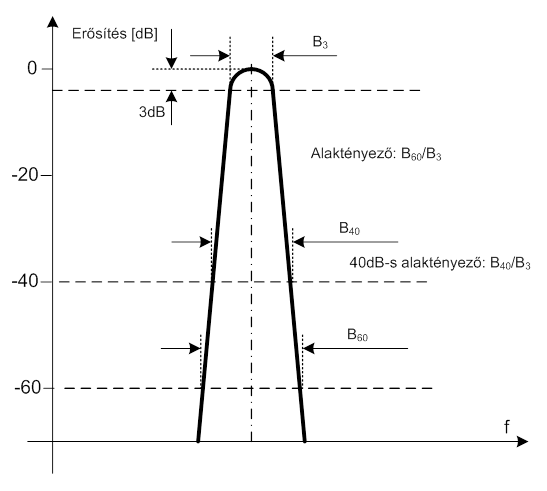
Az alaktényezőt általában a lineáris frekvencia tengelyre szimmetrikus és állandó sávszélességű szűrők jellemzésére használják, de más alkalmazás is ismert.
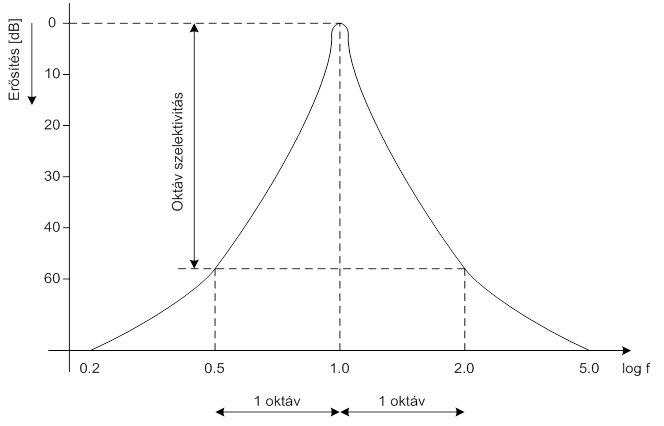
A konstans relatív sávszélességű szűrők jellemzésére, amelyek karakterisztikája a logaritmikus frekvencia tengelyre nézve szimmetrikus, az oktáv, vagy terc szelektivitás fogalmakat alkalmazzák. Ez a szűrő csillapítását adja meg a sávközép frekvenciához viszonyítva egy oktávnyira, vagy egy tercnyire.
7.1.1.3. A szűrő válaszideje
Ha a jel „hirtelen” kerül a szűrő bemenetére, az energiatárolók miatt, nyilvánvalóan idő szükséges ahhoz, hogy a kimeneten a válasz megjelenjen. Legyen a jel harmonikus, és frekvenciája a szűrő átengedési sávján belüli. Ebben az esetben a harmonikus jel amplitúdóját a szűrő 1:1 arányban átengedi, de a kimeneten a jel állandósult értéke csak T=1/B idő eltelte után jelenik meg, ahol „B” a szűrő sávszélessége.
A szűrő „TR válaszideje” mellett, szokás még a szűrő „felfutási idejéről” és „beállási idejéről” is beszélni, de ez utóbbinak csak akkor van jelentősége, ha a szűrő válaszában van egy jelentősebb lappangási idő is. A felfutási idő természetesen rövidebb, mint a válaszidő.
Általánosságban:
|
|
(7.11) |
Ezt az összefüggést a konstans sávszélességű szűrők esetében alkalmazzák.
A konstans relatív sávszélességű szűrők esetében kissé módosul ez a formula:
|
|
(7.12) |
ahol
|
b |
relatív sávszélesség |
|
|
n R |
az „f” frekvencia TR válaszidőben történő előfordulása |
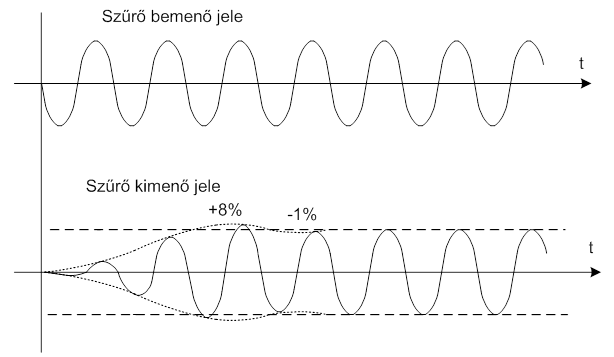
Ez azt jelenti, hogy b=1% esetén nR~100 lesz. Ezek a megfogalmazások más módon írják le azt a szabályt, hogy „B” sávszélességgel történő analízishez minimálisan 1/B idő szükségeltetik.
A 7.7. ábra ábra egy tercszűrő időbeli válaszát mutatja „hirtelen” ráadott harmonikus jel esetében. Mivel a relatív sávszélesség 23.1% azt gondolnánk, hogy 4.3 periódus után állandósul a szűrő kimenete. Ugyanakkor az ábrán az látszik, hogy a kellő pontossághoz 5-6 periódus szükséges. A két, becsléshez alkalmazott összefüggést valójában extrém esetre írtuk fel, arra, hogy a szűrő bemenetére „hirtelen” kerül a harmonikus gerjesztés. Ha olyan analóg szűrőt alkalmaznak, amelynél az analízis „csúsztatással” történik, tehát a szűrő átviteli sávját meghatározott sebességgel mozgatják a frekvencia tengely „mentén”, a gerjesztés nem ugrásszerű. Ezzel együtt, becslés céljára, még „sweep”-elés (csúsztatás) esetén is ezeket a formulákat szokás alkalmazni.
7.1.1.4. Analóg detektorok és rekorderek
Az analóg szűrési technika „hőskorában” természetesen szükség volt olyan analóg áramkörökre is, amelyek az analizált jelekkel a szükséges és meghatározott matematikai műveleteket el tudták végezni. Ezeknek az analóg detektoroknak a mai digitális technikák birtokában megszűnt a jelentősége, de a teljesség kedvéért tömören ismertetjük ezeket is.
A híradástechnikában a zajokat a hasznos jelre szuperponálódó, olyan véletlen feszültség, vagy áram „jelekként” interpretálják, amelynek lineáris átlagértéke zérus.
A zaj teljesítményének mérőszáma tehát a négyzetes átlag lesz, ami tulajdonképpen a zaj varianciája, hiszen a zaj-jel csak AC komponenseket tartalmaz. Az átlagolás „kellően” hosszú idő alatt történik, erre utal a T0 bevezetése. Minél hosszabb ugyanis az átlagolási idő, annál kevésbé függ a kapott érték a T0 időtartamtól. Határértékként így valóban a varianciát kapjuk:
|
|
(7.13) |
feltételezéssel:
|
|
(7.14) |
ahol
|
x MS |
négyzetes átlag (Mean Square) |
|
|
x RMS |
négyzetes átlag gyöke (Root Mean Square), más néven effektív érték |
A fentieket általánosítva az alábbiakat mondhatjuk:
|
Össz-jelteljesítmény=DC teljesítmény+AC teljesítmény |
(7.15) |
Tekintettel arra, hogy a jell (feszültség, vagy áram) négyzete a teljesítménnyel arányos, másként is fogalmazhatunk:
|
Négyzetes átlag=Átlag négyzete+ Variancia |
(7.16) |
Ha tehát általánosságban az x(t) időben változó jel átlaga, „σ” a jel szórása, és „s” a jel tapasztalati szórása, akkor a négyzetes átlag a valós, a gyakorlatban mérhető (empirikus) jelek esetében az alábbi képlet szerint számítható:
|
|
(7.17) |
A fentiek alapján, a mérnöki gyakorlatban az xRMS2 négyzetes átlagot a standard eltérésnek is tekintik, ha a jel lineáris átlaga zérus. A műszerek bementén ezért gyakran látható az alábbi megjelölés: „AC” (vagy „AC only”) és „DC”, ami azt jelenti, hogy a jel egyen-összetevője nélkül, vagy azzal együtt történik a mérés.
A valószínűségszámításból ismert összefüggéssel is igazolható a fenti összefüggés.
Legyen f(x) az „x” valószínűségi változó sűrűségfüggvénye. A variancia számítása a következő módon történik:
|
|
(7.18) |
Felbontva a zárójelet három tagot kapunk:
|
|
(7.19) |
Ismeretes, hogy:
|
és továbbá |
(7.20) |
Behelyettesítve látjuk, hogy a variancia számításának kifejezése igen leegyszerűsödik:
|
|
(7.21) |
Az összefüggés a sűrűségfüggvénytől függetlenül érvényes, és esetünkben célszerű a funkcionálok helyett az empirikus mérési adatokból számolható átlagértékkel és a tapasztalati szórással dolgozni. Ennek figyelembevételével a fenti összefüggés átalakul:
|
|
(7.22) |
Átrendezve igazolva látjuk azt az összefüggést, amelyet a jel DC és AC összetevőire bontva bemutattunk:
|
|
(7.23) |
A szűrő kimenetén tehát megjelenik egy időben változó AC jel. Egyrészt ahhoz, hogy a jel teljesítmény spektrumának komponenseit megkapjuk, a kimenő jel négyzetére van szükség. Másrészt az időben ingadozó amplitúdójú és változó előjelű jel statisztikai mérőszáma a négyzetes középérték. Vigyázat! Változó előjelű harmonikus jel lineáris átlaga ugyanis zérus is lehet, ha a jel szimmetrikus az idő tengelyre!
Diszkrét értékek esetében a négyzetes átlag gyökét az alábbi módon számoljuk:
|
|
(7.24) |
Az időben változó jel folytonos változó, ezért a négyzetes átlag gyökét integrálással határozzuk meg. Ha az átlagolás időtartama T1≤t≤T2, akkor az összefüggés az alábbi lesz:
|
|
(7.25) |
Említettük, hogy a harmonikus jel lineáris átlaga zérus, ezért a villamosságtanban a váltakozó áram és feszültség esetében a négyzetes átlag gyökét alkalmazzák, és hasonlóképpen van ez az információhordozó jel esetében is.
Tanulságos egy U0 amplitúdójú harmonikus jel esetében bemutatni a négyzetes átlag gyökének számítását:
|
|
(7.26) |
|
|
|
(7.27) |
|
|
|
(7.28) |
Tekintettel arra, hogy a négyzetes átlagot definíciója szerint a periódusidőre, és annak egész számú többszörösére számítjuk, a zárójeles kifejezés második tagja kiesik.
|
|
(7.29) |
A négyzetes jel előállítása analóg áramkörök alkalmazásával történhet úgy, hogy a jel pillanatnyi értékét négyzetre emeljük, így megkapjuk a pillanatnyi teljesítményt, és egy meghatározott idejű átlagolással ennek integrálját képezzük (MS: mean square). Minél hosszabb az átlagolási idő, annál kisebb a kapott értékek ingadozása, de persze, hosszú az analízishez szükséges időtartam.
Ha a bemenő jel dimenziójának megfelelően szeretnénk a spektrális tartalmat megjelentetni, tehát az amplitúdó spektrumra van szükség, akkor az előzőekben képzett négyzetes átlagból gyököt kell vonni, így kapjuk az RMS: Root Mean Square értéket.
Gyakran szükség van a kimenet-bemenet arány logaritmikus megjelenítésére is, méghozzá dB értékben. Ilyenkor logaritmikus áramkörök alkalmazására van szükség.
Az analóg technikában a jel négyzetes átlagának gyökét többféle módon képezik:
-
Analóg szorzó áramkör alkalmazásával a jelet önmagával megszorozzák, majd egy kapacitás segítségével megtörténik az átlagolás. A négyzetgyökvonást a visszacsatolásba iktatott négyzetre emelő szorzóáramkörrel valósítják meg. Egy precíziós egyenirányító áramkörrel először képezik a jel abszolút értékét, majd az így kapott jel egy logaritmikus erősítő bemenetére kerül. Az erősítő kimenő jelét megkétszerezik, és ezt követően egy exponenciális átviteli jellegű műveleti erősítő bemenetére kapcsolják. Az átlagolás és négyzetgyökvonás az előbbiekhez hasonló módon történik.
-
FET tranzisztor segítségével közvetlenül megtörténik a bemenőjel négyzetre emelése, ezt követi az átlagolás és a gyökvonás.
-
Termo-csatolásos módszerrel úgy, hogy a bemenő jelet, vele arányos árammá konvertálva egy parányi fűtőszálat melegítenek. A fűtőszál hőmérséklete a váltakozó jel négyzetével arányos. A fűtőszál hőmérséklet változását termisztor, termoelem, vagy egy kettős tranzisztoros kapcsolás figyeli.
Az analóg feldolgozó áramkörök (detektorok) kimenő jelét régebben
-
kijelzőre
-
megjelenítőre, vagy/és
-
regisztrálóra
kapcsolták. Az analóg, vagy digitális kijelző tette lehetővé az analizátorok beállítását, a mért értékek real-time megfigyelését. A megjelenítésben a mai napig is használatos oszcilloszkópok játszották a fő szerepet, míg a regisztrálók családja volt hivatott a szűrés eredményét papír alapú regisztrátumon megörökíteni. A regisztrálók a korabeli műszertechnika és finommechanika csúcstechnikáját képviselték, mert előírt pontossággal és igen nagy frekvencia tartományban képesek voltak a jelszintek rögzítésére. Az igényes regisztrálók mindegyike szabályozókörre épült. A bemenetükre kerülő jel a szabályozókör alapjeleként funkcionált, és a papíron mozgó írótoll (vagy fehér viasszal bevont felületű színes papíron csúszó karcoló tű) pozíciója volt tekinthető a szabályozott jelnek. Az írótoll pozícióját mérték, és szabályozási eltérés esetén a kívánt helyzetbe mozgatták. Magasabb frekvenciák mérése esetében (akusztika, rezgések) a karcoló tűt rugalmas vezetékkel csapágyazták. A rekordereket minden esetben egyfajta aluláteresztő szűrőként kellett kezelni.
A regisztrátum (papír) mozgatásáról külön, precíziós elektromechanikus szerkezet gondoskodott, hiszen a papír mozgása az idő tengelyt, vagy spektrumok esetében a frekvencia tengelyt jelenítette meg. Az akusztikában ezen felül lehetséges volt polár-koordinátás szintrögzítésre is, mert a hangszórók és mikrofonok iránykarakterisztikáját csak így lehetett megjeleníteni. Ebben az esetben a kör alakú papír síkban történő forgatásával a szöghelyzetnek megfelelően lehetett a mért értéket rögzíteni. Az analóg szűrők (analizátorok) használata során külön kellett ügyelni a regisztrálás (írás) sebességére is, figyelembe véve a rekorder adta lehetőségeket. Nagyobb írássebesség magasabb vágási frekvenciát eredményezett, de ez szükségképpen rövidítette az átlagolási időt. A kisebb átlagolási idők kismértékű, míg a nagyobb átlagolási idők jelentősebb jelszint ingadozást eredményeztek.
7.1.2. Analóg analizátor (szűrő) típusok
Az analóg technikában az alábbi analizátor típusok voltak jellemzőek:
-
Diszkrét (léptető szűrős) analizátorok
-
Csúsztatott szűrős analizátorok
-
Párhuzamos (real-time) analizátorok
-
Idő-kompressziós analizátorok (real-time).
Az idő-kompressziós analizátorok tulajdonképpen már átvezetnek a digitális technikába, de a működésük alapját még az analóg heterodin analizátor adja.
A négy analizátor típus felépítését tömören összefoglaljuk.
Az első két típus esetében feltételeznünk kell, hogy az analizálandó jel stacionárius , mert az analízist a sávokban nem egyszerre, hanem időben eltolva végezzük.
7.1.2.1. Diszkrét (léptető szűrős) analizátorok
A 7.8. ábra ábra a rögzített középfrekvenciájú sávszűrőkkel felépített analizátor tömbvázlatát mutatja. A jel ebben az analizátorban a kondicionálás (erősítő fokozat) után közvetlenül egy sorozat párhuzamosan kapcsolt sávszűrőre kerül, amelyek együttesen lefedik az analízis szempontjából érdekes frekvencia tartományt, ld.: 7.8. ábra
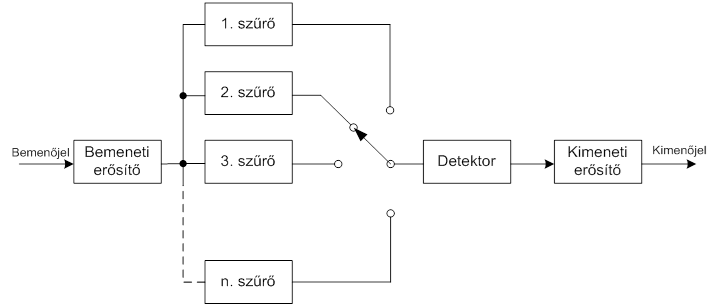
A detektort szekvenciálisan kapcsolják a sávszűrőhöz, amely sorban egymás után méri a sávszűrők kimenetén megjelenő jelet. Az egyes sávokban való tartózkodás idejét az analizálandó jel becsült spektruma alapján kellett beállítani, hasonlóképpen tekintettel kellett lenni a detektorok „feléledési” idejére is. A sávszűrők kimenetének léptetését szinkronizálták az analizátorhoz kapcsolt rekorderrel, pontosabban annak papírsebességével, és az írás sebességével.
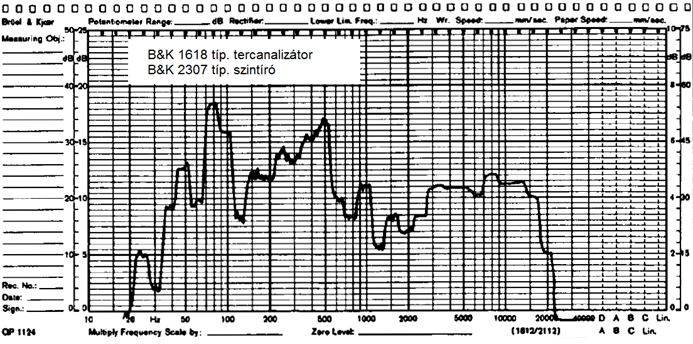
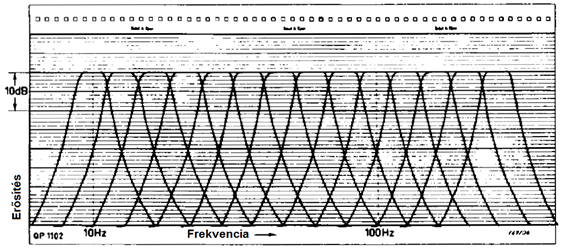
A 7.10. ábra ábra egy léptető szűrős analizátorral felvett terc spektrumot mutat. Ilyen felépítésű analizátorokat kizárólag oktáv és terc sávos szűrésre alkalmaztak, mert a keskeny sávú analízis, a nagyszámú szűrő alkalmazása miatt, az analizátor előállítási költségeit aránytalanul megnövelte volna.
7.1.2.2. Hangolható, „csúsztatott” szűrős analizátorok
A keskenysávú analízis céljaira sokkal jobban megfelel a hangolható középfrekvenciájú szűrő, amelynek tömbvázlatát a (7.11. ábra) ábrán láthatjuk. A szűrőt igény szerint be lehet állítani mind konstans sávszélességre, mind pedig konstans relatív sávszélességre.

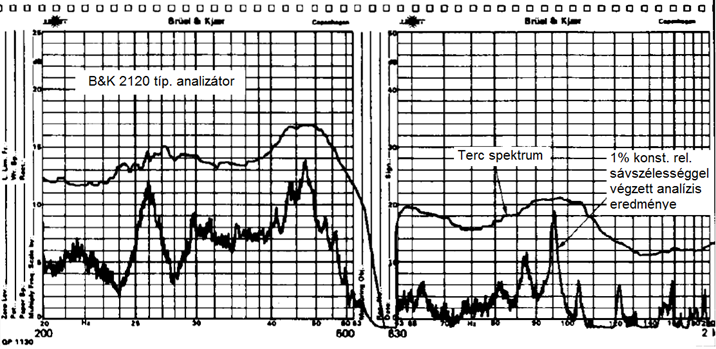
A 7.12. ábra ábra ugyannak a jelnek a spektrumát mutatja, amelyet a 7.12. ábra ábrán láthatunk tercsávos analízis után, annyi módosítással, hogy csak a 200…2 kHz tartományt mutatjuk be. Sajnos a regisztráló papír más célra készült, de így is látható, hogy 600 Hz után 630 Hz sávközép frekvenciával folytatódik. A regisztrátum felső görbéje a konstans sávszélességű tercsávos, míg az alsó az 1%-os relatív sávszélességgel végzett analízis eredményét mutatja. Látjuk, hogy a hangolható (csúszatott) szűrős analízis eredményeként folytonos spektrumot kapunk, persze tudnunk kell, hogy a görbe minden egyes pontja az adott szűrő sávszélességben megjelenő spektrum integrálját adja.
7.1.2.3. Real-time párhuzamos analizátorok
Ez az analizátor típus lehetővé teszi, hogy a vizsgált jelről folyamatosan, és egyszerre kapjunk spektrumképet. Lényegesen gyorsabb a vizsgálat, és természetesen jobban igazodik a jel gyors változásaihoz. Az analizátor tömbvázlatát a 7.13. ábra ábra mutatja.
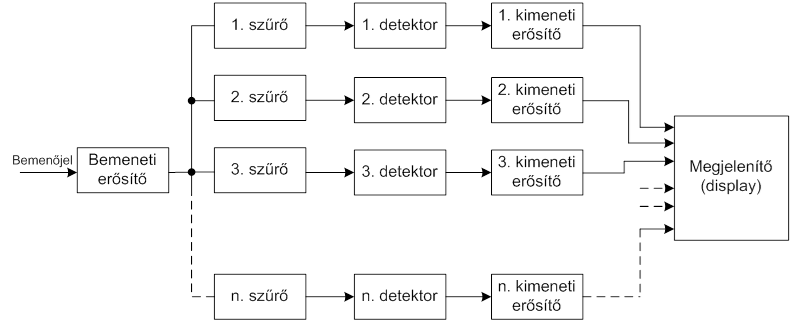
A tömbvázlatnak megfelelő módon épültek fel az első tercsávos real-time analizátorok. Tekintettel a jel spektrumának gyors időbeli változására, a megjelenítésre olyan monitorokat építettek, amelyek a spektrumot világító oszlopok formájában mutatták (a megjelenített kép a hisztogramokra emlékeztetett).
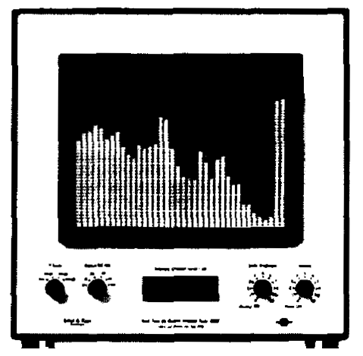
Az analóg real-time analizátorokat a digitális szűrési technika „legyőzte” ugyan, de elszórtan még lehet ilyen eszközökkel munkahelyeken találkozni. A korszerű digitális analizátorok által a számítógép monitorára adott eredmény nagyjából ma is ugyanolyan, mint az egykori analóg berendezések esetében volt.
7.1.2.4. Idő-kompressziós, real-time analizátorok
A tercsávos real-time analizátorok a megvalósíthatóság szempontjából még éppen a technikai ésszerűség határán helyezkednek el. A frekvencia sávot tovább csökkentve, keskenysávú analizátort párhuzamos szűrőkkel és detektorokkal építeni egyszerűen nem lenne gazdaságos, a készülék a magas ár miatt nem lett volna piacképes. A keskenysávú real-time analízist más módon kellett megoldani, így születtek az első idő-kompressziós analizátorok, amelyek működésének alapját a következőkben röviden ismertetjük.
A rendszer működésének alapja az, hogy a vizsgálandó jelet rögzítik (régen FM magnetofonokkal, manapság természetesen korszerű jelrögzítőkkel, illetve számítógépben), majd a felvett jelet ismert sebességre felgyorsítva analizálják a folyamatot, tercsávos párhuzamos analizátorokkal. A real-time analízis ugyanis megköveteli a párhuzamos működést.
A szűrönkénti, egyenként történő analízishez szükséges időt (szűrő „feléledési” ideje) már bemutattuk korábban. Determinisztikus jel esetében a szűréshez szükséges idő a szűrő TR válaszidejével megegyező, ezt láttuk a 7.1.1.3. szakasz fejezetben:
|
|
(7.30) |
Ugyanakkor sztochasztikus jeleknél , keskenysávú analízis esetében, a szűréshez szükséges időt tekintve a szűrő válaszidejét a szűrőben való tartózkodás TD ideje váltja fel. Ennek következtében már nem a válaszidő, hanem a TA átlagolási idő határozza meg a szűréshez szükséges időt. Az átlagolási idő és a szűrő sávszélessége befolyásolják az analízissel kapott eredmény bizonytalanságát (pontosságát), amit az „s” empirikus szórás jellemez. Az RMS detektorral végzett keskenysávú analízis esetében, az analizált jel empirikus szórását, a sávszélességből és az átlagolási időből az alábbi összefüggés révén kapjuk:
|
|
(7.31) |
ahol
|
B |
sávszélesség |
|
|
T A |
átlagolási idő |
A sztochasztikus jelek esetében általában normál amplitúdó eloszlást feltételezhetünk . Az analízis eredménye a helyes értéket annál jobban megközelíti, minél nagyobb az átlagolási idő. Végső soron ez az egyetlen paraméter, amellyel az empirikus szórást befolyásolni lehet. A sávszélességhez ugyanis nem lehet „hozzányúlni”, mert adott esetben ez az analizátor fix jellemzője, amely vagy terc/oktáv, vagy keskenysáv.
Az empirikus szórás értékét mutatja a BTA szorzat függvényében, az alábbi táblázat:
|
BT A |
10 |
20 |
30 |
40 |
50 |
80 |
100 |
|
s [dB] |
1.5 |
1.0 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
Azért, hogy mind a determinisztikus, mind pedig a sztochasztikus jelekre egyaránt alkalmazható feltételt találjunk, az előzőekben ismertetett szabályt némiképpen módisítani kell. Az átlagolás két feltételét összefoglaljuk a szűrőben való TD tartózkodási idő segítségével. A tapasztalati összefüggés a következő:
|
|
(7.32) |
ahol
|
B |
a szűrő sávszélessége |
|
|
T D |
a szűréshez szükséges idő (tartózkodási idő) |
|
|
K |
tapasztalati állandó |
Az idő-kompressziót az analóg analizátorokban egy igen szellemes és egyszerű úton valósítják meg.
Tekintettel arra, hogy a TD idő és a „B” sávszélesség szorzata állandó, a sávszélesség virtuális csökkentésének (tehát a keskeny sáv irányába történő elmozdulásnak) egyik lehetséges módja az, ha a TD időt M-szeresére megnöveljük. Ennek olyan hatása van, mintha a sávszélességet M-ed részére csökkentettük volna. Ezt úgy érik el, hogy a vizsgálandó jelet tárolják, majd M-szeresére felgyorsítva kapcsolják az analizátor bemenetére. Ilyen módszerrel lehetségessé vált a jelek keskenysávú real-time analízise. Napjaink digitális technikája esetében ez nem jelent problémát, az analóg technikában a jelrögzítés mérőmagnetofonok segítségével történt, és a szalag sebességét gyorsították fel a visszajátszás során.
Gyakran okoz gondot a csatornánkénti TD tartózkodási idő szükséges (előírt) hossza is, mert az analízis összes ideje tetemesé válhat. Az idő-kompressziós módszerrel a csatornánkénti TD időt is lehet csökkenteni, mégpedig úgy, hogy virtuálisan megnöveljük a „B” sávszélességet. Ezt a felbontás lerontása nélkül kell biztosítani azáltal, hogy a jelet adott sebességgel (valós időben) rögzítik, majd azt az analízis céljára „M”-szer gyorsabban visszajátsszák.
A 7.15. ábra ábra mutatja, hogy ebben az esetben minden frekvenciát meg kell szorozni M-mel, és emiatt a felbontás ugyanolyan lesz, mintha a szűrő sávszélessége M-szer nagyobb lenne. Ennek eredményeként viszont a TD időt osztani lehet M-mel, ami virtuálisan annak felel meg, mintha az analízist M-szer gyorsabban végeztük volna. Ez volt végső soron az idő-kompresszió célja.
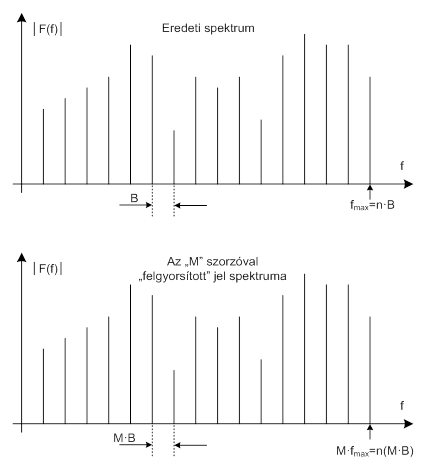
A nehézkes jelrögzítést napjainkban kiváltotta a digitalizálás, és a rendelkezésre álló tekintélyes memóriakapacitás. A módszert „kvázi” real-time analízisnek nevezték, mert a jel egy részét „ki kellett vágni” a jelfolyamból. A mai, korszerű digitális technikában a mintavétel és a feldolgozás megfelelő ütemezésével a real-time üzemmód valósággá válhatott.
7.1.3. Stacionárius jelek analízise a gyakorlatban
A következőkben röviden összefoglaljuk a determinisztikus és sztochasztikus stacionárius jelek analóg analízisével kapcsolatos gyakorlati tudnivalókat.
7.1.3.1. Diszkrét (léptetős) szűrős analízis
Az analízis sávszélességét a szűrő sávszélessége határozza meg, ami terc és oktáv lehet. Már jeleztük korábban, hogy a keskenysávú szűrés ebben a verzióban műszakilag nem megoldható. Az analízis során – a rekordereket is figyelembe véve - jellemzően az alábbi paramétereket lehetett beállítani:
-
Átlagolási idő
-
DC vagy AC jelrögzítés
és régebbi, írószerkezetekhez kapcsolt analizátorok esetében ezeken felül:
-
Rekorder írási sebessége
-
Papírsebesség
Példaként megjegyezzük, hogy 100 mm szélességű („függőleges tengely”) regisztráló papír esetében egy tercsáv 5 mm szélességűnek adódott a vízszintes tengely mentén.
Átlagolási idő megválasztása
Determinisztikus jelek esetében fő követelmény, hogy a szűrő okozta hullámosság elfogadható mértékű legyen. Ha egy adott sávban egyetlen harmonikus komponens fordul elő, akkor a hullámosság kisebb lesz, mint 0.25 dB, ha
|
|
(7.33) |
ahol „f” a harmonikus jel frekvenciája. Rendes körülmények között sok harmonikus komponens fordul elő egy tercsávon belül. Ilyen esetben „f” az a minimális frekvencia különbség, amely két komponens között előre becsülhető.
Magasabb frekvenciákon, ahol már igen sok komponens jelenik meg egy tercsávon belül, célszerűbb a sztochasztikus jelek esetében szokásos átlagolási idővel kalkulálni.
Sztochasztikus jelek esetében a jel amplitúdójának „s” empirikus szórása, tehát a megkívánt (előírt) bizonytalanság ismeretében meg lehet megbecsülni az átlagolási időt, az összefüggést az idő-kompressziós analízisnél már láttuk:
|
|
(7.34) |
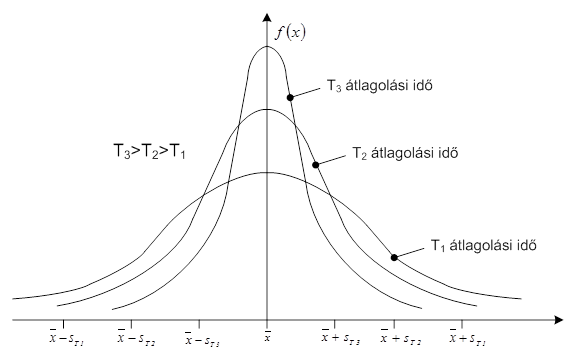
Tájékozódás céljából, táblázatosan összefoglaltuk az empirikus szórás értékeit decibelben, az átlagolási idő függvényében, adott terc sávközép frekvenciákon:
|
Terc sávközép frekvencia [Hz] |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
TA [s] |
2 |
6.3 |
20 |
63 |
200 |
630 |
2k |
6.3k |
20k |
|
0.1 |
1.2 |
0.7 |
0.4 |
0.2 |
|||||
|
0.3 |
1.2 |
0.7 |
0.4 |
0.2 |
|||||
|
1 |
1.2 |
0.7 |
0.4 |
0.2 |
|||||
|
3 |
1.2 |
0.7 |
0.4 |
0.2 |
|||||
|
10 |
1.2 |
0.7 |
0.4 |
0.2 |
|||||
|
30 |
1.2 |
0.7 |
0.4 |
0.2 |
|||||
|
100 |
0.7 |
0.4 |
0.2 |
||||||
|
300 |
0.4 |
0.2 |
|||||||
Oktávsávok esetében a sávszélesség háromszor nagyobb, ezért a fenti táblázatban látható átlagolási időket értelem szerűen harmadolni kell.
A jelminta hosszának megválasztása
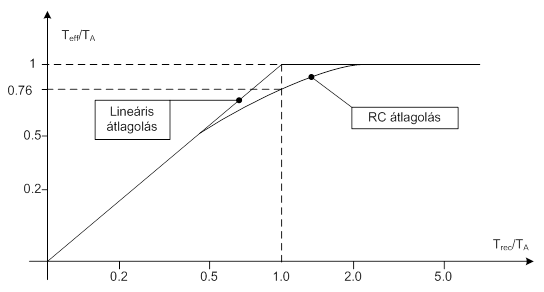
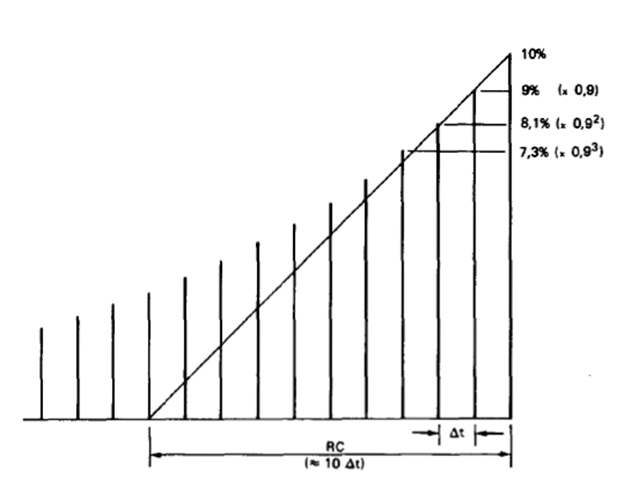
Ha a sztochasztikus jelből rögzített hosszúságú (analóg, vagy digitális) mintát készítettünk, akkor a minta idejénél (Trec) mindenképpen legyen nagyobb az átlagolási idő (TA). Az integrálás effektív (Teff) idejére, a jelminta hosszúsága és az átlagolási idő által gyakorolt hatást mutatja a következő ábra. Látható, hogy exponenciális (analóg RC) jellegű, más néven felejtő átlagolás esetén, ha a jelminta hossza és az átlagolási idő megegyeznek, akkor az effektív integrálási idő ezen idők 76%-ára csökken. A szakirodalomban találunk leírást arra vonatkozóan, hogy semmilyen további javulás nem várható statisztikai funkcionálok (jellemzők) esetében, ha az átlagolási időt az RC jellegnél, a jelminta kétszeresénél nagyobbra választják. Lineáris átlagolásnál az átlagolási idő és a jelminta hossza célszerűen legyen azonos.
A jelrögzítésre, ha csak lehetséges, a DC üzemmód volt ajánlott, mert az átlagolási időt erre specifikálták és az analízis gyorsabb volt ebben az üzemmódban. A DC üzemmód egyik feltétele ugyanakkor a detektor és erősítő 50 dB-nél nagyobb dinamikája volt.
7.1.3.2. Hangolható szűrős (csúsztatott) analizátorok alkalmazása a gyakorlatban
Ennek az analizátor típusnak alkalmazásakor igen sok szempontra kellett figyelemmel lenni. Ezek a következők:
-
Konstans abszolút sávszélességű, vagy konstans relatív sávszélességű szűrőt alkalmazunk
-
Lineáris, vagy logaritmikus a frekvencia skála
-
Aktuális sávszélesség Hz-ben, vagy százalékban
-
Átlagolási idő
-
Sávban tartózkodás ideje (ez határozza meg a csúsztatás - sweep - idejét)
Régebbi időkben ezeken felül
-
Rekorder írási sebessége
-
Papírsebesség
Az első öt feltételt részletesebben is megvizsgáljuk, az írássebességgel és papírsebességgel nem foglalkozunk, ezek jórészt aktualitásukat vesztették.
Konstans sávszélességet akkor alkalmaznak, ha a frekvencia skála lineáris, ha a várható frekvencia spektrumra harmonikus, vagy más determinisztikus összetevők jellemzőek, és, ha más, konstans sávszélességű analízis eredményével kell a kapott értékeket összehasonlítani.
Konstans relatív sávszélességet akkor kell alkalmazni, ha a frekvencia lépték logaritmikus, ha a jel stacionárius sztochasztikus jellegű, és domináns rezonancia frekvenciák is előfordulnak. Például akkor, ha akusztikai, vagy rezgésmérésről van szó, és akkor, ha más, tercsávos analízissel kapott eredménnyel kell az analízis eredményét összehasonlítani.
Lineáris frekvencia skála alkalmazása akkor célszerű, ha a spektrumban egymáshoz kapcsolódó harmonikus összetevők várhatóak, esetleg egymáshoz képest azonos frekvencia-távolságban, mint például az oldalsávok. Alkalmazható akkor is, ha a frekvencia tartomány korlátozott, és, ha más, hasonló módon kapott eredményekkel való összevetés szükséges.
Logaritmikus frekvencia skála ajánlott, ha konstans relatív sávszélességű szűrőket alkalmazunk az analizátorban, ha a frekvencia tartomány nagy, ha kisebb frekvenciaingadozásokat is meg kell jeleníteni, vagy, ha olyan átviteli tulajdonságokat kell kimutatni, amelyek például 10, vagy 20 dB/dekád meredekség formájában jelentkeznek.
Sávszélesség tekintetében is vannak kötöttségek. Determinisztikus jelek esetében kívánatos, hogy az egymáshoz közeli frekvencia komponenseket minél jobban el lehessen különíteni. Ennek feltétele, hogy az alkalmazott sávszélesség a minimális sávfelbontás 1/3 része legyen.
Sztochasztikus jelek esetében a megkívánt relatív sávszélesség legyen kisebb, mint a becsült spektrum legkeskenyebb csúcsához tartozó frekvencia sáv. A legtöbb esetben ez csak léptető szűrős analizátorral érhető el, mert az 1%-os relatív konstans sávszélesség a legkisebb, amely a kereskedelmi analizátorok esetében adott. Determinisztikus és sztochasztikus jelek szuperpozíciója esetében a sávszélességet a determinisztikus jelhez célszerű igazítani.
Átlagolási idő tekintetében a korábbiakban leírtak a mértékadók.
Sávban tartózkodás ideje (T D ) egy egyszerű összefüggésből számítható ki:
|
|
(7.35) |
ahol
|
v sweep |
a csúsztatás sebessége |
|
|
B |
sávszélesség |
|
|
T D |
sávban tartózkodás ideje |
A T D időt több tényező befolyásolja. Ezek a szűrő válaszideje (feléledési ideje), az átlagolási idő és régebbi rendszereknél a rekorder papírsebessége.
Ha a T D idő megegyezik a szűrő feléledési idejével, akkor az egész szűréssel kapott spektrum a frekvencia tengely mentén azonos mértékben jobbra lesz eltolódva. Ez a gyakorlatban nem elfogadható. A sáveltolódással kapcsolatos általános összefüggés az alábbi:
|
|
(7.36) |
Ha KR=4, akkor például a sáveltolódás 1/4 lesz, ami rögzített szűrők esetében, az átlagos frekvencia hiba tekintetében még egy elfogadható kompromisszum is lehet. A KR érték megválasztásánál tudni kell, hogy a sáveltolódás „B” sávszélesség esetében a B/KR aránnyal adható meg.
|
|
(7.37) |
Az átlagolási idő is befolyásolja a szűrőben való tartózkodás idejét. A következő táblázat bemutatja több jellemző, közöttük a sáveltolódás lehetséges mértékét a KA tényező függvényében.
|
|
(7.38) |
A KA tényező nagyságát a detektor karakterisztikájának maximális változása határozza meg, ennek értéke jellemzően 8.7 dB/TA. Az átlagolási idő szokott jelölése és TA.
A következő táblázat a KA tényező kiválasztásában ad támpontokat.
|
KA |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
Szűrő alaktényezője |
15 |
8 |
5.6 |
4.5 |
3.8 |
|
Csúcsdetektálási hiba [dB] |
1.2 |
0.5 |
0.4 |
0.2 |
0.15 |
|
Csúcseltolódás [×B] |
0.3 |
0.2 |
0.13 |
0.1 |
0.1 |
|
Minimumok hibája [dB] |
3 |
1 |
0.5 |
0.25 |
0.2 |
|
Minimumok eltolása [×B] |
0.5 |
0.25 |
0.17 |
0.13 |
0.1 |
7.1.3.3. Idő-kompressziós real-time analízis a gyakorlatban
A real-time analízis révén keletkező spektrummal kapcsolatban fontos korlátozásokat kell figyelembe venni:
-
Az eredeti időbeli jelből kivett minta időtartama (hossza) korlátozza a felső határfrekvenciát.
-
A jelminta időtartama véges, ez alapvetően négyszög időablakot jelent, és vonalas (diszkrét) spektrumot eredményez.
-
Ezeken felül, régebben, a jelminta hosszát az adott memória nagysága korlátozta.
Az idő-kompressziós analizátor műveleti idejének meghatározása a következő tényezők figyelembe vételét teszi még szükségessé:
Sávszélesség
Négyszög súlyozó függvénnyel végzett analízis esetében az analizáló sávszélesség megegyezik a spektrum felbontásával, amelynek értéke „β”. Már jeleztük, hogy a spektrum vonalas lesz, a vonalak közötti távolság (frekvencia sáv) pedig egyszerűen úgy adódik, hogy a kiválasztott frekvencia tartományt osztjuk a vonalak számával. A digitális korszakban a „β” értéket a jelminta idejének hossza dönti el, hiszen a jelminta idejének reciproka a sávszélesség:
|
|
(7.39) |
Megjegyezzük, hogy Hanning-súlyozó függvény alkalmazása esetében 1.5·β zaj sávszélességet kell alkalmazni.
Átlagolási idő
Az átlagolás 1/β időintervallumokban történik, amint az alábbi ábrán látható.
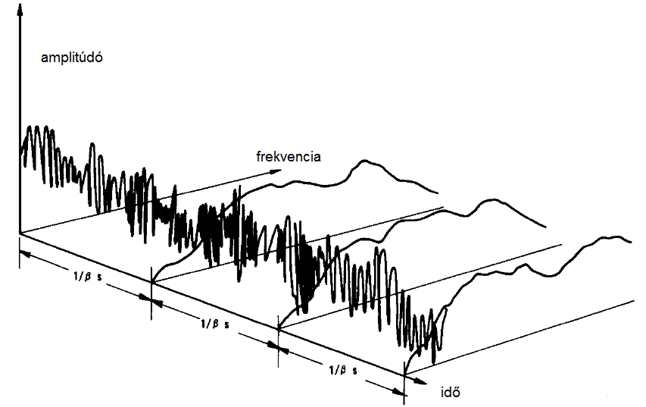
Minden különálló spektrum a tárolt (tárolható) jelminta átlagából keletkezik. Ezért úgy tekinthető, hogy a spektrumok teljessége a teljes analízis idejének átlagából származik. Az átlagolást minden különálló spektrumban lineáris súlyozással is el lehet végezni, de ez azt jelenti idő tartományban, hogy a jelről „pillanatfelvételt” készítünk, ezt analizáljuk, és figyelmen kívül hagyjuk a jel időbeli folytonosságát.
A folytonos analízist ezért úgy programozzák, hogy a szomszédos idősávok bizonyos hányadát figyelembe veszik. A módszert a korszerű digitális szűrés esetében is alkalmazzák, megfelelő rekurzív algoritmussal.
A szomszédos idősávok súlyozása analóg technikában a következő algoritmus szerint történik:
Az új spektrum 10 %-át hozzáadják az addig meghatározott spektrum 90%-ához, és így egy hhoz hasonló kép áll elő, mint amit analóg RC szűrővel történő átlagolásnál kaphatunk. A súlytényezők csökkenése ugyan nem exponenciális, de megközelíti azt.
|
|
(7.40) |
ahol „S” a teljes spektrum és „Sn” az új sáv átlaga.
A jobb érthetőség kedvéért az algoritmust a következő ábrán rajzos formában is bemutatjuk:
Az „effektív” átlagolási idő tehát a már figyelembe vett és az új sáv arányának függvénye. Részletes levezetés nélkül jelezzük, hogy a 0.9 – 0.1 arány a mintavételi idő 10-szereződését, és az effektív átlagolási idő 20-szorozódását jelenti. Ha az arányokat 0.99 – 0.01 értékre módosítják, akkor az előbbi mintavételi idők további látszólagos 10-szereződése lesz ennek eredménye.
7.1.3.4. Folytonos, nem stacionárius jelek analízise a gyakorlatban
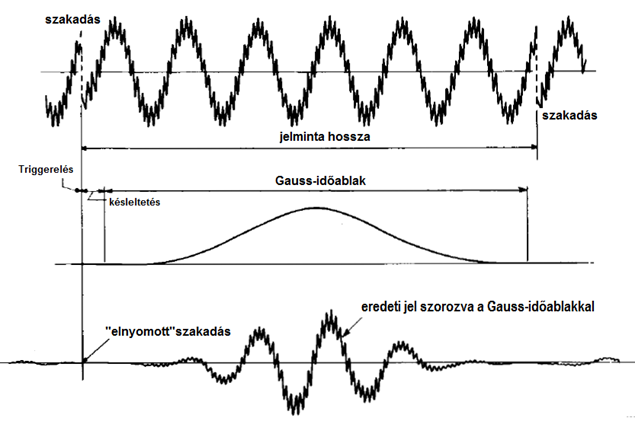
Az idő-ablakot a nem stacionárius folytonos jelek mentén mozgatva, meg lehet határozni az ablakozott rész frekvencia spektrumát. Az eredmény megjelenítése 3D-ben célszerű, mert így egyrészt a frekvenciától való függés (spektrum), másrészt a spektrum-kép időbeli változása is megjeleníthető.
A nem stacionárius időbeli jelek analízise esetében az időbeli ablakozásnak nagy szerepe van. Ha az időablak négyszög formájú, akkor a két végén „hirtelen” változás történik. (Elméletben végtelen meredekséggel, a gyakorlatban persze bizonyos átmenettel.) A szakadás megszüntethető, és lényegesen jobb eredmény kapható, ha az ablak „lágyabb” átmenetű, például Gauss-függvény alakú.
A gyakorlatban használatos ablakok a jelminta más-más részét hangsúlyozzák ki, de mindegyik ablak jobb, mint a négyszög ablak. A nem stacionárius folytonos jelből vett mintát akkor lehet a legkönnyebben analizálni, ha a minta a teljes jelhez képest rövid, mert így hasonló a helyzet, mintha stacionárius jelet vizsgálnánk.
Az ilyen típusú jelek analízise során az alábbi tényezőket kell figyelni:
-
Az időablak típusát
-
Az időablak hosszát
-
Az inkrementális lépések megválasztását
Az időablakozás és a hozzá kapcsolódó spektrum nem érthető a Fourier transzformáció néhány fontos összefüggésének felelevenítése nélkül.
A legfontosabb az ablakozás szempontjából a konvoluciós tétel, amelynek révén a konvolúciós integrál szorzattá transzformálható . A tételt a leggyakrabban a Laplace operátor térben alkalmazzuk, amikor a bemenőjel Laplace transzformáltját az átviteli függvénnyel megszorozva a kimenőjel Laplace transzformáltját állítjuk elő. Időtartományban ennek a műveletnek a konvoluciós integrál felel meg. A konvolució jelölése a két függvény között egy csillaggal történik.
|
|
(7.41) |
A konvolució azonban nem csak a Laplace transzformációhoz kapcsolódik.
A Fourier transzformáció is tartalmaz ennek megfelelő szabályokat. A legfontosabbak ezek közül a témához kapcsolódóan az alábbiak:
|
|
(7.42) |
A kimenőjel spektrumát tehát egyszerűen úgy állíthatjuk elő, hogy a bemenőjel spektrumát a frekvencia átviteli függvénnyel megszorozzuk. A folyamatot egyetlen kiragadott részlet segítségével könnyen elképzelhetjük, ha kiválasztunk egy összetevőt a bemenőjel spektrumából ωi körfrekvenciánál, és ezt a frekvencia átviteli függvény ωi körfrekvenciához tartozó értékével megszorozzuk. Az időtartományban az integrálszámítás lényegesen bonyolultabb.
A megszokott formájú konvolucióban a g(t) függvény az átviteli tag súlyfüggvénye, tehát maga is időfüggvény. A konvoluciót tehát időtartományban végezzük.
Ha egy lépéssel továbbmegyünk, és a konvoluciót a frekvenciatartományra is kiterjesztjük a Fourier transzformációs szabályoknak megfelelően, akkor az időablakozás frekvenciatérbeli hatása érthetővé válik.
A konvolucióban felcseréljük az idő és a frekvencia tartományt, azaz a változókat, és így az alábbi összefüggéseket kapjuk:
|
|
(7.43) |
Tekintettel arra, hogy F(jω) és G(jω) komplex függvények, a szorzatuk is komplex szorzat, ami azt jelenti, hogy szorozzuk az amplitúdókat, és összegezzük a fázisszögeket. Az integrálás ebben az esetben vektor-összegzést jelent.
Ha tehát egy f(t) folytonos időbeli jelből ki akarunk „vágni” egy meghatározott hosszúságú mintát, akkor egy g(t) négyszög időablakkal kell az f(t) függvényt megszorozni. A két időtartománybeli jel szorzata a frekvenciatartományban a megfelelő jelek spektrumainak konvolucióját eredményezi.
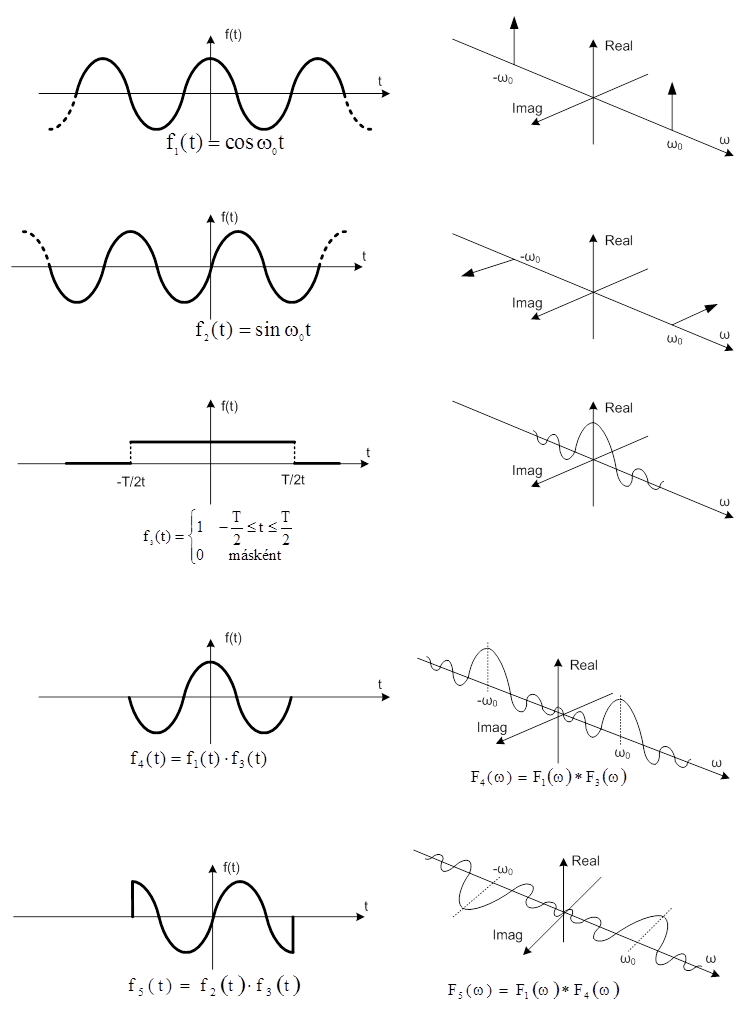
A folyamat képi megjelenítése a (7.21. ábra) ábrán követhető nyomon. Felülről sorrendben az első két függvény egy-egy koszinusz, illetve szinusz függvény, mellettük jobbra a komplex Fourier transzformáltjuk, amelyek Dirac-impulzusok +ωi és -ωi körfrekvenciáknál. Láttuk, hogy , tehát a komplex Fourier transzformált valós része koszinusz, képzetes része pedig szinusz függvény, ha figyelembe vesszük az Euler-összefüggést. Ez tükröződik vissza a spektrumokon is. A harmadik függvény egy négyszög időablak (T időtartamú impulzus), amellyel a folytonos harmonikus függvényekből egy-egy mintát szeretnénk „kimetszeni”. Az impulzus spektruma a jobboldalon látható, és csak valós résszel rendelkezik. A koszinusz jellel való szorzás (ablakozás) eredménye a spektrumban az, hogy az impulzus spektruma a koszinusz függvény -ωi és +ωi körfrekvenciáinál jelenik meg, és csak valós része van. Jól látszik, hogy az ablakozott koszinusz jel lineáris átlaga nem zérus (a pozitív és negatív hullám-felek eredője nem zérus), ezért jelenik meg a spektrumban zérus körfrekvenciánál is összetevő.
A szinusz függvény ablakozása imaginárius spektrumot eredményez, ugyancsak a függvény -ωi és +ωi körfrekvenciáin, és ismét az impulzus spektruma jelenik meg. A spektrumnak nincs összetevője a zérus körfrekvencián, mert az ablakozott szinusz jel lineáris átlaga zérus.
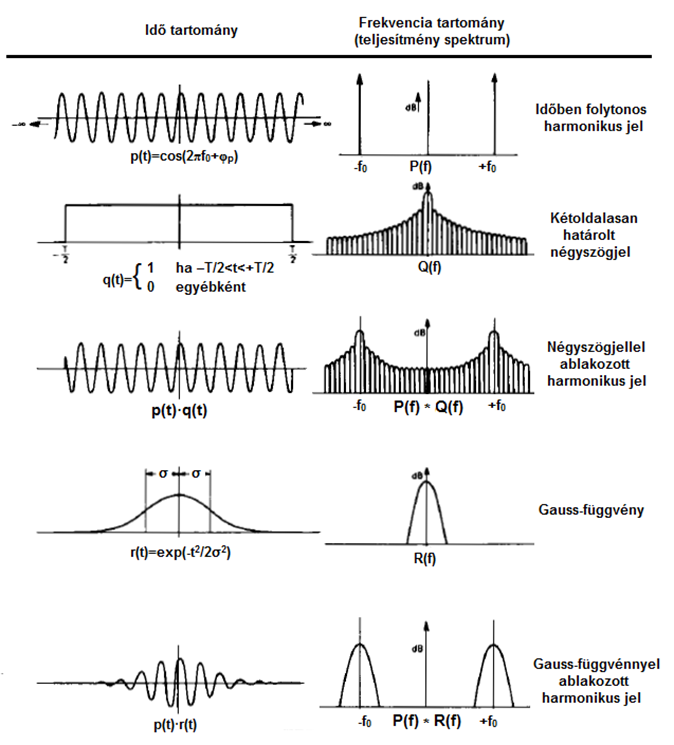
A konvolucióval létrejött spektrum megjelenítése lényegesen egyszerűbb, ha a teljesítmény spektrum közlése a feladat, mert ebben az esetben a 3D-s kép helyett csak a valós koordinátarendszerben kell ábrázolni az eredményt.
A következő ábrán ugyancsak harmonikus jelen történő „ablakozást” látunk két időablak esetében, és jobboldalon a teljesítmény spektrum látható. A folytonos, periodikus harmonikus függvény Fourier transzformáltja (komplex spektruma) ±f0 frekvenciáknál egy-egy Dirac-impulzus. A nem periodikus négyszög-impulzus és a Gauss-függvény spektruma folytonos, és a függőleges tengelyre szimmetrikus. A frekvenciatérbeli konvolució eredményeként az ablakok spektruma a harmonikus jel ±f0 frekvenciáin jelenik meg. Látható, hogy a négyszögjel két végén végbemenő hirtelen változás (végtelen meredekség) igen széles sávú spektrumot eredményez. Az eredeti harmonikus jel frekvenciáján van ugyan egy jól elkülöníthető csúcs, de az oldalsávok teljesítménye nem elhanyagolható. A Gauss-függvénnyel történő ablakozás a harmonikus jelből fokozatosan növekvő amplitúdójú részletet „vág ki”, a hirtelen ugrás megszűnik, és a spektrum ennek következtében „szűkebb” lesz. A teljesítmény spektrumban a megjelenő Gauss-spektrum csúcsaihoz tartozó ±f0 frekvenciák felelnek meg az eredeti folytonos jel frekvenciáinak. Az oldalsávok persze itt sem elhanyagolható mértékűek, ennek nagysága a Gauss-függvény alakjától, pontosabban annak szórásától függ.
Az időablak típusának megválasztása
Az analóg szűrési gyakorlatban az alábbi időablakokat szokás alkalmazni:
-
Négyszög ablak T időtartammal
-
Hanning (cos2) ablak
-
Hamming ablak (Hanning ablak egy kismértékű emeléssel)
-
Gauss ablak
Táblázatban foglaltuk össze a fenti időablakokhoz tartozó szűrési tulajdonságokat:
|
Típus |
3dB sávszélesség β=1/T |
Zaj sávszélesség B eff |
Legmagasabb oldalsáv [dB] |
Oldalsávok csúcsainak meredeksége |
|---|---|---|---|---|
|
Négyszög |
0.9 β |
1.0 β |
-13 |
-20 dB/dekád |
|
Hanning |
1.4 β |
1.5 β |
-32 |
-60 dB/dekád |
|
Hamming |
1.3 β |
1.4 β |
-42 |
-20 dB/dekád |
|
Gauss |
1.8 β |
1.9 β |
nincs |
nincs |
A különböző típusú és „T” időtartamú időablakok frekvencia menetét hasonlítjuk össze a következő ábrán:
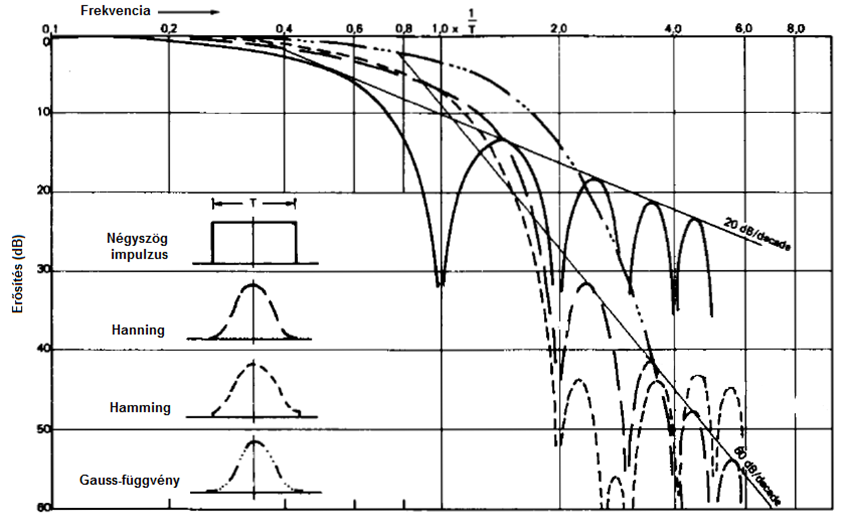
Az időablak hosszának megválasztása
Természetes, hogy az ablak hossza az analizálni kívánt nem stacionárius, folytonos jel hosszától függ, gondoljunk példaképpen a beszédben kiejtett hangzókra, amelyek időtartama átlagban 40 ms körüli. A rövid minta következménye természetesen nagy sávszélesség lesz a frekvenciatartományban, gondoljunk az impulzus spektrumára. A különböző ablak típusok Teff effektív hossza (összehasonlítás céljából) az effektív, vagy zaj sávszélességgel határozható meg, ha a jelminta véletlenszerű, és nagyjából stacionárius:
|
|
(7.44) |
A Teff érték tulajdonképpen a TA helyettesítésére szolgál abban a korábban már megismert összefüggésben, amely az átlagolási idő és a hiba várható eloszlása közötti kapcsolatot adja meg.
|
|
(7.45) |
Láttuk, hogy minél hosszabb az átlagolási idő, annál kisebb a hiba, az eredmény bizonytalansága, empirikus szórása.
Konstans relatív sávszélességű analízis esetében előfordulhat, hogy a kapott eredményt nem a szűrő sávszélessége, hanem az időablak alakja határozza meg.
Az inkrementális lépések megválasztása
Láttuk, hogy Teff dönti el az inkrementális lépések szélességét. Ugyanakkor, ha a fenti elméleti képlet szerint állapítjuk meg a frekvencia inkrementumot, akkor a gyakorlatban hibát követhetünk el.
A lépések sávszélességét célszerű keskenyebbre választani, például a következő minta szerint:
Egy Hanning ablak effektív sávszélessége 1.5β, a képlet alapján számítható Teff=0.67T. Az inkrementális lépések számításához 0.5T értéket célszerű választani.
7.1.4. Tranziens jelek analízise
A gyakorlatban sokféle módszer ismert, és gondot jelent, hogy ezek nem adnak azonos értékű eredményt. Ezért az alkalmazott módszer kiválasztásához több szempontot kell figyelembe venni. A helyes módszer kiválasztásához az alábbi két ábra szolgálhat segítségül:
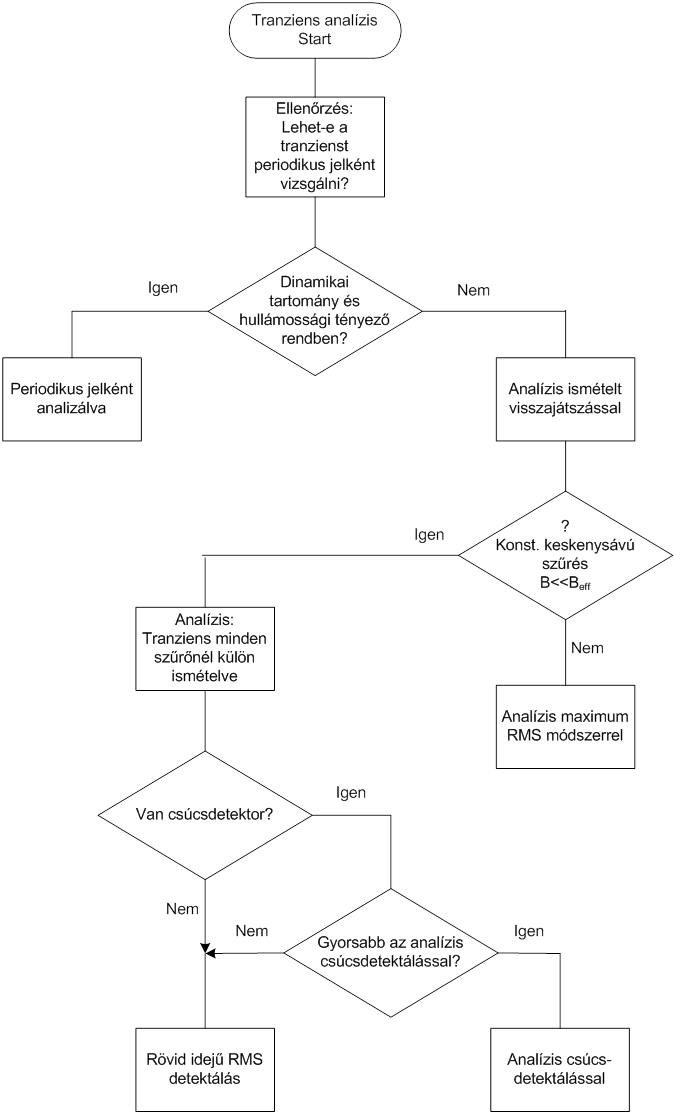
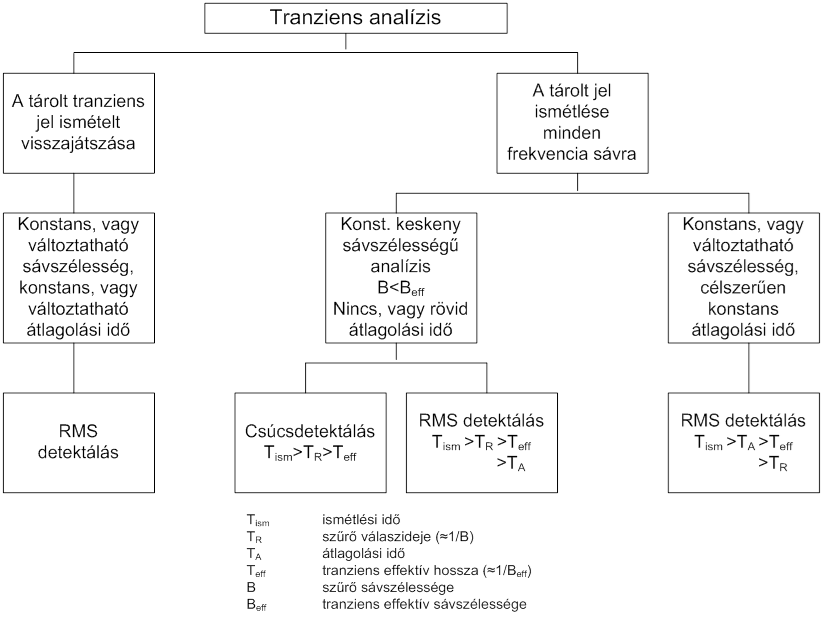
Analízis periodikus jelként
Ebben az esetben a tárolt tranziens jelet „Tism” ismétlési idővel periodikusan visszajátsszák, ügyelve arra, hogy a Tism hosszabb legyen, mint maga a tranziens jel. Ezt láthatjuk a (7.24. ábra) ábrán. Ilyen módon a tranzienst mesterségesen periodikussá alakítják, és az így kapott vonalas spektrum alakja könnyen rokonítható az eredeti tranziens jel folytonos spektrumával. A detektorokkal RMS átlagolást kell végezni, TA átlagolási idővel, amely nagyobb, mint az ismétlés ideje, mert így csillapíthatók az ingadozások.
A periodikus jelként történő analízis módszerének előnyei:
-
Hasonló analizálási technikák alkalmazhatóak, mint a folytonos jelek esetében.
-
A kapott eredményt a sávszélesség kevéssé befolyásolja, mind konstans sávszélesség, mind pedig konstans relatív sávszélesség alkalmazható.
-
Feltéve, hogy az átlagolási idő elegendően nagy (ismétlés idejének figyelembe vételével), az átlagolási idő növelése már nem befolyásolja az eredményt.
-
A spektrum inkább folytonosnak látszik, mert a csúcsok közel esnek egymáshoz.
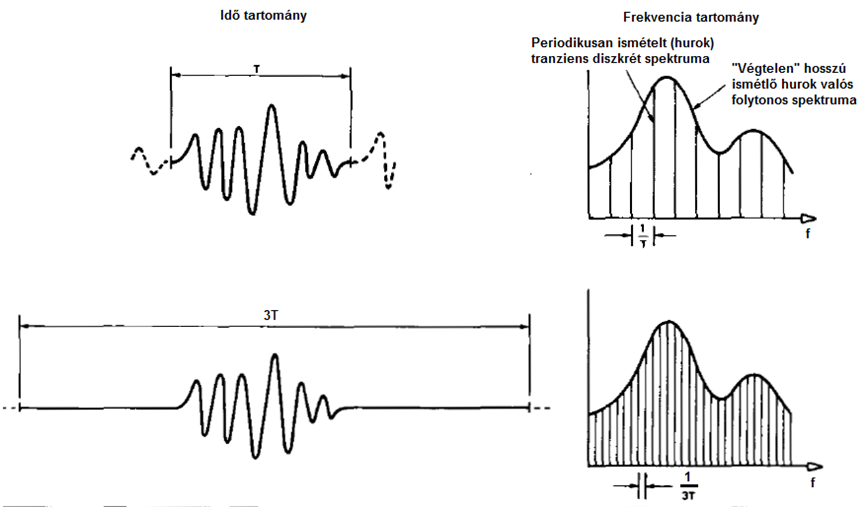
Az analizátor sávszélességével kapcsolatban fontos követelmény viszont, hogy az legyen nagyobb, mint az analízissel kapott vonalas spektrum vonaltávolsága:
|
|
(7.46) |
A spektrumvonalak távolságát viszont az ismétlési idő határozza meg.
Az átlagolási idő T A legyen lényegesen nagyobb, mint az ismétlési idő, a hullámosság csökkentése érdekében. Az elméletben alátámasztható gyakorlati érték az alábbi:
|
|
(7.47) |
Általában 3-nál nagyobb értékkel szokás indulni, és a kapott eredmény szemrevételezése után növelik a szorzót.
A szűrési, vagy TD tartózkodási időt hasonló módon kell megállapítani a sweep-eléshez, amint a stacionárius jelek esetében láttuk.
Tranziens analízis állandó keskeny sávszélességgel
Ezt a módszert akkor szükséges választani, ha az ismétlési időt nem lehet a szükséges mértékben lerövidíteni. Ebben az esetben a tranziens jelet minden egyes szűrő beállítás mellett ismételni kell, megvárva a szűrő válaszát. A szűrő válaszideje jellemzően hosszabb, mint a tranziens jel hosszának ötszöröse, mint ahogy a méréstechnikában is szokásos a leolvasási időt az időállandó ötszörösének venni. Frekvencia térben kifejezve a feltételt a következőképpen lehet megfogalmazni:
|
|
(7.48) |
Teff ebben az esetben a tranziens effektív időtartama, amely nem azonos az ismétlési idővel. A módszer lassú és körülményes, de a kapott spektrum pontos. A spektrumvonalak csúcsain át húzott burkológörbe a tulajdonképpeni jelspektrum.
Ha a szűrési, vagy TD tartózkodási idő nem kisebb, mint az ismétlési idő, akkor a spektrumvonalak távolsága éppen a szűrő sávszélességének felel meg:
|
|
(7.49) |
Tranziens analízis állandó változó sávszélességgel
A keskenysávú analízist a rendelkezésre álló szűrő sávszélessége és a jelminta effektív időbeli hosszának reciprokja közötti arány korlátozza. Szükség esetén az analízist el lehet végezni konstans relatív sávszélességű szűréssel is, például tercsáv-analizátorral.
Az átlagolási időnek a jelmintánál alapvetően hosszabbnak kell lennie, így természetesen az analízishez szükséges idő is hosszabb, mint a keskenysávú módszernél.
Az átlagolási idő meghatározásához az alábbi formula áll rendelkezésre:
|
|
(7.50) |
ahol Teff a jelminta (impulzus) hossza.
Az ismétlési idő és az átlagolási idő közötti kapcsolat pedig az alábbi:
|
|
(7.51) |
A szűrési idő TD (szűrőben töltött idő) rögzített középfrekvenciájú tercszűrők esetében legyen legalább akkora, mint az ismétlési idő.
7.1.5. Cepstrum analízis
B. P. Bogert, M. J. R. Healy, J. W. Tukey „The Quefrency Analysis of Time Series for Echoes: Cepstrum, Pseudo-Autocovariance, Cross-ceprstrum and Saphe Cracking” című, a Proceedings of the Symposium on Time Series Analysis kiadványban megjelent (M. Rosenblatt, Ed. Wiley, New York, 1963 [7.1.] cikke 1963-ban mutatta be azt a módszert, amelynek segítségével a földrengések igen összetett rezgésképéből szét lehetett „választani” az epicentrumban (forrás) kipattant lökéshullámokat, a földkéreg, mint bonyolult átviteli tulajdonságokkal rendelkező passzív rendszer válaszát (kvázi „súlyfüggvényét”), és az echókat (visszahatásokat, „visszhangokat”). Rendszertechnikai kifejezésekkel fogalmazva: el kellett különíteni a földkéreg impulzus-válaszától a forrás által kibocsátott rezgésjeleket.
Bogert újítása azért nagyon fontos újdonság és nélkülözhetetlen gyakorlati módszer a jelanalízisben, mert J. Trampe Broch „On the Applicability and Limitations of the Cross-Corelation and the Cross-Spectral Density Techniques” című, a B&K Technical Review No 4. 1970 [7.2.] megjelent publikációjában, a későbbiekben megmutatta, hogy a hagyományos módszerrel, nevezetesen az autokorrelációs függvény segítségével felderített csúcsok, amelyek például a visszhanggal kapcsolatba hozhatók lennének, sajnálatos módon erősen függenek a frekvencia spektrum alakjától. Ráadásul a földkéregben való terjedés különféle szűrő hatásoknak is ki van téve. A teljesítmény spektrum logaritmusának felhasználásával is történtek próbálkozások, de ezek az eredmények is hasonlóan érzékenyek a szűrésre. Csak a cepstrum képes olyan késleltetett csúcsokat is kimutatni, amire az auto-és keresztkorreláció már nem volt alkalmas.
A gépészeti méréstechnika szempontjából természetesen nem a cepstrum analízis eredeti célja fontos, hanem az, hogy a Bogert-féle publikációt követően szédítő sebességgel kezdték a módszert alkalmazni különböző tudományterületeken, ahol hasonló dekonvoluciós problémákkal küzdöttek. A szeizmikus vizsgálatok után, másodikként, a beszédanalízis területén alkalmazták, mert a cepstrum alkalmas a hangképző szervek frekvencia átviteli tulajdonságainak, és önmagában a „tiszta” hang frekvenciaspektrumának szétválasztására. A hangképző szervek esetleges deformitásai, betegségei ennek segítségével beazonosíthatóvá váltak.
A gépészeti méréstechnika szempontjából természetesen nem ez a két alkalmazás, hanem az alábbi műszaki lehetőségek játszanak szerepet:
-
géprezgések periodikus összetevőinek detektálása és azonosítása,
-
turbinalapátok hibái,
-
csapágyak hibái,
a megfelelő felharmonikusak és oldalsávok elkülönítésének segítségével.
Bogert és társai a bevezetőben említett publikációjukban az általuk javasolt cepstrum analízis eljárás fogalmaira és egységeire olyan elnevezéseket találtak ki, amelyek az eredeti frekvencia analízisből származtak, de néhány betű felcserélésével teljesen új szavak születtek az új fogalmak megjelölésére. Mindeközben persze, a megjelölések hangalakja a felhasználóban a hagyományos frekvencia analízissel való rokonság érzetét kelti, nem alaptalanul.
Nézzünk ezek közül néhányat, angol nyelven, mert így érzékelhető a betűk cseréje. A quefrencia dimenziója idő, ez a soron következő definícióból is nyilvánvaló lesz.
|
Frekvencia analízis |
Cepstrum analízis |
|---|---|
|
frequency [Hz] |
quefrency [s] |
|
spectrum |
cepstrum |
|
filtering |
liftering |
|
harmonic |
rahmonic |
|
phase |
saphe |
A cepstrum analízist több szakirodalom joggal nevezi dekonvoluciónak . Az elnevezés jogos, és igen szemléletesen tükrözi a cepstrum analízis lényegét. Az idő tartományban mért „válaszjelek”, amelyet a földrengéseket észlelő szeizmológiai állomások regisztrálnak, valójában konvoluciós integrálok „eredményei”. Ugyanis, a rendszertechnikában megszokott módon, időtartományban az „y(t)” kimenőjel (válaszjel) az alábbi módon adható meg az átviteli tag „g(t)” impulzus válaszának (súlyfüggvény) és az „u(t)” gerjesztő jelnek ismeretében:
|
|
(7.52) |
A gépészeti méréstechnikai alkalmazásokban legyen az u(t) függvény egy gép (géprendszer) belső zaja, vagy rezgésforrásának jele, g(t) pedig az impulzusválasz, amely a gép belsejétől a mérési pontig terjedő összetett, és nehezen modellezhető rendszert jellemzi.
A méréssel detektálható y(t) válaszjelből idő tartományban nem lehet az eredeti két összetevőt szétválasztani, de amint olvashattuk, az autokorrelációs spektrum sem volt erre alkalmas.
Bogert és társai a konvoluciós integrál frekvencia tartománybeli megfelelőjéből indultak ki, és arra alapozva, hogy a szorzatból logaritmusképzéssel összeg állítható elő, megalkották a cepstrum fogalmát. A cepstrum lényegében az átviteli függvény és a gerjesztés spektrumának logaritmikus összege. Ezt mutatjuk be a következőkben.
A konvolució megfelelője frekvencia tartományban a frekvencia függvények szorzata. Az egyenlet logaritmusát képezve, az egyenlet összeggé alakul.
|
|
(7.53) |
A két összetevő a linearitási törvény alapján külön-külön Fourier transzformálható, így áll elő a cepstrum, amely a két kérdéses időfüggvényből származó spektrum összege:
|
|
(7.54) |
Az egyenlet lényegében a „dekonvolució”, azaz az időfüggvényekhez rendelt spektrumok szétválasztásának folyamatát mutatja.
Napjainkban a cepstrum két formája ismeretes és alkalmazott, ezek a
-
teljesítmény cepstrum és a
-
komplex cepstrum.
Ez utóbbi elnevezésben ugyan benne foglaltatik a komplex jelző, de a cepstrum valójában nem komplex, csak reális része van, erről a későbbiekben még lesz szó.
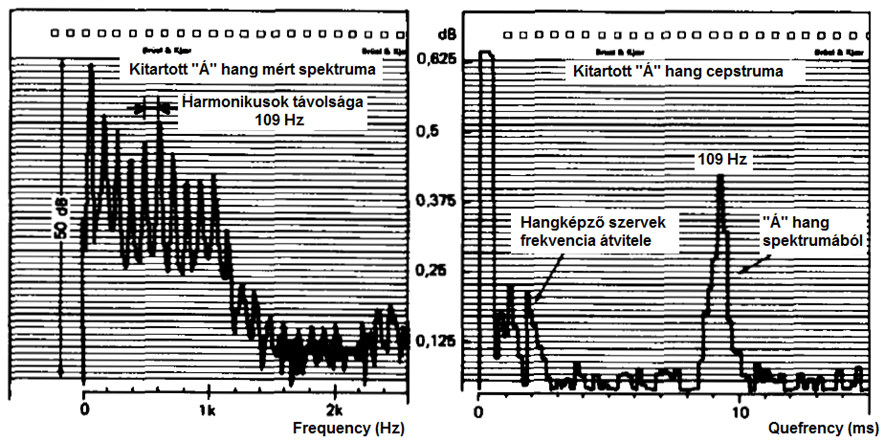
A következő ábra baloldalán a kitartott emberi „Á” hangméréssel felvett spektrumát (válasz spektruma), jobboldalán pedig a cepstrumát mutatja. A spektrumból az eredeti hang frekvenciája nem szűrhető ki, mert a hang több felharmonikussal együtt jelenik meg. A hangképző szervek frekvencia átviteléről egyszerűen pedig nincsen információ.
A jobboldali cepstrumban viszont a hangképző szervek frekvencia átvitele és az eredeti „Á” hang már jól elkülönítetten jelenik meg. Az átviteli tagra (láncra) jellemző quefrenciák általában alacsonyabb értéknél jelennek meg (kisebb a spektrum fluktuációja), így könnyen felismerhetőek, erre jó példa az alábbi ábra jobboldala.
Teljesítmény cepstrum
Matematikailag és történelmileg ez az első forma, hiszen az idézett munkában a cepstrum mint „A teljesítmény spektrum logaritmusának teljesítmény spektruma” van definiálva.
A „miért” kérdésre azonnal érthető a válasz: A bevezetőben ismertetett összefüggések általános formában mutatták be a cepstrum analízis lényegét. Tudomásul kell azonban vennünk, hogy az analizálandó jelek túlnyomó része sztochasztikus jellegű. Az ilyen jeltípusok frekvencia analízise „egyszerű” Fourier transzformációval nem lehetséges, csak az autokorreláció révén.
Nézzük az egyes lépéseket sorjában:
Az időbeli jel Fourier transzformáltja a szokott módon képezhető:
|
|
(7.55) |
A jel teljesítmény spektruma:
|
|
(7.56) |
Végezetül a cepstrum:
|
|
(7.57) |
Fontos egy másik megközelítésben, a quefrency dimenziója miatt, hogy az „R xx (τ)” autokorrelációs függvény és a teljesítmény spektrum között az alábbi összefüggés áll fenn (Wiener-Hincsin tétel):
|
|
(7.58) |
Az autokorrelációs függvény stacionárius és ergodikus folyamat esetében az időközépérték segítségével meghatározható. Meg kell jegyezni, hogy nem stacionárius jelek esetében az autokorrelációs függvény nem csak „τ” eltolási időnek, hanem a „t 0 ” kiindulási időpontnak függvénye is.
|
|
(7.59) |
Ezért az eltolási idő „τ” nem csupán az autokorrelációra, hanem a cepstrumra is jellemző.
A quefrency dimenziója tehát idő .
Nem is lehet más, hiszen a módszer a konvoluciós integrál eredményeként kapott válaszfüggvény dekonvolucióját jelenti. A konvoluciós integrálban ugyanis az átviteli tag súlyfüggvényét ugyancsak folytonosan „τ” idővel toljuk el a bemenő függvényhez képest, és „τ” szerint integrálunk.
A cepstrum megítélésénél fontos, hogy magas quefrency értékek a spektrum gyors fluktuációját jelentik, míg kis quefrency értékek éppen az ellenkezőjét, lassú változásokat mutatnak a jel spektrumában.
Hátra van még a cepstrum mértékegységének kérdése. Tekintettel arra, hogy spektrumot leginkább logaritmikus léptékben adjuk meg, és a mértékegység „dB”, a cepstrum mértékegysége „(dB)2 ” lesz. (Eredetileg a cepstrum megalkotói a teljesítmény második Fourier transzformáltjára „amplitúdó spektrum” elnevezést használtak, amelynek dimenziója viszont „dB” lenne. A második transzformáció a későbbi szerzőknél vagy előre, vagy vissza Fourier transzformáció, ahol csak a léptékek különböznek.)
Komplex cepstrum
Ezt a cepstrum formát A. V. Oppenheim, R. W. Schafer, és T.G. Stockham írták le publikációjukban, amely a „Nonlinear Filtering of Multiplied and Convolved Signals IEEE Trans. Audio & Electroacoustics, Vol. AU-16. No 3, Sept. 1968 [7.3.] jelent meg.
A nevétől eltérően ez egy valós értékű függvény, az elnevezésnek az oka abban áll, hogy a komplex cepstrumot a komplex spektrumból eredeztetik. A legfontosabb tulajdonsága az, hogy a fázis információ nem „vész el”. Ennek következtében a szűrési műveletek után az eredeti jel teljes egészében visszaállítható. Lényegében alkalmas lineáris szűrési technikák alkalmazásával a konvolucióval és szorzással képezett jelek eredeti összetevőinek szétbontására.
A szerzők a komplex cepstrumot a következőképpen definiálták:
„Az időbeli jel komplex spektruma komplex logaritmusának inverz Fourier transzformáltja”.
A szöveg az alábbi műveletekkel írható le:
|
|
(7.60) |
A szerzők a teljesítmény cepstrumtól való eltérés hangsúlyozására a komplex cepstrumot K x (τ) formában jelölték.
Ismeretes, hogy a komplex spektrum F x (f) a következő alakban írható fel:
|
, |
(7.61) |
A transzformált F x (f) a Fourier transzformáció eredményeként jött létre:
|
|
(7.62) |
A komplex exponenciális függvény a valós és képzetes részre való bontás helyett amplitúdót és fázist ad meg. Ha az F x (f) transzformált természetes logaritmusát képezzük a komplex cepstrum eredeti definíciója szerint, akkor az amplitúdó és fázis információ szétválnak:
|
|
(7.63) |
A komplex spektrum a definíciója szerint tehát:
|
|
(7.64) |
A komplex spektrum A(f) és e jΦ(f) szorzat alakjából tehát e komplex cepstrum esetében is összeg lesz a logaritmus révén.
Valós f x (t) függvény komplex spektruma páros konjugált lesz. Így A(f) és lnA(f) páros is páros lesz, Φ(f) pedig páratlan. Ezért a komplex L(f) függvény konjugált páros, amelynek inverz Fourier transzformáltja valós időfüggvény lesz.
A komplex cepstrum révén lehetővé válik az, hogy a mérhető válaszjel komplex cepstrumából kivonva az átviteli függvény komplex cepstrumát megkapjuk a forrás eredeti jelének komplex cepstrumát, amelyből azután a jel időbeli alakja visszaállítható. Az átviteli függvény komplex cepstruma jellemzően alacsony quefrency értékeken jelentkezik, így könnyű az azonosítás és az eltávolítás.
A következő példán jól követhető a visszhang megszűntetése.
A következő ábra legfelül látható, 1. képén három, periodikusan lecsengő szinuszos jel látható, egymástól τ 0 időbeli távolságra. Az első eredeti jelnek tehát két, csökkenő amplitúdójú visszhangja van. Ez az additív jellegű periodicitás megjelenik a logaritmikus amplitúdó spektrumon (2. kép) és fázismeneten (3. kép) is. Ez a két kép tehát már nem a megszokott spektrum, hanem azok logaritmusa. Az amplitúdó spektrumban látható kiemelés a harmonikus jel frekvenciája, a folytonos, sinx/x jellegű spektrum összetevő pedig az időbeli jel impulzus formája miatt jelenik meg.
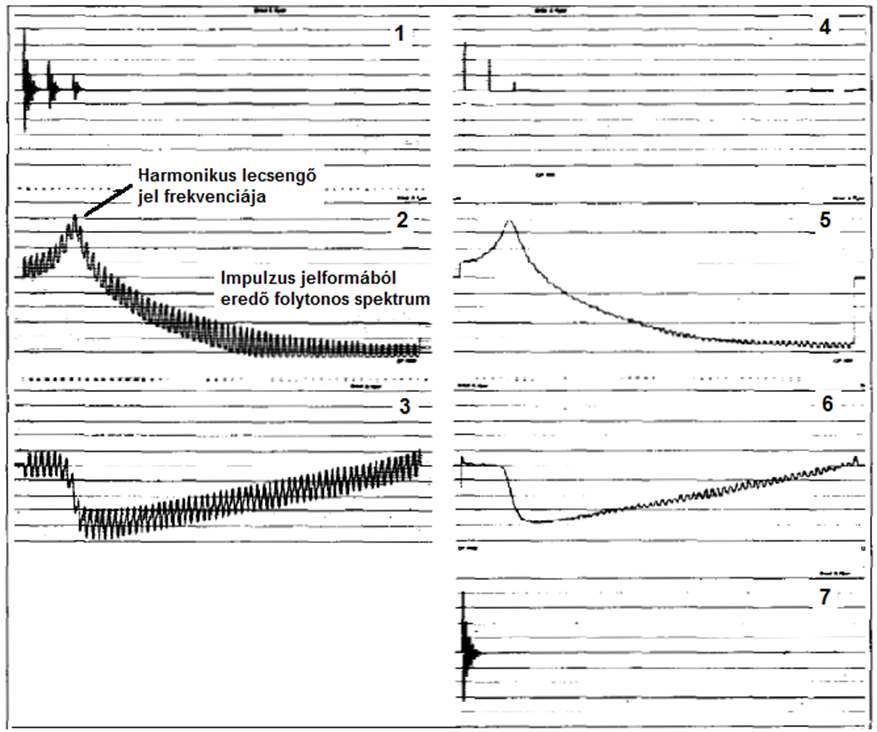
Az inverz Fourier transzformálás után, tehát a komplex cepstrumban , az ismétlődést olyan formában látjuk viszont a 4. képen, hogy a harmonikus jelhez tartozó Dirac-impulzusok τ 0 távolságra helyezkednek el. Eltávolítva a két visszhangot jelentő impulzust (második és harmadik), a „kijavított” komplex cepstrumot visszatranszformálják logaritmikus spektrummá (5. és 6. kép), majd egy inverz logaritmusképzést követően sor kerül a második inverz Fourier transzformálásra is. A folyamat végén, a 7. képen látható az eredeti, visszhangmentes jel időbeli alakja.
Irodalmak
[7.1.] The Quefrency Analysis of Time Series for Echoes: Cepstrum, Pseudo-Autocovariance, Cross-ceprstrum and Saphe Cracking. Proceedings of the Symposium on Time Series Analysis . Wiley. 1963.
[7.2.] On the Applicability and Limitations of the Cross-Corelation and the Cross-Spectral Density Techniques. B&K Technical Review No 4.. 1970.
[7.3.] Nonlinear Filtering of Multiplied and Convolved Signals . IEEE Trans. Audio & Electroacoustics. Sept. 1968.