16. fejezet - A mérésadatgyűjtő számítógép algoritmusai
Vissza		Előre

16. fejezet - A mérésadatgyűjtő számítógép algoritmusai

Tartalom

Algoritmus: valamely feladat megoldási lépéseinek leírása.

Típusi: periodikus , nem periodikus (kezelő vagy egy esemény váltja ki)

Állapot változók: a mérési folyamat állapotát leíró, vagy működését meghatározó analóg illetve mintavételes változók.

Típusai:

mért: egy bemenet mérése alapján meghatározott változó érték
számított: két vagy több mért értéke alapján képzett (számított) változó érték

16.1. Az analóg és digitális jelek mérése, és előzetes feldolgozása

A mérési feladat elemei a számítógép számára:

mintavételezés
átkódolás
méréskorrekció
digitális szűrés
átszámítás fizikai értékre

Ezeket a műveleteket a mérést irányító számítógép periódikusan hajtja végre.

16.1.1. Mintavételezés

Csak az állandó mintavételezési idejű rendszerekkel foglalkozunk.

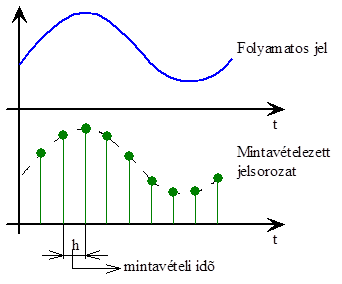
16.1. ábra - Analóg mintavételezés

A mintavételezési törvény alkalmazása

Ha a mintavételezendő jel sáv korlátozott, vagyis megadható egy f_max frekvencia, amelynél nagyobb frekvenciájú jelet nem tartalmaz, a mintavételezendő jelet egyértelműen jellemzi az f_max frekvencia kétszeresénél nagyobb frekvenciával vett minták sorozata. A helyesen megválasztott mintavételezési frekvencia tehát:

f _s > 2*f _max

(16.1)

ahol

	$f_{s}$	a mintavételezés frekvenciája,
	$f_{\max}$	a mérendő jelben előforduló legmagasabb frekvenciájú komponens.

Ha csak a feltétellel megadott mintavételi frekvenciát alkalmazzuk, azaz az f_max frekvencia kétszeresével mintavételezünk, nem kapjuk meg azt a mintavételezett jelet, amelyből visszaállíthatnánk az eredeti mintavételezett jelet, mint ahogy azt a 16.2. ábra ábra mutatja.

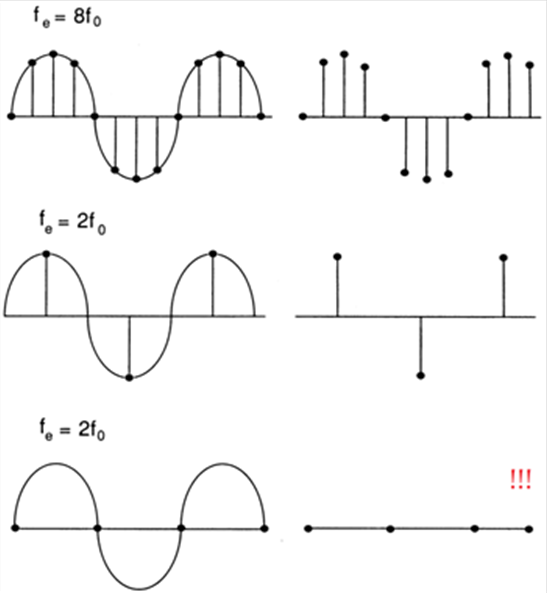
16.2. ábra - A szinuszos jel mintavételezése

A valóság azonban az, hogy a jelek nem sávkorlátozottak, ezért gyakorlati javaslatot kell adni arra vonatkozóan, hogy milyen értékű legyen a mintavételezés frekvenciája. Ez egy közepes bonyolult matematikai formula, amelyből meghatározható, hogy az alul mintavételezéssel milyen torzítást okozunk.

A gyakorlatban az f _max értékének 6-25-szeresével meghatározott mintavételi frekvenciát alkalmazunk ipari berendezésenként f _sample -ként!

16.1.2. Átkódolás és kódkonverzió

Átkódolásra szükség van mind az analóg, mind a digitális bemeneti és kimeneti jeleknél egyaránt.

Az analóg bemeneteknél az analóg érték mintavételes átalakításához szükséges lépéseket kell megtennünk. Így az A/D átalakító által szolgáltatott számábrázolási formát át kell alakítani a számítógépben történő számábrázolási formára.

Mivel a digitális jelek ábrázolása a számítógépben az adatátviteli kódoktól eltérő, a megfelelő átkódolási műveleteket programmal kell végrehajtani.

Átkódolásra van szükség az analóg kimenetek és a kezelő számára a megfelelő formátumú táblázatok, naplók előállításához is.

Átkódoláshoz soroljuk a fixpontos/lebegőpontos , illetve a lebegőpontos/fixpontos átalakításokat is. Erre azért van szükség, mert az A/D átalakítók által adott adat, illetve a D/A átalakítók beállításához szükséges adat egész típusú, fixpontos , míg a számítógép általában lebegőpontos formátumban végzi a műveleteket.

Az adatátvitel biztonsága érdekében a digitális be/kimeneti jeleket is sokszor redundáns módon kódolják (a feltétlenül szükséges információn túl további kiegészítő információkat is kódolnak).

A redundáns kódok a torzult információ felismerését, illetve a hiba kijavítását teszik lehetővé.

16.1.3. Méréskorrekció

A méréskorrekció célja a mért értékek pontosságának növelése. A korrekció történhet korrekciós egyenletek alapján, vagy ezek sorba fejtésével kapott közelítő egyenletek alapján, illetve táblázatban megadott adatok felhasználásával. Gyakran alkalmazott korrekciótípus a mérőműszer referencia feltételének megváltozását figyelembe vevő méréskorrekció.

Például

hőelemes hőmérsékletmérés referencia hőmérsékletének megváltozása

$U_{t h} = k_{t h} (ϑ - ϑ_{k}^{})$

(16.2)

ahol

	$U_{t h}$	hőelem által adott feszültség érték
	$ϑ$	a mérendő hőmérséklet
	$k_{t h}$	hőelem típustól függő konstans érték
	$ϑ_{K}$	a környezeti hőmérséklet, kompenzáció hőmérsékleti hely

Gázmennyiség szűkítő elemes mérésénél alkalmazható korrekciós egyenlet:

$Q_{p o n t o s í t o t t} = Q_{m é r t} \sqrt{\frac{ρ_{n é v l e g e s}}{ρ_{m é r t}}} \cdot \frac{T_{n é v l e g e s}}{T_{m é r t}} \cdot \frac{p_{m é r t}}{p_{n é v l e g e s}}$

(16.3)

ahol

	$Q_{m é r t}$	mért mennyiség
	$ρ_{m é r t}$	mért sűrűség
	$T_{m é r t}$	mért hőmérséklet
	$p_{m é r t}$	mért nyomás érték
	$ρ_{n é v l e g e s}$	névleges sűrűség ([kg/m^3])
	$T_{n é v l e g e s}$	névleges hőmérséklet (20 fokC)
	$p_{n é v l e g e s}$	névleges nyomás érték (1 bar)

16.1.4. Digitális szűrések megvalósítása a gyakorlatban

A digitális szűrés a számítógépben levő jeleken tetszőleges algoritmussal leírható digitális jelfeldolgozási algoritmus.

16.1.4.1. Átlagoló szűrő

Az átlagoló szűrőt, amely egy FIR típusú aluláteresztő szűrő, a bemeneti mintevételes jel zajszűrésénél alkalmazzák.

$y [k] = \frac{1}{N} \sum_{i = 0}^{N - 1} u [k - i]$

(16.4)

ahol

	y[k]	a kimenő jel az $k \cdot h$ pillanatban
	u[k-i]	a bemenő jel az $(k - i) \cdot h$ pillanatban

Az n-edik időpillanatban a jel átlag-értéke (az előző N pont átlaga).

16.1.4.2. Exponenciális szűrő

Az exponenciális szűrőt, a bemeneti mintavételes jel zajszűrésénél alkalmazzák.

$y [k] = \frac{h}{T} (A \cdot u [k - 1] - y [k - 1]) + y [k - 1]$

(16.5)

ahol

	y[k]	a kimenő jel az $k \cdot h$ pillanatban
	y[k-1]	a kimenő jel az $(k - 1) \cdot h$ pillanatban
	u[k-1]	a bemenő jel az $(k - 1) \cdot h$ pillanatban

A szűrő az $\frac{A}{1 + s T}$ egytárolós tag mintavételes megfelelője.

Az aluláteresztő szűrő mintavételes algoritmusa:

	$T \frac{d y}{d t} + y = A \cdot u$	(16.6)
	$T \frac{y_{n} - y_{n - 1}}{h} + y_{n - 1} = A \cdot u_{n - 1}$	(16.7)

Differenciálegyenlet megoldása, amelynek a differencia egyenlettel történő helyettesítése megadott mintavételi időtartammal:

$y_{n} = \frac{h}{T} (A \cdot u_{n - 1} - y_{n - 1}) + y_{n - 1}$

(16.8)

Általánosan

$y_{n} = b_{0} \cdot u_{n - 1} + a_{1} \cdot y_{n - 1}$

(16.9)

A következő időpillanatban a jel értéke rekurzív formulával adható meg (h mintavételi idő esetén.).

16.1.4.3. Logikai adaptív szűrő

A bemeneti jelen megjelenő kiugró értékű véletlenszerű zavarok hatásának kiküszöbölésére alkalmazható.

Az algoritmussal minden egyes mérésnél (mintavételezésnél) meghatározunk (D_k) értékeket, az N darab korábbi értékre vonatkozó jelváltozás gradiens értékét (D_k, D_k-1,..... D_k-(N-1)).

	${\bar{D}}_{k} = \frac{\sum_{i = k}^{k - (N - 1)} D_{i}}{N}$	(16.10)
	$σ_{k} = {[\frac{\sum_{i = k}^{k - (N - 1)} {(D_{i} - {\bar{D}}_{k})}^{2}}{N}]}^{\frac{1}{2}}$	(16.11)

Meghatározzuk ezek átlagértékét és szórását és ennek alapján avatkozunk be a jel szűrésébe.

$[(D_{k} - {\bar{D}}_{k - 1}) < 3 σ_{k - 1}]$

(16.12)

akkor változatlan szűrőegyenletet alkalmazunk.

$[(D_{k} - {\bar{D}}_{k - 1}) > = 3 \cdot σ_{k - 1}]$

(16.13)

A bemeneti jelen nagy értékű pillanatnyi zavarjel jelenik meg, akkor a szűrő kimenetét „befagyasztják”.

$y [k] = y [k - 1]$

(16.14)

Ha adott mintavételi idő után a feltétel még mindig fennáll $[(D_{k} - {\bar{D}}_{k - 1}) > = 3 \cdot σ_{k - 1}]$ , az azt jelenti, hogy a bemeneti jel megváltozott, ekkor

$y [k] = x [k]$

(16.15)

a szűrő algoritmus a megváltozott bemeneti jel környezetében dolgozik tovább.

16.1.4.4. Másodrendű szűrő

$T^{2} \frac{d^{2} y}{d t^{2}} + 2 ξ \cdot T \frac{d y}{d t} + y = u$

(16.16)

Differenciálegyenlet differencia egyenletté alakításával kapjuk.

	${\frac{d y}{d t} \|}_{t_{n}} ≅ \frac{y [k] - y [k - 1]}{h}$	(16.17)
	$\begin{array}{l} {\frac{d^{2} y}{d t^{2}} \|}_{t_{n}} ≅ \frac{\frac{y [k] - y [k - 1]}{h} - \frac{y [k - 1] - y [k - 2]}{h}}{h} \\ = \frac{y [k] - 2 \cdot y [k - 1] + y [k - 2]}{h^{2}} \end{array}$	(16.18)
	$\begin{array}{l} y [k] = \frac{h_{}^{2}}{T^{2} + 2 ξ T h + h_{}^{2}} \cdot u [k - 1] - \frac{2 T^{2} + 2 ξ T h}{T^{2} + 2 ξ T h + h_{}^{2}} \cdot y [k - 1] \\ + \frac{T^{2}}{T^{2} + 2 ξ T h + h_{}^{2}} \cdot y [k - 2] \end{array}$	(16.19)

Látható, hogy a kimenet meghatározásához a k. időpillanatban a megelőző két mintavételi időpillanatban szükséges a kimenet ismerete. Ez általánosan is igaz, ahányad rendű a szűrő, annyi korábbi mintavételi időpillanatbeli kimeneti jel értékre van szükségünk a szűrési egyenlet kiszámításához.

16.1.5. Átszámítás fizikai értékekre

A fizikai értékekre való átszámítás az A/D átalakító által szolgáltatott mintavételes adatot visszaalakítja fizikai mértékegységekben kifejezett értékké annak érdekében, hogy a folyamatváltozó feldolgozásakor közvetlenül a folyamatváltozó valós értékét alkalmazhassuk.

Az átszámítás lineáris jelleggörbéjű jeladó esetén az adat lineáris transzformációját jelenti.

$\frac{m - m_{k e z d ő}}{m_{v é g s ő} - m_{k e z d ő}} = \frac{p - p_{k e z d ő}}{p_{v é g s ő} - p_{k e z d ő}}$

(16.20)

ahol

	m	a folyamatváltozó fizikai mértékegységben kifejezett értéke
	m _kezdő	a folyamatváltozó fizikai mértékegységben kifejezett kezdőértéke
	m _végső	a folyamatváltozó maximális értéke A/D átalakítónál
	p	a folyamatváltozó A/D átalakítás utáni számértéke
	p _kezdő	kezdőérték az A/D átalakításnál
	p _végső	végérték az A/D átalakításnál

$m = m_{k e z d ő} + \frac{p - p_{k e z d ő}}{p_{v é g s ő} - p_{k e z d ő}} (m_{v é g s ő} - m_{k e z d ő})$

(16.21)

16.1. táblázat - Átszámítás fizikai értékekre

folyamatváltozó	m _kezdő = 10at	m = 17.5 at	m _végső = 25 at
áramtávadó	4 mA	12 mA	20 mA
áram-feszültség átalakító (250 ohm-mal)	2 V	6 V	10 V
A/D átalakító 11 bites átalakító [ ]	p_kezdő = 409	p = 1228	p_végső = 2047

folyamatváltozó

m _kezdő = 10at

m = 17.5 at

m _végső = 25 at

áramtávadó

4 mA

12 mA

20 mA

áram-feszültség átalakító (250 ohm-mal)

2 V

6 V

10 V

A/D átalakító

11 bites átalakító [ ]

p_kezdő = 409

p = 1228

p_végső = 2047

$\begin{array}{l} m = m_{k e z d ő} + \frac{p - p_{k e z d ő}}{p_{v é g s ő} - p_{k e z d ő}} (m_{v é g s ő} - m_{k e z d ő}) \\ = 10 + \frac{1228 - 409}{2047 - 409} (25 - 10) = 17,5 a t \end{array}$

(16.22)

Nem lineáris jelleggörbéjű érzékelő esetén:

Szakaszonkénti lineáris (egyenesekkel) közelítéssel

Közelítő polinommal

számítjuk át az értékeket.

Általánosan alkalmazott harmadrendű polinom:

$m = a_{3} \cdot p^{3} + a_{2} \cdot p^{2} + a_{1} \cdot p + a_{0}$

(16.23)

ahol

	m	a folyamatváltozó fizikai mértékegységben kifejezett értéke
	p	a folyamatváltozó A/D átalakítás utáni számértéke

az a_k értékeket (k=0..3) az adott átalakításhoz meg kell határoznunk.

16.2. Számított állapotváltozók képzése

A számított állapotváltozókat a számítógép mért, vagy más számított állapotváltozókkal végzett aritmetikai, illetve logikai műveletek eredményeként állítja elő. Az ilyen típusú állapotváltozókat abban az esetben szokás képezni, ha

a jel méréssel történő meghatározása aránytalanul költséges,

fizikailag nem lehetséges,

célszerűen egy algoritmussal meghatározható az értéke egy adott időtartamra vonatkozó mérési adatok alapján.

Számított állapotváltozók a következők lehetnek:

A mért és számított értékek idő szerinti első deriváltja.
A mért és számított értékek idő szerinti integrálja.
Egyéb tetszőleges érték meghatározása.

16.2.1. Idő szerinti differenciálási formula

$y [k] = \frac{2}{3} \frac{(u [k] - u [k - 1])}{h} + \frac{u [k - 1]}{3}$

(16.24)

16.2.2. Idő szerinti integrálási formulák

Az integrálási formulák közös tulajdonsága, hogy az adott időpillanatig meghatározott integrál értéket az y[k] kimenő változóban tárolják.

A y[k] kimenő változó értéke a k=0 mintavételi időpontban az integráló tag kezdeti értéke .

Az integrálási értékek meghatározása csak a mintavételi időpontokban történik. Ez azt jelenti, hogy az aktuális mintavételi időpontot megelőző mintavételi pontig meghatározott integrál értékhez hozzáadjuk a aktuális bemeneti jellel (és korábbi értékeivel) meghatározott adott lépéshez tartozó részintegrál értékét.

16.2.2.1. Téglány (Euler) integrálás

Az integrálási eljárás a bemenő jel nulladrendű tartós közelítését alkalmazza.

$\begin{array}{l} y [k] = \int_{0}^{t_{n}} u (t) \cdot d t = \sum_{k = 1}^{n} u [k - 1] \cdot h \\ = y [k - 1] + u [k - 1] \cdot h \end{array}$

(16.25)

16.2.2.2. Trapéz integrálás

Az integrálási eljárás a bemenő jel elsőrendű polinomiális közelítését alkalmazza.

$\begin{array}{l} y [k] = \int_{0}^{t_{n}} u (t) \cdot d t = \sum_{k = 1}^{n} \frac{u [k - 1] + u [k]}{2} \cdot h \\ = y [k - 1] + \frac{u [k - 1 + u [k]}{2} \cdot h \end{array}$

(16.26)

16.2.2.3. Simpson integrálás

Az integrálási eljárás a bemenő jel másodrendű (súlyozott) polinomiális közelítését alkalmazza.

$\begin{array}{l} y [k] = \int_{0}^{t_{n}} u (t) \cdot d t \\ ≅ y [k - 1] + \frac{u [k - 2] + 4 \cdot u [k - 1] + u [k]}{6} \cdot h \end{array}$

(16.27)

Irodalmak

[16.1.] Chi-Tsong-Chen. Analog And Digital Control System Design. Sounders College Publishing . 2006.

[16.2.] Chi-Tsong-Chen. Linear System Theory and Design. Oxford University Press. 1999.

[16.3.] Gajic, Zoran . Modern Control Systems Engineering. 1996.

Vissza		Előre
15. fejezet - Analóg kimenetek	Főoldal	Tárgymutató