3. fejezet - A mikromechanikában használt effektusok és funkcionális anyagok
Vissza		Előre

3. fejezet - A mikromechanikában használt effektusok és funkcionális anyagok

Tartalom

3.1. Mechanikus-elektromos átalakítások
3.2. Termikus-elektromos átalakítások
3.3. Mágneses- elektromos átalakítások
3.4. Optikai-elektromos átalakítások

A legtöbb effektus korrekt leírásához szilárdtest-fizikai, atomfizikai és kvantummechanikai ismeretek szükségesek. Ezért az effektusok magyarázatával itt nem foglalkozunk, csak a jelenségek megnevezése és alkalmazása a cél.

3.1. Mechanikus-elektromos átalakítások

Tenzometrikus és piezorezisztív effektus. Mechanikai feszültség hatására a vezető és félvezető anyagoknál ellenállás változás következik be. Az ellenállást a jól ismert képlettel lehet leírni:

$R = ρ \cdot \frac{l}{q}$

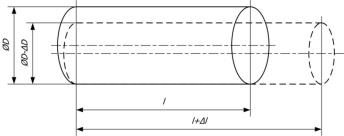
ahol ρ az anyag fajlagos ellenállása, l a prizmatikus (keresztmetszetét tekintve a hossz mentén nem változó) vezető rúd hossza, q ugyanennek a keresztmetszete. Ha a vezető rúdra erő hat (például húzóerő), az anyagban mechanikai feszültség ébred. Az alakváltozás során a rúd megnyúlik, és egyidejűleg a keresztmetszete is lecsökken (3.1. ábra). Ezt nevezzük tenzometrikus hatásnak. A mechanikai feszültség hatására azonban a fajlagos ellenállás is megváltozik, nem tekinthető állandónak. Ezt piezorezisztív hatásnak nevezzük (lásd később). A valóságban a két hatás együttesen, és egymástól szétválaszthatatlanul lép fel, és együttesen hozzák létre a k bélyegállandót, amit idegen kifejezéssel gauge-factor-nak hívunk.

forrás: MOGI

3.1. ábra - Prizmatikus rúd mechanikai alakváltozása

A bélyegállandó egyszerűsített kifejezéséhez teljes differenciálással, és egyszerűsítésekkel, a másodrendű tagok elhanyagolásával juthatunk el.

$k = \frac{\frac{d R}{R}}{\frac{d l}{l}} = (1 + 2 ν) + \frac{\frac{d ρ}{ρ}}{\frac{d l}{l}} \frac{d l}{l} = ε$

ahol ν a Poisson-tényező (értéke hozzávetőlegesen 0,3), és ε a fajlagos nyúlás. Szavakkal kifejezve a bélyegállandó azt mutatja meg, hogy egységnyi fajlagos nyúlás hatására (amikor dl=l, azaz a megnyúlás egyenlő a kezdeti hosszal, vagyis az anyagot képzeletben még egyszer akkorára nyújtjuk) a vezető rúd mekkora fajlagos ellenállás változást szenved. A bélyegállandó a legfontosabb szenzorjellemző, mert ez adja meg a kapcsolatot a mechanikai és a villamos mennyiségek között.

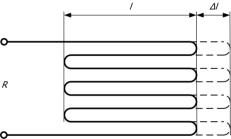
A méréstechnikában ú. n. nyúlásmérő bélyegeket alkalmaznak, amelyek lényegében vékony szigetelő hordozón elhelyezett meander alakú (több szál egymás mellé hajtogatva) ellenálláspályákat tartalmaznak (3.2. ábra).

forrás: MOGI

3.2. ábra - A nyúlásmérő bélyeg elvi kialakítása

Ezzel a konstrukcióval elérhető, hogy az alakváltozásból bekövetkező ellenállás-változás összeadódjék. Több szálat azért célszerű alkalmazni, mert egy szál érzékenysége kicsi, és a mérés jel/zaj viszonya rossz (a szálak villamosan soros, deformáció szempontjából pedig párhuzamos kapcsolásúak).

A bélyeg elnevezés onnan származik, hogy ezeket a szenzorokat ráragasztják a mérendő elemre, és ettől kezdődően a bélyeg ugyanúgy deformálódik, mint a mérendő elem megfelelő felülete. Ezért a ragasztásnak nagyon vékonynak és megbízhatónak kell lennie. Ellenkező esetben a bélyeg „kúszik”, driftje van.

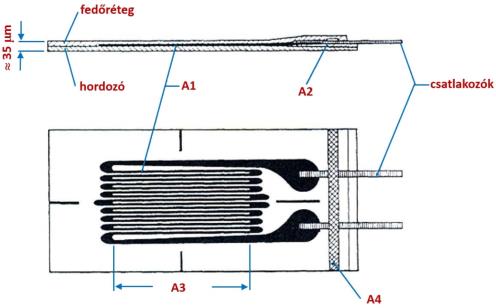
forrás: Tränkler: Sensoren

3.3. ábra - Nyúlásmérő bélyeg gyakorlati kialakítása

A méréstechnikában a maratott, fólia típusú bélyegek a legelterjedtebbek, ezek előállítási technológiája nagyon hasonló a nyomtatott áramköri lapok előállítási technológiájához (3.3. ábra). Névleges ellenállásuk 120, 350, 600, vagy 1000W szokott lenni. Érzékenységük, a bélyegállandó (gauge factor) 1,8...2,2 között van, az effektusban a tenzometrikus hatás a meghatározó. Linearitásuk nagy, 4000 me-ig kb. 0,1% (με-nak a fajlagos nyúlás 10^-6 részét nevezik). A fémes alapú bélyegekkel a mérhető legkisebb nyúlás kb. 0,1 me körül van.

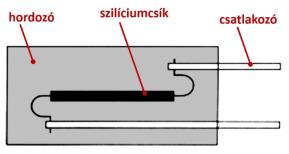
forrás: Tränkler: Sensoren

3.4. ábra - Félvezető nyúlásmérő bélyeg

Nyúlásmérő bélyegek anyagául azonban nemcsak különböző fémötvözetek, hanem félvezetők is alkalmazhatók. A félvezető bélyegeknél a szigetelő hordozón rendszerint egyetlen prizmatikus rudat helyeznek el (3.4. ábra). A félvezető anyagból készült bélyegek több jellemzőjükben különböznek a fémes alapú bélyegektől. Az egyik legfontosabb, hogy ezeknél a bélyegállandót elsősorban a piezorezisztív komponens határozza meg, a tenzometrikus hatás szinte elhanyagolható. A piezorezisztív hatásból adódóan a bélyegállandó, vagyis a szenzor érzékenysége majdnem két nagyságrenddel nagyobb. Ez (a gauge-factor) azonban csak szűk tartományban tekinthető állandónak, ami nyilvánvalóan hátrányos tulajdonság. Szintén hátrányos, hogy a félvezető bélyegek — hasonlóan minden félvezető eszközhöz — a hőmérséklet változására érzékenyek. Névleges ellenállásuk 120W , a bélyegállandó (gauge factor) 100..120 (itt mindkét előjel lehetséges, mert a tenzometrikus hatás elhanyagolható). Linearitásuk (ez függ a terheléstől) 1000 me-ig <1%, de 5000 me felett jelentősen lecsökken. A mérhető legkisebb nyúlás a nagy érzékenység miatt sokkal kisebb, mint a fémes bélyegeknél : kb. 0,001 me körül van. A mérhető legnagyobb nyúlás viszont sokkal kisebb, mint a fémes bélyegeknél, amelynek okát a szilícium tulajdonságaiból kell levezetni: a szilícium rideg anyag, nincs folyáshatára, hanem nagy igénybevételnél az üveghez hasonlóan egyszerűen eltörik.

forrás: Tränkler: Sensoren

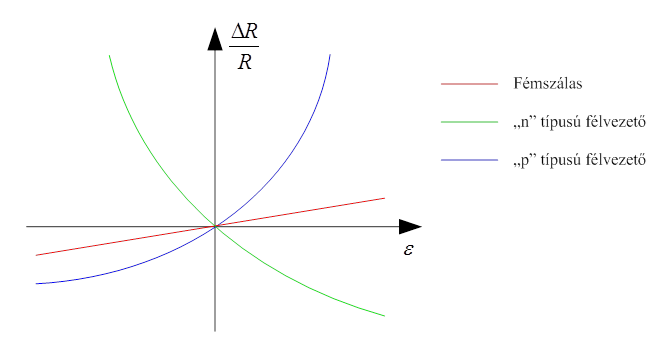
3.5. ábra - A nyúlásmérő ellenállások érzékenységének változása

Az ábrán (3.5. ábra) jól látható, hogy a fémeknél valóban bélyegállandóról van szó, míg a félvezetőknél a bélyegállandó a megnyúlással változik. Ebből következik, hogy a félvezető bélyeg kifejezetten a kis alakváltozásokra alkalmas, ekkor a munkapont környezetében megengedhető a görbült karakterisztika egyenessel közelítése, azaz a bélyegállandó valóban állandónak tekinthető.

A mikrotechnikában a fémes alapú bélyegeket nagyon ritkán használják, annál gyakrabban előfordul viszont a félvezető anyag használata, már csak azért is, mert a szerkezeti anyag is leggyakrabban szilícium. Így logikus, hogy a szenzort is ugyanabból az anyagból alakítsák ki. A mikromechanikában nem ragasztják a bélyegeket a deformálódó elemre, hanem rendszerint annak anyagából állítják elő, hanem abba integrálják, mint ahogyan az a következő ábrán (3.6. ábra) is látható.

forrás: Gardner: Microsensors

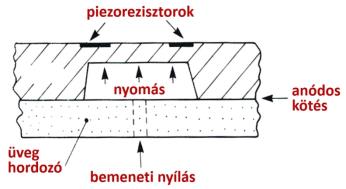
3.6. ábra - Mikromechanikai nyomásmérő vázlata

Mint az előzőkben láttuk, a félvezető anyagokból készült bélyegeknél a piezorezisztív hatás a döntő, emiatt a nyúlásmérő szenzorokat a szakirodalom gyakran piezorezisztorként említi. A piezorezisztivitást nem szabad a piezoelektromos effektussal összekeverni, ezért még egyszer leírjuk: piezorezisztivitásnak a mechanikai feszültség hatására bekövetkező fajlagos ellenállás-változást nevezzük.

A piezorezisztivitással rendelkező anyagok:: szilícium (n- ill. p típusú Si), germánium (Ge), gallium-arzenid (GaAs), polikristályos szilícium (Si), indium-antimonid (n-InSb).

Piezo- és inverz piezoelektromos effektus: a piezoelektromos effektus lényege, hogy mechanikai feszültség hatására elektromos polarizáció (töltésszétválasztás) lép fel bizonyos anyagokban. A fordított (inverz) effektus során villamos feszültség (villamos tér) hatására az anyagban alakváltozás jön létre. A jelenség megfordítható, tehát ugyanabban az anyagban oda-vissza működik.

A Curie-fivérek 1880-ban figyelték meg, hogy egyes ásványi anyagok, mint pl. a kvarc, mechanikai feszültségi állapot hatására villamosan polarizálódnak, és felületükön villamos töltést halmoznak fel. Számos előnyös tulajdonsága miatt piezoelektromos átalakítók céljára gyakran a kvarcot (SiO₂) használják fel. A kvarc előnyös tulajdonságai a következők:

nagy szilárdság 0,5…0,7 GPa (acél:0,5…1,5 GPa),
viszonylag nagy ellenálló képesség hőmérsékleti hatások ellen, mintegy 500 °C-ig a piezoelektromos tényező alig változik,
igen nagy szigetelési ellenállás, kb. 10¹⁴ …10¹⁵Wcm,
nagy linearitás, hiszterézis nélkül.

A kvarc hátrányos tulajdonsága a viszonylag kis érzékenység. Természetesen más anyagok (például a PZT, ólom-cirkonát-titanát) sokkal nagyobb piezoelektromos állandóval rendelkeznek, de ezek viszont sokkal érzékenyebbek a környezeti behatásokkal (például a hőmérséklettel vagy légnedvességgel) szemben. Ezért ezeket az anyagokat inkább az aktuátortechnikában, mint a szenzortechnikában használják.

forrás: MOGI

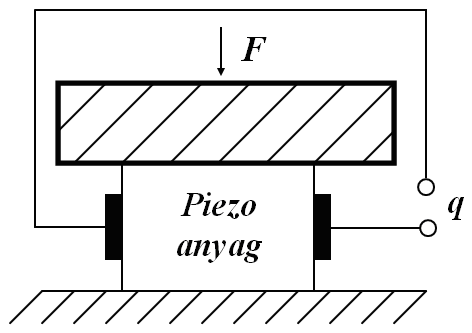
3.7. ábra - A piezoelektromos szenzor vázlata

A 3.7. ábra a piezoelektromos érzékelők elvi vázlatát mutatjuk be. Lényeges, hogy az F erőhatás egyenletes elosztása miatt egy járulékos tömeget kell alkalmazni, ami a dinamikai tulajdonságokat rontja. A keletkezett töltések az anyagban ébredő mechanikai feszültséggel arányosak, k egy anyagra jellemző állandó, A a piezoelektromos anyag (kristály) felülete.

$q = \frac{k \cdot F}{A}$

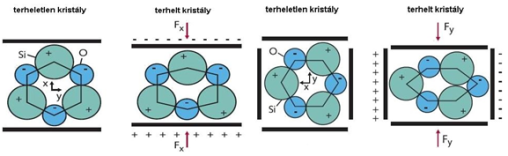
A piezoelektromos effektus lehet longitudinális és transzverzális is, a kvarc esetében például attól függően, hogy a szenzor mely kristálytani irány szerint van orientálva (3.8. ábra).

forrás: TU Ilmenau

3.8. ábra - Longitudinális és transzverzális piezoelektromos effektus

A piezoelektromos eszközöknek akarva-akaratlanul kapacitásuk van, a két fegyverzet és a közöttük lévő szigetelő tulajdonságú anyag dielektrikumként működve kondenzátort alkot. Ebből következően a töltésszétválasztás után a fegyverzetek között villamos feszültséget is lehet mérni. A képletben C₂ az eszköz saját kapacitása, amely a szükségképpen létrehozott kondenzátor tulajdonsága, és amely a piezo effektussal mindig együtt, attól szétválaszthatatlanul jelentkezik.

$U_{k i} ≅ - \frac{q}{C_{2}}$

Az inverz piezoelektromos effektus esetén az elektródákra U villamos feszültséget kell kapcsolni, a fellépő villamos erőtér a kristályszerkezetet deformálja, ami az x elmozdulás formájában jelentkezik.

$x = - \frac{k \cdot U}{A}$

Tekintettel arra, hogy a piezo anyag szigetelő, a fegyverzetek között állandósult állapotban (statikus esetben) áram gyakorlatilag nem folyik. Dinamikus működtetéskor a piezo aktuátor kapacitív terhelésként jelentkezik, hiszen a kondenzátor feltöltéséhez és kisütéséhez töltések áramlására van szükség, ezt nevezzük villamos áramnak.

A felhasználható anyagok:: kvarc (SiO₂), gallium-arzenid (GaAs), cink-oxid (ZnO), lítium-niobát (LiNbO₃), litium tantalát (LiTaO₃), ólom-cirkonát-titanát (PZT), polivinil-fluorid (PVDF).

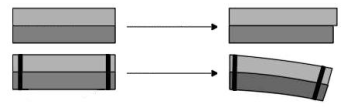
Ikerfém anyagok (bimetálok): egybehengerelt, különböző hőtágulású anyagpárok a hőmérséklet változásának hatására mechanikai deformációt szenvednek, és ezzel elmozdulást hoznak létre (3.9. ábra).

forrás: Wikipédia

3.9. ábra - A bimetall effektus

Anyagpárok: alumínium-szilícium (Al- Si), arany-szilícium (Au- Si), vas-nikkel-mangán (FeNi₂₀Mn₆- FeNi₄₂), polivinil-fluorid-politrifluor-etilén,-poliimid (PVDF/PTE- PI).
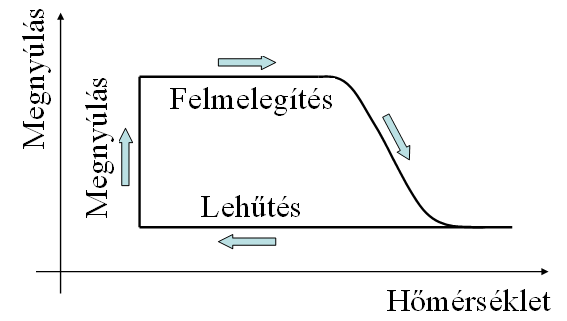
Emlékezőfémes effektus (SMA: Shape Memory Alloy): Bizonyos anyagok esetén, ha a martenzit kristályszerkezetű anyagot (T< T_á) deformáljuk, ezután felmelegítjük, amelynek hatására (T>T_á) az anyag kristályszerkezete ausztenitessé alakul, az anyag felveszi eredeti formáját, úgymond „emlékezik” az előző (hideg állapotban deformált) alakjára. A lehűlés után, tehát a martenzitté történő visszaalakulása után azonban nem változik már az alakja. Ezt nevezi a szakirodalom az egyutas effektusnak (3.10. ábra).

forrás: Janocha: Aktoren

3.10. ábra - Az egyutas emlékezőfémes effektus

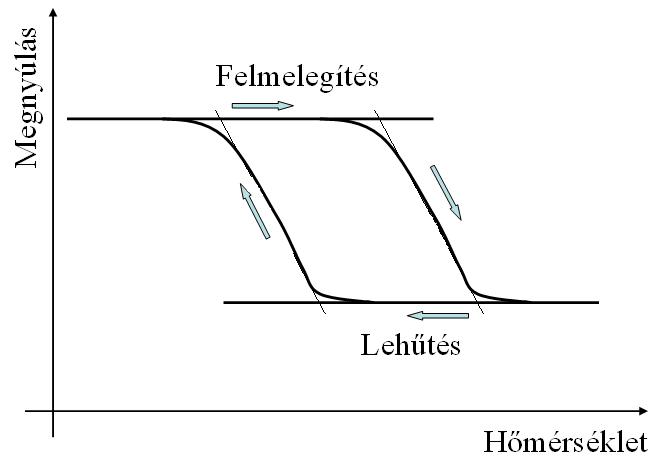
Ismeretes, és az aktuátor technikában gyakrabban alkalmazott jelenség a kétutas effektus, 3.11. ábra. Ekkor az alakváltozások kisebbek, mintegy feleakkorák, mint az egyutas effektusnál, de a martenzites-ausztenites átalakítás hőhatásra sokszor ismételhető. Megjegyzésre érdemes, hogy az SMA anyagok hőhatásra nem megnyúlnak (mint a fémes anyagok), hanem rövidülnek, és ennek mértéke a kétutas effektusnál kb. 3-5%.

forrás: Janocha: Aktoren

3.11. ábra - A kétutas emlékezőfémes effektus

Anyagok: nitinol (Ni-Ti), réz-cink-alumínium (Cu-Zn-Al), réz-alumínium-nikkel (Cu-Al-Ni) ötvözetek (az arányok és egyéb adalékok általában gyártási titkokat képeznek).

Elektrosztatikus erőhatás: a mikrotechnikai módszerekkel viszonylag nehéz tekercseket előállítani. Ebből következik, hogy a mikroaktuátoroknál az elektromágnest, mint szerkezetet ritkán használják. Ezzel szemben előtérbe kerülnek az elektrosztatikus mozgatások. Ezeket könnyen elő lehet állítani a mikromechanikai technológiákkal, és ebből következően gyakrabban találkozunk olyan aktuátorokkal, amelyeknél a mozgatóerőt nem elektromágneses, hanem elektromos erőtérrel hozzák létre. Az elektrosztatikus aktuátorok mikromechanikai alkalmazásának tulajdonképpen az az oka, hogy nagyon kisméretű légrések alakíthatók ki, amelyből következően nem kellenek extrém nagy feszültségek a megfelelő villamos tér létrehozásához. Az erőhatás ugyanis a villamos térerősségtől függ, hasonlóan a mágneses terekhez, ahol az erőhatás a mágneses indukcióval függ össze. Az elektrosztatikus terek létrehozásához nem kellenek tekercsek, csak vezető anyagból készült fegyverzetekre és a közöttük lévő dielektrikumra van szükség. Az elektrosztatikus erő a töltések (q1 és q2 ) nagyságán kívül azok távolságától (r) függ, méghozzá négyzetesen. Ez a másik gyakorlati oka annak, hogy a kis méretek tartományában nagyobb jelentősége van az elektrosztatikus aktuátoroknak mert a mikrorendszereknél az r távolság a mikrométeres tartományban lehet.

$F = k \frac{q_{1} q_{2}}{r^{2}}$

A k tényező értéke $k = \frac{1}{4 π ε_{0}}$ , ahol ε₀ =8,85·10 ^-12 C²/Nm² .

A mikrotechnikában az elektrosztatikus effektust használó aktuátorokban elérhető energiasűrűség azonos nagyságrendben van az elektromágneses effektust használó aktuátorok energiasűrűségével (hozzávetőlegesen 0,5 Ws/m³).

3.2. Termikus-elektromos átalakítások

Hőmérséklet mérés rezisztív úton: Ohm első törvénye alapján az elektromos ellenállás a hőmérséklet függvénye. Ez alapján lehetőség nyílik hőmérséklet mérésére.

$R_{T 2} = R_{T 1} (1 + α (T_{2} - T_{1}))$

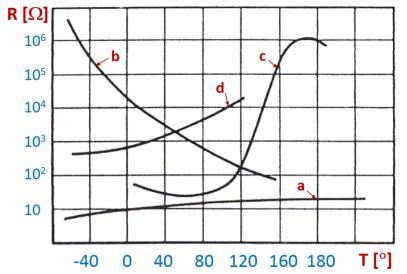
A képletben R_T2 a T₂ hőmérsékleten mérhető ellenállás, R_T1 a T₁ hőmérsékleten mérhető ellenállás, α a hőmérsékleti tényező, idegen kifejezéssel a temperature coefficient, rövidítve T_c, T₂-T₁ pedig a hőmérséklet különbség. Fontos megjegyezni, hogy a fémek karakterisztikája általában lineáris, vagy annak tekinthető, a félvezetőknél viszont a karakterisztika soha nem tekinthető lineárisnak. A lineáris karakterisztika előnye mellett ugyanakkor megjelenik egy hátrány is: ez a kis meredekség (érzékenység, 3.12. ábra, a görbe).

Anyagok: nagy tisztaságú, és lehetőleg korrózióálló fémek: platina (Pt, α= 0,00351 ·1/°C), nikkel (Ni), réz (Cu), ezüst (Ag), arany (Au), alumínium (Al), wolfram (W).

forrás: Lambert: Szenzorok

3.12. ábra - A különböző hőmérséklettől függő ellenállások összehasonlítása

A b görbe egy negatív hőmérsékleti tényezővel rendelkező (Negative Temperature Coefficient, NTC) félvezető szenzor karakterisztikája, a magyar műszaki terminológiában sokszor termisztornak nevezik. A karakterisztika soha nem lineáris, viszont nagy érzékenységgel rendelkezik, amely pontról pontra változik. Határértékek érzékelésénél előszeretettel használják, annak ellenére, hogy bizonyos típusok öregedésre hajlamosak. Külön csoportot képeznek a 3.12. ábra c karakterisztikájával rendelkező ú. n. PTC szenzorok, amelyek szintén félvezetők. Ezeket gyakran hővédelemre használják oly módon, hogy bizonyos hőmérséklet felett a PTC a körben folyó áramot korlátozza, lecsökkenti, és ezzel a túlzott melegedést akadályozza meg.

Külön családot képeznek azok az anyagok, amelyeknél a hőmérséklet hatására bekövetkező ellenállás változás más fizikai effektusok eredménye. Ilyen például a félvezetőknél a töltéshordozók mozgékonyságából következő ellenállás változás, amely az abszolút hőmérséklet függvénye (3.12. ábra, d görbe).

Anyagok: szilícium, poliszilícium (Si).

Megint más lehetőséget kínál a nyitóirányú szilíciumdiódák nyitófeszültségének hőmérséklet függése, amely nem nagy ugyan (kb. -2 °C), de stabil, és széles tartományban állandó. A dióda áram-feszültség karakterisztikája a következő ábrán (3.13. ábra) látható.

Három részre szokás osztani: I.— nyitóirány, II.— záróirány, III.— letörési tartomány.

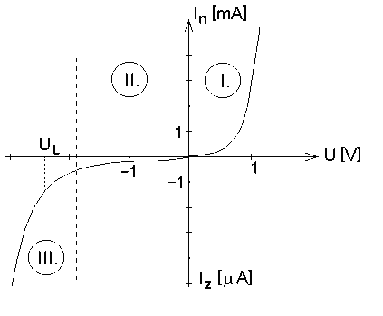
forrás: MOGI

3.13. ábra - Félvezető diódák karakterisztikája

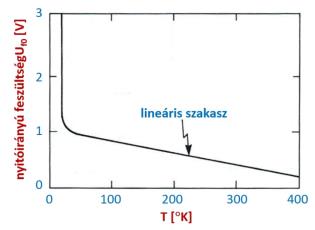
A szilícium diódák nyitóirányú feszültségének hőmérséklettől függése meglehetősen széles hőmérséklet tartományban állandó, mint ahogyan az a következő ábrán (3.14. ábra) látható. Nem szabad figyelmen kívül hagyni, hogy a hőmérséklet skála abszolút hőmérsékletben van skálázva, a szobahőmérséklet 300 °K közelében van.

forrás: Gardner: Microsensors

3.14. ábra - A nyitóirányú pn átmenet hőmérsékletfüggése

Anyag: egykristályos szilícium (Si).

A termisztoroknál (hőmérséklettől függő ellenállásoknál, Negative Temperature Coefficient, 3.12. ábra, b görbe) polikristályos fémoxidokat használnak, az ellenállás változása messze nem lineáris, jellemzően a hőmérséklet növekedésével csökkenő tendenciájú. Ezeket nagy általánosságban NTC szenzoroknak szokás nevezni. Vannak olyan anyagkombinációk is, amelyek ezzel ellentétesen a hőmérséklet növekedésével meredeken emelkedő ellenállás változással reagálnak, ezeket a szakirodalom PTC (Positive Temperature Coefficient, 3.12. ábra, c görbe) ellenállásoknak nevezi.

Anyagok: bárium-titán-oxid (BaTiO₃), [Ba_0,3Sr_0,7]TiO₃, [Ba_0,8Pb_0,2]TiO₃.

Az áram termikus hatása: hő előállítása elektromos árammal, ez talán a legismertebb jelenség, az áram hőhatása minden elektromos vezetékben jelentkezik, amelynek ellenállása (R) van.

$P = U \cdot I = \frac{U^{2}}{R} = I^{2} \cdot R$

Anyagok: platina (Pt), nikkel (Ni), titán (Ti), króm-nikkel ötvözetek (Cr-Ni), polikristályos szilícium (Si).

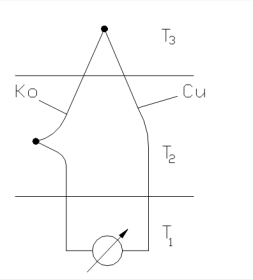
Seebeck - effektus: Ha két különböző anyagú vezetőt egymással érintkezésbe hozunk (tipikusan összehegesztjük), a nyitott kör két pontja közt feszültség mérhető, amennyiben az összeérintett pont és a vezetők másik végpontja között hőmérsékletkülönbség van. Ezt termofeszültségnek nevezzük (3.15. ábra).

forrás: Wikipédia

3.15. ábra - Termoelektromos effektus

A termofeszültség értéke attól függ, hogy mekkora a két fém elektródpotenciálja a platinához képest. Mennél távolabb esnek ezek egymástól, annál nagyobb lesz a termofeszültség értéke.

Anyagok: nikkel-króm-nikkel (Ni-CrNi), vas-réz-nikkel (Fe-CuNi), platina- platina-ródium (Pt- PtRh).
Peltier-effektus: bizonyos anyagpárok esetén, ha a körben áram folyik, úgy hőáramlás indul meg az egyik vezetőtől a másik irányában, tehát villamos áram hatására hőmérséklet különbség hozható létre. Az áram irányától függően fűtésre és hűtésre egyaránt használható, utóbbi a gyakoribb. A Seebeck- és a Peltier- effektus megfordítható jelenségek.

Anyagok: PtRh₆, (Rh: ródium) SbBi- SeTe, ATO- ITO- kerámiák, ón-dioxid-antimon (Antimony Tin Oxid, SnO₂-Sb), indium-oxid-ón (Indium Tin Oxid, In₂O₃-Sn)
Piroelektromos effektus: bizonyos dielektrikumok villamos tér hatására polarizálódnak. Ez a polarizáció azonban hőmérsékletfüggő, így állandó villamos tér mellett az anyag hőmérséklet mérésére is használható.

Anyagok: bárium-titanát (BaTiO₃), lítium-niobát (LiNbO₃), triglicin-szulfát (TGS), kerámiák és újabban polimerek.

3.3. Mágneses- elektromos átalakítások

Ferromágnesesség: a ferromágneses anyagok mágneses tér hatására változtatják permeabilitásukat. A lágy és a kemény mágneses anyagok egyaránt ide tartoznak. Tekintettel arra, hogy a tekercsek készítése mikromechanikai méretekben nehézkes, a ferromágnességnek (elektromágneses aktuátorok) sokkal kisebb jelentősége van, mint az elektrosztatikus effektusnakAnyagok: vas (Fe), nikkel (Ni), vas-nikkel ötvözetek (FeNi₇₈) és a kemény mágneses anyagok: alumínium-nikkel-kobalt (AlNiCo), szamárium-kobalt (SmCo₅), neodímium-vas-bór (Fe-Nb-B).

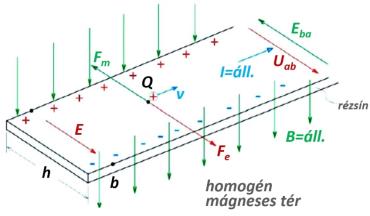
Hall-effektus: Amennyiben a vezető anyag (3.16. ábra, rézsín) az áram irányára merőleges mágneses térben (B) van, az áramló elektronokra (Q) a Lorentz-erő hat, emiatt azok a vezető egyik oldalán sűrűsödnek, a másik oldalán ritkulnak. Ebből következik, hogy a vezetés és a mágneses tér irányára is merőleges irányban feszültség, nevezetesen a Hall-feszültség mérhető (Edwin Herbert Hall, 1879). A fellépő Lorentz-erő:

$\bar{F_{m}} = Q \cdot \bar{v} \times \bar{B}$

forrás: BME VIK

3.16. ábra - A Hall-effektus magyarázata

A Lorentz-erő hatására a pozitív töltések a vezető a oldalán, a negatív töltések a b oldalán sűrűsödnek. A töltés szétválasztódás miatt fellépő elektrosztatikus térerősség erőt fejt ki:

$\bar{F_{e}} = Q \cdot \bar{E}$

Ez az erő F_m-mel ellenkező irányú erőt fejt ki a v sebességgel haladó Q töltésekre. A kialakuló E villamos térerősség nagyságát az erők egyensúlyából, az abszolút értékek egyenlőségéből (F_m = F_e), vagyis a Q·E = Q·v·B képletből határozható meg:

$\bar{E} = \bar{v} \cdot \bar{B}$

A B mágneses indukcióval rendelkező térbe helyezett I árammal átjárt vezetőben tehát elektrosztatikus tér alakul ki, és az ebből származó Hall-feszültség:

$U_{a b} = \int_{a}^{b} \bar{E} d \bar{s} = \bar{v} \bar{B} h$

U _ab a töltés egyesítő F_e erőhöz, a fellépő E_ba elektromotoros erő a töltés szétválasztásához szükséges F_m erőhöz kapcsolódik. A gyakorlatban a nagy U_ab elérése érdekében a félvezető anyagból készült Hall-szondát (Hall elemet, Hallotront) elsősorban a B mágneses indukció mérésére használják (I arányos v-vel). (forrás: Dr. Nagy István)

forrás: Fraden: Modern Sensors

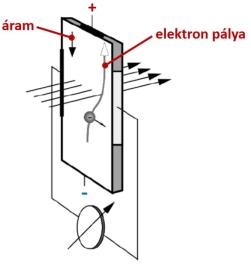
3.17. ábra - A Hall-effektus

A gyakorlatban alkalmazott Hall-érzékelő vázlatát a fenti ábra (3.17. ábra) mutatja. A Hall-feszültség (U_H) mind a mágneses indukciótól (B), mind az átfolyó áramerősségtől (I) függ. Adott Hall-generátor esetében az érzékenységet az eszközre jellemző k tényező határozza meg. A vektori szorzat miatt a maximális Hall-feszültség akkor érhető el, ha az indukció merőleges az érzékelő síkjára, valamint a gerjesztő áram vektorára.

$U_{H} = k \cdot (I \times B)$

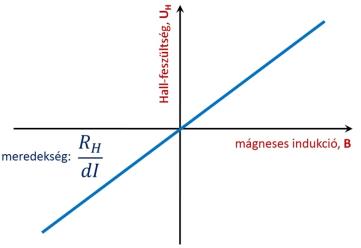
A Hall-feszültség az eszköz fizikai működéséből következően a mágneses tér előjelét is megmutatja, egy jellegzetes karakterisztikát mutat a 3.18. ábra. A karakterisztika meredeksége az eszközön áthajtott áramtól függ, és a lineáris karakterisztika eléréséhez értelemszerűen az áramot állandó értéken kell tartani.

forrás: Tränkler: Sensoren

3.18. ábra - A Hall-feszültség függése a mágneses indukciótól

A Hall-effektust felhasználó négy kivezetéses eszközöket a szakirodalom Hall-szonda, Hall-elem, vagy Hallotron néven egyaránt nevezi.

Anyagok: az effektus fizikai sajátosságából adódóan az elemek alábbi fő- és mellékcsoportjának kombinációja: AIII- BV, AII- BVI, AIV- BVI. Például: gallium-arzenid (GaAs), indium-antimonid (InSb), kadmium-szulfid (CdS).

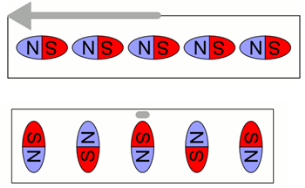
Magnetostrikciós effektus: bizonyos ferromágneses anyagok kristályai mágneses tér hatására anizotróp deformációt szenvednek, azaz mágneses tér hatására alakváltozás következik be (3.19. ábra). Ha ez a magnetizálás az ún. Curie-hőmérséklet alatt történik, akkor a deformáció hosszváltozás formájában jelentkezik (James Joule 1842).

forrás: Wikipédia

3.19. ábra - A magnetostrikció magyarázata

Anyagok: nikkel (Ni), permalloy (FeNi₇₇+ adalékok), vacoflux 50 (FeCo₄₉ + adalékok), terfenol-D (Tb_(x)Dy_(1-x)Fe_(y)), valamint a lantanidák (Sm: szamárium, Tb: terbium, Dy: diszprózium) ötvözetei FeSm₃₈, FeTb₄₆.
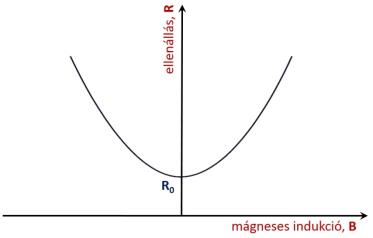
Magnetoellenállás, magnetorezisztor: Ellenállás jellegű eszköz, szintén a Hall-effektust használja fel azáltal, hogy a Lorentz-erő által eltérített töltéshordozók az anyagban hosszabb utat kényszerülnek befutni, amit kívülről az ellenállás megváltozásaként érzékelünk. Mennél nagyobb a mágneses indukció, annál nagyobb az eszköz ellenállása. A magnetorezisztorok nem képesek a mágneses indukció előjelét detektálni, szemben a klasszikus 4 kivezetővel ellátott Hall-generátorokkal, mint ahogyan az a következő ábrán (3.20. ábra) látható.

forrás: Tränkler: Sensoren

3.20. ábra - A magnetorezisztor karakterisztikája

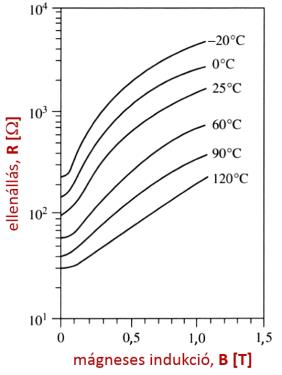
A magnetorezisztorok ellenállása azonban nemcsak a mágneses tértől, hanem a hőmérséklettől is függ, méghozzá jelentősen. A szenzor hőmérsékletfüggését a mágneses indukció függvényében mutatja a 3.21. ábra.

forrás: Tränkler: Sensoren

3.21. ábra - A magnetorezisztor ellenállása a mágneses indukció (T) függvényében különböző hőmérsékleteknél

Anyagok: egyrészt értelem szerűen a Hall-effektusnál látott anyagok, másrészt a nikkel (Ni), vas (Fe), kobalt (Co) két és háromalkotós ötvözetei.

3.4. Optikai-elektromos átalakítások

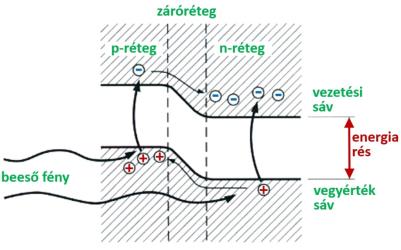
Belső fotoelektromos effektus: a félvezető pn átmenetére érkező elektromágneses sugárzás hatására a beérkező fotonok töltéshordozókat generálnak, és ezek a pn átmenet potenciálgátjának két oldalán helyezkednek el (3.22. ábra).

forrás: Wikipédia

3.22. ábra - A belső fotoelektromos effektus

forrás: Wikipédia

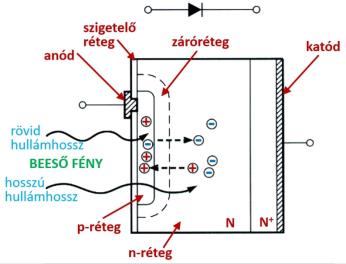
3.23. ábra - Fotodióda vázlatos keresztmetszete

A fotodiódák vázlatos keresztmetszetét a 3.23. ábra mutatja. A fotodiódákat fényelemként is (ezt fotofeszültségű, vagy fotovoltaikus üzemmódnak nevezik), és — zárófeszültséget adva a diódára — zárófeszültségű üzemmódban is lehet működtetni.

forrás: Tränkler: Sensoren

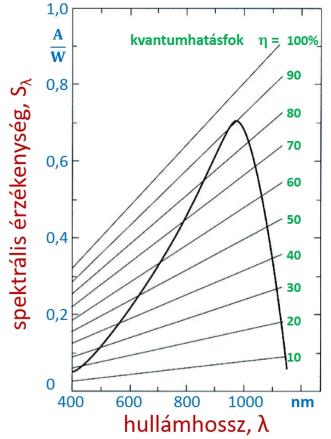
3.24. ábra - A szilícium fotodiódák spektrális érzékenysége

A félvezető fotodiódák sugárzási érzékenysége a fotodióda anyagától függ (anyagjellemző), tehát kötött, különböző adalékolási módszerekkel is csak nagyon kis mértékben változtatható. Szilícium esetében (3.24. ábra) a sugárzási érzékenység maximuma nagyjából a 950 nm-es hullámhossznál (a közeli infra tartományban) van, értéke kb. 0,7 A/W.

Anyagok: egykristályos félvezetők, például szilícium (Si), germánium (Ge), gallium-arzenid (GaAs).
Fordított fotoelektromos effektus: félvezető dióda nyitóirányú áramával az elektronokat magasabb energiaszintre lehet kényszeríteni, majd az elektronok alacsonyabb energiaszintre ugorva adott frekvenciájú elektromágneses sugárzást bocsátanak ki. Ezeket fényemittáló diódáknak LED-eknek (Light Emitting Diode) nevezzük. A fizikai működésből következően a LED-ek által kibocsájtott fény hullámhossza a félvezető anyagától függ.

forrás: Texas: Optoelektronikai kézikönyv

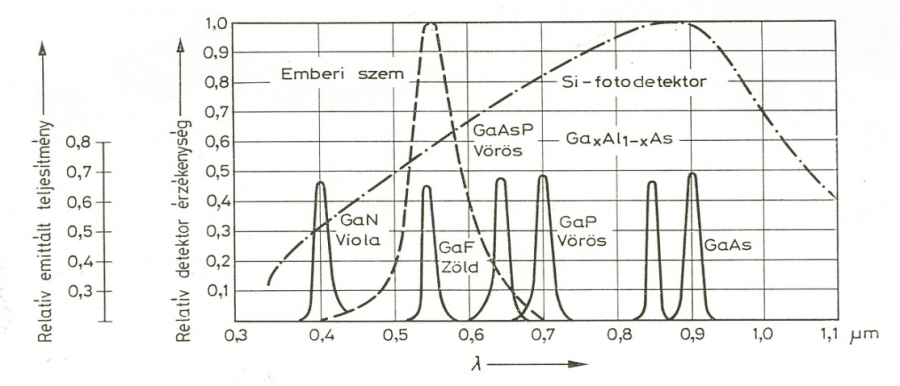
3.25. ábra - A LED-ek sugárzási karakterisztikája, valamint az emberi szem, és a szilícium fotodióda spektrális érzékenysége

A 3.25. ábra a különböző hullámhosszúságú (különböző színű) LED-ek sugárzásának spektrális eloszlását, és az emberi szemnek, valamint a szilícium fotodiódának a relatív (%-osan megadott) érzékenységét láthatjuk.

Ebbe a csoportba tartoznak a lézerdiódák is. Ezek kis áramoknál LED-ként működnek, majd egy bizonyos áramérték felett létrejön a lézer effektus, amely felett már lézerként működnek.

Anyagok: gallium-arzenid-foszfid (GaAs_(x)P_(1-x)), Al_(y)Ga_(1-y), As_(x)P_(1-x).
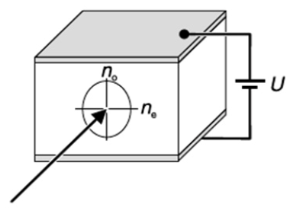
Elektro-optikai effektus (Pockels- / Kerr-effektus, 1974): elektrosztatikus tér hatására az anyag változtatja az optikai törésmutatóját. A Pockels-effektus esetében az optikailag kettőstörő anyag kettőstörő tulajdonsága változik elektromos tér hatására, és ez a változás egyenesen arányos a villamos erőtérrel. A Kerr-effektus csak abban különbözik ettől, hogy a kettőstörés exponenciálisan nő az elektromos tér függvényében. A szokásos elrendezést a 3.26. ábra mutatja.

forrás: www.uni-obuda.hu

3.26. ábra - A Pockels effektus magyarázatához

Anyagok: litium-niobát (LiNbO₃), gallium-arzenid (GaAs), indium-foszfid (InP).
Elaszto-optikai (feszültségoptikai) effektus: mechanikai deformáció (mechanikai feszültség) hatására az anyag változtatja az optikai törésmutatóját (3.27. ábra). Polarizált fény segítségével lehet a jelenséget jól megfigyelni átlátszó anyagoknál. (David Brewster)

forrás: Wikipédia

3.27. ábra - Az elaszto-optikai effektus bemutatása

Anyagok: litium-niobát (LiNbO₃), gallium-arzenid (GaAs), indium-foszfid (InP), és számos műanyag.
Fotorefraktív effektus: Fény hatására bizonyos anyagok változtatják a törésmutatójukat. Nemlineáris effektus.

Anyagok: bárium-titanát (BaTiO₃ ), lítium-niobát (LiNbO₃), folyadékkristályok, szerves anyagok, fotopolimerek, üvegek.
Magneto-optikai effektus: az anyag a mágneses tér hatására változtatja a törésmutatóját.

Anyagok: litium-niobát (LiNbO3), gallium-arzenid (GaAs), indium-foszfid (InP), platina-mangán-antimon ötvözet (PtMnSb).

Vissza		Előre
2. fejezet - A mikromechanika anyagai	Főoldal	4. fejezet - Jellegzetes mikromechanikai technológiák