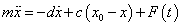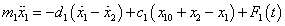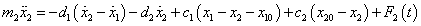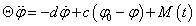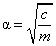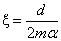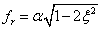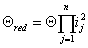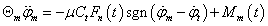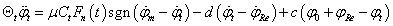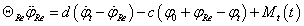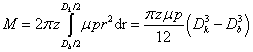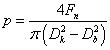4. fejezet - Tervezési lépések és modellezési eljárások
- 4.1. Hajtáslánc dinamikai modellezése a tengelykapcsoló működése szempontjából
-
- 4.1.1. A fizikai modellek megalkotásának és alkalmazásának általános szempontjai
- 4.1.2. Dinamikai modellek megvalósítása lengőrendszerek csatolt modelljeivel
- 4.1.3. A hajtáslánc dinamikai modellje
- 4.1.4. Háromtömegű egyszerűsített hajtásláncmodell alkalmazása a tengelykapcsoló vizsgálatához
- 4.1.5. További szempontok tengelykapcsolók tervezéséhez
- 4.2. Irányítási rendszerek alkalmazása tengelykapcsolók automatikus működtetéséhez
- Irodalmak:
4.1. Hajtáslánc dinamikai modellezése a tengelykapcsoló működése szempontjából
Ebben a fejezetben áttekintést nyújtunk a hajtásláncok, ill. különös tekintettel a tengelykapcsolók tervezési folyamata során alkalmazott dinamikai modellezési és szimulációs eljárásokról. A fejezet célja az általános kép kialakítása, ezért közel sem törekedtünk teljességre sem pedig szigorú formalitásra.
4.1.1. A fizikai modellek megalkotásának és alkalmazásának általános szempontjai
A fizikai modellek megalkotása és alkalmazása a tervezési feladatok során több lépésből álló feladat. Ezek a lépések röviden a következőképpen foglalhatók össze:
-
A probléma felvetése (megfogalmazása)
-
A probléma absztrakciója
-
A modell matematikai megfogalmazása
-
A modell alkalmazása
-
A kapott eredmények összevetése a valósággal
Ezek között a lépések között sorrendi kapcsolat található ezért mindegyikük azonos jelentőségű a modellezési feladat megoldása során.
Első lépésként meg kell fogalmazni a problémát. Ez sok esetben annak a tervezési feladatnak a sajátságaiból adódik, amelyiknek a támogatásához modellt akarunk készíteni (pl. a feladatkitűzés eleve formális műszaki specifikáció által történik), ez azonban nem minden esetben nyilvánvaló. A feladat megfogalmazásakor meg kell határozni a tervezés (modellezés) célját, és fel kell felmérni a kiindulási információkat (pl. műszaki követelmények, szabványok, stb.).
A megfelelően megfogalmazott problémától el kell vonatkoztatnunk ahhoz, hogy modellt tudjunk építeni a probléma megoldásához. Az elvonatkoztatás célja, hogy a probléma számos tulajdonsága közül azokat emeljük ki, amelyek a modellezni kívánt jelenség szempontjából fontosak. Ez a folyamat mindig függ az adott feladat kitűzésétől, eltérő célok eltérő absztrakciót igényelnek.
Az absztrakt modellt meg kell fogalmaznunk matematikai formában, mivel a modellvizsgálat eredményeként számszerűsített jellemzőket kell kapnunk a fizikai folyamatról. A modell matematikai megfogalmazása különböző megközelítések szerint történhet, azonban a vizsgálandó problémák (hajtáslánc-modellezés) szempontjából jellemző az absztrakt fizikai modellre épülő, ún. white box megközelítés.
A modell alkalmazása a matematikai modellen végzett kísérletet jelent. Ez jellemzően valamilyen, a matematikai modellt magában foglaló szimuláció elvégzése. Fontos, hogy ez nem csak egyszeri alkalmazást jelent, mivel a szimuláció többször is elvégezhető és a kapott eredmények, ill. az újabb felmerülő problémák alapján többször el is kell végezni (másképpen: fejlesztési iteráció).
Végezetül a modell eredményeit össze kell vetni a valóságos tapasztalatokkal (pl. mérési eredményekkel). Ezzel az összevetéssel meghatározható, hogy a modell milyen pontossággal írja le a valóságot, ill. hogy a modell által tett előrejelzések igazak lesznek-e a modell érvényességi tartományán belül (validáció) [4.1.] .
4.1.2. Dinamikai modellek megvalósítása lengőrendszerek csatolt modelljeivel
A gépjárművek és a gépjármű-alrendszerek mozgásának vizsgálata általában valamilyen dinamikai probléma vizsgálatára vezethető vissza. Ezeknek a dinamikai problémáknak az elemi építőegysége jellemzően az ún. egyszabadságfokú, vagy egytömegű lengőrendszer[1], ami egy tömegpontszerűen kezelt test (tömeg) és a testet egy másik testtel összekötő rugó és lengéscsillapító együttes, absztrakt modellje.
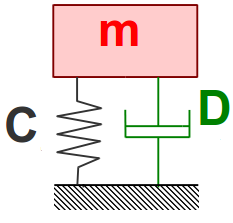
Feltéve, hogy a vizsgált egytömegű lengőrendszer csak egy irány mentén végezhet mozgást, a rendszer modellje a dinamika alapegyenlete (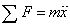 ) szerint a következő, közönséges másodrendű differenciálegyenlet alkalmazásával írható le:
) szerint a következő, közönséges másodrendű differenciálegyenlet alkalmazásával írható le:
|
|
ahol m a tömeg, 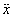 a tömeg gyorsulása,
a tömeg gyorsulása, 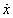 a tömeg sebessége, x a tömeg pillanatnyi pozíciója, x
0
a rugó terheletlen hossza, c a rugóállandó, d a csillapítási tényező, F(t) az esetleges (időben változó) külső gerjesztő erő.
a tömeg sebessége, x a tömeg pillanatnyi pozíciója, x
0
a rugó terheletlen hossza, c a rugóállandó, d a csillapítási tényező, F(t) az esetleges (időben változó) külső gerjesztő erő.
A bemutatott egyenletet mozgásegyenletnek nevezzük [4.2.] . Megfigyelhető, hogy az egyes erőkomponensek (a csillapításból, ill. a rugóerőből adódóak) a test sebességétől, ill. pillanatnyi pozíciójától függenek. Ezt a megfontolást felhasználva két lengőrendszer összekapcsolható olyan formában, hogy a két testet összekötő elemekben ébredő erőkomponensek nem a testek abszolút sebességétől és pozíciójától függenek, hanem egymáshoz viszonyított helyzetüktől, ill. sebességkülönbségüktől. Az ilyen módon összekapcsolt lengőrendszert kéttömegű lengőrendszernek nevezzük.
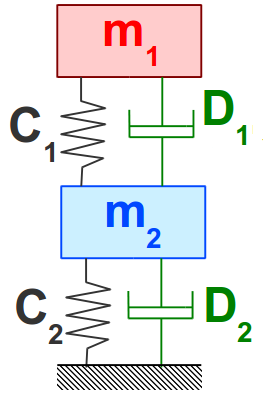
A fenti megfontolások alapján a kéttömegű lengőrendszer első tömegének a mozgásegyenlete a következőképpen írható:
|
|
Az előzőhöz hasonlóan a második tömegé:
|
|
ahol a jelölések a megfelelő indexálást figyelembe véve megegyeznek az egytömegű lengőrendszernél bemutatott jelölésekkel.
A kéttömegű lengőrendszerhez hasonlóan tetszőlegesen sok tömegből, ill. a közöttük lévő tetszőleges kapcsolatokból álló lengőrendszer is definiálható. Ilyen esetben a lengőrendszert annyi egyenlet írja le, ahány szabadságfoka van, vagyis ahány tömeg alkotja.[2] Terjedelmi okokból nem térünk ki az összetett lengőrendszerek formális tárgyalására.
A lengőrendszerek nem csak longitudinális, hanem forgómozgást végző formában is értelmezhetők. Ezeket a lengőrendszereket torziós lengőrendszernek nevezzük [4.3.] . Ez a megközelítés különösen fontos a tengelykapcsolók vizsgálatánál, mivel a tengelykapcsolók, ill. a hajtáslánc hozzájuk kapcsolódó részei is rendszerint forgómozgást végeznek.
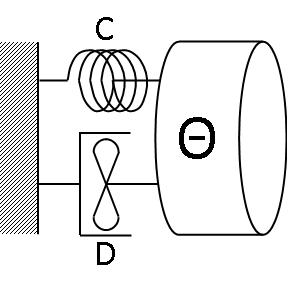
Forgómozgást végző rendszer esetén a dinamikai egyenletek azonos alakúak a korábban bemutatott egyenletekkel, viszont a mozgásmennyiségek és a jellemző paraméterek a forgómozgásnak feleltethetők meg. Az egytömegű lengőrendszer viselkedését leíró egyenlet torziós lengőrendszer esetén a következőképpen írható:
|
|
ahol Θ a tömegnek a torziós lengőrendszer forgástengelyére számított tehetetlenségi nyomatéka, 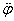 a tömeg szöggyorsulása,
a tömeg szöggyorsulása, 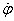 a tömeg szögsebessége, φ a tömeg pillanatnyi pozíciója, φ
0
a rugó terheletlen pozíciója, c a torziós rugóállandó, d a torziós csillapítási tényező, M(t) az esetleges (időben változó) külső gerjesztő nyomaték.
a tömeg szögsebessége, φ a tömeg pillanatnyi pozíciója, φ
0
a rugó terheletlen pozíciója, c a torziós rugóállandó, d a torziós csillapítási tényező, M(t) az esetleges (időben változó) külső gerjesztő nyomaték.
A differenciálegyenlettel adott lengőrendszer a megfelelő kezdeti feltételek (x(0),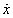 (0)) hozzárendelésével kezdetiérték-feladatot jelent, amely numerikus módszerekkel megoldható. A különböző numerikus módszerek alkalmazásának számos módja van, többek között léteznek erre a célra szolgáló szoftverrendszerek, amelyek akár grafikus eszközökkel is segítik a felhasználót a probléma matematikai megfogalmazásában és megoldásában. Ilyen rendszer például a MATLAB/Simulink, amely elterjedten alkalmazott eszköz a dinamikai modellek és a hozzájuk kapcsolódó irányítási rendszerek szimulációs problémáinak megoldásában.
(0)) hozzárendelésével kezdetiérték-feladatot jelent, amely numerikus módszerekkel megoldható. A különböző numerikus módszerek alkalmazásának számos módja van, többek között léteznek erre a célra szolgáló szoftverrendszerek, amelyek akár grafikus eszközökkel is segítik a felhasználót a probléma matematikai megfogalmazásában és megoldásában. Ilyen rendszer például a MATLAB/Simulink, amely elterjedten alkalmazott eszköz a dinamikai modellek és a hozzájuk kapcsolódó irányítási rendszerek szimulációs problémáinak megoldásában.
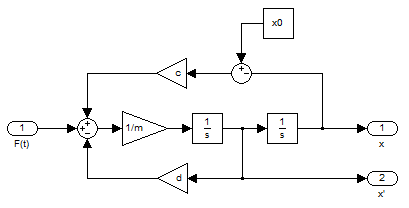
Figyeljük meg a műveletvégző elemek megfeleltethetőségét a mozgásegyenlet szerint! (1/s az integrálás műveletét jelöli az integrálás Laplace-transzformáltjának jelölése szerint)
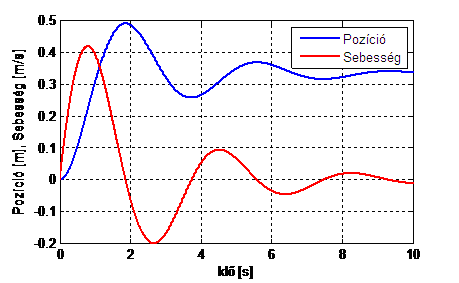
(a mozgásegyenletek megoldásai (0,0) kezdeti feltételekkel, m=1 kg, c=3 N/m, d=0,8 Ns/m, x0=0 m)
A lengőrendszerek vizsgálata szempontjából nem csak az időtartományban kapott megoldásfüggvények jelentősek, hanem az is, hogy, ha F(t) gerjesztőerő harmonikus, vagy harmonikus komponenseket tartalmaz, akkor F(t) frekvenciájának függvényében milyen viselkedést mutat a lengőrendszer. Ennek leírásához – terjedelmi korlátok miatt bővebb magyarázat nélkül – vezessük be a (csillapítatlan) sajátkörfrekvencia fogalmát. A sajátkörfrekvencia a lengőrendszer tulajdonsága, értéke a rugóállandótól és a tömegtől függ, a következő összefüggés szerint:
|
|
Hasonlóképpen vezessük be a csillapítási arányszám fogalmát is:
|
|
A csillapítási arányszám kitüntetett értékekkel rendelkezik. Ha ξ<1, alulcsillapítottnak, ha ξ>1, túlcsillapítottnak, ha ξ=1 akkor kritikusan csillapítottnak, ha pedig ξ=0 akkor csillapítatlannak nevezzük a rendszert. A saját körfrekvencia és a csillapítási arányszám ismeretében számítható az ún. rezonanciafrekvencia:
|
|
A rezonanciafrekvencia tulajdonsága, hogy adott amplitúdójú F(t) gerjesztőerő esetén a lengőrendszer kitérése maximális, ha F(t) frekvenciája megegyezik a rezonanciafrekvenciával. A rezonanciaállapot, ill. a lengőrendszer maximális kitérése a gyakorlatban általában kerülendő, mivel a szerkezet tönkremenetelét okozhatja. A lengések amplitúdójának szerkezetre káros mértékű növekedése azonban nem csak a rezonanciafrekvencia értékénél, hanem annak környezetében is felléphet. Ahhoz, hogy minden frekvencián megvizsgálhassuk a rendszer viselkedését, elő kell állítani a rendszer ún. frekvenciaátviteli függvényét. (A frekvenciaátviteli függvény meghatározását terjedelmi okokból nem mutatjuk be. A gyakorlatban célszerű az elterjedt numerikus módszereket alkalmazni a frekvenciaátviteli függvény meghatározásához.) A frekvenciaátviteli függvény a gerjesztés frekvenciájának a függvényében megadja a gerjesztés és a gerjesztett rendszer amplitúdójának a viszonyát, valamint a gerjesztett rendszer lengéseinek a fázisát a gerjesztéshez viszonyítva. Ebből következően a jellemző ábrázolásmódja egy olyan diagrampár, ahol az egyik diagram az amplitúdóviszonyt, a másik pedig a fázist ábrázolja a frekvencia függvényében. Ezeknek a diagramoknak több, egymástól elsősorban elnevezésükben eltérő, de tartalmilag azonos változata is elterjedt, ilyenek pl. a lengéstani irodalomban megtalálható rezonanciadiagramok, vagy a rendszertechnikában használatos Bode-diagramok.
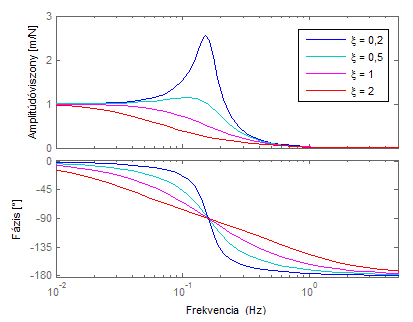
(erőgerjesztés és elmozdulás közti átvitel)
Az előzőleg bemutatott tulajdonságból következik, hogy a gépszerkezetek tervezésénél célszerű arra törekedni, hogy a csillapítási arányszámot növeljük, vagy a rezonanciafrekvenciát a szerkezet paramétereinek (tömeg, rugómerevség) megváltoztatásával olyan értékűre „hangoljuk”, ahol rendeltetésszerűen nem, vagy csak nagyon rövid ideig üzemel a rendszer.
Fontos megemlíteni, hogy a fentebb bemutatott modellek, illetve matematikai megfogalmazásaik lineárisak. Ez matematikai szempontból azt jelenti, hogy az egyenletek baloldala a mozgásmennyiségek legfeljebb elsőfokú (lineáris) függvénye, gyakorlati szempontból pedig azt, hogy érvényes rájuk a szuperpozíció elve. Ez az egyszerűsítés a gyakorlati alkalmazások során nem mindig állja meg a helyét, ilyen esetekben kiegészítő módszerek alkalmazása válik szükségessé.
4.1.3. A hajtáslánc dinamikai modellje
A gépjármű-hajtásláncok dinamikai modellje számos, különböző megközelítés szerint felépíthető. Az alkalmazott módszereket meghatározzák az aktuális tervezési, vizsgálati célok, elsősorban a 4.2.1. szakasz pontban megfogalmazott általános elvek szerint. Eltérő modelleket célszerű alkalmazni például a belsőégésű motorok által gerjesztett rezgések hatásainak vizsgálatához, a nyomatékváltók tervezési feladataihoz, vagy éppen a tengelykapcsolók működésének vizsgálatához. A különböző modellek bonyolultságukat, az alkalmazott matematikai módszereket, vagy éppen a számításigényüket tekintve jelentősen eltérőek lehetnek, azonban közös jellemzőjük, hogy a megvalósítás általában valamilyen többtömegű csatolt lengőrendszer mozgásegyenleteinek megoldását jelenti.
Általánosan elmondható, hogy a hajtáslánc minél több alrendszerét vagy alkatrészét különböztetjük meg önálló tömegként (minél több tömegből álló lengőrendszermodellt alkotunk) annál pontosabb eredményeket kapunk és annál részletesebben vizsgálhatjuk a hajtásláncban fellépő tranziens jelenségeket.
Példaként a tengelykapcsolók kapcsolási folyamatainak, ill. a kapcsolás során fellépő rezgések járművezetőre gyakorolt hatását a LuK tengelykapcsoló-gyártó az alábbi, hat tömegből álló csatolt lengőrendszer-modell alkalmazásával vizsgálja [4.4.] . A modell előnye, hogy alkalmazásával közvetlenül vizsgálhatók a járművezetőt érő erőhatások, ill a járművezető mozgásállapota. Hátránya, hogy a leíráshoz szükséges hat egyenlet bizonyos problémák esetén nehezebben kezelhető, mint más, egyszerűbb modellek.

A modellben Θ m a belsőégésű motor, ill. lendkerék, Θ t a tengelykapcsoló-súrlódótárcsa. Θ e az erőátviteli berendezések (nyomatékváltó, kiegyenlítőmű, féltengelyek), Θ k a hajtott kerekek, Θ b a karosszéria, Θ j a járművezető redukált tehetetlenségi nyomatéka. Látható, hogy az összes tömeg, azok is, amelyek alapvetően nem forgómozgást végeznek, a belsőégésű motor forgattyústengelyére számított tehetetlenségi nyomatékként van jelen a modellben. Ez a tömegek és tehetetlenségi nyomatékok redukciójának következménye, ami a Steiner-tétel alkalmazásával adódik, amely a hajtáslánc elemeire általánosan a következő alakban írható:
|
|
ahol Θ red egy adott elem redukált tehetetlenségi nyomatéka, Θ az adott elem tehetetlenségi nyomatéka a saját forgástengelyére számítva, i j a j-edik módosítás (nyomatékváltó, vagy kiegyenlítőmű módosítása, kerék gördülési sugarából adódó módosítás, stb.), n a módosítások száma az adott elem és a redukált elem között.
Ezzel a módszerrel a probléma megoldása jelentősen egyszerűsíthető, mivel a mozgásegyenletek megoldásánál már nem kell tekintettel lenni a módosítások hatásaira (természetesen ehhez a gerjesztőnyomatékokat, erőket is a módosítások figyelembevételével kell meghatározni).
A modell másik meghatározó tulajdonsága, hogy a tengelykapcsoló-súrlódótárcsa és a lendkerék, valamint a nyomatékváltó kapcsolatát részben Coulomb-súrlódást leíró elemekkel modellezi. Ez az elem nehézséget okozhat a modell felépítésénél és alkalmazásánál, mivel a lengőrendszer mozgásegyenleteit nemlineárissá teszi. Másrészről viszont belátható, hogy legalább egy, Coulomb-súrlódást leíró elem alkalmazása megkerülhetetlen a tárcsás tengelykapcsolók dinamikai modelljében, azok működési alapelvéből adódóan. A nemlineáris tulajdonságokból adódó problémák kezelése érdekében ilyen esetekben célszerű a modellt két, szakaszonként lineáris modellre bontani, a jellemző munkapont(ok) körül linearizálni, vagy olyan numerikus megoldási módszert alkalmazni a mozgásegyenletek megoldásához, amely a nemlineáris egyenleteket is képes megoldani.
A fenti modellen túl, a hajtáslánc egyszerűbb modelljei is létrehozhatók és alkalmazhatók. Gyakori például a bemutatott modell öt tömeget magába foglaló változata (járművezető nélkül), amely csak a járműkarosszériáig bezáróan vizsgálja a hajtáslánc viselkedését.
Más megközelítésben a tengelykapcsoló viselkedése vizsgálható olyan modell alkalmazásával is, amelyikben a hajtott kerekek és a járműkarosszéria egy tömeget képez és végtelen tehetetlenségű. Ezzel a közelítéssel a hajtáslánc modellje egy kéttömegű lengőrendszer modelljévé egyszerűsödik [4.5.] . Nyilvánvaló, hogy ezzel az egyszerűsített modellel nem vizsgálható a tengelykapcsoló összes üzemállapota, hanem jellemzően csak a kapcsolás kezdeti, nagy sebességkülönbségű szakasza, ill. bizonyos lengéstani tulajdonságok.
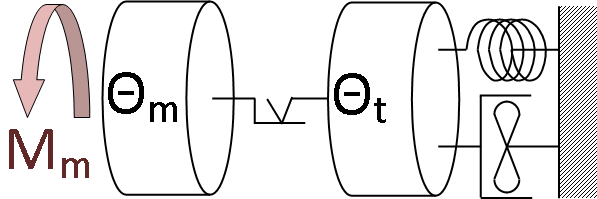
4.1.4. Háromtömegű egyszerűsített hajtásláncmodell alkalmazása a tengelykapcsoló vizsgálatához
Az előzőleg bemutatott modellek tulajdonságai alapján adódik, hogy a tengelykapcsolók összes üzemállapotban történő vizsgálatához a hajtáslánc egy legalább három tömegből és egy nemlineáris elemből (Coulomb-súrlódás) álló modelljére van szükség [4.6.] [4.7.] .
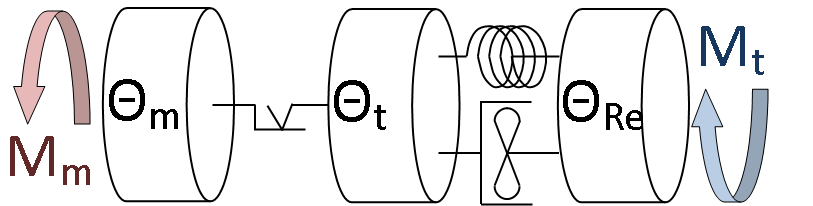
Ez a modell egy olyan torziós lengőrendszerként hozható létre, amelyben a modellt alkotó három tömeg a következő: a motor forgattyústengelyének és a kapcsolódó alkatrészeknek a tehetetlenségi nyomatéka, a tengelykapcsoló súrlódótárcsájának a tehetetlenségi nyomatéka, és a nyomatékváltó, valamint a jármű összes többi részének (kiegyenlítőmű, kerekek, karosszéria) redukált tehetetlenségi nyomatéka. A modell matematikai megfogalmazása az alábbi egyenletrendszer szerint írható:
|
|
||
|
|
||
|
|
ahol Θ
m
a motor (forgattyústengely és kapcsolódó alkatrészek) tehetetlenségi nyomatéka, 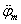 a motor szöggyorsulása, μ a tengelykapcsoló súrlódótárcsájának súrlódási tényezője,
a motor szöggyorsulása, μ a tengelykapcsoló súrlódótárcsájának súrlódási tényezője, 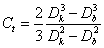 tengelykapcsoló-állandó. D
k
a tengelykapcsoló súrlódófelületének külső átmérője, D
b
a tengelykapcsoló súrlódófelületének belső átmérője, F
n
(t) a tengelykapcsolót összenyomó, időben változó normálerő,
tengelykapcsoló-állandó. D
k
a tengelykapcsoló súrlódófelületének külső átmérője, D
b
a tengelykapcsoló súrlódófelületének belső átmérője, F
n
(t) a tengelykapcsolót összenyomó, időben változó normálerő, 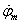 a motor szögsebessége, M
m
(t) az időben változó motornyomaték, Θ
t
a tengelykapcsoló súrlódótárcsájának tehetetlenségi nyomatéka,
a motor szögsebessége, M
m
(t) az időben változó motornyomaték, Θ
t
a tengelykapcsoló súrlódótárcsájának tehetetlenségi nyomatéka, 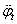 a tengelykapcsoló súrlódótárcsájának szöggyorsulása,
a tengelykapcsoló súrlódótárcsájának szöggyorsulása, 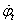 a súrlódótárcsa szögsebessége, d a súrlódótárcsa és a nyomatékváltó közötti torziós csillapítási tényező, c a súrlódótárcsa torziós csillapítórugóinak torziós rugómerevsége, φ
0
a torziós rugó nyugalmi pozíciója, Θ
Re
a nyomatékváltó, és a teljes redukált járműtömeg tehetetlenségi nyomatéka,
a súrlódótárcsa szögsebessége, d a súrlódótárcsa és a nyomatékváltó közötti torziós csillapítási tényező, c a súrlódótárcsa torziós csillapítórugóinak torziós rugómerevsége, φ
0
a torziós rugó nyugalmi pozíciója, Θ
Re
a nyomatékváltó, és a teljes redukált járműtömeg tehetetlenségi nyomatéka, 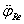 a redukált járműtömeg szöggyorsulása,
a redukált járműtömeg szöggyorsulása, 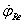 a redukált járműtömeg szögsebessége, φ
Re
a redukált járműtömeg pozíciója, M
t
(t) a redukált járműtömegre ható, időben változó terhelés (pl. gördülési és légellenállás, stb.).
a redukált járműtömeg szögsebessége, φ
Re
a redukált járműtömeg pozíciója, M
t
(t) a redukált járműtömegre ható, időben változó terhelés (pl. gördülési és légellenállás, stb.).
Figyelembe kell venni, hogy a modell, az előzőekben bemutatott lineáris rendszerekhez képest kibővült 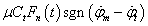 nemlineáris taggal, amire a Coulomb-súrlódás leírása miatt van szükség. Ez a tag súrlódásból adódó nyomatékot határozza meg a motor és a súrlódótárcsa szögsebesség-különbségének előjelétől függően.
nemlineáris taggal, amire a Coulomb-súrlódás leírása miatt van szükség. Ez a tag súrlódásból adódó nyomatékot határozza meg a motor és a súrlódótárcsa szögsebesség-különbségének előjelétől függően.
A modellt részletesebben szemlélve felmerülhet, hogy M m (t), F n (t) és M t (t) függvények nincsenek egyértelműen meghatározva. Ennek oka, hogy a vizsgált problémától függően többféleképpen is megadhatók. Legegyszerűbb esetben ezek a függvények összetartozó idősorokként, vagy szimbolikusan adott közelítőfüggvényekként (pl. polinomfüggvények) illeszthetők a modellhez. Összetettebb modellek esetén ezek a függvények a teljes problémát leíró modell egy-egy önálló részmodelljeként tekinthetők. Például M m (t) megadható a belsőégésű motor nyomaték-fojtószelepállás-motorfordulatszám karakterisztikája alapján.
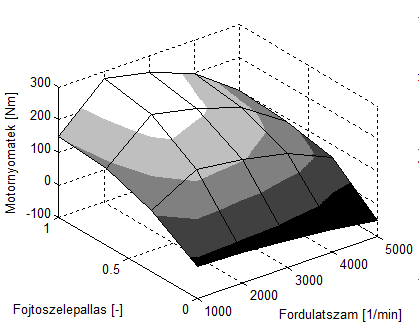
A motorkarakterisztika kiegészíthető a járművezető egy egyszerűsített modelljével, ami fordulatszám-szabályozást valósít meg egy PI szabályozóval, előállítva ezzel a motorkarakterisztikához szükséges másik szükséges információt, a fojtószelepállást, mint a szabályozás beavatkozójelét. Ezzel a módszerrel biztosítható, hogy a kapcsolási folyamatok szimulációja során a motor fordulatszáma nem csökken nagymértékben, mivel a járművezető-modell megpróbálja azt állandó értéken tartani. A motorfordulatszámot visszacsatolva a járművezető modellje és a motorkarakterisztika hozzákapcsolható a hajtáslánc modelljéhez. A modell tovább bővíthető a tengelykapcsoló-pedál működtetését és a tengelykapcsoló rugóját leíró modellekkel, ezáltal F n (t) pillanatnyi értéke is meghatározható. M t (t) pillanatnyi értéke jellemzően a gördülési ellenállás és a légellenállás ismert összefüggései, valamint mérések alapján határozható meg.
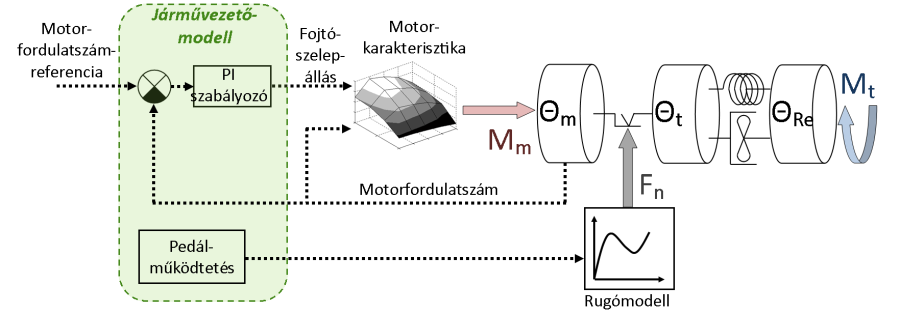
Az ilyen módon adott modellt szimulációs környezetben megvalósítva több különböző, a tengelykapcsoló működésére jellemző tranziens üzemállapotot vizsgálhatunk. Példaként a 2.2. szakasz fejezetben is tárgyalt, a jármű álló helyzetből történő indulási folyamatának szimulációját mutatjuk be.
A szimuláció a következők szerint történik:
-
A motor fordulatszáma 1000 ford./perc, amit a járművezető megpróbál állandó értéken tartani
-
A járművezető t=0,5 s-nél egyenletes sebességgel elkezdi felengedni a tengelykapcsoló-pedált és ezáltal zárni a tengelykapcsolót
-
A pedálelmozdulás függvényében a súrlódási nyomaték növekedni kezd
-
A motorfordulatszám fokozatosan csökken, ahogy a tengelykapcsolón keresztül egyre nagyobb terhelés éri a motort
-
t=1 s-ig a jármű nem mozdul meg, mivel csak ekkor visz át a tengelykapcsoló annyi nyomatékot, ami a járművet a nyugalmi állapotából ki tudja mozdítani (nyugvó súrlódás legyőzése)
-
A tengelykapcsoló fokozatos zárásával egyre nagyobb nyomatékot visz át, ezáltal a jármű gyorsul, és a motor, valamint a nyomatékváltó közti fordulatszám-különbség fokozatosan kiegyenlítődik
-
Amikor a fordulatszám-különbség kiegyenlítődik, a súrlódótárcsa nyugalmi helyzetbe kerül a motorhoz (lendkerékhez) képest és az összekapcsolódott hajtáslánc fokozatosan eléri az állandósult sebességet
A kapcsolási folyamat során elsősorban a szögsebesség-különbségek, ill. a szögsebesség-kiegyenlítődés vizsgálata által vonhatunk le következtetéseket a rendszer működésére vonatkozólag, ezért a szimulációban is elsősorban ezeket a mennyiségeket vizsgáljuk.
Első szimulációs eredményként egy olyan esetet mutatunk be, ahol a hajtáslánc kialakítása dinamikai szempontból nem megfelelő, ezért rezonanciaállapot alakul ki, amely károsíthatja a szerkezetet. Az ábrán látható rezonancia a kapcsolási folyamat során kismértékben változó súrlódási tulajdonságok, ill. a nemlineáris rugókarakterisztika következtében a súrlódónyomatékon keresztül történő gerjesztés következtében jön létre [4.4.] . A gerjesztés frekvenciája 22…24 Hz.
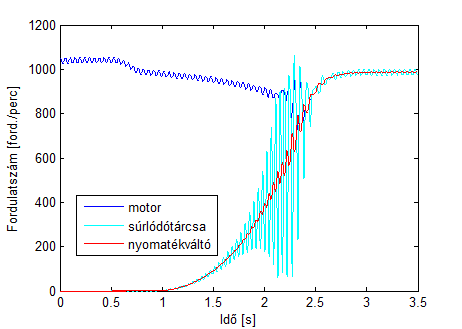
(háromtömegű torziós lengőrendszer modelljén előállított szimulációs eredmény)
Előállítva a rendszer frekvenciaátviteli függvényét a súrlódótárcsára ható gerjesztőnyomaték és a súrlódótárcsa szögsebessége között, a Bode-diagramon látható, hogy a frekvenciaátviteli függvény amplitúdóviszonyának maximuma van a 24 Hz-es frekvenciánál. Ez közelítőleg egybeesik a gerjesztés frekvenciájával ezért kialakul a rezonanciaállapot. Adódik, hogy a rezonanciaállapot kialakulása elkerülhető, ha a rendszert úgy módosítjuk, hogy a lokális maximum megszűnjön, vagy más frekvenciaértékhez kerüljön. Ez több paraméter változtatásával is elérhető, de nem minden változtatás előnyös egyéb konstrukciós szempontok miatt. A súrlódótárcsa tehetetlenségi nyomatékának megnövelésével például egyetlen paraméter változtatásával el tudjuk „hangolni” a rezonanciafrekvenciát olyan tartományba, amelyik már jellemzően nem esik egybe a gerjesztés frekvenciatartományával. Ennek a módosításnak a frekvenciaátvitelre gyakorolt a hatása látható az alábbi ábrán is.
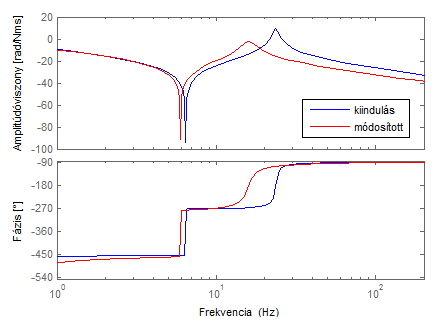
(háromtömegű torziós lengőrendszer modelljén előállított szimulációs eredmény)
A módosítás után a szimulációt ismételten végrehajtva a kapott eredményeken látható, hogy a módosítás következtében a rezonanciaállapot kialakulása megszűnt a kapcsolási folyamat során.
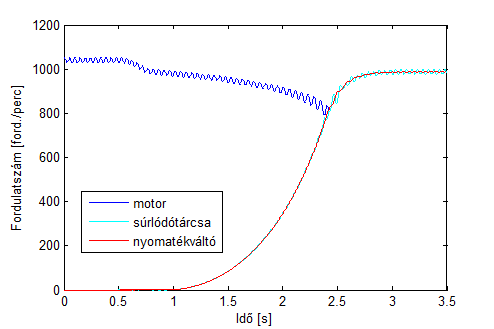
(háromtömegű torziós lengőrendszer modelljén előállított szimulációs eredmény)
A modell nem csak a sebességkülönbségek és a frekvenciaátviteli tulajdonságok vizsgálatára alkalmas, vizsgálhatók vele olyan járulékos jelenségek, amelyek ideális esetben nem befolyásolják közvetlenül a kapcsolási folyamatot, de jelentős hatással lehetnek a szerkezet élettartamára. Ilyen vizsgálat lehet például a kapcsolási folyamat során keletkező veszteségteljesítmény, ill. a kupplungszerkezet túlhevülésének vizsgálata, amelyből következtetéseket lehet levonni a a szerkezet esetleges meghibásodására, ill. a várható élettartamára vonatkozólag. Mivel az alkalmazott modell meghatározza a motor és a súrlódótárcsa sebességét, ezért képezhető belőlük a sebességkülönbség.
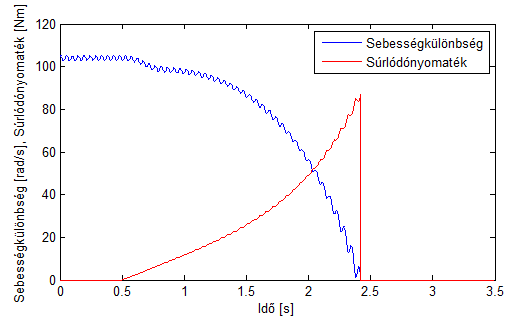
(háromtömegű torziós lengőrendszer modelljén előállított szimulációs eredmény)
A sebességkülönbség és a súrlódónyomaték ismeretében számítható a pillanatnyi veszteségteljesítmény, ami a kapcsolási folyamat során a súrlódásból adódik. A veszteségteljesítmény idő szerinti integrálja alapján számítható a kumulált veszteség, amit felhasználva felső becslés adható a hőmérsékletnövekedés értékére a vizsgált alkatrészek hőkapacitása alapján.
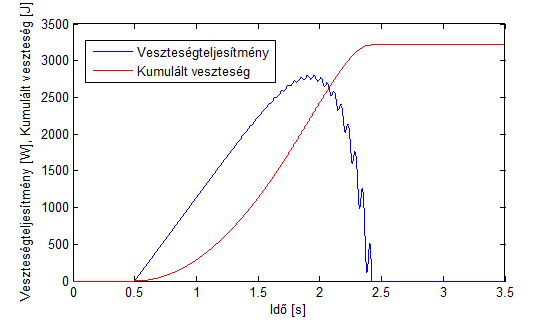
(háromtömegű torziós lengőrendszer modelljén előállított szimulációs eredmény)
4.1.5. További szempontok tengelykapcsolók tervezéséhez
A tengelykapcsolók tervezésénél az egyik legfontosabb szempont, hogy a tengelykapcsoló a tervezési nyomatékot megfelelő biztonsággal képes legyen átvinni, másfelől viszont korlátozott a tengelykapcsoló súrlódótárcsáját terhelő felületi nyomás, valamint a tengelykapcsoló átmérője. A felsorolt megfontolásoknak megfelelően a tengelykapcsolót úgy méretezzük, hogy a felületi nyomásra teljesüljön a p ≤ p max összefüggés, ahol p max a maximálisan megengedhető felületi nyomás. Ezen túl a tengelykapcsoló súrlódó felületeit nyomatékra ellenőrizzük, ill egyéb kötéseit (pl. tengely-agy kapcsolat, súrlódóelemek rögzítése, stb.) nyomatékra méretezzük. Az említett számítások alapösszefüggése a súrlódófelületeken átvihető névleges nyomaték számítására szolgáló összefüggés, ami a következőképpen írható:
|
|
ahol z a súrlódófelületek száma, μ a tengelykapcsoló súrlódótárcsájának súrlódási tényezője, D k a tengelykapcsoló súrlódófelületének külső átmérője, D b a tengelykapcsoló súrlódófelületének belső átmérője, r a sugár, p pedig a felületi nyomás, ami a következő összefüggés szerint határozható meg:
|
|
ahol F n a tengelykapcsolót összenyomó normálerő [4.8.] .
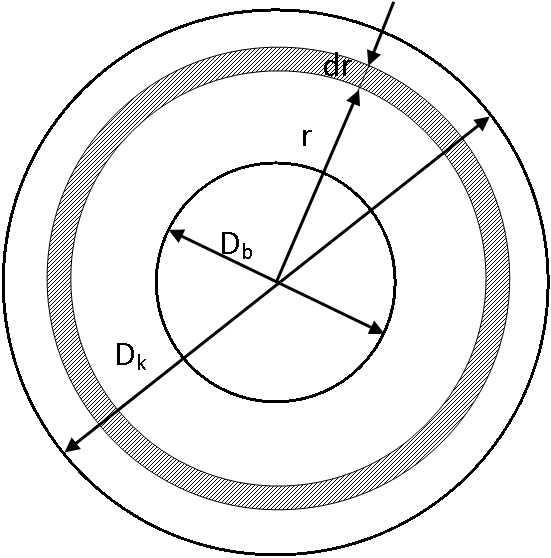
Fenti összefüggésekkel kapcsolatban érdemes kiemelni, hogy az átvihető nyomaték a külső és a belső átmérő harmadik hatványának különbségétől függ. A gyakorlatban egyes esetekben egyszerűsítésként szokás az átmérők négyzetének különbségével és a középátmérővel számolni, azonban ez a közelítés csak akkor ad elfogadhatóan pontos eredményt, ha a 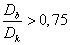 (jellemzően pl. kis átmérőjű, soklemezes nedves tengelykapcsolók esetén).
(jellemzően pl. kis átmérőjű, soklemezes nedves tengelykapcsolók esetén).
A tengelykapcsolók és kötőelemeik részletes méretezésének bemutatására nem térünk ki, mivel a vonatkozó irodalom (pl. [4.8.] [4.9.] ) könnyen hozzáférhető, és részletes leírást ad a problémakörről.
A gépjármű-tengelykapcsolók tervezésénél további szempont a tengelykapcsolót alaphelyzetben zárva tartó rugó megfelelő kialakítása. A rugó karakterisztikája befolyásolja a járművezető által kifejtett erő nagyságát és a kapcsolási folyamatot is. A járművezető tehermentesítése és az egyenletes kapcsolási folyamat biztosítása érdekében általában tányérrugókat alkalmaznak erre a célra [4.10] .
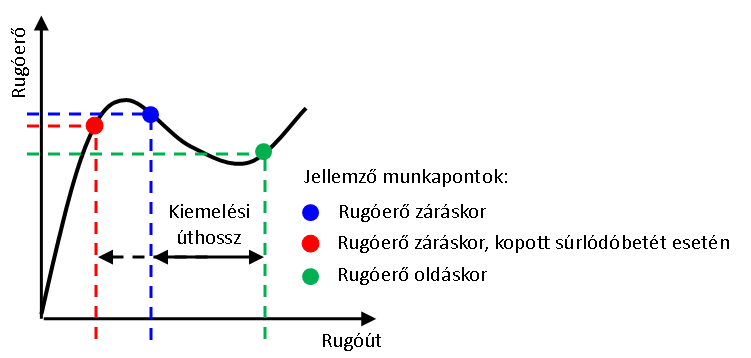
Ezen túlmenően, a tengelykapcsoló axiális merevségének vizsgálatakor figyelembe kell venni a súrlódótárcsa és a ház axiális merevségét is.
4.2. Irányítási rendszerek alkalmazása tengelykapcsolók automatikus működtetéséhez
4.2.1. Tengelykapcsoló automatikus működtetése
A tengelykapcsolók automatikus működtetése szerteágazó problémakör, aminek a relevanciáját az ilyen megoldások egyre szélesebb körű járműipari alkalmazása adja. A tengelykapcsolók részben, vagy teljes mértékben automatizált működtetése több különböző szempont szerint is célszerű lehet. Ilyen szempontok lehetnek például:
-
terhelés alatt kapcsolható, több tengelykapcsolót alkalmazó nyomatékváltók kapcsolási folyamatának megvalósítása
-
hagyományos szerkezeti felépítésű nyomatékváltók működtetésének automatizálása
-
a kapcsolási folyamat minőségi jellemzőinek javítása
Általában elmondható, hogy a tengelykapcsolók automatikus működtetésére nincsenek általános megoldások, hanem adott jármű által meghatározott szempontrendszer szerint történik az irányítási rendszer kialakítása. Mivel a legtöbb automatizálási törekvés megközelíthető abból a szempontból, hogy célja az emberi közreműködés kiváltása, vagy akár az emberi közreműködés minőségi jellemzőit meghaladó irányítási megoldás megvalósítása, ezért a tengelykapcsolók automatizált működtetésének irányítási problémái is vizsgálhatók ebből a szempontból. Ezen túl a különböző automatizált tengelykapcsolóműködtető-rendszerek működési elvének áttekintéséhez célszerű figyelembe venni az irányítási rendszerek felépítésével kapcsolatos alapvető általános ismereteket is.
A problémakör további tárgyalása során – terjedelmi okokból – csak a tengelykapcsolók indítási folyamatával kapcsolatos automatizálási kérdések köréből mutatunk példákat. Ennek megfelelően a szerepeltetett működési elvek, ábrák és összefüggések egyszerűsítettek és hiányosak abban az értelemben, hogy lehetőség szerint nem tartalmazzák azokat az elemeket, amelyek nincsenek közvetlen összefüggésben az indítási folyamat automatizálásával.
A legegyszerűbb irányítási rendszerek, amelyek a tengelykapcsolók működtetéséhez alkalmazhatók, olyan vezérlések (nyílt hatásláncú irányítási rendszerek [4.15.] ), amelyek valamilyen előre meghatározott kiemelőcsapágy-elmozduláskarakterisztika szerint mozgatják a kiemelőcsapágyat a 2.1. szakasz fejezetben bemutatott elektrohidraulikus, elektropneumatikus, esetleg elektromechanikus beavatkozó szervek (aktuátorok) segítségével. A kiemelőcsapágy működtetése mellett gyakori megoldás, hogy az irányítási rendszer egyidejűleg módosítja a belsőégésű motor fojtószelepállását is, megnövelt teljesítményleadást biztosítva a kapcsolási folyamat során. Visszatekintve a korábban bemutatott szimulációs modellhez (amely a járművezető viselkedésének egyszerűsített modelljét is tartalmazta), az ilyen módon működtetett tengelykapcsoló jellemezhető a modell elemeivel. Ilyen vezérléssel megvalósított automatizált tengelykapcsoló működési vázlata látható az alábbi ábrán.
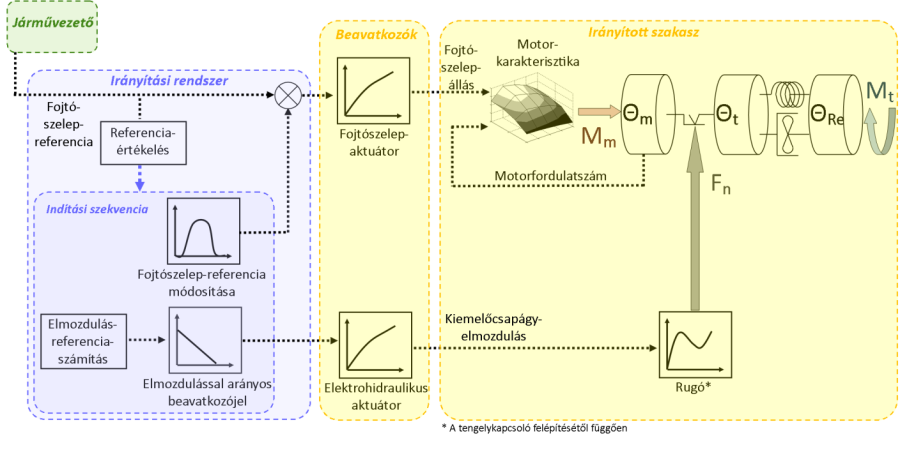
A korábban bemutatott modellhez képest különbség, hogy az ábrán nem egy modell elemei, hanem a megvalósított elemeket reprezentáló jelölések láthatók (tehát pl. a járművezető modellje helyett a járművezető, a hajtáslánc modellje helyett a hajtáslánc, stb.). További különbség, hogy ebben az esetben a járművezetőről nem feltételezzük, hogy szabályozóként működne (mindazonáltal ettől a feltételezéstől függetlenül működhet ilyen módon), valamint megjelent az irányítási rendszer és a beavatkozószervek.
A kapcsolási folyamat minőségét alapvetően befolyásolja az irányítási rendszer. A bemutatott példában az irányítási rendszer legfontosabb tulajdonsága, hogy nyílt hatásláncú, tehát nem tartalmaz semmilyen visszacsatolást az irányított szakasz állapotváltozóiról (pl. mozgásmennyiségek). Működése azt az egyszerű elvet követi, hogy, ha a járművezető a fojtószelep-referencián (gázpedálálláson) keresztül közli az indulási szándékát, akkor a vezérlés egy előre meghatározott karakterisztika szerint zárja a tengelykapcsolót, a kapcsolási folyamat során pedig kismértékben megnöveli a fojtószelep-referencia értékét, megnövelt motorteljesítmény-leadást biztosítva ezáltal [4.16] . Működési elvéből következően ez az irányítási rendszer csak a legegyszerűbb esetekben alkalmazható, mivel nem biztosítható, hogy az előre meghatározott kapcsolási karakterisztika a környezeti feltételek jelentős változása (pl. vízszintes felület helyett meredek emelkedőn történő indulás) esetén is megfelelő kapcsolási folyamatot fog biztosítani (ld. még.: 2.2. szakasz).
Az említett problémák kiküszöbölése érdekében általában valamilyen zárt hatásláncú irányítást, vagyis szabályozást valósítanak meg az automatizált tengelykapcsolókat működtető irányítási rendszerek. Az alkalmazott szabályozási köröknek számos különböző megvalósítása lehetséges abban az értelemben, hogy a rendszer melyik állapotváltozója (ill. állapotváltozói) az irányított jellemző. Mivel a kapcsolási folyamat során elsősorban a belsőégésű motor és a hajtáslánc sebességének (fordulatszámának) tranzienseivel szemben támaszthatunk minőségi követelményeket ezért a legelterjedtebben alkalmazott megoldások a belsőégésű motor, ill. a nyomatékváltó fordulatszámának szabályozása a kapcsolási folyamat során. A továbbiakban a belsőégésű motor fordulatszám-szabályozására épülő szabályozási megoldásokon keresztül mutatunk be néhány egyszerűbb szabályozási lehetőséget.
A legegyszerűbb eset a belsőégésű motor fordulatszám-szabályozása olyan módon, hogy közben a tengelykapcsoló működtetése továbbra is vezérelt, vagyis előre meghatározott karakterisztika szerint történik. Ennek a szabályozási megoldásnak a működési vázlata (benne foglalva a szabályozás hatásvázlatát is) látható az alábbi ábrán.
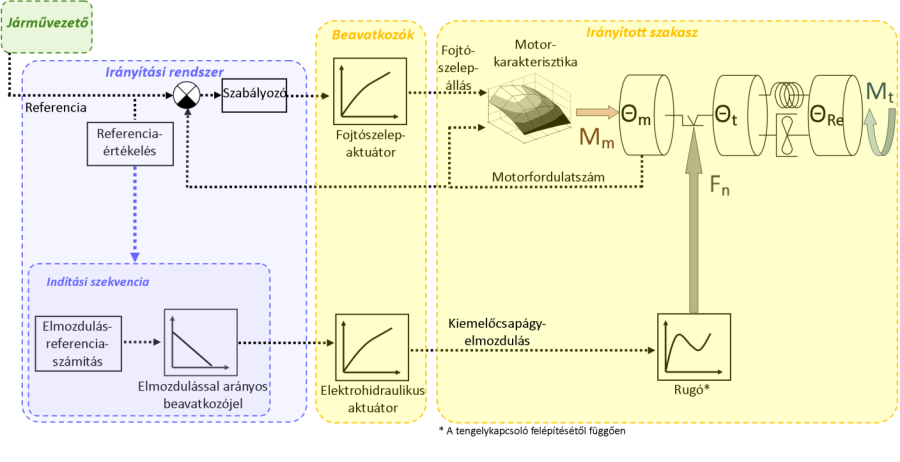
Az ábrán látható, hogy a motor fordulatszáma az irányított jellemző, amely a negatív visszacsatolás révén szabályozási kört képez (Az ábrán a ![]() jelölés a különbségképzést jelenti). Ezt az irányítási megoldást önállóan ritkán alkalmazzák, de számos automatizált tengelykapcsoló-rendszer alapját képezi
[4.12.]
. A belsőégésű motor kapcsolás közbeni fordulatszám-szabályozásával kapcsolatban megjegyzendő, hogy, bár a bemutatott ábra az irányítási rendszert egyetlen, összefüggő egységként jelöli, a szabályozás, ill. az irányítás megvalósítása általában két alrendszer, a beágyazott hajtásláncirányító egység (Traction Control Unit - TCU) és a beágyazott motorirányító egység (Engine Control Unit - ECU) együttes, összehangolt működése révén történik.
jelölés a különbségképzést jelenti). Ezt az irányítási megoldást önállóan ritkán alkalmazzák, de számos automatizált tengelykapcsoló-rendszer alapját képezi
[4.12.]
. A belsőégésű motor kapcsolás közbeni fordulatszám-szabályozásával kapcsolatban megjegyzendő, hogy, bár a bemutatott ábra az irányítási rendszert egyetlen, összefüggő egységként jelöli, a szabályozás, ill. az irányítás megvalósítása általában két alrendszer, a beágyazott hajtásláncirányító egység (Traction Control Unit - TCU) és a beágyazott motorirányító egység (Engine Control Unit - ECU) együttes, összehangolt működése révén történik.
A belsőégésű motor szabályozásán túl lehetőség van a tengelykapcsoló-működtetés szabályozására is. Ennek a jelentősége elsősorban abban áll, hogy az üzemi körülmények változása (pl. hőmérséklet, kopás, stb.) jelentősen befolyásolhatja a kapcsolási folyamatot, ami az előre definiált karakterisztika szerinti tengelykapcsoló-működtetés esetén a kapcsolási folyamat minőségi jellemzőinek romlásához vezethet. Ennek elkerülése érdekében bevezethető a tengelykapcsoló-működtetés szabályozása. Az alábbi egy olyan rendszer működési- ill. hatásvázlatát mutatja, amely a belsőégésű motor fordulatszám-szabályozása mellett a kiemelőcsapágy pozíciószabályozását is megvalósítja.
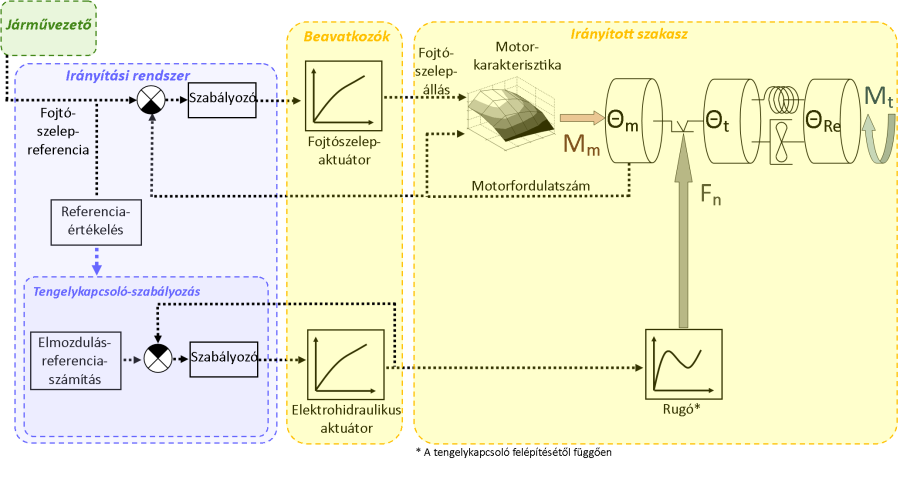
A bemutatott szabályozási módszereknek számos további változata létezik. Mivel a kapcsolási folyamat minőségi jellemzői a motor fordulatszám-tranziense mellett ugyanúgy a hajtáslánc többi elemének fordulatszám-tranzienseihez is köthetők, ezért gyakori a bemutatott szabályozásokhoz hasonló fordulatszám-szabályozás alkalmazása a nyomatékváltó oldalán is, akár a motor fordulatszám-szabályozásával együttesen. A kapcsolási folyamat minőségi jellemzőinek javítása érdekében (pl. ún. félaktív rezonanciacsökkentés céljából) a fordulatszám-szabályozás közvetett módon, a tengelykapcsoló működtetése révén is megvalósítható [4.11.] . Szintén jellemző megoldás a belsőégésű motor és a nyomatékváltó fordulatszám-különbségének szabályozása is [4.13.] [4.14.] . A legösszetettebb szabályozási megoldások egy ún. állapotbecslési algoritmus segítségével képesek meghatározni olyan állapotváltozók értékét is, amelyek nincsenek közvetlenül mérve, vagy a mért jelet jelentős zaj terheli. Az ilyen módon meghatározott értékek felhasználásával további szabályozási körök képezhetők, akár konkurens kialakítással is, amely kialakítás lehetővé teszi, hogy az üzemállapot jelentős megváltozása esetén a megváltozott feltételeknek leginkább megfelelő szabályozás lépjen működésbe [4.11.] [4.13.] .
4.2.2. A dinamikai modell alkalmazása irányítási módszerek modellalapú fejlesztéséhez
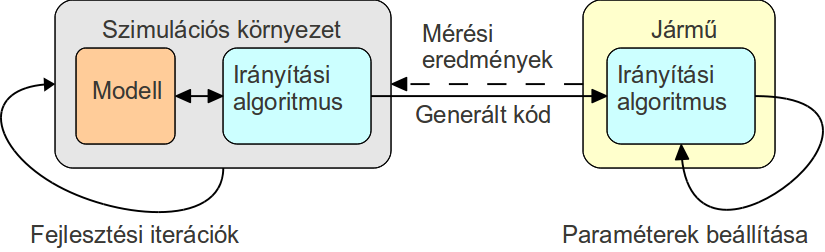
Irányított rendszerek esetén a szimulációs modell felhasználható arra a célra, hogy az irányítási algoritmus fejlesztési iterációinak egy részét a szimulációs környezetben tegyük meg. A tengelykapcsolók automatizált működtetése esetén az említett irányítási megoldásokat célszerű szimulációs környezetben, a bemutatott dinamikai modellel párhuzamosan fejleszteni.
A szimulációs környezetben létrehozott irányítási algoritmus automatizált eszközökkel átültethető a járműbe olyan módon, hogy a szimulációs környezetben megvalósított irányítási algoritmusból a beágyazott rendszerekben alkalmazható programkód generálható a megfelelő eszközök segítségével.
A szimulációs modell, ill. az általa biztosított szimulációs környezet, valamint az irányítási algoritmus fejlesztése nem sorrendi, hanem iteratív folyamat. Ez azt jelenti, hogy a fejlesztési iterációk jelentős része elvégezhető a szimulációs környezetben, majd, miután az ilyen módon fejlesztett irányítási algoritmus megfelelő viselkedést mutat szimulációs körülmények között, átültethető a járműbe épített beágyazott rendszerbe az említett módszerek alkalmazásával. A járműves mérések és tapasztalatok visszacsatolhatók a szimulációs környezet, ill. modell fejlesztésébe. A cél, hogy a fejlesztési iterációk ciklusainak a lehető legnagyobb hányadát a szimulációs környezetben tegyük meg, mivel ezáltal gyorsítható és olcsóbbá tehető az irányítási rendszer fejlesztése.
Irodalmak:
[4.1.] Modellalkotás. NTK. Budapest . 2013. 17-35p.
[4.2.] Mozgástan. NTK. Budapest . 1997. 470-536p.
[4.3.] Járművek és mobil gépek I., . Budapest . 2010. 29p.
[4.4.] Ursachen und Abhilfen. LuK Symposium. 1998. 139-159p.
[4.5.] Transient responses of a 2-dof torsional system with nonlinear dry friction under a harmonically varying normal load. Journal of sound and vibration. 2005. 1223-1234p.
[4.6.] Automotive clutch models for real time simulation. Proceedings of the Romanian Academy Series A. 2011. 109-116p.
[4.7.] Improved optimal control of dry clutch engagement. Proceedings of the 16th IFAC World Congress. 2005.
[4.8.] Gépelemek I.. GATE egyetemi jegyzet. Gödöllő . 1978. 219p.
[4.9.] Mechanikus tengelykapcsolók. Műszaki Könyvkiadó. Budapest . 1966. 339-424p.
[4.10.] Mezőgazdasági traktorok elmélete és szerkezete. FVM MGI. Gödöllő . 2004. 293-310p.
[4.11.] Software for automatized transmissions. LuK Symposium. 2006. 155-169p.
[4.12.] Modeling torque transmissibility for automotive dry clutch engagement. American Control Conference. 2008. 306-311p.
[4.13.] trol of dry clutch engagement for vehicle launches via a shaft torque observer. American Control Conference. 2010. 676-681p.
[4.14.] Evaluation of control strategies for automotive powertrains with backlash. AVEC ’02 International Symposium on Advanced Vehicle Control. 2002.
[4.15.] Rendszer és irányítástechnika. Műszaki Könyvkiadó. Budapest . 2001. 320-328p..
[4.13.] Simulation and control of an automotive ary clutch. American Control Conference. 2004. 4078-4083p.
[1] Megj.: a lengőrendszer ennek az absztrakt fizikai modellnek csupán a megnevezése, amiből nem következik, hogy egy ilyen rendszer minden üzemi körülmények között periodikus mozgást (lengést) végez.
[2] Itt csak azokat az eseteket tárgyaljuk, amikor egy tömeg legfeljebb egy szabadságfokkal rendelkezik, tehát csak egy irány mentén képes elmozdulni. Ellenkező esetben az egyenletek száma nem egyezik meg a tömegek számával, mivel általánosan a szabadságfokok száma határozza meg, hogy hány egyenlet szükséges a lengőrendszer leírásához.