1. fejezet - A képalkotás alapjai
Vissza		Előre

1. fejezet - A képalkotás alapjai

Tartalom

1.1. Fénytani alapismeretek

1.1.1. A fény tulajdonságai

A fény elektromágneses rezgés. Kettős, hullám-, illetve részecsketermészete van, ezért bizonyos jelenségeket hullámtani, másokat pedig kvantummechanikai tárgyalással lehet leírni.

A fény hullámhossza:

$λ_{0} = \frac{c}{γ}$

(1.1)

ahol

	λ ₀	a fény hullámhossza vákuumban
	c	a fény terjedési sebessége vákuumban (közelítőleg: 3x108 m/s)
	v	a fény frekvenciája

Általában a fény keletkezésével és elnyelésével (detektálásával) kapcsolatos esetekben kvantummechanikai leírás szükséges, míg terjedésekor a hullámtani, sőt sokszor – a még egyszerűbb – ún. geometriai optikai tárgyalásmód is elegendő.

Fénynek az elektromágneses spektrumnak az emberi szem által látott tartományát (VIS) és a mellette lévő ibolyántúli (UV), valamint infravörös (IR) tartományokat hívjuk. (Lásd. 1.1. ábra)

A látható fény tartománya 380 < λ₀ < 780 nm, amelynek részleteit a látott színek szerint nevezünk el.

A hullámtani tárgyalásmód használatakor hullámfelületekkel jellemezzük a fény terjedését.

A geometriai optika bevezeti a fénysugarak fogalmát, amelyeken a hullámfelületek ortogonális trajektóriáit értjük. Ezen sugároptikai leírás segítségével a legtöbb elemi optikai képalkotást megmagyarázhatjuk.

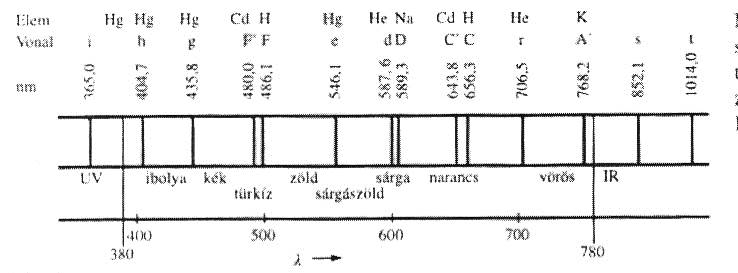
1.1. ábra - Spektrumszínek és spektrumvonalak

Mivel az atomok emissziós sugárzásai nagyon pontos hullámhosszakon történnek, ezért ezek jeleivel dolgozunk az optikában, ha pontos hullámhosszra akarunk hivatkozni.

1.1.2. Fény terjedése közegekben. A törésmutató és az Abbe-szám

A fény lassabban terjed anyagi közegekben, ekkor sebességét v-vel, hullámhosszát λ-val jelöljük. Frekvenciája változatlan marad.

$λ = \frac{v}{ν}$

(1.2)

A különböző színű fények hullámhossza és terjedési sebessége más és más. (lásd Táblázat 1.1)

1.1. táblázat - A fény terjedési sebessége különböző anyagokban

Anyag	Sebesség km/s	Anyag	Sebesség km/s
hidrogén	299 959	glicerin	204 152
oxigén	299 918	koronaüveg	197 980
levegő	299 914	kanada balzsam	194 553
nitrogén	299 912	flintüveg	186 013
víz	225 059	nehézflint	170 374
etil-alkohol	220 312	gyémánt	124 105

A sebesség vákumbanihoz képesti csökkenését egy viszonyszámmal, a törémutatóval fejezzük ki.

$n = \frac{c}{v}$

(1.3)

A levegő törésmutatója 20 °C-on és 1013 mbar nyomáson n = 1,0003, így a továbbiakban n = 1-nek vesszük.

A víz törésmutatója: 1,33

A leggyakoribb, tradicionális optikai anyag az üveg, amelynek átlagos törésmutatója: 1,5, míg a különféle üvegek törésmutatója: 1,45 < n < 1,95 között változik.

A törésmutató is színfüggő, vagyis egy adott anyagnak nem egyetlen törésmutatója van, hanem minden színre más és más.

Az üveg törésmutatója is változik a fény színe szerint. Ernst Abbe-ról Abbe-számnak nevezzük a következő összefüggést:

$v_{e} = \frac{n_{e} - 1}{n_{F} - n_{C}}$

(1.4)

A nevezőben a spektrum kék, illetve vörös színeire vonatkozó törésmutatók különbsége, a számlálóban pedig egy közepes (pl. „e”, vagy „d”) színre vonatkozó törésmutató szerepel.

ν indexe a közepesnek választott színre utal. λ_e = 546,1 nm, λ_d = 587,6 nm. Az emberi szem legérzékenyebb a λ = 555 nm-re, így az ehhez közel álló színeket szokás alapul venni közepes hullámhosszként.

Néhány optikai üveg betű-számjelét, törésmutatóit és Abbe-számát az (Táblázat 1.2) táblázatban láthatjuk.

1.2. táblázat - Optikai üveg adatok

Az üveg jele	n_F’	n_e	n_C’	ν_e
BK7	1.52283	1.51872	1.51472	63.96
K5	1.52910	1.52458	1.52024	59.20
ZK N 7	1.51470	1.51045	1.50633	60.98
BaK 4	1.57648	1.57125	1.56625	55.85
SK 15	1.63108	1.62555	1.62025	57.79
SK 16	1.62814	1.62286	1.61777	60.08
F 2	1.63310	1.62408	1.61582	36.11
SF 2	1.66238	1.65222	1.64297	33.60
SF 6	1.82970	1.81265	1.79750	25.24
SF 10	1.74805	1.73430	1.72200	28.19

A törésmutató indexeként az 1.1. ábra szerinti spektrumvonalak jeleit használjuk pl. n_d, n_e, n_c, n_F. Ha egy törésmutató jele (n) mellett nincs index, akkor megállapodásszerűen a d vonalra kell gondolni, vagyis

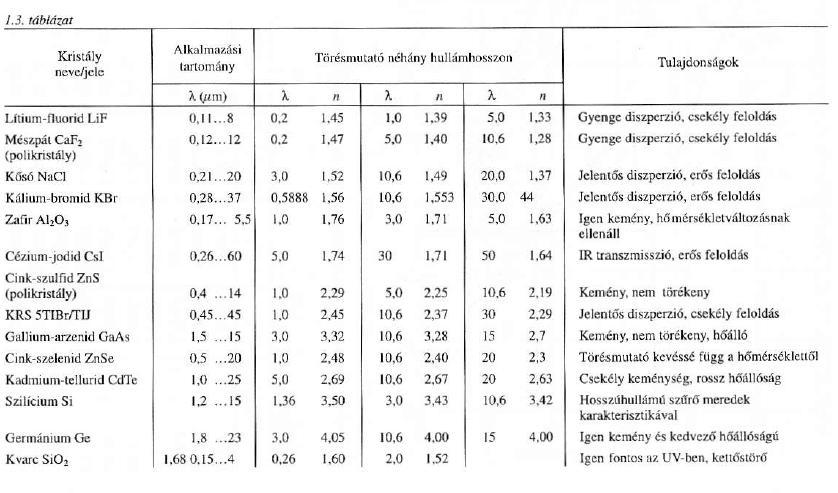
Ezekről néhány jellemzőt találhatunk az (Táblázat 1.3) táblázatban.

n = nd

Az üveg mellett különféle kristályokat is használunk az optikában.

1.3. táblázat - Optikai kristály adatok

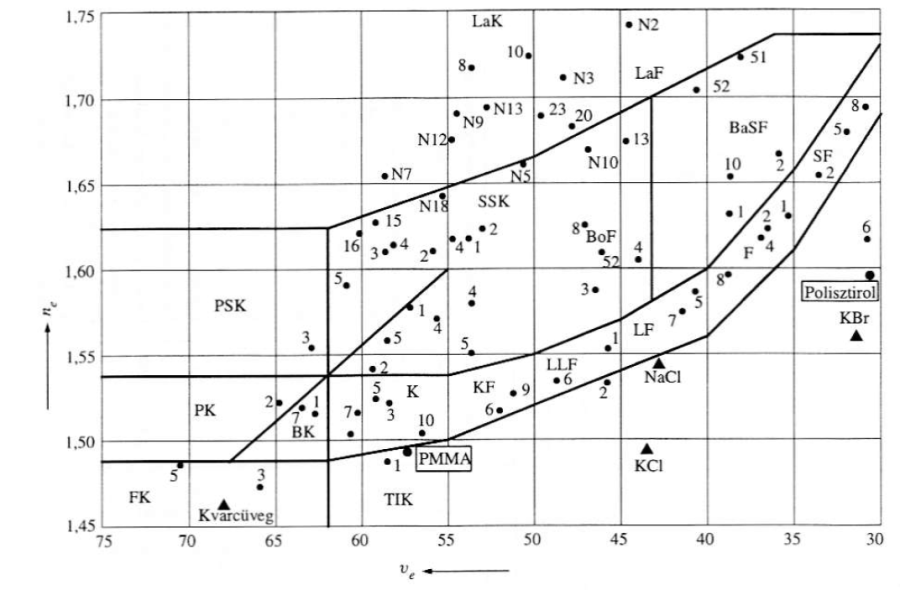
Az optikai üvegeket és kristályokat a katalógusok diagramban is meg szokták adni, a közepes törésmutató és az Abbe-szám függvényében.

Egy ilyen összeállítást mutat az 1.2. ábra.

1.2. ábra - Az optikában használatos anyagok a törésmutató és az Abbe-szám függvényében

1.1.3. A fény viselkedése közegek határfelületein

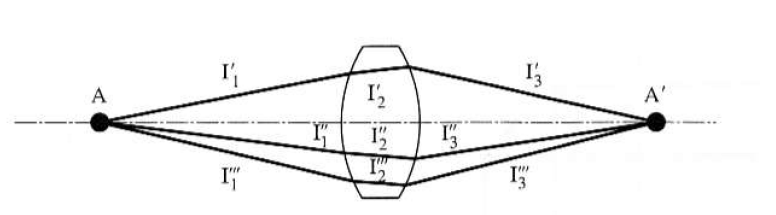
A Fermat-elv

Két pont között a fénysugár azokon az utakon halad, amelyek megtételéhez a legrövidebb időre van szükség más útvonalakkal szemben.

1.3. ábra - Képalkotás a Fermat-elv alapján

$t_{1}^{'} = \frac{l_{1}^{'}}{c}; t_{2}^{'} = \frac{l_{2}^{'} n}{c}; t_{3}^{'} = \frac{l_{3}^{'}}{c}$

mivel $n = \frac{c}{v}$

így

	$t_{1}^{"} = \frac{l_{1}^{"}}{c}; t_{2}^{"} = \frac{l_{2}^{"}}{v} = \frac{l_{2}^{"} n}{c}; t_{3}^{"} = \frac{l_{3}^{"}}{c}$
	$t_{1}^{'} + t_{2}^{'} + t_{3}^{'} = t_{1}^{"} + t_{2}^{"} + t_{3}^{"}$

és így továbbb.

A t₂ kifejezéskor a számlálóban megjelent l₂n szorzatot – vagyis a geometriai távolság és a közeg törésmutatójának szorzatát – optikai úthossznak nevezzük.

Eszerint egy lencse képalkotását, vagyis egy tárgypontból kiinduló több fénysugárnak a képpontban való találkozását úgy képzelhetjük el, hogy valamennyi, a lencsén keresztülhaladó fénysugár azonosan minimális időket fut, miközben más-más utakat tesz meg. Ez úgy lehetséges, hogy a lencsén belül v, a levegőben c sebességgel terjed a fény, így a részidők összege egyenlő lehet egy megfelelő alakú lencse esetén.

A tárgy és képpont közötti utak befutásához szükséges idő:

$T = \sum_{i = 1}^{n} \frac{l_{i} \cdot n_{i}}{c} = \frac{1}{c} \sum_{i = 1}^{n} l_{i} \cdot n_{i}$

(1.5)

Vagyis a két pont között a fénysugár olyan utakon fog haladni, hogy azok mentén az optikai úthosszak összege egyenlő legyen.

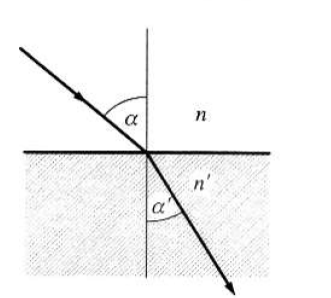
1.4. ábra - Fénytörés két közeg határán

A Snellius–Descartes-törvény szerint két közeg határán a fénysugár megváltoztatja irányát, megtörik.

	$\frac{\sin α}{\sin α'} = \frac{v}{v'} = \frac{c / n}{c / n'} = \frac{n'}{n}$
	$n \sin α = n' \sin α'$	(1.6)

Sűrűbb közegből ritkább közegbe haladó fénysugár felvehet egy olyan beesési szöget, amelynél törési szögként 90º adódik. Ekkor a fénysugár nem lép ki a sűrűbb közegből – totálreflexiót szenved. (1.5. ábra)

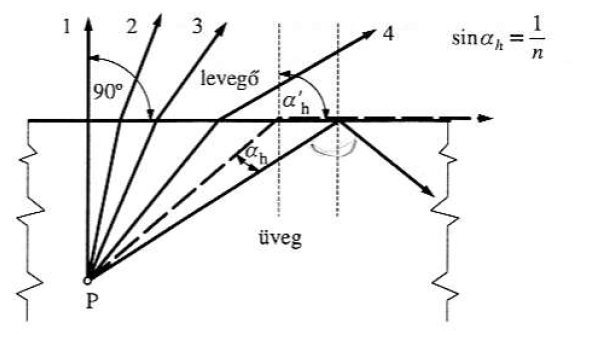
1.5. ábra - A totálreflexió

$\frac{\sin α_{h}}{\sin α_{h}^{'}} = \frac{n'}{n}$

A határszögnél nagyobb beesési szöggel érkező fénysugarak nem tudnak kilépni a közegből, totálreflexiót szenvednek.

Példa

Üveg-levegő felületre:

	n=1,52
	n’=1
	αh=90°
	$\sin α_{h} = \frac{1}{1,52}$
	αh=41,1° határszög

45º-os prizma esetén az oldallapokra merőleges fénysugarak az átfogó felületéről úgy verődnek vissza, mintha az tükör lenne, hiszen a visszaverődéskor a 45º > 41,1º, tehát totálreflexió áll fenn.

Alkalmazási példa: optikai szálak

Optikai szálakban a mag és a köpeny határfelületén totálreflexió jön létre. (1.6. ábra)

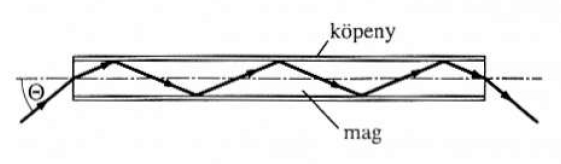
1.6. ábra - Az optikai szál működési elve

Van egy maximális Θ szög, amelynél nagyobb szöggel érkező fénysugarak nem tudnak az optikai szálba belépni.

$\sin Θ_{\max} = \sqrt{n_{k ö p e n y}^{2} - n_{m a g}^{2}}$

(1.7)

Az optikai szálakat felhasználási cél szerint három csoportra oszthatjuk:

informatikai célra egyetlen elemi szál sok, modulált információt vihet át. Ezeknél nem található külön mag és köpeny, hanem a törésmutató belülről kifelé folyamatosan csökken (gradiens szál);
fénykábelként sok elemi szálat köteggé fogunk össze, és világítási célból továbbítjuk velük a fényt;
képtovábbító szálkötegek esetében vigyázunk arra, hogy a köteg egyik végén a szálak relatív helye ugyanolyan legyen, mint a másik végén, így képet lehet továbbítani velük.

A síkpárhuzamos (planparalell) lemez

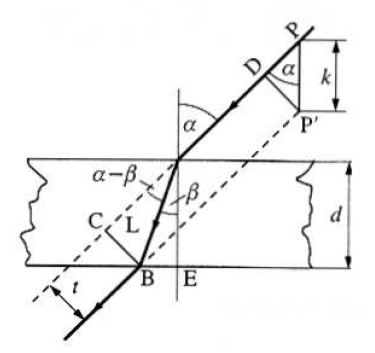
A síkpárhuzamos lemez d vastagságú átlátszó, fénytörő anyagból pl. üvegből, műanyagból készül. A határoló felületek egymással párhuzamosak. A levegőből az első felülethez érkező fénysugár az anyagba lép, sebessége csökken.

A sugár a beesési merőleges felé törik. A lemezen áthaladva az előbbi közegbe, pl. a levegőbe lép ki, és itt eredeti sebességét nyeri vissza. A sugár a beesési merőlegestől törve, eredeti irányával párhuzamosan folytatja útját. Ezen áthaladás alatt két jelenséget tapasztalunk:

fénysugár eredeti irányától t távolságban eltolódott,
P fénypont, amelyből a fénysugár eredetileg elindult, látszólag a síkpárhuzamos lemezhez k-val közelebb P’-be került.

1.7. ábra - A síkpárhuzamos lemez

1.2. A geometriai optika alapjai

1.2.1. A geometriai optika alaptörvényei

A fény egyenes vonalban terjed. Ez természetesen homogén, izotróp közegben érvényes.
Különböző közegek határain a fénysugár megtörve folytatja útját. A fénytörést a Snellius–Descartes-törvény írja le.
Különböző közegek határán a fény egy része visszaverődik. Ezt a tükör-törvény írja le, miszerint a beeső, a visszavert fénysugár és a beesési merőleges egy síkban fekszik, valamint a beesési és visszaverődési szög egyenlő. A szögeket a beesési merőlegestől mérjük, amely a fénysugár döféspontjában a felület normálisa.
A fénysugarak függetlenségének elve kimondja, hogy a tér egy pontján keresztül akárhány fénysugár áthaladhat egymás zavarása nélkül. E törvény nyilván nem érvényes pl. koherens lézerfények találkozása esetén, amelyek egymásra hatásakor interferencia jön létre.
A fénysugarak megfordíthatóságának elve szerint ha fény a tér egyik pontjából egy bizonyos útvonalon halad a tér egy másik pontjába, akkor a visszafelé indított fénysugár ugyanazon úton fog haladni.

1.2.2. Előjelszabályok (megállapodások)

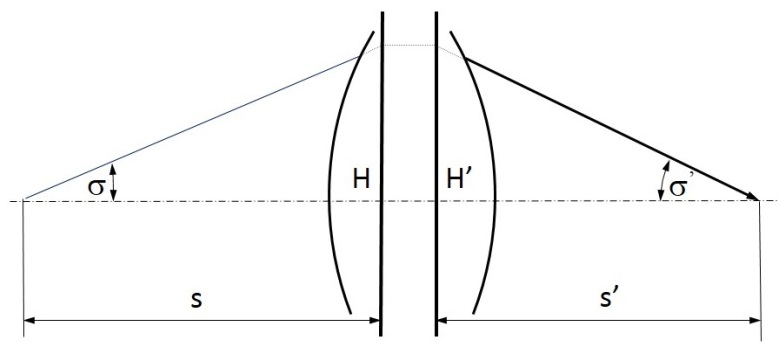
A sugármenet-rajzokat úgy vesszük fel, hogy a fénysugarak balról jobbra haladjanak (1.8. ábra).

Az optikai tengely mentén a gömbfelülettől balra eső távolságok negatívok, a jobbra esőek pozitívok.
Az optikai tengely feletti távolságok (pl. h) pozitívok, a tengely alattiak pedig negatívok.

A távolságok előjelei olyanok, mintha egy felvett koordináta-rendszer origója az S pontban lenne.
A fénysugarak optikai tengellyel bezárt szögei (Ϭ, Ϭ’) akkor pozitívok, ha az optikai tengelyt a fénysugárba az óramutató járásával ellentétes irányban lehet 90°-nál kisebb szöggel beforgatni. Ellenkező esetben a szögek negatívok.

Eszerint az (1.8. ábra) ábrán: s és Ϭ’ előjele negatív, h, s’, és Ϭ -é pedig pozitív.
A felület döféspontjában a fénysugarak beesési (i), illetve törési (r) szögei akkor pozitívok, ha a beesési merőlegest a fénysugárba az óramutató járásával ellenkező irányba lehet 90°-nál kisebb szöggel beforgatni. Ellenkező esetben a szögek negatívok.

Eszerint i és r pozitív.
A gömbfelületek görbületi sugarai akkor pozitívok, ha a felület balról nézve konvex, és akkor negatívok, ha balról nézve konkáv.

Eszerint R pozitív.
A fókusztávolság előjele pozitív gyűjtő-, negatív pedig szórólencse esetében.

1.2.3. Egyetlen gömbfelület képalkotása

Egy lencse (vagy tükör) leképező rendszerként használva képet alkot a tárgyról. A képalkotás akkor ideális, ha a tárgy és a képe arányos (torzulásmentes), a lencse pontot ponttá, egyenest egyenessé, síkot síkká képez le. A geometriai optikának a fényelhajlás miatt korlátja van, ezért pl. pontot egy valóságos lencse egy kis folttá tud csak leképezni. Ezzel a jelenséggel az optikai átviteli függvényekről szóló 1.7. szakasz fejezetben foglalkozunk.

Paraxiális képalkotásról beszélünk akkor, ha a leképzésben részt vevő fénysugarak az optikai tengelyhez képest csak kis szögeket zárnak be, vagyis tengelyközelben haladnak. Ilyenkor a szögfüggvények (sin, tg) helyett a szögek ívmértékben vett nagyságát használhatjuk.

Metszéki távolságoknak (s, s’) nevezzük a gömbfelület tengelypontjától a tárgy (P), illetve a képpontig (P’) terjedő mennyiségeket.

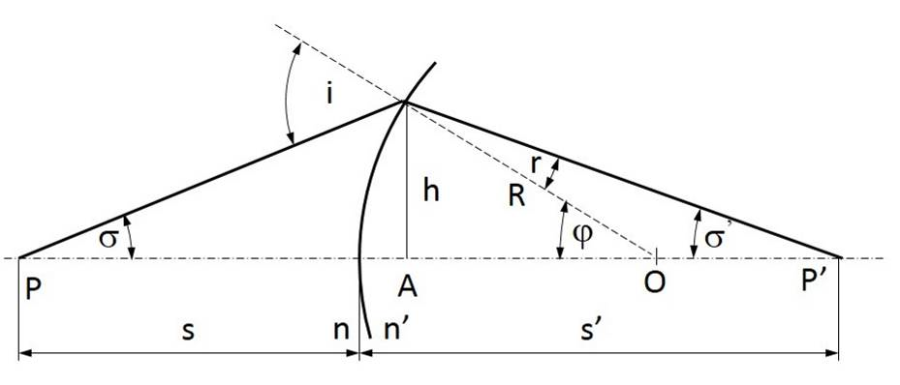
1.8. ábra - Gömbfelület képalkotása

A Snellius–Descartes-törvény szerint:

nsini=n’sinr

Kis szögek esetében (paraxiális eset):

ni=n’r

(1.8)

Az előjel szabályok alkalmazásával az egyes szögekre a megfelelő háromszögekből:

$\begin{array}{l} i = σ + φ \\ φ = r - σ' ahonnan r = σ' + φ \\ σ = - \frac{h}{s} \\ σ' = - \frac{h}{s'} \\ φ = \frac{h}{R} \end{array}$

Ezeket az (1.8)-ba helyettesítve:

	$n (σ + φ) = n' (σ' + φ)$
	$n (- \frac{h}{s} + \frac{h}{R}) = n' (- \frac{h}{s'} + \frac{h}{R})$

h-val végig osztva és beszorozva:

$- \frac{n}{s} + \frac{n}{R} = - \frac{n'}{s'} + \frac{n'}{R}$

Az ismeretlen a képtávolság:

	$\frac{n'}{s'} = \frac{n}{s} + \frac{n'}{R} - \frac{n}{R}$
	$\frac{n'}{s'} = \frac{n}{s} + \frac{n' - n}{R}$	(1.9)
	$s' = \frac{n'}{\frac{n}{s} + \frac{n' - n}{R}}$	(1.10)

Az összefüggés szerint egy r sugarú gömbfelülettől s távolságra fekvő tárgypont képe a felülettől s’ távolságra keletkezik.

A képlet átrendezésével, egy-egy oldalra gyűjtve a tárgyoldali (veszszőtlen) és a képoldali (vesszős) mennyiségeket az Abbe-féle invariánst kapjuk.

$n (\frac{1}{r} - \frac{1}{s}) = n' (\frac{1}{r} - \frac{1}{s'})$

(1.11)

Ha a gömbfelületre párhuzamos fénysugarak érkeznek (a tárgy a végtelenben van), akkor a fénysugarak a képoldalon a fókuszpontban találkoznak. (1.9) – ből s= - ∞ és s’=f’ helyettesítéssel:

$\frac{n'}{f'} = \frac{n' - n}{r}$

(1.12)

A jobb oldalon lévő mennyiséget törőértéknek nevezzük, és dioptriában adjuk meg:

	$φ = \frac{n'}{f'} = \frac{n' - n}{r}$	(1.13)
	$φ = \frac{n}{f} = \frac{n' - n}{r}$	(1.14)

(Dioptriában való számoláskor a fókusztávolságokat méterben kell helyettesíteni!)

A Langrange-féle invariáns

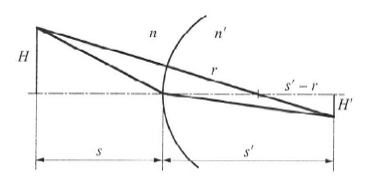
1.9. ábra - Vázlat a Lagrange-féle invariánshoz

A Snellius–Descartes-törvény szerint a törési pontban kis szögek esetén:

$n \frac{H}{- s} = n' \frac{- H'}{s'}$

másképpen

$n s' H = n' s H'$

de az (1.8. ábra) ábrából

	$\begin{array}{l} h = s σ = s' σ' \\ s = s' \frac{σ'}{σ} \end{array}$
	$n s' H = n' \frac{σ'}{σ} s' H'$

ahonnan

$n σ H = n' σ' H'$

Ezt nevezzük Lagrange-féle invariánsnak, ami azt fejezi ki, hogy a fénysugár paraxiális tartományban úgy törik, hogy a törésmutató, a tárgy, ill.képszög és a tárgy, ill. képnagyság szorzata állandó marad.

1.2.4. Kardinális elemek: fősíkok, főpontok, csomópontok

A fősíkok az első és utolsó felületével jellemzett optikai rendszerbe a tengellyel párhuzamosan belépő fénysugarak és a rendszert elhagyó megfelelő fénysugarak meghosszabbításainak metszéspontjai által kifeszített felületek (1.10. ábra).

A főpontok a fősíkoknak és az optikai tengelynek a döféspontjai (H,H’)

Minden optikai rendszernek két fősíkja (és főpontja) van: tárgyoldali és képoldali fősíkok (főpontok).

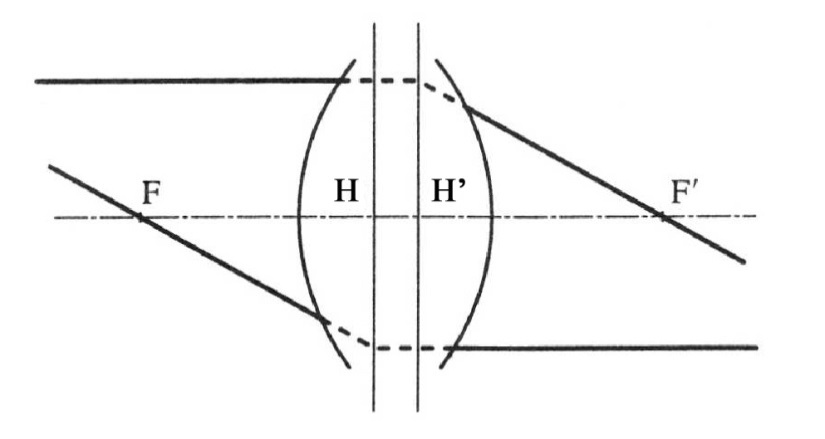
1.10. ábra - A fősíkok és a főpontok szerkesztése

A fősíkoktól mérjük a fókusztávolságokat, a tárgytávolságot, illetve a képtávolságot.

A főpontokra nézve az optikai rendszer nagyítása 1-szeres és pozitív (egyenes állású).

A fősíkok sorrendje és helye az adott optikai rendszertől függ. Egy optikai rendszer főpontjai egymás konjugáltjai, vagyis ha az egyikbe helyezünk egy tárgyat, akkor annak képe a másikban lesz.

A csomópontok

Egy optikai rendszer egyik csomópontjába (N) irányított fénysugár a rendszert önmagával párhuzamosan hagyja el, úgy, mint ha a másik csomópontból (N’) indult volna (1.11. ábra).

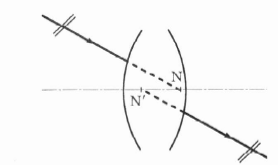
1.11. ábra - A csomópontok származtatása

A csomópontok egymás konjugáltjai.

A Lagrange-féle invariáns szerint (lásd az (1.12. ábra) ábrát):

$n σ H = n' σ' H'$

Newton-formulából: (lásd a következő pontban az 1.16 összefüggést):

	$\frac{H'}{H} = \frac{f}{z} = - \frac{z'}{f'}$
	$\frac{H'}{H} = \frac{n σ}{n' σ'} = \frac{n}{n'} = \frac{f}{z} = \frac{- z'}{f'}$

Ugyanis a csomópontokra nézve Ϭ = Ϭ’

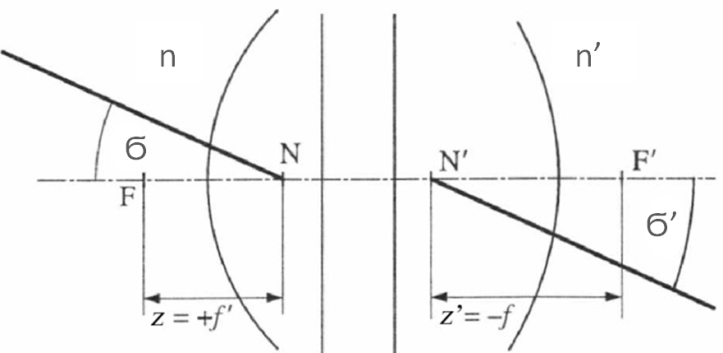
1.12. ábra - Vázlat a csomópontok helyének számításához

innen

$z' = - \frac{n}{n'} f'$ illetve $z = \frac{n'}{n} f$

De a lencse dioptriája mindkét oldalon azonos, így a reciproka is.

$\frac{f'}{n'} = \frac{f}{n}$ , így z’=f és $z = \frac{n'}{n} f = f'$

Értelmezés: A csomópontok helye a Newton-féle koordináta-rendszerben, tehát a fókuszpontokból számítva a következő:

A tárgyoldali csomópont a tárgyoldali fókuszponttól éppen a képoldali fókusztávolságnyira van, míg a képoldali csomópont a képoldali fókuszponttól éppen tárgyoldali fókusztávolságnyira van, és a távolságokat előjelesen kell érteni.

Ha az optikai rendszer tárgy-, és képtere azonos törésmutatójú (pl. levegő), akkor a csomópontok és a főpontok egybeesnek.

1.2.5. Newton-formula

Ábrázoljunk egy optikai rendszert a fősíkjaival és a fókuszpontjaival! Mérjük a tárgy illetve a kép távolságát a fókuszpontoktól (z illetve z’) (1.13. ábra).

Az (1.13. ábra) ábrából hasonló háromszögek felhasználásával:

$\frac{h}{- z} = \frac{- h'}{f} é s \frac{- h'}{z'} = \frac{h}{f'}$

(1.15)

A nagyítás (β) felhasználásával

$β = \frac{h'}{h} = \frac{- z'}{f'} = \frac{f}{z}$

(1.16)

Az utolsó egyenlőség felhasználásával a Newton-formula:

zz’=-ff’

(1.17)

a Newton-formula segítségével írhatók az alábbiak:

$\begin{array}{l} z z' = - f f' \\ (s + f) (s' - f') = - f f' \\ s s' + f s' - s f' - f f' = - f f' \\ 1 + \frac{f}{s} - \frac{f'}{s'} = 0 \\ \frac{f'}{s'} - \frac{f}{s} = 1 \end{array}$

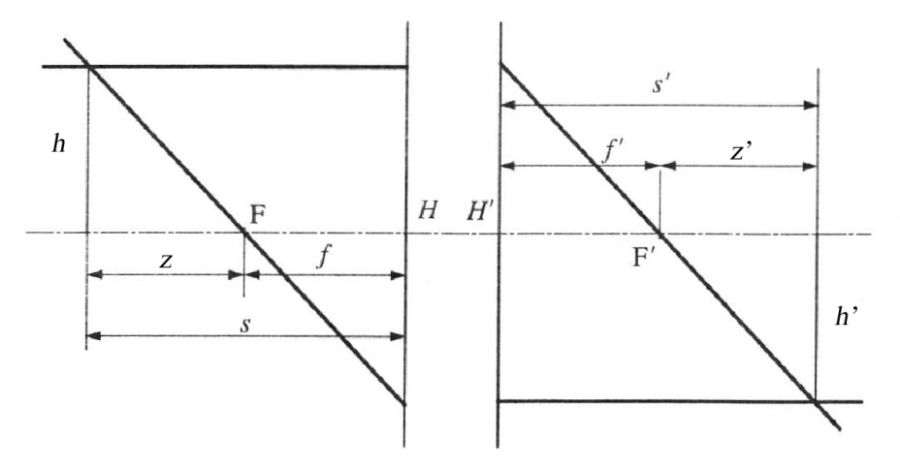
1.13. ábra - Vázlat a Newton-formulához

Ez az összefüggés „vékony” lencse esetén megadja a tárgy és kép távolsága közötti összefüggést. Amennyiben a tárgy- és képtér is levegő (vagy azonos közeg) akkor f’=f és így

$\frac{1}{s'} - \frac{1}{s} = \frac{1}{f}$

(1.18)

Vigyázzunk az előjelekre: s negatív esetén a középiskolás fizikában tanult

összefüggés adódik.

$\frac{1}{f} = \frac{1}{k} + \frac{1}{t}$

1.2.6. A vékony lencse

1.14. ábra - Vázlat a vékonylencse számításhoz

Vékony lencsénél a metszéki és a tárgy-, illetve képtávolságok azonosak.

A vékony lencse absztrahálás eredménye. Ilyenkor eltekintünk a lencse vastagságától.

Egy egyszerű lencse két gömbfelületből áll, tehát az egyetlen gömbfelület képalkotására levezetett összefüggéseinket kell kétszer alkalmazni.

$\begin{array}{l} \frac{n_{1}^{'}}{s_{1}^{'}} - \frac{n_{1}}{s_{1}} = \frac{n_{1}^{'} - n_{1}}{r_{1}} \\ \frac{n_{2}^{'}}{s_{2}^{'}} - \frac{n_{2}}{s_{2}} = \frac{n_{2}^{'} - n_{2}}{r_{2}} \end{array}}$

mivel vékony a lencse:

	$\begin{array}{l} s_{2} = s_{1}^{'} \\ n_{1}^{'} = n_{2} = n \\ n_{1} = n_{2}^{'} = 1 \end{array}$
	$\begin{array}{l} \frac{n}{s_{1}^{'}} - \frac{1}{s_{1}} = \frac{n - 1}{r_{1}} \\ \frac{1}{s_{2}^{'}} - \frac{n}{s_{1}^{'}} = \frac{1 - n}{r_{2}} \end{array} \| ebből \frac{n}{s_{1}^{'}} = \frac{1}{s_{1}} + \frac{n - 1}{r_{1}}$

Átalakítva:

$\frac{1}{s_{2}^{'}} - \frac{1}{s_{1}} = (n - 1) (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

(1.19)

(1.18) felhasználásával a vékony lencse fókuszképlete:

$\frac{1}{f^{'}} = (n - 1) (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

(1.20)

másképpen:

ha s₁= - ∞, akkor s₂’=f’

1.2.7. A lineáris, longitudinális és szögnagyítás

A lineáris nagyítás (β)

$β = \frac{y^{'}}{y}$

(1.21)

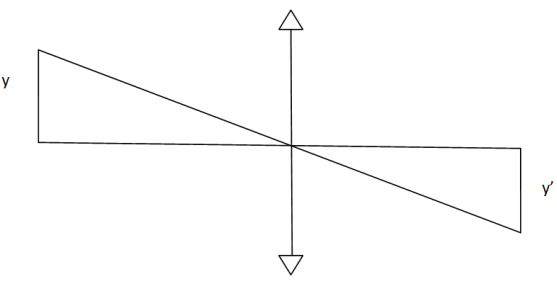
1.15. ábra - A lineáris nagyítás számítása

Kifejezhető még a Newton-formula segítségével:

$β = \frac{f}{z} = \frac{- z'}{f'} = \frac{f}{f + s} = \frac{f' - s'}{f'}$

(1.22)

A szögnagyítás (γ) (1.16. ábra)

1.16. ábra - A szögnagyítás számítása

$γ = \frac{t g σ'}{t g σ}$

(1.23)

Kifejezhető még a következőképpen:

$γ = \frac{t g σ'}{t g σ} = \frac{\frac{h}{s'}}{\frac{h}{s}} = \frac{s}{s'}$

(1.24)

A csomópontokra nézve a szögnagyítás γ=1

Számítsuk ki a lineáris és a szögnagyítás szorzatát:

$γ = \frac{s}{s'} = \frac{z - f}{z' + f'}$

mivel $β = \frac{f}{z}$ , amiből $z = \frac{f}{β}$

és $β = - \frac{z'}{f'}$ , amiből $z' = - f' β$

$γ = \frac{\frac{f}{β} - f}{- f' β + f'} = \frac{f}{f'} \frac{\frac{1}{β} - 1}{- β + 1} = \frac{f}{f'} \frac{1 - β}{β (1 - β)} = \frac{f}{f'} \frac{1}{β}$

ebből

$β γ = \frac{f}{f'}$

(1.25)

ha f=f’, akkor

$β = \frac{1}{γ} é s γ = \frac{1}{β}$

(1.26)

(1.24) felhasználásával

$β = \frac{f}{f'} \frac{s'}{s}$

(1.27)

ha f=f’, akkor

$β = \frac{s'}{s}$

(1.28)

Longitudinális nagyítás (α)

$α = \frac{d z}{d z'}$

(1.29)

dz deriválást jelent z szerint

A Newton-formulából

$z z' = - f f'$

ebből

$z' = - f f' \frac{1}{z}$

deriváljunk z szerint

$\frac{d z'}{d z} = f f' \frac{1}{z^{2}}$

Tehát

$α = f f' \frac{1}{z^{2}}$

(1.30)

$\frac{f}{f}$ -el beszorozva

$α = \frac{f'}{f} \frac{f^{2}}{z^{2}} = \frac{f^{'}}{f} β^{2}$

mivel $β = \frac{f}{z}$ , így

$α = \frac{f^{'}}{f} β^{2}$

(1.31)

Ha f = f’, akkor:

$α = β^{2}$

(1.32)

Számítsuk ki a lineáris és a szögnagyítás hányadosát!

$\frac{β}{γ} = \frac{f}{f^{'}} \frac{s^{'}}{s} \frac{s^{'}}{s}$ ,

mivel $β = \frac{f}{f^{'}} \frac{s^{'}}{s}$ , és $γ = \frac{s}{s^{'}}$

Beszorozva $\frac{f}{f^{'}} \frac{f^{'}}{f}$ -fel

$\frac{β}{γ} = (\frac{f}{f^{'}} \frac{s^{'}}{s}) (\frac{s^{'}}{s} \frac{f}{f^{'}}) \frac{f^{'}}{f} = α$ ,

mivel a zárójeles mennyiség ß és (1.31) szerint $α = \frac{f'}{f} β^{2}$

Így tehát

$α = \frac{β}{γ}$

(1.33)

1.3. Valóságos lencsék számításai

1.3.1. Vékony lencsék eredője

Két elemi vékony lencsét egymás mellé helyezve, dioptriáik, vagyis törőértékeik összeadódnak:

$φ = φ_{1} + φ_{2}$

(1.34)

mivel azonos közegekben $φ = \frac{1}{f}$ , ezért

$\frac{1}{f} = \frac{1}{f_{1}} + \frac{1}{f_{2}}$

(1.35)

f-re kifejezve

$f = \frac{f_{1} f_{2}}{f_{1} + f_{2}}$

(1.36)

1.3.2. Légközzel elválasztott két vékony lencse eredője

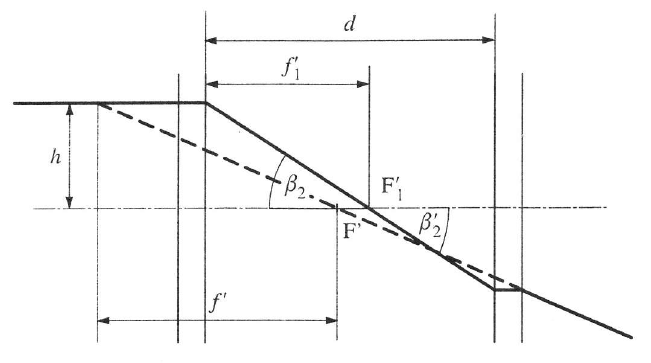
Más a helyzet akkor, ha a két vékony lencse között d távolság van (1.17. ábra).

Eredő gyújtótávolság számításához a szögnagyítás a 2. lencsére:

$γ = \frac{s_{2}}{s_{2}^{'}} = \frac{t g β_{2}^{'}}{t g β_{2}} = \frac{f_{1}^{'}}{f^{'}}$

(1.37)

mivel $t g β_{2} = \frac{h}{f_{1}^{'}}$ és $t g β_{2}^{'} = \frac{h}{f'}$

$f_{1}^{'} t g β_{2}^{'} = f^{'} t g β_{2}^{'}$

1.17. ábra - Vázlat az eredő gyújtótávolság számításához

Mint ismeretes:

$\frac{f_{2}^{'}}{s_{2}^{'}} - \frac{f_{2}}{s_{2}} = 1$

amiből

$\frac{f_{2}^{'}}{s_{2}^{'}} = 1 + \frac{f_{2}}{s_{2}} = \frac{f_{2} + s_{2}}{s_{2}}$

innen s₂=f₁’-d felhasználásával

$s_{2}^{'} = \frac{f_{2}^{'} s_{2}}{f_{2} + s_{2}} = \frac{f_{2}^{'} (f_{1}^{'} - d)}{f_{2} + (f_{1}^{'} - d)}$

Ezt behelyettesítve (1.37)-be

$γ = \frac{f_{1}^{'}}{f^{'}} = \frac{(f_{1}^{'} - d) (f_{2} + f_{1}^{'} - d)}{f_{2}^{'} (f_{1}^{'} - d)}$

és innen

$f^{'} = \frac{f_{1}^{'} f_{2}^{'}}{f_{1}^{'} + f_{2} - d}$

(1.38)

illetve levegőben lévő lencsék összerakásakor:

$\frac{1}{f} = \frac{1}{f_{1}} + \frac{1}{f_{2}} - \frac{d}{f_{1} f_{2}}$

(1.39)

A vékony lencsével ekvivalens vastag lencséről akkor beszélünk, ha a két lencsének azonos a fókusztávolsága, a törésmutatója és az első görbületi sugara. (Tehát a vastagságban és a hátsó görbületi sugárban térnek el).

Az (1.38) összefüggés nevezőjében lévő kifejezést jelöljük Δ-val.

Ezt nevezzük optikai tubushossznak.

	$Δ = f_{1}^{'} + f_{2} - d$	(1.40)
	$f^{'} = \frac{f_{1}^{'} f_{2}^{'}}{Δ}$	(1.41)

Miután az így létrejött valóságos lencse két fősíkkal kell rendelkezzen, ezek helyét is kiszámíthatjuk. Legyen p’ a képoldali fősík és a második vékony lencse távolsága és p a tárgyoldali fősík és az első vékony lencse távolsága. Ezekkel a valóságos lencse fősíkjainak helyei

	$p^{'} = s_{2}^{'} - f^{'} = \frac{f_{2}^{'} (f_{1}^{'} - d)}{Δ} - f^{'} = \frac{f_{2}^{'} (f_{1}^{'} - d)}{Δ} - \frac{f_{1}^{'} f_{2}^{'}}{Δ}$
	$p^{'} = \frac{f_{2}^{'} f_{1}^{'} - f_{2}^{'} d - f_{1}^{'} f_{2}^{'}}{Δ} = - \frac{f_{2}^{'} d}{Δ}$

Hasonló levezetéssel:

$p = \frac{f_{1} d}{Δ}$

Összefoglalva:

$\begin{matrix} f = \frac{f_{1} f_{2}}{Δ} & f^{'} = \frac{f_{1}^{'} f_{2}^{'}}{Δ} \\ p = \frac{f_{1} d}{Δ} & p^{'} = - \frac{f_{2}^{'} d}{Δ} \end{matrix}$

(1.42)

1.3.3. A vastag lencse

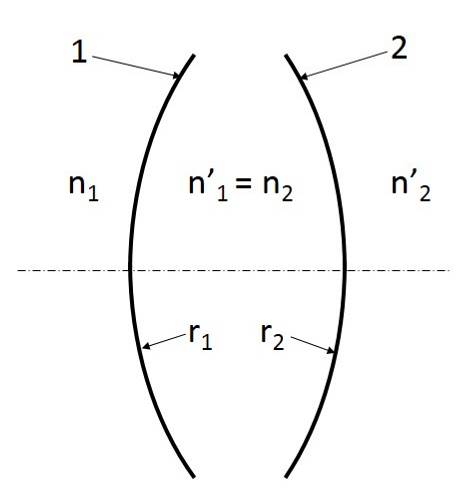
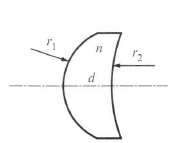
Alkalmazzuk most a görbületi sugarakat is tartalmazó (1.42) összefüggést a „vastag” lencsére, vagyis egy két (r₁ és r₂) görbületi sugarú gömbfelületből álló, d vastagsággal és n törésmutatóval rendelkező valóságos lencsére! (1.18. ábra)

1.18. ábra - Vastag lencse

	$f = \frac{n r}{n^{'} - n}$
	$f^{'} = \frac{n' r}{n' - n}$
	$n_{1} = 1 n_{1}^{'} = n r = r_{1}$
	$f_{1} = \frac{r_{1}}{n - 1} f_{1}^{'} = \frac{n r_{1}}{n - 1}$

majd ezt a 2. felületre:

	$f_{2} = \frac{n r_{2}}{1 - n} f_{2}^{'} = \frac{r_{2}}{1 - n}$
	$Δ = f_{1}^{'} + f_{2} - d = \frac{n r_{1}}{n - 1} + \frac{n r_{2}}{1 - n} - d = \frac{n r_{1} - n r_{2} - (n - 1) d}{n - 1}$
	$f = f^{'} = - \frac{n r_{1} r_{2} (n - 1)}{{(n - 1)}^{2} [n (r_{1} - r_{2}) - (n - 1) d]}$
	$\frac{1}{f} = (n - 1) \frac{n (r_{2} - r_{1}) + (n - 1) d}{n r_{1} r_{2}}$

Fennáll egy azonosság:

$\frac{r_{2} - r_{1}}{r_{1} r_{2}} = \frac{1}{r_{1}} - \frac{1}{r_{2}}$

ezzel

$\frac{1}{f} = (n - 1) (\frac{1}{r_{1}} - \frac{1}{r_{2}} + \frac{n - 1}{n} \frac{d}{r_{1} r_{2}})$

(1.43)

d = 0 esetében

$\frac{1}{f} = (n - 1) (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

vagyis megkapjuk a vékony lencse képletét (pl. szemüvegnél így számolhatunk).

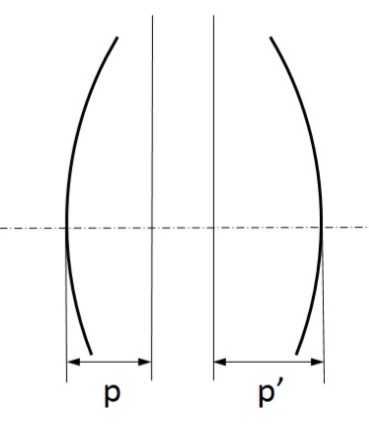
1.19. ábra - Vázlat a vastag lencse fősíkjainak számításához

Számítsuk ki a fősíkok helyeit is a lencsegörbületek segítségével (1.43)-ből. (1.19. ábra)

	$p = \frac{f_{1} d}{Δ} = \frac{r_{1} d}{n - 1} \frac{n - 1}{n (r_{1} - r_{2}) - (n - 1) d}$
	$p^{'} = - \frac{f_{2}^{'}}{Δ} = + \frac{r_{2} d}{n - 1} \frac{n - 1}{n (r_{1} - r_{2}) - (n - 1) d}$

Rendezve:

$\begin{array}{l} p = \frac{r_{1} d}{n (r_{1} - r_{2}) - (n - 1) d} \\ p^{'} = \frac{r_{2} d}{n (r_{1} - r_{2}) - (n - 1) d} \end{array}$

(1.44)

Ha d = 0, akkor p= p’= 0 a két fősík egybeesik.

p– t az első lencsefelülettől p’-t a hátsó lencsefelülettől kell mérni.

1.3.4. Több felületből álló lencserendszerek

A vastag lencsénél kétszer alkalmaztuk a gömbfelületre vonatkozó összefüggéseket. Ha több lencsés optikai rendszerünk van, akkor a gömbfelületre vonatkozó összefüggések sorozatos alkalmazásával a következő öszszefüggésekhez jutunk:

Eredő fókusztávolság:

$f = \frac{n_{1}}{n_{k}^{'}} \frac{s_{1}^{'} s_{2}^{'} s_{3}^{'} ... s_{k}^{'}}{s_{2} s_{3} ... s_{k}}$

(1.45)

Eredő lineáris nagyítás:

$β = \frac{n_{1}}{n_{k}^{'}} \frac{s_{1}^{'} s_{2}^{'} s_{3}^{'} ... s_{k}^{'}}{s_{1} s_{2} s_{3} ... s_{k}}$

(1.46)

ahol

	k	a gömbfelületek száma
	n ₁	a tárgytér törésmutatója
	n’ ₂	a képtér törésmutatója

Nagyításról csak véges tárgytávolság (s₁)esetén beszélhetünk!

1.4. Teleszkopikus rendszerek

A teleszkopikus rendszerek olyan kéttagú összetett optikai rendszerek, amelyeknél Δ = 0, vagyis az egymás felé eső két fókuszpont egybeesik.

Két ilyen rendszer lehetséges:

	f ₁ > 0 f₂> 0	Kepler-távcső
	f ₁ > 0 f₂ < 0	Galilei-távcső

1.4.1. Kepler-távcső (csillagászati távcső)

A rendszer szögnagyítása

$γ = \frac{t g β'}{t g β} = \frac{- h}{f_{2}^{'}} \frac{f_{1}}{(-) - h} = - \frac{f_{1}}{f_{2}^{'}}$

(1.47)

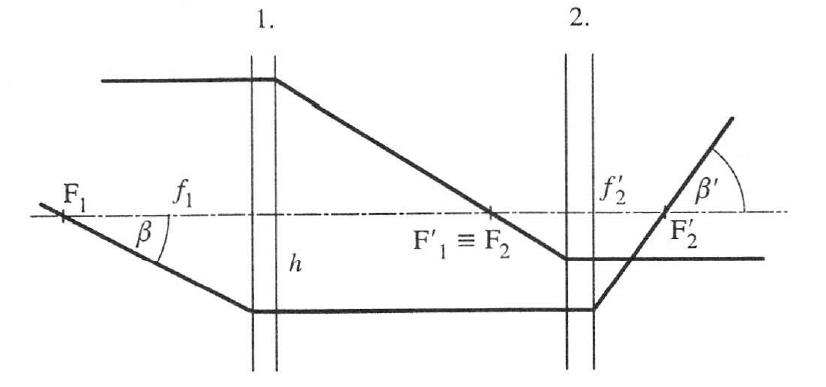
1.20. ábra - A Kepler-távcső

γ negatív előjele a fordított állású képet jelzi.

A rendszer akkor nagyít, ha $| f_{1} | > | f_{2} |$

1.4.2. Galilei-távcső (színházi vagy terresztikus távcső)

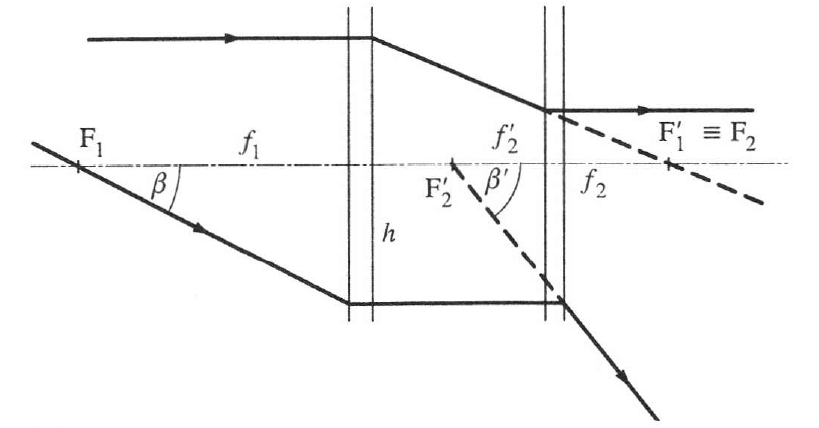
1.21. ábra - A Galilei-távcső

A szögnagyítás (1.21. ábra)

$γ = \frac{t g β'}{t g β} = \frac{- h}{- f_{2}^{'}} (-) \frac{f_{1}}{- h} = \frac{f_{1}}{f_{2}^{'}} > 0$

(1.48)

Ha $| f_{1} | > | f_{2}^{'} |$ , akkor nagyít.

1.5. Rekeszek

A rekeszek az optikai rendszeren áthaladó fénysugarak egy részének kizárását, vagy a kép határolását végzik. Tengelyszimmetrikus rendszereknél a rekeszek általában szintén tengelyszimmetrikusak, sokszor kör alakúak.

Feladatuk szerint kétféle rekesz van: apertúrarekesz és mezőrekesz.

1.5.1. Apertúrarekesz

Az apertúrarekesz feladata a lencserendszer nyílásának határolása, vagyis a szélső sugarak kizárása (1.21. ábra).

A P-vel jelölt rekesznek két képét külön is használjuk: a rekesztől balra eső részrendszer által a rekeszről alkotott kép neve: belépő pupilla (EP). Az apertúrarekesztől jobbra eső részrendszer által a róla alkotott kép neve: kilépő pupilla (AP).

A belépő és kilépő pupillák egymás konjugáltjai az egész rendszerre vonatkozóan.

Ha egy sugarat a belépő pupilla közepe felé irányítunk, akkor az – miközben az apertúrarekesz közepén átmetszi az optikai tengelyt, úgy fogja elhagyni az optikai rendszert, mintha a kilépő pupilla középpontjából indult volna.

Ha a rendszer torzításmentes, akkor ezen belépő és kilépő fénysugár párhuzamos.

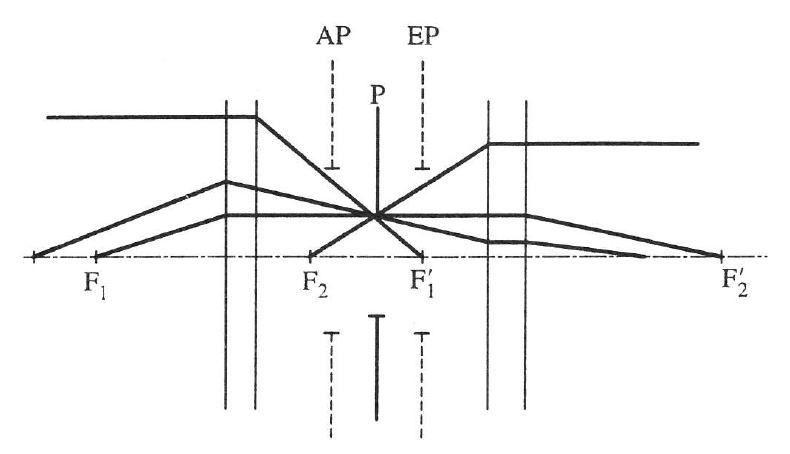
1.22. ábra - Az apertúrarekesz

Minden olyan fénysugár, amelyik a tárgypontból a belépő pupilla széle felé halad, át fog jutni az optikai rendszeren. Ezek segítségével meg lehet határozni az egyes lencsetagok szükséges átmérőjét. Ezen sugarak a rendszerből úgy fognak kilépni, mintha a kilépő pupilla széléből indulnának.

Az apertúrarekesz helye (az optikai tengely mentén) hatással van a képminőségre, hiszen általa a szélső sugarak más-más része záródik ki a képalkotásból.

Természetes rekeszhely

Van egy ún. természetes rekeszhely, amelyet kétféleképpen definiálhatunk:

Ha az apertúrarekesz a természetes rekeszhelyen van, akkor a belépő és a kilépő pupillák éppen a fősíkokban vannak.

Megfordítva: ha egy fősugarat az egyik fősík tengelypontja felé irányítunk, akkor az a másik fősík tengelypontja felől fog eltávozni, miközben a valóságos fénysugár éppen a természetes rekeszhelyen metszi az optikai tengelyt.

Fotoobjektívek rekesze az ún. íriszblende. A fotoobjektívek fényerejének a belépő pupilla átmérőjének és a fókusztávolságnak a hányadosát nevezik.

Távcsöveknél az apertúrarekesz éppen az objektív széle, foglalata, ezért azonos a belépő pupillával.

Ennek képe – az egész rendszer által leképezve – viszont a kilépő pupilla. Az emberi szem pupillája ideális esetben a távcső kilépő pupillája helyére kerül, és nagyságuk közel egyenlő.

Így pl. ha egy objektív fényereje 1 : 5,6 az azt jelenti, hogy

$\frac{1}{5,6} = \frac{\emptyset E P}{f}$

ezt nevezik másképpen relatív nyílásnak.

1.5.2. Mezőrekesz, nyílások

A mezőrekesz feladata az, hogy a képnek éles széle legyen. Elhelyezése a tárgy-, vagy a képtérben történik.

A mezőrekesz az az átmérő, amelyik a belépő pupilla középpontjából a legkisebbnek látszik.

A mezőrekesz képei a nyílások: a belépő nyílás a mezőrekesznek a tárgyoldali részrendszer által alkotott képe. A kilépő nyílás a képoldali részrendszer által alkotott rekeszkép.

Mikroszkópnál a mezőrekeszt az okulár síkjában helyezzük el. Fényképezőgépnél a film síkjában lévő téglalap alakú nyílás a mezőrekesz.

1.6. Képméret, képszög, fősugár

A képméret a nem végtelenben lévő tárgyról alkotott kép nagysága.

A képszög a fősugarak átal alkotott kép félszöge.

A fősugár a tárgypontból a belépő pupilla középpontjába mutató sugár. Kiterjedt tárgy esetén több fősugár van, hiszen minden tárgypontból indul egy fősugár.

1.7. Optikai átviteli függvények

A képalkotó optikai rendszerek működését úgy is szemlélhetjük, hogy eltekintünk a rendszerek optikai jellegétől, és mindössze azt vesszük észre, hogy milyen összefüggés van a tárgyak és képeik között. Nem törődve azzal, mi hozta létre ezt a transzformációt, a kapcsolatot függvényekkel írjuk le. Hasonló feladatokat már más tudományterületek eredményesen megoldottak, pl. az elektronikai rendszerek esetében bevezették az átviteli függvényeket a bemeneti és a kimeneti jelek közötti kapcsolatok leírására. Az optikai rendszerek esetében hasonlóan járunk el, megkülönböztetésül optikai átviteli függvényekről beszélünk.

Az optikai átviteli függvények ma már széles körben elterjedtek. Az optikai rendszereket minősítők és a felhasználók számára a legfontosabb információkat adják, a tervezők számára pedig analitikus tervezőmunkájuk eredményének végső ellenőrzését jelentik. Forradalmi változást jelentettek az optikai átviteli függvények a hibaminimumra törekvő automatikus finomkorrigáló számítógépprogramok fejlődéstörténetében az 1970-es években. Ekkor ugyanis azok a programok, amelyek már „készre” korrigálták a rendszereket, eredményüket illetően elmaradtak azoktól az új programoktól, amelyeken még ezután elvégeztek egy olyan korrekciót is, amelynek célfüggvénye az optikai átviteli függvény számítása alapján került kialakításra.

Felmerült a kérdés: szükség van-e akkor más hibafüggvény-aberráció számítására, miért nem lehet közvetlenül az optikai átviteli függvényekre optimalizálni a leképző rendszerek tervezési folyamatát? A válasz az, hogy az optikai átviteli függvények annyira eredő jellemzői az egész optikai rendszer bármely eleme által okozott hibáknak, hogy visszafelé – néhány speciális esettől eltekintve – nem lehet egyértelműen megmondani, hogy mi okozta a rendszer átviteli függvényének romlását. Mivel a hagyományos aberrációk elmélete ezzel ellentétben viszont rendelkezik a hiba okokra vonatkozó következtetés lehetőségével, így mind a mai napig használjuk a klasszikus technikát, és csak a végső fázisban térünk át az optikai átviteli függvények használatára.

Tekintettel leszünk ugyanakkor a más tudományterületeken már elterjedten használt fogalmakra (pl. moduláció, frekvencia, fázis), és azokhoz igazodóan vezetjük be az optikai megfelelőiket (pl. kontraszt, térfrekvencia).

Mint látni fogjuk, a matematikai formulák nagyon hasonlóak. Ez praktikussága mellett azzal az előnnyel is jár, hogy viszonylag könnyen lehet majd vegyes rendszereket tárgyalni, amelyekben az optikai leképző rendszer pl. elektronikus detektorral csatoltan működik.

Az optikai átviteli függvények használata könnyebbé teszi a sorba kapcsolt optikai rendszerek tárgyalását is, eredő optikai átviteli függvények képzésével.

1.7.1. Elemi alakzatok képalkotása

Általános értelemben az optikai leképzést úgy tekinthetjük, mint a tárgytér fényeloszlása és a képtér fényeloszlása közötti transzformációt. A leképzendő tárgy minden egyes pontjának van valamilyen felületi fényessége, és ez a keletkezett képre is elmondható. Ideális esetben a megfelelő tárgy- és képpontok között homogén lineáris kapcsolat áll fenn.

Az optikai rendszereknél az átviteli függvény szempontjából nem foglalkozunk az időbeliséggel, vagyis állandó megvilágítású tárgyak statikus képét vizsgáljuk. A transzformációt akkor tartjuk jónak, ha a pontot ponttá, egyenes vonalat egyenes vonallá alakítja át a rendszer, miközben a szükséges nagyítás létrejön. A nagyításra vonatkozóan pedig elvárjuk, hogy az a képtér minden tartományában azonos legyen, vagyis egyenes szakaszt nagyítás szoros hosszúságú egyenes szakasszá képezze le.

Egyetlen pont képének fényeloszlás függvényét pontszórás függvénynek, egyetlen vonalét vonalszórás függvénynek, egyetlen élét pedig élszórás függvénynek nevezzük.

Az optikai rendszerek által alkotott kép minősége sokszor jelentősen változik a kép közepétől (az optikai tengelytől) távolodva. A képsík egy kis tartományában feltételezhető, hogy a képminőség azonos (izoplanatikus tartományok).

Ugyanez a detektorok esetében csak bizonyos munkaponti tartományokban igaz, nagyon kis és nagyon nagy fénymennyiségeknél nemlineáris jelenségekkel kell számolnunk. A képet akkor érezzük élesnek, ha részletgazdagságban nem marad el a tárgyétól, vagy ha a tárgyak szélei a képen kontrasztosan jelennek meg. Ez utóbbit úgy képzelhetjük el, hogy a képen az éles sötét-világos részek átmenetszerűen jönnek létre. Annál rosszabb egy kép, minél nagyobbak ezek az átmenetek (1.23. ábra). Egy vékony vonal képének mindkét oldalán is megtalálhatók ezek az átmenetek (1.24. ábra), sőt egyetlen pont képe körkörösen átmenetszerűen jön létre (1.23. ábra).

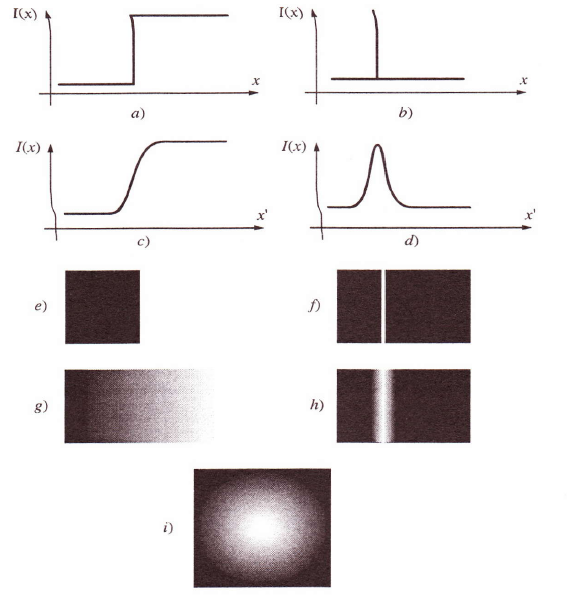
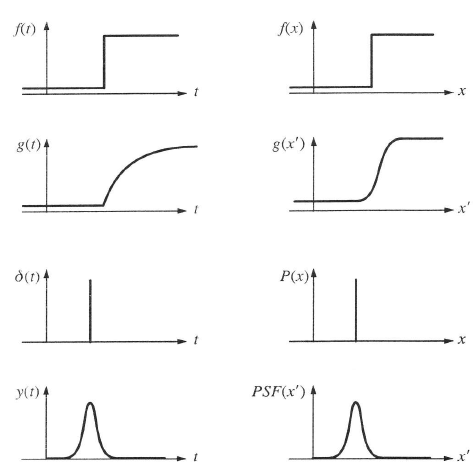
a) sötét-világos félsíkok (pl. kések) fényintenzitás-eloszlása a tárgyon. x a késélre merőleges hosszúság, I(x) a tárgy felületi fényessége vagy egyszerűen intenzitása; b) sötét háttéren lévő világos vonal fényeloszlása a tárgytérben; c) az a) szerinti tárgy képének fényeloszlása; d) a b) szerinti tárgy képének fényeloszlása (x’ az x-szel párhuzamos és annak megfelelő irány a képtérben); e) az a) szerinti tárgysík rá merőleges irányból nézve; f) a b) szerinti tárgysí k rá merőleges irányból nézve; g) a c) szerinti kép rá merőleges irányból nézve; h) pontszórásfüggvény; i) egy sötét háttérben lévő világos pont képe rá merőleges irányból nézve (fényeloszlásának függvénye a d) ábráéhoz hasonlít)

1.23. ábra - Elemi alakzatok szórásképei

1.7.2. Az optikai átviteli függvény rendszertechnikai származtatása

Az időbeli vagy dinamikai rendszerek vizsgálatával foglalkozó rendszertechnika kialakította azt az általános tárgyalásmódot, amit analógiaként felhasználhatunk az optikai átviteli függvények fogalmának bevezetésénél. A rendszertechnika általánosította azokat a villamosságtanban, mechanikában, hőtanban stb. hasonlóan tárgyalható rendszerelemeket, amelyekre egyaránt jellemző, hogy időben változó bemeneti jelekre f(t) időben változó kimeneti jeleket g(t) hoznak létre ún. válaszfüggvényként.

Definiálásra került az átviteli függvény T(ω), amely a kimeneti jelek és a bemeneti jelek Laplace-transzformáltjainak F(ω), illetve G(ω) hányadosa. (1.24. ábra)

Mivel az ún. impulzusfüggvény, vagy Dirac-függvény speciális Laplace-transzformálttal rendelkezik

ℒ [δ (t)] = 1), így az átviteli függvény az erre adott válaszfüggvény transzformáltjával egyenlő.

Mindezek az optikai rendszerek esetében is felhasználhatók. Itt a Laplace-transzformáció helyett elegendő a Fourier-transzformációt használni:

$ℱ [f (x)] = \int_{- \infty}^{\infty} f (x) e^{- i ω x} d x$

(1.49)

Míg az időbeli rendszereknél a vízszintes tengelyen a t szerepel, addig az optikai rendszereknél a helykoordináta x. Időbeli rendszereknél ω=2πf, ahol f a frekvencia, vagyis a másodpercenkénti periódusok száma (1.49).

Optikai rendszereknél

ω=2πv

A v a térfrekvencia, vagyis a milliméterenkénti periódusok száma. Optikai rendszereknél a Dirac-bemenetnek egy fénylő csillag felel meg a sötét égbolton, amelyre $ℱ [P (x)] = 1$ , így ennek válaszfüggvényét Fourier-transzformálva előállítjuk az optikai átviteli függvényt (OTF). A Fourier-transzformáció képletéből látható, hogy az eredmény komplex függvény lesz, amelyet Euler-alakban ábrázolva abszolút értékre és fázisra bonthatjuk.

1.24. ábra - Az optikai átviteli függvény, mint a rendszertani átviteli függvény analógiája

$\begin{array}{l} T (ω) = \frac{G (ω)}{F (ω)} & O T F (ω) = \frac{G (ω)}{F (ω)} \\ G (ω) = ℒ [g (t)] & G (ω) = ℱ [g (x')] \\ G (ω) = ℒ [f (t)] & F (ω) = ℱ [f' (x)] \\ ℒ [δ (t)] = 1 & ℱ [P (x)] = 1 \\ T (ω) = ℒ [y (t)] & O T F (ω) = ℱ [P S F (x')] \end{array}$

Hasonló felbontással találkozunk a rendszertechnikában, ahol az abszolút érték részét és a fázisrészt egymás alatt a frekvencia függvényében szokás ábrázolni. Az optikában is ezt tesszük.

$O T F (v) = M T F (v) e^{- i P T F (v)}$

(1.50)

Az OTF az MTF és a PTF jelölést a nemzetközi irodalom miatt tartjuk meg (optical transfer function, modulation transfer function, illetve phases transfer function), utóbbit szokás még egyszerűen ϕ(ν)-vel jelölni.

Definicíószerűen MTF(0) = 1 vagyis nulla térfrekvencián a modulációs átviteli függvény értéke egységnyi, míg PTF(0) = 0, vagyis a fázisátviteli függvényérték ugyanott zérus.

Valamely tetszőleges tárgy f(x) leképzésekor keletkező kép g(x΄) intenzitáseloszlását a leképző optikai rendszer OTF-jének ismeretében úgy kaphatjuk meg, hogy az 1.24. ábra szerinti összefüggésből kifejezzük. G(ω)-t és azt inverz-Fourier-transzformáljuk:

$g (x') = ℱ^{- 1} [G (ω)] = ℱ^{- 1} [O T F (ω) ℱ [f (x)]]$

(1.51)

Egy rendszer optikai átviteli függvényét tehát egyszer kell csak meghatározni, azután bármely tárgy képét segítségével kiszámíthatjuk. Eredményünk tartalmazni fogja a képalkotási hibák hatását is.

1.7.3. Az optikai átviteli függvények szemléletes magyarázata

Tekintsük az 1.25. ábra szerinti sűrűn csíkos tárgyat. A négyszögszerű jelsorozat mutatja a tárgy fényeloszlását. A kép fényeloszlását rárajzoltuk a tárgyéra (egységnyire normálva a nagyítást). Látható, hogy a képen a sarkos fényeloszlás helyett színusszerű jelenik meg, sőt a jelsorozat amplitudója sem olyan nagy mint a tárgyé.

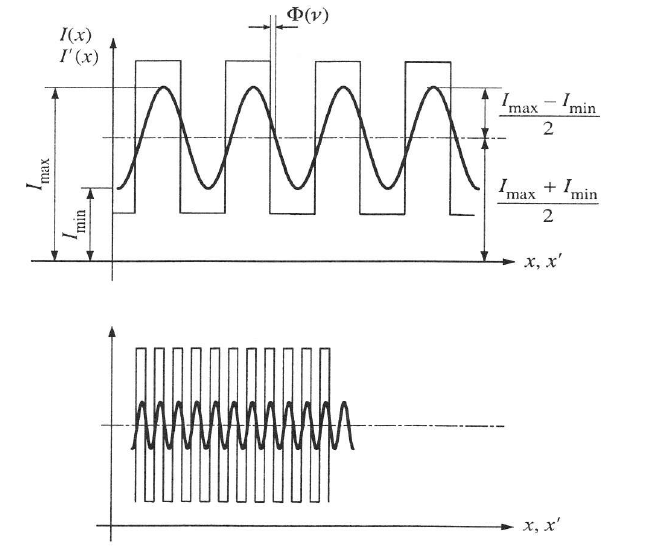
A tárgy fényeloszlássa a négyszög-, a képe pedig a szinusszerű. A térfrekvencia növelésével a képkontraszt csökken.

1.25. ábra - A csíkos tárgy képalkotása.

Megfigyelhető az is, hogy a kép- és tárgyjel között egy kis Φ(ʋ) nagyságú fáziseltolódás is van. A jel amplitúdócsökkenés és a fáziseltolódás általában annál nagyobb, minél sűrűbb, vagyis nagyobb térfrekvenciájú a tárgyfüggvény.

Kontrasztnak nevezzük a sötét és a világos részek viszonyát. E viszonyt a híradástechnikai moduláció fogalomnak megfelelően a jel középvonalától mért amplitúdó és a középvonalnak a vízszintes tengelytől mért magassága hányadosaként definiáljuk.

$K = \frac{\frac{I_{\max} - I_{\min}}{2}}{\frac{I_{\max} + I_{\min}}{2}} = \frac{I_{\max} - I_{\min}}{I_{\max} + I_{\min}}$

(1.52)

Látható, hogy a kontraszt maximális értéke egységnyi lehet, általában pedig 0-1 közé esik. (Akkor lehetne egységnyi, vagyis 100%-os, ha az I_min=0 lenne, ez pedig akkor állhat elő, ha az optikai rendszer a kép fekete területére semmilyen fényt nem juttatna).

Az (1.25. ábra) ábrából az is látható, hogy egyetlen élátmenet leképzésének hiányossága miatt áll elő a kontrasztcsökkenés, hiszen a rendszer csak bizonyos meredekséggel képes átvinni a hirtelen emelkedő négyszögjelet – így minél sűrűbb a négyszögjelsorozat, annál kisebb értékre tud felemelkedni a válaszjel, mire a négyszöggel ismét csökkenni kezd. Tehát a térfrekvencia növekedésével a kontraszt csökkenni fog.

Ha a kontraszt csökkenését a térfrekvencia függvényében ábrázoljuk, megkapjuk a kontrasztátviteli vagy modulációs átviteli függvényt.

Az 1.26. ábra szerinti két függvény nem más, mint az OTF(ʋ) komplex optikai átviteli függvény abszolút értéke és fázisa.

Persze egy valóságos tárgy általában nem periodikus struktúrájú. Mint a függvénytanból tudjuk, felírható azonban függvénysorként, vagyis különféle frekvenciájú összetevők összességeként. Miután az egyes összetevő frekvenciák átvitele nem azonos, ezért a tárgy leképzése nem lesz ideális. Általában igaz, hogy a magasabb frekvenciákon csökken a kontraszt és növekszik a fázishiba. Ez olyan, mint a rendszertechnikában a felülvágó szűrők hatása.

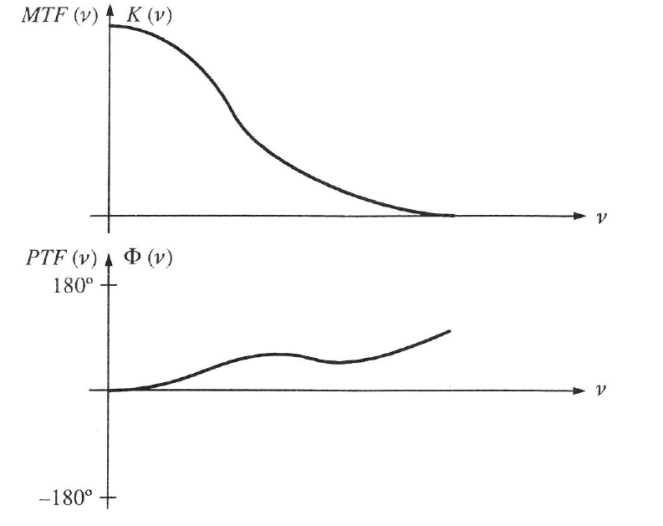
1.26. ábra - A modulációs átviteli függvény és a fázisátviteli függvény

Itt a függőleges tengely léptéke szög, mivel egyetlen periódust 360º-nak tekintünk, és ehhez képest léptékezzük a fáziseltolódást.

A fázishiba jelentéséhez megjegyezzük, hogy azt úgy kell elképzelni, mintha az egyes képrészletek (pl. a négyszöggel felfutó vagy lefutó éle) nem pontosan oda kerülne a képen, ahová ideális képszerkesztés útján.

A vízszintes tengelyen a ʋ térfrekvencia található ciklus/mm egységben. Az ábra alatt szokás ábrázolni a fázishiba változását szintén a térfrekvencia függvényében.

1.7.4. Az apertúrafüggvény és kapcsolata az optikai átviteli függvénnyel

E fejezet tanulmányozását a könyv II. részének ismeretében könnyebben elvégezhetjük. Azért szerepeltetjük mégis itt, és nem a hullámoptikai részek után, mert az optikai átviteli függvények megértését teljesebbé teszi.

A fény hullámtani leírásakor elektromágneses rezgésekről, hullámokról beszélünk. Az elektromos térerőt, amelynek változásaként is leírhatjuk a fényt, a következő képlettel szemléltethetjük:

$E_{0} (t) = U_{0} e^{i (ω t + φ)} = U_{0} \cos (ω t + φ) + i U_{0} \sin (ω t + φ)$

(1.53)

Ha összevonjuk az időtől független tagokat: $E_{0} (t) = U_{0} e^{i φ} \cdot e^{i ω t}$ alakot kapjuk. Ebben az alakban jelöljük E-vel az időtől független részt:

$E = U_{0} e^{i φ}$

(1.54)

és nevezzük ezt komplex amplitúdónak, hiszen az időbeli rezgésnek ez jelenti az amplitúdóját.

Itt U₀ a rezgés amplitúdója, t az idő, j a kezdő fázisszög, i az imaginárius egység. Az összefüggés valós része a cosinuszos terjedés leírását szemlélteti. A továbbiakban a komplex amplitúdónak lesz csak jelenősége, mert a másik tényező csak az időtől függ, mi pedig a helytől függő viszonyokat vizsgáljuk.

Tekintsük az (1.27. ábra) ábrát!

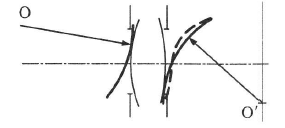
1.27. ábra - A hullámaberráció értelmezése

Képzeljük el az optikai leképzést úgy, mintha a lencsébe bemenő fényhullám komplex amplitúdója megszorzódna egy – a lencsére jellemző ún. pupillafüggvénnyel, és így alakulna ki a kimeneten a fényhullám komplex amplitúdója. A pupillafüggvényre vonatkozóan két dolgot kell számításba vennünk. Egyrészt lehet a lencsének τ(u,v) átbocsátási tényezője, másrészt megváltoztathatja a fényhullámok gömbszerűségét, amelyet az 0’ középponttól rajzolt referenciagömbtől való W(u,v) eltéréssel vehetünk figyelembe. Ezekkel a pupillafüggvény

$P (u, v) = \sqrt{τ (u, v) e^{i \frac{2 π}{λ} W (u, v)}}$

(1.55)

Itt a négyzetgyök értelme az intenzitás képzésénél látható, amikor is négyzetre emelés miatt eltűnik.

λ a fény hullámhossza, $\frac{2 π}{λ} W (u, v)$ pedig a W(u,v) hatására létrejövő fáziseltolódás.

A leképzés síkjában a fényhullám komplex amplitúdója egydimenziós esetben:

$E (x') = \int_{- \infty}^{\infty} P (u) e^{i 2 π u X'} d u - n a k$

(1.56)

adódik, amely összefüggésről felismerhető, hogy az nem más, mint egy Fourier-transzformáció! Kimondható tehát, hogy a képsíkon a fényhullám komplex amplitúdója arányos a pupillafüggvény Fourier-transzformációjával.

Kétdimenziós esetre:

$E (x', y') = \int_{- \infty}^{\infty} \int P (u, v) e^{- i 2 π (u x' + v y')} d u d v$

(1.57)

A képsíkon egy pont képének intenzitását úgy kaphatjuk meg, ha az amplitúdót ismerjük, hogy azt négyzetre emeljük, pontosabban, a komplex amplitúdó ismeretében

$I (x' y') = E (x', y') E * (x', y')$

E*(x’,y’) az E(x’,y’) komplex konjugáltját jelenti.

Mivel az optikai átviteli függvény a pontszórásfüggvény Fourier-transzformáltja,

$O T F (v) = \int_{- \infty}^{\infty} \int I (x', y') e^{- i 2 π (v x' + μ y')} d x' d y'$

A behelyettesítéseket elvégezve egydimenziósan írva:

$O T F (v) = \int_{- \infty}^{\infty} P (u) P * (u) d u$

(1.58)

Miután az ilyen összefüggést autokorrelációnak nevezzük, kijelenthető, hogy az optikai átviteli függvényt a pupillafüggvény autokorrelációjaként is előállíthatjuk.

1.7.5. Aberrációmentes optikai rendszer átviteli függvénye

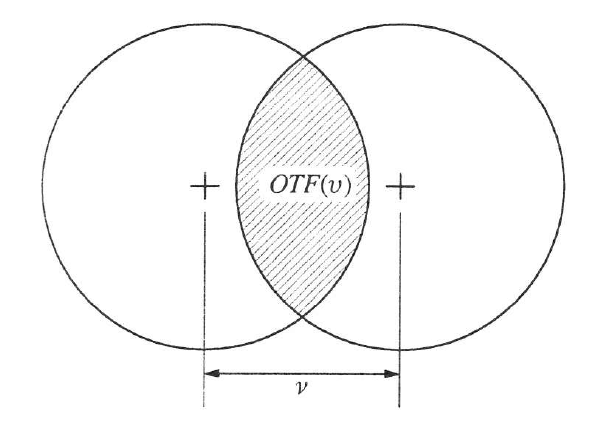
Ha az optikai rendszer aberrációmentes, akkor W(u,v) hullámaberráció zérus, az $e^{- i \frac{2 π}{λ} W (u, v)}$ tényező egységnyi lesz, tehát P(u,v) kivihető az integrál jel elé. Az integrálandó függvény ekkor a pupilla területének és önmagával eltolt területének az 1.28. ábra szerinti metszete lesz az eltolás mértékének függvényében. Az eltolás mértéke pedig arányos a térfrekvenciával. (Mindez az autokoreláció miatt van így.)

Látható, hogy ʋ = 0 esetén a terület maximális (ezt tekintjük 1-nek), amikor pedig a két kör érinti egymást, akkor a terület zérus lesz. Ekkor a u = ʋ_határ_. vagyis a felbontóképesség elvi határa így határozható meg.

A függvény jellegét az alábbi összefüggéssel írhatjuk le:

$O T F (v_{r e l}) = \frac{2}{π} (arc c o s v_{r e l} - v_{r e l \sqrt{1 - v_{r e l}^{2}}})$

(1.59)

ahol

	$v_{r e l} = \frac{v}{v_{h a t á r}}$ és $v_{h a t á r} = \frac{1}{λ \frac{f}{D}}$
	$\frac{f}{D}$ a lencse relative nyílása

1.28. ábra - Aberrációmentes rendszer átviteli függvényének szemléltetése

1.29. ábra - Aberrációmentes rendszer átviteli függvénye

Kör Alakú apertura esetén

$v_{h a t á r} = \frac{1}{1,22 λ \frac{f}{D}}$

(1.60)

1,22 az elsőfajú Bessel-függvény miatt kerül be.

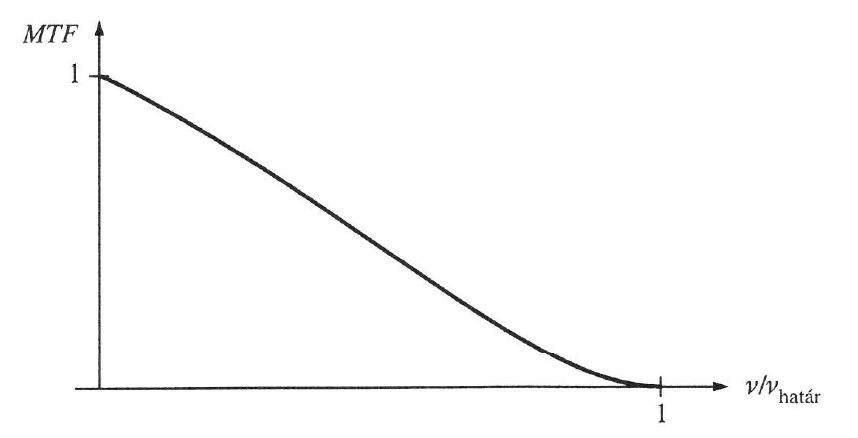
Az 1.29. ábra az aberrációmentes optikai rendszerek átviteli függvényét mutatja. Mivel a vízszintes tengely relatív koordinátájú, ebben ábrázolva az összes tengelyszimmetrikus optikai rendszer egyetlen függvénynyel ábrázolható.

Az (1.30. ábra) ábrán különböző mértékben rekeszelt optikai rendszer modulációs átviteli függvényei láthatóak.

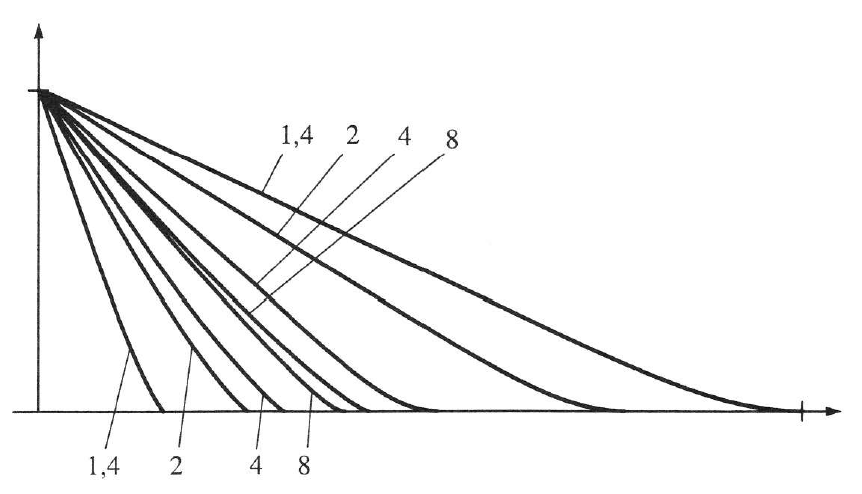
1.30. ábra - Aberrációval terhelt és aberrációmentes rendszerek átviteli függvényei a rekeszelés függvényében

Feltüntettük az egyes rekeszállásoknak megfelelő aberrációmentes átviteli függvényeket is. Mint látható, két ellentétes folyamat játszódik le rekeszeléskor: egyrészt javult a rendszerek átviteli függvénye, hiszen kizáródnak a szélső nyalábok, csökken az abberáció, másrészt romlik az adott rekesznek megfelelő aberrációmentes átviteli függvény. Az adott objektívnél 8-os rekeszértéknél összesimul a valós és az aberrációmentes átviteli függvény. Ha tovább rekeszelünk, akkor már csak romolhat a rendszer, hiszen az aberrációmentes függvény romlik, a valós pedig nem lehet jobb nála. Minden objektívnél van egy olyan rekeszérték, amelynél előáll ez a helyzet.

Miután az aberrációmentes rendszereknél a képminőséget csak a diffrakció korlátozza, az ilyen rendszereket diffrakciókorlátozott, vagy diffrakciólimitáló rendszerekként is említi az irodalom.

1.7.6. Sorba kapcsolt rendszerek átviteli függvénye

Összetett rendszereknél az eredő átviteli függvény az integrál alatt összeszorzódik a két rendszerre:

$O T F (v) = \int_{- \infty}^{\infty} \int P_{1} (u, v) P_{1}^{*} (u, v) P_{2} (u, v) P_{2}^{*} (u, v) d u d v$

(1.61)

Négy esetet különböztetünk meg:

Az egyes rendszerek aberrációmentesek. Ekkor a W(u,v) hullámaberráció zérus, ezért az imaginárius tag elmarad, a határtérfrekvenciát a legkevésbé fényerős rendszer ʋ határa szabja meg, de a nagyobb fényerejű nem rontja az eredményt.
Az egyes rendszerek aberrációval terheltek, ilyenkor minden elemi rendszer hat az eredőre.
A hullámaberációk a kitevőben algebrailag összegződnek (tehát javíthatják is egymást).
Ha az egyes összetevő rendszerek között valódi kép jön létre, és azt leképezi a következő rendszer, akkor az MTF-ek összeszorzódnak, a PTF-ek pedig összeadódnak.

Vissza		Előre
Műszaki Optika	Főoldal	2. fejezet - Radiometria – fotometria