2. fejezet - Radiometria – fotometria

A CIE fényerő észlelő egy olyan sugárzást érzékelő eszköz, amelynek relatív spektrális érzékenységi görbéje a V(λ) vagy V’(λ) láthatósági függvénnyel megegyezik, tehát az emberi szem spektrális érzékenységére vonatkoztatott fotometriai mennyiségek és a radiometriai mennyiségek között számszerűen kifejezhető összefüggések vannak [2.4.] . Tehát a radiometriai illetve a fotometriai mennyiségek között a kapcsolatot az emberi szem spektrális érzékenysége teremti meg.

Más szóval ez azt jelenti, ha a fényforrások által kisugárzott fényben megjelelő energia terjedésének törvényeit vizsgáljuk, akkor azt a radiometria eszközeivel tesszük. Ha figyelembe vesszük azt, hogy az emberi szem a különböző spektrális összetételű, de azonos teljesítményű fényforrásokat másképpen érzékeli, akkor a jelenségeket a fotometria fogalmaival írjuk le, tehát a fotometriában a fény energetikai jellemzőinek meghatározásakor tekintetben vesszük az emberi szem spektrális érzékenységét is, és a méréseket etalon fényforrásra vezetjük vissza [2.19.] .

A geometria eszköztárában a szög fogalma két egymást metsző egyenes egymástól való elhajlását jelenti. E két egyenes metszéspontja körül behúzott egységnyi sugarú kör területén a két egyenes által kimetszett l hosszúságú ívdarabbal, azaz ívmértékkel magát a szöget jellemezzük [2.4.] . Nem egységnyi, hanem R sugarú kör esetén a szög

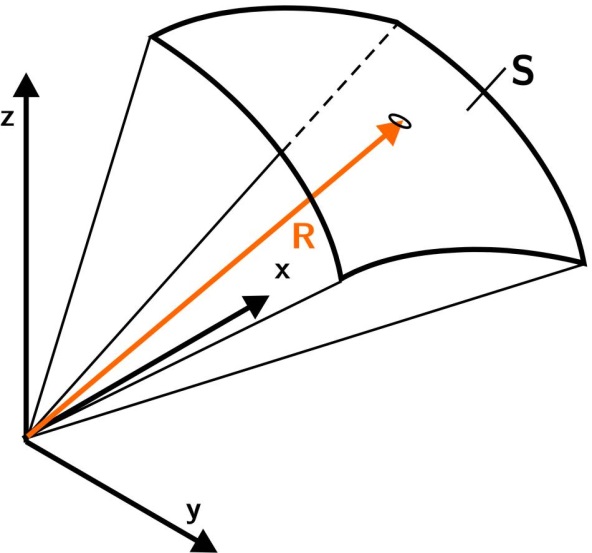
Az SI-rendszer szerint tehát a síkszög egysége a radián.

Ha az előzőek analógiájára értelmezzük egy R sugarú gömbből kimetszett S felület és egy gömb sugara négyzetének arányát, akkor eljutunk a térszög fogalmához, melynek mértékegysége a szteradián.

Egységnyi sugarú gömb esetén a lehetséges legnagyobb, az egész teret befogó térszög mértéke 4π szteradián.

Tapasztalati tények alapján állítható, hogy a fénynyalábban energia áramlik, és ezen energia áramlásának irányát a fénysugarak iránya adja meg. A fényforrások által kisugárzott fény a látható összetevő mellett láthatatlan sugárzást is tartalmaz, így a teljes sugárzási energiának csak egy része a látható fény által szállított fényenergia [2.12.] .

A „fény” szót használják a látható tartományon kívül található optikai sugárzás megnevezésére is, azonban szigorú értelemben a fény a CIE fénymérő észlelő szerint súlyozott sugárzás.

Ha valamely főnyaláb adott metszetén dt idő alatt dW _e sugárzási energia, illetve dW _v fényenergia áramlik át, akkor a teljesítmény jellegű

sugárzási teljesítményt (energiaáramot), illetve a

fényáramot tudjuk definiálni.

A sugárzási teljesítmény mértékegysége a watt, a fényáramé a lumen.

A sugárerősség a sugárforrást elhagyó, az adott irányt tartalmazó dΩ térszögben terjedő dΦ _e sugárzott teljesítmény és a dΩ térszög hányadosa:

Egysége a W⋅sr ^-1

Fotometriai értelemben ezzel analóg mennyiség a fényerősség, amely a fényforrást elhagyó, az adott irányt tartalmazó dΩ térszög hányadosa:

Egysége a candela = lumen⋅sr^-1. A candela (cd) az SI-rendszer alapmértékegysége, és definíció szerint olyan fényforrás fényerőssége adott irányban, amely 540⋅10¹² Hz frekvenciájú monokromatikus fényt bocsát ki, és sugárerőssége ebben az irányban 1/683 watt/szteradián, azaz a fekete sugárzó 1/600000 cm²–nyi felületének fényerőssége a felületre merőleges irányban, a platina dermedési hőmérsékletén, 101325 Pa nyomáson.

A sugársűrűsség adott irányban az Ie sugárerősségnek és a dS felületelem látszólagos nagyságának, a dScosν vetületnek a hányadosa és mértékegysége W⋅m^-2⋅sr^-1.

A fénysűrűség, a fényforrás felületi fényessége vagy világossága adott irányban, az Iv fényerősségnek és a dS felületelem látszólagos nagyságának, a dScosϑ vetületének hányadosa,

Mértékegysége a cd⋅m ^-2 . Használatos még a stilb (sb) egység is, amely 1 cd/cm ² , s ebben a gyertya fénysűrűsége kb. 1 sb, a Napé derűs időben kb. 10⁵ sb.

A besugárzott teljesítmény a felület egy adott pontján az oda beeső dΦ _e sugárzási teljesítmény és a felületelem dS területének a hányadosa

Egysége a W⋅m^-2.

A megvilágítás a felület egy adott pontján az oda beeső dΦ _e sugárzási teljesítmény és a felületelem dS területének a hányadosa

Egysége a lux = lm⋅m^-2.

Azt a fény- vagy sugárforrást, melynek méretei a forrás és az érzékelő közötti távolsághoz képest kicsik, pontszerű forrásnak nevezzük. Az ilyen források fényét a geometriai optika egyenesekkel, a fénysugarakkal jellemzi. A pontszerű fényforrás által keltett árnyékok kontúrvonala éles, kemény. Ilyen forrásnak tekinthető a Nap, az ívfény, a fény szóródását biztosító, bura nélküli izzó.

Pontszerű fényforrások alkalmazása esetén a fényforrás és a felület megvilágítási viszonyaira a távolságtörvény a jellemző, mely szerint pontszerű fényforrás esetén a fényforrás megvilágítása a felülettől való távolság négyzetével arányosa csökken.

A pontszerű sugárzók kemény fényével ellentétben definiálhatók olyan források, melyek lágy fényt sugároznak. Az ilyen típusú sugárzást nevezzük szórt vagy diffúz fénynek. Tulajdonsága, hogy az árnyékhatás jelentéktelen. Nem érvényesek rá a pontszerű fényforrások törvényszerűségei. Az ideálisan diffúz felület az ún. Lambert-féle felület, amit a Lambert-féle koszinusztörvény jellemez. E törvény kimondja, hogy a visszaverő felület fényerőssége a felület normálisával bezárt szög koszinuszával arányos.

Az ábra alapján könnyen belátható, hogy a fénysűrűség azért állandó bármely irányból tekintve, mert a csökkentett intenzitást egy szintén a szög koszinuszával arányosan csökkenőnek látszó felület sugároz ki.

A radiometriai és fotometriai  mérések célja a fény által transzportált energia, vagy a sugárzási teljesítmény számszerű kiértékelése. A sugárzásdetektorok három fő csoportra oszthatók, aszerint hogy működésük a fény melyik fizikai hatásán alapszik [2.17.] .

A fotometria legfontosabb feladata különböző fotometriai mennyiségek: a fénysűrűség, a megvilágítás, a fényáram és a fényerősség mérése. Ha a mérést a szemünkkel végezzük, akkor vizuális vagy szubjektív fotometriáról, ha azonban valamilyen fényre érzékeny eszközzel, akkor fizikai vagy objektív fotometriáról beszélünk.

Az emberi szem a fényerősség mértékének abszolút meghatározására alkalmatlan, azonban két szomszédos felület fényerősségének összehasonlítását nagy biztonsággal tudja elvégezni. A vizuális fotométerek egy tipikus példája a Ritchie-féle fotométer. Egy derékszögű szimmetrikus gipszprizmát egyik oldalról egy ismert fényerősségű forrás világít meg adott távolságról. A prizma másik oldalán elhelyezkedő, ismeretlen fényerősségű forrásprizmától mért távolságát addig változtatjuk, míg a prizma két oldalát vizuálisan egyenlő világosnak nem találjuk. Ilyenkor a prizma éle gyakorlatilag láthatatlanná válik. Ha a források méreteikhez képest nagy távolságban helyezkednek el, akkor a távolságtörvény alapján az ismeretlen fényerősség meghatározható [2.4.] .

Objektív fotometriáról akkor beszélünk, ha a szem helyett a sugárzásmérést egy érzékelő mérő-eszközre bízzuk, és az általa szolgáltatott jelet értékeljük. Mivel ezek az érzékelő eszközök az elektromágneses spektrum látható, infravörös és ultraibolya részében is érzékenyek, ezért itt fotometria helyett optikai sugárzásmérésről beszélhetünk. A sugárzásmérő eszközök (detektorok) a fizikai működés szempontjából három fő csoportra oszthatók – hő, fényelektromos és fotográfiai hatáson alapulókra.

Ha a sugárzás időben állandó és kellően intenzív, akkor teljesülnek a kalorimetrikus sugárzásmérési módszer feltételei. A termoelemes sugárzásmérés esetén a termoelem forrasztási pontjára ható sugárzás eredményeként keletkező termofeszültség – mely galvanométerrel mérhető – arányos a sugárzási teljesítménnyel.

A termoelem helyett elterjedtebben alkalmazzák a termooszlopokat. A termooszlop tulajdonképpen több, sorba kapcsolt termoelem, így a termoelemeken megjelenő feszültségek összege mérhető.

Egy fekete fémlapba termoelemes hőmérő illetve elektromos izzítást lehetővé tevő izzószál van beépítve. A fekete fémlap a ráeső sugárzás hatására melegedni kezd. Adott idő után a sugárzás hatására felvett, illetve a hő veszteség által leadott hő egyensúlyba kerül, a fémlap állandó hőmérsékletet vesz fel. A mérendő sugárzás kiiktatása után a fémlapot a benne elhelyezett fűtőszál segítségével az egyensúlyi hőmérsékletre hevítjük fel. A bevezetett elektromos teljesítmény egyenlő a felvett sugárzási teljesítménnyel. Így a fűtőszálba bevezetett elektromos áram erősségéből, illetve a feszültségből meghatározható a sugárzási teljesítmény abszolút mértéke. A platina- vagy félvezetőlemezkék, melyek a sugárzás hatására létrejövő felmelegedés miatt megváltoztatják vezetőképességüket a bolométeres sugárzásmérést teszik lehetővé [2.20.] .

Mivel a bolométerek a mérőáramkörökben mint ellenállások működnek, külön figyelmet kell szentelni a feszültség-áram-karakterisztikájuknak. A kis áramok tartományában a jelleggörbéjük közel lineáris, közel ohmos terhelést képviselnek. Az áram növekedésével azonban a keletkező hő visszahat az elemre, fokozatosan eltér a lineáris karakterisztikától, majd egy maximumérték után az áram növekedését csökkenő feszültség kíséri, ezt negatív ellenállású tartománynak nevezzük. A bolométereket mérési célokra általában a lineáris tartományban használják. Az érzékelő lemezeket kiegyenlíthető hídba kapcsolva alkalmazzák. A gyakorlatban három fő típusukat különböztetik meg, a fém bolométereket, a félvezető bolométereket, illetve a szupravezető bolométereket.

A Golay-cella alkalmazása esetén, a sugárzás hatására felmelegedő cella a hőjét a gáznak átadva, közvetve a gáz hőtágulása révén membrán deformációt hoz létre, mely mérhető. A Golay-cellák a legérzékenyebb sugárzásdetektorok közé tartoznak.

Gyakran nevezik pneumatikus sugárzásdetektornak, mivel a gázhőmérővel azonos elven működik. A gyakorlatban a Golay-detektorok egy kis hővezető-képességű, gázzal töltött cellából állnak. A cella egyik oldalán egy alkalmasan megválasztott abszorpciójú filmréteg van, a túloldalán pedig az ún. membrántükör helyezkedik el. A cellában elhelyezett gáz a sugárzás hatására megváltoztatja térfogatát, és a tükröt elmozdítja. A detektor részét képezi egy optikai rendszer is. A fényforrásból kilépő fényt egy kondenzor egy rácson keresztül a tükörre juttatja. A rács és a tükör között elhelyezkedő optika a fényt úgy fókuszálja, hogy a rács egyik felének a képe fedje a másik felének a képét, ha nincs membrábdeformáció. A deformáció bekövetkezte után a rács elmozdul, ez a kondenzátor túloldalán fényváltozást eredményez.

A fényelektromos hatás elvén működő sugárzásmérők alapeszközei a fényelemek, a fotoellenállások, fotodiódák és a fotocellák. A fényelemek tulajdonképpen pn-n átmenetet tartalmazó fotodetektorok. A megvilágított pn-n átmenet áramforrásként szerepel, energiáját a gerjesztett töltéshordozópárok szétválasztásából és felhalmozódásából kapja. A fotoellenállás működésének alapja az, hogy a sugárzás hatására többlet-töltéshordozók keletkeznek, amelyek hatással vannak a kristály vezetőképességére. A CdS, illetve a CdSe fotoellenállások nagy előnye, hogy érzékenységi görbéjük nagyon jól megközelíti a szem érzékenységi görbéjét. Emellett azonban rendelkeznek hátrányos tulajdonságokkal is. Ezek közé tartozik a nagy időállandó és az úgynevezett drift.

A fotodiódák és a fényelemek szerkezeti kialakításukat tekintve szinte megegyezők. Alapvető különbség az üzemeltetés módjában van. A zárófeszütséges, fotodióda üzemmódban a pn-n átmenet ellenállása nagy lesz. Ebben az esetben mérhető a megvilágítás hatására fellépő fotoáram. A fotodióda-üzemre a viszonylag gyors működés a jellemző. A gáztöltésű fotocellákat szintén széles körben alkalmazzák sugárzásmérésre. A fotoáram arányos a katódra eső sugárzás teljesítményével. Az egyszerű fotocella helyett a gyakorlatban úgynevezett elektronsokszorozó fotocellákat alkalmaznak. A mérendő sugárzás hatására a katódból kilépő elektronok a pozitív feszültségű elektródból másodlagos elektronokat váltanak ki. Ez tulajdonképpen azt jelenti, hogy az elektromos válaszjel elcsúszik a megvilágítás intenzitásának függvényében, illetve annak függvényében, hogy a cella a mérést megelőzően mennyi ideig volt megvilágítva. Ha ezt több fokozaton keresztül végezzük, akkor az anódra jutó elektronok száma elérheti az elsődlegesek számának 10⁸ szorosát is.

A fotográfiai hatáson alapuló sugárzásmérés alapgondolata az, hogy egy fotográfiai réteg expozíciója és az előhívott kép optikai denzitása között jól definiálható összefüggés van. Az expozíció a megvilágítás és az expozíciós idő szorzata [2.16.] .

Ha egy optikai közegre fényt bocsátunk, annak egy része a közegen áthatol, egy másik része elnyelődik, a maradék pedig visszaverődik. Ennek megfelelően értelmezni tudunk egy transzmissziós vagy áteresztési tényezőt, amely az áteresztett és a beeső sugárzott teljesítmények vagy fényáramok aránya. Ebből származtatott mennyiség a denzitás vagy feketeség, amely az áteresztési tényező reciprok értékének 10-es alapú logaritmusa.

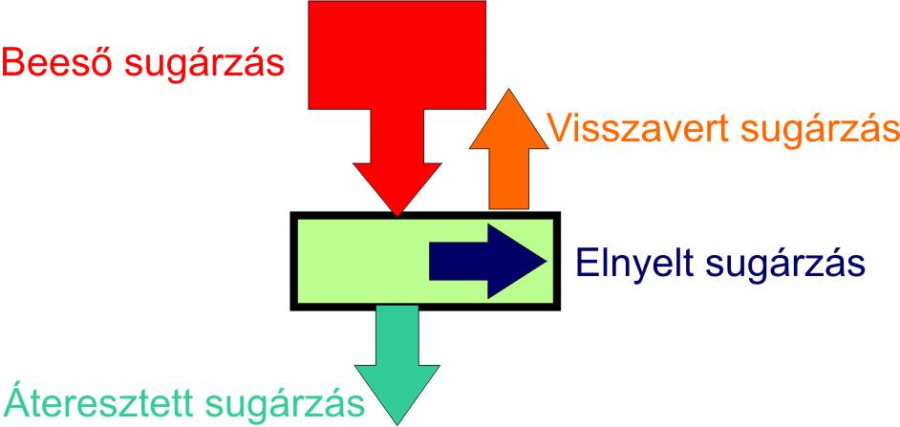
τ az áteresztési tényező.

A jelleggörbe függőleges tengelyén az optikai denzitás látható, míg a vízszintes tengelyen az expozíció logaritmusa. A görbén rendre a következő szakaszok különböztethetők meg. Az alapfátyol a nyersanyagon az elérhető legkisebb denzitást jelöli. A lineáris szakasz alatt található az alsó könyök, felette pedig a felső könyök. A felső könyök után a görbe eléri a maximumát, ami azt a denzitást jelöli, amely a nyersanyaggal maximálisan elérhető. Innen az expozíció növelésével a denzitás csökken, ez a szolarizáció szakasza. A görbének egy jellemző paramétere a lineáris szakasz meredeksége, a gamma-érték. Egy ezüsthalogén alapú fekete-fehér nyersanyag kidolgozása a hívásból és a rögzítésből áll. Ha exponált és kidolgozott fotografikus nyersanyag egy adott pontjára fénynyalábot bocsátunk, megmérjük a bebocsátott illetve az áteresztett fényáramokat, ezekből kiszámíthatjuk a denzitást. Mivel a nyersanyag feketedése számos tényezőtől függ, ezért abszolút intenzitásmérésre nem alkalmas, azonban ha két azonos fénynyaláb ugyanazon a fotográfiai nyersanyagon, azonos expozíciós idők mellett azonos feketedést eredményez, akkor a két nyaláb intenzitása azonos.

A denzitométerek segítségével lehet az áteresztési tényezőt, illetve a denzitást meghatározni. A gyakorlatban alkalmazott denzitométerek működési elv szempontjából két csoportba oszthatók. A közvetlen leolvasásúak esetében a vizsgálandó lemezen áthaladó fény az elektromos érzékelő jelét megváltoztatja, s így a változást közvetlenül leolvashatjuk. Az összehasonlító elven működők kétsugaras berendezésekben a mérendő és az összehasonlító fényáram összehasonlításából lehet következtetni az ismeretlen minta denzitására [2.16.] .

Logikusnak tűnik, hogy a fotometriai mennyiségek tárgyalásánál azok mérésénél a fénynek az emberi szemre gyakorolt hatását vegyük alapul. Ennek azonban az a hátránya, hogy szemmel a fotometriai mennyiségeket nem tudjuk számszerűen meghatározni, mivel a szembe jutó fényáram és a detektált fényérzet nem arányos egymással. Amellett, hogy a fényérzetet még számtalan fizikai és szubjektív paramétertől függ, probléma az is, hogy a növekvő fényárammal szem érzékenysége jelentősen csökken. Kihasználható előny viszont, hogy az emberi szem nagy biztonsággal tudja meg különböztetni a megvilágításbeli különbségeket, melyekre igen érzékeny. Két azonos tulajdonságú felület azonos színű megvilágítása mellett, az ember szemmel történő megfigyeléssel képes eldönteni a megvilágítások bizonyos határon belüli egyezőségét. Ez az izokromatikus fotometria alapgondolata, és a fent leírtaknak megfelelően, úgynevezett kiegyenlítő mérési módszerek alkalmazását teszi lehetővé [2.18.] . Az eltérő szerkezeti és elvi kialakítású izokromatikus fotométerekben ezen kiegyenlítés történhet polarizációs szűrőpárokkal, fényhatároló rekeszekkel, forgótárcsákkal, szürke ékekkel, de lehetséges pusztán a távolságtörvény megfelelő alkalmazásával is. Ebben az esetben merőleges beesésnél az a távolságra levő I ₁ fényerősségű és az b távolságra elhelyezett I ₂ fényerősségű fényforrások akkor eredményeznek egyenlő megvilágítást, ha

Ismerve az egyik fényerősséget és a hozzá tartozó távolságot, a másik távolság megfelelő változtatásával a keresett fényerősség meghatározható.

Probléma léphet föl két különböző színű fény összehasonlításakor, mivel az izokromatikus fotometria módszerei csak nagyon kis mértékű színkülönbség esetében alkalmazhatók [2.18.] . Ilyenkor válik szükségessé a heterokromatikus fotométerek alkalmazása, mint amilyen például a gyakran alkalmazott, és széles körben elterjedt villogásos fotométer. Alkalmazása során egy felületet felváltva világítanak meg két különböző színű, és erősségű fénnyel, amit a szem érzékel. A szemet érő fény villogtatásának frekvenciájának növelésével egy keverékszín válik érzékelhetővé. Az egyik fényforrás fényáramát addig szabályozzák, míg a fényvillogás meg nem szűnik, ilyenkor a megvilágítások értékei azonosak.