3. fejezet - Fényforrások
Vissza		Előre

3. fejezet - Fényforrások

Tartalom

3.1. A fényforrások működését leíró alapfogalmak és törvények
3.2. A sugárzás fontosabb törvényei
3.3. A Planck-törvény
3.4. A Wien-törvény
3.5. Rayleigh–Jeans-törvény
3.6. A Stefan-Boltzmann-törvény
3.7. Nem abszolút fekete-test jellegű sugárzók
3.8. A Kirchhoff törvény
3.9. Fényforrások hatásfoka
3.10. Fénykibocsátás az abszolút fekete test sugárzása alapján
3.11. A Nap sugárzása
3.12. Izzólámpák
3.13. Elektromos kisülés gázokban
3.14. Gázkisülő lámpa
3.15. Nagyintenzitású ívlámpák
3.16. Ellenőrző kérdések
Felhasznált irodalom

Optikai rendszerek tervezésekor alapos vizsgálat alá kell venni a rendszerben alkalmazott fényforrásokat is, hiszen az optikai rendszer többi elemének tervezése nagymértékben függ az alkalmazott elektromágneses sugárzás hullámhosszától és intenzitásától. A fény keletkezését, elektromágneses hullám lévén, az elektromos töltések sebességváltozása okozza. A mindennapi életben fellelhető fényforrások nagyobbik részénél több-kevesebb pontossággal alkalmazhatók is az elektronok rezgésére és keringésére vonatkozó elméletek, azonban a fénykibocsátás leírásának pontosabb elméleteinél figyelembe kell vennünk a fény részecsketermészetét és a kvantummechanika törvényszerűségeit is.

A leggyakrabban előforduló fényforrások általában az alábbi két nagy csoport egyikébe sorolhatók, bár a csoportok között nincs éles határvonal:

Termikus fényforrások esetében a fénykibocsátás a magas hőmérséklet eredménye.
Elektromos kisülés gáztéren keresztül, amikor a fénykibocsátás a feszültség hatására létrejövő ionizációk és ütközések eredménye.

A fényforrások egy speciális típusával, a lézerrel egy másik fejezet foglalkozik.

3.1. A fényforrások működését leíró alapfogalmak és törvények

A testeket sugárzáshoz való viszonyulásuk alapján a következőképpen csoportosíthatjuk [3.1.] :

Ha α = 1, akkor ρ = 0 és τ = 0.

Ez esetben a test a ráeső sugárzó energiát teljesen elnyeli. Az ilyen testeket abszolút fekete testnek, vagy egyszerűen fekete testnek nevezik.
Ha ρ = 1, akkor α = 0 és τ = 0.

Ez azt jelenti, hogy a test a ráeső sugárzó energiát teljesen visszaveri. Ha a visszaverődés szabályos, akkor a test tükröző. Ha a visszaverődés diffúz, a testet abszolút fehér testnek nevezzük.
Ha τ =1, akkor α = 0 és ρ = 0.

Ilyenkor a teljes sugárzó energia áthalad a testen, az ilyen test átlátszó.

Az abszolút fekete test viselkedését jól modellezi a falán kis nyílással ellátott üreges test. Az üreg nyílásánál az abszorpciós tényező közel egységnyi, azaz a nyílásra eső, és azon belépni szándékozó sugárzás energiája az üregbe bejutva, azon belül szinte teljesen elnyelődik [3.1.] .

3.2. A sugárzás fontosabb törvényei

A fizikai törvényszerűségeiről a legrégebbi ismereteink természetesen azokról a területekről származnak, ahonnan a legkönnyebb volt pontos mérési eredményeket szerezni. Ezek közé tartozik a tér, idő, a mozgás és a hő. Az is könnyen belátható, hogy törvényszerű összefüggések megkonstruálása legelőször azoknál a jelenségeknél sikerült, amelyek megfigyelhető lefolyása gyakran a külső, kísérő körülményektől és beavatkozásoktól függetlenül folyt. A megfigyelt fizikai törvényt, már a kezdeti időktől rendszerint egy matematikai formulában próbálták kifejezni. Ez biztosította, és tette lehetővé, hogy az általunk választott feltételek mellett végbemenő folyamatokat, adott körülmények között előre tudjuk meghatározni, időbeli lefolyásukat pedig a lehető legpontosabban kiszámítani. Az érvényes a sugárzást leíró törvényszerűségekre is, melyek összefüggéseit sok spontán megfigyeléssel, tervezett kísérleti vizsgálattal igyekeztek leírni. Megjegyzendő, hogy az alábbiakban ismertetésre kerülő általános törvényszerűségeket természetesen csak az abszolút fekete test által kibocsátott vagy elnyelt sugárzásra lehet értelmezni, érvényességük pontosan csak légüres térben végbemenő sugárzásokra vonatkozik, más, például gáznemű közegekben végbemenő sugárzás esetében csak jó közelítésnek tekinthetők [3.4.] .

3.3. A Planck-törvény

Max Karl Ernst Ludwig Planck (1858 –1947) Nobel-díjas német fizikus, a kvantummechanika megalapítója. Gyermekkorát Kielben és Münchenbe töltötte, egyetemi tanulmányai során a kor hírességeinek előadásait hallgathatta, olyanokét, mint Hermann von Helmholtz, Gustav Kirchhoff, valamint Karl Weierstraß. Magánúton tanulmányozta Rudolf Clausius feljegyzéseit, ennek a köszönhető, hogy érdeklődése a hőtan felé fordult. 1879-ben nyújtotta be doktori disszertációját „A mechanikai hőtan második főtétele” címmel, majd 1880-ban a habilitációs értekezését „Izotróp testek egyensúlyi állapota különböző hőmérsékleteken” címmel. 1889-ben Helmholtz közbenjárásával Berlinbe hívták, hogy Kirchhoff utóda legyen, ahonnan 1926-ban vonult nyugdíjba; az ő utóda Erwin Schrödinger lett. 1894-ben kezdett a Kirchhoff által már 1859-ben megfogalmazott feketetest-sugárzás problémájával foglalkozni. A klasszikus fizikára alapozva levezetett Rayleigh-Jeans-törvény a magas frekvenciákon nem illeszkedett a mérési eredményekhez. A Wilhelm Wien által, és róla elnevezett törvény sem volt kielégítő, hiszen az a magas frekvenciájú eredményeket igazolta, de alacsony frekvenciákon nem egyezett a mérésekkel. Plancknak sikerült tisztán matematikai megfontolásokra alapozva e két törvényt egyetlen összefüggéssel helyettesítenie. 1918-ban elnyerte a Nobel-díjat a plancki hatáskvantum felfedezéséért, amit csak 1919-ben vehetett át. Minden idők egyik legnagyobb fizikusa 1947-ben halt meg; a göttingeni városi temetőben nyugszik.

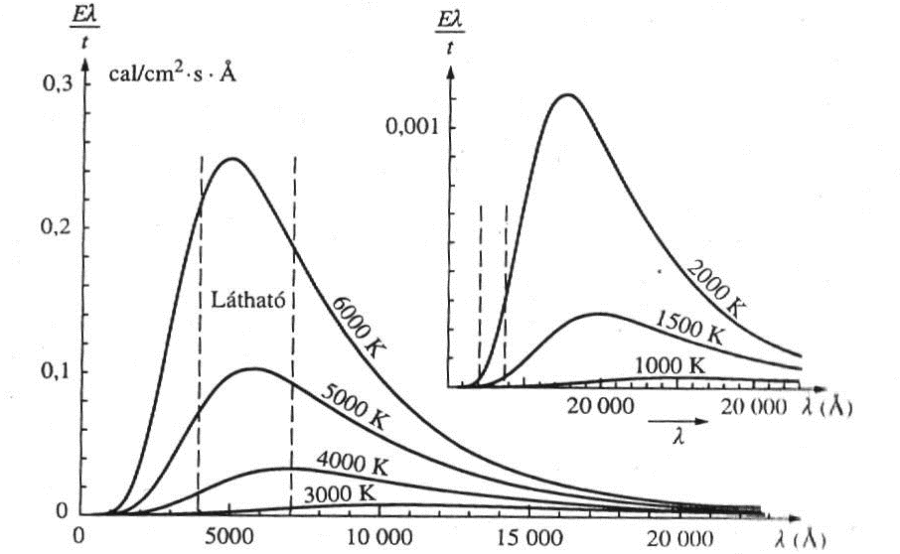
Az E emisszióképesség azt az energiamennyiséget jelenti, amelyet a test egységnyi felülete egységnyi idő alatt a teljes hullámhossz tartományban kisugároz. Emellett azonban rendkívüli jelentőséggel bír annak ismerete, hogy különböző testhőmérsékleteken hogyan változik a kisugárzott energia hullámhossz függvényében.

A Planck törvény segítségével kiszámítható a sugárzás intenzitásának nagysága fekete test esetén, adott sugárzó testre vonatkozó abszolút hőmérséklet és a sugárzási hullámhossz esetén.

$E_{0} = \frac{c_{1} λ^{- 5}}{e^{\frac{c_{2}}{λ T}} - 1}$

ahol a λ a hullámhossz, T a sugárzó test abszolút hőmérséklete, c₁ és c₂ állandók. A c₁ állandó a h=6,626068⋅10^-34m²kgs^-1 Planck-állandó és a c=299792458ms^-1 fénysebesség négyzetének szorzata.

c ₂ állandó az alábbiak szerint határozható meg:

$c_{2} = \frac{c h}{k}$

ahol c=299792458ms^-1, h=6,626068⋅10^-34m²kgs^-1 és k=1,3806503⋅10^-23m²kgs^-2K^-1 az úgynevezett Boltzmann-állandó.

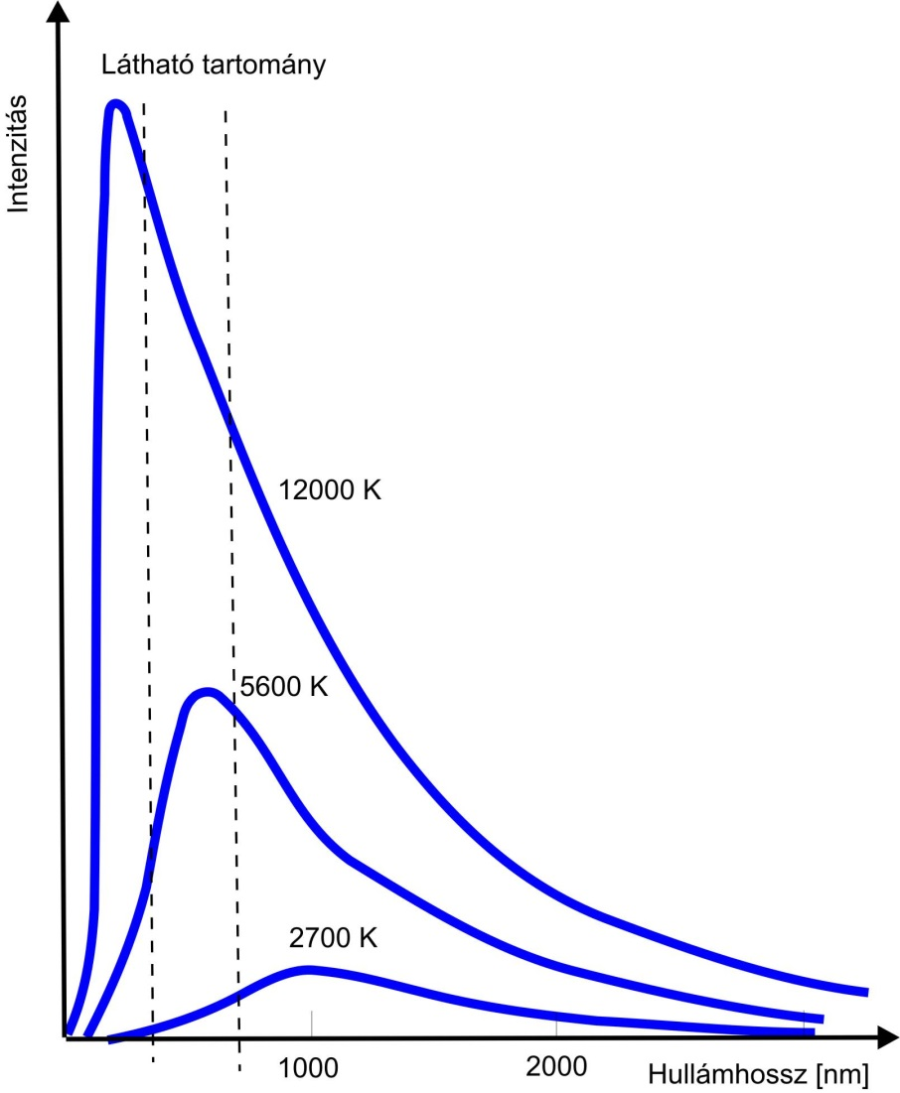
3.1. ábra - A Planck-törvény grafikus ábrázolása

A Planck-törvény ábrájából következtethető, hogy a sugárzás intenzitása a hőmérséklettel nagyon határozottan nő. Az egyes hőmérséklethez tartozó intenzitás-görbék maximumai, növekvő hőmérséklettel csökkenő hullámhosszakat adnak.

3.4. A Wien-törvény

Wilhelm Wien (1864–1928) német fizikus. Munkásságának legjelentősebb része az elektromágnesesség és a hőtan elméletéhez kapcsolódik. A legismertebb, nevéhez fűződő megállapítás a Wien-féle eltolódási törvény, mely a fekete test sugárzásának számítására vonatkozik. A hősugárzás területén végzett munkásságáért 1911-ben Nobel-díjat kapott. Általános iskolai tanulmányait Rastenburgban és Heidelbergben végezte. Egyetemi tanulmányait a göttingeni, majd a berlini egyetemen folytatta. 1883-85 között Hermann von Helmholtz mellett, annak laboratóriumában dolgozott, 1886-ban szerezte meg doktori fokozatát a fémek környezetében bekövetkező fényelhajlási jelenségek vizsgálatával. 1896-1899 között Aachen-i egyetemen adott elő, majd 1900-ban a würzburgi egyetemre került, ahol Wilhelm Conrad Röntgen utóda lett. 1896-ban tapasztalati úton meghatározta a fekete test sugárzási törvényét, ezt róla nevezik Wien törvénynek. Hőtani eredményi csoportjába tartozik továbbá a Wien-féle eltolódási törvény, vagy más néven Wien I. törvénye, mely segítségével egy test emisszióképességének maximális értéke határozható meg. A törvény szerint az abszolút fekete test emisszióképességének hullámhossz szerinti maximumhelye fordítva arányos a termodinamikai hőmérséklettel. Az eltolódási törvény a gyakorlatban is megfigyelhető, egy test fokozatos hevítéséhez tartozó színváltozásával. Alacsony hőmérsékleten a hevített test vöröses színű. A hevítés fokozásával, azaz a hőmérséklet emelésével a test színe fokozatosan változik a világos vöröstől, sárgásfehéren keresztül egészen, a magas hőmérsékleten tapasztalható kékes színig. Wien II. törvénye kevésbé ismert ugyan, azonban jelentősége szintén nagy. A törvény a maximális intenzitásérték hőmérsékletfüggését adja meg, mely szerint annak maximális értéke a hőmérséklet ötödik hatványával arányos.

A Planck-törvény segítségével számszerűen meghatározható a sugárzás nagysága, ha ismeretes a sugárzó test abszolút hőmérséklete és a sugárzás hullámhosszúsága. Wien-törvény kapcsolatot teremt a sugárzó test abszolút hőmérséklete és a sugárzás hullámhosszúsága között, és megmutatja, hogy mekkora a fekete test sugárzás intenzitásának nagysága, adott sugárzó testre vonatkozó abszolút hőmérséklet és a sugárzási hullámhossz esetén.

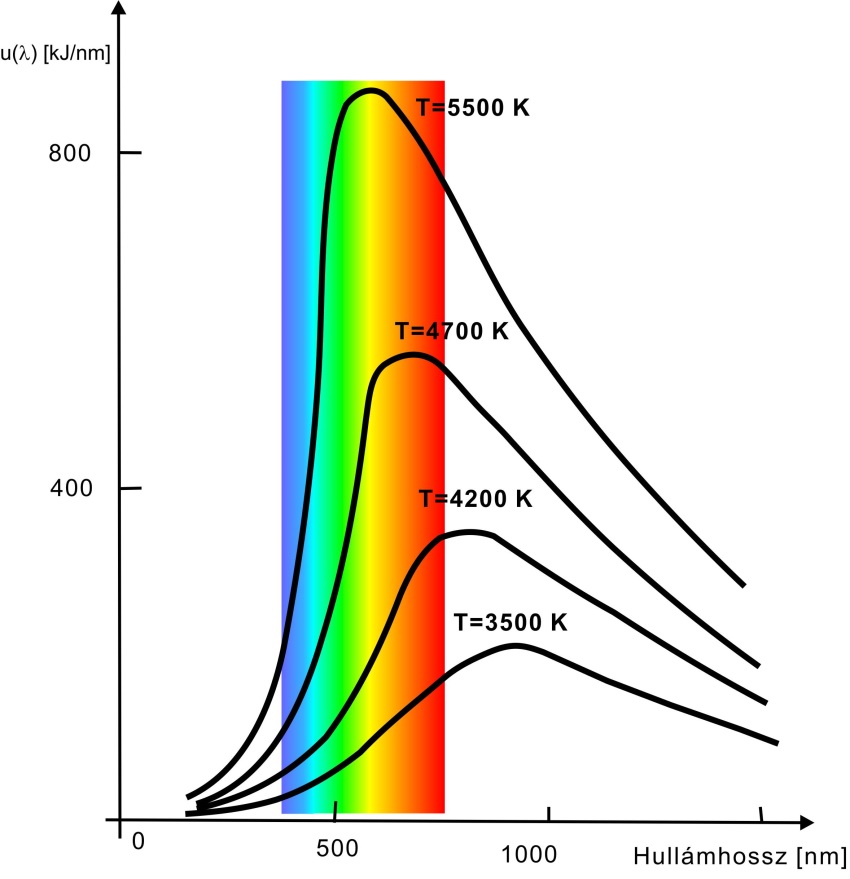
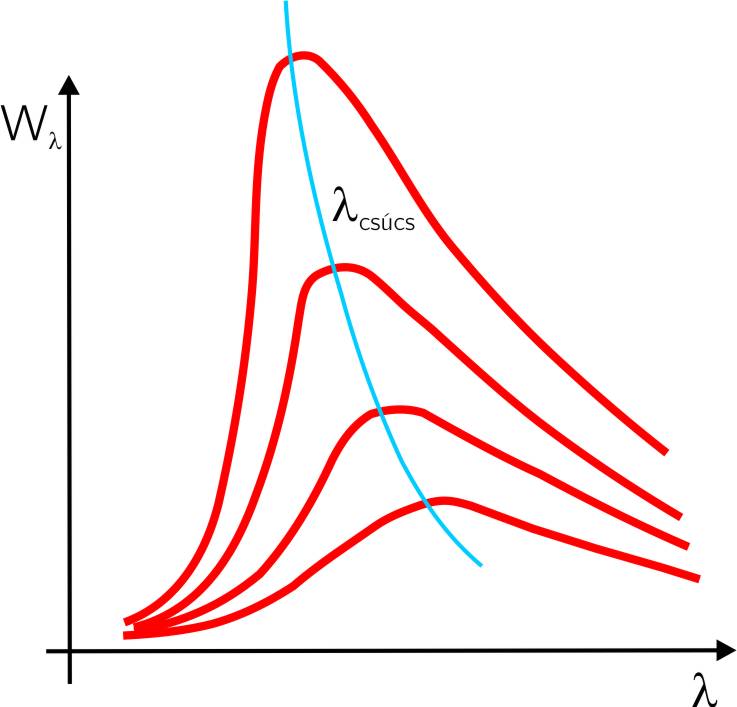
A Wien-törvényt grafikusan ábrázolva látható, hogy azok a hullámhosszak, amelyeknél E₀ maximális értéket ér el, növekvő hőmérséklettel egyre kisebb λ értékek felé tolódnak el. A Wien-törvényből kiadódik a T=állandó görbék szélső értékeinek helye a λ függvényében

$λ_{E_{0} λ_{\max}} T = á l l a n d ó$ ,

vagyis az intenzitás-maximumokhoz tartozó hullámhosszak és a megfelelő abszolút hőmérsékletek szorzata állandó [3.2.] . Ezt nevezik Wien-féle eltolódási törvénynek.

3.2. ábra - A Wien-féle eltolási törvény szemléltetése

3.3. ábra - A Wien-féle eltolási törvény ábrázolása

3.5. Rayleigh–Jeans-törvény

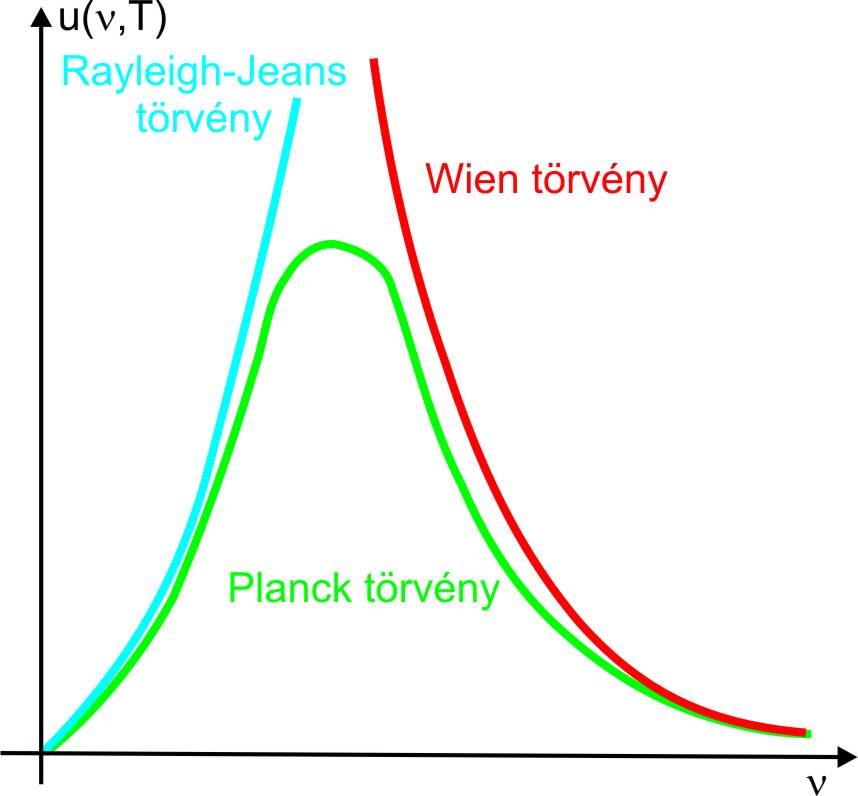
3.4. ábra - Rayleigh–Jeans-törvény és a Wien-törvény

A Wien-törvény csak a sugárzás nagy frekvenciáin írja le helyesen a tapasztalati eloszlást, a frekvenciát csökkentve bekövetkezne az úgynevezett infravörös katasztrófa. Ezzel szemben a Rayleigh–Jeans-törvény csak az alacsony frekvencián követi helyesen a tapasztalati eloszlást; a frekvenciát növelve itt az úgynevezett ultraibolya-katasztrófa következne be. Tehát sem a Wien- törvény, sem a Rayleigh–Jeans-törvény nem adja vissza a tapasztalati intenzitáseloszlást a teljes frekvencia tartományon. Max Planck vizsgálta az energiaeloszlás és az entrópia közti kapcsolatot. A Wien-féle és a Rayleigh–Jeans-féle alakot az entrópia második deriváltja segítségével kombinálta össze, és a Boltzmann-féle termodinamikai valószínűséget alkalmazta, mely eredményeként az ismert, Planck-féle sugárzási formulát kapta, mely a kis frekvenciákra a Rayleigh–Jeans-törvényt, míg a nagyfrekvenciákra a Wien-törvényt adta, és belőle a Stefan–Boltzmann-törvény is levezethető.

3.6. A Stefan-Boltzmann-törvény

Ludwig Eduard Boltzmann (1844–1906) osztrák fizikus. Számos tudományos eredménye közül az egyik legjelentősebb a feketetest-sugárzásra vonatkozó Stefan- Boltzmann -féle törvény megalkotása. Róla nevezték el többek között a Boltzmann-állandót, és a Boltzmann-féle transzportegyenletet. 1863-ban iratkozott a Bécsi Egyetemre, fizikát hallgatott. Külön érdekesség, hogy tanára volt a magyar származású, az optika terén is maradandót alkotó Petzval József is, valamint Josef Stefan, aki irányítása mellett 1866-ban a Bécsi Egyetemen doktori fokozatot szerzett a kinetikus gázelmélet terén végzett vizsgálataival, majd 1867-től az ő asszisztense lett. Josef Stefan (1835 – 1893) szlovén fizikus mérte meg először a feketetest által az összes hullámhosszon kisugárzott energiát. Azt tapasztalta, hogy egy abszolút fekete test kisugárzott összes energiája a hőmérséklet negyedik hatványával arányos. Ezt Boltzmann 1879-ben elméletileg is megalapozta, ezért nevezik az eredményt Stefan-Boltzmann-törvénynek. Számos ismert és nagyhírű egyetemen töltött esztendő után 1893-ban visszatért Bécsbe, hogy egykori mentora, Josef Stefan után az Elméleti Fizikai Intézetének vezetője legyen.

Az abszolút fekete test felületének területegysége által időegység alatt kisugárzott teljes energiamennyiség értéke a Planck-törvény és az összsugárzásra vonatkozó összefüggés felhasználásával:

$E_{0} = \int_{0}^{\infty} E_{0 λ} d λ = \int_{0}^{\infty} \frac{c_{1} λ^{- 5}}{e^{\frac{c_{2}}{λ T}} - 1} d λ$

Az integrálás után

$E_{0} = C_{0} T^{4}$

ahol a C₀=5,67⋅10^-8Wm^-2K^-4 állandó az abszolút fekete test sugárzási együtthatója. A Stefan-Boltzmann-törvény tehát kimondja, hogy a test egységnyi felületéről időegység alatt kisugárzó összes energia a sugárzó test abszolút hőmérsékletének negyedik hatványával arányos.

3.7. Nem abszolút fekete-test jellegű sugárzók

A Stefan-Boltzmann-törvény csak abszolút fekete testre vonatkozik, de átalakítással szürke testekre is alkalmazható. Ebben az esetben:

$E_{0} = ε C_{0} T^{4}$

A ε < 1 relatív emisszióképesség, vagy más néven a test feketeségi foka mindig kisebb, mint a fekete testé. Nyilvánvaló, hogy egy valós test viselkedése eltér az abszolút fekete testétől.

3.8. A Kirchhoff törvény

Gustav Robert Kirchhoff (1824–1887) német fizikus. Egyetemi előadói karrierjét1847-ben kezdte a Berlini Egyetemen, majd három évvel később már a fizika rendkívüli tanára a Breslaui Egyetemen. A Heidelbergi Egyetemre fizikaprofesszorrá1855-ben nevezték ki, itt született Bunsennel közösen a színképelemzés módszere. 1845-ben közölte a róla elnevezett Kirchhoff-törvényeket, melyek segítségével lehetséges villamos hálózatokban az áram, a feszültség és az ellenállások számítása. 1859-ből származik a sugárzási törvénye, mely szerint bármely testnél egy adott hullámhosszon és hőmérsékleten a spektrális emisszióképesség és az abszorpcióképesség hányadosa állandó. 1875-től a Berlini Egyetem matematikai fizika professzora.

Kirchhoff törvénye a test emisszióképessége és abszorpcióképessége, azaz elnyelőképessége között állapít meg összefüggést [3.2.] . Kirchhoff törvénye a fentiek alapján tehát a következőképpen is megfogalmazható: Az emisszióképesség és abszorpcióképesség viszonya minden testre vonatkozóan ugyanakkora és csak az abszolút hőmérséklet függvénye egyben egyenlő az abszolút fekete test ezen hőmérsékletéhez tartozó emisszióképességével. Kirchhoff törvénye nem csak a teljes sugárzásra vonatkozólag adható meg, hanem a részsugárzásra is alkalmazható, s ez esetben az alábbi formában fogalmazható meg: Egy adott hullámhosszhoz tartozó emisszóképességnek és az ugyanazon hullámhosszhoz tartozó abszorpcióképességhez az aránya valamennyi testre nézve azonos, és ez az arány csak a hullámhossz és a hőmérséklet függvénye.

3.9. Fényforrások hatásfoka

A fényforrások jelentős részénél a kisugárzott energiának csak kis része esik a látható fény tartományába. A nagyobbik rész a világítás szempontjából elvész, így a hatásfok alacsony marad. A fénykibocsátás gazdaságosságának megítélésekor figyelembe kell venni az emberi szem spektrális érzékenységét is. A fotometriával, illetve radiometriával fogalakozó fejezetben megismert összefüggések alapján a szem legnagyobb érzékenységének megfelelő zöld színnél azt találjuk, hogy a fény teljesítmény-egyenértéke 680 lumen/watt. Vagyis ennyi lenne az elérhető legnagyobb fényhasznosítás, ha a forrás csak ezen az egy hullámhosszon sugározna. A valós helyzet ennél sokkal rosszabb, pl. egy 30 wattos izzó fényhasznosítása csak kb. 2%. A világítástechnika fejlődésében a fentiek alapján a nagyobb hatásfok elérése érdekében egyre nagyobb hőmérsékletű termikus sugárzókat használunk, amelyek energiájuk jelentős részét a látható tartományban bocsátják ki. Ezek többnyire gázkisüléseken, illetve lumineszcencián alapulnak.

3.10. Fénykibocsátás az abszolút fekete test sugárzása alapján

A folyamatos spektrális eloszlású fényforrások legáltalánosabb példája a magas hőmérsékleten izzó szilárd test. Tapasztalataink azt mutatják, hogy a sugárzás erőssége a növekvő hőmérséklettel szintén nő, és a sugárzás intenzitásának maximuma, spektrálisan a hőmérséklet növekedésével a rövidebb hullámhosszak felé tolódik el. A termikus fényforrások vizsgálata során használt modell az abszolút fekete test, amely minden hullámhosszon minden sugárzást egyformán elnyel. A különböző hőmérsékletű abszolút fekete testek sugárzási görbéit az ábra mutatja.

Abszolút fekete test a valóságban természetesen nem létezik. Gyakorlati megvalósításakor, egy a sugárzást át nem eresztő, belül kormozott falú edényen kis lyukat fúrnak. A lyukon át behatoló sugárzás az alacsony reflexiójú falakon való többszörös diffúz visszaverődések következtében gyakorlatilag abszorbeálódik, mielőtt a lyukból kijutna.

3.5. ábra - Különböző hőmérsékletű abszolút fekete test sugárzási görbéi

A Planck-féle sugárzási törvény elméleti megalapozásakor érdemes megemlíteni, hogyan képzelték a termikus fényforrások keletkezését. A molekulák rendezetlen hőmozgásának energiája bizonyos mértékben az elektronoknak illetve az atomoknak adódik át, és ezeket rendszertelen rezgésekre gerjeszti. A rezgő töltések elektromágneses hullámokat bocsátanak ki, ami mindenféle frekvenciát tartalmaz. Megfordítva, a beeső sugárzás hatására, a részecskék rezgésbe jönnek, tehát a sugárzásból energiát nyernek el, amely vagy kibocsátódik, vagy az ütközések miatt hővé alakul. A törvény megalkotásakor Planck arra a klasszikus fizika által megoldatlan problémára igyekezett választ adni, hogy az adott frekvenciával rezgő elemi oszcillátorok nem vehetnek fel tetszőleges, folytonosan változó értéket, hanem csak egy legkisebb energiakvantumnak, az egész számú többszöröseit.

3.11. A Nap sugárzása

A hőmérsékleti sugárzók legalapvetőbb példája központi csillagunk, a Nap. Sugárzásának döntő többségét felületének egy viszonylag vékony rétege, a fotoszféra bocsátja ki. Sugárzásenergia-eloszlása a 600 K hőmérsékletű feketetest sugárzásához hasonlít a legjobban. A Nap folytonos spektrális eloszlású színképében diszkrét helyeken sötét, ún. Fraunhoffer-féle vonalak figyelhetők meg. Ennek oka a nap légkörében keresendő: a napkorona, vagy kromoszféra lényegesen alacsonyabb hőmérsékletű gázokból áll, mint a fotoszféra, és így elnyeli azoknak a hullámhosszaknak egy részét, amelyek megegyeznek a gázok gerjesztési energiaszint-különbségeivel.

A Föld légköre szintén elnyel a sugárzásból bizonyos hullámhosszakat, és bizonyos tartományokban jelentős szóródást is okoz. Így a Nap sugárzásának spektrális eloszlása jelentős mértékben eltér a Föld felszínén és a légkörön kívül.

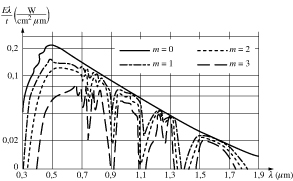
3.6. ábra - A Nap sugárzásának spektrális eloszlása m=0 a légkörön kívül; m=1 a Föld felszínén; a merőleges beesésnél; m=2 Nap állása 60°; m=3 Nap állása 70°

A Naphoz hasonlóan keletkezik a többi csillag fénye is, így fénykibocsátásuk spektrális eloszlása elsősorban az adott égitest felületi hőmérsékletétől függ, ami általában a 3500-5000K tartományba esik.

A csillagok színképét az alábbiak szerint osztályozzák:

	Q	Újonnan fellángolt csillagok, szupernóvák
	W	Rendkívül forró, 50000K felszíni hőmérsékletű csillagok
	B	20000K felszíni hőmérsékletű ún. héliumcsillagok
	A	Kb. 10000K felszíni hőmérsékletű ún. hidrogéncsillagok, a színképben már megjelennek a fém- és hidrogénvonalak
	F	6000-8000K felszíni hőmérsékletű csillagok, a színképben egyre több fémvonallal
	G	6000K hőmérsékletű csillagok nagyszámú sötét abszorpciós vonallal, ilyen a Nap is
	K	A színképet a fémek sötét abszorpciós vonalai jellemzik, megjelennek a molekulák vonalai is, a hőmérséklet kb. 4500K
	M	3500K hőmérsékletű vöröses csillagok, molekulaabszorpciós sávokkal
	RN	Hidegebb ún. széncsillagok
	S	Ritkán előforduló hideg csillagok színképtípusa

3.12. Izzólámpák

A mesterséges hőmérsékleti sugárzók leggyakoribb típusát a különféle izzólámpák alkotják. Ezekben villamos árammal 1000-3000K környékére felmelegített áramvezető izzószál atomjai világítanak folytonos spektrális eloszlással. Az izzószál általában spirál, vagy dupla spirál alakúra húzott volfrámszál, amelyet üveg- vagy kvarcburában helyeznek el. A volfrámszál méretei (hossz, keresztmetszet) az izzó teljesítményét határozzák meg, míg hőmérséklete és felületének nagysága a kisugárzott energiát [3.3.] .

A lámpa élettartamát a wolframszálnak a magas hőmérséklet miatti, párolgása határozza meg. A párolgás hatása kettős: egyrészt a szál átmérőjét csökkentve végül is meghibásodáshoz vezet, másrészt a burán lecsapódó anyag a lámpa hatásfokát csökkenti. Ez a fényáram csökkenés a lámpa élettartama során elérheti a 20%-ot. A párolgás csökkentésére a burát semleges gázzal (pl. nitrogén vagy argon) töltik fel, ez azonban a hővezetés miatt veszteséget is okoz. Ha az izzószálas lámpán a feszültséget növeljük, a fényáram jelentősen növelhető, viszont az élettartam ugrásszerűen csökken. Hasonló módon az alulfűtött izzók élettartama jelentősen növelhető.

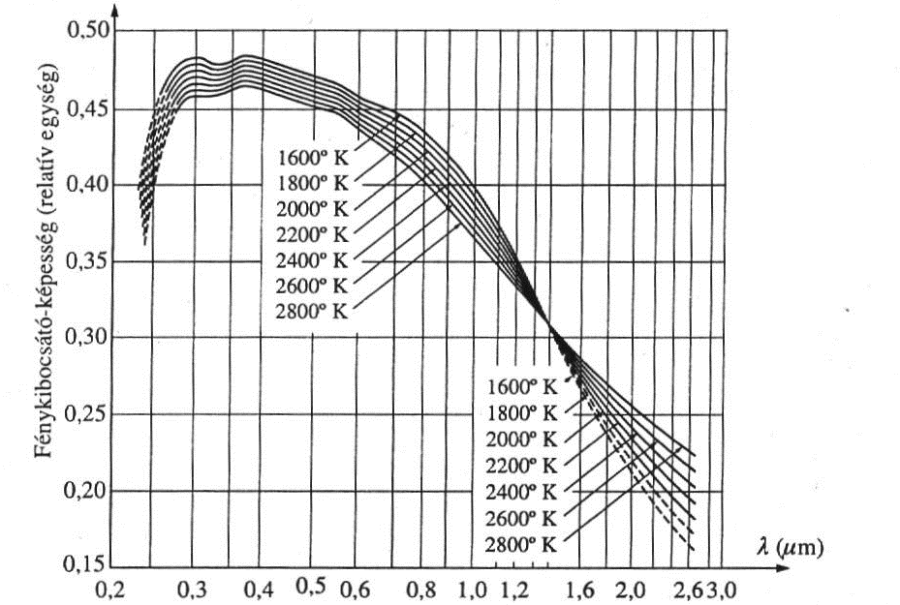
3.7. ábra - Különböző hőmérsékletű volfrámszálak kibocsátó képessége

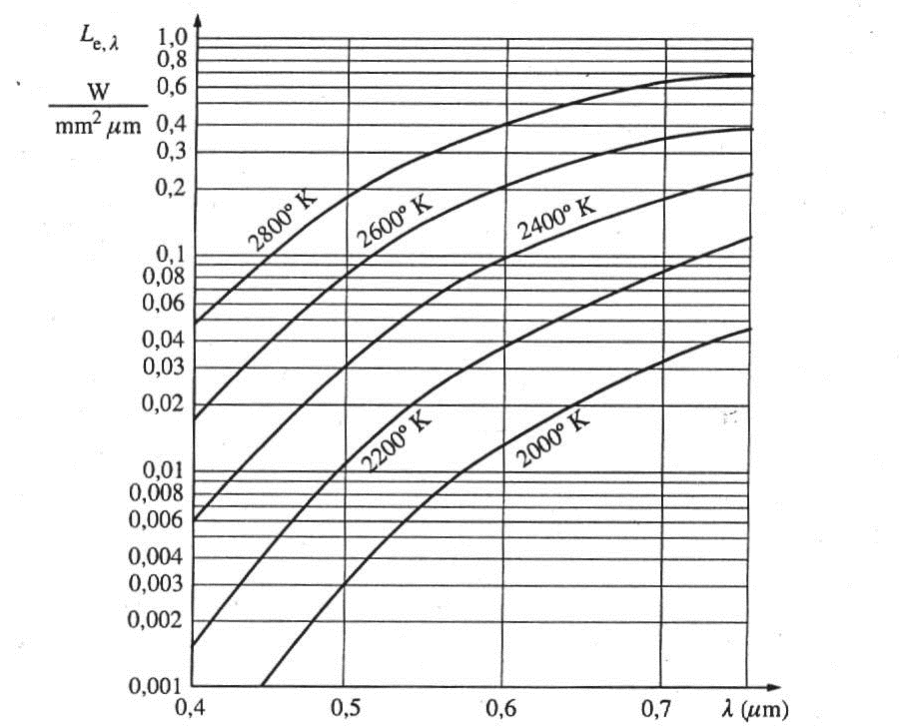
3.8. ábra - Különböző hőmérsékletű volfrámszálak spektrális felületi fénysűrűsége

Az izzólámpák egy speciális csoportját alkotják a halogénizzók. Itt az élettartam növelése céljából a lámpát halogénelem-tartalmú gázzal töltik fel. A halogén anyaggal az elpárolgó volfrámrészecskék reakcióba lépnek, a burára kicsapódó fémhalogén visszadiffundál az izzószálba. A burában így kialakuló ciklus, jelentősen megnöveli az élettartamot, és a lámpa fényáram csökkenését is megakadályozza, egyúttal lehetővé teszi a magasabb izzószál-hőmérsékletek elérését, és így a nagyobb fényhasznosítást és fényáramot.

Az izzószál az abszolút fekete test sugárzásával szemben ún. szürke testnek tekinthető. Ennek sugárzási eloszlása a látható tartományban megközelítőleg olyan, mint a hasonló hőmérsékletű fekete testé, de a kisugárzott összes intenzitás kevesebb.

3.13. Elektromos kisülés gázokban

Ha egy semleges részecskéket tartalmazó gáztérre feszültséget kapcsolunk, alaphelyzetben nem jön létre megfigyelhető változás. Ha azonban a térben szabad elektronok is jelen vannak, ezek a feszültség hatására felgyorsulva, és az atomokkal illetve molekulákkal ütközve, gerjesztett állapotot hoznak létre, és sugárzást bocsátanak ki. Ez az alapelve a gázkisüléses lámpáknak.

A gázcsőben a hőmozgás és a külső sugárzás hatására létrejövő szabad töltések száma viszonylag kevés, így a szabad elektronok forrása elsősorban a katód, ahonnan az alábbi jelenségek hatására léphetnek ki a töltések:

hő hatására létrejövő emisszió a katód fűtésének segítségével
megfelelő nagy térerő hatására létrejövő emisszió
másodlagos emisszió, amit a katódba becsapó pozitív ionok hoznak létre.

Ha a gáztérben a feszültség nagyobb, mint az első gerjesztett állapothoz tartozó minimális gerjesztési feszültség, monokromatikus fénykibocsátás jön létre ω frekvenciával.

$ω = \frac{2 π e U}{h}$

h a Planck-féle állandó, és az e az elektron töltése.

A feszültséget növelve magasabb gerjesztési állapotok is létrejönnek, és további hullámhosszokon is energia sugárzódik ki. Amikor a feszültség nagyobb, mint az ionizációs potenciál, a részecskék ionizálódnak az ütközések következtében, és az így keletkező pozitív és negatív töltések az anód és a katód felé gyorsulva tovább növelik az áramot. Alacsony nyomáson az elektronok és az ionok rekombinációjának valószínűsége kicsi, és a katódba csapódó ionok további elektronok kiválását okozzák. Amikor ez a másodlagos emisszió elegendően nagy a kisülési áram fenntartásához, parázskisülésről, vagy más néven glimmkisülésről beszélünk. A parázskisülést állandó áramsűrűség jellemzi. Ha növekszik az áram, növekszik a kisülési keresztmetszet, míg a feszültség állandó marad. Ha a feszültséget tovább növeljük, a glimmkisülés átmegy ívkisülésbe, ami hirtelen feszültségcsökkenéssel jár, jelezve egy másfajta elektronemissziós jelenség kialakulását. Ívkisülés esetén a katódba csapódó pozitív ionok annyira felhevítik az elektródát, hogy a hő hatására kilépő elektronok tartják fenn a folyamatos kisülést. Az energiát egyrészt a nagy hőmérsékletű elektródok, másrészt az ív 4000-8000K hőmérsékletű plazmája sugározza ki.

3.14. Gázkisülő lámpa

A gázkisülő lámpák, vagy közismert nevükön a neoncsövek, alacsony nyomású gázzal töltött, hideg elektródás fényforrások. A neontöltésű cső piros, a héliumtöltésű narancsos fénnyel világít. Higany hozzáadásával a neon fénye kékesfehérré tehető. Színes üvegcsövet alkalmazva, szinte tetszőleges színű fény hozható létre. A csőben a gáz nyomása 0,5 és 10Hgmm között van. A gyújtási feszültség 3000V.

3.15. Nagyintenzitású ívlámpák

A folyamatos fényű mesterséges fényforrások közül az ívlámpák szolgáltatják a legnagyobb teljesítményt. A szén-, és a nagynyomású higany és xenonív fénye megközelíti, illetve néha meg is haladhatja a Nap fényességét (1500 cd/mm²).

A nagynyomású higanyívlámpák zárt térben hozzák létre a kisülést, rendkívül nagy fényerőt biztosítva. A nagy teljesítmény miatt folyamatos hűtést igényelnek. További hátrányuk, hogy robbanásveszélyesek, így csak megfelelő mechanikai foglalással, védőházban használhatóak. Spektrális eloszlásuk erősen vonalas karakterisztikájú.

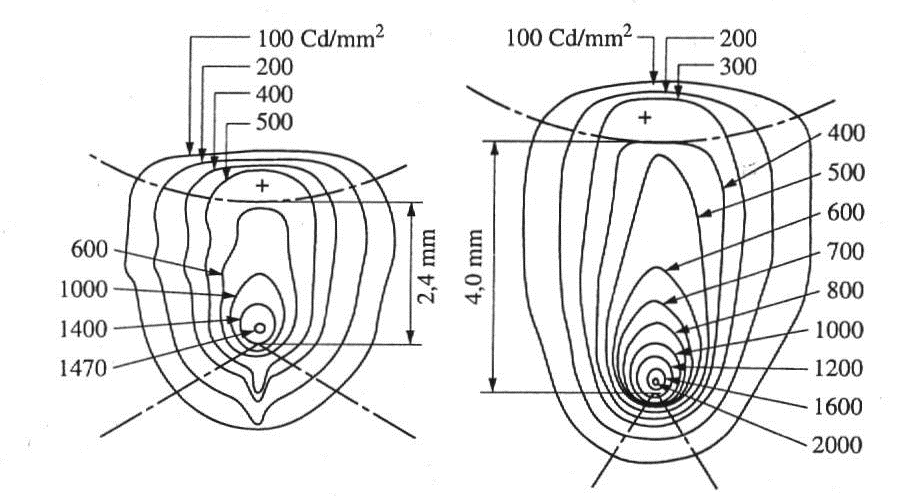
3.9. ábra - 2,5 kW teljesítményű higany-xenon ív fényességeloszlása

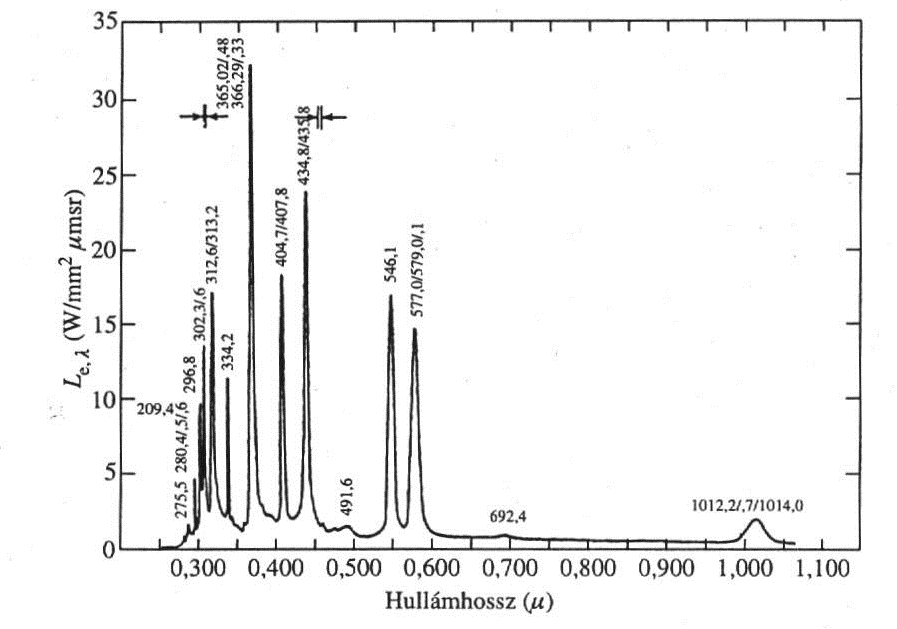
3.10. ábra - Nagynyomású higanyívlámpa spektrális eloszlása

A nagy intenzitású ívfénylámpák legrégebben használt típusa szénelektródával működött. Vetítőgépekben, színpad megvilágításnál, légvédelmi reflektorokban alkalmazták. Az ívet szabad térben, levegőn hozták létre. Az elektródák fogyása miatt a szénrudakat folyamatos előtolással mozgatni kellett, hogy az elektródatávolság állandó maradjon. A higanyív vonalas spektrumának javítására jó eredménnyel használhatók bizonyos semleges gázok. Ezek alapján fejlesztették ki a nagynyomású gázívlámpák családját, amelyek a látható tartományban egyenletesnek tűnő spektrális eloszlást mutatnak.

3.16. Ellenőrző kérdések

A leggyakrabban előforduló fényforrások általában az alábbi két nagy csoport egyikébe sorolhatók: a termikus fényforrások esetében a fénykibocsátás a magas hőmérséklet eredménye, elektromos kisülés gáztéren keresztül történő fénykibocsátás során a feszültség hatására létrejövő ionizációk és ütközések az okok. Világítson rá e két fénykibocsátás típus közötti alapvető különbségre és mutasson példákat mindkét típusra!
A testeket sugárzáshoz való viszonyulásuk alapján az abszorpciós, reflexiós és transzmissziós tényezőjük alapján hogyan csoportosíthatók? Mondjon példákat ezen csoportosításra!
Az abszolút fekete test viselkedését jól modellezi a falán kis nyílással ellátott üreges test. Az üreg nyílásánál az abszorpciós tényező közel egységnyi, azaz a nyílásra eső, és azon belépni szándékozó sugárzás energiája az üregbe bejutva, azon belül szinte teljesen elnyelődik. Hogyan magyarázza ez a fekete sugárzással jól közelíthető viselkedést?
A Planck-törvény segítségével kiszámítható a sugárzás intenzitásának nagysága fekete test esetén, adott sugárzó testre vonatkozó abszolút hőmérséklet és a sugárzási hullámhossz esetén. Ismertesse az összefüggést és magyarázza el az egyes tényezők jelentését, szerepét!
Wien-törvény kapcsolatot teremt a sugárzó test abszolút hőmérséklete és a sugárzás hullámhosszúsága között. Megmutatja, hogy mekkora a sugárzás intenzitásának nagysága fekete test esetén, adott sugárzó testre vonatkozó abszolút hőmérséklet és a sugárzási hullámhossz esetén. Ábrázolja a Wien-törvényt grafikusan Planck-törvény segítségével, adjon magyarázatot arra, hogy az intenzitás-maximumokhoz tartozó hullámhosszak és a megfelelő abszolút hőmérsékletek szorzata miért állandó!
A Stefan-Boltzmann-törvény kimondja, hogy a test egységnyi felületéről időegység alatt kisugárzó összes energia a sugárzó test abszolút hőmérsékletének negyedik hatványával arányos. Hol van jelentősége ennek a megállapításnak?
Kirchhoff törvénye a test emisszióképessége és abszorpcióképessége, azaz elnyelőképessége között állapít meg összefüggést. Mit mond ki?
A fényforrások jelentős részénél a kisugárzott energiának csak kis része esik a látható fény tartományába. A nagyobbik rész a világítás szempontjából elvész, milyen hatással van ez a fényforrás hatásfokára?
Abszolút fekete test a valóságban természetesen nem létezik. Gyakorlati megvalósításakor, egy a sugárzást át nem eresztő, belül kormozott falú edényen kis lyukat fúrnak. A lyukon át behatoló sugárzás az alacsony reflexiójú falakon való többszörös diffúz visszaverődések következtében gyakorlatilag abszorbeálódik, mielőtt a lyukból kijutna. Magyarázza meg, hogy ez a modell miért helyettesítheti a fekete sugárzót?
A Nap folytonos spektrális eloszlású színképében diszkrét helyeken sötét, úgynevezett Fraunhoffer-féle vonalak figyelhetők meg. Mi ennek az oka?
A mesterséges hőmérsékleti sugárzók leggyakoribb típusát a különféle izzólámpák alkotják. Ezekben villamos árammal felmelegített áramvezető izzószál atomjai világítanak folytonos spektrális eloszlással. Milyen szerkezetű egy ilyen fényforrás, mik a jellemzői?
A lámpa élettartamát a wolframszálnak a magas hőmérséklet miatti, párolgása határozza meg. Milyen hatásai vannak a párolgásnak?
Mi történik, ha az izzószálas lámpán a feszültséget növeljük? Hogyan viselkednek az alulfűtött izzók, hogyan növelhetők élettartamuk jelentősen?
Mi az alapelve a gázkisüléses lámpáknak?
A nagynyomású higanyívlámpák zárt térben hozzák létre a kisülést, rendkívül nagy fényerőt biztosítva. Mik az előnyeik és a hátrányaik?

Felhasznált irodalom

[3.1.] Fülöp, Z.. Hőtechnikai alapmérések. Tankvk.. Budapest . 1979.

[3.2.] Karácsony, J.. Optika. Editura Ábel. 2008. ISBN 9789731140728.

[3.3.] Budó, Á.. Kísérleti fizika. Nemzeti Tankvk.. Budapest . 3. köt. 1999.

[3.4.] Jenkins, F. és et al.. Optika. Panem-McGraw-Hill. Budapest . 1997.

[3.5.] Gróf. Gyula. Hőközlés. BME . Budapest. 1999.

Vissza		Előre
2. fejezet - Radiometria – fotometria	Főoldal	4. fejezet - Színtan