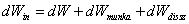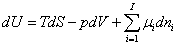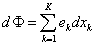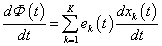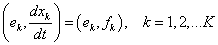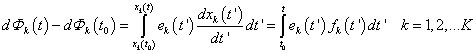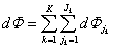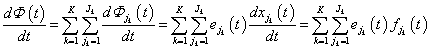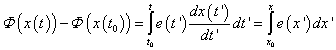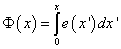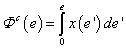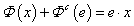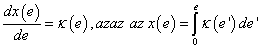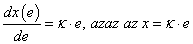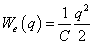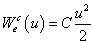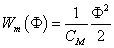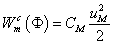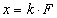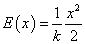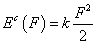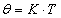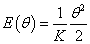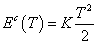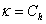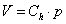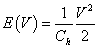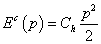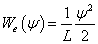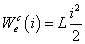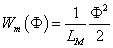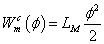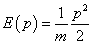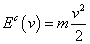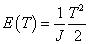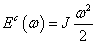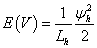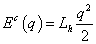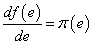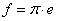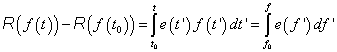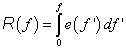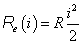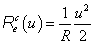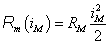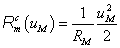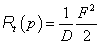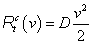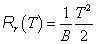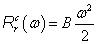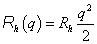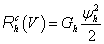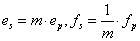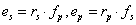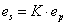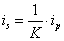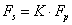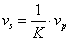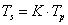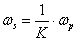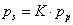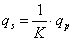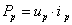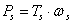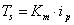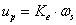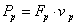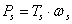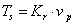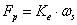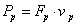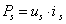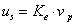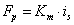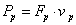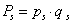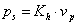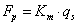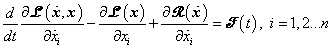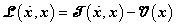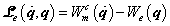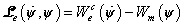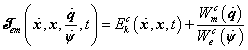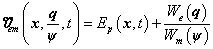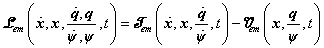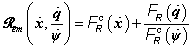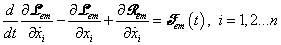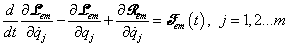7. fejezet - Rendszerek és modellezési analógiák

A mechatronikai eszközök és berendezések több fizikai-mérnöki diszciplína, így a mechanika, elektrotechnika és elektronika, pneumatika és hidraulika, irányítástechnika és informatika elemeiből felépített alrendszerek és szinergikus együttese. Ezért – mind elemzési, irányítási, de elsősorban tervezési szempontból – célszerű a különböző fizikai területek elemeinek modellezési analógiákat felhasználó értelmezése és leírása, és ezeknek a modelleknek a segítségével történő egységes kezelése. Ezt alapjában véve a műszaki rendszerek energetikai megközelítésével lehet elérni, amely lehetővé teszi a mérnöki termodinamika koherens módon történő bekapcsolását is.

A mechanikai rendszereknek a Lagrange-egyenletekkel történő leírása és a villamos rendszerek matematikai leírásában fellépő analógiákat már Maxwell észrevette, melyek aztán az elektromechanikai energia-átalakítók egységes matematikai leírását készítették elő. Ezzel a kezelésmóddal hasonló módon származtathatók a mechanikai rendszerek Newton-egyenletei és a villamos hálózatok Kirchoff-egyenletei.

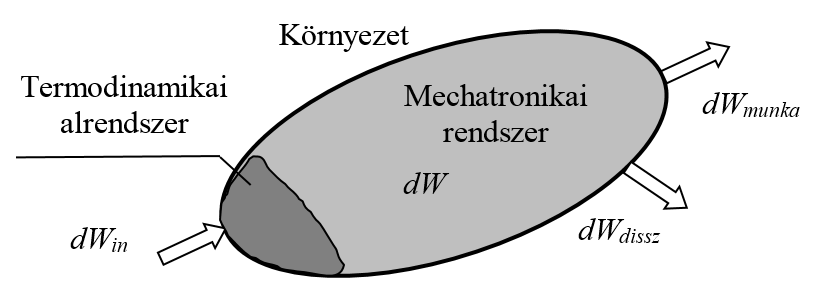
Egy mechatronikai rendszer általános energetikai reprezentációját az 7-1. ábra mutatja be, melyet a környezetével energia-csatolásban lévő rendszerként jelenítettünk meg.

A rendszerbe bevitt energiát alapvetően három fő részre oszthatjuk a (7.1) módon, ahol a jobb oldalon az egyes tagok a rendszer üzemelésére fordított energiát, a környezet számára végzett munkát és a rendszer által disszipált energiát jelenti. A rendszerben mindig elkülöníthetünk egy termodinamikai alrendszert, amely a reverzibilis termikus effektusokat reprezentálja.

Erre az alrendszerre felírhatjuk a Gibbs-egyenletet

ahol az U, V, S, ni, p, T, μi jelölik, sorban, a belső energiát, térfogatot. entrópiát, a kémiai komponensek mol számait, a nyomást, hőmérsékletet és a komponensek kémiai potenciáljait. Ez a formula a termodinamikai alrendszer belső energia-megváltozását reprezentálja a kölcsönhatásban lévő energiaformák, azaz a hő-, hidraulikus-pneumatikus és kémiai energiák kölcsönös megváltozásával.

A (7.2) energia-formulának az egész rendszerre történő kiterjesztését az általánosított Gibbs egyenletben fogalmazzuk meg

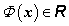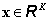ahol a az állapotváltozók valós értékű energia-állapot függvénye.

A 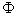energia-állapot függvény a rendszer teljes energiáját reprezentálja a rendszerben előforduló, egymással kölcsön-hatásban lévő és átalakuló energia-formákkal és az azokat jellemző állapotváltozókkal. A rendszer időbeli viselkedését meg-határozó dinamikus leírást a Gibbs-egyenlet alapján kapjuk meg a (7.3) összefüggésben az időbeli differenciálhányadosok bevezetésével

Mivel a (7.4) egyenletben a 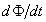teljesítménydimenziójú (W), ezért a baloldalon található szorzatok egyenként szintén teljesítmény dimenziót adnak, ezért a (7.4) egyenlettel a 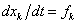jelölés bevezetésével az

az un. teljesítmény-konjugált változókat, illetve teljesítmény-konjugált változó-párokat definiáljuk. Figyelembe véve az egyes időpontokra megadott (7.4) teljesítmény kifejezéseket az egyes energiaformákra az azokat jellemző állapotváltozókkal a (0,t) időintervallumban a teljes energia-mennyiségeket a (7.6) integrálok adják meg.

A különböző fizikai területeknek a (7.3) és (7.4) általánosított összefüggésekben megjelenő teljesítmény-konjugált mennyiségeit a (7.2) Gibbs-egyenlet alapján értelmezzük. Így az xk változók az adott fizikai területek extenzív mennyiségeit – a (7.2) egyenletben az S entrópiát, a V fluidum térfogatot és az ni anyagmennyiséget (tömeget) –, a 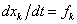deriváltak az extenzívek áramait, míg az ek változók az ezen extenzíveknek megfelelő intenzív mennyiségeket – a (7.2) egyenletben a hőmérsékletet, a nyomást és a kémiai potenciált – jelölik. Ezeknek a mennyiségeknek az általános meghatározását az alábbi definíciókkal adjuk meg.

Definíciók

Ha a V térfogatot a Vn, n=1,2…N, részekre osztjuk, akkor a részek térfogatából additíve a V térfogat adódik, azaz

.

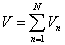
Extenzív mennyiség: azon fizikai mennyiségeket, amelyek részekre osztásnál (illetve összerakásnál) a térfogathoz hasonlóan transzformálódnak, extenzív mennyiségeknek nevezzük.

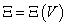
- legyen egy extenzív mennyiség modellje, és legyen

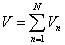
Akkor

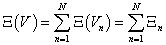
Másként:

Ha 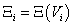és 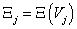, akkor

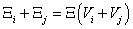
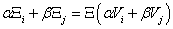
Intenzív mennyiség: azon fizikai mennyiségeket, amelyek részekre osztásnál (illetve összetevésnél) az értéküket nem változtatják, intenzív mennyiségeknek nevezzük.

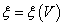- legyen egy intenzív mennyiség modellje, és legyen

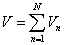
Akkor

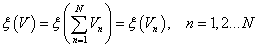
Másként:

Ha 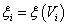, 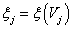és 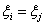, akkor

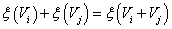
Az egyes fizikai – és mérnöki – diszciplínák extenzív és intenzív mennyiségeit az 7-1. táblázat foglalja össze. Ezek az adott fizikai területeken jól ismert mennyiségek, de ebben az általánosított kontextusban hasonló – analóg – jellemzőkként kezelhetjük azokat. A táblázat azt is tartalmazza, hogy az egyes fizikai területek mely mennyiségei alkotják azok jellemző teljesítmény-konjugált párjait. Lényegében ezeknek a mennyiségnek a modelljei és a közöttük fennálló függvénykapcsolatok adják meg a mechatronikai rendszerek egységes kezeléséhez szükséges analógiák alapjait.

Az extenzív mennyiségek tárolhatók, akár statikus, akár dinamikus formában, míg az intenzívekben fellépő különbségek – inhomogenitások – képezik azokat az e hajtóerőket (effort), melyek az extenzívek f áramlását (flow) hozzák létre. Az 7-1. táblázat által megadott bármely mennyiségpár esetén könnyen ellenőrizhetjük ezt az állítást, mivel – csak példaszerűen felsorolva – feszültségkülönbség töltésáramot hoz létre, nyomáskülönbség fluidumok térfogatáramát generálja, vagy az eltérő hőmérsékletek entrópia áramot hoznak létre. Azt is könnyen ellenőrizhetjük, hogy a táblázat egyes soraiban megadott intenzívek és extenzív áramok szorzatai valóban teljesítmény dimenziójú mennyiségek.

A rendszer modellezéséhez annak struktúráját térben elkülönített, koncentrált paraméterű, csatolt rendszerelemek egyszintű hálózataként írjuk le a 7-2. ábra által vázolt módon, mely elemek az 7-1. táblázatnak megfelelően elektromos, mágneses, mechanikai – transzlációs és rotációs –, hidraulikus és pneumatikus, fizikai kémiai, kémiai és termikus jellegűek lehetnek, akkor a rendszer (7.3) teljes energiáját – annak extenzív jellege következtében – eloszthatjuk a hálózat egyes elemeire a (7.7) módon, ahol Jk jelöli a k-adik energia-formához tartozó rendszerelemek számát.

Innen az (7.4) felhasználásával az egyes rendszerelemeken átáramló teljesítmények pillanatnyi összegét kapjuk a

formában.

A hálózat egyértelmű leírásához az (7.8) összegen túl az egyes rendszerelemek közötti ok-okozati kapcsolatokat is meg kell adni, ami az extenzív áramok irányainak, azaz az elemek közötti energiaközvetítés irányainak a rögzítését jelenti. Ez egyúttal az egyes elemeken megjelenő (7.8) teljesítményáramlások irányait is meghatározza.

Ugyanakkor azt is figyeljük meg, hogy az egyes elemeken megjelenő teljesítmény, vagy a (7.6) kifejezés alapján az adott elemen átáramló energia ismerete önmagában nem határozza meg a teljesítmény-konjugált változókat, mivel egy egyenletünk van két változóval. A teljes meghatározáshoz a rendszerelemek karakterisztikáit kell még megadni, amely függ az elem jellegétől. Itt a továbbiakban csak az 7-1. táblázat első 5 sorában felsorolt villamos, mágneses, mechanikai és hidraulikus-pneumatikus elemek jellemzőit tekintjük át és összegezzük – természetesen a termikus kapcsolatokkal együtt –, mivel a mechatronikai rendszerek felépítésében az ilyen elemek a dominánsak.

Egy rendszerelem karakterisztikája az intenzív és extenzív jellemzők közötti függvénykapcsolatot jelenti. A rendszerelemeket bemenet-kimenet modellekkel leírva az intenzívek bemenet-kimenet különbségei az elemeken kialakuló e hajtóerők, melyeknek az elemeken átáramló f extenzív áramokkal való összefüggései alkotják az elemek karakterisztikáit. Mivel az e·f=f·e szorzat nem határozza meg az elemekre vonatkozó ok-okozati kapcsolatokat, ezért azokat – a hálózat előzőekben említett irányultságát felhasználva – kell specifikálnunk. Ha egy rendszer-elem bemenetén megjelenő f áram az elsődleges, azaz az ok, akkor az okozat az elemen kialakuló e(f) hajtóerő, ahogy ezt a 7-3. ábra a) része illusztrálja. Ha azonban a rendszerelemre az e hajtóerő hat elsődlegesen mint ok, akkor az okozat az elemen áthajtott f(e) áram. Ezt a 7-3. ábra b) része illusztrálja.

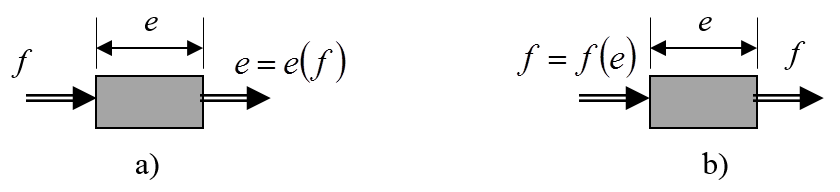
A rendszerelemek közötti energiaközvetítés teljesítmény-kapukon keresztül történik, így a mechatronikai rendszerek egyes részei és elemei közötti fizikai csatolásokat egységesen a teljesítmény kapcsolatokkal tudjuk megadni.

A teljesítmény-átvitellel jellemzett fizikai kapcsolatok mellett az egyes rendszerelemek között információ-átvitellel jellemzett kölcsönhatásokat is definiálnunk kell.

Definíciók

Egy fizikai terület azon intenzív és extenzív-áram jellemzőit, melyek szorzata teljesítmény dimenz i ójú, teljesítmény-konjugált mennyiségeknek nevezzük.

Teljesítmény-kapu (power port): egy rendszerelem két teljesítmény-konjugált változójával jellemzett bemenete vagy kimenete.

Információ-kapu: egy rendszerelem valamely változóval jellemzett bemenete vagy kimenete.

Két rendszerelem teljesítmény-kapukon keresztüli kölcsönhatását teljesítmény-kötésnek (power bond) nevezzük.

Két rendszerelem információ -kapukon keresztüli kölcsönhatását információ -kötésnek ( information bond) nevezzük.

A rendszerelemeket energetikai szempontból feloszthatjuk energiát tároló, azaz konzervatív, energiát disszipáló, azaz disszipatív, és energiát transzformáló elemekre, valamint energiaforrásokra.

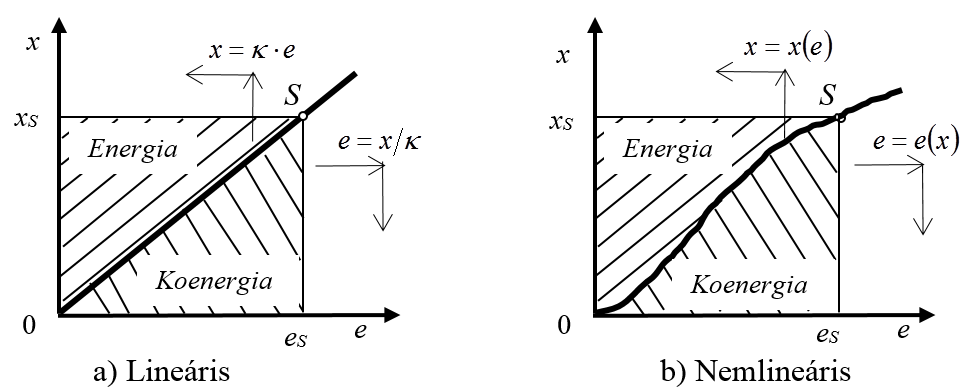
Egy energiatároló, azaz konzervatív rendszerelem karakterisztikáját a 7-4. ábra mutatja be a) lineáris és b) nemlineáris esetben. Ez alapjában véve az 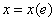függvénykapcsolatot jelenti, amely a konzervatív elemen felhalmozott x extenzív mennyiségét adja meg az elemre eső e hajtóerő függvényében, vagy éppen fordítva: a felhalmozott x függvényében adja meg a rendszerelemen kialakuló e hajtóerőt az 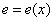függvénykapcsolat formájában.

A (7.9) és (7.10) integrálok geometriai képét a 7-4. ábra karakterisztika feletti területe adja meg. Ha a 7-4. ábra által ábrázolt – akár lineáris, akár nemlineáris – karakterisztikán kijelöljük az S pontot, akkor ezzel egyértelműen meghatározzuk az x és e állapotváltozókat.

A konzervatív rendszerelemmel társított energiát a (7.6) egyenletből kiindulva határozhatjuk meg behelyettesítve az 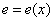összefüggést és ezzel a

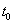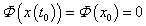összefüggéshez jutunk. A =0 és választás esetén a

integrál fejezi ki az elem energia-állapotát az e és x állapotváltozókkal az üres állapothoz viszonyítva. Ezt a területet az xS koordinátáig számítva a konzervatív elemnek a karakterisztika S pontjával kijelölt energia-állapotát azzal egyenértékűen adjuk meg. Ezzel az is jól látható, hogy a konzervatív elem aktuális állapota nem függ attól, hogy a t0 és t időpontok között mely állapotokban volt, azaz milyen folyamatban érte el a végső energia-állapotot. Ez a dinamikus rendszerek egyik fontos tulajdonsága, ezért mindig feltételezzük, hogy a konzervatív elem karakterisztikája a 7-4. ábra által bemutatott módon a változók kölcsönösen egyértelmű függvénye, amit a dielektrikus vagy ferromágneses hiszterézis jelensége esetén a hiszterézis görbe közép-vonalával történő közelítéssel érünk el. Ekkor a hiszterézis veszteséget egy disszipatív tag hozzáadásával lehet pótolni.

Természetesen az lényeges, hogy a hálózat dinamikus folyamatai a karakterisztikán melyik irányban mozdítják el az állapotváltozókat. Ugyanis – az ok-okozati kapcsolatokat és a kölcsönösen egyértelmű leképezéseket figyelembe véve – bármelyik állapotváltozó növekménye a másik növekményét, és egyúttal az elemen tárolt energia mennyiségének növekményét idézi elő, míg a fordított irányú elmozdulás a tárolt energia csökkenését. Mivel azonban mind az energia-felvétel, mind pedig annak leadása veszteségmentes, azért az ideális konzervatív elemeken ez a folyamat reverzibilis.

Figyelembe véve, hogy a 0eSSxS0 téglalap területe a 7-4. ábra mindkét változatán az (eS·xS) szorzattal egyenlő jól látható, hogy a karakterisztika alatti terület az eS pontig a rendszerelem energiájával egyértelmű kapcsolatban van. Ezt a karakterisztika alatti területet a

integrál adja meg és koenergiának (coenergy) nevezzük. Az energia és koenergia összege az elem karakterisztikájának tetszőleges pontjában az (x·e) szorzattal egyenlő, azaz

A koenergia fogalmát alapvetően csak az energiával összefüggésben értelmezhetjük, bár lineáris karakterisztika esetén, ahogy ez a 7-4. ábra a) részén jól látható, a két mennyiség egyenlő, így bármelyik – a 7-2. táblázat és a 7-3. táblázat által megadott – kifejezést használhatjuk a számításokban. Ugyanakkor azt is érdemes megjegyezni, hogy a koenergia fogalom – és analitikus formulája – az elektromechanikai rendszerek Lagrange-egyenletekkel történő modellezésében és számításában játszik fontos szerepet, mivel az elektromechanikai Lagrange-függvény meghatározásához szükség van a koenergia fogalmára, ahogy ezt a későbbiekben látni fogjuk, de – többek között – a villamos hálózatok számításában Kirchhoff hurokegyenleteit valamint csomóponti egyenleteit lehet az energia-koenergia páros felhasználásával származtatni.

A 7-4. ábra által ábrázolt karakterisztikákat, illetve az azokkal leírt rendszerelemeket egyszerűbben, egyetlen paraméterrel is jellemezhetjük, mégpedig a függvények meredekségének tetszőleges pontban történő megadásával a

módon, amely lineáris esetben a

formát ölti. A κ paraméter lényegében az adott rendszerelem valamely állapotában az extenzív mennyiség, azaz végső soron az energia felhalmozási képességét jelenti. Lineáris esetben tehát a rendszerelem meghatározásához elégséges a konstans értékű κ paraméter megadása.

A konzervatív rendszerelemek energiatárolása két, jellegükben különböző módon történik. Statikus módon, a villamos rendszerek elnevezését általánosítva kapacitív elemekkel (jelölésük összefoglalva: C), és dinamikus módon, melyeket – ugyancsak a villamos rendszer-elemek elnevezését használva – általánosított induktív elemeknek nevezzük (jelölésük I). Az 7-1. táblázat által megadott fizikai területek konzervatív rendszerelemeinek konstitutív paramétereit, karakterisztikáit, energia és koenergia kifejezéseit a 7-2. táblázat és a 7-3. táblázat foglalja össze.

Az energiatároló rendszerelemek ideális objektumok, melyek veszteség nélkül tárolják és adják vissza a tárolt energiát. Ez valós rendszerek modellezése esetén természetesen nem ad megfelelő leírást, mert bármelyik valós rendszer működése energiaveszteséggel jár. Ezt a termodinamika második főtétele értelmében, amely úgy is fogalmazható, hogy minden valós fizikai rendszer disszipatív, azaz a folyamatokban az energia egy része hő formájában veszteségként "szétszóródik". Ezt az ideális elemekhez megfelelően csatolt disszipatív elemek alkalmazásával modellezhetjük. Hasonló módon pótolhatjuk a rendszerelemeket hálózatba foglaló teljesítmény-kötések általi veszteségeket. Ugyanakkor a disszipatív elemek, mint az extenzív áramlásokkal szembeni ellenállások, vagy a hálózat egyes ágaira eső teljes intenzív különbségeket megfelelően megosztó objektumok fontos elemei az energetikai hálózatoknak.

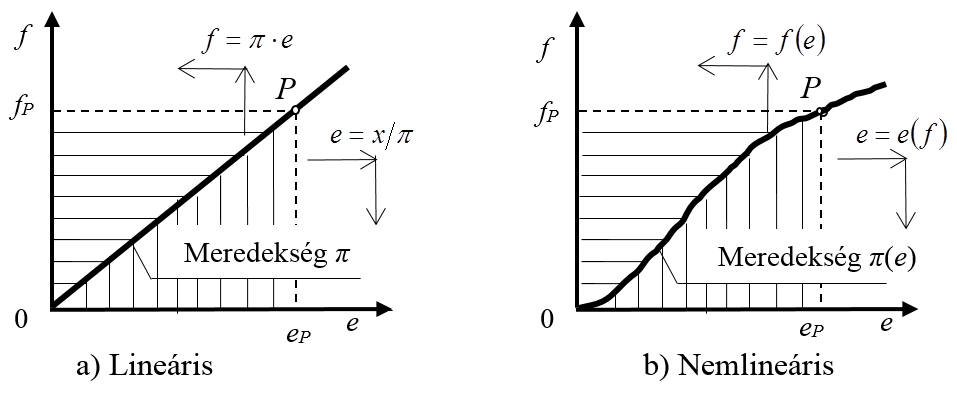
A disszipatív elemek karakterisztikájának általános képét mutatja be az 7-5. ábra mind a) lineáris, mind b) nemlineáris rendszerelemek esetében. Egy elem karakterisztikája az f=f(e) és az inverz e=e(f) függvénykapcsolatokat jelenti, melyeket – kölcsönösen egyértelmű leképezések lévén – szintén egy paraméterrel jellemezhetünk: a függvények meredekségének tetszőleges pontban történő megadásával a

módon, amely lineáris esetben a

formát ölti.

Ha az 7-5. ábra által ábrázolt – akár lineáris, akár nemlineáris – karakterisztikán kijelöljük a P pontot, akkor ezzel egyértelműen meghatározzuk a disszipatív elemen kialakuló f és e állapot-változókat. Ugyanakkor itt is megtaláljuk – a konzervatív elemekhez hasonlóan – karakterisztika feletti terület energetikai értelmezését. Képezve ugyanis az elemen átáramló teljesítmény integrálját az f=f(e) inverz karakterisztikát felhasználva az

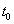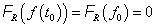összefüggéshez jutunk, amely a =0 és választás esetén a

egyenletet szolgáltatja.

Az (7.18) integrál definiálja a Rayleigh-disszipáció függvényt, melynek a disszipatív rendszerek Lagrange-egyenletekkel való kezelésében van alapvető szerepe. A disszipatív elemek konstitutív paramétereit a 7-4. táblázat mutatja be.

A különböző fizikai és mérnöki területek rendszereinek modellezési analógiái azt mutatják, hogy az analógiák a mechanikai és elektromos rendszerek között a legjobbak, így a mechanikai rendszerekre kidolgozott Lagrange-módszert a villamos rendszerekre. illetve ennek alapján az elektromechanikai rendszerekre közvetlenül ki lehetett terjeszteni.

A Lagrange-módszer lényege, hogy az egész modellezendő rendszert általánosított koordinátákkal és azok deriváltjaival tudjuk leírni, kiindulva a pontmechanika általánosított fogalmaiból. Ez az 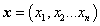általánosított koordináták és deriváltjaik 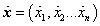meghatározását jelenti, melyekkel a mechanikai Lagrange-egyenleteket a

formában írjuk fel, ahol a Lagrange-függvény a

alakú. Itt a 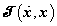a mechanikai rendszer teljes kinetikus energiáját, 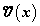a teljes potenciális energiát, 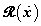az energia-veszteséget leíró Rayleigh-féle disszipáció függvényt, míg 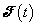a rendszerre ható külső erőket jelenti. A két energiaforma különbségéből álló Lagrange-függvényre vonatkozó (7.21) Lagrange-egyenletek rendszere megadja a rendszer erőhatásainak a Newton-módszerrel előállítható mérlegegyenleteit.

A bemutatott analógiák alapján villamos hálózatok esetében hasonló fogalmakat tudunk definiálni, ezért a Lagrange-módszert közvetlenül ki lehetett terjeszteni az elektromos, és ezen túl az elektromechanikai rendszerekre is.

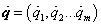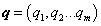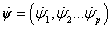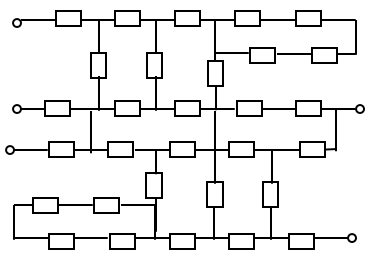
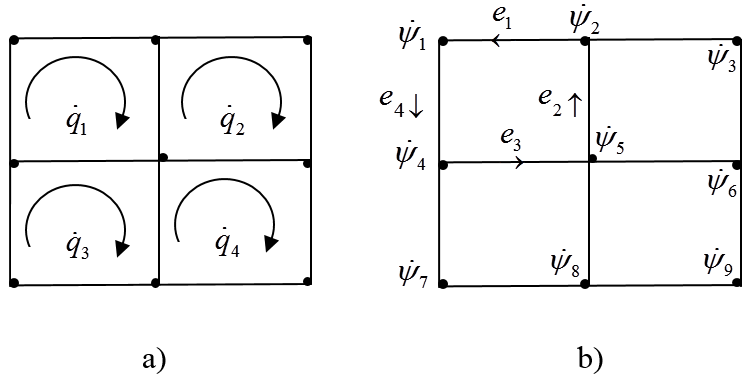
Villamos hálózatok esetén két eljárás is lehetővé teszi a megfelelő általánosított koordinátákkal történő jellemzést: a hurokáramokkal és huroktöltésekkel, illetve a csomóponti potenciálokkal és 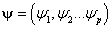csomóponti fluxusokkal, ahogy ezt a 7-6. ábra illusztrálja. A 7-6. ábra a) részén látható hurokáramok nyilván teljesítik a csomóponti áramösszegekre vonatkozó Kirchhoff-törvényt, míg a csomóponti potenciálok összege – figyelembe véve az 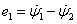, , 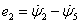, , 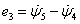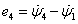azaz 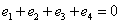egyenleteket – kiadja Kirchhoff huroktörvényét. Jegyezzük meg tehát előzetesen, hogy az általánosított koordináták ily módon történő definíciójával a Lagrange-módszer a jól ismert Kirchoff-egyenleteket állítja elő.

A villamos-mechanikai analógiák alapján intuitíve belátható, hogy, mivel – a 7-2. táblázat és a 7-3. táblázat alapján – a kinetikus energia a mechanikai rendszer 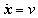változóival jellemzett dinamikájában jelenik meg, így ennek villamos megfelelőjét a 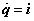hurokáramokkal adott 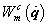koenergiával lehet kifejezni. Hasonló analógia alapján a statikus jellegű potenciális energiának a töltésekkel kifejezett 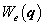villamos energia a megfelelője, így az elektromos Lagrange-függvényt az

kifejezés alkotja.

Hasonló módon az elektromos Lagrange-függvényt a csomóponti feszültségekkel is ki tudjuk fejezni a

módon. A (7.23) függvény alkalmazása esetén a Lagrange-egyenlet a villamos hálózat hurokáramokkal történő leírását adja, míg a (7.24) függvény alkalmazása a csomóponti feszültségekkel írja le a hálózatot. Az első esetben az általános erőket ideális feszültségforrások, a második esetben pedig ideális áramforrásokkal adjuk meg.

Összekötve most a mechanikai és elektromos komponenseket az elektromechanikai kinetikus – dinamikus – energiát a

függvény adja meg, míg a potenciális – statikus – energiának a kifejezése

alakú. Mindezek alapján a elektromechanikai Lagrange-függvényt az

formában írhatjuk fel, ahol a 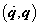mennyiségekkel kifejezett tagok esetén a villamos alrendszert hurokáramokkal írjuk le, míg a 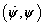mennyiségek alkalmazása a csomóponti feszültségekkel modellezett villamos alrendszer-modellt jelent.

Végül az elektromechanikai Rayleigh-függvényt

formában adjuk meg, így a teljes elektromechanikai Lagrange-egyenletrendszert

Mindezen függvényeket felhasználva az elektromechanikai Lagrange-függvénnyel a mechanikai egyenleteket a

míg a villamos Lagrange-egyenletet a

vagy

formában kapjuk meg.

A Lagrange-módszer alkalmazása különösen a nemlineáris rendszerelemeket is tartalmazó rendszerekben lehet eredményes, amire egy példát mutatunk be egy elektromechanikai (lineáris) erőgép tervezése kapcsán.