3. fejezet - Matematikai eszközök SISO LTI rendszerek vizsgálatához
- 3.1. Vizsgálat (komponensekre bontás) az időtartományban
- 3.2. Vizsgálat a frekvencia-, illetve Laplace-operátoros tartományban
-
- 3.2.1. Fourier-sorfejtés
- 3.2.2. Kidolgozott feladatok Fourier sorokhoz kapcsolódóan
- 3.2.3. Fourier-transzformáció
- 3.2.4. Laplace-transzformáció
- 3.2.5. Fourier-sorfejtés, Fourier- és Laplace-transzformáció áttekintő táblázat
- 3.2.6. Laplace-transzformáció alkalmazása
- 3.2.7. Kifejtési (reziduum) tétel (s-re nézve valós együtthatójú racionális törtfüggvények inverz Laplace-transzformációja)
- 3.2.8. Időállandó
- 3.2.9. Kidolgozott feladatok Laplace-transzformáció alkalmazására
- 3.3. Közönséges állandó együtthatós elsőrendű differenciálegyenletek megoldása Laplace-transzformációval
- 3.4. Kapcsoló üzemmód
Adottnak tekintjük a rendszer differenciálegyenletét, amelyről azt feltételezzük, hogy az (2.107) alakú. A differenciálegyenletből (az együtthatók értékéből) kiindulva kívánunk következtetni a rendszer általános tulajdonságaira.
Vizsgálati módszer : A bemenőjel et komponensekre bontjuk , az e lemi komponensek elemi hatását meghatározzuk , majd az időinvariancia és szuperpozíció elvének kihasználásával az elemi hatások at összegezzük.
Világosan kitűnik, hogy a jelen fejezetben leírtak csak lineáris, időinvariáns rendszerek esetén alkalmazhatók.
A bemenőjelet mind az idő-, mind a frekvencia-, illetve Laplace-operátoros tartomány ban komponensekre lehet bontani.
3.1. Vizsgálat (komponensekre bontás) az időtartományban
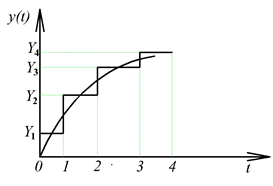
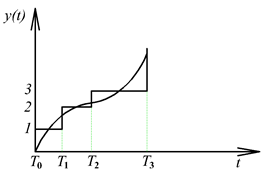
Ebben a fejezetben a 2.12.4 fejezetben leírt lineáris, időinvariáns, kauzális egy bemenetű egy kimenetű rendszerekkel találkozunk. A felbontás alapvetően két módon történhet. A jeleket az időben függőleges impulzusokra bonthatjuk az időtengely mentén, vagy vízszintes ugrások sorozatára bonthatjuk a függőleges tengely mentén (ld. 3-1. ábra). A felbontáshoz az impulzus és ugrás függvényeket kell definiálnunk.
Impulzusokra és lépésekre bontás
3.1.1. Dirac-impulzus és egységugrás
(2.107) megoldása tetszőleges mellett meglehetősen nehézkes. Ehelyett az jelet megpróbáljuk komponensekre bontani, majd a szuperpozíció elvét kihasználva a komponensek hatását összegezzük. Az jel impulzusok sorozatára bontható. Először diszkrét időben adjuk meg a definíciókat, mert diszkrét időben sok olyan tulajdonság egyszerűen belátható, amelyek folytonos időben komoly matematikai nehézségek elé állítanak bennünket. Természetesen folytonos időben is törekszünk a matematikai egzaktságra, de a diszkrét idejű összefüggés összegzését a folytonos időben integrálra cserélve megsejthetjük, hogy folytonos időben milyen összefüggéseket kell belátnunk.
Diszkrét időben
A rendszerek bekapcsolásának modellezéséhez szükséges a diszkrét idejű egységugrás fogalma, amelynek a definíciója (ld. 3-2. ábra):
|
|
( 3.1 ) |
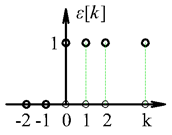
A (3.1) definícióból következik
|
|
( 3.2 ) |
A diszkrét idejű egységimpulzus definíciója (ld. 3-3. ábra):
|
|
( 3.3 ) |
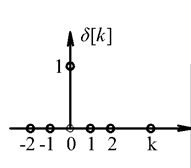
Az eltolást a diszkrét idejű egységimpulzus esetén is értelmezhetjük
|
|
( 3.4 ) |
továbbá
|
|
( 3.5 ) |
(3.3) definíciójából triviálisan következik, de később fontos szerepe lesz:
|
|
( 3.6 ) |
Könnyen belátható, hogy egy diszkrét idejű függvény konvolúciója az egységimpulzussal egy adott K érték mellett a függvény K helyen felvett értékét adja vissza.
|
|
( 3.7 ) |
A diszkrét idejű egységugrás és egységimpulzus kapcsolatát kétféleképpen adhatjuk meg:
-
Az egységugrás értéke a k helyen kiszámítható az egységimpulzus függvényből.
|
|
( 3.8 ) |
-
Az egységugrás két szomszédos helyen felvett értékének különbsége megegyezik az egységimpulzus függvény megfelelő helyen felvett értékével
|
|
( 3.9 ) |
Folytonos időben
Az egységugrás definíciója
|
|
( 3.10 ) |
Az eltolást a folytonos időben is értelmezhetjük
|
|
( 3.11 ) |
A definícióból látható, hogy az függvénynek nincs határozott értéke a helyen. Vannak szerzők, akik 0, 0.5 vagy 1 értéket adnak neki. Ennek nincs jelentősége, mert az egységugrás általában a bemeneten jelenik meg, bennünket általában a kimenet érdekel, és valós rendszereknél a kettő között integráló hatás van, így a kimenőjelre matematikai értelemben nincs hatása annak, hogy a időpontban -nak milyen véges értéket választunk. Azért érdemes a 0.5 értéket választani, mert pl. az ugrásokból álló négyszögjel Fourier-sora a szakadásnál a kétoldali határérték számtani középértékét adja vissza. Mérnöki megközelítésben nincs ennek jelentősége. Célunk a valós fizikai rendszer működésének leírása. A valós fizikai rendszer bekapcsolásakor lezajló fizikai jelenségeket az egyszerűség kedvéért nem modelleztük, így a rendszer időpontbeli matematikai viselkedése intuíciókat adhat, hogy a fizikai rendszer bekapcsolási jelenségeit hogyan képzelhetjük el, de ez inkább csak egy szellemi kaland lehet. Amennyiben a matematikai egzaktságot úgy is meg tudjuk tartani, hogy értékét nem definiáljuk a helyen, akkor a legjobb, ha azzal is kifejezzük a bekapcsolási folyamatokkal kapcsolatos bizonytalanságot, hogy erre vonatkozóan nem adunk esetlegesen félrevezető információt.
A diszkrét idejű egységimpulzus megfelelőjének matematikai értelmezése a folytonos időben még ennél is nehezebb. A mechanikában az impulzus definíciója egyértelmű. A tömegre ható erő integrálja. Állandó tömeget feltételezve ugyanazt az impulzust érhetjük el, ha kisebb az erő, de tovább hat, vagy ha nagyobb erővel, de rövidebb ideig hatva. Ezt általánosítva definiáljunk egy egységimpulzus függvényt:
|
|
( 3.12 ) |
(3.12) azért egységimpulzus, mert idő szerint integrálja 1 lesz az eredmény, hasonlóan, mint (3.6) diszkrét időben.
|
|
( 3.13 ) |
Formálisan a helyettesítéssel:
|
|
( 3.14 ) |
(3.14) hagyományos értelemben nem tekinthető függvénynek, mert 1/0 nem egy valós számérték. Az sem elegendő, ha azt mondjuk rá, hogy végtelen, mert pl. a 7/0 és a 0.2/0 is végtelen. Fordítsuk meg a dolgot és használjuk fel (3.13)-at és (3.14)-et definícióként: egységimpulzusnak (további elnevezések: Dirac-delta, Dirac-impulzus) nevezzük azt a kiterjesztett értelmű függvényt (disztribúciót), amely a pont kivételével mindenütt nulla. A pontban pedig olyan értéket vesz fel, hogy
|
|
( 3.15 ) |
teljesüljön. Az egységugráshoz hasonlóan a Dirac-impulzus hatását is általában egy integrálási művelet után vizsgáljuk, így a fenti definíció egy jó gyakorlati megközelítés. Azt fejezi ki, hogy a Dirac-impulzus mechanikai rendszereknél egy kalapácsütést jelent. E definíciót (2.108) segítségével kiterjeszthetjük az egységimpulzus deriváltjára: egy olyan kiterjesztett értelmű függvény (disztribúció), amely a pont kivételével mindenütt nulla. A pontban pedig olyan értéket vesz fel, hogy teljesüljön. Hasonló módon magasabb rendű deriváltakat is definiálhatunk.
definíciójából következik (vö. (3.8)):
|
|
( 3.16 ) |
A (3.16) integrál értéke a időpontban nincs meghatározva, hasonlóan a (3.10) definícióhoz. Így kijelenthetjük, hogy a disztribúciót értelmezhetjük úgy, mint általános értelemben vett deriváltja.
A (3.4) és (3.5) is könnyen általánosítható folytonos időben. A egy olyan kiterjesztett értelmű függvény (disztribúció), amely a pont kivételével mindenütt nulla. A pontban egy olyan értéket vesz fel, hogy teljesüljön.
A pedig olyan kiterjesztett értelmű függvény (disztribúció), amely a pont kivételével mindenütt nulla. A pontban pedig olyan értéket vesz fel, hogy teljesüljön.
A (3.7) formális általánosítása is egyszerű a folytonos időben. A folytonos függvény konvolúciója kiterjesztett értelmű függvény (disztribúció) -val vett eltoltjával a függvény pontbeli értékével egyezik meg. Mivel páros függvény, ezért a konvolúció számításában az argumentumának előjelét megcserélhetjük.
|
|
(3.17) |
Számunkra (3.17) azért kiemelt jelentőségű, mert (3.17) segítségével egy folytonos függvényhez hozzá tudjuk rendelni egy adott pontbeli értékét. A mérnöki gyakorlatban ezt nevezzük (mérésnek) mintavételezésnek. Ha (3.17)-t elvégezzük a (ahol és rögzített szám) mintavételi pontok sorozatára, akkor egy folytonos idejű jelnek előállíthatjuk a diszkrét idejű megfelelőjét.
|
|
(3.18) |
A fentiekből következik, hogy a Dirac-impulzus nem tekinthető hagyományos értelemben vett függvénynek, de a Dirac-impulzusnak a fenti származtatása az egységimpulzusból fizikailag könnyen értelmezhető, a mérnöki gyakorlatban ezt az értelmezést alkalmazzuk. Ugyanakkor a (3.15) definíció nem ad támpontot több alapvető matematikai művelet elvégzésére. A Dirac-impulzus egzakt matematikai kezelésére vezettük be a 2.12.5 pontban a disztribúció fogalmát. A Dirac-impulzussal kapcsolatos intuitív megállapításaink egzakt matematikai eszközökkel is bizonyíthatók, a további elemzést az olvasóra bízzuk.
A diszkrét idejű jelek felbontása a 3-4. ábra látható
Impulzusokra és lépésekre bontás
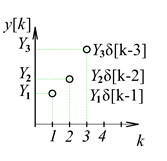
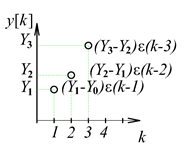
3.1.2. Impulzusokra bontott bemenőjel hatásának összegzése
Először a diszkrét idejű rendszereket vizsgáljuk, majd ezt kiterjesztjük folytonos idejű rendszerekre. A továbbiakban általában a bemenőjel egy ún. belépő függvény. Ez azt jelenti, hogy létezik egy olyan K, illetve érték, amelyre , illetve . Az egyszerűség kedvéért azt feltételezzük, hogy ha egyéb megjegyzést nem teszünk, akkor , illetve . A legtöbb esetben mindez formálisan csak annyit jelent, hogy az időre vonatkozó összegzésben és integrálok számításában a helyett a 0 az alsó határ. A kauzalitás miatt a rendszer válasza is csak a bekapcsolás után indulhat, de az állapotváltozó jellegű változóknak lehet nullától eltérő kezdeti értéke. Ebben a 3.1.2 pontban matematikai szempontból nincs szükség a belépő jelekre tett kikötésre, de a frekvencia-, illetve Laplace-operátoros tartományban (Laplace-transzformált jelek esetén, ld. 3.2.4, 3.2.6, 3.2.7, 3.2.8 pontok) élnünk kell ezzel a feltételezéssel.
Diszkrét időben
A 2.1.11. fejezetben leírt (2.98) alakú ARMA rendszerekkel foglalkozunk.
|
|
(3.19) |
A (2.98) jobb oldalán az összegzés r-ig tart. (i=r+1, …, n) bevezetésével egyszerűbbé tehetjük a későbbi tárgyalást, megjegyezzük, hogy a i<r sorszámú együtthatók között is lehet nulla. Ha első n számú () és r számú () értéke ismert, akkor (3.19) segítségével a további kimenőjel kiszámítható.
A lépésről lépésre számítás helyett kiszámoljuk, hogy a rendszer miként reagál egyetlen bemenőjelre, vagyis egyetlen „ütésre”. Amikor a diszkrét idejű rendszerek bemenőjele egy diszkrét idejű egységimpulzus, akkor a kimenőjelet súlyfüggvénynek vagy impulzusválasznak nevezzük (az irodalomban mindkét elnevezés elterjedt) és -val jelöljük (ld. 3-5. ábra) (megjegyezzük, hogy az irodalomban használják még a jelölést is).
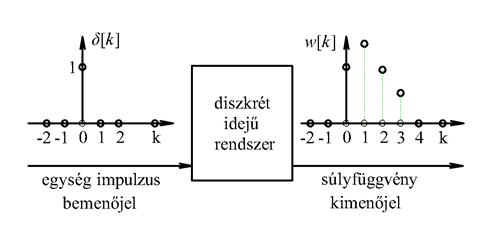
Tegyük fel, hogy és ismert. Kihasználjuk azt, hogy
|
|
(3.20) |
Ez azt jelenti, hogy egy adott i –edik időpontban egy nagyságú és i lépéssel eltolt impulzussal gerjesztjük a rendszert. E bemenőjelre a rendszer válasza egy arányosan megnövelt és időben eltolt súlyfüggvény: (ld. 3-6. ábra).
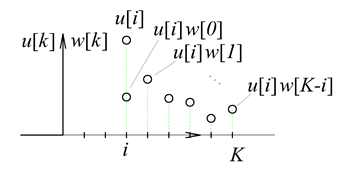
Bármely k-adik időlépésben az időinvarianciát és a szuperpozíció elvét kihasználva időeltolással összegezzük ezeket a hatásokat
|
|
(3.21) |
A (3.21) úgy is értelmezhető, hogy a kimenőjel értéke egy k-adik időpillanatban a rendszerre az összes múltbeli időpontban ható bemenőjel súlyozott átlaga, innen a súlyfüggvény elnevezés. A (3.21) kifejezésben nincsenek állapotváltozók, így kezdeti értékek sem adhatók meg, csak a rendszer tulajdonsága és az bemenőjel határozza meg az kimenőjelet. Itt az összegzés csak az tartományra szorítkozik, de nincs elvi akadálya, hogy akár -ből induljon.
Az impulzusnak véges energiája van, így egy valós fizikai rendszernél a kauzalitás miatt csak belépő függvény lehet (a bemenő jel csak a jövőre hathat), a linearitás miatt nem lehet irreverzibilis változás, minden valós rendszer működése közben van valamilyen energiaveszteség, így valós rendszer esetén biztosan lecsengő, értékei nullához tartanak.
Ha létezik olyan K időpont, amelyre igaz az, hogy , akkor a rendszert „véges impulzus válaszú” rendszernek nevezzük, és ezekre a rendszerekre az angol név alapján a FIR (Finite Impulse Response) rövidítést használjuk. Értelemszerűen definiálhatjuk az IIR végtelen impulzusválaszú (Infinite Impulse Response) rendszereket is.
Folytonos időben
(2.107) alakú differenciálegyenlettel leírható rendszerekkel foglalkozunk. A (2.107) egyenletben alkalmazott jelölésekkel n=r ( (i=r+1, …, n)) és
|
|
(3.22) |
A (3.22) megoldása tetszőleges mellett meglehetősen nehézkes. Ehelyett az jelet a diszkrét idejű rendszereknél alkalmazott eljáráshoz hasonlóan komponensekre (impulzusok sorozatára) bontjuk, majd a szuperpozíció elvét kihasználva a komponensek hatását összegezzük. A diszkrét idejű rendszerhez hasonlóan bevezethetjük a súlyfüggvényt (impulzusválaszt) ld. 3-7. ábra. (Az irodalomban használatos még a jelölés is)
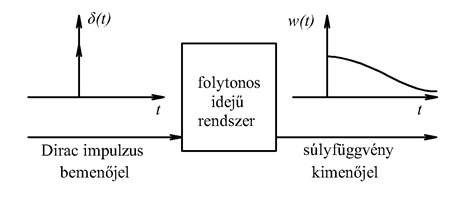
Valós fizikai rendszer esetén w(t) lecsengő belépő időfüggvény (ezt a tulajdonságát később kihasználjuk)
Tegyük fel, hogy w(t) ismert (például mérés alapján). Formálisan (3.21) összegzést kell átírni folytonos időbe, k helyére t kerül és az összegzés helyett integrált kell írnunk, továbbá tekintettel kell lenni arra, hogy akár Dirac-impulzus is lehet, így az összegzésben, illetve integrálszámításban a t=0 pontot is figyelembe kell venni, ahol nem folytonos és az értékét csak az integrálja határozza meg. Ebből következik, hogy az integrál alsó határának a 0 bal oldali közelítését kell választani, ezt jelöljük 0-val.
|
|
(3.23) |
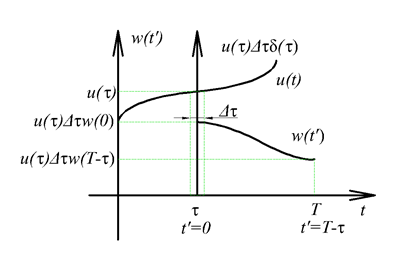
A (3.23) úgy is értelmezhető, hogy az u(t) bemenőjel értelmezési tartományát nagyságú időintervallumokra osztjuk, minden időintervallumot egy impulzusnak tekintjük, amelynek a nagysága . Ezt az impulzust egy, az impulzussal megegyező nagyságú Dirac-impulzussal helyettesítjük. Ennek megfelelően a τ időpillanatban a rendszer bemenőjele lesz. Erre a -val eltolt és nagyságú impulzusra a válasz egy eltolt és arányosan lecsökkentett súlyfüggvény (ld. 3-8. ábra). Meg kell jegyezni, hogy ha tart nullához, akkor a nagyságú impulzus is tart nullához, így a rendszer válasza végtelen sok végtelenül kicsi impulzus hatásából adódik össze.
|
|
(3.24) |
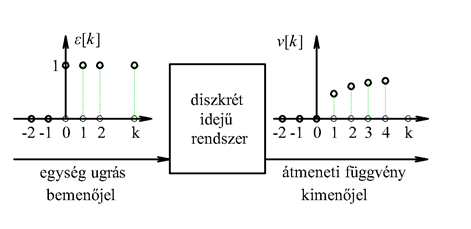
Az u(t) bemenőjelet nem csak függőlegesen, hanem vízszintesen is feloszthatjuk, ekkor elemi ugrásfüggvényeket kapunk. A rendszer válaszát az egységugrás bemenőjelre átmeneti függvénynek nevezzük és -vel jelöljük (ld. 3-10. ábra). Valós fizikai rendszerek esetén .
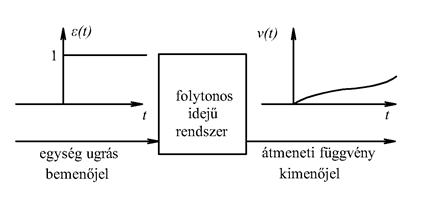
Formálisan, ha a bemenőjelet integráljuk, akkor a kimenő jelet is integrálni kell, így az egységugrás bemenőjelre adott válasz a súlyfüggvény integrálja lesz.
|
|
(3.25) |
Természetesen a (3.25) átfogalmazható úgy, hogy az átmeneti függvény időszerinti deriváltja a súlyfüggvény. A kimenőjel az átmeneti függvény és a bemenőjel ismeretében is meghatározható. A időpillanatban a bemenőjel mértékben változik meg. Ezt a változást nagyságú ugrásfüggvénnyel, vagyis bemenőjellel modellezzük. E bemenőjelre a rendszer válasza egy olyan átmeneti függvény, amelynek a nagysága meg van szorozva -val és az időben el van tolva -val. Ennek az átmeneti függvénynek az értéke egy adott T időpontban . Ezeket az elemi átmeneti függvényeket kell összegezni, de figyelembe kell venni, hogy u(t)-nek lehetett egy kezdeti ugrása is a t=0 időpontban. Az összegzés eredménye:
|
|
(3.26) |
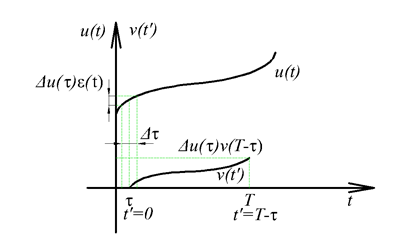
Összefoglalásul megállapíthatjuk, hogy folytonos idejű modell esetén az u(t) bemenőjel az időtartományban felbontható impulzusok vagy ugrások sorozatára, továbbá definiálhatók a rendszer működését általánosan leíró időfüggvények (súly- és átmeneti függvény). Az időtartományban a bemenőjel felbontásával és az időtartománybeli rendszerfüggvények segítségével egy konvolúciós integrállal ((3.23), illetve (3.26)) a rendszer kimenőjele kiszámítható. A probléma az, hogy a konvolúciós integrál számítása folytonos időben továbbra is bonyolult, ez a matematikai művelet lényegesen leegyszerűsödik a frekvencia-, illetve Laplace-operátoros tartományban, és részben ez az oka (de nem az egyetlen), hogy folytonos idejű rendszerek esetén áttérünk a frekvencia-, illetve Laplace-operátoros tartományra.
3 - 1 feladat Diszkrét idejű konvolúció
Egy diszkrét idejű rendszer diszkrét idejű impulzusválasza (súlyfüggvénye) legyen
, , és , ha
-
Számítsa ki a rendszer válaszát, ha a bemenőjel diszkrét idejű egységugrás.
-
Mekkora a rendszer erősítése?
Megoldás
A diszkrét idejű az egységugrásra úgy tekintünk mint diszkrét idejű az egységimpulzusok sorozatára. Jelölje az egységugrás -edik időpillanatbeli értékére adott impulzusválasz függvényének -adik időlépésbeli értékét. Írjuk be egy táblázatba és első öt értékét.
|
k |
|
|
|
|
|
|
|
0 |
1 |
1 |
||||
|
1 |
3 |
1 |
4 |
|||
|
2 |
2 |
3 |
1 |
6 |
||
|
3 |
0 |
2 |
3 |
1 |
6 |
|
|
4 |
0 |
0 |
2 |
3 |
1 |
6 |
Látható, hogy túllendülés nélkül a lépésben beáll az állandósult értékre. Így a táblázatból kiolvasható, hogy a rendszer erősítése 6.
3 - 2 feladat (Házi feladat, megoldását nem közöljük)
Egy diszkrét idejű rendszer diszkrét idejű impulzusválasza (súlyfüggvénye) legyen
, , , , , , , ,
, , , , , és , ha
-
Számítsa ki a rendszer válaszát, ha a bemenőjel diszkrét idejű egységugrás.
-
Számítsa ki a rendszer válaszát, ha a diszkrét idejű bemenőjel a következő:
, , , , , , , ,
, , , , , és , ha
-
Mekkora a rendszer erősítése?
3 - 3 feladat (Házi feladat, megoldását nem közöljük)
Egy diszkrétidejű rendszer diszkrétidejű ugrásválasza (átmenetifüggvénye) legyen
, , és , ha
-
Számítsa ki a rendszer válaszát, ha a diszkrét idejű bemenőjel a következő:
-
és , ha
-
Mekkora a rendszer erősítése?
3 - 4 feladat (Házi feladat, megoldását nem közöljük)
Egy diszkrét idejű rendszer diszkrét idejű ugrásválasza (átmeneti függvénye) legyen
, , , , , , , ,
, , , , , és , ha
-
Számítsa ki a rendszer válaszát, ha a bemenőjel diszkrét idejű egységugrás.
-
Számítsa ki a rendszer válaszát, ha a diszkrét idejű bemenőjel a következő:
, , , , , , , ,
, , , , , és , ha
-
Mekkora a rendszer erősítése?
3.2. Vizsgálat a frekvencia-, illetve Laplace-operátoros tartományban
Tapasztalat:
Ha egy függőleges helyzetű rugó alsó végére egy tömeget akasztunk és a rugót ugyancsak függőlegesen szinuszosan mozgatjuk a felső végénél fogva, akkor a tömeg is szinuszosan fog lengeni a gerjesztéssel azonos frekvenciával, de a gerjesztéstől eltérő fázisban és amplitúdóval. Azt is érezzük, hogy ha a gerjesztés amplitúdója állandó marad, de a frekvenciáját növeljük, akkor a tömeg mozgásának amplitúdója fokozatosan csökken, és a fáziskésése növekszik. Tendenciájában ez a legtöbb valós rendszerre igaz.
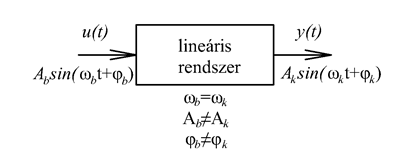
E tapasztalat indít arra, hogy a jeleket nem az időben, hanem a frekvencia-, illetve Laplace-operátoros tartományban bontjuk komponensekre. A frekvencia-, illetve Laplace-operátoros tartományban a felbontás matematikai alapja az, hogy szinuszos gerjesztés esetén egy lineáris differenciálegyenlet inhomogén megoldása a gerjesztő függvénnyel azonos frekvenciájú szinuszos függvény (ld. 3-12. ábra). Ez egyben rámutat az alkalmazás korlátaira, az itt leírtak nemlineáris rendszerekre általában nem (vagy csak nagyon körülményesen) alkalmazhatók. Meg kell jegyezni, hogy mérnöki szemmel a differenciálegyenletek infomogén megoldása egy gerjesztés hatására kialakuló állandósult állapot. A 3-12. ábra úgy értelmezhető, hogy ha a lineáris rendszert szinuszosan gerjesztjük, akkor a tranziens lezajlása után, az állandósult állapotban a kimenőjel szinuszosan fog változni.
Kihasználjuk még, hogy a periodikus függvények Fourier-sorba fejthetők. A Fourier-sorba fejtés általánosítható első lépésben véges energiájú nem periodikus, majd belépő függvényekre. A függvényeknek e három típusú felbontása különböző frekvenciájú komponensekre formális analógiát mutat a sík és térvektorok merőleges (ortogonális) komponensekre bontásával. E formális analógia mélyebb matematikai összefüggéseinek a feltárása olyan matematikai hátteret igényelne, amely messze túlmutatna e tananyag keretein. Ennek ellenére didaktikai szempontból építünk erre a formális hasonlóságra, mert a vektorok felbontásának szemléletessége nagymértékben segítheti a frekvencia-, illetve Laplace-operátoros tartománybeli összefüggések könnyebb megértését és tán a képletek megjegyzését is. A frekvencia-, illetve Laplace-operátoros tartománybeli gondolkodás képessége számos villamosmérnöki és szabályozástechnikai probléma megoldását segítheti.
Idézzük fel, amit a síkvektorok komponensekre bontásáról tudunk.
-
A síkvektorok esetén definiálva van a skaláris szorzás.
-
Egy v síkvektor abszolút értékének (hosszának) négyzete egyenlő a vektor önmagával vett skaláris szorzatával (3.27), itt megjegyezzük, hogy ha a síkvektort komplex számokkal írjuk le, akkor a vektor (komplex szám) abszolút értékét úgy kapjuk, hogy a komplex számot a komplex konjugáltjával szorozzuk.
|
|
(3.27) |
Legyen v egy síkvektor, valamint és két egymásra merőleges egységvektor. és a sík ortonormált bázisa, mivel bármely v vektor egyértelműen kifejezhető és segítségével a következő alakban (ld. 3-13. ábra)
|
|
(3.28) |
ahol az együtthatókat skaláris szorzással számíthatjuk ki.
|
|
(3.29) |
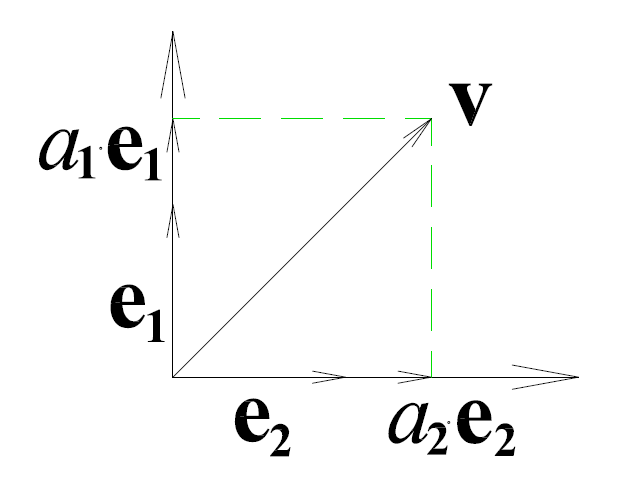
Az ortogonalitás feltétele, hogy és vektorok skaláris szorzata 0, . A normáltsághoz az kell, hogy és vektorok egységvektorok legyenek, vagyis az önmagukkal vett skaláris szorzatuk 1 legyen, . A sík, mint a síkvektorok tere teljes, ha tetszőleges és értékekkel (3.28) egy síkban létező vektort ír le.
További fontos és jól ismert összefüggés, hogy a vektor hosszának (a vektor abszolút értékének) négyzetét az együtthatók négyzetösszegével is kiszámíthatjuk (a keresztszorzatok az ortogonalitás miatt kiesnek).
|
|
(3.30) |
A fenti állítások triviálisnak hatnak és könnyen általánosíthatjuk 3D térvektorokra. Azt szeretnénk, ha hasonló könnyedséggel tudnánk a függvények felbontását is kezelni.
A fentiekből látható, hogy a kulcselem a skaláris szorzás, en nek segítségével definiálhatjuk a vektorok nagyságát (hosszát, mértékét), az ortogonalitást, továbbá a komponensek együtthatóit is skaláris szorzással számít hat juk ki.
Általános értelemben vett vektorok lineáris terét Hilbert-térnek nevezzük, ha a térben értelmezve van a skaláris szorzás, és a tér teljes a skaláris szorzásból származó normára nézve.
Egy tér teljes, ha minden benne haladó Cauchy-sorozat konvergens. A tér pontjaiból álló sorozatot akkor nevezzük Cauchy-sorozatnak, ha minden pozitív valóstávolság értékhez találunk olyan N egész számot, hogy az N-nél nagyobb indexű elemek közül bármely kettő közti távolság kisebb, mint a megadott távolság.
Ha tekintettel szeretnénk arra lenni, hogy egy komplex függvény normája is valós szám legyen (ld. (3.27) egyenlettel kapcsolatos megjegyzést), akkor a intervallumon értelmezett és abszolút integrálható valós vagy komplex függvények skaláris szorzatát a következő módon definiálhatjuk
|
|
(3.31) |
ahol a felülvonás a komplex konjugáltat jelöli (a valós függvényeket (3.31) speciális esetének tekintjük). Folytonos függvények esetén (3.31) minden további megkötés nélkül kielégíti a skaláris szorzás definícióját, de részben a mérnöki gyakorlat miatt, részben azért, hogy a vizsgált függvénytér teljes legyen, meg kell engednünk nem folytonos függvényeket is. Ebben az esetben (3.31) csak akkor elégíti ki a skaláris szorzás minden feltételét, ha az olyan függvényeket, amelyek csak nullamértékű halmazon különbözőek, más megfogalmazásban majdnem mindenütt megegyező értékűek, azonosnak tekintjük. A mérnöki gyakorlatban mindig élhetünk ezzel a megkötéssel és az integrál értékére sincs hatása, ha a függvényértékek nulla mértékű halmazon különböznek (az integrálszámításra a skaláris szorzásban betöltött szerepe miatt kell tekintettel lennünk). A függvények értelmezési tartománya nem csak véges zárt intervallum lehet, hanem nyílt vagy akár végtelen intervallum. Az abszolút integrálhatóságot azért kell kikötni, hogy (3.31) véges értéket adjon.
A (3.31) skaláris szorzatból számított norma (ezt szokás -normának is nevezni)
|
|
(3.32) |
Azokat a függvényeket, amelyekre a (3.32) norma véges értéket ad, szokás az osztályba tartozó függvényeknek nevezni, amelyekről belátható, hogy Hilbert-teret alkotnak.
Az függvény (3.28) kiterjesztéseként értelmezett felbontásához szükség van a (3.28)-ban szereplő és vektorok megfelelőjére a függvényosztályban. Matematikai megfogalmazásban szükségünk van egy ortonormált bázisra. Ehhez intuícióul szolgálhat a Fourier-sorfejtés, ezért idézzük fel az erről tanultakat.
3.2.1. Fourier-sorfejtés
Az olyan periodikus függvényeket (ld. 3-14. ábra) lehet Fourier-sorba fejteni, amelyek abszolút integrálja egy hosszúságú periódusra véges (A gyakorlatban előforduló esetekben ezzel egyenértékű feltétel, hogy (3.32) szerinti normája legyen véges).
|
|
(3.33) |
Ismertnek tekintjük a Fourier-sorok első szokásos, inkább csak matematikusok által használt alakját
|
|
(3.34) |
Ha folytonos és véges sok differenciálható darabból áll, akkor (3.34) rekonstruálja az eredeti függvényt. Olyan eseteket is megengedünk, amikor szakaszosan folytonos (-nek véges számú ugrása van, (példaként ld. 3-14. ábra)), ilyen függvények esetén (3.34) a szakadás helyén a kétoldali határérték számtani közepét adja vissza. Ez a megjegyzés a matematikai korrektség miatt fontos, de a mérnöki gyakorlatban nincs jelentősége, mert valós fizikai folyamatot leíró jelnek akkor van ugrása, ha rövid tranziensű jelenségeket elhanyagolva idealizáljuk a rendszer működését. Ez a tulajdonság öröklődik a később tárgyalandó inverz Fourier és Laplace-transzformáltakra is.
Megjegyezzük, hogy az ún. alapharmonikus körfrekvenciája, az alapharmonikus frekvenciája értelem szerűen adódik: .
(3.34) könnyen átírható arra az alakra, amely a mérnöki gyakorlatban a legelterjedtebb.
|
|
(3.35) |
A későbbiek szempontjából fontos kitérni a (3.35) fizikai értelmezésére. Egy periodikus függvény, amely kielégíti a (3.33) feltételt előállítható úgy, hogy először vesszük a függvény átlagát, majd ehhez hozzáadjuk amplitúdójú és körfrekvenciájú koszinuszos alapharmonikust a fáziseltolással, majd sorra a koszinuszos felharmonikusokat amplitúdóval, felharmonikus körfrekvenciával és fáziseltolással. Így a periodikus jelet megszámlálhatóan végtelen koszinuszos függvényből állítjuk elő. Hogy az alap- és felharmonikusok a jelben jelen vannak, azt onnan is láthatjuk, hogy ezek megfelelő szűrővel kinyerhetők a jelből, rezonanciára hajlamos rendszereknél rezonanciát okozhatnak. Villamos áramkörök esetén az értéket egyenáramú összetevőnek is szokás nevezni. A (3.35)-ból kiolvasható, hogy egy periodikus jelben az alapharmonikus és a felharmonikusok milyen amplitúdóval és fázisszöggel szerepelnek. Az amplitúdóértékeket szokás a frekvencia (esetenként a körfrekvencia) függvényében ábrázolni. A 3-15. ábra példaként egy négyszögjel alap- és felharmonikusainak az amplitúdóit ábrázoljuk (A periódusidő 10s, a négyszögjel nagysága 1, a számítás részleteit ld. 3-5 mintafeladatban)
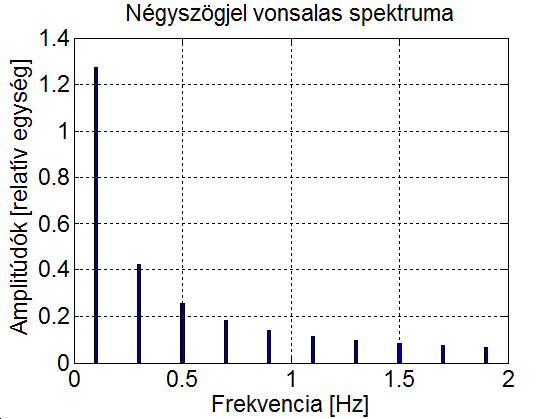
Bár a fizikai tartalmat (3.35) mutatja a legjobban, az általánosításhoz át kell térni a Fourier-sorok komplex alakjához. Abból indulunk ki, hogy
|
|
(3.36) |
A (3.36) segítségével (kihasználva, hogy =1) (3.35) a következő komplex alakra írható
|
|
(3.37) |
ahol az komplex együtthatók és a amplitúdók összefüggése a következő
|
|
(3.38) |
Látható, hogy egy valós függvényt komplex függvények összegével állítunk elő, így a komplex komponensek fizikailag önmagukban nehezen értelmezhetők, különösen a negatív előjellel szereplő körfrekvenciát nem tudjuk megmagyarázni, de az azonos abszolút értékű pozitív és negatív sorszámú komponensek egymástól függetlenül nem léteznek, egymástól függetlenül nem változnak, az információt együtt hordozzák. A (3.38)-ből kitűnik, hogy és egymásnak komplex konjugáltja, az komplex együtthatók abszolút értéke és fázisszöge szoros kapcsolatban van az adott komponens amplitúdójával és fáziseltolásával. Hangsúlyozzuk, nincs negatív körfrekvencia, csak a (3.36) felbontás miatt a mindig pozitív értékű körfrekvencia negatív előjellel is szerepel a függvény komplex felbontásában. A negatív frekvenciáknak az Euler forma miatt matematikailag van jelentőségük. A (3.37) előnye az, hogy formális hasonlóságot mutat a (3.28) kifejezéssel.
Így már kimondhatjuk: az függvényosztálynak az komplex függvények (ahol és ) ortonormált bázisát alkotják, ha ezen osztályba tartozó két függvény (jelölje ezeket és ) skaláris szorzatát a következő módon definiáljuk:
|
|
(3.39) |
Az együttható azért kell, hogy a bázis ne csak ortogonális legyen, hanem normált is.
|
|
(3.40) |
Az ortogonalitás azt jelenti:
|
|
(3.41) |
(3.29) általánosításaként (3.39) alapján az komplex együtthatók közvetlenül számíthatók
|
|
(3.42) |
A későbbiek miatt hangsúlyozzuk ki, hogy az komplex együttható függvénye -nak.
Ha az függvényosztályról beszélünk, akkor (3.36) szigorúan véve csak a intervallumra vonatkozik,
|
|
(3.43) |
Természetesen (3.43) ezen az intervallumon kívül is visszaadja a periodikus függvényt.
A (3.27) és (3.30) általánosítása is fontos szerepet játszik a mérnöki gyakorlatban. A fizikai összefüggések feltárásához alkalmazzuk a (3.35) alakot
|
|
(3.44) |
Periodikus jelek leginkább a villamosmérnöki gyakorlatban fordulnak elő. A (3.44) fizikai tartalmára egy nagyon egyszerű villamos áramköri példán keresztül világítunk rá. A példa megértéséhez elegendő az Ohm törvényt ismerni és azt tudni, hogy a feszültség és áram szorzata a teljesítmény. Legyen és az ellenállás feszültsége, árama és pillanatnyi teljesítménye. Ismert:
|
|
(3.45) |
Tegyük fel, hogy az ellenállást fűtésre használjuk. A feszültség és az áram időfüggvényét egyetlen számmal (normával) szeretnénk jelölni. A szoba hőmérsékletére az átlagteljesítménynek van hatása, így célszerű olyan normát választani, hogy abból az átlagteljesítmény könnyen számítható legyen, ezt a normát a villamos mérnökök effektív értéknek hívják. A (3.45) helyébe a következő egyszerűsített formát szeretnénk felírni:
|
|
(3.46) |
A (3.45) és (3.46)-ból az következik, hogy a feszültség és áram esetén az effektív értéket a következőképpen kell definiálni:
|
|
(3.47) |
ahol lehet vagy . Azt feltételezzük, hogy és periodikus, a periódusidő . Vegyük észre, ha a skaláris szorzás definíciója (3.39) alakú, akkor a villamos jeleknél bevezetett effektív érték megegyezik a jel normájával. Az effektív értéket az átlagteljesítményből származtattuk, így egy villamos jel átlagteljesítménye normájának négyzetével arányos (kiemeljük, hogy ez nem jelent egyenlőséget). (3.44)-ből következik, hogy egy villamos jel effektív értékének négyzete megegyezik az összetevők effektív értékének négyzetösszegével, vagyis (3.44) üzenete az, hogy a jel átlagteljesítménye a komponensek átlagteljesítményének összege. Szokás a jelösszetevők amplitúdónégyzetét is ábrázolni a frekvencia függvényében, ezt szokás teljesítményspektrumnak is nevezni (ismét hangsúlyozzuk, bizonyos jelek esetén ez csupán arányosságra utal, bizonyos jeleknél ez fizikailag nem értelmezhető), periodikus függvényeknek az amplitúdóérték spektrumához hasonlóan a teljesítményérték-spektrumuk is vonalas.
A (3.35) alakú felbontásban a koszinuszos komponensek ortogonálisak, de nem normáltak, ezért kell az ½ szorzó a összegzésénél. Ezzel szemben a (3.43) felbontás ortonormált, így
|
|
(3.48) |
3.2.2. Kidolgozott feladatok Fourier sorokhoz kapcsolódóan
3 - 5 feladat négyszögjel Fourier sor a
Határozza meg a 3-16. ábraán látható négyszögjel Fourier sorát
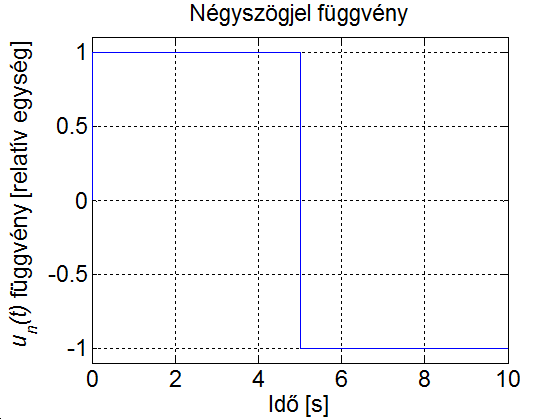
Megoldás
A jel szimmetriájából következik, hogy a Fourier-sor csak páratlan szinuszos tagokat tartalmaz, ezért célszerű a Fourier sor (3.34) alakját használni a következő formában:
|
|
(3.49) |
ahol és a bázis függvényekből áll. Az ábráról leolvasható a periódus idő és az alapharmonikus értéke
|
|
(3.50) |
Az együtthatókat ebben az esetben is skaláris szorzással határozhatjuk meg. A villamosmérnöki gyakorlatban a periodikus függvényeket általában a idő helyett szög függvényében ábrázoljuk és a Fourier sor együtthatóinak kiszámítása is egyszerűbb, ha helyett szerint integrálunk.
|
|
(3.51) |
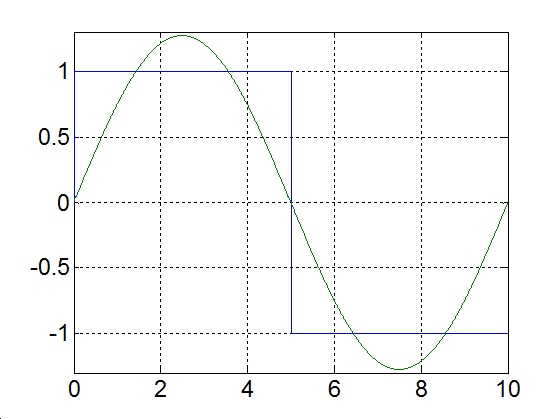
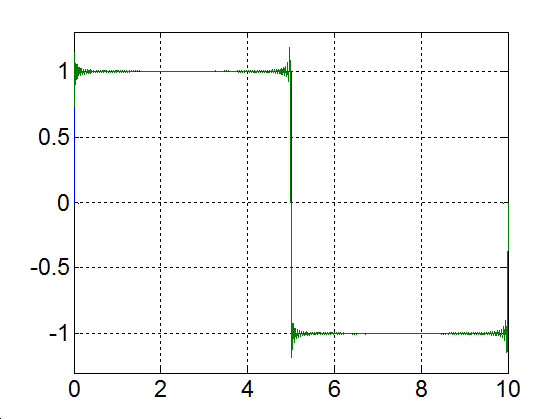
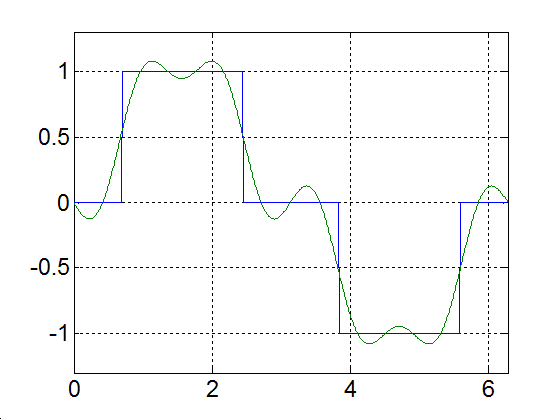
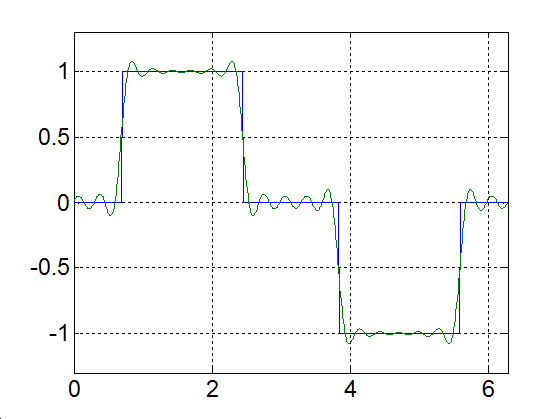
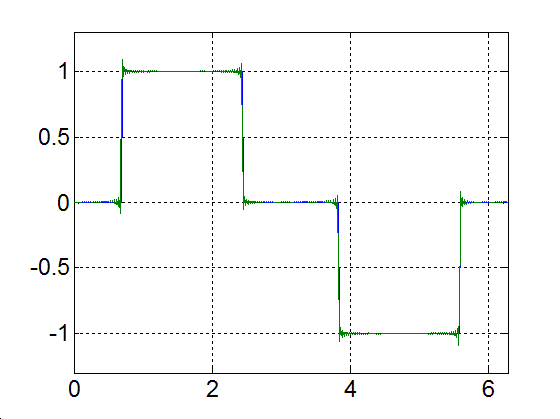
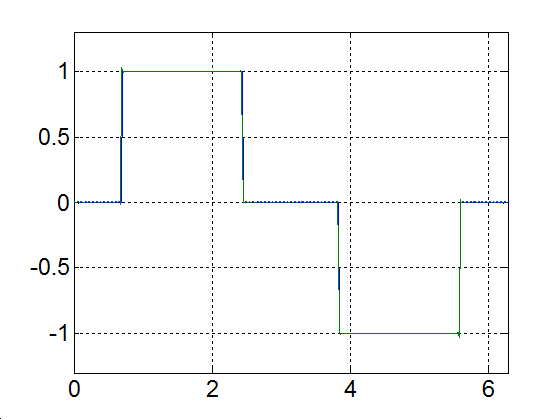
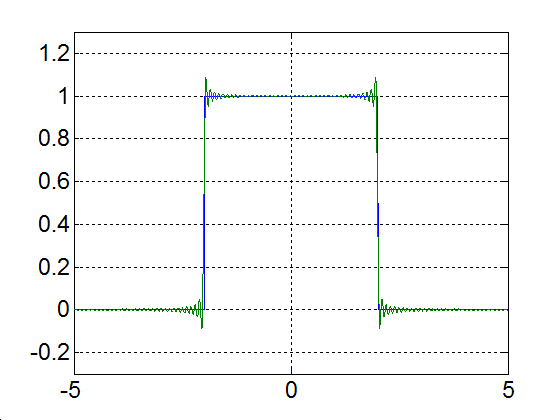
Rajzoljuk meg a következő függvényt, különböző számú felharmonikust figyelembe véve
|
|
(3.52) |
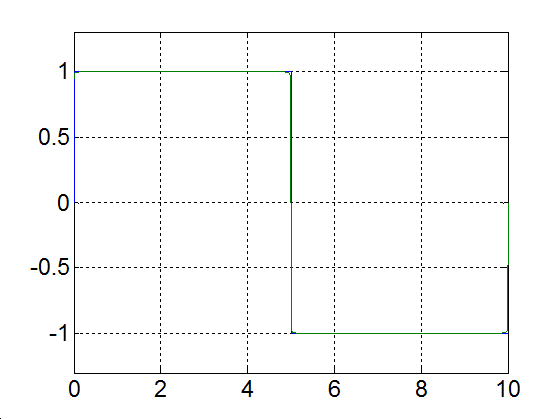
|
Alap-harmonikus |
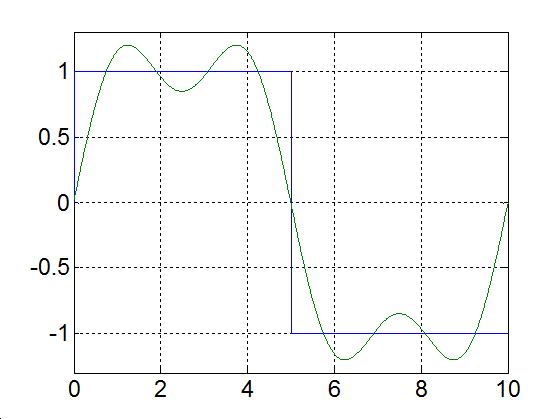
Alap- és az első felharmonikus |
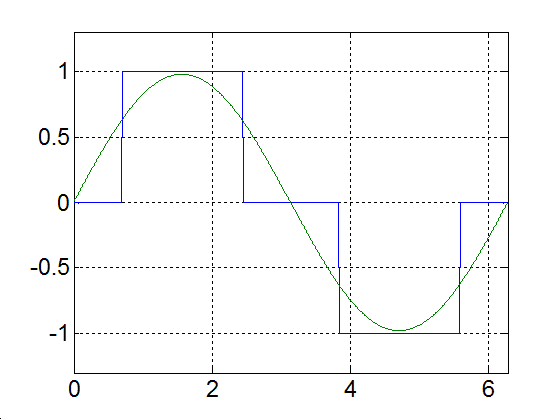
|
Alap- és az első két felharmonikus |
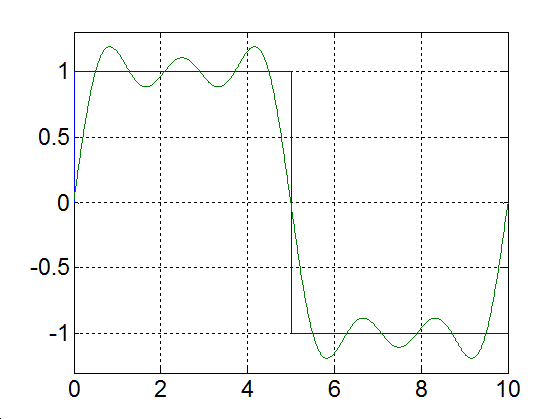
Alap- és az első kilenc felharmonikus |
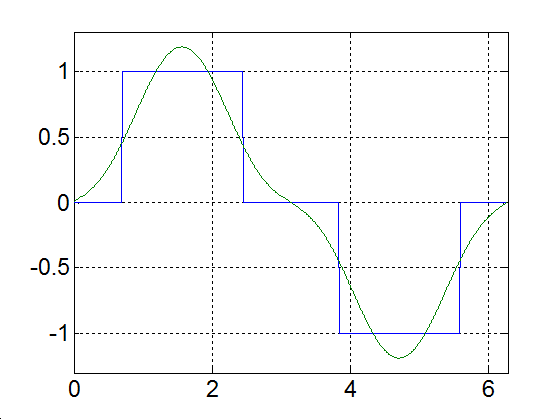
|
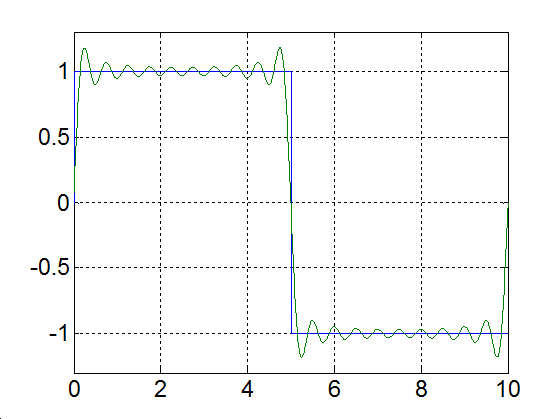
Alap- és az első száz felharmonikus |
Alap- és az első ezer felharmonikus |
3-17. ábra Négyszögjel Fourier sorfejtése
A fenti számítások a következő MATLAB program segítségével végezhetők el.
t=0:0.01:10;
max=size(t);
max=max(2);
for i=1:max
f(i)=sign(sin(t(i)/5*pi));
end
plot(t,f)
set(gca, 'fontsize', 17);
ylabel('{\it u_n(t)} függvény [relatív egység]');
xlabel('Idő [s]');
title('Négyszögjel függvény');
axis([0 10 -1.1 1.1]);
grid
pause
for ib=1:10
ii=2*ib-1;
af(ib)=4/pi/ii;
end
for is=1:max
fi(is)=0;
for l=1:10
ii=2*l-1;
fi(is)=fi(is)+af(l)*sin(is/max*2*pi*ii);
end
end
plot(t,f,t,fi)
axis([0 10 -1.3 1.3]);
grid
pause
bar( [0.1 0.3 0.5 0.7 0.9 1.1 1.3 1.5 1.7 1.9],af, 0.07)
set(gca, 'fontsize', 17);
ylabel('Amplitúdók [relatív egység]');
xlabel('Frekvencia [Hz]');
title('Négyszögjel vonsalas spektruma')
grid
3 - 6 feladat Fourier sorfejtés gyakorlati alkalmazása
A 3-18. ábra egy szünetmentes áramforrás egyszerűsített rajzát szemlélteti.
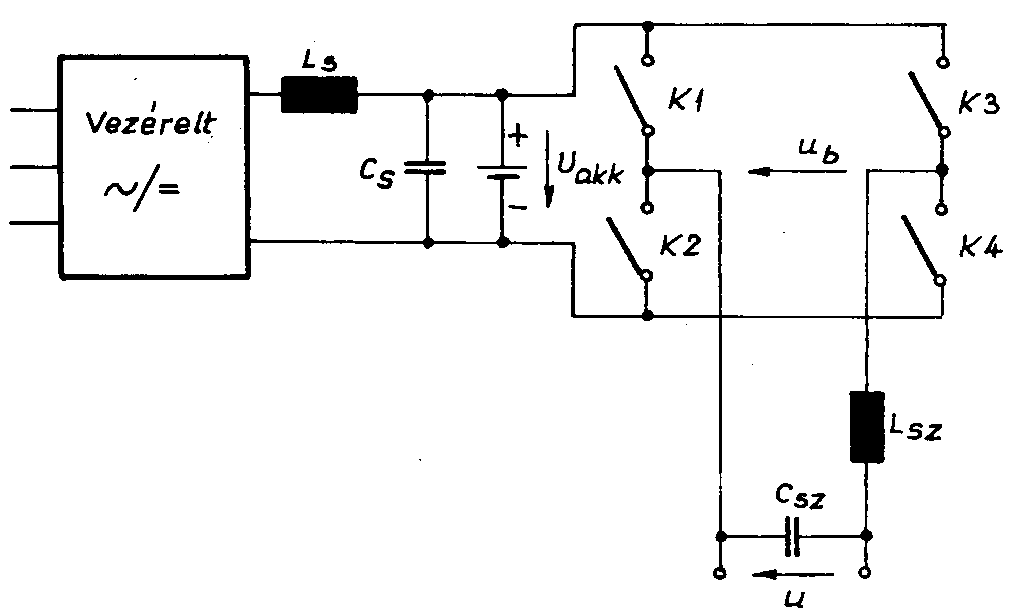
A szünetmentes áramforrás részei:
-
vezérelt egyenirányító
-
simító szűrő
-
akkumulátor
-
inverter (K1…K4)
-
kimeneti szűrő .
Mindaddig, míg van hálózati feszültség, a vezérelt egyenirányító táplálja az invertert, és gondoskodik arról, hogy az akkumulátor feltöltött állapotban legyen. Hálózati feszültség kimaradásakor az akkumulátor a benne tárolt energia révén szünetmentesen tudja tartani az inverter, illetve a fogyasztó táplálását.
Az inverter – működési elvéből adódóan – csak különböző előjelű négyszög alakú impulzusok kiadására képes. Tegyük fel, hogy mindkét fél-periódusban szimmetrikusan kiadunk egy szélességű impulzust. Az egyszerűség kedvéért az impulzust relatív egységben, az függvényében ábrázoljuk (az időt radiánban mérjük, ld. 3-19. ábra)
A fogyasztók többsége azonban szinuszos feszültséget igényel, ezért szükséges a kimeneti szűrőkör.
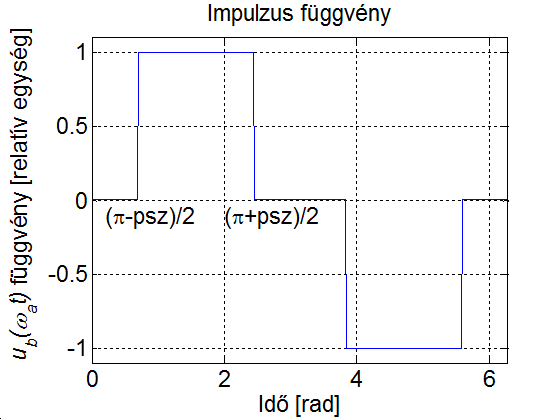
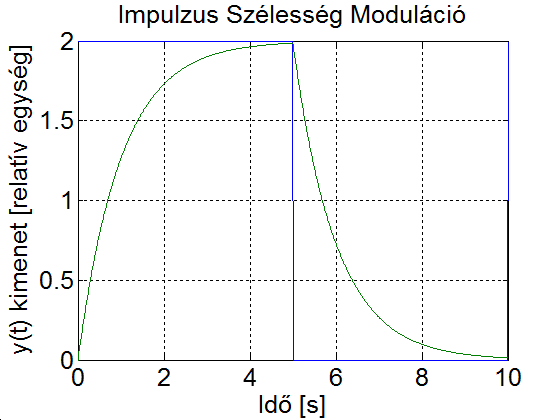
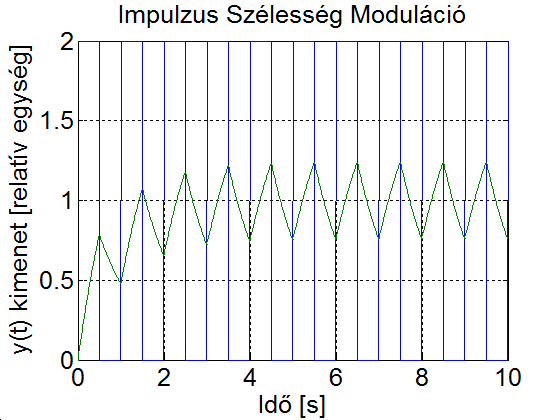
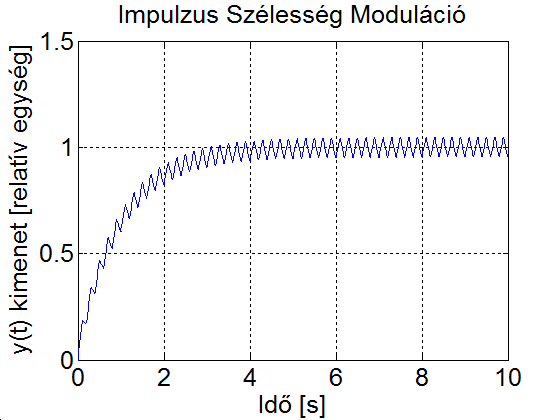
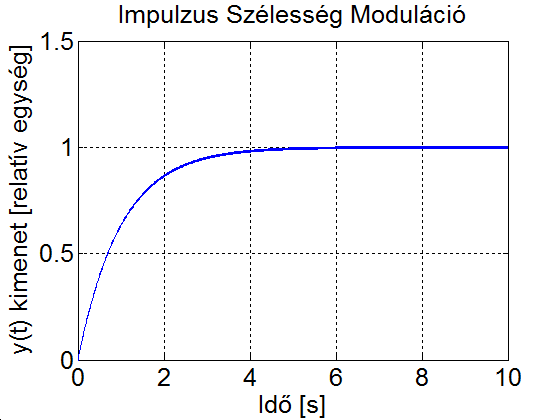
Az alapharmonikus feszültség szabályozása, de nem utolsó sorban a szűrőkör árának és méretének csökkentése érdekében is, úgynevezett PWM (Pulse Width Modulation = impulzus szélesség moduláció) eljárást szokás alkalmazni. Az egyik legegyszerűbb PWM-módszer a 3-19. ábra látható. Az áramforrás kimenő feszültségének effektív értékét az inverter által előállított szimmetrikus impulzus jel szélességének változtatásával lehet módosítani. Ha egy félperióduson belül az impulzusok számát növeljük, akkor egyidejűleg változtathatjuk a kimenő feszültség effektív értékét és felharmonikus tartalmát. A PWM lényege a szűrés szempontjából bban áll, hogy változatlan effektív érték mellett az alapharmonikushoz képest az alacsony rendszámú felharmonikusok nagyságát lecsökkentjük vagy teljesen megszüntetjük azon az áron, hogy közben a nagyobb rendszámú felharmonikusokat relatívan megnöveljük; a nagyobb rendszámú felharmonikusok pedig kisebb méretű, és ezért olcsóbb szűrőkörrel csökkenthetők, mint az alacsony rendszámúak.
-
Határozza meg a feszültség jel effektív értékét az impulzus időben kifejezett szélességének függvényében.
-
Ábrázolja függvényében az első három felharmonikus nagyságának alakulását!
-
Mekkorára kell -t választani, ha az rendszámú felharmonikust meg akarjuk szüntetni?
Megoldás
-
Az effektív érték (3.47) definíciója alapján
|
|
(3.53) |
-
A jel szimmetriájából következik, hogy a Fourier-sor csak páratlan szinuszos tagokat tartalmaz, ezért célszerű a Fourier sor (3.34) alakját használni a következő formában:
|
|
(3.54) |
ahol és a bázis függvényekből áll. Az együtthatókat ebben az esetben is skaláris szorzással határozhatjuk meg.
|
|
(3.55) |
Felhasználva a
|
|
(3.56) |
azonosságot:
|
|
(3.57) |
|
|
(3.58) |
A 3-20. ábra az és együtthatók vonatkoztatott abszolút értékét mutatja nagyság függvényében. Az a teljes kitöltésű négyszög alakú jel alapharmonikusa. Az előjele a -edik felharmonikus fázisával van kapcsolatban.
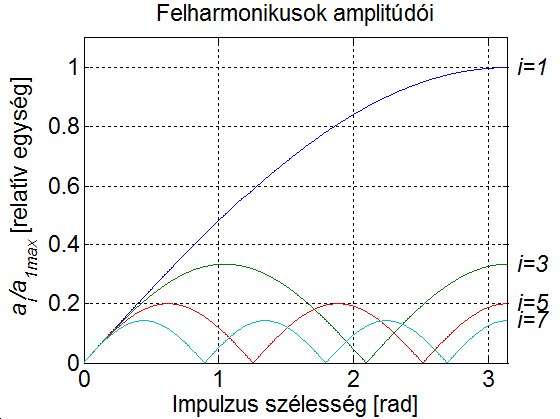
-
Az kifejezéséből látható, hogy megfelelő választásával tetszőleges rendszámú felharmonikus megszüntethető. A rendszámú felharmonikus megszűnését jelentő
egyenlőség akkor teljesül, ha
Mivel , ezért
impulzus szükséges.
Megjegyezzük, hogy ha egy félperiódusban több impulzust adunk ki, akkor az impulzusokat egyenként Fourier-sorba fejthetjük és ezeket a sorokat tagonként összegezhetjük. Belátható, hogy az impulzusok helyének megfelelő választásával annyi felharmonikus küszöbölhető ki, ahány impulzus esik egy félperiódusra. Ugyanakkor nem szabad megfeledkezni arról, hogy az impulzusszélesség moduláció közben az alapharmonikus értéke is csökken, így néhány felharmonikus értéke relatívan növekedhet.
3 - 7 feladat Fourier sorfejtés MATLAB programmal
Készítse el az előző feladat számításait MATLAB programmal a következő adatokkal
és
Megoldás
t=0:0.01:2*pi;
max=size(t);
max=max(2);
for i=1:max
if abs(sin(t(i)))>0.64
f(i)=sign(sin(t(i)));
else
f(i)=0;
end
end
plot(t,f)
set(gca, 'fontsize', 17);
ylabel('{\it u_b(\omega_at)} függvény [relatív egység]');
xlabel('Idő [rad]');
title('Impulzus függvény');
axis([0 2*pi -1.1 1.1]);
text(0.2,-0.1,['{\fontsize{17}(\pi-psz)/2}'])
text(2,-0.1,['{\fontsize{17}(\pi+psz)/2}'])
grid
a1max=4/pi*sin(pi/2);
for i=1:max
a1(i)=abs(4/pi*sin(pi/2)*sin(i/max*pi/2))/a1max;
a3(i)=abs(4/pi/3*sin(pi/2*3)*sin(i/max*pi*3/2))/a1max;
a5(i)=abs(4/pi/5*sin(pi/2*5)*sin(i/max*pi*5/2))/a1max;
a7(i)=abs(4/pi/7*sin(pi/2*7)*sin(i/max*pi*7/2))/a1max;
end
pause
plot(t/2,a1,t/2,a3,t/2,a5,t/2,a7)
set(gca, 'fontsize', 17);
ylabel('{\it a_i/a_{1max}} [relatív egység]');
xlabel('Impulzus szélesség [rad]');
title('Felharmonikusok amplitúdói');
axis([0 pi 0 1.1]);
grid
text(pi,1,['{\it \fontsize{17} i=1}'])
text(pi,a3(max),['{\it \fontsize{17} i=3}'])
text(pi,a5(max),['{\it \fontsize{17} i=5}'])
text(pi,a7(max),['{\it \fontsize{17} i=7}'])
pause
psz=pi-2*asin(0.64);
for ib=1:10
ii=2*ib-1;
af(ib)=4/pi/ii*sin(ii*psz/2)*sin(pi/2*ii);
end
for is=1:max
fi(is)=0;
for l=1:10
ii=2*l-1;
fi(is)=fi(is)+af(l)*sin(is/max*pi*2*ii);
end
end
plot(t,f,t,fi)
axis([0 2*pi -1.3 1.3]);
grid
|
Alap-harmonikus |
Alap- és az első felharmonikus |
|
Alap- és az első két felharmonikus |
Alap- és az első kilenc felharmonikus |
|
Alap- és az első száz felharmonikus |
Alap- és az első ezer felharmonikus |
3-21. ábra Szimmetrikus impulzus Fourier sorfejtése
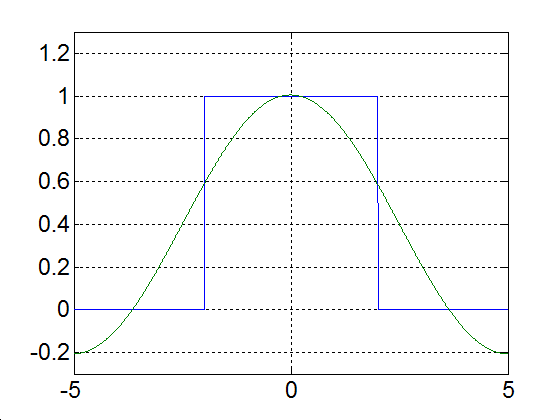
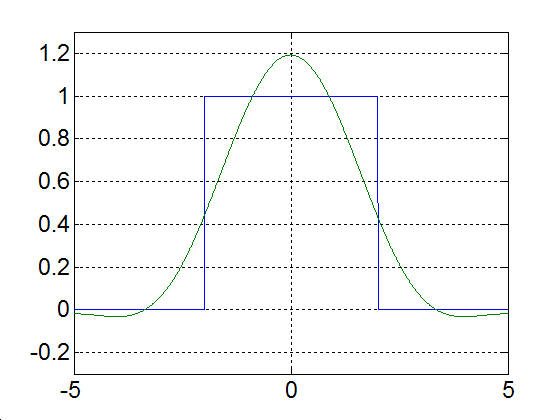
3 - 8 feladat Egy impulzus jel Fourier sora ( komplex együtthatókkal)
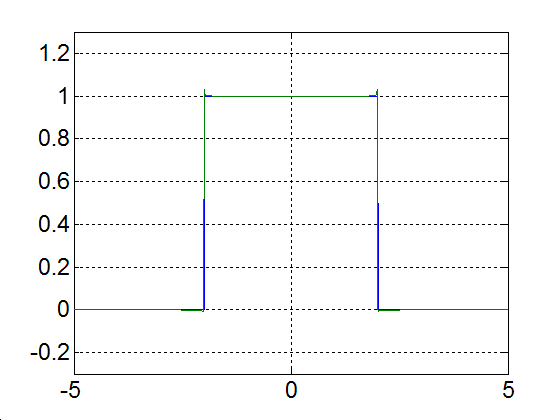
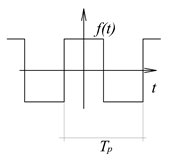
Határozza meg a 3-22. ábraán látható impulzus jel Fourier sorát. Legyen a periódus idő, és az impulzus szélessége, az impulzus nagysága az egyszerűség kedvéért legyen 1. Az ábráról leolvasható a periódus idő és az impulzus szélessége ( és ). Az alapharmonikus értéke:
|
|
(3.59) |
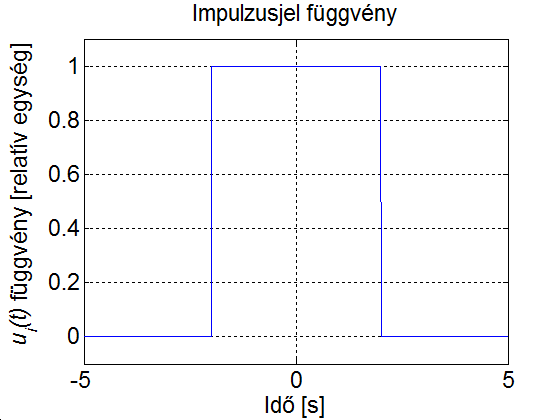
Megoldás
Használjuk a Fourier sorok (3.37) komplex alakját, az együtthatók (3.42) alapján számítva, és kihasználva a sorfejtendő függvény 0 vagy 1 értéket vehet fel.
|
|
(3.60) |
ahol . , -a jel egy periódusra vonatkozó átlagértéke- a 3-22. ábraáról közvetlenül kiolvasható, de (3.60) összefüggésből l'Hopital szabállyal is ugyanazt az eredményt kapjuk
|
|
(3.61) |
Látható, hogy az összes együttható valós, ez (3.37) és (3.38) alapján azt jelenti, hogy a Fourier sorok (3.35) alakja esetén a koszinuszos tagok fáziseltolása nulla.
|
|
(3.62) |
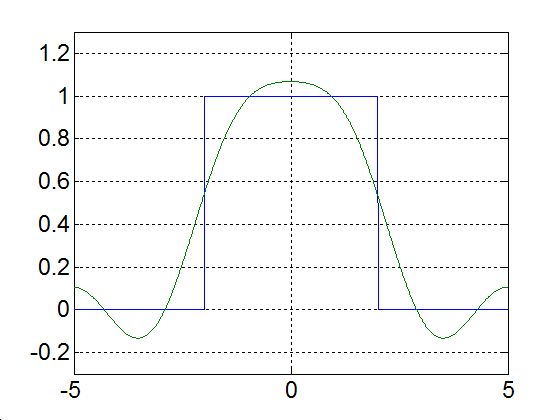
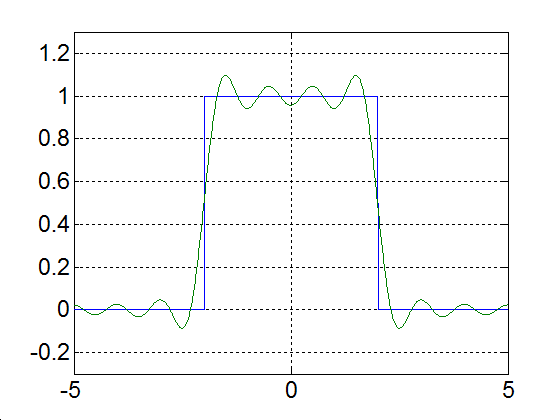
|
Alap-harmonikus |
Alap- és az első felharmonikus |
|
Alap- és az első két felharmonikus |
Alap- és az első kilenc felharmonikus |
|
Alap- és az első száz felharmonikus |
Alap- és az első ezer felharmonikus |
3-23. ábra Egy impulzus Fourier sorfejtése
A MATLAB fájl
t=-5:0.01:5;
max=size(t);
max=max(2);
Tsz=4;
Tp=10;
dr=Tsz/Tp;
for i=1:max
f(i)=0;
if t(i)>-(dr)*5
f(i)=1;
end
if t(i)>(dr)*5
f(i)=0;
end
end
plot(t,f)
set(gca, 'fontsize', 17);
ylabel('{\it u_i(t)} függvény [relatív egység]');
xlabel('Idő [s]');
title('Impulzusjel függvény');
axis([-5 5 -0.1 1.1]);
grid
pause
nn=1001;
for ib=1:nn
af(ib)=sin(ib*pi*dr)/ib/pi;
end
for is=1:max
fi(is)=dr;
for l=1:nn
fi(is)=fi(is)+af(l)*2*cos((-max/2+is/max)*2*pi*l);
end
end
plot(t,f,t,fi)
axis([-5 5 -0.3 1.3]);
grid
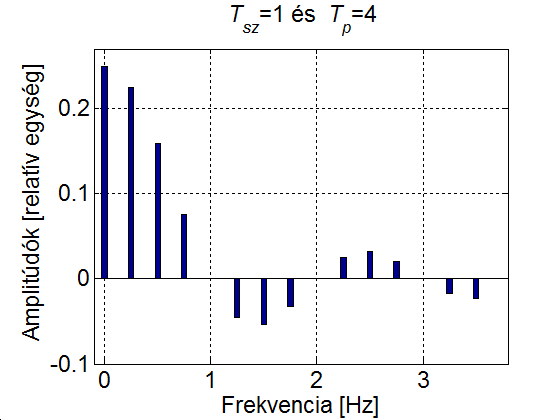
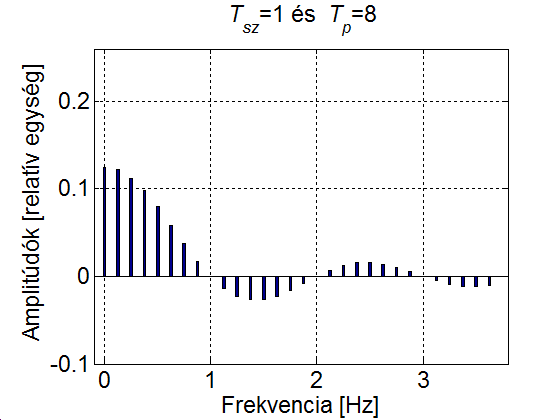
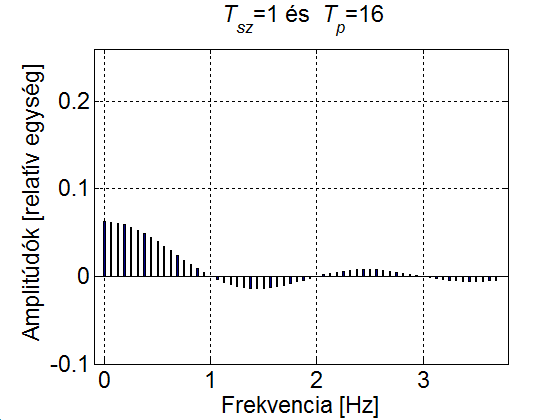
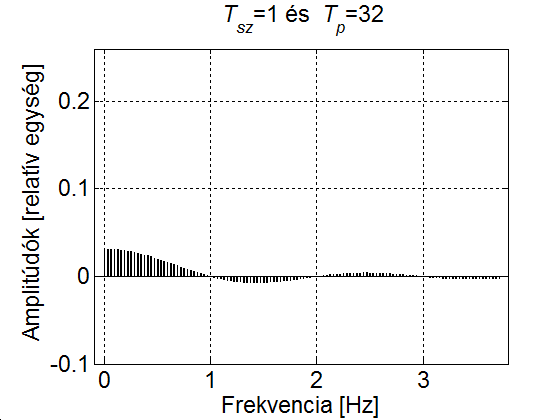
3 - 9 feladat Egy impulzusjel vonalas spektruma
Vizsgáljuk meg, hogy miként változik az impulzus jel spektruma, ha az impulzus szélessége állandó (), ugyanakkor a periódusidő növekszik. Csak a pozitív tartományt ábrázoljuk (a negatív tartomány ennek tükörképe).
Megoldás
Tsz=1;
Tp=4;
dr=Tsz/Tp;
nn=15/4*Tp;
fr(1)=0;
af(1)=dr;
for ib=2:nn
fr(ib)=(ib-1)/Tp;
af(ib)=sin((ib-1)*pi*dr)/(ib-1)/pi;
end
bar( fr,af, 0.2)
set(gca, 'fontsize', 17);
ylabel('Amplitúdók [relatív egység]');
xlabel('Frekvencia [Hz]');
title(['{\it T_{sz}}=1 és {\it T_p}=' int2str(Tp)])
grid
axis([-0.1 3.8 -0.1 0.26]);
|
|
|
|
|
|
3-24. ábra Egy impulzus jel vonalas amplitúdó spektruma
A 3-24. ábra szemléletesen mutatja, hogy a növelésével az amplitúdók egyre csökkennek és a vonalak (a felharmonikusok) egyre sűrűbben lesznek. Ez természetesen a (3.60) képletből is kiolvasható, ahol az is látszik, hogy ha az amplitúdó értékeket megszorozzuk -vel, akkor az aktuális értéktől függetlenül az amplitúdó spektrum burkológörbéje egy függvény.
|
|
(3.63) |
Más szavakkal, a vonalas amplitúdó spektrum nem más, mint a mintavételezése, ahol a mintavételezés sűrűsége növekszik, ha a periódus időt növeljük.
3.2.3. Fourier-transzformáció
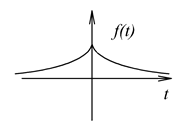
A Fourier-transzformáció megértéséhez célszerű a 3-9 feladatot tanulmányozni, ahol egy állandó nagyságú impulzus periodikusan ismétlődött. Minél nagyobb a periodusidő, annál távolabb kerülnek egymástól az impulzusok. Ha azt akarjuk, hogy egyetlen impulzusunk legyen, akkor a periódus időt végtelenre kell növelni. Ezt általánosítva, nem periodikus jelek esetén szokás azzal a szemléletes képpel élni, miszerint tegyük fel, hogy a jel periodikus, csak a periódus ideje végtelen, amikor a végtelenben befejeződött egy periódus, akkor kezdődik a következő, ugyancsak végtelen hosszú periódus. Vegyük észre, hogy (3.43) és (3.40) sehol sem használja ki a jel periodikusságát, így formálisan kiterjeszthető olyan abszolút integrálható (lecsengő) nem periodikus jelekre (ld. 3-25. ábra), ahol , de itt kell tennünk néhány megjegyzést.
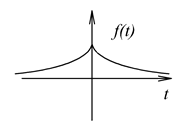
-
Ha , akkor az alapharmonikus nulla,
-
Az 1. megjegyzésből az következik, hogy az kitevőjében alakban tetszőleges körfrekvencia megjelenik, ezért a (3.43) összegzés nem mehet sorszám szerint formálisan, a (3.43) összegzésben megszámlálhatatlanul sok összeget kellene figyelembe venni, ami ilyen formában nem működik. Így nem az -t léptetjük, helyette lépésekben kell az összegzést elvégezni, a (3.43) összegzés helyett egy szerinti integrált kell felírni.
-
Ha és abszolút integrálható, akkor (3.42) minden -ra nullát ad, ezért a formálisan az így kiszámított értékeknek önmagukban nincs semmilyen információtartalma. Fizikailag ezt úgy magyarázhatjuk, hogy a nem periodikus jel megszámlálhatatlanul végtelen, nulla amplitúdójú koszinuszos összetevőből áll. Mivel megszámlálhatatlanul sok nullaértékű tagot összegezünk, ezért az összeg lehet nem nulla. Az információt nem az amplitúdóban kell keresnünk. Ezért az amplitúdóérték helyett bevezetjük az amplitúdósűrűség fogalmát. Ha pusztán formálisan nézzük, akkor a (3.42) összefüggésben kiszámított nulla nagyságú amplitúdókat elosztjuk az alapharmonikus frekvenciájával, vagyis megszorozzuk a végtelen nagyságú periódus idővel és így alakban véges értékeket kapunk. Az amplitúdósűrűséget is ábrázolhatjuk akár a frekvencia, akár a körfrekvencia függvényében. Ekkor egy folytonos amplitúdósűrűség spektrumot kapunk. De itt ennél sokkal több van, így egy alapvetően más művelethez jutunk. Ahelyett, hogy egy függvényt komponensek összegére bontanánk, a függvényt leképezzük egy másik függvényre. Más megfogalmazásban egy függvény transzformációt végezünk el.
E megjegyzésekre tekintettel (3.42) és (3.43) általánosítását abszolút integrálható nem periodikus jelek esetén Fourier-transzformációnak és inverz transzformációnak nevezzük. Ezekk a következő alakban írhatók fel:
Pusztán jelöléstechnikai kérdés, (3.64) és (3.65) helyett szokásos a következő jelölés
Megjegyezzük, hogy bizonyos szerzők a körfrekvencia helyett a frekvenciát használják, ekkor
Mivel a Fourier-transzformációt a Fourier-sorokból származtattuk, ezért a komplex amplitúdósűrűség függvénynek a fizikai tartalmát is a Fourier-sorokból érthetjük meg.
Ugyan minden frekvenciához tartozó komponens önmagában nézve nulla amplitúdóval szerepel az összegzésben, de ha sávokat nézünk, akkor az egyes frekvenciasávok súlya már mérhető. Ha összehasonlítjuk két értékét, Pl. az és helyettesítési értéket, és azt találjuk, hogy , akkor azt mondjuk, hogy ugyan mind az és mind az körfrekvenciájú összetevő nulla amplitúdójú, de az körfrekvenciájú összetevő súlya még is kétszerese az körfrekvenciájú összetevő súlyának az jelben. Az komplex szám argumentuma az adott frekvenciájú összetevő fáziseltolását adja meg. Hogy ezek az összetevők jelen vannak a jelben azt onnan is tapasztalhatjuk, hogy lengésre hajlamos rendszereknél rezonanciajelenséget is megfigyelhetünk. Ezt az alkalmazástól függően vagy ki akarjuk használni, vagy el akarjuk kerülni, pl. szabályozásnál instabilitást nem engedünk meg.
3.2.3.1. Teljesítmény spektrum
Az amplitúdósűrűséghez hasonlóan bevezethetjük a teljesítménysűrűséget, talán ez az, ami fizikailag legjobban értelmezhető és mérhető. Ennek segítségével meghatározhatjuk, hogy egy frekvencia sávra a jel teljes átlagteljesítményéből mennyi jut. Csak arra kell ügyelnünk, hogy formálisan a negatív előjelű frekvencia tartományban is integrálni kell, különben a komplex függvény integrálásakor nem kaphatunk valós teljesítmény értéket (ld. (3.36) ). Egy jel effektív értékének négyzete a Fourier-transzformált jelből közvetlenül kiszámítható. xxxxxx
|
|
(3.70) |
3.2.3.2. Frekvenciaátviteli függvény (frekvenciakarakterisztika)
A Fourier-transzformációt széles körben alkalmazzuk, egyrészt ennek segítségével határozhatjuk meg a jelek spektrumát, másrészt a rendszerek leírására is használhatjuk. A 3-12. ábraból kiindulva kiszámíthatjuk, hogy egy konkrét frekvenciájú gerjesztés válasza (az inhomogén differenciálegyenlet megoldása) mi lesz, hogyan változik meg az amplitúdó és a fázisszög a gerjesztés frekvenciája (pontosabban körfrekvenciája) függvényében. Sok esetben ezt nem direktben számítjuk, mert bizonyos közbenső számításoknál a Fourier-transzformált nem értelmezhető. Fourier-transzformációnak van egy fontos korlátja. A gyakorlatban előforduló olyan egyszerű jelek esetén sem alkalmazható, mint az egységugrás jel. A megoldás a következő fejezetben olvasható.
3.2.4. Laplace-transzformáció
A Fourier-transzformáció alkalmazásakor akkor ütközünk akadályba, ha olyan nem periodikus jelekre is ki akarjuk terjeszteni a frekvencia tartománybeli vizsgálatot, amelyek nem abszolút integrálhatóak. Ennek az a módja, hogy ezeket a függvényeket is abszolút integrálhatóvá tesszük, ezt azzal érjük el, hogy egyszerűen beszorozzuk az függvényt egy függvénnyel (ahol egy megfelelően megválasztott érték és csak úgynevezett belépő függvényeket engedünk meg. Szemléletesen a tartományban lenullázzuk a függvényt és a tartományban lekalapáljuk, hogy lecsengő legyen. A Laplace-transzformálhatóság feltétele így:
|
|
(3.71) |
Ezt követően már az függvényt formálisan Fourier-transzformálhatjuk és visszatranszformálhatjuk azzal a kikötéssel, hogy a tartományban a függvény nulla:
Az eredeti függvényt is könnyen visszakaphatjuk
|
|
(3.74) |
A tartományban a függvény nulla, ezért (3.64)-ban az alsó integrálási határ is nulla, továbbá az helyettesítéssel élünk
|
|
(3.75) |
A -0 azt fejezi ki, hogy az integrálást úgy kell elvégezni, hogy az esetlegesen a időpillanatban fellépő Dirac-impulzus hatását figyelembe tudjuk venni. Alkalmazzuk formálisan az inverz Fourier-transzformációt, ekkor az függvényt kapjuk vissza, amelyet az függvénnyel meg kell szorozni, hogy az eredeti függvényt kapjuk. Mivel nem függ a körfrekvenciától, így bevihető az integráljel alá. Kihangsúlyozzuk, hogy a (3.75) képletben csak a 0≤t tartomány szerepel, így az inverz Laplace-transzformációval is csak ezt a tartományt tudjuk visszaállítani.
|
|
(3.76) |
A Laplace- és az inverz Laplace-transzformáció szokásos jelölése még:
A Laplace-transzformált függvény fizikai tartalmát nehéz lenne megmagyarázni, ugyanakkor ez egy nagyon jól használható matematikai eszköz. Gyakran előfordul, hogy olyan jelekkel végzünk műveletet, amelyeknek nem létezik a Fourier-transzformáltja, ezért kénytelenek vagyunk a Laplace-transzformációhoz folyamodni. De a végeredményről egyéb fizikai megfontolásokból tudjuk, hogy Fourier-transzformálható, így a végső lépésben a helyettesítéssel megkapjuk a jel spektrumát (Fourier-transzformáltját). Nagyon fontos, hogy a mérnöki gyakorlatban sokszor a jel fizikai tulajdonságai alapján mondjuk ki, hogy a jel matematikai értelemben eleget tesz-e a Fourier-, illetve Laplace-transzformálhatóság feltételének.
3.2.5. Fourier-sorfejtés, Fourier- és Laplace-transzformáció áttekintő táblázat
3. 1 Tábláza t
|
Függvény típusok |
|||
|
Periodikus függvények |
Lecsengő függvények |
Belépő függvények |
|
|
|
|
|
|
|
Feltétel |
|||
|
|
|
|
|
|
Komponensre bontás (skaláris szorzással) |
|||
|
|
|
|
|
|
Jel visszaállítása a komponensekből |
|||
|
|
|
|
|
|
„Pütagorász-tétel” általánosítása Parseval-tétel |
|||
|
|
|
||
3.2.6. Laplace-transzformáció alkalmazása
E fejezetben közölt szabályok, állítások bizonyítása a függelékben található.
3.2.6.1. Azonosságok összefoglalása
Tegyük fel, hogy
akkor érvényesek a következő szabályok
Hasonlósági szabály
Csillapítási szabály
Eltolási szabály
Konvolúciós szabály
Szorzás idővel
Integrálási szabály
Differenciálási szabály ,
ahol baloldali határértéke helyen
Többszörös differenciálási szabály:
ahol az függvény -dik deriváltjának baloldali határértéke a helyen
Megjegyzések
-
Ha van egy függvény, amely folytonos és hagyományos értelemben deriválható a teljes tartományban, és ezt a függvényt Laplace-transzformáljuk, akkor az csak a tartományra vonatkozik, vagyis formálisan a tartományban a függvényt lenullázzuk és a tartományról miden információt elveszítünk, így pl. nem tudunk különbséget tenni a konstans 1 és az egységugrás függvény között. Mindkettőnek a Laplace-transzformáltja. Általában, ha , akkor a Laplace-transzformácó alkalmazásával az függvényt belépő függvénnyé alakítjuk, vagyis a Laplace-transzformáció szempontjából figyelembe vett függvénynek ugrása van a helyen. (ld. 3-26. ábra) Ez az ugrás kihat Laplace-transzformáltjának értékére, hiszen a Laplace-transzformáció a esetre vonatkozik. Szemléletesen azt is mondhatjuk, hogy a Laplace-transzformációból hiányzó értékre vonatkozó információt kell pótolni a deriválási szabálynál.
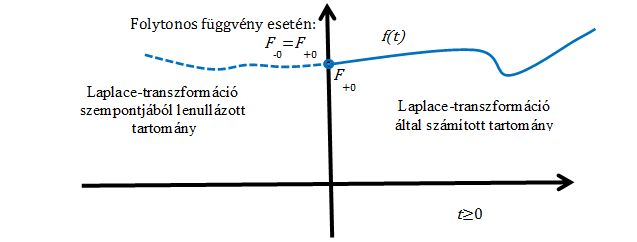
Ha a deriválási szabályból kapott eredményt inverz Laplace-transzformáljuk,
|
|
( 3.79 ) |
A Laplace-transzformáció kizárólag belépő függvényekre vonatkozik, ha egy nem nulla értékből induló belépő függvényt deriválunk, akkor az mindenképp generál egy Dirac-impulzust. Ha a függvény mégsem belépő, hanem folytonos, akkor ez a Dirac-impulzus felesleges és le kell vonnunk.
Visszatérve a példánkhoz, a konstans 1 függvénynek és az egységugrás függvény Laplace-transzformáltja egyaránt . Mindkettő esetén , de értéke különbözik, ahogy a két függvény deriváltja sem azonos.
|
|
( 3.80 ) |
Az első esetben a derivált azonosan nulla, a második esetben egy Dirac-impulzus és ez megfelel az előzetes elvárásainknak. További példák a deriválási szabály alkalmazására folytonos és ugrásfüggvény esetén a 3.2.9 pontban kidolgozott feladatok között találhatók.
-
A mérnöki gyakorlatban a Laplace-transzformációt bekapcsolási jelenségek vizsgálatára használjuk. Mérnöki szempontból fontos, hogy a fenti matematikai megfontolások gyakorlati alkalmazásakor a fizikai hátteret is tisztázzuk. Ha (2.107) alakú differenciálegyenlettel leírható rendszerek megoldását keressük Laplace-transzformáció segítségével, akkor a gerjesztés általában egy ugrás függvény, ahol . Ha véletlenül olyan esettel találkozunk, ahol , akkor valószínűsíthetően célszerű átgondolni a rendszermodellt, és új állapotváltozót bevezetni. Hasonlóan a gerjesztés magasabb rendű deriváltjainak baloldali határértéke a 0 pontban általában 0. Ezzel szemben és az idő szerint az első derviáltja, pontosabban az állapotvállozók, általánosított értelembe vett energia jellegű mennyiséget írnak le, így valóságos esetben (véges gerjesztés mellett) folytonosak. Ha egy rendszer alakú differenciálegyenletének mindkét oldalát Laplace-transzformáljuk és feltételezzük, hogy folytonos és , akkor
|
|
( 3.81 ) |
Ha ezt követően a kapott eredményt inverz Laplace-transzformáljuk, akkor -t csak a tartományban belépő függvényként kapnánk vissza. A folytonosságot úgy tudjuk visszaállítani, ha visszacsempésszük az értéket
|
|
( 3.82 ) |
Ilyen formában a kezdeti értéket expliciten is megjeleníthetjük a rendszer differenciálegyenletében. Ezt később kihasználjuk a hatásvázlat készítésekor is.
-
A fenti matematikai fejtegetés fizikai háttere a következő. Laplace-transzformációval mindig bekapcsolási jelenségeket vizsgálunk, és mindig energiamentes
|
|
( 3.83 ) |
kezdeti állapotból indulunk ki. Ha a rendszer mégsem energiamentes a vizsgálódásunk kezdetén, akkor egy pillanatszerű energiaközléssel (végtelenül nagy teljesítményű beavatkozással), vagyis egy Dirac-impulzussal beállítjuk a megfelelő kezdeti értéket. Pl. egy motor fordulatszámát egy olyan esetben vizsgáljuk, amikor a motor üresjárásban elérte az üresjárási fordulatszámot, majd ugrásszerűen megváltoztatjuk a terhelést, és arra vagyunk kíváncsiak, hogy a terhelésrádobás hatására miként változik a fordulatszám, akkor úgy kell eljárnunk, hogy először egy pillanatszerű mozgási energiaközléssel, vagyis egy Dirac-impulzussal beállítjuk az üresjárási fordulatszámot, és ezt követően jöhet a terhelésrádobás. További magyarázat található a 3.3 alfejezetben.
-
Különbséget kell tenni a következő három eset között , , és az eltolási szabály csak az utolsó esetre vonatkozik. Az első két esetben valamilyen trükkre van szükség, hogy a Laplace-transzformálandó függvényt az első esetben (ld. 3-11 feladat függvény), a második esetben alakúra alakítsuk át (ld. 3-12 feladat)
-
Az eltolási szabály határeseteként , ekkor
3.2.6.2. Végérték-tételek:
A kezdetiérték-tétel alkalmazhatóságának feltétele az, hogy az függvénynek létezzen a nulla körüli Taylor-sora
|
|
(3.84) |
Ha Taylor-sorának első tagja nulla , akkor a kezdeti érték tétel segítségével a kezdeti meredekség meghatározható
|
|
(3.85) |
Az állandósult érték tétel alkalmazhatóságának feltétele az, hogy létezzen az állandósult érték
|
|
(3.86) |
Pl. ha valós együtthatójú racionális törtfüggvény és részlettörtre bontható, akkor (3.86) tétel a következő esetekben alkalmazható:
-
Ha van legalább két olyan pólus, amelynek az értéke nulla, akkor a többi pólustól függetlenül (3.86) mindkét oldala a végtelenhez tart.
3.2.6.3. Néhány függvény Laplace-transzformáltja
Megjegyzés: a fenti Laplace-transzformáltak a 0≤t tartományra vonatkoznak, így az időfüggvények elé ε(t) szorzótényező írható. Erre az inverz Laplace-transzformációnál is tekintettel kell lennünk. Hangsúlyozzuk, a Laplace-transzformáció a bekapcsolási jelenségek vizsgálatára szolgál.
3.2.7. Kifejtési (reziduum) tétel (s-re nézve valós együtthatójú racionális törtfüggvények inverz Laplace-transzformációja)
A legtöbb gyakorlati esetben egy s-re nézve valós együtthatójú racionális törtfüggvényt kell inverz Laplace-transzformálni és ehhez nem szükséges a (3.76) egyenletet közvetlenül felhasználni. Legyen alakú és azt is feltételezzük, hogy a számlálóban lévő polinom fokszáma kisebb a nevezőben lévő polinom fokszámánál (ha ez nem teljesülne, akkor polinom osztással valódi törteket kell kapnunk).
3.2.7.1. Egyszeres gyökök esetén
Ha Den(s)-nek csak egyszeres gyökei vannak és a pólusok száma n, akkor az függvény felírható a következő alakban:
|
|
(3.93) |
ahol pi a nevező polinomjának i-dik gyöke (az átviteli függvény pólusa). A gyökök között lehet nulla, és komplex konjugált pár is. Szorozzuk meg (3.93) mindkét oldalát -vel, és végezzük el az határátmenetet.
|
|
(3.94) |
Mivel az összeg minden tagja – kivéve az L-ediket- zérushoz tart. (3.94) alapján:
|
|
(3.95) |
Általánosan felírhatjuk
|
|
(3.96) |
Így exponenciális időfüggvények összegét kapjuk. Ha valós, akkor
|
|
(3.97) |
é s lehet komplex konjugált pár, ebből következően é s is komplex konjugált párt alkot, így (3.97) összegzésben megjelennek komplex tag párok, amelyek összevonhat ó k valós függvénnyé. Vezessük be a következő jelölést:
|
|
(3.98) |
Ebben az esetben az inverz Laplace-transzformáció eredménye:
|
|
(3.99) |
3.2.7.2. Többszörös pólusok esetén
A részlettörtek számának meg kell egyeznie a pólusok számával. Ha a pólus Lm -szeres, akkor a következő részlettörteknek is szerepelniük kell:
|
|
(3.100) |
A (3.100) inverz Laplace-transzformáltja
|
|
(3.101) |
Az egyszeres gyökök együtthatóinak kiszámítását nem befolyásolja, hogy vannak többszörös gyökök.
Többszörös gyökök esetén általában valamilyen trükkre van szükség. Ha csak egy többszörös gyökünk van, akkor (3.100) összeg közös nevezőre hozásával a számláló -ed fokú polinom lesz, amelynek együtthatója van, így az számú együttható kiszámításához számú egyenletet lehet felírni.
Az egyszeres gyökökre bevezetett ötlet többszörös gyökök esetén csak a legnagyobb sorszámú együtthatóra alkalmazható. Ezt célszerű kiszámítani, mert ezzel csökkenthető a közös nevezőre hozáskor a megoldandó egyenletrendszer egyenleteinek száma.
|
|
(3.102) |
3.2.8. Időállandó
A fentiek alapján az -re nézve valós együtthatójú racionális törtfüggvények inverz Laplace-transzformációjának eredményeként (ld. (3.97), (3.99) és (3.101)) exponenciális tagokat kapunk. A kitevőben a idő együtthatója a pólus, pontosabban az összevonás után (ld. (3.99)) a pólus valós része. Az alakú függvény esetén, ahol a értéket nevezzük az függvény időállandójának (ld. 3-16 feladat).
Az függvény néhány tulajdonsága (ha ):
-
A függvény bármely pontjában felrajzoljuk az érintőt, az az időtengelyt a időpontban metszi.
-
A függvény bármely pontjában felvett értékének kb. 37%-a lesz a függvény értéke egy időállandónyi idő elteltével a időpontban.
-
A függvény bármely pontjában felvett értékének kb. 5%-a lesz a függvény értéke három időállandónyi idő elteltével a időpontban.
-
A függvény bármely pontjában felvett értékének kb. 1%-a lesz a függvény értéke öt időállandónyi idő elteltével a időpontban.
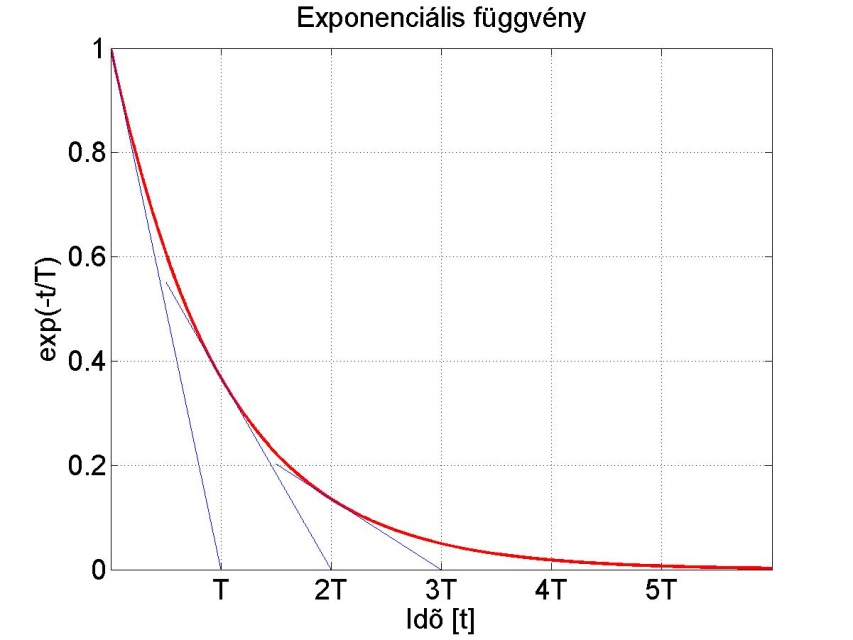
Geometriailag könnyen értelmezhetjük a negatív időállandót. A függvény bármely pontjában felrajzoljuk az érintőt, akkor az az időtengelyt a időpontban metszi, ha (exponenciálisan növekszik, mert ). Ha a függvény érték konstans, akkor az időállandót tekinthetjük végtelennek. (konstans érték) alapján.
Komplex konjugált pólusok esetén (ld. (3.99) és 3-28. ábra) a szinuszosok lengések amplitúdója csökken, ha a pólus valós része negatív (illetve az amplitúdók exponenciálisan növekednek, ha a pólus valós része pozitív).
Definíció
Összegezve kijelenthetjük, hogy a (2.107) alakú differenciálegyenlettel leírható rendszerek kimenő jelének változására, illetve olyan jelek esetén, amelynek a Laplace-transzformáltját egy -re nézve valós együtthatójú racionális törtfüggvény ír le, bevezethetjük az időállandó fogalmát, amelyet úgy definiálunk, mint a jel Laplace-transzformáltját leíró, -re nézve valós együtthatójú racionális törtfüggvény pólusai valós része reciprokának mínusz egyszerese. Ebből következik, hogy egy jelnek több időállandója is lehet, ha több pólusa van, és ahogy létezhetnek többszörös pólusok, így létezhetnek többszörös időállandók. Mivel egy rendszer kimenőjelének változása a rendszert leíró differenciálegyenlettől függ, így az időállandókat is a rendszerhez kötjük.
A (3.97), (3.99) és (3.101) kifejezéseket átírhatjuk úgy, hogy e kifejezésekben a pólus helyett az időállandó szerepeljen az -edik pólus, az és -edik komplex konjugált, illetve többszörös pólus esetén az adott pólushoz (pólusokhoz) tartozó exponenciális időfüggvény az időállandóval a következő alakot öltik:
|
|
(3.103) |
|
|
(3.104) |
|
|
(3.105) |
Be kell vezetnünk a domináns időállandó fogalmát.
Definícó
Domináns időállandónak nevezzük a rendszer legnagyobb időállandóját, ha a rendszernek vagy csak egy időállandója van, vagy a legnagyobb időállandója legalább háromszor akkora, mint a második legnagyobb időállandó. Hasonlóan a beszélhetünk domináns pólusról, ha a második legkisebb pólus legalább háromszor akkora, mint a legkisebb pólus.
Sok esetben elegendő, ha csak a domináns időállandóval számolunk és a többi időállandót elhanyagoljuk. Értelemszerűen, ha a legnagyobb időállandó egy többszörös pólushoz, vagy komplex konjugált póluspárhoz tartozik, akkor nem beszélhetünk domináns időállandóról. Ilyen esetben használatos a domináns póluspár kifejezés.
A (3.145) rendszeregyenletet átírhatjuk a következő alakúra
|
|
( 3.106 ) |
ahol és
A (3.106) formának az az előnye, hogy a rendszer időállandója és erősítése közvetlenül megjelenik a differenciálegyenletben. Ha , akkor az adott kezdeti értékéről indulva időállandóval éri el a állandósult értéket.
3.2.9. Kidolgozott feladatok Laplace-transzformáció alkalmazására
3 - 10 feladat Függvényábrázolás
Készítsen egy Matlab programot, amely ábrázolja a következő két időfüggvényt. Határozza meg mindkét esetben a kezdeti értéket.
a) eset
|
|
(3.107) |
b) eset
|
|
(3.108) |
Megoldás
(3.99) alapján
a) eset
|
|
(3.109) |
A kezdetiérték törvény alapján
|
|
(3.110) |
b) eset
|
|
(3.111) |
A kezdetiérték törvény alapján az előzővel azonos értéket kapunk
|
|
(3.112) |
(3.109) és (3.111) alapján a MATLAB program
t=0:0.05:30;
% a) esetben
f=4*exp(-0.2*t).*cos(5*t+pi/4);
% b) esetben
f=4*exp(-0.2*t).*cos(0.2*t+pi/4);
plot(t,f)
set(gca, 'fontsize', 17);
ylabel('f(t) függvény [relatív egység]');
xlabel('Idő [s]');
title('Komplex konjugált póluspár esete');
axis([0 30 -4 4]);
grid
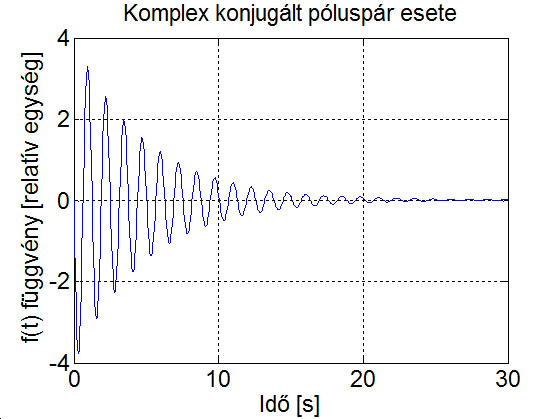
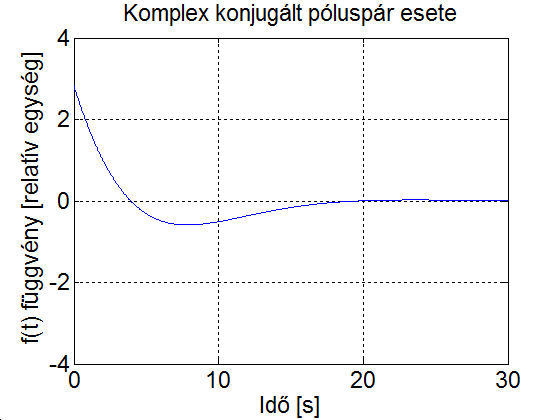
Mindkét esetben az időállandó , ebből következően a lengések amplitúdója kb. 25 időegység alatt csökken az eredeti érték kb. 1%-ára. Az első esetben a lengések periódus ideje egység, ez kisebb az időállandónál, így jól látható, hogy több perióduson zajlik le, amíg az amplitúdó jelentősen csökken (ld 3-28. ábra). A második esetben nagyobb az időállandónál, így gyakorlatilag egy periódus alatt a lengések amplitúdója 1% alá csökken (ld. 3-29. ábra).
3 - 11 feladat a csillapítási tétel alkalmazására
Határozza meg az alábbi függvények Laplace-transzformáltját, ahol ezt kihangsúlyozandó a szorzót odaírtuk.
, emlékeztetőül:
Megoldás
A csillapítási tétel alapján:
esetén az idővel szorzás szabálya is alkalmazható
3 - 12 feladat az eltolási tétel alkalmazására
Vázolja fel az alábbi függvényeket és határozza meg a Laplace-transzformáltjukat.
Megoldás
Azonos átalakítással és az eltolási tétel alkalmazásával:
3 - 13 feladat az inverz Laplace-transzformáció alkalmazására
(ha a Laplace-operátoros tartomány ban nincs exponenci ális tag)
Határozza meg az alábbi függvények inverz Laplace-transzformáltjait. Az összefüggések a intervallumban érvényesek.
Megoldás
Az inverz transzformáció részlettörtekre bontással, illetve a kifejtési tétel alkalmazásával végezhető el. Az összefüggések a intervallumban érvényesek.
3 - 14 feladat az inverz Laplace-transzformáció alkalmazására
(ha a Laplace-operátoros tartomány ban van exponenci ális tag)
Határozza meg az alábbi, exponenciális tagot is tartalmazó függvények inverz Laplace-transzformáltját.
Megoldás
Az inverz transzformáció az eltolási tétel alkalmazásával, illetve a periodikus függvényre vonatkozó formula alapján végezhető el. Az összefüggések a intervallumban érvényesek.
3 - 15 feladat Végérték tétel alkalmazása
Határozza meg az alábbi Laplace-transzformált függvények kezdeti és állandósult értékét a végérték tételek alapján.
Megoldás
Kezdeti értékek
Állandósult értékek
az állandósult érték tétel alkalmazásának feltétele nem teljesül, ld. (3.86) tétel utáni megjegyzés.
az állandósult érték tétel alkalmazásának feltétele nem teljesül, ld. (3.86) tétel utáni megjegyzés.
3 - 16 feladat Kezdeti meredekség
A kezdeti érték tétel segítségével határozza meg meredekségét a időpontban.
Megoldás
Abból kell kiindulni, hogy a Laplace-transzformáció csak a tartományra érvényes, ezért szigorúan nézve csak a függvényt tudjuk Laplace-transzformálni, amelynek szakadása van a időpontban, ezt felfoghatjuk úgy, hogy a kezdeti meredekség végtelen.
Ha a tényleges meredekséget kívánjuk meghatározni, akkor a függvény eltolásával kell gondoskodni arról, hogy a időpontban a kezdeti érték nulla legyen. A és függvény kezdeti meredeksége megegyezik, ugyanakkor az utóbbi függvény folytonos és a kezdeti értéke nulla, ezért
|
|
(3.113) |
A (3.113) összefüggésből az olvasható ki, hogy a függvény a időpontban 2 értékről indul és a időpontban berajzolt érintő 0.25 időegység után éri el az időtengelyt. Vagyis az időállandója .
3 - 17 feladat Deriválási szabály alakalmazhatóságának illusztrálása
Kiindulva a szinusz és koszinusz függvény Laplace transzformáltjából (ld. táblázat). A Laplace-transzformált függvények idő szerinti deriválására vonatkozó szabály felhasználásával határozza meg a következő két függvény deriváltjának Laplace-transzformáltját
|
|
(3.114) |
Megoldás
A koszinusz függvény Laplace-transzformáltja
|
|
(3.115) |
Ha ezt az időszerint deriváljuk, akkor ezt meg kell szorozni -sel és le kell vonni a kezdeti értéket, az függvény esetben 1-et, az függvény esetben 0-át
|
|
(3.116) |
|
|
(3.117) |
Inverz Laplace-transzformálva a táblázat alapján
|
|
(3.118) |
|
|
(3.119) |
3 - 18 feladat Deriválási szabály alakalmazhatóságának illusztrálása
Kiindulva a szinusz és koszinusz függvény Laplace transzformáltjából (ld. táblázat). A Laplace-transzformált függvények idő szerinti deriválására vonatkozó szabály felhasználásával határozza meg a következő két függvény deriváltjának Laplace-transzformáltját
|
|
(3.120) |
Megoldás
A szinusz függvény Laplace-transzformáltja
|
|
(3.121) |
Ha ezt az időszerint deriváljuk, akkor ezt meg kell szorozni -sel és le kell vonni a kezdeti értéket, amely mindkét függvény esetében 0-át
|
|
(3.122) |
Inverz Laplace-transzformálva a táblázat alapján
|
|
(3.123) |
3 - 19 feladat Deriválási szabály alakalmazhatóságának illusztrálása
Kiindulva a szinusz és koszinusz függvény Laplace transzformáltjából (ld. táblázat). A Laplace-transzformált függvények idő szerinti deriválására vonatkozó szabály felhasználásával határozza meg a következő két függvény deriváltjának Laplace-transzformáltját
|
|
(3.124) |
Megoldás
Trigonometrikus azonosságok alpján
|
|
(3.125) |
|
|
(3.126) |
|
|
(3.127) |
Inverz Laplace-transzformálva a táblázat és ismert trigonometrikus azonosság alapján
|
|
(3.128) |
|
|
(3.129) |
3 - 20 feladat Deriválási szabály alakalmazása egység sebeségugrás Laplace-transzformáltjának meghatározására
Kiindulva az egységugrás függvény Laplace transzformáltjából (ld. táblázat). A Laplace-transzformált függvények idő szerinti deriválására vonatkozó szabály felhasználásával határozza meg az egység sebesség ugrás függvény Laplace-transzformáltját.
Megoldás
Induljunk ki, a következő ismertnek tekintett öszefüggésből
|
|
(3.130) |
A deriválási szabályt alkalmazva helyettesítéssel
|
|
(3.131) |
könnyen kifejezhető:
|
|
(3.132) |
3 - 21 feladat Deriválási szabály alakalmazása koszinusz négyzet függvény Laplace-transzformáltjának meghatározására
Kiindulva a szinusz függvény Laplace-transzformáltjából (ld. táblázat) határozza meg a következő Laplace-transzformált függvényt
|
|
(3.133) |
Megoldás
Először határozzuk meg függvény deriváltját
|
|
(3.134) |
Laplace-transzformáltját ismertnek tekintjük továbbá tudjuk, hogy ,
|
|
(3.135) |
könnyen kifejezhető:
|
|
(3.136) |
3 - 22 feladat Deriválási szabály alakalmazása szinusz négyzet függvény Laplace-transzformáltjának meghatározására
Kiindulva a szinusz függvény Laplace-transzformáltjából (ld. táblázat) határozza meg a következő Laplace-transzformált függvényt
|
|
(3.137) |
Megoldás
Először határozzuk meg függvény deriváltját
|
|
(3.138) |
Laplace-transzformáltját ismertnek tekintjük továbbá tudjuk, hogy ,
|
|
(3.139) |
könnyen kifejezhető:
|
|
(3.140) |
3 - 23 feladat Idővel megszorzott függvény Laplace-transzformáltjának meghatározására
Kiindulva a szinusz függvény Laplace-transzformáltjából (ld. táblázat) határozza meg a következő Laplace-transzformált függvényt
|
|
(3.141) |
Megoldás
Bevezetve a következő jelölést
|
|
(3.142) |
Alkalmazva az idővel szorzás szabályt
|
|
(3.143) |
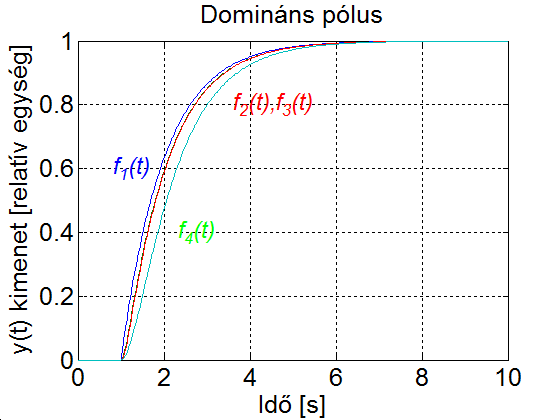
3 - 24 feladat Domináns időállandó vizsgálata
Ábrázoljuk függvényt, és határozzuk meg a függvények kezdeti meredekségét (mind a négy esetben ). A feladatban egy-, két- és három-energiatárolós tagokra kapcsolt egységugrás válaszainak (átmeneti függvények) Laplace-transzformáltja szerepel.
Megoldás
Látható, hogy a négy esetben minimális eltérés van a felfutásban, és a beállási idő praktikusan nem különbözik. pl. ha megvizsgáljuk, hogy mennyi idő alatt csökken az eltérés az állandósult értéktől 1% alá, akkor ebben alig van különbség. A 3-30. ábra nem látszik a különbség és között, mivel esetén a legkisebb 0.01 értékű időállandó hatása hamar megszűnik. A különbségek közvetlenül a bekapcsolás után vannak. Jól megfigyelhető, hogy az egy-energiatárolós tag egy határozott meredekséggel indul, és ha az időállandónál sokkal kisebb tartományt vizsgálunk, akkor a változás jól közelíthető egy egyenessel. A kettő vagy több energiatárolós tagok nulla meredekséggel indulnak, ezt a végérték tétellel könnyen beláthatjuk.
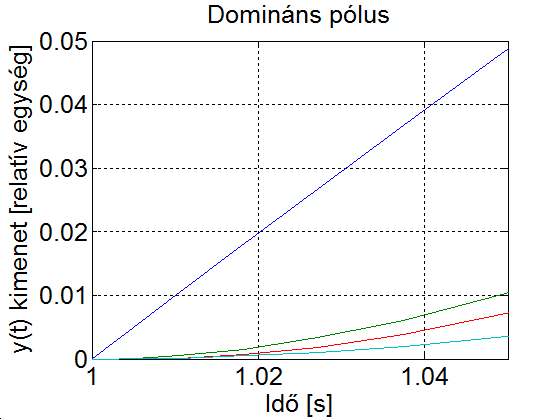
Kezdeti meredekségek meghatározása
|
|
(3.144) |
behelyettesítve
3 - 25 feladat (Házi feladat, megoldását nem közöljük)
Ábrázolja és határozza meg az alábbi függvények Laplace-transzformáltját, ahol .
3.3. Közönséges állandó együtthatós elsőrendű differenciálegyenletek megoldása Laplace-transzformációval
A deriválási szabály miatt a differenciálegyenlet a Laplace-transzformációval algebrai egyenletté alakul.
Bevezető példaként adott egy (2.107) alakú elsőrendű differenciálegyenlet
|
|
( 3.145 ) |
ahol az állapotváltozó kezdeti értéke. Itt utalnunk kell a derivált függvény Laplace transzformálásának szabályára, továbbá (3.81) és (3.82) értelmezésére. Ha a (3.145) egyenletet Laplace-transzformáljuk, akkor azt feltételezzük, hogy folytonos és hagyományos értelemben deriválható, belépő-függvény. és értéke egyaránt nulla a tartományban. folytonosságáról úgy gondoskodhatunk, ha kielégítjük az kezdeti érték feltételt. A deriválási szabályt figyelembe véve :
|
|
( 3.146 ) |
Érdekes, és fizikailag értelmezhető eredményre jutunk, ha a (3.146) egyenletet inverz Laplace-transzformáljuk
|
ahol |
( 3.147 ) |
Értelmezés
A (3.147) egyenletet elemezve arra a következtetésre juthatunk, hogy gondolkozhatunk úgy, hogy a Laplace-transzformáció energiamentes kezdeti állapottal foglalkozik, ezért egy impulzus segítségével tudjuk beállítani a szükséges kezdeti értéket, vagyis gondoskodni arról, hogy teljesüljön. Ez egy ugrást jelent a tárolt energia (állapotváltozó) értékében, szemléletesen azt mondhatjuk, hogy a Laplace-transzformáció a tartománnyal foglalkozik. A múlt hatását (az állapotváltozóban felhalmozott energiát) egy impulzusnyi ütéssel koncentráltan közöljük a rendszerrel, és ennek hatására alakul ki a szükséges kezdeti érték, hogy onnan folytatódjon a folyamat. Ha , akkor az egy újabb - nagyságú - kalapácsütés, így a két Dirac-impulzus közül az elős a múlt összegzése, a második egy a tartományban érkező új hatás, ezért . Ezzel megszüntetjük folytonosságát, de azért mert a múlt hatása mellett a tartományban érkezett egy új impulzusszerű hatás. Szemléletesen két részből álló kalapácsütéssel súlytunk a rendszerre. Az egyik rész a múltat jeleníti meg a tartományban, és a kezdeti értéket állítja be, a másik rész a tartományban érkező új külső gerjesztés. Természetesen, ha később érkezik a bemenetre egy időben eltolt Dirac-impulzus, akkor a időpillanatban jelent egy kalapácsütést és ugrást az állapotváltozó értékében. Ez a gondolatmenet kiterjeszthető magasabb rendű differenciálegyenletekre is.
kifejezhető a (3.146) egyenletből
|
|
( 3.148 ) |
Az állapotváltozó a (3.148) kifejezésében az első tag a kezdeti értéktől, a második tag a nulla kezdeti értékről indulva csak a gerjesztéstől függ. A (3.148) kifejezésből az is kiolvasható, hogy a (3.145) alakú, elsőrendű differenciálegyenletet esetén az együttható az állapotváltozó Laplace-transzformált kifejezésében a pólus mínusz egyszerese . A (3.148) kifejezés inverz Laplace-transzformációját elvégezve
|
|
( 3.149 ) |
Ha a (3.149) kifejezést összevetjük a (3.23) egyenlettel, akkor beláthatjuk, hogy a (3.145) differenciálegyenlettel leírt rendszernek a súlyfüggvénye (impulzusválasza) a következő
|
|
( 3.150 ) |
A (3.23) egyenlet kapcsán tett megjegyzésünk, (miszerint a (3.23) egyenlettel a rendszer válaszát csak energiamentes kezdeti állapotból kiindulva számíthatjuk ki), összhangban van azzal, hogy a (3.149) kifejezés második tagja nulla kezdeti értékről indulva csak a gerjesztéstől függ. Így a (3.145) differenciálegyenlet megoldását két részre bontottuk egy kezdeti érték és egy gerjesztés függő tagra. Ez egy teljesen más felbontás, mint ami általános a differenciálegyenletek elméletében, ahol homogén (mérnöki terminológiával tranziens) és inhomogén (mérnöki terminológiával állandósult) tagokat szokás megkülönböztetni. Ebben a megközelítésben (3.148) és (3.149) első tagja a múlt (a tartomány) hatására, a második tagja a tartományban érkező hatásokra adott választ tartalmazza, a homogén és inhomogén megoldás szétválasztása nélkül.
Néhány konkrét esetet megvizsgálva:
Ha , akkor a (3.148) helyett a következőt írhatjuk
|
|
( 3.151 ) |
Így az inverz Laplace-transzformált.
|
|
( 3.152 ) |
(3.152) úgy értelmezhető, hogy a időpillanatban az állapotváltozó értéke a Dirac-impulzus hatására az értékről értékre ugrik, majd időállandóval exponenciálisan lecseng.
Ha , akkor (3.148) helyett a következőt írhatjuk
|
|
( 3.153 ) |
Így az inverz Laplace-transzformált
|
|
( 3.154 ) |
Könnyen belátható, hogy , és ez egyben a (3.145) differenciálegyenlet inhomogén megoldása. A tag a homogén megoldás esetén, a tag a homogén megoldás kiegészítése esetben. Ennek megfelelően (3.154) úgy értelmezhető, hogy a kezdeti és állandósult érték különbsége időállandóval exponenciálisan tart a nullához. Más szavakkal, egy-energiatárolós rendszer esetén a rendszer bármilyen átkapcsolása után exponenciális időfüggvényt követve jut át az egyik állandósult állapotból a másikba. Például egy meleg nyári napon a hűtőszekrényből kiveszünk egy üveg sört, és ott felejtjük a konyhaasztalon, akkor annak a hőmérséklete jó közelítéssel exponenciálisan éri el a konyha levegőjének hőmérsékletét. Szintén exponenciálisan változik a szoba hőmérséklete, ha a fűtést be- illetve kikapcsoljuk. Hasonló mondható el, ha szinuszosan kezdjük el gerjeszteni a rendszert, akkor a szinuszos gerjesztéshez is tartozik egy szinuszos állandósult állapot (a differenciálegyenlet inhomogén megoldása), akkor a bármely kezdeti értékből kiindulva az aktuális és állandósult szinusz függvény különbsége exponenciálisan tart nullához. Mindez matematikailag következő módon vezethető le:
Ha az , akkor (3.148) helyett a következőt írhatjuk
|
|
( 3.155 ) |
A második tagot gyöktényezős alakra kell hozni
|
|
( 3.156 ) |
Így az inverz Laplace-transzformált felírásához a második tagot is részlettörtekre kell bontani. Maradva a komplex alaknál a második tag három pólusa:
|
|
( 3.157 ) |
A kifejtési tételt alkalmazva a második tagra
|
|
( 3.158 ) |
A komplex együtthatókat Euler formára átírva
|
|
( 3.159 ) |
|
|
( 3.160 ) |
Az időfüggvényt átalakítva
|
|
( 3.161 ) |
(3.161) valós alakban is felírható
|
|
( 3.162 ) |
Jobban látható az első, exponenciális tag szerepe, ha átírjuk a következő alakúra
|
|
( 3.163 ) |
A (3.163) második tagja az inhomogén (állandósult) megoldás. A időpillanatban tényleges és az állandósult érték különbsége
|
|
( 3.164 ) |
Ez a különbség tűnik el időállandóval exponenciálisan. Más szavakkal exponenciálisan simul az állandósult értékhez.
3.3.1. Kidolgozott felagatok közönséges állandó együtthatós elsőrendű differenciálegyenletekkel kapcsolatban
3 - 26 feladat elsőrendű differenciálegyenlet megoldására konkrét numerikus értékekkel
Adott a következő differenciálegyenlet
|
|
( 3.165 ) |
ahol az állapotváltozó kezdeti értéke . Legyen
Megoldás
(3.165) egyenletet Laplace-transzformálva, és figyelembe véve a kezdeti értékre vonatkozó deriválási szabályt
|
|
( 3.166 ) |
kifejezhető
|
|
( 3.167 ) |
állapotváltozó (3.167) kifejezésében az első tag a kezdeti értéktől függ, a második a gerjesztéstől. Az inverz Laplace-transzformációt elvégezve
|
|
( 3.168 ) |
3 - 27 feladat soros RL kör egyenáramú gerjesztésének megváltoztatása
Van egy soros RL áramkörünk és egy kapcsolónk (ld. 3-31. ábra). A kapcsolóval az egyik ellenállást rövidre tudjuk zárni. Tegyük fel, hogy a kapcsolót periodikusan kapcsolgatjuk és 0.2 időegységig nyitva, majd ugyanennyi ideig zárva tartjuk. Határozza meg az induktivitás áramát.
Legyen R1=5Ω, R2=5Ω, és L=0.1H, a generátor feszültsége V.
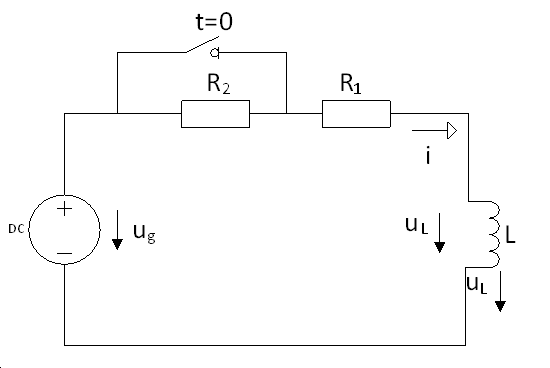
Megoldás
Jelülje az áramkörben található ellenállások eredő értékét
|
|
(3.169) |
Legyen az áramkör eredő ellenállásán eső feszültség. Az áramkörre felírható Kirchhoff hurokegyenlet:
A (3.165) egyenletet Laplace transzformálva:
|
|
(3.172) |
(3.166) átrendezése után (tetszőleges gerjesztés mellett):
|
|
(3.173) |
Inverz Laplace-transzformálva
|
|
( 3.174 ) |
Ha a kapcsoló zárva van, akkor az áram állandósult értéke és az időállandója . Ha a kapcsoló nyitva van, akkor az áram állandósult értéke: és az időállandója . Van egy-egy állandósult érték a kapcsoló két állapotának megfelelően, és a kapcsoló minden egyes átkapcsolásakor a megfelelő időállandóval térhetünk át az egyik értékről a másikra (ld. 3-32. ábra).
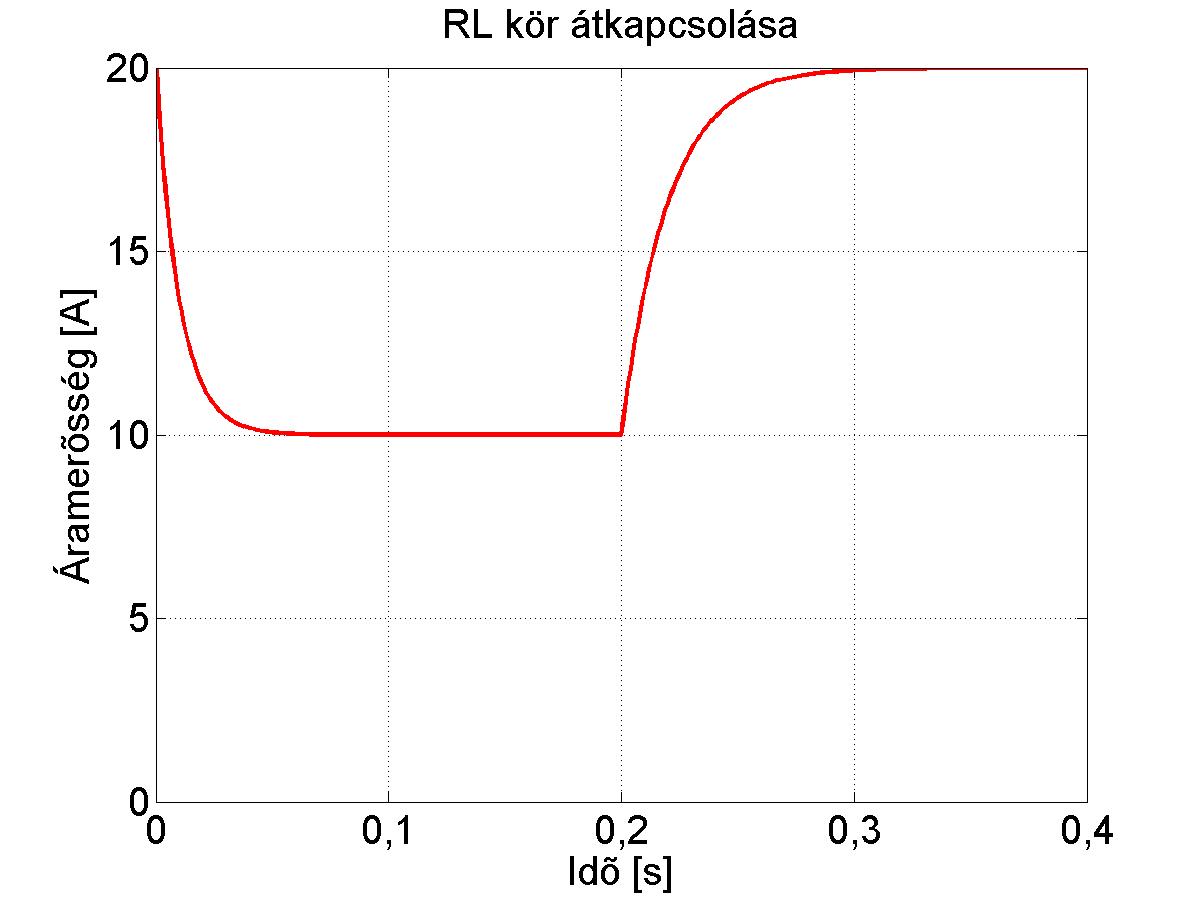
3-28 feladat soros RL kör szinuszos gerjesztéssel
Adott a 3-33. ábrán látható soros RL kör.
Legyen R=5Ω és L=0.1H. A generátor feszültsége csúcsértékű 50Hz frekvenciájú váltakozó feszültség, a bekapcsolás pillanatában a kezdő fázishelyzet pedig 0 fok. Fizikai megfontolások alapján az induktivitás áramának kezdeti értéke nulla. Írja fel az induktivitás áramának időfüggvényét.
Megoldás
Az áramkörre felírható Kirchhoff hurokegyenlet:
A (3.176) egyenletet Laplace transzformálva:
|
|
(3.177) |
(3.177) átrendezése után (tetszőleges gerjesztés mellett):
|
|
(3.178) |
Legyen az RL kör gerjesztése szinuszos feszültség. A t=0 időpillanatban bekapcsoljuk a kapcsolót. A valóságban kicsi az esély arra, hogy pont egy nulla átmenetnél zárjuk a kapcsolót. Ezért legyen az RL körre kapcsolt feszültség alakú. Megjegyezzük, hogy az áramkör kikapcsolása fizikailag nem egyszerű, mert az induktivitásban tárolt energia fenntartja az áramot és egy egyszerű kapcsoló esetén az érintkezők eltávolításakor egy ív alakul ki, de e jelenség vizsgálata nem e tantárgy kereteibe tartozik.
Mivel a t=-0 időpillanatban a kapcsoló nyitott volt, ezért , a gerjesztő feszültség pedig
|
|
(3.179) |
|
|
(3.180) |
|
|
(3.181) |
Behelyettesítve
|
|
(3.182) |
|
|
Az első tag a tranziens összetevő, a második az állandósult megoldás
|
|
(3.183) |
Szinuszos gerjesztés bekapcsolása esetén exponenciálisan tűnik el a különbség az aktuális érték és az állandósult érték között. (ld. 3-34. ábra). Esetünkben a gerjesztés periódus ideje megegyezik az RL kör időállandójával, ezért 5 periódus elteltével csökken a tranziens összetevő a kezdeti értékének kb. 1%-ára.
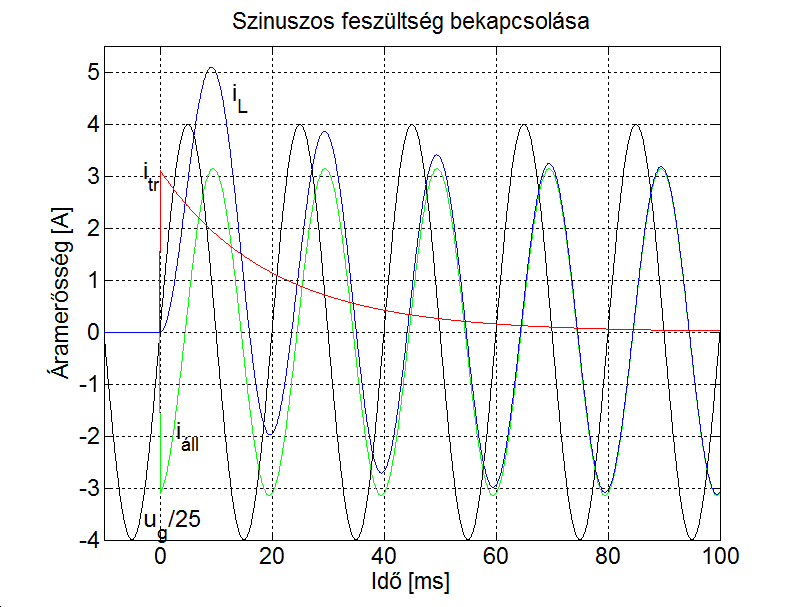
A feladatot megoldó MATLAB kód
t=-10/1000:0.05/1000:100/1000;
tm=t*1000;
R=5; L=0.1; Ug=100; omega=100*pi;
max=size(t); max=max(2);
Iall=Ug/(L*sqrt((R/L)^2+(omega)^2));
fi=atan(omega/(R/L));
f1=Ug*sin(100*pi*t)/25;
f2=Iall*sin(100*pi*t-fi);
f3=-Iall*sin(-fi)*exp(-t*R/L);
for I = 1:max
if t(I) <0
f2(I)=0;
f3(I)=0;
end
end
f4=f2+f3;
plot(tm,f1,'k',tm,f2,'g',tm,f3,'r',tm,f4,'b')
set(gca, 'fontsize', 17);
ylabel('Áramerősség [A]');
xlabel('Idő [ms]');
title('Szinuszos feszültség bekapcsolása');
text(-3,3,'i_{tr}','FontSize',18)
text(-3,-3.7,'u_g/25','FontSize',18)
text(3,-2,'i_{áll}','FontSize',18)
text(13,4.5,'i_L','FontSize',18)
axis([-10 100 -4 5.5]);
grid
Természetesen, ha pl. az ellenállás értékét ötszörösére növelve ötödére csökkenmtjük az RL kör időállandóját, akkor egy perióduson belül hozzá simul az állandósult értékhez (ld. 3-35. ábra).
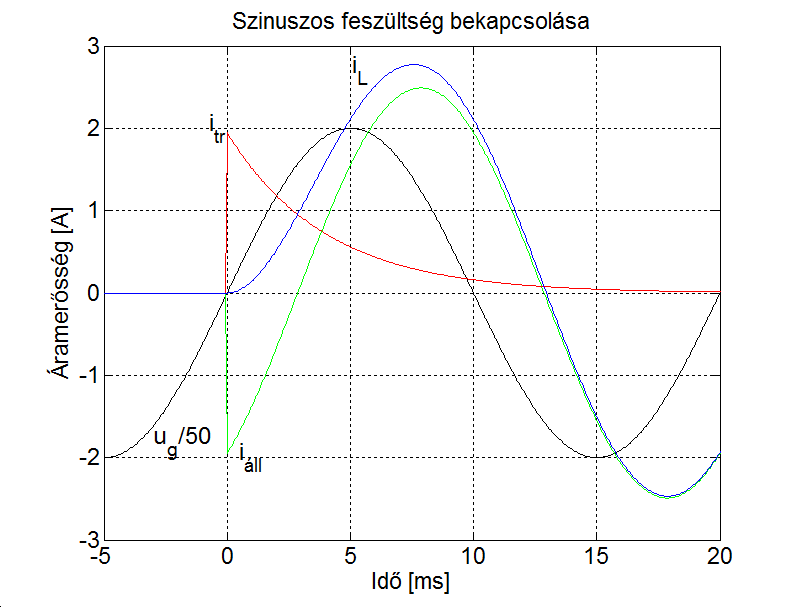
3.4. Kapcsoló üzemmód
A mérnöki gyakorlatban többször előfordul, hogy a rendszer kimenőjelének az értékét a bemenőjel folyamatos kapcsolgatásával tartjuk egy előírt értéktartományban. Tipikusan ilyen a legtöbb fűtésrendszer, továbbá a teljesítményelektronikai rendszerek Impulzus Szélesség Szabályozása (Pulse Width Modulation) idetartozik. A működés legfontosabb feltétele, hogy a kapcsolások ciklusideje lényegesen kisebb legyen a rendszer domináns időállandójánál.
3 - 29 feladat Kapcsoló üzemmód
Adott a következő differenciálegyenlet
|
|
( 3.184 ) |
ahol és egy 50% kitöltésű négyszög impulzus, amely értéke 0 és 2 lehet. Rajzolja fel az állapotváltozó időfüggvényét, ha a rendszer időállandója kisebb, illetve nagyobb, mint a négyszög impulzus periódusideje.
Megoldás
|
3-36. ábra A periódusidő ötszöröse az időállandónak |
3-37. ábra A periódusidő megegyezik az időállandóval |
|
3-38. ábra A periódusidő ötöde az időállandónak (a négyszög impulzus nincs kirajzolva) |
3-39. ábra A periódusidő ötvenede az időállandónak (a négyszög impulzus nincs kirajzolva) |