2. fejezet - Alapfogalmak, a fizikai jelenségek matematikai leírása
- 2.1. Valós fizikai rendszer fogalma
- 2.2. A jel fogalma
- 2.3. A be- és kimenetek fogalma
- 2.4. Az absztrakt rendszer fogalma
- 2.5. Lineáris és nemlineáris rendszerek fogalma
- 2.6. Determinisztikus, sztochasztikus és kaotikus rendszerek fogalma
- 2.7. Kauzalitás fogalma
- 2.8. Paraméter és változó fogalma
- 2.9. Elosztott és koncentrált paraméterű leírás fogalma
-
- 2.9.1. Vektormezővel leírható rendszerek koncentráltparaméterű modellje
- 2.9.2. Villamos jelenségek elosztott paraméterű leírása a Maxwell egyenletekkel
- 2.9.3. Kirchhoff egyenletek származtatása (koncentrált paraméterű modellekhez)
- 2.9.4. Kétpólusokkal modellezett stacioner állapotú villamos és mágneses áramkörök
- 2.9.5. Hálózatszámítási analógiák
- 2.10. Lineárisan független egyenletek kiválasztása
- 2.11. Koncentrált paraméterű determinisztikus leírás
-
- 2.11.1. Statikus rendszerek fogalma
- 2.11.2. Dinamikus rendszerek fogalma
- 2.11.3. Rendszerek simasága
- 2.11.4. Időinvariáns és autonóm rendszerek fogalma
- 2.12. Dinamikus rendszerek általános összefüggései
-
- 2.12.1. Állapot, állapotjelző, állapotváltozó és állapotegyenletek fogalma
- 2.12.2. Lineáris, egy bemenetű egy kimenetű diszkrét idejű rendszer
- 2.12.3. Állapottér-reprezentáció
- 2.12.4. Változó struktúrájú rendszerek
- 2.12.5. Lineáris, egy bemenetű egy kimenetű folytonos idejű rendszer
- 2.12.6. Általánosított derivált
- 2.12.7. Differenciálegyenletek megoldása analóg számítógépes megközelítéssel
- 2.13. A stabilitás fogalma
- 2.14. Kidolgozott feladatok koncentrált paraméterű rendszerekhez kapcsolódóan
- 2.15. Alapvető vizsgálati módszerek
2.1. Valós fizikai rendszer fogalma
Definíció
Valós fizikai rendszer egy olyan fizikai objektum, amely mérhető külső kényszer hatására mérhető módon megváltozik.
Értelmezés
Számos esetben találkozunk olyan műszaki problémával, ahol van valamilyen külső kényszer és ennek hatására valami megváltozik. A későbbi szóhasználat egyszerűsítésére bevezetjük a „valós fizikai rendszer” fogalmát: ez egy olyan fizikai objektum, amely mérhető külső kényszer hatására mérhető módon megváltozik (ld. 2-1. ábra). E tananyag fókuszában az áll, hogy miként lehet a valós fizikai rendszereket matematikailag leírni.
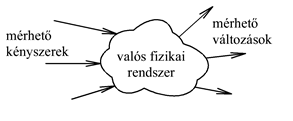
A műszaki életben előforduló valós fizikai rendszereket többféle szempont szerint lehet kategóriákba sorolni és egy valós fizikai rendszernek többféle matematikai leírása létezhet. A megfelelő leírási mód nemcsak magán a valós fizikai rendszeren múlik, hanem függ a vizsgálat tárgyától is. Például nem mindegy, hogy a valós fizikai rendszer változási folyamataira (tranziens viselkedésére) vagy csak a végállapotára (állandósult állapotára) vagyunk kíváncsiak. Ugyanazon valós fizikai rendszer esetén más-más matematikai eszközt használhatunk e két különböző vizsgálatra. Ezért nagyon fontos, hogy a mérnöki munkában először a vizsgálat tárgyát és célját pontosan definiáljuk, és csak utána válasszunk alkalmas matematikai eszközt a probléma elemzésére és megoldására.
2.2. A jel fogalma
Definíció
A jel egy változó fizikai mennyiség absztrakt információ tartalma.
Értelmezés
A jel egy változó fizikai mennyiség absztrakt információtartalma, jellemzően egy időfüggvény, de mint később a 2.11.2 fejezetben látni fogjuk, bizonyos jelek értelmezéséhez a függvény fogalom általánosítását is meg kell engednünk. Ebből következik, hogy a jel elveszíti az eredeti fizikai mennyiség mértékegységét, sőt még az abszolút nagyságát is elveszítheti, ha áttérünk az ún. relatív egységre. A relatív egységet úgy kapjuk, ha a jelet elosztjuk egy jellemző értékével (általában a névleges értékével), így az értékét százalékosan tudjuk kifejezni. Azonos funkciójú, de különböző fizikai kapacitású, illetve teljesítményű rendszerek ilyen módon válhatnak összehasonlíthatóvá. Ha van például két motorom és mindegyikre 100V feszültséget kapcsolok, akkor ez így nem mond semmit, nem sokat tudok a motor üzemállapotáról, mert lehet, hogy az egyik motor tönkremegy (mert egy eredetileg 10 voltra tervezett kis motor), a másik el sem tud indulni (mert több kV-ra tervezett hatalmas motor). Két motor túlterhelhetősége annak alapján hasonlítható össze, hogy a névleges értékük hányszorosát viselik el. A relatív egység használata számos előnnyel jár a mérnöki gyakorlatban.
A jeleket különböző szempontok szerint szokás osztályozni. Jelen tananyag a nevéből adódóan a rendszerekre fókuszál, ezért a jelek osztályozását a rendszerek osztályozásához kapcsolódóan végezzük el.
2.3. A be- és kimenetek fogalma
Definíció
A valós fizikai rendszerre ható és időben változni képes kényszereket nevezzük fizikai bemeneteknek.
A valós fizikai rendszernek a fizikai kényszerek hatására bekövetkező bármely változása lehet fizikai kimenet, ezek közül azt tekintjük fizikai kimenetnek, amelyet az adott vizsgálatban közvetlenül vagy közvetve mérünk .
Értelmezés
A valós fizikai rendszerre ható és időben változni képes kényszereket nevezzük fizikai bemeneteknek, ezek közül megkülönböztetjük az irányított (mesterségesen változtatható) és a környezet által meghatározott (ezért sokszor nem ismert) fizikai bemenetet. A fizikai bemenetekhez tartozó jelet (a bemenőjelet) gerjesztésnek is nevezzük. Az előbbi felosztásnak megfelelően a gerjesztéseken belül megkülönböztethetünk beavatkozó és zavaró jelet. Ez utóbbiról sokszor nincs pontos információnk, de valós fizikai rendszereknél ezzel mindig számolni kell. A zavaró jeleket is két nagy csoportra bonthatjuk, nevezetesen a zaj- és terhelésjellegű jelekre. Ha a terhelést ismerjük, akkor azt bemenőjelnek is tekinthetjük. Szokásosan a beavatkozó jelet az u, míg a zavaró jelet (az angol disturbance után) a d betű jelöli.
A valós fizikai rendszernek a fizikai kényszerek hatására bekövetkező bármely változása lehet fizikai kimenet, ezek közül azt tekintjük fizikai kimenetnek, amelyet az adott vizsgálatban közvetlenül vagy közvetve mérünk. A fizikai kimenethez tartozó kimenőjelet sokszor válaszjelnek nevezzük, és szokásosan y betűvel jelöljük. Meg kell jegyeznünk, hogy a fizikai kimenet definíciójában semmilyen megkötés vagy útmutatás nincs arra vonatkozóan, hogy miként válasszuk ki a mérendő fizikai mennyiséget, ezért azzal később külön kell foglalkozni, hogy a mérésekből a valós fizikai rendszer teljes (vagy az adott vizsgálat szempontjából érdekes részleges) működése rekonstruálható-e. Más szavakkal a mérés tartalmazza-e a számunkra érdekes információt.
A valós fizikai rendszer vizsgálatának az első lépése a fizikai be- és kimenetek meghatározása. Egy rendszernek az adott használattól vagy a vizsgálat tárgyától függően más és más fizikai bemenetei, illetve kimenetei lehetnek. Csak egy nagyon egyszerű példát alapul véve: egy kerékpár kanyarodását első közelítésben a kormány elforgatásával tudjuk elérni. Már abban is van különbség, hogy hol van a kezünk a kormányon, minél szélesebben fogjuk, annál kisebb erővel (kényszerrel) tudjuk elforgatni. Kis sebességeknél biztosan elegendő a kormányra koncentrálni, de aki nagy sebességnél pusztán a kormányt forgatja, az hamar rájön, hogy kanyarodáshoz a súlypontáthelyezés is elengedhetetlen. Vannak, akik úgy is tudnak kanyarodni, hogy közben nem fogják a kormányt. Az ő esetükben a kerékpár haladási iránya szempontjából a súlypontáthelyezést lehet bemeneti kényszernek tekinteni, ugyanakkor a kormány elfordulása a kiadódó mennyiségek közé sorolandó, így lehet fizikai kimenet. Azt is sok kerékpáros tapasztalhatta, hogy egy kavics, vagy az útpadka ugyancsak eltérítheti a kerékpárt eredeti irányából. Így ha nem sima úton haladunk, akkor a talaj egyenetlenségeit is bemeneti kényszernek (zavarójelnek) kell tekinteni. Ismét más kényszert és kiadódó változó mennyiséget kapunk, ha pl. a kerékpár által megtett utat vizsgáljuk.
A mechatronikában gyakran egyenáramú szervomotort alkalmazunk mozgatásra. Gyakori ipari előfordulása és egyszerűsége miatt e tananyagban is több példában alkalmazzuk az egyenáramú motort. A motort, mint valós fizikai rendszert vizsgálva az egyértelmű, hogy a motor működését az armatúra tekercsen keresztül tudjuk befolyásolni, de nem mindegy, hogy az armatúra tekercs áramát vagy feszültségét írjuk-e elő. Az áramvezérlés esetén az armatúra-áram a kikényszerített mennyiség és az armatúra-feszültség a motor fordulatszámától függően kiadódik. A feszültségvezérlés esetén az armatúra-feszültség a kikényszerített mennyiség, és az armatúraáram a terheléstől függően fog kiadódni. Ugyancsak a motornak kiadódó mennyisége lehet a nyomatéka, fordulatszáma és szögelfordulása. Az is világos, hogy ezek a kiadódó mennyiségek egymástól nem függetlenek. A motor enkóder jeléből a szögelfordulásást közvetlenül a szögsebességet közvetve ki tudjuk számítani, és fordítva.
A fenti példák annak szemléltetésére szolgálnak, hogy a fizikai be- és kimenetek meghatározása nem mindig triviális, ezért bármilyen vizsgálatot ezek pontos elemzésével kell kezdeni.
2.4. Az absztrakt rendszer fogalma
Definíció
A rendszer egy valós fizikai rendszer valamilyen pontosságú és meghatározott működési tartományra érvényes absztrakt modellje, amely a bemenőjelek és a kimenőjelek között teremt matematikai kapcsolatot
Értelmezés
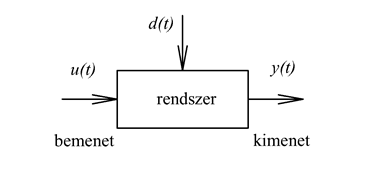
A rendszer egy valós fizikai rendszer valamilyen pontosságú és meghatározott működési tartományra érvényes absztrakt modellje, amely a bemenőjelek és a kimenőjelek között teremt matematikai kapcsolatot (ld. 2-2. ábra). Megjegyezzük, hogy a rendszerhez választhatunk olyan bemenőjelet, amely a valós fizikai rendszert tönkretenné, és a rendszer matematikailag kiszámíthat olyan kimenőjelet, amelynek kiadására a valós fizikai rendszer fizikailag képtelen. Ezért fontos, hogy egy rendszer vizsgálatakor meggyőződjünk annak érvényes működési tartományáról.
Az előző fejezetben leírtaknak megfelelően a bemenőjelek közül a 2-2. ábran megkülönböztettük a zavaró és a beavatkozó jelet. A zavaró jelet sok esetben elhanyagoljuk. Ha erről külön nem teszünk említést, akkor a beavatkozó jel megegyezik a bemenőjellel. A be- és a kimenőjeleken kívül a rendszernek lehetnek további belső jelei. Ha a későbbiekben a rendszer, be- és kimenet szavakat a „fizikai” jelző nélkül használjuk, akkor mindig az absztrakt matematikai értelmükre gondolunk.
A mérnöki munkában valós fizikai rendszereket kell alkotnunk, és ehhez ismernünk kell azok működését, valahogy le kell tudni írni a belső változásokat. A valós fizikai folyamatok lezajlásáról részben a korábbi tapasztalatunk (fogalmazhatunk úgy, hogy a mérnöki ösztön) alapján, részben a folyamatokat leíró egyenletek alapján nyilatkozunk. Tisztán matematikai egyenletekkel sohasem tudjuk teljes pontossággal leírni a körülöttünk lévő világot, mindig szükség lesz a mérnöki tapasztalatra. A mérnöki munka szépsége e két megközelítés összhangjának megteremtésében rejlik. A Rendszertechnika tárgy pusztán a matematikai megközelítéssel foglalkozik.
A továbbiakban azt vizsgáljuk, hogy milyen matematikai kapcsolat adható meg a bemenetek és a kimenetek között.
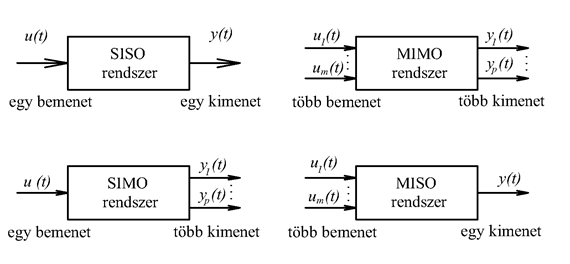
A rendszereket szokás a be- és kimenetek száma szerint csoportosítani (ld. 2-3. ábra). A klasszikus szabályozástechnikában elsősorban egy bemenetű egy kimenetű rendszerekkel (angolul Single Input Single Output SISO) találkozunk. A modern szabályozáselmélet foglalkozik több bemenetű több kimenetű rendszerekkel (angolul Multiple Input Multiple Output MIMO). Természetesen beszélhetünk egy bemenetű több kimenetű (SIMO) és több bemenetű egy kimenetű (MISO) rendszerekről is.
2.5. Lineáris és nemlineáris rendszerek fogalma
Definíció
A lineáris rendszerek legfontosabb tulajdonsága, amely egyben definícióként is használható, hogy érvényes rájuk a szuperpozíció elve.
Értelmezés
Ez az egyik legfontosabb tulajdonság, amelyet minden vizsgált rendszerről el kell dönteni. A lineáris rendszerek matematikailag sokkal könnyebben kezelhetők, mint a nemlineáris rendszerek. Kézenfekvő, hogy a lineáris rendszereket lineáris egyenletekkel (algebrai, közönséges és parciális differenciálegyenletekkel) írhatunk le. A lineáris rendszerek leggyakrabban kihasznált tulajdonsága a bemeneti hatások szuperponálhatósága (ld. 2-4. ábra). Ezt használhatjuk ki, ha méréssel kell eldönteni egy valós fizikai rendszerről, hogy lineáris-e. Pl. egy ellenállás esetén rákapcsolunk egy feszültséget (mint bemenőjelet), és megmérjük az ennek hatására kialakuló áramot (mint kimenő jelet). Ha az adott feszültséget felére, illetve kétszeresére változtatjuk, és azt tapasztaljuk, hogy ekkor az áram is felére, illetve kétszeresére nő, akkor az ellenállás az adott működési tartományban lineáris. Hasonlóan, ha egy rugót megterhelünk egy erővel, és az erőt felére vagy kétszeresére változtatjuk, akkor a rugó megnyúlása is a fele, illetve a kétszerese lesz. Gyakori, hogy egy rendszer csak egy adott működési tartományban lineáris (csak egy adott működési tartományban érvényes rá a szuperpozíció elve.) Pl. ha a rugót teljesen összenyomtuk, vagy teljesen kinyújtottuk, akkor az erő további növelése nem okoz változást.
Könnyen belátható, hogy két lineáris rendszer soros vagy párhuzamos kapcsolásából keletkező eredő rendszer is lineáris. Ezt a tulajdonságot is gyakran kihasználjuk.
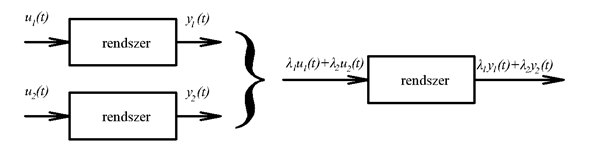
Azok a rendszerek, amelyek nem írhatók le lineáris egyenletekkel, nemlineárisak. A nemlineáris rendszerek is osztályozhatók annak függvényében, hogy miben rejlik a nemlineáris jelleg. A továbbiakban elsősorban lineáris rendszerekkel foglalkozunk.
MIMO rendszerek esetén a 2-4. ábraán látható bemeneti és kimeneti mennyiségek általános esetben vektorosan értendők. A vizsgálati módszer gyakran az, hogy csak az egyik bemenetre adunk gerjesztést és megvizsgáljuk a rendszer válaszát, majd egy másik bemenetre adunk gerjesztést annak a válaszát is megvizsgáljuk, végül a két bemenetre együttesen adunk gerjesztést. Ha a rendszer lineáris, akkor a két benetet együttesen gerjesztve a rendszer válasza a két külön válasz összege.
A valós fizikai rendszerek működésében valahol biztosan jelentkezik a nemlineáris jelleg. Elég arra gondolnunk, hogy mindig található olyan nagy fizikai bemenőjel, amely tönkre tudja tenni a valós fizikai rendszert, és ekkor a linearitás értelemszerűen megszűnik. Így a linearitás egy működési tartományra és pontossági követelményre jellemző tulajdonság. Fordított megközelítésben, a nemlineáris valós fizikai rendszert vizsgálva a legtöbb esetben egy munkapont körül kijelölhető egy olyan tartomány, ahol a működés lineárisnak tekinthető. Legyen a munkaponti egyenlet, amely az munkaponti bemenőjel és az munkaponti kimenőjel között adja meg a kapcsolatot:
|
|
( 2.1 ) |
Módosítsuk a bemenőjelet a munkapont körül
|
|
( 2.2 ) |
|
|
( 2.3 ) |
A rendszer az adott munkapontban lineáris, ha
|
|
( 2.4 ) |
Sok esetben a rendszer a munkapontban sem lineáris, de lineárisan közelítjük. Ezt nevezik munkaponti linearizálásnak, és gyakran élünk ezzel a lehetőséggel. Megjegyezzük, hogy léteznek más linearizálási módszerek is. Mechanikai rendszereknél általában az egyesúlyi helyzetet keressük meg, és e körül linearizálunk. A Rezgéstanban számos ilyen feladattal találkozhattak.
Néhány gyakori oka a nemlineáris viselkedésnek: mágneses köröknél a telítődés és a hiszterézis, mechanikai rendszereknél a súrlódás, kotyogás és a mozgás korlátozása, teljesítményelektronikai berendezések esetén a kapcsoló üzemmód, elektronikai áramkörökben az offszet, valamint bármely irreverzibilis változás.
2.6. Determinisztikus, sztochasztikus és kaotikus rendszerek fogalma
Definíció
Determinisztikus rendszerről akkor beszélünk, ha egy konkrét bemenőjelre a rendszer teljes ismeretében mindig egy konkrét kimenőjel analitikusan kiszámítható.
Definíció
Sztochasztikus rendszer egy konkrét bemenőjelre adott válasz á t nem tudjuk pontosan meghatározni, csak annak a valószínűségi eloszlását. A rendszer tartalmaz valamilyen véletlenszerűségen alapuló elemet.
Definíció
Olyan nemlineáris dinamikával rendelkező determinisztikus rendszereket nevezünk kaotikusnak, amelyek hosszú távú viselkedése csak statisztikailag írható le.
Értelmezés
Kihangsúlyozzuk, hogy sokszor nem az a kérdés, hogy maga a valós fizikai rendszer determinisztikus vagy sztochasztikus, sokkal inkább a leírási mód a kérdés. Számos esetben egy valójában determinisztikus, de összefüggéseiben nagyon bonyolult folyamatot egyszerűbb sztochasztikus szabályokkal leírni. A véletlen számok generálásának egy tipikus eszköze a dobókocka. Ha egy geometriailag pontosan megmunkált, homogén anyag kitöltésű dobókockát elgurítunk, akkor az azonos valószínűséggel áll meg bármely oldalán. Ez így egy tipikus sztochasztikus folyamat. Kisgyerekek gyakran azzal próbálják a „hatos” dobásának az esélyét megnövelni, hogy a dobókockát úgy fogják a kezükbe, hogy a „hatos” felfelé legyen. Ez nem sokat szokott segíteni, ha csak azt a dobást tekintjük érvényesnek, amikor a dobókocka ténylegesen gurul egy keveset. Az eldobás erejét nem tudjuk olyan pontosan szabályozni, hogy a dobókocka mindig ugyanúgy álljon meg. A folyamatot a kezünk pontatlansága teszi sztochasztikussá. Ezzel szemben, ha pontosan tudjuk, hogy egy robot miként fogta meg a dobókockát (vagyis tudjuk a kezdeti állapotot) és pontosan tudjuk, hogy milyen irányba, milyen erővel az asztaltól milyen távolságban dobta el a dobókockát (vagyis pontosan tudjuk a rendszer bemenőjelét), továbbá ismerjük a dobókocka fizikai paramétereit (vagyis ismerjük a rendszeregyenleteket), akkor a folyamat determinisztikussá válik. Meg van az elvi esély, hogy előre ki tudjuk számítani, hogy mit fog egy robot dobni. Hasonlítsuk össze egy labda és egy dobókocka elgurítását. Egy labda és egy nagy síkfelület esetén, ha egy kicsivel megváltoztatjuk a labda kezdeti helyzetét a gurítás pillanatában, akkor mindig ugyanennyivel fog megváltozni a végállapot. Ezzel szemben, ha egy dobókockának kicsivel megváltoztatjuk a kiindulási állapotát, akkor ez lehet, hogy nincs hatással a végső állapotra, de előfordulhat, hogy a kezdeti feltételek apró megváltoztatása miatt a dobókocka eggyel többször billen át, vagy elmarad az utolsó átbillenése. Lineáris rendszerek esetén a szuperpozíció elvéből következően, a bemenőjel megváltoztatásával arányos lesz a kimenőjel megváltozása. Egy periodikusan működő nemlineáris rendszer esetén is tetszőleges időtávra pontosan meg tudjuk mondani a kimenőjel értékét. Vannak olyan rendszerek, ahol a kezdeti érték minimális megváltozása is teljesen megváltoztatja a jel későbbi alakulását. Ilyen rendszerek válhatnak kaotikus működésűvé. A kaotikus jelenségek tipikus példája az időjárás. Ahogy az időjárást befolyásoló változókat egyre pontosabban tudjuk mérni, és egyre bonyolultabb számításokat tudunk végezni, úgy egyre pontosabb rövidtávú prognózisokat tudunk készíteni (ebből látszik a rendszer determinisztikus volta), de minél hosszabb távra próbálunk előretekinteni, úgy a prognózis egyre bizonytalanabbá válik.
Valós fizikai rendszerek esetén mindig szükség van valamilyen mérésre és a méréshez mindig társul zaj. Tipikusan a zajok és azok hatása tekinthető sztochasztikusnak. Vagyis sok esetben a determinisztikus és sztochasztikus jel együtt jelenik meg. Fontos feladat lehet ezek szétválasztása. Ennek egyik módja a jel szűrése. A szűrést elvégző szűrőre úgy tekinthetünk, mint matematikai eljárást megvalósító rendszerre, ahol a bemenet a zajos jel, a kimenet a szűrt jel. A mérnöki gyakorlatban sokszor előbb készül el az absztrakt matematikai modell, és ahhoz keresünk valós fizikai rendszert. Ennek kapcsán egy újabb fontos fogalmat kell tisztázni. Külön megkell említeni a kaotikus rendszereket, amelyek valójában deteminisztikusak, de bizonyos szempontból sztochasztikusnak látszanak.
2.7. Kauzalitás fogalma
Definíció
Egy rendszert akkor nevezünk kauzálisnak, ha a rendszer kimenőjele bármely időpillanatban nem függ az adott időpont utáni bemenőjelektől (gerjesztésektől), vagyis a jövőbeni események nem hatnak a jelenre.
Értelmezés
Természetesen minden valós fizikai rendszer és minden a méréssel azonos időben működő jelfeldolgozó algoritmus kauzális. A kauzalitás lehet a kritériuma annak, hogy egy adott matematikai algoritmus megvalósítható-e a vizsgálattal, vagy a méréssel egy időben (valós időben) pl. később látni fogjuk, hogy egy ideális aluláteresztő szűrő nem kauzális, ezért elvileg lehetetlen, hogy a méréssel egy időben működve megvalósítsuk. Egy mérési adatsoron elvégzett utólagos jelfeldolgozó algoritmus esetén a kauzalitás nem feltétlenül szükséges, mivel ezeket az algoritmusokat egy múltbeli időpontban úgy alkalmazzuk, hogy ahhoz a múltbeli időponthoz képest a vizsgálandó jövő ismert. Példaként könnyen beláthatjuk, hogy ha különböző frekvenciájú és különböző amplitúdójú szinuszos jeleket kívánunk szűrni egy ideális aluláteresztő szűrővel, és egy nullátmenet után azt tapasztaljuk, hogy a jel meredeken nő, akkor ez lehet egy nagy amplitúdójú kis frekvenciájú jel, amelyet át kell engedni, vagy lehet egy nagy frekvenciájú kis amplitúdójú jel, amelyet el kell nyomni. A nullátmenetnél nem tudjuk, hogy mit kell tennünk, de a jel egészét áttekintve könnyen eldönthetjük, hogy az adott jelet átengedni, vagy elnyomni kell.
Sociális, illetve társadalmi rendszerek lehetnek jövőbelátók (anticipatívak), pl. a jelen tőzsdei folyamatait a jövő vélt vagy valós ismerete befolyásolja.
2.8. Paraméter és változó fogalma
Definíció
A valós fizikai rendszert leíró egyenletek együtthatói a paraméterek .
Értelmezés
Első közelítésben azt mondhatjuk, hogy egy valós fizikai rendszer matematikai leírásában szereplő állandókat paraméternek, az időben változni képes mennyiségeket változóknak nevezzük. Az előbbire példa az ellenállás (első közelítésben), az utóbbira a feszültség és az áram.
|
|
(2.5) |
Sokan ragaszkodnak ehhez a szigorú megkülönböztetéshez, azonban a szakirodalomban találkozunk időben változó paraméter kifejezéssel is. A paramétert abban az értelemben használjuk, hogy azok a valós fizikai rendszert leíró egyenletek együtthatói. A változó paraméterű rendszer változó együtthatójú egyenletekkel leírható rendszert jelent.
Gyakran előfordul, hogy egy valós fizikai rendszernek létezik egy közmegegyezésen alapuló paraméteres leírása, amely bizonyos pontossággal, bizonyos működési tartományban jól használható (ld. Ohm törvény (2.5)). Ha a pontosságot vagy a működési tartományt növelni kívánjuk, akkor előfordulhat, hogy az egyszerűbb leírásban állandónak tekintett és állandó értékű paraméterként viselkedő mennyiség változásait is figyelembe kell venni, pl. egy áramkörben a hőmérséklettől függően változhat az ellenállás értéke. Tegyük fel, hogy (2.5) egy aszinkronmotor forgórészköri tekercs ellenállásán eső feszültséget írja le. Ez az ellenállás üzemi hőmérsékleten akár 50%-kal is megnövekedhet a szobahőmérsékleten mért értékhez képest. Ha a számításainkat pontosítani akarjuk, akkor a hőmérsékletet tekinthetjük egy új változónak, amelynek értékét egy meglehetősen bonyolult f hőtani függvény segítségével számíthatjuk ki. A hőmérsékletet megadó f függvény függ az áramtól, a külső hőmérséklettől, a motor fordulatszámától és számos egyéb körülménytől.
|
|
( 2.6 ) |
A hőmérséklet meghatározása nagy számítási kapacitást igényel, különösen, ha arra is tekintettel kívánunk lenni, hogy a hőmérséklet nem egyenletes eloszlású a tekercsen belül. Ugyanakkor a (2.5) egyenletre nem önmagában van szükség, ez beépül egy nagyobb, a motor működését leíró rendszerbe. Általában törekszünk lineáris rendszerek használatára. Ha a (2.6) egyenletet alkalmazzuk, akkor a motor működését leíró rendszer biztosan elveszíti a linearitását. E rendszert felhasználhatjuk a motor működésének szabályozásakor. Pl. mérjük a motor aktuális áramait és fordulatszámát, majd ezekből a mérési eredményekből és a motor működését leíró rendszer segítségével kell kiszámítanunk, hogy mekkora feszültségeket kell a motor kapcsaira kapcsolni a kívánt működés elérése érdekében. Ha bonyolult a rendszer, sokat kell számolni, akkor mire kiszámítjuk a motorra kapcsolandó feszültséget, a mérési eredmények érvényüket vesztik. Pl. ha egy autóban van ez a motor, akkor rég nekimentünk a falnak, mire kiszámítjuk, hogy fékezni kellene. Természetesen, ahogy egyre olcsóbban, egyre nagyobb kapacitású számítástechnikai eszközöket tudunk vásárolni, úgy egyre bonyolultabb modelleket tudunk a méréssel egy időben számolni. De a rendszer bonyolultságának mindig lesz egy határa, és elképzelhető, hogy a méréssel egy időben számítható modell még mindig nem ad kellő pontosságú eredményt.
Egy kompromisszumos megoldás lehet, hogy egy tipikus működést feltételezve offline módon kiszámítjuk, hogy az R ellenállás az időben miként változik, azaz egyszerűen időben változó paraméterként kezelhetjük.
|
|
(2.7) |
A pontosságot úgy tudtuk megnövelni a (2.5) összefüggéshez képest, hogy nem veszítettük el a linearitást, a számítási igényt sem növeltük meg jelentősen, de (2.7) csak akkor ad jobb eredmény, ha a tipikus működéstől nem térünk el jelentősen.
Az időben változó paraméter használatának van egy másik fontos előnye, miszerint megőrizhető a rendszer linearitása. A példánkban (2.6) egy pontosabb, mindig érvényes, de nemlineáris modell, (2.7) csak egy tipikus működés esetén érvényes, de lineáris modell.
2.9. Elosztott és koncentrált paraméterű leírás fogalma
Definíció
Az elosztott paraméterű leírás esetén a tér minden pontjában meghatározunk valamilyen matematikai összefüggést, leginkább pa rciális differenciálegyenletek formájában.
Koncentrált paraméterű leírás esetén a vizsgált valós fizikai rendszer összefüggései t egy adott térrészben kiátlagoljuk, és egyetlen egyenlettel helyettesítjük.
Értelmezés
Talán ez az első és legnagyobb elágazás, de addig nem foglalkozhattunk ezzel, amíg a paraméter fogalmát nem tisztáztuk. Az elosztott szó itt a térbeli eloszlásra utal. Az elosztott paraméterű leírás esetén a tér minden pontjában meghatározunk valamilyen matematikai összefüggést, leginkább parciális differenciálegyenletek formájában. Tipikusan a hullámjelenségek (akár elektromágneses, akár mechanikai), anyagon belüli hő- és belsőfeszültség-eloszlások tartoznak ide. Ezeket az egyenleteket leginkább végeselem módszerrel oldjuk meg. Ez a témakör más tananyagokba tartozik.
Koncentrált paraméterű leírást akkor alkalmazhatunk, ha a vizsgált valós fizikai rendszer összefüggései egy adott térrészben kiátlagolhatók és összevont egyenlettel helyettesíthetők. Ezzel az egyszerűsítéssel a mérnöki gyakorlatban nagyon gyakran élünk. Pl. Ha egy rúd tartó szerepet tölt be, akkor egy térfogattal és tömeggel jellemezhető merev test. Ha hangvillaként használjuk, akkor a hullámok vizsgálatához minden pontját külön kell számítani, ezért az elosztott paraméterű modellre van szükség. Akkor is elosztott paraméterű modell szükséges, ha azt számítjuk ki, hogy erő hatására hol törik el a rúd.
Ebben a tananyagban - a továbbiakban - csak koncentrált paraméterű leírást alkalmazunk. Ettől függetlenül néhány később tárgyalt kategória alkalmazható elosztott paraméterű leírás esetén is. A koncentrált paraméterű leírásnak oka lehet, hogy rövidebb számítási időt igényel. Pl. egy robot tervezésekor azt szeretnénk tudni, hogy akár statikus, akár dinamikus terhelés esetén hol lépnek fel a legnagyobb belső feszültségek, ezért hol kell erősíteni, vagy hol lehet még biztonsággal gyengíteni a mechanizmust, akkor biztosan elosztott paraméterű leírást kell alkalmazni, és előfordulhat, hogy egy dinamikai vizsgálatnál egy 10 perces mozgás közben ébredő erők kiszámítása egy órán keresztül tart. A tervezési fázisban ez megengedhető. Ezzel szemben, a robot szabályozásánál, mérünk valamit és a lehető legrövidebb időn belül valahogy be kell avatkoznunk a robot mozgására vonatkozó céljaink elérése érdekében. Nem engedhető meg, hogy percekkel később számítsuk ki, hogy valamikor a múltban hogy kellett volna beavatkozni. A gyorsabb beavatkozás érdekében kénytelenek vagyunk lemondani a pontosságról.
2.9.1. Vektormezővel leírható rendszerek koncentráltparaméterű modellje
Ebben a fejezetben koncentrált paraméterű rendszert leíró egyenletek strukturális hasonlóságát, pontosabban hálózatok számítási módszereit vizsgáljuk. A koncentrált paraméterű leírás mindig valamilyen közelítést, illetve elhanyagolásokat jelent. Az elhanyagolások a villamos áramkörök számításánál (ott is inkább az alacsony frekvenciás gerjesztések esetén) a legkisebbek. Talán ez az oka, hogy a villamos áramkörök számítása van a legjobban kidolgozva, így más fizikai jelenségek leírására sokszor villamos analógiát használunk. E jegyzetben is a villamos áramkörök számítását vizsgáljuk meg részleteiben és a kapott eredményeket általánosítjuk.
Sok fizikai jelenséget egy vektormező divergenciájával és rotációjával lehet a legtömörebben leírni. Ezekből az egyenletekből koncentrált paraméterű modelleket alkothatunk, és ehhez kapcsolódóan származtathatunk fizikai mennyiségeket, létrehozhatunk hálózatokat.
Definíció
A megmaradási törvényekből származtatott koncentrált paraméterű fizikai mennyiségeket extenzív fizikai mennyiségeknek nevezzük. Sok esetben az extenzív fizikai mennyiségek egy vektormező divergenciájából származtathatók. Tipikusan extenzív fizikai mennyiségek a különböző típusú energiák és anyagmennyiségek, de ide tartozik a térfogat (hidrosztatika), az impulzus és impulzus momentum is.
Értelmezés
Elosztott paraméterű modellekben a megmaradási törvények divergencia egyenletek formájában írhatók fel, amelyek a forrásokra és a nyelőkre vonatkoznak, és azt fejezik ki, hogy a tér egy adott pontjában a legkülönbözőbb típusú anyag és energiákhoz köthető áramok átfolynak (befolynak és/vagy kifolynak), vagyis a tér minden pontjához a forrás értékére vonatkozó skalár értéket rendelünk, így a tér forrás sűrűségét kapjuk. Szokásos még az a megközelítés, hogy ha két térrészt egyesítünk, akkor (linearitást feltételezve) az eredő térrészben az extenzív fizikai változót jellemző érték a két térrész extenzív fizikai változói értékének az összege. Ezt úgy is megfogalmazhatjuk, hogy a térrészek egyesítésekor a extenzív fizikai változók additívak (linearitást feltételezve). A forrás sűrűségből összegzéssel számíthatjuk egy adott térrészre az összesített forrásokat (nyelőket). Az így kapott érték csak egy adott pillanatra vonatkozik, és ebből adódik, hogy egy újabb típusú fizikai változót definiáljunk.
Definíció
Extenzív fizikai mennyiségek rátájának nevezzük az adott extenzív fizikai mennyiség egy adott felületen mérhető időegység alatti változását.
Értelmezés
A jelenségek leírásánál általában a változásokra, pontosabban áramlására vagyunk kiváncsiak. Pl. töltésáram, térfogatáram, hőáram stb.
Az extenzív fizikai mennyiségek változásának két oka lehet, az egyik egy forrás vagy nyelő jelenléte, a másik a fizikai mennyiség vándorlása, illetve áramlása. Ez utóbbinak oka a vektormező örvényességében (illetve örvénymentességében) keresendő. Az extenzív fizikai mennyiségekhez találhatunk egy másik fizikai mennyiséget, amely az extenzív fizikai mennyiségek áramlását okozza.
Definíció
A vektormező örvényességi tulajdonságából származtatott fizikai mennyiségeket nevezzük intenzív fizikai mennyiségnek. Tipikusan intenzív fizikai mennyiség a nyomás, villamos feszültség és hőmérséklet.
Értelmezés
A rotáció a vektormező örvényességére, vagyis az áramlások okára vonatkozik. A tér minden pontjához egy vektor rendelhető, amely tekinthető egy általánosított erőnek, vagyis az egységnyi nagyságú extenzív mennyiségre gyakorolt hatásnak az adott pontban. Szokásos az a megfogalmazás, hogy a térrészek egyesítésekor az eredő térrészben az intenzív fizikai változó kiegyenlítődik, ez az egyesített térrészek súlyozott átlaga. Természetesen az örvényesség okára nézve az intenzív fizikai változók is additívak, vagyis, ha egy újabb örvényességi forrást iktatunk be, akkor a két forrás hatása valamely intenzív fizikai változók esetén is összegződnek (linearitást feltételezve). Az analóg mennyiségeket a 2.2 táblázat első felében foglaltuk össze.
Az extenzív és intenzív fizikai mennyiség fogalma erősen kötődik ahhoz, hogy két térfogatot egymás mellé helyezve egyesítünk, és ekkor igaz az, hogy az intenzív mennyiségek összeadódnak és az extenzív mennyiségek kiegyenlítődnek. Az absztrakt mezőket nem csak egymás mellé tehetjük, hanem egymásba is helyezhetjük (ennek elképzelése sok esetben nem egyszerű). Egy ilyen absztrakt mező egyesítés megvalósítható úgy, hogy az extenzív fizikai mennyiségek egyenlítődnek ki, és az intenzív fizikai mennyiségek adódnak össze. Tipikus koncentrált paraméterű példaként említhetjük az áramköri elemek soros és párhuzamos kapcsolását. Párhuzamos kapcsolásnál a feszültség egyenlítődik ki, és az áramok adódnak össze, soros kapcsolódásnál megfordítva, az áramok egyenlítődnek ki és a feszültségek adódnak össze. Később a 2.2 táblázatban is látni fogjuk, hogy értelmezéstől függően bizonyos fizikai mennyiségek szerepe felcserélhető.
2.9.2. Villamos jelenségek elosztott paraméterű leírása a Maxwell egyenletekkel
(elsősöknek nem ajánlott)
E pontban az elektromágneses mezőt, mint egy elosztott paraméterű modellt mutatjuk be. A (2.8), (2.9), (2.10) és (2.11) egyenleteket szokás differenciális Maxwell egyenleteknek nevezni.
|
|
( 2.8 ) |
ahol H a mágneses térerősség és J a vezetési áramsűrűség vektora, valamint D az eltolási vektor. ( tag az ún. eltolási áram). Az üzenet a következő: A mágneses tér mindig örvényes és ennek forrása valamilyen áram: vezetési vagy eltolási.
|
|
( 2.9 ) |
ahol E az elektromos térerősség és B a mágneses indukció vektora.
|
|
( 2.10 ) |
|
|
( 2.11 ) |
ahol a töltéssűrűség.
Lineáris, homogén és izotróp közeget feltételezve
|
|
( 2.12 ) |
|
|
( 2.13 ) |
|
|
( 2.14 ) |
ahol és a közeg permittivitása és permeabilitása (az index nélküli érték az egy adott közegre vonatkozik, amely felbontható a vákuumra vonatkozó értékre (0 indexszel jelölve) és annak szorzójaként megjelenő relatív értékre.), a nem villamos eredetű elektromotoros-erő, amely szintén oka lehet az elektronok áramlásának, pl. egy akkumulátorban kémiai hatások tartják fent a villamos áramot.
2 .1 Táblázat I dőben állandó elosztott paraméterű elektromos jelenségek formális analógiája
|
Elektrosztatika
|
Stacionárius (rezisztív) áramlási tér
*
|
Stacionárius mágneses tér
|
* Származtatott egyenlet:
Stacionárius jelenségek statikai egyenletekkel írhatók le, és ilyen esetben rendszertechnikai értelemben nem beszélhetünk állapotváltozóról. A rendszertechnikában az állapotváltozó mindig valamilyen dinamikai tulajdonsághoz (tároló elemhez) köthető és az állapotváltozókra mindig valamilyen differenciálegyenlet írható fel. Ugyanakkor a stacioner állapot leírására is szükségünk van valamilyen fizikai mennyiségekre és ezeknek megfelelő matematikai változókra. A 2.1 táblázat kiegészíthető nem villamos jelenségekkel is.
2.9.3. Kirchhoff egyenletek származtatása (koncentrált paraméterű modellekhez)
(elsősöknek nem ajánlott)
Ebben a pontban időben állandó jelenségekkel foglalkozunk. A cél az, hogy a 2.1 táblázatban megadott differenciális törvényekből (elosztott paraméterű modellből), koncentrált paraméterű modellt alkossunk.
-
Csomóponti egyenletek
A divergencia egyenleteket a Gauss–Osztrogradszkij-tétel (divergenciatétel) segítségével a vektor felületi integráljává alakítjuk át. A zárt felületet részekre bonthatjuk és az adott felületen a vektort egyszerűen kiátlagolhatjuk. Így jutunk el a koncentrált paraméterű Kirchhoff I. (csomóponti) törvényhez.
Elektrosztatika
|
|
( 2.15 ) |
Stacionárius (rezisztív) áramlási tér
|
|
( 2.16 ) |
Stacionárius mágneses tér
|
|
( 2.17 ) |
-
Hurokegyenletek
A rotáció egyenleteket a Stokes tétel segítségével a vektor vonal integráljává alakítjuk át. A zárt görbét görbeszakaszokra bonthatjuk és az adott görbeszakaszok mentén a vektort egyszerűen kiátlagolhatjuk. Így jutunk el a koncentrált paraméterű Kirchhoff II. (hurok) törvényhez.
Elektrosztatika
|
|
( 2.18 ) |
Stacionárius (rezisztív) áramlási tér
Mivel nem villamos eredetű, így nem szokás szerepeltetni a (2.9) Maxwell egyenletben. Ugyanakkor oka az elektronok áramlásának az áramkörben, vagyis oka az örvényességnek, ahogy egy szivattyú is keringetni tudja a folyadékot egy zárt csőhálózatban. Így célszerű figyelembe venni az örvényességre vonatkozó egyenletben. A szuperpozíció elvét kihasználva
|
|
( 2.19 ) |
Értelmezés
A szummában szereplő egy adott hosszegység végpontjai között mérhető feszültségkülönbség, ugyanakkor az értékhez tartozó távolságot nullának kell tekintenünk. Vagyis a szummában szereplő nullától különböző , illetve értékek mind villamos jellegűek, ezért azt mondhatjuk, hogy a külső elektromotoros erőből származó feszültséggel az áramkör villamos jellegű feszültségei tartanak egyensúlyt. Az ideális vezetőn belül az elektromos térerősség ugyancsak nulla. tipikusan egy akkumulátor (szárazelem) sarkai között üresjárásban mérhető feszültség különbség. Ha a szárazelemet terheljük, akkor a sarkain mérhető feszültség csökken a szárazelem belső villamos ellenállásán eső feszültség miatt. az összegzés jobb oldalán található, ezért általában ténylegesen az iránya ellentétes az áramkörben folyó áram irányával. Ezért tud az akkumulátoron belül az elektron a pozitív kimenettől a negatív kimenet felé vándorolni. Váltakozó áramú körökben az indukált feszültség -hez hasonló szerepet tölt be.
Stacionárius mágneses tér
|
|
( 2.20 ) |
-hez hasonlóan, úgy tekinthetjük, hogy az , magneses motoros erőt is egy nulla hosszúságú szakaszon iktatjuk be a mágneses körbe.
2.9.4. Kétpólusokkal modellezett stacioner állapotú villamos és mágneses áramkörök
Ebben a pontban időben állandó jelenségekkel foglalkozunk, így a tároló elemek kívül esnek e pont tárgykörén. Az előző pontban egy adott felület részre, illetve görbeszakasz mentén kiátlagoltuk az aktuális vektoriális mennyiséget, ebben a pontban a kiátlagolás után egy adott térrészben mind a keresztmetszet mentén, mind egy hosszúság mentén homogén eloszlást feltételezünk, továbbá az anyagminőséget is azonosnak tekuntjük a tér minden pontjában, és ezért az adott térrészt egyetlen koncentrált paraméterel jellemezzük.
2.9.4.1. Elektrosztatika
Tegyük fel, hogy egy adott henger alakú térrészben minden pontjában az és vektorok a henger palástjával párhuzamosan azonos irányba mutatnak, nagyságuk a henger minden pontjában azonos, és , továbbá a henger anyaga homogén, permittivitása a tér minden pontjában azonos. Legyen a henger hossza , egy merőleges keresztmetszetének területe . Egy ilyen homogén elektrosztatikus tér csak egy kondenzátor fegyverzetei között alakítható ki.
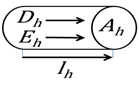
A homogén elektromos tér esetén (2.13) alapján:
|
|
( 2.21 ) |
A hengeren áthaladó villamos (eltolási) fluxus (2.15) és a hengeren eső feszültség (2.19) alapján
|
; |
( 2.22 ) |
(2.21) egyenletet átalakítva kapjuk a kondenzátorokra vonatkozó ismert összefüggéseket
|
|
( 2.23 ) |
2.9.4.2. Stacionárius (rezisztív) áramlási tér
Tegyük fel, hogy egy adott henger alakú térrészben minden pontjában az és vektorok a henger palástjával párhuzamosan azonos irányba mutatnak, nagyságuk a henger minden pontjában azonos, és , továbbá a henger anyaga homogén és vezetőképessége . Legyen a henger hossza , egy merőleges keresztmetszetének területe .
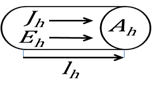
Az elektromotoros erő hatását különválasztva, tisztán az elektromos térerősség hatására kialakuló áramsűrűség nagysága (2.14) alapján:
|
|
( 2.24 ) |
A hengeren átfolyó áram (2.16) és a hengeren eső feszültség (2.19) alapján
|
|
( 2.25 ) |
(2.24) egyenletet átalakítva kapjuk az ismert Ohm törvényt
|
|
( 2.26 ) |
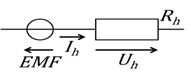
Külön kell figyelembe venni az adott szakaszon esetlegesen megjelenő elektromotoros erő hatását, ennek megfelelően a henger általános helyettesítő kapcsolása a 2-7. ábraán látható.
2.9.4.3. Stacionárius mágneses tér
Hasonló egyenletek írhatók fel mágneses tér esetén is
Tegyük fel, hogy egy adott henger alakú térrész minden pontjában az és vektorok a henger palástjával párhuzamosan azonos irányba mutatnak, nagyságuk a henger minden pontjában azonos, és , továbbá a henger anyaga homogén és mágneses permeabilitása . Legyen a henger hossza , egy merőleges keresztmetszetének területe .
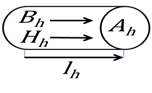
A gerjesztés (mágneses motoros erő) hatását különválasztva, tisztán az elektromos térerősség hatására kialakuló áramsűrűség nagysága (2.13) alapján
|
|
( 2.27 ) |
A hengeren áthaladó fluxus (2.17) és a hengeren eső gerjesztés (2.20) alapján
|
|
( 2.28 ) |
(2.27) egyenletet átalakítva kapjuk a mágneses Ohm törvényt
|
|
( 2.29 ) |
Külön kell figyelembe venni az adott szakaszon esetlegesen megjelenő gerjesztés (mágnesesmotoros erő) hatását, ennek megfelelően a henger helyettesítő kapcsolása a 2-9. ábraán látható.
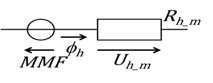
2.9.5. Hálózatszámítási analógiák
Két rendszer közötti analógia abból a tényből származtatható, hogy a rendszer működése hasonló alakú egyenletek segítségével írható le. Rendszerek közötti átjárhatóságról, analógiáról Harry F. Olson írt először (Dynamical Analogies, 2. kiadás, Van Nostrand, pp. 27–29, 1958) azzal a céllal, hogy segítséget nyújtson a mérnökök számára különböző rendszerek elemzéséhez és teljesítményeinek meghatározásához. Sok esetben a vizsgált rendszert kétpólusú, koncentrált paraméterű elemekből álló hálózatként írhatjuk le. Minden elemet egy paraméterrel, valamint az átmenő és keresztváltozó kapcsolatát leíró egyenlettel adhatunk meg. Az átmenő változó értéke a kétpólus két kivezetésén azonos, a keresztváltozó a két kivezetés különbségi értéke.
Definíció
Átmenő változó: Egy extenzív fizikai mennyiség rátája egy kétpólusra vonatkoztatva, ahol a kétpólusnak van egy belépő és egy kilépő felülete. Tipikus példa az elektronok, mint extenzív fizikai mennyiség áramlását leíró villamos áram, .
Értelmezés
A megmaradási tételből logikailag is levezethető, hogy ha egy adott térrészben nem változik egy adott extenzív fizikai mennyiség értéke, akkor a térrészt határoló felületen a be- és kiáramló extenzív fizikai mennyiség előjeles összegzése nullát ad. Elosztott paraméterű rendszerek esetén a divergencia egyenletből Gauss–Osztrogradszkij-tétel segítségével jutunk hasonló eredményre. Ebből vezethető le Kirchhoff I. (csomóponti) törvénye. Általánosságban kimondhatjuk: a koncentrált paraméterű modellek esetén az átmenő változók számítására a Kirchhoff I. törvényével analóg csomóponti egyenletet használhatjuk.
Definíció
Keresztváltozó: Az intenzív fizikai mennyiségnek egy kétpólus sarkain mérhető különbségét nevezzük keresztváltozónak. Tipikus példa a villamos feszültség, .
Értelmezés
Az elosztott paraméterű rotációs egyenletből a Stokes tétellel kaphatunk vonalintegrállal számított mennyiséget. A rotációból származtatott koncentrált paraméterű keresztváltozók közös jellemzője, hogy Kirchhoff II. törvényével analóg hurokegyenlet írható fel rájuk. Külön kell tárgyalni az örvénymentes mezőket, ezeket szokás potenciálos vagy konzervatív mezőnek nevezni.
2.9.5.1. A kétpólusú elemeknek
A kétpólusú elemeknek három típusát különböztethetjük meg
Definíció
-
Á-típusú tároló: olyan tároló, amely átmenő változó révén tárolja az energiát (általánosított értelmű energiát). A kétpólus két kivezetésén az átmenő változó időszerinti deriváltja arányos a két kivezetésen mért keresztváltozó különbségével. Tipikus példa az induktivitás. A tárolt energia és a kétpólusra felírható egyenlet
|
|
( 2.30 ) |
-
K-típusú tároló: olyan tároló, amely keresztváltozó révén tárolja az energiát (általánosított értelmű energiát). A kétpólus két kivezetésen mért keresztváltozó különbségének deriváltja arányos az átmenő változóval. Tipikus példa a kapacitás. A tárolt energia és a kétpólusra felírható egyenlet:
|
|
( 2.31 ) |
-
P-típusú elem: olyan elem, amely esetén a kétpólus két kivezetésen mért keresztváltozó különbsége arányos az átmenő változóval (Proporcionális-elem). Általában nem tárol energiát, hanem általában épp ellenkezőleg, elnyeli azt, más szavakkal hatására energia disszipálódik a rendszerből. De az elektrosztatikus és mágneses körök esetén pont ez az elem tárolja az energiát. Tipikus példa az ellenállás. Az energiára (ellenállás esetén a disszipált energiát jelent), és a kétpólusra felírható egyenlet:
|
|
( 2.32 ) |
2 . 2 Táblázat analógiák
|
Extenzív mennyiség |
Intenzív mennyiség |
Koncentrált paraméterű leírás kétpólus elemekkel (az . elemre felírva ) |
|||||||
|
vektormező
|
koncentrált forrás |
vektormező
|
koncentrált örvényesség |
átmenő változó
|
keresztváltozó |
P-típusú elem |
K-típusú tároló |
Á-típusú tároló |
|
|
|
|
extenzív mennyiségből származtatva
|
(eredő mennyiség) |
|
|
|
|||
|
Elektros z tatika |
eltolási vektor |
elektromos töltés |
elektromos térerősség |
nulla potenciálos |
villamos fluxus nem töltés rátája!!! |
feszültség különbség |
kondenzátor, helyén annak reciproka szerepel |
nem definiált |
nem definiált |
|
Elektromos áramkör |
eltolási vektor |
elektromos töltés |
elektromos térerősség |
elektro-motoros erő |
elemen átfolyó elektromos áram |
feszültség esés |
ellenállás |
kondenzátor |
önindukciós tekercs |
|
Mágneses kör * |
mágneses indukció |
nulla, forrásmentes |
mágneses térerősség |
gerjesztés (magneto-motoros erő) |
elemen áthaladó mágneses fluxus |
elemre jutó gerjesztés |
mágneses ellenállás |
nem definiált |
hiszterézises és örvényáramú veszteséges vasmag |
|
Hidraulikai rendszer Összenyomhat-atlan folyadék |
sebesség mező |
nulla forrásmentes |
sebesség mező |
szivattyú hatása |
térfogatáram |
nyomás esés |
csővezeték elem (nem lineáris) |
térfogat tartály |
hidraulikus tömeg |
|
Pneumatikus rsz. összenyomható közeg |
sebesség mező |
sebesség mező |
szivattyú hatása |
levegő térfogatáram |
nyomás esés |
csővezeték (fojtó) elem (nem lineáris) |
térfogat tartály |
nem definiált |
|
|
Lineáris mechanikai rsz. |
nem használt |
távolság nem divergenciából származtatott |
erő gradiens |
nulla, (potenciálos) |
relatív sebesség |
eredő erő |
csillapított mozgású elem |
rugó |
két ponton kapcsolódó tömeg |
|
Forgó mechanikai rsz. |
nem használt |
szögelfordulás nem divergenciából származtatott |
nyomaték gradiens |
nulla, (potenciálos) |
szögsebesség |
eredő nyomaték |
csillapított mozgású elem |
rugó |
két ponton kapcsolódó inercia |
|
Lineáris mechanikai rsz. |
normált Dirac impulzus |
impulzus |
gyorsulás mező |
nulla, (potenciálos) |
erő |
relatív sebesség |
csillapított egyenes mozgású elem** |
két ponton kapcsolódó tömeg |
rugó |
|
Forgó mechanikai rsz. |
normált Dirac impulzus momentum |
impulzus momentum |
szög-gyorsulás mező |
nulla, (potenciálos) |
nyomaték |
relatív szögsebesség |
csillapított forgó mozgású elem** |
két ponton kapcsolódó forgó tömeg |
rugó |
|
Tisztán termikus |
hőmennyiség |
hőmérséklet gradiens |
hő-áram |
hőmérséklet esés |
hővezető elem |
hő-kapacitás |
nem definiált |
||
* A mágneses kör esetén a többi példával ellentétben a D disszipatív elem tárolja és a K-típusú tároló disszipálja az energiát
**értéke a fenti elemek értékének reciproka
Megjegyzés: látható, hogy az elektromos és a mágneses jelenségek esetén az extenzív és intenzív fizikai változókat két-két különböző vektormezőből származtatjuk, ezzel szemben az áramlási problémáknál ugyanannak a vektortérnek vesszük a divergenciáját és a rotációját. Matematikailag az elektromos, illetve a mágneses jelenségek leírásakor elegendő lenne egy-egy vektormezőt definiálni. Vákuum jelenlétében nincs értelme ennek a szétválasztásnak. Ezt a szétválasztást az anyag tulajdonságai indokolják. Az elektromos tér forrása a töltés, de az anyagon belül több különböző módon létrejöhet töltés szétválasztás. Az eltolási vektor és az elektromos térerősség megkülönböztetésének pont az az alapja, hogy az előbbi figyelembe veszi, az utóbbi figyelmen kívül hagyja az anyagon belül az elektromos tér hatására kialakult töltésszétválasztás hatását. Hasonlóan, az anyagon belül az atomi szinten található párosítatlan elektronoknak (az adott elektronpályákon csak egy-egy elektron kering, a részletek a kvantum fizika tárgykörébe tartoznak) van egy állandó mágneses momentuma, amely erősítheti a küldő mágneses tér hatását. Ez modellezhető az anyagon belüli elemi köráramokkal (pl. ahogy az elektron kering az atommag körül), s ez a hatás a mágneses indukcióban megjelenik, de a mágneses térerősségben nem. Ez azt jelenti, hogy a mágneses indukció a teljes mágneses teret (a külső és belső áramok hatását együttesen) írja le, ezzel szemben a mágneses térerősséget kizárólag a külső áramokból számítjuk a gerjesztési törvény alapján, vagyis a külső áramok hatását írjuk le.
További analógiák Függelék Rendszerek és modellezési analógiák című fejezetében találhatók.
2.10. Lineárisan független egyenletek kiválasztása
Összetett rendszereknél, ahol az egyenleteket többféle módon lehet felírni, gondot jelenthet a lineárisan független egyenletek kiválasztása. Tipikusan ilyen rendszerek a különböző hálózatok, beleértve a mágneses és áramköröket, a víz, gáz és egyéb csőhálózatokat, de ide tartozik több koncentrált paraméterű hővezetési probléma is. Ezekre jellemző, hogy csomóponti és hurokegyenletet írhatunk fel. Elsősorban a lineárisan független hurkok kiválasztása okoz gondot, melyhez a gráfelmélet nyújthat segítséget.
2.10.1. Gráfelméleti alapok:
A gráfelmélet a kombinatorika egy fontos ága, amelynek létezik tisztán halmazelméleti megközelítése. A műszaki életben azért népszerű, mert a gráfelméleti fogalmak szemléletesen megjeleníthetők, és a gráfokkal könnyen leírható az áramkörök, csőhálózatok topológiája. A gráfelméleti terminológiák csekély mértékben eltérnek a műszaki életben használt terminológiáktól, ezért a gráfelméleti tárgyalásnál mindkettőt megadjuk, a későbbi alkalmazási példáknál csak a műszaki terminológiákat használjuk. Ebben a megközelítésben a következő definíciókat vezethetjük be:
Gráfelméleti definíciók
2.10.1.1. Gráf:
Csúcsok (műszaki megfelelője: csomópontok) és élek (műszaki megfelelője: ágak) halmazának egymáshoz rendelése oly módon, hogy egy él két csúcsot köt össze és egy csúcshoz több él is csatlakozhat. A csúcsokat pontokkal, az éleket vonalakkal jelöljük (ld. 2-10. ábra). Rajztechnikailag előfordulhat, hogy két él a kétdimenziós papíron keresztezi egymás, valójában az élek csak egy csúcsban találkozhatnak.
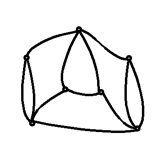
2.10.1.2. Irányított gráf:
Olyan gráf, amelyben az élekhez irányt rendelünk, vagyis megkülönböztetjük az élek kezdő- és végpontját. (ld. 2-11. ábra). A továbbiakban csak irányított gráfokkal foglalkozunk.
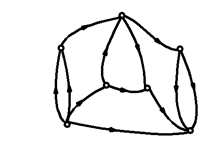
2.10.1.3. Egyszerű gráf:
Olyan gráf, amelyben bármely két csúcsot legfeljebb egy él köt össze, továbbá nem tartalmaz olyan élt, amelynek a kezdete és vége is ugyanahhoz a csúcshoz csatlakozik (ld. 2-12. ábra). A továbbiakban az első eset előfordulását megengedjük, de kizárjuk a második esetet.

2.10.1.4. Részgráf:
Olyan gráf, amelyet úgy kapunk, hogy egy gráfból kiemelünk csúcsokat és éleket. (ld. 2-13. ábra).

2.10.1.5. Út:
Olyan részgráf, amelyet úgy kapunk, hogy első lépésben a gráfból kiválasztunk egy élt és annak két végén található két csúcsot. Így egy út legalább egy élből és két csúcsból áll. Ezt tovább bővíthetjük úgy, hogy minden lépésben az utat bővítjük egy éllel és egy ahhoz csatlakozó csúccsal. Az élnek olyan csúcsból kell indulnia, amelyhez csatlakozó élek közül e lépést megelőzően csak egy szerepelt az út részgráfban, és az újonnan kiválasztott él másik vége egy olyan csúcs, amely korábban nem szerepelt az útban (ld. 2-14. ábra). Ebből következik, hogy ha egy gráfnak m db csúcsa van, akkor egy olyan útnak, amely tartalmazza a gráf minden csúcsát m-1 db éle van.
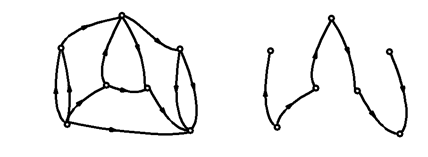
2.10.1.6. Összefüggő gráf:
Olyan gráf, amelynek bármely két csúcsa között található legalább egy út. Az út fenti definíciójából következik, hogy az út is mindig összefüggő gráf.
2.10.1.7. Kör (műszaki megfelelője: hurok):
Olyan összefüggő részgráf, amelyben minden csúcshoz pontosan két él csatlakozik (ld. 2-15. ábra). Látható, hogy egy körből bármely élt elhagyva utat kapunk.
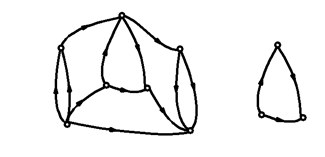
2.10.1.8. Fa:
Olyan összefüggő részgráf, amelyikben nincs kör, azaz bármely két csúcsa között csak egy út található (ld. 2-16. ábra). Az út a fának egy speciális este. A fa hasonlóan generálható, mint az út, az egyetlen különbség az, hogy amikor egy új éllel és csúccsal bővítjük a fát, akkor annak a feltételnek nem kell teljesülnie, hogy az élnek olyan csúcsból kell indulnia, amelyhez csatlakozó élek közül e lépést megelőzően csak egy szerepelt a fa részgráfban. Vagyis egy csúcsból tetszőleges számú él indulhat ki, ahogy az élő fatörzs is több felé ágazhat el.
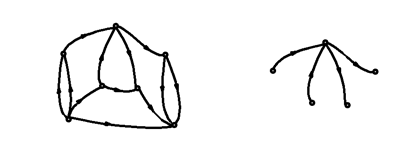
2.10.1.9. Feszítőfa:
Egy összefüggő gráfban egy olyan fa, amely a gráf minden csúcsát tartalmazza (ld. 2-17. ábra). A feszítőfára is igaz, hogy ha egy összefüggő gráfnak m db csúcsa van, akkor egy feszítőfának m-1 db éle van. Lineárisan független egyenletek generálásában fontos szerepe van a feszítőfának.

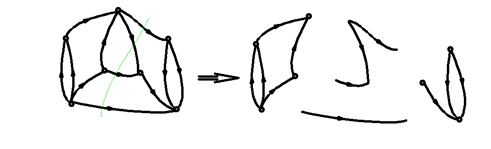
2.10.1.10. Vágat
Egy összefüggő gráfban az élek olyan halmaza, amelyet ha kiveszünk egy összefüggő gráfból az 2 független, de magában összefüggő gráfra esik szét (ld. 2-18. ábra). Más megközelítésben az összefüggő gráf csúcsait két részre osztjuk, és vesszük azokat az éleket, amelyek a két részt kötik össze. Speciális eset, amikor a csúcsokat úgy osztjuk szét, hogy az egyik részbe egy csúcs kerül, a másik részbe az összes többi.
2.10.2. Áramköri hálózatok leírása gráfokkal
Ahogy a bevezetőben is említettük az itt leírt módszer a műszaki élet számos más területén is használható. A továbbiakban áttérünk a műszaki szóhasználatra.
Az első lépés a formális analógia alapján a hálózatgráf felrajzolása. Ehhez a csomópontokat és az azokat összekötő ágakat kell meghatároznunk. Az 2-1 és 2-2 feladatban találunk példát villamos áramkörök és hálózat gráfjára (ld. 2-23. ábra és 2-24. ábra).
2.10.3. Hálózatot jellemző mátrixok
Ha ismerjük a hálózat struktúráját, definiálhatjuk a hálózatot jellemző mátrixokat:
Hurokmátrix (Körmátrix): lineárisan független hurkokra vonatkozó információt tartalmazza. Többféleképpen felírható. Első lépésben kijelölünk egy feszítőfát. Ha a feszítőfához bármely fennmaradó ágat hozzávesszük, akkor garantáltan keletkezik egy hurok. A nem feszítőfa ágak kapják az alacsonyabb sorszámokat és a hurkokat úgy generáljuk, hogy veszünk egy nem feszítőfa ágat és megnézzük, hogy ez a faágakkal hogyan képez egy hurkot úgy, hogy a hurok irányítása egyezzen meg a hurokban szereplő nem faág irányításával. Ezt mátrixosan is felírjuk, úgy, hogy a mátrix oszlopai az egyes ágakat jelölik, a sorai a hurkokat. Az egyes hurkokban az ágakra vonatkozóan a következő értékeket írjuk
-
0, ha az adott ág nincs benne a hurokban
-
-1, ha az adott ág szerepel a hurokban, a hurokkal ellentétes irányítással
-
1, ha az adott ág szerepel a hurokban, a hurokkal megegyező irányítással
példa az 2-19. ábra alapján, ahol a kiválasztott feszítőfa élei pirosak :
|
|
( 2.33 ) |
Itt: Az 1, 2 és 3 ágak nem részei a feszítőfának. Egy adott sorban a nem feszítőfa ágak közül mindig egynek lesz az értéke 1, a másik kettőé pedig 0, így a hurokmátrixban kialakul esetünkben egy 3x3-as egységmátrix.
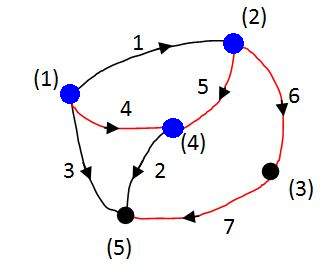
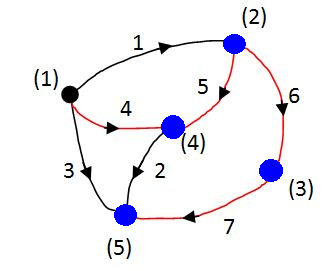
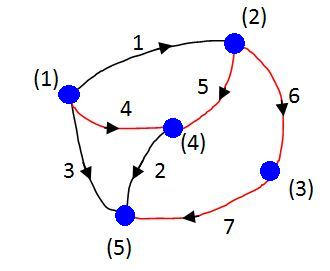
Vágatmátrix: azt az információt tartalmazza, hogy az összefüggő mátrixot milyen ághalmazok kihagyásával lehet két részre osztani. Egy gráfot általában többféleképpen lehet két részre bontani, de ezek a felbontások nem mindig függetlenek egymástól. Lineárisan független vágatokat is a feszítőfa segítségével lehet generálni. A feszítőfa bármely ágát elvágva, két egymástól független, de külön-külön összefüggő részgráfot kapunk. A feszítőfával együtt az összes többi ágat is elvágjuk, amelyek összekötik a kialakuló két részgráfot. A vágatmátrixban az elvágott ágakat szerepeltetjük.
A vágatmátrixnak n-1 sora van (feszítőfa ágainak száma) és m oszlopa (ágak száma). A mátrixba írt értékek a következőképpen értelmezhetőek az elvágott ág iránya szerint:
-
0 – nincs elvágva (nem tartozik a vágathoz)
-
(-1) – ellenkező irányú az elvágott feszítőfa ágával
-
1 – egyirányú az elvágott feszítőfa ágával
példa az 2-20. ábra alapján, ahol a kiválasztott feszítőfa élei pirosak:
|
|
( 2.34 ) |
Itt: 4-5-6-7 a feszítőfa ágai. Az ezek közül éppen elvágott ág viseli az 1-es értéket közöttük, így egy egységmátrix alakul ki.
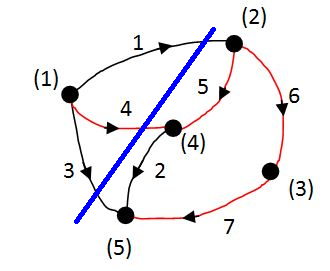
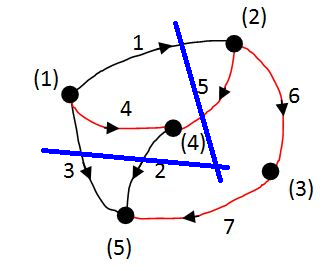
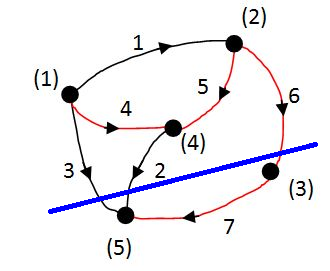
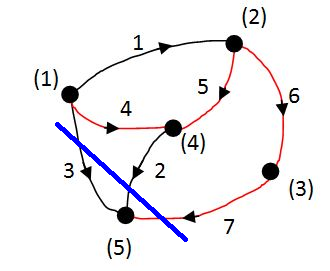
Csomóponti mátrix: A vágatmátrix speciális esete. A lineárisan független vágatokat nem a feszítőfa segítségével generáljuk. Helyette az összefüggő gráfot úgy osztjuk két részletre, hogy a csomópontokat egyenként kiemeljük a gráfból, és az adott csomóponthoz tartozó ágakat vágjuk el.
|
|
( 2.35 ) |
2.10.4. Áramkörök számítása
A hurok és csomóponti egyenleteket szeretnénk felírni, a csomóponti mátrix és hurok mátrix segítségével. Legyen az ágak száma és a csomópontok száma , így a feszítőfa ágak (egyben a lineárisan független csomópontok, illetve vágatok) száma és a nem feszítőfa ágak (egyben a lineárisan független hurkok) száma .
Minden ágban van egy ellenállás (általános esetben impedancia) és azzal lehet sorba kapcsolva egy feszültség generátor vagy párhuzamosan egy áramgenerátor (ld. 2-21 ábra).
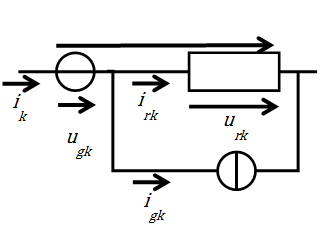
Az ágak, illetve az ellenállások áramát valamint feszültségét rendezzük egy-egy oszlopvektorba:
és , illetve és
Hasonlóan rendezzük egy-egy oszlopvektorba a generátor-feszültségeket és generátor-áramokat:
Az ellenállásokat rendezzük egy négyzetes mátrix átlójába:
Csomóponti mátrixot jelölje: ,
A hurokmátrixot jelölje:
Tegyük fel, hogy valamint ismert, és kiszámítandó és , így összesen ismeretlenünk van, vagyis egyenletre van szükség. Ohm törvény alapján egyenletet írhatunk fel. A csomóponti és hurok egyenletek száma , illetve . Ez összesen egyenlet.
A csomóponti és hurok egyenleteket mátrixos alakba rendezhetjük:
|
|
( 2.36 ) |
|
|
( 2.37 ) |
Az Ohm törvény mátrixos alakban:
|
|
( 2.38 ) |
(2.36) egyenletet átalakítva:
|
|
( 2.39 ) |
(2.37) egyenletet átalakítva és (2.38) behelyettesítéssel :
|
|
( 2.40 ) |
Mind (2.39), mind (2.40) egyenlet bal oldalán egy mátrixszal van megszorozva. Formálisan a mátrix inverzével kell balról beszorozni, hogy megkapjuk értékét. Ez a művelet akkor ad egyértelmű eredményt, ha a mátrix négyzetes. Az mátrix szorzóját úgy tehetjük négyzetessé, ha a (2.39) és (2.40) egyenleteket egymás alá írjuk
|
|
( 2.41 ) |
|
|
( 2.42 ) |
|
|
( 2.43 ) |
Most már nincs akadálya a mátrixinverziónak.
|
|
( 2.44 ) |
ismeretéeben a (2.38) Ohm törvény segítségével könnyen megkapható, de a fenti levezetéshez hasonlóan közvetlenül felírható. Ebben a kifejezésben megjelenik az ellenállás mátrix inverze. Mivel diagonális, így elemenként invertálható. Az impedancia reciproka az admittancia, amelynek a jele , ezért az ellenállás mátrix inverzét szokás admittancia mátrixnak nevezni és betűvel jelölni.
|
|
( 2.45 ) |
Felmerül a kérdés:mi a feltétele annak, hogy a (2.44) illetve (2.45) egyenletben található mátrixinverzió elvégezhető legyen. A mérnöki válasz: Ha egyetlen ellenállás, illetve admittancia értéke sem nulla, akkor az áramkör minden ágában kialakul egy áram és feszültség, a feladatnak egyértelműen megoldhatónak kell lennie. Így fizikai megfontolások alapján állítjuk, hogy az adott mátrixnak invertálhatónak kell lennie. Ezzel szemben, ha van két párhuzamosan kapcsolt olyan ág, amelyek különböző értékű feszültséggenerátort tartalmaznak és a velük sorba kapcsolt ellenállás értéke nulla, illetve van két sorban kapcsolt különböző értékű áramgenerátor és a velük páruzamosan kapcsolt ellenállás admittanciájának értéke nulla, akkor egy fizikailag értelmezhetetlen állapot alakul ki. Ezért a feladatnak matematikailag is megoldhatatlannak kell lennie.
Matematikailag az szükséges, hogy az invertálandó mátrix rangja legyen . Ha a csomóponti egyenletek helyett vágat egyenleteket írunk fel és a 2.10.3 pontban leírtak szerint sorszámozzuk az ágakat, akkor könnyen belátható, hogy az mátrixnak a második felében a mátrixnak az első felében van egy-egy egységmátrix (példaként ld. (2.33) és (2.34)). Ha a mátrixot meg szorozzuk az diagonális mátrixszal, akkor a mátrixban található 1-esek helyére az adott ág ellenállásának értéke kerül (természetesen a megfelelő előjellel), hasonlóan ha a mátrixot meg szorozzuk az diagonális mátrixszal, akkor a mátrixban található 1-esek helyére az adott ág admittanciájának értéke kerül (természetesen a megfelelő előjellel). Mindez nem befolyásolja a mátrix alapvető struktúráját, így ha az , illetve mátrix diagonáljában nincsenek nullák, akkor az invertálandó mátrix sorai garantáltan lineárisan függetlenek. Ha egy-két ellenállás értéke nulla, az nem jelenti automatikusan azt, hogy a mátrix nem invertálható. Az áramkörbe elhelyezhető néhány új ideális feszültséggenerátor, illetve áramgenerátor úgy, hogy az ne okozzon gondot. Az állítás csupán annyi, ha vannak olyan ágak, amelyekben nincs a feszültséggenerátorral sora kapcsolt nem nulla értékű ellenállás, illetve az áramgenerátorral nincs párhuzamosan kapcsolt nem nulla értékű admittancia, akkor tetszőleges elrendezésnél nem garantálható, hogy van egyértelmű megoldás. Így az adott mátrixok sem invertálhatóak.
2.10.5. Módszerek az invertálandó mátrix méretének lecsökkentésére:
2.10.5.1. Hurokáramok módszere
A 2-22. ábrán két hurok található. A hurokban keringő áramot nevezzük hurokáramnak. Az 2-22. ábráról leolvasható, hogy az 1. hurok árama megegyezik az 1. ellenállás áramával. A 2. hurok árama ellentétes a 3. ellenállás áramával, továbbá a 2. ellenállás áram a két hurokáram összege.
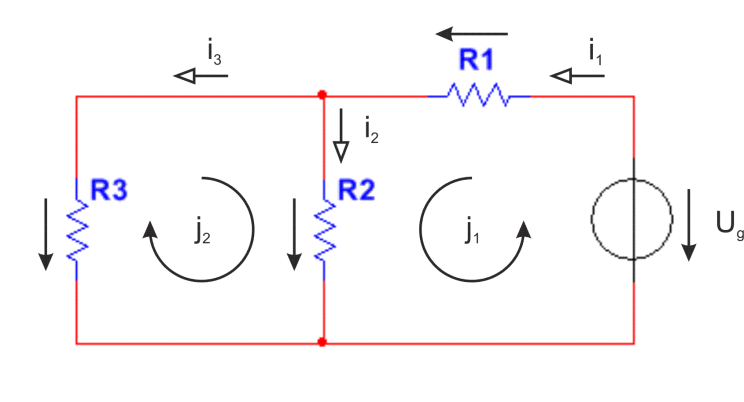
Általánosságban a hurokáramok és az ágáramok között a hurokmátrix segítségével teremthetünk kapcsolatot. A hurok mátrix oszlopai azt az információt tartalmazzák, hogy az adott ág melyik hurokban és milyen irányítással szerepel. Ha a hurokmátrix egy oszlopát összeszorozzuk a hurokáramok oszlopával, akkor megkapjuk az adott oszlopnak megfelelő ág áramát. Természetesen ehhez a mátrix művelethez a hurokmátrixot transzponálni kell.
|
|
( 2.46 ) |
|
|
( 2.47 ) |
ahol
a hurokmátrix transzponáltja
- az adott hurokban keringő áramok vektora
A hurokmátrix transzponálására azért van szükség, mert az ágakban akarunk összegezni.
A csomóponti egyenletből tudjuk, hogy:
|
|
( 2.48 ) |
ezt felhasználva, és behelyettesítve (2.47) alakját:
|
|
( 2.49 ) |
|
|
( 2.50 ) |
(2.50) mindig teljesül, mert a kiválasztott csomópontokról és a kiválasztott hurkokról tartalmaz információt. Az mátrix egy sora egy csomópontra, a mátrix egy oszlopa egy hurokra vonatkozik. A mátrixszorzásnál egy csomópontot egy hurokkal szorzunk össze áganként. Ha az adott csomópont nem szerepel az adott hurokban, akkor biztosan nullát kapunk. Ha az adott csomópont szerepel az adott hurokban, akkor a csomóponthoz tarozó ágak közül pontosan 2 található meg a hurokban. Ha ennek a két ágnak a csomópont szerint azonos az irányítása (mindkettő a csomópontba mutat, vagy mindkettő kifelé mutat), vagyis a két ághoz tartozó érték az mátrixban azonos előjelű, akkor az egyik ág irányítása megegyezik a hurokirányítással, a másik pedig garantáltan nem. Vagyis az adott sor és oszlop összeszorzásakor garantáltan értéket kapunk. Ha a két ág a hurokban kap azonos előjelet (irányítást), akkor a csomópontnál lesz ellentétes az előjelük. Tehát ebben az esetben is nullát kapunk.
Hurokegyenletek:
|
|
( 2.51 ) |
Nekünk a hurokáramokra van szükségünk, ezért helyettesítsük (2.51) egyenletbe először értékét (2.38) Ohm törvény alapján, majd értékét (2.47) alapján, végül az egyenletet átrendezve fejezzük ki a hurokáramok oszlopvektorát:
|
|
( 2.52 ) |
|
|
( 2.53 ) |
|
|
( 2.54 ) |
Végül kifejezhetjük az ellenállások áramát:
|
|
( 2.55 ) |
Hurokellenállás mátrix:
– ez közvetlenül felírható (számításnál hasznos), az átlóban lévő elemek az egyes hurkokban lévő ellenállások összegei. Az adott sorban és oszlopban lévő elemek pedig az adott hurkok közös ágakhoz tartozó ellenállások előjeles összegei. Az előjel a hurkok irányításától függ, ha a két hurok irányítása ellentétes, akkor negatív, ha megegyező, akkor pozitív (ld. (2.56)).
Megjegyzés
A hurkok köszös ágai csak a feszítőfa ágak közül kerülhetnek ki. A hurokáramok módszerének nem csak az az előnye, hogy kisebb mátrixot kell invertálnunk, hanem a hurkok megfelelő kiválasztásával befolyásolni tudjuk az invertálandó mátrix kondícióját, és ezzel numerikus problémákat kerülhetünk el. Pl. van néhány ág, amelynek az ellenállása nagyságrendekkel kisebb a többi ág ellenállásánál, akkor azokat az ágakat nem választjuk be a feszítőfába.
|
|
( 2.56 ) |
2.10.5.2. Vágatfeszültségek módszere
A vágatfeszültségek módszere hasonlít a hurokáramokéhoz, de itt nem egyes hurkokhoz rendeljük a bennük keringő áram értékét, hanem az egyes vágatokhoz a bennük fellépő feszültséget. Ezekből feszültségekből képezünk egy vágatfeszültség-vektort (vQ). Ha ezzel megszorozzuk a vágatmátrix transzponáltját (QT) megkapjuk az ágfeszültségek vektorát.
|
|
( 2.57 ) |
A hurok egyenletből tudjuk, hogy:
|
|
( 2.58 ) |
ezt felhasználva, és behelyettesítve alakját (2.57) alapján
|
|
( 2.59 ) |
|
|
( 2.60 ) |
(2.60) mindig teljesül, ennek belátását az olvasóra bízzuk.
Vágategyenletek:
|
|
( 2.61 ) |
Nekünk a vágatfeszültségekre van szükségünk, ezért helyettesítsük (2.61) egyenletbe először értékét (2.38) Ohm törvény alapján, majd értékét (2.59) alapján, végül az egyenletet átrendezve fejezzük ki a vágatfeszültségek oszlopvektorát:
|
|
( 2.62 ) |
|
|
( 2.63 ) |
|
|
( 2.64 ) |
Végül kifejezhetjük az ellenállások feszültségét:
|
|
( 2.65 ) |
2.10.5.3. Csomóponti potenciálok módszere
A vágatfeszültségek módszeréhez hasonlóan alkotunk egy csomóponti potenciálvektort (φ) oly módon, hogy egy tetszőleges csomópontot zérusnak választva, az összes többinek az ehhez viszonyított potenciálját összeírjuk. Mivel sorba haladunk a csomópontokon, a vektorban szomszédos értékek a rendszerben is szomszédos csomópontokhoz tartoznak, így ha bármelyik két szomszédos értéket kivonjuk egymásból, akkor a hozzájuk tartozó két csomópont közötti potenciálkülönbséget (feszültséget) kapjuk.
|
|
( 2.66 ) |
A kapott csomóponti potenciálvektorral megszorozva a rendszer csomóponti mátrixát megkapjuk a rendszer ágfeszültség vektorát.
|
|
( 2.67 ) |
A vágatfeszültségek módszeréhez hasonlóan, formálisan a vágatmátrix helyére az csopóponti mátrixot helyettesítve kapjuk:
|
|
( 2.68 ) |
|
|
( 2.69 ) |
2.10.6. Kidolgozott feladatok áramkörök számítására
2 - 1 feladat
Adott a 2-23. ábrán látható áramkör. Tegyük fel, hogy az összes ellenállás, valamint a feszültség generátor értéke ismert. ( , az ággal ellentétes irányítású). Számítsuk ki az összes ág áramát.
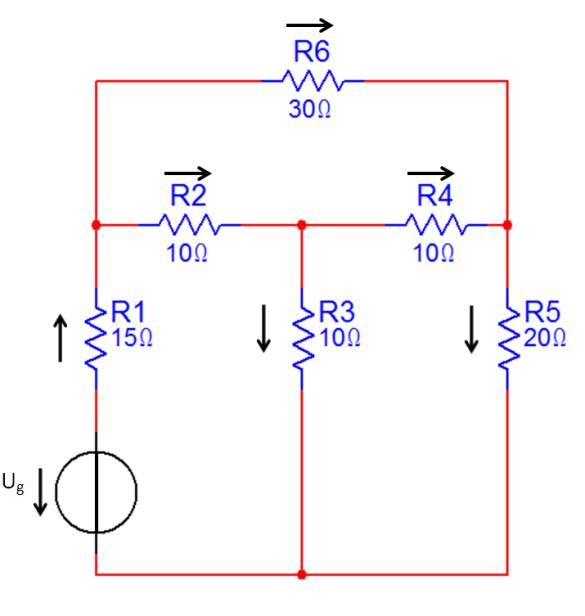
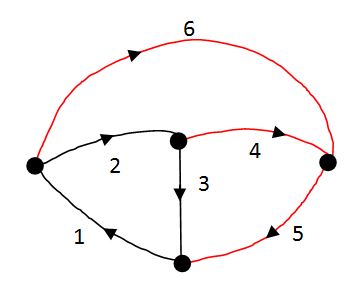
Írjuk fel a hurok- és csomóponti mátrixot a 2-23. ábrán látható hálózatgráf alapján.
|
|
( 2.70 ) |
|
|
( 2.71 ) |
|
|
( 2.72 ) |
A feszültség generátorok oszlopvektora és az ellenállások diagonál mátrixa
|
|
( 2.73 ) |
|
|
( 2.74 ) |
A hurokellenállás mátrix
|
|
( 2.75 ) |
|
|
( 2.76 ) |
A hurokellenállás mátrixot invertálva
|
|
( 2.77 ) |
|
|
( 2.78 ) |
|
|
( 2.79 ) |
Mivel nincs áramforrásunk, ig (a generátoráram) kiesik a (2.55) képletből.
|
|
( 2.80 ) |
Megoldás:
|
|
( 2.81 ) |
2 - 2 feladat
Adott a 2-24. ábrán látható R-L-C áramkör. Tegyük fel, hogy az összes ellenállás, kondenzátor, induktivitás, valamint a váltakozó áramú feszültség és áramgenerátor értéke ismert. ( , ). Számítsuk ki az összes ág áramát.
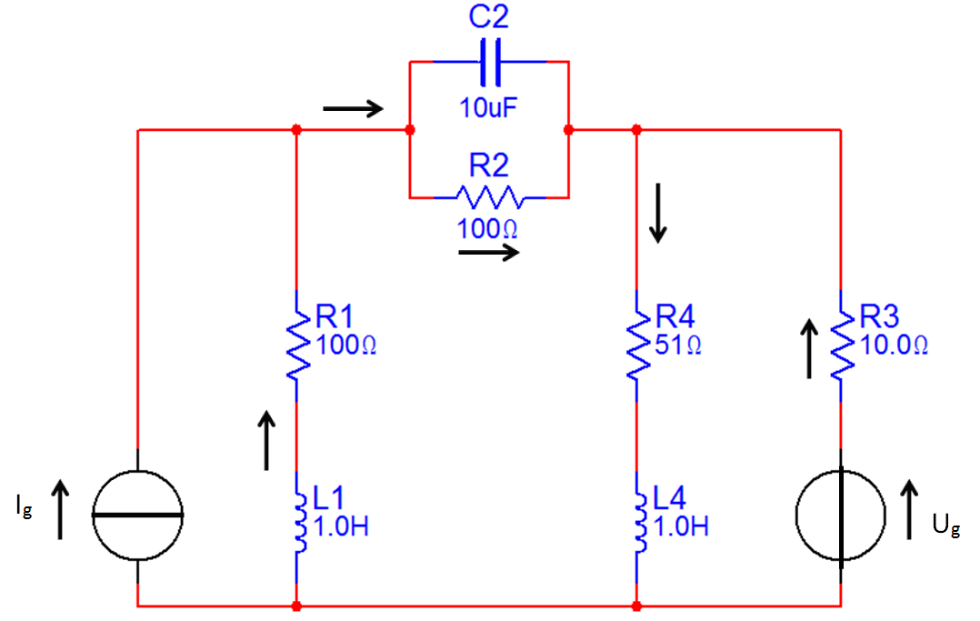
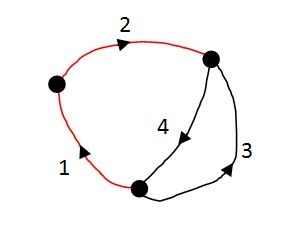
Az egyes ágak impedanciái
|
|
( 2.82 ) |
|
|
( 2.83 ) |
|
|
( 2.84 ) |
|
|
( 2.85 ) |
Írjuk fel a hurok- és csomóponti mátrixot a 2-24. ábrán látható hálózatgráf alapján. A feszítőfa két ága az 1. és 2. ág.
|
|
( 2.86 ) |
|
|
( 2.87 ) |
A feszültség és áramgenerátorok oszlopvektora valamint az impedancia diagonál mátrixa
|
|
( 2.88 ) |
|
|
( 2.89 ) |
|
|
( 2.90 ) |
A hurokimpedancia mátrix
|
|
( 2.91 ) |
|
|
( 2.92 ) |
Ebben az esetben komplex értékű mátrixot kell invertálni. A hurokáramok
|
|
( 2.93 ) |
Az ágáramok
|
|
( 2.94 ) |
2 - 3 feladat (Házi feladat, megoldását nem közöljük)
Az ábrán látható ellenállás hálózat tartalmaz még egy állandó értékű ideális Ug feszültség- és egy Ig áramgenerátort. A generátorok helyzete az Ön sorszámától függ, ezért ezeket csak az ellenállás hálózat mellé rajzoltuk le.
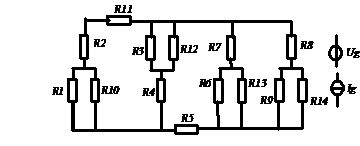
Feladatok:
-
Rajzolja fel az áramkör hálózat-gráfját (jelölje ki a pozitív irányokat).
-
A gráfban jelöljön ki egy feszítőfát, és ennek segítségével írjon fel egy-egy lehetséges csomóponti és hurokmátrixot.
-
Írja fel a hurokellenállás mátrixot
-
Írja fel a feszültég- és áramgenerátor oszlopvektorát.
-
Hurokáramok módszerét alkalmazva határozza meg az ágáramokat.
Adatok
Rk=k Ohm
Ug= sorszám*10 V Helye: sorba kapcsolva az Rn ellenállással, ahol n=1+Mod14(sorszám).
Ig= sorszám*10 A Helye: párhuzamosan kapcsolva az Rn ellenállással, ahol n=1+Mod14(sorszám).
2.11. Koncentrált paraméterű determinisztikus leírás
A továbbiakban koncentrált paraméterű determinisztikus rendszereket feltételezve azt vizsgáljuk, hogy a bemenetek és a kimenetek közötti kapcsolat milyen típusú egyenletekkel írható le. A rendszereket az őket leíró egyenletek szerint csoportosítjuk.
2.11.1. Statikus rendszerek fogalma
Definíció
Ha bármely pillanatban a bemenőjelek pillanatnyi értékei egyértelműen meghatározzák az adott pillanatban a kimenőjelek értékeit, akkor statikus rendszerről beszélünk.
Értelmezés
A statikus rendszernek nincs memória jellege, nincs szükség a bemenőjelektől eltérő belső állapotok definiálására, sem a múltbéli, sem a jövőbeni történések nem befolyásolják a jelent. Ezekben a rendszerekben az idő nem jelenik meg. Lineáris statikus rendszerek esetében a bemenetek és kimenetek között algebrai egyenletek írhatók fel.
Idetartoznak az ellenállás hálózatok, ha a feszültség- és áramgenerátorok ismeretében az egyes ellenállások feszültségét és áramait számítjuk, a robotok kinematikai vizsgálatai, a digitális technikában a kombinációs hálózatok. Nem véletlen az elnevezés, idetartoznak a mechanika statikai problémái. Az erők, mint bemenetek hatására ellenerők, mint kimenetek alakulnak ki. Kicsit más a helyzet, ha lehajlásokat is kell számolni, mint pl. a szilárdságtanban. A lehajlások kialakulásához idő kell, de sok esetben bennünket csak a végállapot érdekel, és abban értelemszerűen az idő már nem játszik szerepet.
2.11.2. Dinamikus rendszerek fogalma
Definíció
A dinamikus rendszerek a valós fizikai rendszerek működésének időbeni lefolyását is leírják, jellemzően idő szerinti differenciálegyenletek segítségével. Memória jelleggel rendelkeznek és ennek különböző formái lehetnek .
Értelmezés
Példaként könnyen beláthatjuk, hogy ha egy autót, mint rendszert vizsgálunk úgy, hogy bemeneteinek a gáz és fékpedál helyzetét tekintjük, akkor e bemeneti értékek egy adott pillanatbeli értékéből (az autó további paramétereinek ismeretében) az autó gyorsulása az adott pillanatban kiszámítható. Vagyis ha a fék és gázpedál a rendszer bemenete, valamint a gyorsulás a kimenet, akkor statikai egyenletet kapunk. Ezzel szemben, ha a kimenetnek a gyorsulás helyett a sebességet, vagy az elmozdulást választjuk, akkor ismernünk kell a múltbeli történéseket. Pusztán pl. a fékpedál egy pillanatbeli helyzetéből nem tudjuk kiszámítani az aktuális sebességet, illetve helyzetet. Tudnunk kell, hogy milyen sebességről indultunk, és mennyi ideje nyomjuk a féket. Külön kell kezelni az időkésleltetett dinamikus rendszereket. Legegyszerűbb esetben , ahol az időkéseltetés nagysága. Az időkésleltetett rendszerekkel külön fejezetben foglalkozunk. A dinamikai egyenletek felírása előtt további fogalmakat kell bevezetnünk
2.11.2.1. A rendszer jeleinek értelmezési tartománya, illetve a folytonos és diszkrét idejű rendszerek fogalma
Definíció
2.11.2.1.1. Folytonos idejű rendszerek
Folytonos idejű rendszerek esetén a be- és kimenőjel, és a vizsgált időintervallum minden időpont já ban értelmezve van, .
2.11.2.1.2. Diszkrét idejű rendszerek
Diszkrét idejű rendszerek esetén a be- és kimenőjel és a vizsgált időintervallumon csak diszkrét időpontok sorozatában van értelmezve , ahol és .
Értelmezés
Általában a jelfeldolgozó algoritmusok olyan esetekre vonatkoznak, ahol , vagyis a rendszerről csak meghatározott időlépésenként van információnk. A időlépést mintavételezési időnek is nevezzük, ugyanakkor a méréseknél nem mindig biztosítható az állandó és pontos mintavételezési idő. Gyakran számítógépes rendszerrel mérünk, és pl. a Windows operációs rendszer nincs felkészítve arra, hogy bármelyik taszkot (esetünkben a mintavételező taszkot) egy jól meghatározott időben futtassa le (megjegyezzük, hogy drágább kártyák a pontos mintavételezést hardware szinten meg tudják oldani). Azokat az operációs rendszereket, amelyek lehetővé teszik a taszkok időzített lefutását, valós-idejű (real-time) operációs rendszernek nevezzük. Alapbeállításban a legtöbb szimulációs program is változó nagyságú időlépést használ. Erre tekintettel kell lennünk az utólagos digitális jelfeldolgozásnál. Az egyszerűbb leírási mód kedvéért a diszkrét idejű rendszerekre bevezetjük a következő jelöléseket: az és időfüggvények értékeit diszkrét időben és jelöli. Az időfüggvény időpontbeli értékére az alábbi jelölést használjuk: és . A diszkrét idejű rendszerek leírásában a differenciálegyenletek helyett differencia egyenleteket kapunk. Ezek matematikai kezelése egyszerűbb, az egyenleteket lépésről lépésre meg lehet oldani. Sokszor didaktikailag hatékonyabb, ha először diszkrét idejű rendszert vizsgálunk, és ezt általánosítva jutunk el a folytonos idejű rendszerekhez.
2.11.2.1.3. A rendszerek jeleinek ablakozása
Egy ideális rendszer az idők kezdete óta az idők végezetéig működik, így jelei a teljes tartományban értelmezve vannak. Mi méréssel vagy szimulációval csak egy tartományban tudunk információt szerezni a jel változásáról, e tartományon kívül a jelről nem tudunk semmit. Az elnevezés onnan ered, hogy van egy az idők kezdetétől az idők végezetéig tartó jel, és ezt mi egy ablakon át csak egy tartományban látjuk. Sok esetben e tartományon kívül a jel számunkra érdektelen, de vannak olyan esetek, amikor az ablakozás hatását is valamilyen módon figyelembe kell venni.
2.11.2.2. A rendszer jeleinek értékkészlete, folytonos és kvantált értékű rendszerek
Definíció
2.11.2.2.1. Folytonos értékű rendszerek
Ha a rendszer jeleinek értéke egy tartományban folytonosan változhat , és , akkor folytonos értékű rendszerről beszélünk.
Diszkrét értékű (kvantált) rendszerek
Ha a rendszer jelei csak diszkrét értékeket vehetnek fel és , akkor diszkrét értékű (kvantált) rendszerről beszélünk.
Értelmezés
2.11.2.3. A rendszer csoportosítása a jeleinek értelmezési tartománya és értékkészlete alapján
Mind a folytonos idejű, mind a diszkrét idejű rendszer lehet folytonos értékű és kvantált. Ennek megfelelően a négy lehetőség
-
Folytonos idejű és folytonos értékű rendszer
-
Folytonos idejű és diszkrét értékű rendszer
-
Diszkrét idejű és folytonos értékű rendszer
-
Diszkrét idejű és diszkrét értékű rendszer.
Egy egyenletekkel felírt ideális rendszer lehet folytonos idejű és folytonos értékű, de akár mérjük, akár szimuláljuk a rendszer működését, pusztán a számábrázolás korlátossága miatt van egy olyan elvi határ, amelyen belül a változást már nem tudjuk kifejezni, így szigorúan nézve a rendszer diszkrét idejűvé és diszkrét értékűvé válik. Ha a jel változási sebességéhez és a változás mértékéhez képest sokkal kisebb az időlépés és sokkal kisebb a számábrázolásból eredő korlát, akkor a rendszert tekinthetjük folytonos idejű folytonos értékű rendszernek.
Diszkrét idejű és kvantált rendszereket inkább akkor használunk, ha mérésből nyerjük a rendszerről az információt.
2.11.3. Rendszerek simasága
Mind a mintavételezési idő, mind a kvantálási határok megválasztásánál tekintettel kell lennünk arra, hogy a rendszer jelei milyen gyorsan és milyen mértékben változnak.
2.11.4. Időinvariáns és autonóm rendszerek fogalma
Definíció
Az időinvariáns rendszer esetén, ha a rendszer egy gerjesztésre adott válasza , akkor az időben eltolt gerjesztésre adott válasz is egyszerű időbeni eltolással megkapható (ld. 2-26. ábra).
Értelmezés
Más megközelítésben az időinvariancia azt jelenti, hogy a rendszer válasza nem függ attól, hogy mikor adtuk a rendszerre a gerjesztést. Ez természetesen nem mondható el egy változó paraméterű rendszerről, amelyet időben változó (idővariáns) rendszernek nevezünk.

Az időinvarianciával rokon fogalom az autonómia.
Definíció
Matematikai értelemben akkor beszélünk autonóm rendszerről, ha a rendszer működését ún. autonóm differenciálegyenlet-rendszerrel lehet leírni. A alakú közönséges differenciálegyenlet-rendszert akkor nevezzük autonómnak, ha jobb oldala nem függ közvetlenül az időtől (azaz a változótól), vagyis átírható a következő alakúra: .
Értelmezés
Az autonóm differenciálegyenletek számos olyan tulajdonsággal rendelkeznek, ami miatt érdemes ezt a megkülönböztetést megtenni. A fenti megfogalmazásban nincs szó a bemenetről, e fogalom a rendszer aktuális működésére vonatkozik, amelynek a bemenőjel is része. Műszaki nyelvre lefordítva az autonóm rendszer azt jelenti, hogy sem maga a rendszer, sem a külső hatások nem változnak az időben. A rendszertechnikában a rendszert úgy definiáltuk, mint a bemenő- és kimenőjel közötti matematikai kapcsolatot, és ez ilyen formában független a gerjesztés minőségétől. Vagyis az időinvariancia magára a rendszerre vonatkozó és a bemenőjeltől független fogalom, az autonómia a működésre vonatkozik, és ezért függ a bemenőjeltől. Csak egy időinvariáns rendszer működhet autonóm üzemmódban, ennek az a feltétele, hogy a bemenőjel konstans legyen. Pl. egy magára hagyott időinvariáns rendszert leíró differenciálegyenlet lehet autonóm. Ha a bemenőjel időben változik, akkor a rendszer működése nem lehet autonóm.
Ismételten nem az a kérdés, hogy maga a valós fizikai rendszer időinvariáns-e/autonóm-e vagy sem, kérdés az, hogy miként írjuk le. Szigorúan véve a legtöbb valós fizikai rendszer idővariáns, mert az öregedés, kopás és végül a tönkremenetel idővariánssá teszi azt.
Itt visszautalunk a 2.6. fejezetre. Ha az áramot bemenőjelnek, a feszültséget kimenőjelnek tekintjük, akkor a (2.6) által definiált rendszer nemlineáris, de autonóm, a (2.7) által definiált rendszer lineáris, de nem autonóm.
Tegyük fel, hogy R(t) kiszámításakor azt feltételeztük, hogy a motort a t=0 időpillanatban kapcsoltuk be, és ehhez tartozik egy i(t) áram, mint bemenőjel és , mint kimenőjel, valamint R(t), mint a rendszer egyetlen paramétere. Ha a motort nem a t=0 időpillanatban kapcsoljuk be, akkor ez az áramnak, mint bemenőjelnek az időbeni eltolását eredményezi (feltételezve, hogy az egyéb működési körülmények nem változnak). Ha ehhez az időben eltolt i(t-τ) bemenőjelhez az eredeti (időben nem eltolt) rendszert, nevezetesen az R(t) együtthatót használjuk, akkor triviális, hogy a rendszer válaszát nem kaphatjuk meg egyszerű időeltolással. Röviden, ha , akkor a speciális esetektől eltekintve .
2.12. Dinamikus rendszerek általános összefüggései
Először az egyenletek szintjén egy egyszerű példából kiindulva jutunk el az általános rendszeregyenletekhez, és áttekintő képet adunk a kapcsolódó mérnöki feladatokról. Amikor az átfogó kép után a konkrétumokat tárgyaljuk, akkor természetesen ismét vissza kell térnünk az egyszerűbb esetekhez. Először a diszkrét idejű rendszereket vizsgáljuk, és ezt terjesztjük ki folytonos idejű rendszerekre. (Az időkésleltetett rendszerekkel nem foglalkozunk ebben a fejezetben.)
2.12.1. Állapot, állapotjelző, állapotváltozó és állapotegyenletek fogalma
Az állapot szót köznapi értelemben is gyakran használjuk és megjelenik több különböző tudományterületen is, így az állapot szónak több különböző értelmezése létezik. Az állapot rendszerelméleti megközelítésénél a dinamikus rendszerek definíciójából indulunk ki, miszerint azok memória jelleggel rendelkeznek, ezt a memóriát többféleképpen meg lehet valósítani, általánosságban a következőt lehet kimondani.
Definíció
Az állapot a múlt összesített hatása. A rendszer állapotának a következő két tulajdonsággal kell rendelkeznie
-
Bármely T időpillanatban a kimenőjel az adott pillanatbeli állapot és bemenőjel együttes ismeretében egyértelműen meghatározható legyen.
-
Az állapot egy adott T időpillanatban egyértelműen meghatározható legyen a bemenőjel a t≤T időtartománybeli értékének ismeretében.
Az állapotváltozók az állapot egyértelmű leírására szolgálnak .
Értelmezés
Különösen a német szakirodalom megkülönbözteti az állapotjelző és állapotváltozó fogalmát. Az állapotjelző mindig valamilyen energiához tartozó valós fizikai változó, amely közvetlenül vagy közvetve az adott energia nagyságát írja le. Az extenzív és intenzív fizikai változók egyaránt lehetnek állapotjelzők, ha valamilyen tárolóelemhez köthető mennységet írnak le, ezért maga az állapotjelzővel leírt tárolt mennyiség mindenképp additív, vagyis az állapotjelzőkre vonatkozó összegződés és kiegyenlítődés említése zavaró lehet, ez a két kifejezés maradjon meg magára a fizikai változóra. Az állapotváltozókat tágabb értelemben használjuk. Megválasztásában viszonylag nagy szabadságunk van, az egyetlen feltétel, hogy a definícióban megadott két feltételt teljesítsük. A német rendszertechnika könyvekben minden állapotjelző egyben állapotváltozó, de nem minden állapotváltozó állapotjelző. Ezért az állapot fogalma széles körben alkalmazható. Az állapotváltozókat nem kell konkrét fizikai mennyiséghez, illetve energiához kötni, de a definícióból következően mindenképp valamilyen általánosított tároló elemhez kötjük. Ezért felmerül a következő kérdés: minimálisan hány állapotváltozóra van szükség egy rendszer állapotának leírására?
Definíció
Egy rendszer állapotának egyértelmű leírásához minimálisan szükséges állapotváltozók számát a rendszer dimenziójának szokás nevezni.
-
Véges dimenziójú: véges számú állapotváltozóval leírható rendszer. Az állapotváltozók szokásos jelölése:.
-
Végtelen dimenziójú: végtelen számú állapotváltozóval leírható rendszer.
-
Diszkrét állapotú rendszerek: Ha egy véges dimenziójú rendszer állapotváltozói véges számú értéket vehetnek fel, akkor a rendszer lehetséges állapotainak száma is véges.
Értelmezés
Az állapotváltozók valamilyen általánosított értelmű tárolóelemekhez köthetők, és az állapot a diszkrét idejű rendszereknél valamilyen összegzés, a folytonos idejű rendszereknél integrálás eredménye. Egy dinamikai rendszerben az elmozdulás is lehet állapotváltozó, itt a tároló jelleg abból adódik, hogy a nulla ponttól mért távolságot tároljuk és az is világosan látszik, hogy a nulla ponttól mért távolság kis elmozdulások összegzéséből határozható meg. Tovább gondolva, ebből következik, hogy a rendszeregyenleteket a diszkrét időben differencia, a folytonos időben differenciálegyenletekkel írjuk le. A differenciálegyenletek rendszáma megegyezik a tárolóelemek számával. A véges dimenziójú rendszereknél véges számú tároló elem van. Szokás a rendszer dimenzióját a tároló elemek számával megadni. Pl. a későbbiekben külön foglalkozunk egy- és kéttárolós rendszerekkel. A továbbiakban csak véges dimenziójú rendszereket tárgyalunk.
Sokszor olyan fizikai változókat leíró jeleket választunk állapotváltozónak, amelyek valamilyen energiával, vagy annak változásával hozhatók kapcsolatba, ezek az állapotjelzők. Számtalanszor az állapotváltozónak nincs semmilyen fizikai megfelelője, ezek az állapotváltozók. A 2.9.1 pontban definiált Á-típusú tárolók átmenő változóját, a K-típusú tárolók keresztváltozóját célszerű állapotváltozónak választani. A P-típusú elem nem tárol, így ehhez kapcsolódóan nem tudunk állapotváltozót definiálni. Természetesen mindig a valós fizikai rendszerből indulunk ki, és először a valós fizikai rendszer egyenleteit írjuk fel, de sok esetben az így természetes módon felírt egyenletek rendszertechnikai szempontból nem elég rendszerezettek. A természetes módon felírt egyenletek általában magukra a jelenségre koncentrálnak. A rendszertechnikai szemléletben a konkrét beavatkozás és annak hatása, vagyis a bemenőjel és a kimenőjel áll a fókuszban és e két jel között kívánunk matematikai kapcsolatot teremteni. Amikor az alapjelenségből felírjuk az adott problémában szereplő be- és kimenőjel közötti matematikai kapcsolatot, akkor a matematikai egyszerűsítések miatt a fizikai tartalom a konkrét leírásból elveszhet, de pont az a cél, hogy a fizikai jelenségtől független, egységesen használható matematikai eszköztárat alapozzunk meg.
2.12.1.1. Diszkrét állapotú rendszerek
A diszkrét állapotú rendszerek esetén az állapotbeli változások nem az időben folytonosan, hanem egy-egy esemény hatására ugrásszerűen mennek végbe. A digitális technikában a szekvenciális hálózatok tipikusan idetartoznak, ahol minden logikai változó csak két különböző érték egyikét veheti fel.
A legegyszerűbb példa egy olyan fűtésszabályozás lehet, ahol két állapot (fűtés bekapcsolva és fűtés kikapcsolva) között a szerint váltunk, hogy a szoba hőmérséklete nagyobb-e a felső hőmérsékleti korlátnál, vagy kisebb-e a alsó hőmérsékleti korlátnál (ld. 2-27. ábra). (Természetesen )
Kicsit összetettebb példa lehet egy jegykiadó automata. Be kell dobni a pénzt, majd meg kell nyomni egy gombot és az automata kiadja a jegyet. A legegyszerűbb esetben csak egyfajta pénzt fogad el az automata (legyen ez a 100 Ft-os), minden más pénzérme átesik az automatán és azokkal az esetekkel nem foglalkozunk, továbbá a jegy ára 100 Ft, vagyis a 100 Ft bedobása után jár a jegy. Az automatának két állapota van, és kétféle esemény következhet be mindkét állapotban (ld. 2-28. ábra).
A „várakozás” állapotban hiába nyomkodjuk a gombot, nem történik semmi. Ha bedobunk egy 100 Ft-os érmét, akkor átkerülünk a „kiadásra kész” állapotba. A „kiadásra kész” állapotban, ha megnyomjuk a gombot, akkor az automata kiadja a jegyet és visszakerülünk a „várakozás” állapotba. A „kiadásra kész” állapotban maradunk, ha újabb pénzt dobunk be. Ez a pénz így elveszett. Nyilvántarthatjuk, hogy hány pénzt dobtak be, de ahhoz egy számláló kell, amely további állapotok bevezetését igényelné. Pl. bevezethetnénk a „kétjegy kiadására kész” állapotot, de ekkor a „kiadására kész” állapot nevét is célszerű pontosítani (ld. 2-29. ábra), és ez a sor folytatható.
Egy más jellegű bővítést jelent, hogy ha azt is figyelembe akarjuk venni, hogy időnként a jegy kiadása nem sikerül. Visszatérve a 2-28. ábrahoz, ha a „kiadásra kész” állapotban megnyomjuk a gombot, akkor az automata megpróbálja kiadni a jegyet. Ha sikerül a jegykiadás, akkor visszakerülünk a „várakozás” állapotba, ha nem, akkor „kiadásra kész” állapotban maradunk. Így egy eseménynek bizonyos valószínűséggel két kimenetele lehet. Ebben a példában a valószínűséget a hibás működés hozza be, de bizonyos esetekben a működés lényeges tulajdonsága, hogy egy esemény kimenetele véletlenszerűen alakul.
A 2-28. ábraához nagyon hasonlóan írhatunk le egy nyerő automatát. Első lépésben a jegyet a nyereménnyel helyettesítjük (ld. 2-30. ábra).
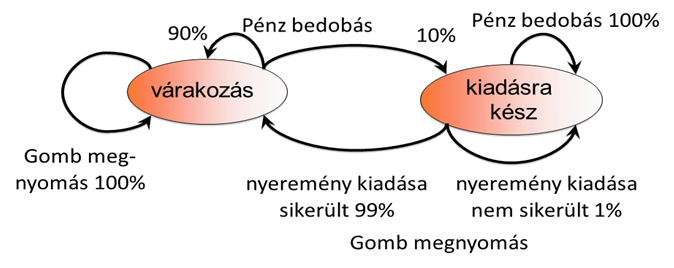
A legnagyobb különbség abban rejlik, hogy a pénz bedobásával nem minden esetben kerülünk át a nyeremény „kiadásra kész” állapotba. Ennek van valamekkora valószínűsége (esetünkben 10%), de a pénz bedobása nem determinálja az állapotváltást, vagyis ez nem egy determinisztikus rendszer. Ebben a példában a nyeremény összege fix. A 2-30. ábraán figyelembe vettük azt is, hogy a nyeremény kiadását valami megakadályozhatja (az esetek 1%-ában), de ekkor nem akarjuk elvenni a nyereményt.
2.12.1.2. A modellek kategorizálásának néhány problémája
Az előző példában a sztochasztikus jelleget megvalósíthatjuk úgy, hogy minden pénzbedobás után generálunk egy egyenletes eloszlású véletlen számot 0 és 1 között. Ha azt szeretnénk, hogy a nyerési esély 10% legyen, akkor 0 és 1 között kijelölünk egy 0.1 hosszúságú intervallumot. Ha a generált véletlenszám ebbe az intervallumba esik, akkor a „várakozás” állapotból átlépünk a „kiadásra kész” állapotba. Ha nem az adott intervallumba esik a generált szám, akkor nem változik az állapot. Az ilyen rendszereket joggal nevezzük sztochasztikusnak. Vannak olyan esetek, amikor nem teljesen egyértelmű, hogy a rendszer determinisztikus vagy sztochasztikus-e. Az előző példában számlálhatjuk, hogy eddig hányszor dobtak be pénzt az automatába, és egy előre meghatározott számsor szerint döntjük el, hogy hányadik pénzbedobó fog nyerni. Ekkor a rendszerünk determinisztikus, de a felhasználó számára sztochasztikusnak tűnik. Itt meg kell jegyezni, hogy maga a számláló is egy végesállapotú rendszer. Ha előre eldöntjük, hogy pl. az első 1000 pénzbedobás közül, melyik fog nyerni, akkor ezzel 1000 állapotot definiálunk. Sok esetben egy bonyolult determinisztikus rendszert egy lényegesen egyszerűbb struktúrájú sztochasztikus rendszerrel írunk le. Bizonyos bonyolult és összetett részek pontos működését statisztikákkal modellezzük.
Sok esetben ugyanazt a fizikai rendszert leírhatjuk néhány diszkrét állapottal, vagy folytonos értékű állapotváltozóval. Példaként egy gyomor állapotát leírhatjuk a két legfontosabb állapottal, jóllakottsággal és éhséggel. Az egyik állapotból a másikba egy-egy esemény bekövetkeztével jut a rendszer. Az éhes állapotból az evéssel lehet a jóllakott állapotba kerülni, és elegendő idejű nem evéssel vissza az éhségbe. Más megközelítésben, a gyomor telítettségére bevezethetünk egy folytonos állapotváltozót, amely értékét a bevitt és a megemésztett táplálék különbségének integráljával számíthatjuk (ld. 2-31. ábra).
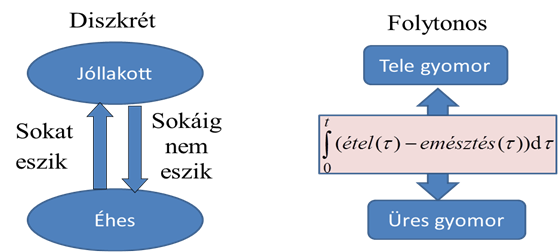
2.12.1.3. Véges dimenziójú rendszerek
Az állapotváltozós leírás nagy előnye az, hogy használható nemlineáris, idővariáns (nem autonóm) MIMO rendszerek esetén is
ahol az állapotváltozók vektora, a beavatkozó jelek vektora, a zavaró jelek vektora, a kimenőjelek vektora, a rendszer működését leíró függvény, kimenőjelet leképező függvény.
A rendszer általános definíciójában (ld. 2.1 pont) a rendszerre vonatkozóan nem szerepelt az idő, a 2.1 pontban megadott definíció nem nyilatkozik arról, hogy maga a rendszer időben változó-e vagy változatlan. Természetesen a be- és kimenőjelek a rendszertől függetlenül időben változhatnak. Ezzel szemben a dinamikai rendszereknél az idő a rendszerre vonatkozóan is fontos szerepet tölt be. Akár közvetlenül is megjelenhet a rendszeregyenletben (ld. változó paraméterű rendszerek), de a memória jelleg csak egy időintervallumban értelmezhető. A memória jelleg miatt a rendszert elvileg az idők kezdetétől meg kellene figyelni, de pont ennek elkerülésére vezettük be az állapot fogalmát. Általában a rendszereket csak egy meghatározott T0 időponttól kezdődően ( tartományban) vizsgáljuk. A legtöbb esetben az egyszerűség kedvért T0=0. A múlt hatását az állapotváltozók kezdeti értékében összegezzük. Ennek fényében a rendszer általános egyszerűsített ábráját (ld. 2-2. ábra) is ki kell egészíteni és a (2.95)-(2.96) rendszer is kiegészítendő az kezdeti értékkel. Tekintettel kell lenni az időre (ld. 2-32. ábra).
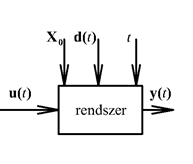
Megjegyzések:
-
Sok esetben a rendszer minden állapotváltozóját mérni tudjuk, ekkor
-
Sok esetben ún. energiamentes kezdeti állapotból indulunk ki, vagyis az állapotváltozók kezdeti értéke nulla. Ha az bemenetet külön nem jelöljük, illetve nem adjuk meg, akkor az azt jelenti, hogy energiamentes állapotban kezdődik a rendszer vizsgálata. Időinvariáns rendszerek esetén nincs szükség a bemenetre. Sokszor a zavaró jelet is elhanyagoljuk, és nem rajzoljuk fel az ábrára.
-
is lehet nulla, ekkor a magára hagyott rendszerről beszélünk.
-
2.9.1. pont alapján sok fizikai jelenség leírásában nagy szerepet játszik egy vektormező divergenciája és rotációja.
A divergenciából származtatott (általános értelmű áramlással kapcsolatos) változók esetén Kirchhoff I. törvényével analóg csomóponti egyenletet kapunk.
A rotáció a vektormező örvényességére, vagyis az áramlások okára vonatkozik. A tér minden pontjához egy vektor rendelhető. A rotációból származtatott fizikai változók közös jellemzője, hogy Kirchhoff II. törvényével analóg hurokegyenlet írható fel rájuk. A csomóponti és hurok egyenletek általában nem tekinthetők állapotegyenletnek, de alapjai lehetnek egy analóg számítási módszer leírásának. Ezzel a 2.9.1. pontban foglalkozunk.
-
A termodinamikában nem szokás a (2.95) alakú állapotegyenleteket felírni, továbbá állapotváltozó helyett az állapotjelző fogalmát használják, mert az egyenleteikben mindig valamilyen energiához tartozó valós fizikai változó jelenik meg. A termodinamikában definiált állapot az adott fizikai jelenség egy pillanatfelvétele, amelyet az intenzív és extenzív állapotjelzőkkel írnak le. Az előbbiek homogén eloszlása sok esetben a termodinamikai rendszer stabil egyensúlyát jelentik. Ezt úgy is meg szokták fogalmazni, hogy az intenzív változók kiegyenlítődésre törekednek és ez kiváltója valamilyen anyag, illetve energiaáramlásnak. Az extenzív mennyiségek általában a rendszer anyag-, illetve energiamennyiségével arányosak.
Ha f folytonos és az állapotváltozók értéke egy T0 időpillanatban ismert, akkor a (2.95) egyenlet állapotváltozóra vonatkozó megoldása a következő alakot ölti.
|
|
( 2.97 ) |
Az egyszerűség kedvéért . Ha relé típusú bemenőjelet is megengedünk, akkor -re nézve nem lesz mindenütt folytonos ( –re nézve megmarad a folytonosság). A legtöbb gyakorlati esetben a (2.95) egyenletből kifejezhető (2.97) alakban, ennek feltétele az, hogy teljesítse az ún. Carathéodory-feltételeket (-nek integrálhatónak kell lennie). Ez a feltétel változó struktúrájú rendszerek esetén nem mindig teljesül. A későbbiekben folytonosságát nem követeljük meg.
2.12.2. Lineáris, egy bemenetű egy kimenetű diszkrét idejű rendszer
A dinamikus rendszerekre jellemző memória jelleg legközvetlenebbül a diszkrét idejű ún. ARMA rendszereknél figyelhető meg.
Definíció
Azt feltételezzük, hogy a kimenőjel a k-adik időlépésben függ a kimenőjel utolsó n értékének lineáris kombinációjától (autoregressziójától (AR)), valamint a bemenőjel utolsó r értékből számított mozgó átlagától (MA). (ld. 2-33. ábra). A mindkét típusú emlékezettel rendelkező rendszereket szokás ARMA rendszereknek nevezni.
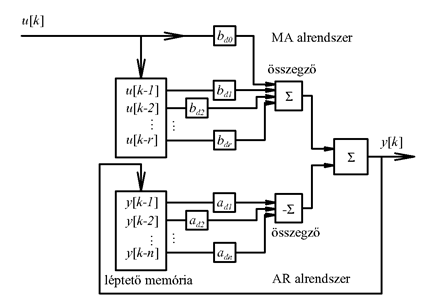
A 2-33. ábrak megfelelő ARMA rendszert a (2.98) alakú egyenlettel írhatjuk le.
|
|
( 2.98 ) |
Ebben a formában a rendszernek n+r számú belső tároló elemmel kell rendelkeznie (ld. 2-33. ábra). Egy-egy tároló elem tartalmát matematikai értelemben változónak, rendszertechnikai értelemben jelnek kell tekinteni. Ennek megfelelően a múlt összesített hatását db értékkel tudjuk megadni. Így, ha ismerjük a kimenőjel db egymás utáni (kezdeti) értékét, valamint ugyanezen időpontok közül az utolsó db időponthoz tartozó és jelenlegi bemenőjel értékét, akkor az kimenőjel (2.98) segítségével lépésről lépésre kiszámítható.
Megjegyzések:
1. Ha , az azt jelenti, hogy a bemenőjel a dinamikus rendszert megkerülve közvetlenül is hat a kimenőjelre,
2. A fizikai megvalósíthatóság feltétele .
3. Matematikai átalakításokkal (2.98) átrendezhető úgy, hogy elegendő legyen legfeljebb n db belső tároló elem.
A későbbiekben a MATLAB Simulink szimulációs szoftvert használjuk. A 2-33. ábra ARMA rendszerének MATLAB Simulink megfelelője a 2-34. ábran látható.
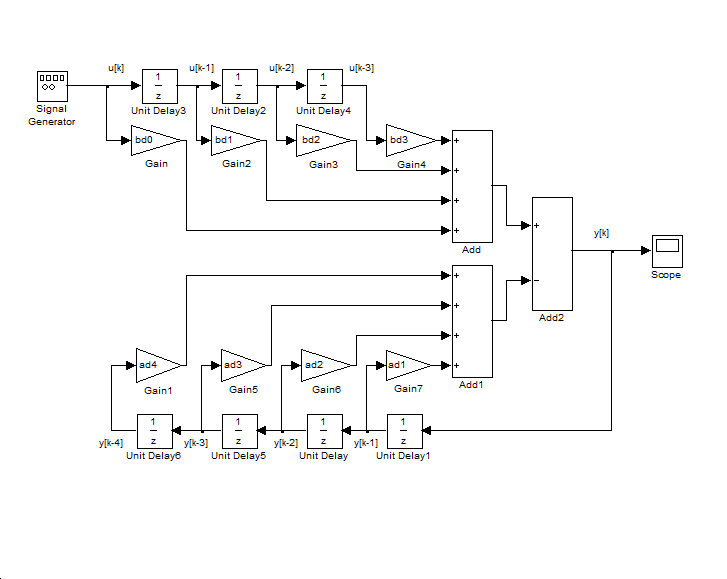
2.12.3. Állapottér-reprezentáció
Az irányításelméletben az időtartománybeli vizsgálatok esetén a (2.95) és (2.96) forma helyett a mátrixos formalizmuson alapuló az ún. állapottér-leírás a legelterjedtebb. Lineáris és időinvariáns (ún. LTI) rendszerek esetén ez az átalakítás könnyen megtehető. Az állapotváltozókat, a be- és kimenőjeleket egy-egy oszlopvektorba rendezzük, így (2.95) és (2.96) helyett két mátrixegyenletet kapunk. Egy LTI rendszer állapottér-egyenletei a következő alakúak.
ahol az állapotváltozók oszlopvektora, a bemenetek oszlopvektora, a kimenetek oszlopvektora , és a rendszert leíró konstans elemű mátrixok. A (2.99) és (2.100) egyenletek szokásos grafikai megjelenítése a 2-35. ábrán látható.
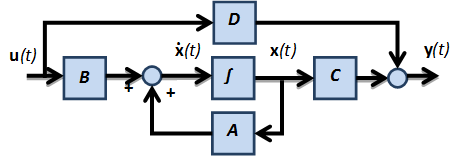
A mátrixos formalizmus nagymértékben megkönnyíti a rendszerrel kapcsolatos számításokat és tervezési feladatok megoldását, azok lineáris időinvariáns esetre nagyon jól kidolgozottak. A 2.6 fejezetben láttuk, hogy a nemlineáris rendszerek is valamilyen kompromisszummal és megkötésekkel (illetve a működéssel kapcsolatos további ismeretek beépítésével a modellbe) kezelhetők lineárisként. Ilyen kompromisszum eredménye a lineáris időben változó rendszerek. Az általános rövidítése, az angol név alapján LTV (Linear Time Varying).
ahol az állapotváltozók oszlopvektora, a bemenetek oszlopvektora, a kimenetek oszlopvektora , és a rendszert leíró mátrixok, amelyek elemei között van olyan, amelyik időben változik .
A kilencvenes években került a kutatók érdeklődésének középpontjába a lineáris változó paraméterű rendszerek. A rövidítés itt is az angol névből származik LPV (Linear Parameter Varying)
ahol az állapotváltozók oszlopvektora, a bemenetek oszlopvektora, a kimenetek oszlopvektora , és a rendszert leíró mátrixok, amelyek elemei között olyan, amelyik értéke egy paramétertől függ.
Az állapottér reprezentáció egyre szélesebb körben használható.
2.12.4. Változó struktúrájú rendszerek
A teljesítményelektronikai berendezések tipikusan a változó struktúrájú rendszerek (Variable Structure System: VSS) csoportjába tartoznak. A teljesítményelektronikai berendezések egyik legjellemzőbb közös tulajdonsága a kapcsoló üzemmód, vagyis a teljesítményelektronikai berendezésekben található félvezető elemeket ki- vagy bekapcsolhatjuk a veszteségek csökkentése érdekében, hiszen ha a kapcsolóelemnek vagy a feszültsége vagy az árama közel nulla, akkor a vesztesége is közel nulla. A változó struktúrájú rendszerek néhány érdekes szabályozástechnikai tulajdonsággal rendelkeznek. Ezt azért kell kiemelnünk, mert a változó struktúrájú rendszerek bizonyos eseteiben a (2.95) egyenletből nem fejezhető ki (2.97) alakban. A problémát az okozza, hogy létezik olyan szabályozási stratégia, amikor a félvezetőelemekkel előállított bemenőjel minden időpillanatban átkapcsol, ezért , ebből következően sehol sem lesz folytonos és nem integrálható, így (2.97) sem létezhet. Természetesen egy valóságos rendszernél ez nem fordulhat elő, ennek ellenére ez az idealizált állapot fontos szerepet játszik a szabályozáselméletben. Gondoljunk arra, hogy a teljesítményelektronikai eszközök mindig kapcsoló üzemmódban működnek. Ilyen esetekkel későbbi tananyagokban külön foglalkozunk. Ekkor a differenciálegyenletek klasszikus elmélete helyett az ún. jobb oldalán nem folytonos differenciálegyenletek elméletét kell alkalmazni.
Egy VSS akkor is lehet aszimptotikusan stabilis, ha a VSS –t alkotó valamennyi struktúra önmagában instabil. A VSS további fontos tulajdonsága, hogy – megfelelő szabályozással ellátva – olyan állapotba kerülhet, amikor a rendszer dinamikája az eredetihez képest csökkentett szabadságfokú differenciálegyenlettel írható le. Ebben az állapotban a rendszer elméletileg teljesen független bizonyos típusú paraméterek változásától és bizonyos típusú külső zavarok (pl. nemlineáris terhelés) hatásától. Ezt az állapotot csúszómódnak (sliding mode) és az erre alapozott szabályozást csúszómód-szabályozásnak nevezik, ami kiemelten fontos szerepet játszik a teljesítményelektronikai eszközök szabályozása területén.
2.12.5. Lineáris, egy bemenetű egy kimenetű folytonos idejű rendszer
Diszkrét időből folytonos időbe kétféle megközelítéssel lehet átlépni. A diszkrét időben lépésről lépésre végzett számítás helyett folytonos időben az integrálás műveletére van szükség. Ez elvezethet az integrális alakhoz, amely a (2.98) egyenlethez hasonlóan közvetlenül megadja az y(t) időfüggvényt. Általában az integrális alakot az időtartományban nem használjuk. Írjuk át a (2.98) egyetletet a következő alakra
|
|
( 2.105 ) |
Egy másik megközelítésben, ha ismerjük egy változó két egymást követő értékét és az időlépést, akkor ismerjük a differenciahányadost, ha egy harmadik értéket is ismerünk, akkor két egymást követő differenciát is ismerünk, és ebből eggyel magasabbrendű differenciahányadost is kiszámíthatunk. A (2.105) egyenletben az kimenőjelnek összesen n+1 számú és az bemenőjelnek összesen r+1 számú egymás utáni értéke szerepel. esetre: van 3+1 db értékünk, 3 db differenciahányadosunk, 2 db differenciahányadosok differenciahányadosa és végül 1 db differenciahányados, melyet differenciahányadosok differenciahányadosából kapunk (ld. (2.106)).
|
|
( 2.106 ) |
Ha , akkor (2.105) helyett (2.106) alapján egy harmadrendű differenciálegyenletet írhatunk fel. Ha az előbbi elvet követjük, akkor általános esetben a kimenőjelnek n-ed és a bemenőjelnek r-ed rendű differenciahányadosát tudjuk felírni. A folytonos időben a differenciahányados megfelelője a differenciálhányados, így (2.98) (pontosabban (2.105)) megfelelője a folytonos időben az alábbi típusú differenciálegyenlet:
|
|
( 2.107 ) |
ahol az idő szerinti i-edik deriváltat jelöli. Az általánosságot nem csökkenti, ha az feltételezéssel élünk. A fizikai megvalósíthatóság feltétele folytonos időben is . Bármely lineáris állandó együtthatós differenciálegyenlet-rendszer átírható (2.107) alakúra.
Később látni fogjuk a (2.107) alakú felírás előnyét, de a mögöttes fizikai tartalom értelmezése ebben a formában nehézkes. Ismert, hogyha egy valós fizikai rendszer működését a fizikai törvényekből kiindulva n db lineáris, állandó együtthatójú elsőrendű differenciálegyenletből álló egyenletrendszerrel írhatjuk le, akkor az átírható egyetlen n-ed rendű differenciálegyenletté. Ebben az átírásban a közvetlen fizikai tartalom általában elvész. Képzeljük el, hogy van egy motor, az egy rugalmas tengelyen keresztül mozgat egy terhet, és bennünket a teher fordulatszáma érdekel, azt választjuk kimenőjelnek. A fizikából kiindulva a motor tekercsének áramára, a motor forgórészének mozgására, a tengely deformálódására és a deformációból a teher mozgására (ld. 2-16-2-19 feladatok). Ha az egyenleteket átírjuk (2.107) formára, akkor nyilvánvalóan a teher fordulatszámának n-edik deriváltja nem lesz azonos pl. a motor áramával.
Még két alapvető problémáról kell szólni (2.107) kapcsán.
-
A (2.107) egyenletből kiolvasható, hogy elő kell írnunk n-szeres és r-szeres differenciálhatóságát, főleg az utóbbi túlzottan szigorú megkötés (a megoldást ld. a 2.12.5 pontban).
-
Továbbá n+r db (i=0,1, … , n-1) és (i=1, … , r) változót kell definiálni, és ugyanennyi (i=1, … , n) és (i=1, … , r) kezdeti értéket kell megadnunk. Később a kezdeti érték fogalmát is pontosítanunk kell. Kérdés, hogy a változók és a kezdeti értékek számát nem csökkenthetjük-e. Később látni fogjuk, hogy (2.107) többféleképpen átrendezhető úgy, hogy elegendő legyen legfeljebb n db változó és n db kezdeti érték bevezetése. (A megoldást ld. 2.12.1. pontban az állapotváltozókra és kimenőjelre vonatkozó egyenletek szétválasztása, (2.95) és (2.96))
2.12.6. Általánosított derivált
A továbbiakban a (2.107) alakú differenciálegyenletekkel leírható rendszerekkel fogunk foglalkozni. Ha r-szeres differenciálhatóságát szigorúan vesszük, és nem akarjuk a rendszereinket túlzottan elbonyolítani, akkor olyan egyszerű működést sem tudunk vizsgálni, hogy valamit be- és kikapcsolunk, vagy a valós fizikai rendszerben valamire kalapáccsal ráütünk. Egy pontosabb modellel ezek a problémák elvileg megoldhatók, figyelembe vehetjük, hogy egy motor bekapcsolásakor a tekercsben az áram hullámként kb. fél fénysebességgel terjed, a kalapács és megütött anyag az ütéskor egy kicsit deformálódik és valójában nem pillanatszerűen csökken a kalapács sebessége nullára. Ha a rendszert nem akarjuk szükségtelenül elbonyolítani, de az alapvető működések vizsgálatáról sem akarunk lemondani, akkor a matematikához kell fordulnunk. Ahhoz, hogy egy nem folytonos függvényt deriválni tudjunk, a függvény fogalmát ki kell terjeszteni. A kiterjesztett értelmű függvény neve disztribúció, amely a hagyományos függvényfogalommal szemben szingularitásokat is megenged (pontos definíciót ld. később).
Definíció
Ha majdnem mindenütt folytonos, akkor az általános értelmű deriváltja az az disztribúció, amely kielégíti a (2.108) egyenletet.
|
|
( 2.108 ) |
ahol az integrálás alsó határánál a azt fejezi ki, hogy az integrálást úgy kell elvégezni, hogy esetleges szakadását a időpillanatban figyelembe tudjuk venni. Ez egyben azt is jelenti, hogy meg kell különböztetni a kezdeti érték jobb és baloldali határértékét.
Értelmezés
Tegyük fel, hogy az időfüggvény folytonos, az idő szerint differenciálható és felírható a következő alakban
|
|
( 2.109 ) |
Ha folytonos és függvény kezdeti értéke a T0 időpillanatban az ismert érték (a múltbeli változások összesített hatása), akkor (2.108) megoldása a (2.108) alakot ölti. és az a cél, hogy (2.108) akkor is megoldása legyen a (2.108) differenciálegyenletnek, ha sem sem folytonosságát nem írjuk elő. Ha megengedjük, hogy az időfüggvénynek szakadása legyen, akkor ez a szakadás a T0 időpillanatban is lehet. Ez azt jelenti, hogy a kezdeti érték fogalmát is pontosítanunk kell.
Definíció
Az nem folytonos függvény T0 időpillanatbeli kezdeti értékén az függvény T0 időpillanatbeli baloldali határértékét értjük.
Értelmezés
Mérnöki terminológiával ez bekapcsolás előtti értéke. Megjegyezzük, hogy minden olyan függvény, amely bármely véges szakaszon integrálható, értelmezhető disztribúcióként, és akkor deriválható is, mint disztribúció. Akkor van gond, ha nem integrálható, mert pl. minden pontjában szakadása van. Természetesen a valóságban ilyen nem fordulhat elő, de egy amúgy jól használható egyszerűsített rendszer produkálhat ilyet. Ebben az esetben ismét két út áll előttünk, vagy a valósághoz közelítve elbonyolítjuk a rendszert, hogy egy ilyen eset ne következhessen be, vagy újabb matematikai eszközöket keresünk, hogy ezt a furcsa esetet is kezelni tudjuk. Mindkét útnak megvan a maga előnye és hátránya. Ezzel a problémakörrel később foglalkozunk, most maradjon itt az a konklúzió, hogy vannak olyan függvények, amelyek a disztribúciók körében sem deriválhatók, és a mérnöki gyakorlatban is találunk olyan rendszereket, amelyeknél (2.108) sem vezet eredményre. Az általános értelmű deriváltra is használjuk a szokásos jelölést (ld. (2.109)). Egy disztribúció is deriválható, és a disztribúció deriváltja is disztribúció. A disztribúcióelmélet túlmutat e tananyag keretein. Bizonyítás nélkül fogadjuk el, hogy e tananyagban a disztribúciókkal elvégzett műveletek hasonló eredményt adnak, mintha az adott műveletet hagyományos függvényeken végeznénk el. Az esetleges eltérésekre mindig külön megjegyzést teszünk.
2.12.6.1. A disztribúció elmélet alapjai
(elsősöknek nem ajánlott)
A disztribúció pontos definíciójához be kell vezetni a próbafüggvényt, amelynek értéke csak egy véges intervallumon különbözik nullától és létezik tetszőleges számú hagyományos értelmű deriváltja (ebből következik, hogy folytonos és korlátos, de még a negatív végtelentől a pozitív végtelenig vett integrálja is véges).
Egy tipikus próbafüggvény
|
|
( 2.110 ) |
Fogalmazhatunk úgy, hogy matematikai értelemben nagyon jól viselkedő függvény (a szokásos függvény műveletet nehézség nélkül el tudjuk végezni függvényen). Az disztribúció, mint általánosított értelmű (ezért matematikailag nehezen kezelhető) függvény definícióját és számunkra legfontosabb tulajdonságait ehhez a matematikailag jól kezelhető függvényhez kötjük. Az disztribúciót a következő integrál segítségével definiáljuk
|
|
( 2.111 ) |
ahol egy tetszőleges disztribúció segítségével a függvényhez hozzárendelünk egy konkrét számértéket. (Megjegyezzük, hogy azt a matematikai műveletet, amikor egy függvényhez egy számértéket rendelünk, funkcionálnak nevezzük.) Bizonyos esetekben bármely t időponthoz hozzárendelhetünk egy konkrét értéket, ezt nevezzük reguláris disztribúciónak. Pl. ha bármely függvényhez hozzárendeljük egy adott intervallumon vett határozott integráljának értékét (hangsúlyozottan egy konkrét számértéket)
|
|
( 2.112 ) |
akkor könnyen beláthatjuk, hogy
|
|
( 2.113 ) |
Ezzel szemben léteznek olyan disztribúciók, amelyeknél bizonyos t időpontokhoz nem rendelhetünk egy konkrét értéket, ezeket nevezzük szinguláris disztribúciónak. Igazán csak ez utóbbiak miatt van értelme bevezetni a disztribúció fogalmát. Legyen erre példa a következő
|
|
( 2.114 ) |
Azt beláthatjuk, hogy (2.114) esetén , ha , de nem tudjuk egy konkrét számmal megadni értékét. A (2.114) által definiált disztribúció fontos szerepet tölt be a rendszertechnikában, ezzel a 3.1.1 pontban fogunk foglalkozni.
A definíció után térjünk vissza a deriváláshoz. Ha (2.111) mindkét oldalát deriváljuk, akkor a jobb oldal nulla, így
|
|
( 2.115 ) |
(2.115) legfontosabb üzenete: Ha egy lehetséges próbafüggvény, akkor is az, ezért ha (2.111) leír egy disztribúciót, akkor (2.115) annak deriváltját írja le. Konklúzióként megállapíthatjuk, hogy minden olyan függvény, amely bármely véges szakaszon integrálható, értelmezhető disztribúcióként, és akkor deriválható is, mint disztribúció. A fenti definíció és konklúzió birtokában már közvetlenül is megadhatjuk egy függvény általánosított deriváltját.
2 - 4 feladat Disztribúció deriváltjának meghatározása
Határozza meg a (2.112) segítségével definiált (2.113) disztribúció deriváltjára vonatkozó összefüggést.
Megoldás
|
|
( 2.116 ) |
Látható, hogy a keresett disztribúció szinguláris. Ennél fontosabb megállapítás: Az egység-ugrás függvény általánosított deriváltja alkalmas mintavételezésre.
2 - 5 feladat Egységugrás jel deriváltjának meghatározása
Határozza meg az egységugrásnak, mint disztribúciónak a deriváltját. Kiindulva a disztribúció definíciójából
|
|
( 2.117 ) |
Megjegyezzük, hogy a próbafüggvényre tett kikötésünk miatt garantáltan egy véges számérték. A disztribúció deriváltjára vonatkozó (2.115) összefüggés alapján és figyelembe véve, hogy a próbafüggvény definíciója értelmében
|
|
( 2.118 ) |
2.12.7. Differenciálegyenletek megoldása analóg számítógépes megközelítéssel
Napjainkban klasszikus analóg számítógépeket nem használunk, de a szemlélet formálásában fontos szerepet játszhat azok felépítésének megismerése. Diszkrét időben a (2.98) egyenlet grafikus megjelenítésének tekinthető a 2-33. ábra. Folytonos időben a (2.107) differenciálegyenlet átírható a (2.98) egyenletnek megfelelő alakúra (az általánosságot nem csökkenti az feltételezés)
|
|
( 2.119 ) |
Az első ötletünk lehet az, hogy kimenőjelet -szer és az bemenőjelet -szer deriválva majd a kapott deriváltak (2.119) egyenletnek megfelelő lineáris kombinációját képezve kimenőjelet előállítjuk és így 2-33. ábraához teljesen hasonló grafikai megoldást kapunk, ahol a léptetések helyére deriváló tagokat kell tennünk, de sajnos ez így nem működik. A helyett az jelet kell kifejeznünk (az általánosságot nem csökkenti az feltételezés)
|
|
( 2.120 ) |
A deriváló tagok helyett integrátorokat kell alkalmaznunk. Az jelet -szer integrálva kapjuk meg az jelet. Közben tagok is előállnak, így azok lineáris kombinációját is képezhetjük (2.120) második összegzésének megfelelően. De ez a módszer is csak esetben működik, mert a bemenőjel deriváltját nem tudjuk megkapni. Ha , akkor valamilyen módon segédváltozókat kell bevezetni. A segédváltozókról belátható, hogy állapotváltozónak tekinthetők. Legyen , és vezessük be a következő jelölést
|
|
( 2.121 ) |
Ha , akkor
|
|
( 2.122 ) |
A (2.121) és (2.122) egyenletet megvalósító MATLAB Simulink program:
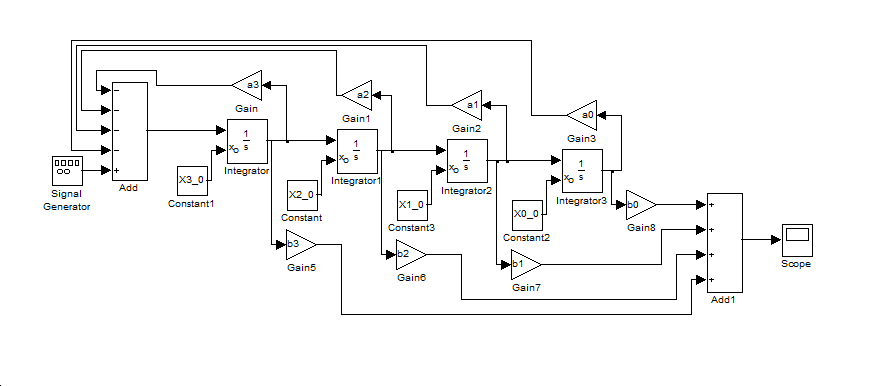
2.13. A stabilitás fogalma
Rendszerek vizsgálata során kulcsfontosságú feladat a stabilitás eldöntése. A későbbi fejezetekben több olyan konkrét módszert mutatunk be, amelyek segítségével a stabilitás eldönthető. Ebben az alfejezetben csak a legfontosabb definíciókat adjuk meg. A stabilitás megítélésében apró szemléletbeli különbségek tapasztalhatók akár annak függvényében is, hogy milyen jellegű feladatot kell megoldani. Ebben a tárgyban a végső cél a szintézis, egy szabályozó tervezése. Az elvárás az, hogy az elkészült rendszer minden üzemállapota stabilis legyen, így a rendszer stabilitásáról beszélünk. Ha analízis a feladatunk, akkor a rendszernek a különböző üzemállapotait néha csak külön-külön vizsgáljuk, ekkor azt hangsúlyozzuk, hogy a stabilitás nem a rendszer, hanem az adott üzemállapot tulajdonsága. Az irányítási feladatok fontos sajátossága, hogy e tárgykörben általában visszacsatolt rendszerekkel találkozunk, ezért legtöbbször a visszacsatolt rendszer stabilitását kell vizsgálnunk. Az a kérdés, hogy a visszacsatolás miként befolyásolja a visszacsatolt rendszer stabilitását.
A stabilitás mérnöki értelemben alapvetően két megközelítésben vizsgálható. Az irodalomban találkozhatunk a gerjesztetlen rendszer, illetve a gerjesztett rendszer stabilitásával. Matematikai értelemben pontosabb az a megfogalmazás, ha autonóm működésű és nem autonóm működésű rendszerek stabilitásáról beszélünk, vagyis matematikai értelemben a ténylegesen gerjesztetlen (az összes bemenet nulla értékű) és konstans gerjesztésű rendszereket azonos módon lehet kezelni. Az időben változó rendszerek a stabilitás szempontjából matematikailag az ún. „gerjesztett” kategóriába sorolandók, még akkor is, ha a bemenetre effektíven nulla értéket kapcsolunk. Talán ezért terjedt el a paraméteresen gerjesztett rendszer kifejezés, amely egyszerűen időben változó, vagyis nem autonóm működésű rendszert jelent. Természetesen autonóm működésű és nem autonóm működésű rendszerek egyaránt lehetnek lineárisak és nemlineárisak, ez a problémakör teljesen más megközelítése.
Lineáris, invariáns rendszerek esetén viszonylag egyszerűbb a helyzet, de nemlineáris rendszerek esetén a stabilitás egy összetett fogalom, és többféle definíció létezik rá. Az is előfordulhat, hogy egy rendszer az egyik definíció szerint stabil, a másik szerint pedig nem. Nemlineáris rendszerek esetén a stabilitás lehet gerjesztés és munkapont függő is.
A stabilitással rokon fogalom az egyensúlyi állapot. A gerjesztetlen és konstans gerjesztésű rendszer stabilitása az egyensúlyi állapot segítségével egyszerűen definiálható, így ezzel gyakran élünk. A gerjesztett, pontosabban a nem autonóm működésű rendszer egyensúlyi állapota összetettebb definíciót igényel, ezért a gerjesztett rendszer stabilitását általában a korlátos működésre alapozva definiáljuk.
2.13.1. Statikus egyensúlyi állapot
Definíció
Egy autonóm rendszer akkor van statikus egyensúlyi állapotban, ha az állapotváltozók értéke konstans.
Értelmezés
Megjegyzés. Ez a definíció kizárja a statikus rendszereket (amelyeknek nincs állapotváltozójuk), ugyanakkor a konstans gerjesztést megengedi. Egy lineáris időinvariáns dinamikus rendszernek egy adott konstans gerjesztés mellett csak egyetlen egyensúlyi állapota létezhet (ellenkező esetben nem lenne érvényes a szuperpozíció elve). Egy nemlineáris rendszernek adott konstans gerjesztés mellett lehet több egyensúlyi állapota is.
Példaként, ha van egy golyónk és egy kanalunk, akkor a kanál helyzetétől függően a golyót többféle módon tudjuk a kanálra helyezni úgy, hogy a golyó ne mozduljon el, vagyis statikus egyensúlyi állapotba kerüljön. Alapvető különbség van két eset között
-
A kanalat szokásosan fogjuk és a golyót a kanál mélyedésébe helyezzük.
-
A kanalat fordítva fogjuk, és a golyót a kanál domborulata tetejére helyezzük.
A különbséget azonnal észrevesszük, ha egy kicsit remeg a kezünk. Az első esetben a golyó kicsit ide-oda gurul, de ismét megáll, ha a kéz remegése megszűnik. A második esetben a golyó legurul a kanálról és sohasem gurul vissza a kanál tetejére. E gondolatkísérlet alapján fogalmazhatjuk meg az első stabilitási definíciót.
2.13.2. Aszimptotikus stabilitás
Definíció
Egy autonóm lineáris differenciálegyenlettel leírható rendszert tetszőlegesen kitérítjük az egyensúlyi állapotából. Az egyensúlyi állapotban ható esetleges konstans gerjesztést nem változtatjuk meg, és magára hagyjuk a rendszert. Ha a rendszer állapotváltozói konvergálnak az egyensúlyi állapotban felvett értékekhez, akkor a rendszert aszimptotikusan stabilisnak nevezzük.
Értelmezés
Ha egy rugóval függőlegesen felfüggesztünk egy tömeget, akkor a tömegre a gravitáció állandó gerjesztésként hat, és kialakul egy egyensúlyi állapot. Ha ebből az állapotból kimozdítjuk a tömeget és elengedjük, akkor a csillapítás miatt egyre csökkenő amplitúdójú lengések után beáll egy új egyensúlyi állapotba. Ha a rendszer lineáris, akkor az új egyensúlyi állapot megegyezik az eredeti egyensúlyi állapottal. Lineáris rendszerek esetén az egyensúlyi állapotra alapozott stabilitás vizsgálata egyszerű, mert csak egy egyensúlyi állapota lehet, és ha az stabilis, akkor aszimptotikusan is stabilis. Nemlineáris rendszerek esetén a fenti definíción enyhíteni kell. Mivel a nemlineáris rendszernek több egyensúlyi állapota is lehetséges, ezért nem követelhetjük meg, hogy tetszőlegesen nagy kitérítés után is mindig az eredeti egyensúlyi állapothoz konvergáljon a rendszer, vagyis az aszimptotikus stabilitás csak egy tartományon belül érvényes. Általában magát az „aszimptotikusságot” sem írhatjuk elő egy nemlineáris rendszer esetén, vagyis nem követelhetjük meg azt, hogy a kitérített rendszer konvergáljon az eredeti egyensúlyi állapothoz. Az egyik tipikus nemlinearítás a súrlódás. Ha a fenti példa tömeg-rugó rendszerében a tömeg pl. egy fal mellett mozog és mozgás közben a tömegre a faltól származó súrlódási erő is hat, akkor a tapadási súrlódás miatt a tömeg általában az eredeti egyensúlyi állapot előtt vagy után beragad.
Így a rendszer szigorúan nézve nem elégíti ki az aszimptotikus stabilitás kritériumát, de műszaki értelemben valahol ezt is stabilisnak érezzük, ezért szükséges az aszimptotikusnál megengedőbb definíció.
2.13.3. Ljapunov stabilitás
Definíció
Egy nemlineáris autonóm működésű rendszert akkor mondunk Ljapunov érelemben stabilisnak, ha az egyensúlyi állapot bármely környezetéhez találunk egy olyan nullánál nagyobb maximális kitérítést, amelynél kisebb kitérítések esetén a rendszer garantáltan visszatér az eredetileg meghatározott környezetbe.
Értelmezés
Ez a definíció egyrészt feltételezi, hogy az állapotváltozóknak van normája, vagyis értelmezhető az egyensúlyi állapot környezete, másrészt nem követeli meg, hogy a rendszer visszatérjen a kiindulási állapotba, csak annak környezetébe. A nemlineáris súrlódással terhelt tömeg-rugó rendszer Ljapunov értelemben stabilis, de nem aszimptotikusan stabilis.
2.13.4. Dinamikus egyensúlyi, illetve állandósult állapot
A statikus egyensúlyi állapot fogalma kiterjeszthető az egyensúlyi mozgásállapotra, tipikusan állandó amplitúdójú, állandó frekvenciájú periodikus lengésekre, ilyen esetben dinamikus egyensúlyi állapotról beszélünk. A mérnöki gyakorlatban az általános értelemben vett egyensúlyi állapotot szokás állandósult állapotnak nevezni.
Hasonlóan nem az eredeti egyensúlyi állapotba tér vissza a tömeg, ha időközben megváltozik a rugó rugalmassági együtthatója.
2.13.5. BIBO stabilitás
Definíció
Korlátos bemenőjelre minden esetben korlátos kimenőjel a válasz. Ezt a feltételt teljesítő rendszert ismételten az angol név után BIBO (Bounded Input Bounded Output) stabilis rendszernek hívjuk.
Ha egy lineáris rendszer valamilyen értelemben stabi lis , akkor a többi értelemben is az.
2.14. Kidolgozott feladatok koncentrált paraméterű rendszerekhez kapcsolódóan
2 - 6 feladat Rendszerek csoportosítása
A definícióból kiindulva adja meg, hogy az alábbi rendszerek közül, melyek lineárisak, kauzálisak, statikusak vagy dinamikusak, továbbá időinvariánsak, illetve autonómak. Ahol ez nem dönthető el egyértelműen, ott adja meg a feltételét annak, hogy a rendszer az adott osztályba tartozzon, ahol
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Az első 12 rendszerre vonatkozó megoldások
|
rendszer sorszáma |
lineáris |
statikus |
kauzális |
időinvariáns |
|
1. |
igen |
igen |
igen |
igen |
|
2. |
igen |
nem |
igen |
igen |
|
3. |
igen |
nem |
nem |
igen |
|
4. |
nem |
igen |
igen |
igen |
|
5. |
nem |
igen |
igen |
igen |
|
6. |
nem |
igen |
igen |
igen |
|
7. |
nem |
igen |
igen |
igen |
|
8. |
igen |
nem |
igen |
igen |
|
9. |
igen |
nem |
nem |
igen |
|
10. |
igen |
igen |
igen |
igen |
|
11. |
nem |
igen |
igen |
nem |
|
12. |
igen |
igen |
igen |
nem |
Rövid magyarázatok
Ha és , akkor ebből következik, hogy
|
|
( 2.123 ) |
Vagyis a szuperpozíció elve érvényes, ezért a rendszer lineáris.
A linearitás hasonlóan belátható a 2., 3., 8. és 12. rendszer esetén.
Legyen és , mivel
|
|
( 2.124 ) |
Vagyis a szuperpozíció elve nem érvényes, ezért a rendszer nemlineáris.
A kétbemenetű rendszer esetén:
Ha és , akkor ebből következik, hogy
|
|
( 2.125 ) |
Vagyis a szuperpozíció elve érvényes, ezért a rendszer lineáris.
Ha és, akkor a speciális esetet leszámítva
|
|
( 2.126 ) |
Vagyis a szuperpozíció elve nem érvényes, ezért a rendszer nem lineáris.
Az és rendszer nem kauzális, mert e két rendszer esetén a kimenet tetszőleges időponthoz tartozó értéke függ a bemenet értékétől. Az első 12 rendszer közül az összes többi rendszer kauzális.
|
|
( 2.127 ) |
A 12-nél nagyobb sorszámú rendszerek: Házi feladat, megoldását nem közöljük
2-7 feladat RL kör bekapcsolása
Írja fel egy soros RL kör differenciálegyenletét, ha a bemenőjel az feszültség ( az ellenálláson és az induktivitáson eső feszültség), a kimenőjel az induktivitás árama.
Megoldás
Az áramkörre felírható Kirchhoff hurokegyenlet:
, , és
|
|
( 2.130 ) |
2 - 8 feladat Hőátadás
Egy tömegű, felületű testre hőáramot kapcsolunk. A tömeg intenzív hőcserében van a környezetével (mint például a radiátor). Tegyük fel, hogy a hőmérséklet kezdeti értéke nulla () Írjuk fel a tömeg hőmérsékletváltozását leíró egyenletet. Legyen a bemenőjel a (t) hőáram és a kimenőjel a radiátor hőmérséklete. További paraméterek: α hőátadási tényező, c fajhő.
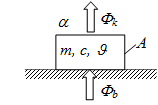
Megoldás
A kilépő hőáram:
|
|
(2.131) |
A be- és kilépő hőáram különbsége a test hőmérsékletét változtatja:
|
|
(2.132) |
2 - 9 feladat Vezető melegedése
Egy tömegű, hosszúságú keresztmetszetű és felületű vezetőn áram folyik. A vezető anyaga legyen réz. Az áram hatására a vezetőben hő keletkezik, amely a felületen hősugárzással, hővezetéssel és hőáramlással távozik. Tegyük fel, hogy a hőmérséklet kezdeti értéke nulla () Írjuk fel a vezető hőmérsékletváltozását leíró egyenletet. Legyen a bemenőjel a vezető áramának négyzete és a kimenőjel a vezető hőmérséklete. További paraméterek: az anyag fajlagos vezetőképessége, α hőátadási tényező, c fajhő.
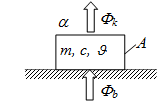
Megoldás
A kilépő hőáram:
|
|
(2.133) |
A be- és kilépő hőáram különbsége a test hőmérsékletét változtatja:
|
|
(2.134) |
|
|
(2.135) |
2 - 10 feladat Folyadéktartály
Határozza meg a 2-39. ábrán látható tartály folyadékszintjének változását leíró egyenletet veszteségmentes kifolyást feltételezve, és egy adott vízszintmagasságból kiindulva. Legyen a bemenőjel a beáramló térfogatáram és a kimenőjel a folyadékszint.
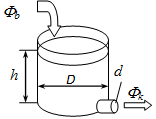
Megoldás
A kilépő térfogatáramot a kiáramlási sebesség felhasználásával tudjuk meghatározni:
|
|
(2.136) |
A be- és kiáramlás különbsége a tartályban lévő folyadék térfogatát változtatja:
|
|
(2.137) |
Mint látható, az egyenlet nemlineáris. Tegyük fel, hogy a tartályban a folyadékszint csak kismértékben ingadozik (h0 körül). Ekkor értéke jól közelíthető lineáris függvénnyel (linearizálás). Kétféleképpen is próbálkozhatunk:
-
felírhatjuk a függvény h0 pontbeli érintőjének egyenletét, vagy
-
vehetjük h0 pont körül felírt Taylor sorának első két tagját.
Az eredmény természetesen mindkét esetben ugyanaz lesz:
|
. |
(2.138) |
Ennek felhasználásával a differenciálegyenlet:
|
. |
(2.139) |
Megjegyzés: tartályos feladatra az integráló tagnál is láthatunk példát (4.6.3). A kettő közti lényegi különbség az, hogy míg ott a kiáramló térfogatáram az időtől függ, itt a tartályban lévő folyadékszinttől.
2 - 11 feladat ARMA rendszer paraméterei (Házi feladat, megoldását nem közöljük)
Adja meg a 2-7, 2-8 és 2-10 feladatban ismertetett rendszer diszkrétidejű ARMA modelljének paramétereit.
2 - 12 feladat Rendszerekegyenletek felírása ( Ideális transzlációs telemanipulációs rendszer )
Írja fel a 2-40. ábraán látható ideális transzlációs telemanipulációs rendszer egyenletét a következő esetekben, mind diszkrét, mind folytonos időben:
-
Legyen a rendszer bemenete a mester oldalon a fogantyú elmozdulása, és a rendszer kimenete a szolga oldali fogantyú elmozdulása. A mester és szolga oldali fogantyút egy merev rúd kapcsolja össze. Ebben a megközelítésben ez egy statikai rendszer. A bemenet egyértelműen meghatározza a kimenetet.
-
Hogy módosul az a) eset, ha az pozícióban eltörik a rúd?
-
Más a helyzet, ha az erőhatást tekintjük a bemenetnek, a szolga oldali erőhatást elhanyagoljuk, és először legyen a kimenet a rúd sebesssége a szolga oldalon. Ekkor egy dinamikai rendszerhez jutunk. Legyen a rendszer tömege és tudjuk, hogy és rúd kezdeti sebessége szintén nulla, továbbá
-
Tovább bővítve, ha az erőhatást tekintjük a bemenetnek, a szolga oldali erőhatás nulla, és a kimenet a rúd pozíciója a szolga oldalon. Ekkor egy másodrendű dinamikai rendszerhez jutunk. A súrlódást elhanyagoljuk. Legyen a rendszer tömege és tudjuk, hogy és a rúd kezdeti sebessége szintén nulla, továbbá
-
Továbbra is az erőhatást tekintjük a bemenetnek, a szolga oldali erőhatás nulla, és a kimenet a rúd pozíciója a szolga oldalon. Ekkor egy másodrendű dinamikai rendszerhez jutunk. A súrlódást vegyük figyelembe egy sebességtől függő erőhatással (ezt nevezik viszkózus súrlódásnak). A viszkózus súrlódási együtthatót jelöljük -vel. Legyen a rendszer tömege és tudjuk, hogy és a rúd kezdeti sebessége szintén nulla, továbbá
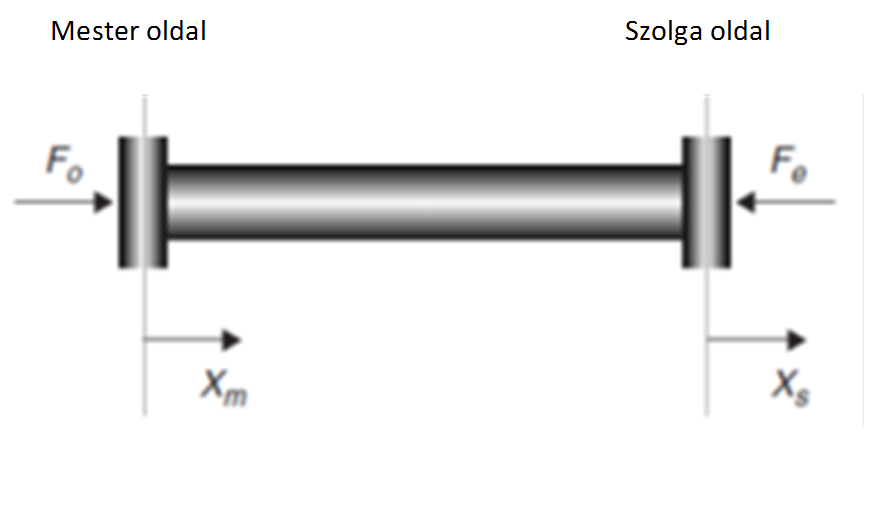
Megoldás
|
Bemenet |
Kimenet |
Diszkrét idejű rendszeregyenletek |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bemenet |
Kimenet |
Folytonos idejű rendszeregyenletek |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Az a) és b) eset nem szorul további magyarázatra. A c) esetben abból indulhatunk ki, hogy állandó erőt és tömeget feltételezve, a középiskolában tanultak alapján,
|
|
(2.140) |
ahol a szolga oldal gyorsulása. A manipulátor kar sebességét az idő függvényében a következőképp számíthatjuk, ha és .
|
|
(2.141) |
(2.140) minden időpillanatban érvényben marad akkor is, ha az erő meváltozik. Tegyük fel, hogy az erő diszkrét időlépésenként lépcsősen változik. Tegyük fel, hogy egy adott t időpillanatban vizsgáljuk a rendszer viselkedését. Ehhez az időponthoz db nagyságú időlépéssel jutunk el
|
|
(2.142) |
Térjünk át a diszkrét idejű felírásra
|
|
(2.143) |
Ha az erő adott egy időpontban adott, akkor az időlépésben a sebesség megváltozása
|
|
(2.144) |
Ezt a változást hozzá kell adnunk a sebesség pontbeni értékéhez, így megkapjuk a sebesség pontbeni értékét
|
|
(2.145) |
A sebesség bármely időpontban összegzéssel számítható ki (a sebesség kezdeti értéke )
|
|
(2.146) |
Ha a sebesség egy adott időpontban ismert, akkor az adott időlépésben a pozíció megváltozása a (2.144) kifejezéshez hasonló gondolatmenettel számítható.
|
|
(2.147) |
Itt is elmondható, hogy a változást hozzá kell adnunk a pozíció pontbeli értékéhez, így megkapjuk a pozíció pontbeli értékét
|
|
(2.148) |
Ismert, hogy a sebességből a pozíció ugyancsak összegzéssel állítható elő, a pozíció kezdeti értéke . Ha egy időpontban vagyunk kíváncsiak értékére, akkor a (2.147) kifejezésben leírt változásokat kell összegezni, de értéket helyettesítsük (2.146) alakjával. Így kettős szummát kapunk
|
|
(2.149) |
Az erő hatására az első időlépésben csak a sebesség változik meg, és csak a második lépésben jelenik meg az erő hatása a pozíciójelben. Ugyanakkor a kezdeti értékek hatását az első két lépésben is figyelembe kell venni. Ez azt jelenti, hogy a (2.149) kifejezés csak a tartományban értelmezhető. Ezzel kapcsolatban egy kérdés merül fel. Honnan kezdjük számolni az időt. Mondhatjuk azt, hogy legyen az idő kezdőpontja az, ahonnan a (2.149) kifejezés él, ekkor néhány negatív időpontban is ismernünk kell az erő, pozíció és a sebesség értékét.
|
|
(2.150) |
Adott esetben mindkét megközelítés lehet helyes. Ez a konkrét esettől és szituációtól függ. A fenti példa legfontosabb üzenete az, hogy attól az időponttól, ahonnan (2.149), illetve (2.150) érvényes, jelnek visszamenőleg két értékét ismernünk kell. Természetesen ez a két érték lehet nulla, de akkor azt kell tudnunk, hogy nulla. Ha nullához tart, akkor e két megközelítéssel számított sorozat különbsége is nullához tart, és ekkor az összegzés helyett integrálni kell, továbbá (2.149), illetve (2.150) azonossá válik, és az egyértelmű számításhoz és ) értékét kell ismerünk.
A (2.149) kifejezést kiszámító matlab program a következő, ahol az idő 10 egység, az erő nagysága 1. A időlépés nagyságát DT jelöli.
K=10/DT;
for i = 1:K-1
F(i)=1;
end
sum=0;
for k1 = 1:K-1
sum=sum+F0*DT*DT;
for i = 1:k1-1
sum= sum+ F(i)*DT*DT;
end
end
sum=sum/m
Ha viszkózus (sebességgel arányos)
|
|
(2.151) |
súrlódás fékezi a mozgást, akkor e súrlódási erővel csökkenteni kell a tömegre ható gyorsító erőt
|
|
( 2.152 ) |
(2.152) alapján (2.145) és (2.146) is módosítandó
|
|
( 2.153 ) |
|
|
( 2.154 ) |
Súrlódás esetén (2.149) is módosul
|
|
( 2.155 ) |
Mivel a (2.155) képletben szerepel a sebesség is, ezért a (2.154) és (2.155) képletben párhuzamosan kell számolnunk. A kettőt egy képletbe összevonni nehézkes. Ugyanakkor a sebesség implicite szerepel a (2.155) képletben is, így célszerűbbnek látszik egy rekurzív formula felírása. Helyettesítsük a (2.148) kifejezésbe (2.153) megfelelően eltolt változatát.
|
|
( 2.156 ) |
Használjuk ki, hogy
|
|
( 2.157 ) |
|
|
( 2.158 ) |
A (2.158) kifejezésből világosan látszik, hogy a kimenőjel egy új értékének kiszámítáhához mind a kimenőjelnek, mind a bemenőjelnek két visszamenő értékét kell ismerni. Ehhez a megállapításhoz logikai úton is eljuthatunk, ha az erő egy tetszőleges -edik időpontban megváltozik, akkor a következő -adik időlépésben a sebesség változik meg, és csak a rákövetkező -dik lépésben jelenik meg az erőváltozás hatása a pozíciójelben. A (2.158) kifejezést megvalósító MATLAB Simulink program a 2-41. ábran látható.
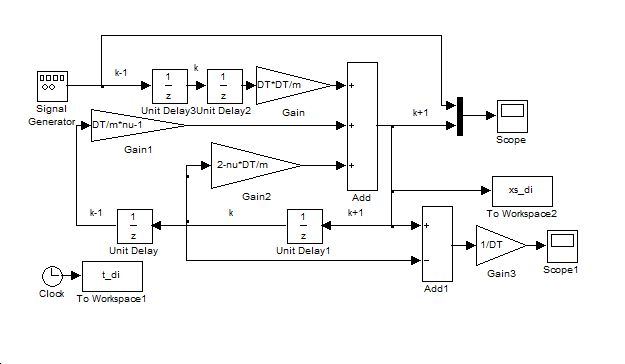
(2.140) minden időpillanatban érvényben marad akkor is, ha az erő folyamatosra változik
|
|
( 2.159 ) |
Ebben az esetben bármely időpontban az összegzés helyett integrálással lehet értékét kiszámítani, ha és .
|
|
( 2.160 ) |
Ismert, hogy a sebességből a pozíció ugyancsak integrálással állítható elő, ismét zérus kezdeti feltétellel és .
|
|
( 2.161 ) |
|
|
( 2.162 ) |
Ha viszkózus (sebességgel arányos)
|
|
( 2.163 ) |
súrlódás fékezi a mozgást, akkor e súrlódási erővel csökkenteni kell a tömegre ható gyorsító erőt
|
|
( 2.164 ) |
(2.164) alapján (2.160) is módosítandó.
|
|
( 2.165 ) |
Súrlódás esetén (2.162) is módosul
|
|
( 2.166 ) |
A kezdeti értékeket is figyelembe véve legyen és
|
|
( 2.167 ) |
A nehézséget az okozza, hogy a sebesség kiszámításához ismernünk kell a sebességet. Az integrál alaknál sok esetben célszerűbb a differenciális alakot használni. Induljunk ki a (2.164) összefüggésből és helyettesítsük a gyorsítás és a sebesség helyére a pozíció első illetve második deriváltját
|
|
(2.168) |
A (2.168) kifejezés csak a kezdeti értékek megadásával válik egyértelművé. A (2.168) kifejezés kétszeres integrálásával a (2.167) kifejezéshez jutunk. Az eredményt a 2-42. ábraán látható analóg számítógéppel is megkaphatjuk.
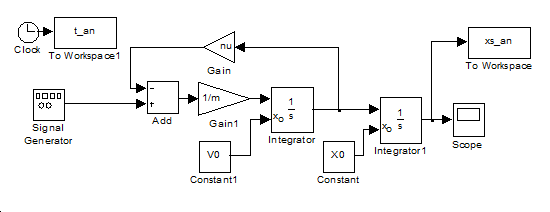
Válasszuk a következő paramétereket:
Tmax=0; DT=1; K=Tmax/DT; nu=0; X0=0; V0=0; F0=1; m=1;
Az erő egy egység és a szimuláció időtartama Tmax=10 egység. Könnyen kiszámítható, hogy az elmozdulás
|
|
( 2.169 ) |
A 2-43. ábran a folytonos idejű modell (kék folytonos görbe) és a diszkrét idejű modell (lépcsős görbék) szimulációs eredményeit hasonlítottuk össze. Látható, hogy (2.149) és (2.150) összefüggés ez alsó és egy felső becslését adja a folytonos idejű eredménynek. (2.149) és (2.150) összefüggés között két időlépésnyi eltérés van, ha a kettő között egy időlépés eltolással számítjuk a diszkrét idejű rendszert, akkor az a folytonos idejű megoldás körül oszcillál.
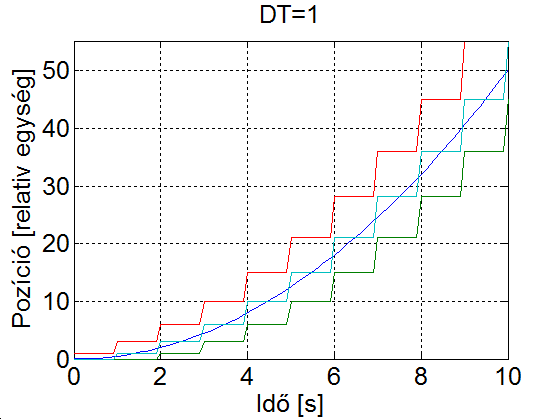
Ahogy az időlépés nagyságát csökkentjük, úgy a diszkrét idejű és folytonos idejű megoldás különbsége egyre kisebb lesz (ld. 2-44. ábra). Ha , akkor a három változat határértékben ugyanahhoz a függvényhez tart. Itt emlékeztetünk arra, hogy egy függvény integrálhatóságának feltétele az, hogy az alsó és felső becslés ugyanahhoz a határértékhez tartson.
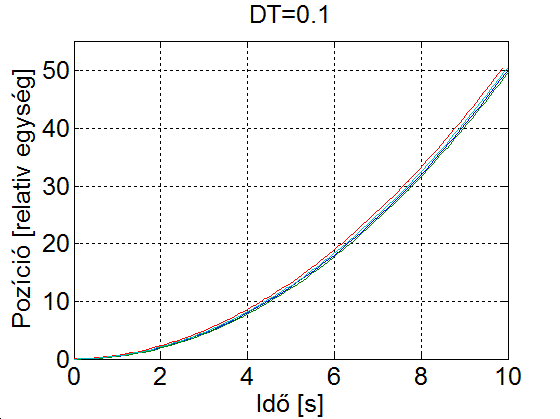
2 - 13 feladat Rendszeregyenletek felírása ( Kerékpár ) (Házi feladat, megoldását nem közöljük)
Adott egy direkt hajtású (a hátsó agyban nem racsnis) kerékpár, nyúlás és kotyogás mentes lánccal (válasszon valóságos adatokat a kerékméretre, az első és hátsó fogaskerékre és a pedál kar hosszára). A kerékpár egyenesen halad.
-
Írja fel a kerékpár rendszeregyenletét. Legyen a rendszer bemenete a pedál elfordulása. Legyen a kimenet a megtett út.
-
Írja fel a kerékpár rendszeregyenletét. Legyen a rendszer bemenete a kerékpáros által a pedálra kifejtett nyomaték. Legyen a kimenet a megtett út. Ismert a kerékpáros és a kerékpár tömege.
-
Hogy módosul a rendszeregyenlet, ha a hátsóagy racsnis a b) esetben
2 - 14 feladat Ideális transzlációs telemanipulációs rendszer ARMA alakja
Adja meg a
2-12 feladat c), d) és e) pontjában ismertetett rendszer diszkrét idejű ARMA modelljének paramétereit.
c) pont
A (2.153) alapján
|
|
( 2.170 ) |
A 2-33. ábra és (2.170) alapján
|
|
( 2.171 ) |
d) pont
A (2.158) kifejezés alapján helyettesítéssel
|
|
( 2.172 ) |
A 2-33. ábra és (2.172) alapján
|
|
( 2.173 ) |
e) pont
A (2.158) kifejezés alapján
|
|
( 2.174 ) |
A 2-33. ábra és (2.174) alapján
|
|
( 2.175 ) |
2 - 15 feladat Kerékpár rendszeregyenleteinek ARMA alakja (Házi feladat, megoldását nem közöljük)
Írja fel a
2-13 feladat b) pont esetében a rendszer ARMA modelljét 0.1s-os mintavétellel.
2 - 16 feladat Egyenáramú motor és merev tengellyel forgatott tömeg
Adott egy külsőgerjesztésű egyenáramú motor, amely egy merev tengelyen keresztül egy terhelést mozgat. A motor villamos áramának dinamikáját elhanyagoljuk, más szavakkal az időállandóját (definíciót ld. 161. oldal) nullának tekintjük. Jelölések: a motor szögsebessége és az elfordulása, , , , , pedig értelemszerűen a motor illetve a teher másodrendű nyomatéka, illetve a viszkózus súrlódást figyelembe vevő paramétere. a motor kapocsfeszültsége, a motor paramétere, Ra az armatúra ellenállása. A rendszer egyenletei:
|
|
( 2.176 ) |
Megoldás
a) feladat
A 2-17 feladat speciális esete.
b) feladat
Fejezzük ki a deriváltakat
|
|
( 2.177 ) |
Vezessük be a következő jelölést
|
|
( 2.178 ) |
Az analóg számítógépes modell a 2-45. ábran látható.
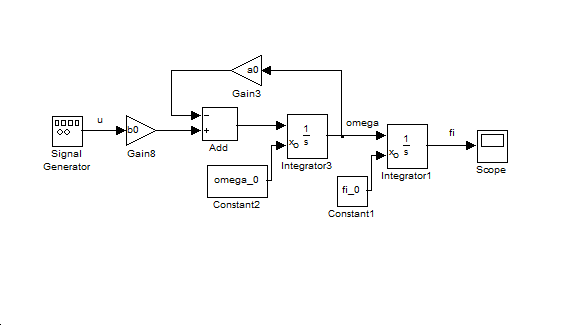
2 - 17 feladat Egyenáramú motor és terhelő nyomaték
Adott egy külsőgerjesztésű egyenáramú motor, amelyet nyomaték terhel. Jelölések: a motor szögsebessége és az elfordulása, és pedig a motor másodrendű nyomatéka, illetve a viszkózus súrlódást figyelembe vevő paramétere. a motor kapocsfeszültsége, a motor paramétere, az armatúra ellenállása, az armatúra tekercs induktivitása. A rendszer egyenletei:
|
|
( 2.179 ) |
Írja át a differenciálegyenlet-rendszert (2.107) alakúra,
-
Legyen az bemenet a motor kapocsfeszültsége és az kimenet a motor fordulatszáma. Az terhelőnyomatékot ebben az esetben tekintsük nullának.
-
Legyen az bemenet a motor kapocsfeszültsége és az kimenet a motor elfordulása. Az terhelőnyomatékot ebben az esetben tekintsük nullának.
-
Legyen az bemenet a motor terhelőnyomatéka és az kimenet a motor fordulatszáma. A motor kapocsfeszültségét ebben az esetben tekintsük nullának.
-
Legyen az bemenet a motor terhelőnyomatéka és az kimenet a motor elfordulása. A motor kapocsfeszültségét ebben az esetben tekintsük nullának.
-
Rajzolja fel (2.179) egyenlettel leírt rendszer analóg számítógépes vázlatát integrátorok segítségével.
Megoldás
e) feladat
Fejezzük ki a deriváltakat
|
|
( 2.180 ) |
|
|
( 2.181 ) |
Vezessük be a következő jelöléseket
|
|
( 2.182 ) |
|
|
( 2.183 ) |
Az analóg számítógépes modell a 2-46. ábran látható.
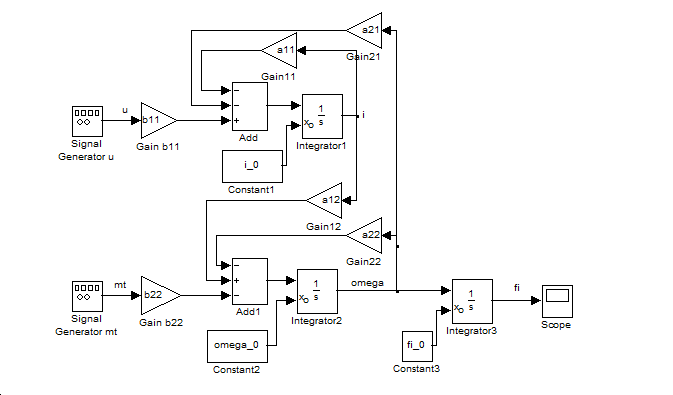
2 - 18 feladat Egyenáramú motor és rugalmas tengellyel forgatott tömeg
Egy külsőgerjesztésű egyenáramú motor egy rugalmas tengelyen keresztül egy terhelést mozgat. A motor villamos áramának dinamikáját elhanyagoljuk, más szavakkal az időállandóját (definíciót ld. 161. oldal) nullának tekintjük. A jelölések: a motor szögsebessége és az elfordulása, és a teher szögsebessége és elfordulása. a tengely torziós rugómerevsége, a tengely elcsavarodása (, , , , , pedig értelemszerűen a motor illetve a teher másodrendű nyomatéka, illetve a viszkózus súrlódást figyelembe vevő paraméter. a motor kapocsfeszültsége, a motor paramétere, Ra az armatúra ellenállása a villamos nyomaték. A rendszer egyenletei:
|
; ; ; |
( 2.184 ) |
Írjuk át a differenciálegyenlet-rendszert (2.107) alakúra.
-
Legyen az bemenet a motor kapocsfeszültsége és az kimenet a teher fordulatszáma.
-
Legyen az bemenet a motor kapocsfeszültsége és az kimenet a teher elfordulása.
Megoldás
A 2-19 feladat speciális esete.
2 - 19 feladat Egyenáramú motor és terhelő nyomaték rugalmas tengelyen keresztül
Egy külsőgerjesztésű egyenáramú motor egy rugalmas tengelyen keresztül egy terhelést mozgat és a terheléshez további terhelő nyomaték kapcsolódik. A motor villamos áramának dinamikáját elhanyagoljuk, más szavakkal az időállandóját (definíciót ld. 161. oldal) nullának tekintjük. A jelölések: a motor szögsebessége és az elfordulása, és a teher szögsebessége és elfordulása. a tengely torziós rugómerevsége, a tengely elcsavarodása (, , , , , pedig értelemszerűen a motor, illetve a teher másodrendű nyomatéka, illetve a viszkózus súrlódást figyelembe vevő paraméter. a motor kapocsfeszültsége, a motor paramétere, Ra az armatúra ellenállása, valamint a villamos nyomaték. A rendszer egyenletei:
|
|
( 2.185 ) |
|
|
( 2.186 ) |
|
|
( 2.187 ) |
|
|
( 2.188 ) |
|
|
( 2.189 ) |
Írjuk át a differenciálegyenlet-rendszert (2.107) alakúra.
-
Legyen az bemenet a motor kapocsfeszültsége és az kimenet a motor fordulatszáma. Az terhelőnyomatékot ebben az esetben tekintsük nullának.
-
Legyen az bemenet a motor kapocsfeszültsége és az kimenet a motor elfordulása. Az terhelőnyomatékot ebben az esetben tekintsük nullának.
-
Legyen az bemenet a motor terhelőnyomatéka és az kimenet a motor fordulatszáma. A motor kapocsfeszültségét ebben az esetben tekintsük nullának.
-
Legyen az bemenet a motor terhelőnyomatéka és az kimenet a motor elfordulása. A motor kapocsfeszültségét ebben az esetben tekintsük nullának.
Megoldás
a) feladat
Ebben az esetben . A (2.185) egyenletből az áramot kifejezve és behelyettesítve a (2.186) egyenletbe:
|
|
( 2.190 ) |
Az így kapott kifejezését helyettesítsük a (2.187) egyenletbe:
|
|
( 2.191 ) |
A (2.188) egyenletből következik
|
|
( 2.192 ) |
A motor fordulatszámára és gyorsulására vonatkozó (2.192) kifejezéseket a (2.191) egyenletbe helyettesítve:
|
|
( 2.193 ) |
kifejezhető a (2.189) egyenletből
|
|
( 2.194 ) |
A (2.194) összefüggéseket felhasználva (2.193) alapján (2.107) alakú kifejezést kapunk
|
|
||||
|
|
|
|
||
|
|
|
( 2.195 ) |
||
b) feladat
Mivel , így (2.195) alapján
|
|
||||
|
|
|
|
||
|
|
|
( 2.196 ) |
||
c) feladat
Ha , akkor (2.190) a következőképp módosítható
|
|
( 2.197 ) |
Hasonlóan (2.191) helyett a következőt írhatjuk
|
|
( 2.198 ) |
értékét (2.189) egyenletből kifejezve () és behelyettesítve a (2.198) egyenletbe
|
|
( 2.199 ) |
A motor fordulatszámát ismét a (2.192) alapján küszöböljük ki
|
|
( 2.200 ) |
Mivel ebben az esetben , így a (2.194) kifejezést is módosítani kell
|
|
( 2.201 ) |
A (2.201) összefüggéseket felhasználva (2.200) alapján (2.107) alakú kifejezést kapunk
|
|
||||
|
|
|
|
||
|
|
( 2.202 ) |
|||
d) feladat
Mivel , így (2.202) alapján
|
|
||||
|
|
|
|
||
|
|
( 2.203 ) |
|||
2 - 20 feladat Diszkrét állapotú érzelmi modell
Tegyük fel, hogy egy tamagoccsi (たまごっち) a teljes életét egy szobában tölti, ahová csak a gazdája és egy idegen léphet be és távozhat (egymástól függetlenül). A tamagoccsinak alapvetően négyféle érzelmi állapota lehet. Szomorú, ha egyedül van a szobában, boldog, ha a gazdájával ketten vannak a szobában, ideges, ha az idegennel ketten vannak a szobában, végül nyugodt, ha az idegen és a gazdája is a szobában van.
Rajzolja le a tamagoccsi diszkrét állapotú érzelmi modelljét.
Megoldás
A feladat kiírása szerint négy állapotunk van, és négy eseményt definiálhatunk (a gazda is és az idegen is érkezhet és távozhat). Ezek az események nem függetlenek egymástól: egy adott szereplő esetében az érkezés után csak távozás következhet, a távozást érkezés követi.
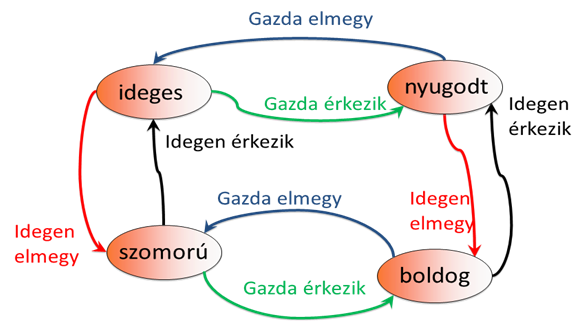
2 - 21 feladat Diszkrét állapotú viselkedésmodell
Tegyük fel, hogy egy tamagoccsi (たまごっち) négyféle tevékenységet folytathat: étkezik, alszik, játszik és unatkozik. A viselkedés szabályai
-
Az étkezés és alvás ideje kötött (ez alatt az idő alatt más tevékenység nem folytatható)
-
Az étkezés és alvás ideje nem követi egymást (alvás után nem következhet étkezés és fordítva)
-
Ha nem alszik és nem étkezik, akkor vagy játszik, vagy unatkozik attól függően, hogy a gazda jelen van-e, vagy sem.
Rajzolja le a tamagoccsi diszkrét állapotú viselkedés modelljét.
Megoldás
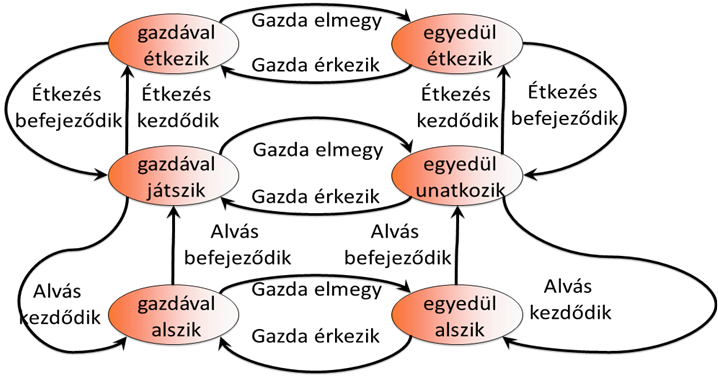
2 - 22 feladat Lifthívó - rendszer diszkrét állapotú modellje
Tegyük fel, hogy három szint és három nyomógomb van. Ha pl. megnyomjuk a 3. gombot, akkor a lift a 3. szintre megy.
Rajzolja le a lifthívó-rendszer diszkrét állapotú modelljét.
Megoldás
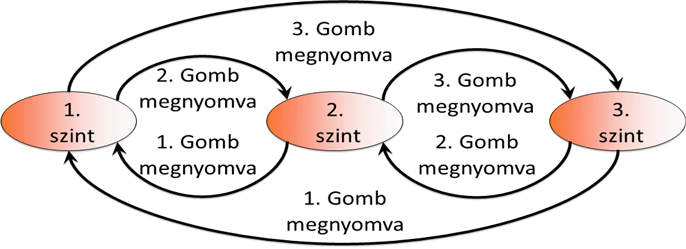
2 - 23 feladat Kombinált (fűtés. melegvíz) kazán szabályozójának diszkrét állapotú modellje
Tegyük fel, hogy a fűtésszabályozó alrendszernek két állapota (fűtés bekapcsolva és fűtés kikapcsolva) van, amelyek között a szerint vált, hogy a szoba hőmérséklete nagyobb-e a felső hőmérsékleti korlátnál, vagy kisebb-e a alsó hőmérsékleti korlátnál. (Természetesen ). A vízcsapok megnyitásakor a melegvíz szolgáltatásnak nagyobb prioritása van.
Rajzolja le a kombinált (fűtés. melegvíz) kazán szabályozójának diszkrét állapotú modelljét.
Megoldás
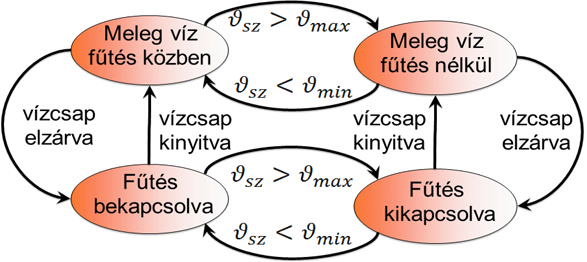
2.15. Alapvető vizsgálati módszerek
Megismerkedtünk a rendszer fogalmával, és annak típusaival. Fel tudjuk írni a rendszer egyenleteket, megismertük az alapvető matematikai műveleteket a rendszeregyenletek megoldására. Áttekintettük a legfontosabb problémaköröket. A következő fejezetben olyan matematikai módszereket ismerünk meg, amelyek leegyszerűsítik a rendszer differenciálegyenleteinek megoldását, illetve amelyek segítségével a rendszer differenciálegyenleteinek megoldásnélkül is következtetni tudunk a rendszer viselkedésére.
A két legfontosabb megközelítés
-
A bemenőjel komponensekre bontása és a kimenőjel kiszámítása konvolúció alkalmazásával (Klasszikus szabályozáselmélet alapja) (ld. 3. és 4. fejezet). A bemenőjel komponensekre bontása történhet az időtartományban is és a frekvencia-, illetve Laplace-operátoros tartományban is. Mivel a konvolúció a frekvencia-, illetve Laplace-operátoros tartományban számítható könnyebben, ezért ezt a megközelítést általában a frekvencia-, illetve Laplace-operátoros tartományban használjuk.
-
Mátrixos formalizmus (Ennek speciális és széles körben elterjedt esete az állapottér-módsze. (A mátrixos formalizmus az idő- és frekvencia-, illetve Laplace-operátoros tartományban egyaránt alkalmazható)