8. fejezet - Véletlen hatások és sztochasztikus folyamatok
- 8.1. Valószínűség, valószínűségi változók és valószínűségi eloszlások
-
- 8.1.1. Eseményalgebra és a valószínűség definíciója
- 8.1.2. Valószínűségi változók és valószínűségi eloszlások
- 8.1.3. A valószínűségi változók jellemző paraméterei
- 8.1.4. Többdimenziós valószínűségi vektor-változók és eloszlások
- 8.1.5. A többdimenziós valószínűségi vektor-változók jellemző paraméterei
- 8.1.6. Gyakran használt diszkrét és folytonos eloszlások
- 8.1.7. Valószínűségi változók függvényei
- 8.1.8. Valószínűségi változók entrópiája és információ-tartalma
- 8.2. Sztochasztikus folyamatok
8.1. Valószínűség, valószínűségi változók és valószínűségi eloszlások
8.1.1. Eseményalgebra és a valószínűség definíciója
A mérnöki gyakorlatban többnyire determinisztikus rendszerekkel és folyamatokkal dolgozunk, melyekben minden hatás, elem és kapcsolat jól meghatározott, és adott körülmények között az azoktól függő változások és események szükségszerűen be is következnek. Az ilyen eseményeket pontosan előre lehet jelezni, matematikai modelljeik segítségével pontosan számolhatjuk – természetesen a számítások hibahatárain belül – az események és folyamatok bekövetkezési idejét és értékét. Ettől lényegileg eltérőek azok a hatások, események és folyamatok, amelyek megadott, jól meghatározott körülmények között is csak bekövetkezhetnek, azaz: vagy bekövetkeznek, vagy nem következnek be. Ha bekövetkeznek, akkor értékük nem adható meg előre. Az ilyen hatások kialakulásának, az események bekövetkezésének ideje és/vagy értéke tehát bizonytalan meghatározottságú, amit úgy szoktunk jellemezni, hogy valószínűleg ekkor és/vagy ilyen értékben fordulnak elő és következnek be. Ezeket az eseményeket és folyamatokat véletlen eseményeknek és folyamatoknak nevezzük.
A véletlenség és valószínűség intuitív fogalma általában induktív értelmezésen és véleményeken alapul, amit olyan kijelentésekkel illusztrálhatunk, mint: „Ez a mérőeszköz várhatólag jól fog működni”; „Az elképzelés valószínűleg hibás”; „A zaj valószínűleg nem lesz elég erős”. Ezek a vélemények adott szituációban érdekesek lehetnek, de csak valamiféle kvalitatív értékelést és jóslást jelentenek. Azonban a véletlen eseményekben és folyamatokban rejlő bizonytalanságot sok esetben kvantitatíve is jellemezni tudjuk, amihez a véletlenség matematikai modelljét az egyes véletlen hatások „bizonytalan” következményeinek megvalósulását jellemző mértékekkel kell megfelelően megfogalmazni.
A valószínűség fizikai hátterű, modell-alapú precíz megfogalmazásához valamely fizikai kísérlet modelljét, az idealizált gondolatkísérlet és e gondolatkísérlet összes lehetséges eredményének fogalmát kell bevezetnünk. A valószínűség fogalmát kizárólag ezekhez a jól definiált modell-objektumokhoz kapcsolhatjuk. Itt analóg módon járunk el azokhoz a modellezési eljárásokhoz, mint pl. a mechanikában a tömegpontok fogalmának, vagy a villamosságban a hurokáramok fogalmának bevezetése és alkalmazása a determinisztikusként modellezett jelenségek vizsgálatában.
Egy gondolatkísérlet – melyet többnyire véletlen kísérletnek nevezünk – bármelyik lehetséges eredményét elemi eseménynek nevezzük, és az elemi események halmaza alkotja az elemi eseményteret. Az elemi eseményeket kockajáték esetén, melyet a valószínűséggel foglalkozó klasszikus megközelítés egyik leggyakrabban alkalmazott illusztrációjaként használhatunk, könnyen azonosíthatjuk az egy dobással megvalósítható 1,2,3,4,5,6 számok valamelyikének megjelenésével. Ekkor az elemi eseményteret az {1,2,3,4,5,6} halmaz alkotja. Ha azonban egy kockadobással, mint fizikai kísérlettel társított gondolatkísérlet összes lehetséges eredményét nézzük, akkor beszélhetünk – többek között – a „páros szám” {2,4,6} eseményről, vagy az {5,6} „legalább öt” eseményről, amelyek a hatelemű eseménytér összes részhalmazából választott, összetett eseményekként értelmezett részhalmazok.
A kockadobás eseményei diszkrét halmazokat alkotnak. Vegyünk azonban egy másik példát, amelyben az események megszámlálhatatlan végtelen számú ponttal jellemezhetők. Legyen ugyanis egy különböző elemekből álló villamos négypólus, amelyben két nem ismert kapacitású kondenzátor található. A négypólus viselkedése – nem tekintve annak struktúráját – természetesen függ a kondenzátorok kapacitásától. A nem ismert kondenzátorok kapacitásának kimérése véletlen kísérletnek tekinthető, amely kontinuum számosságú valós, véletlen értékeket adna, így, feltételezve a C1>0 és C2>0 egyenlőtlenségeket, a (C1,C2) értékpárok elvileg az egész pozitív siknegyedet, azaz egy kontinuum számosságú folytonos halmazt jelölnek ki. Ebben az esetben az elemi eseményeket a (C1,C2) valós értékpároknak megfelelő síkpontok alkotják, míg az összetett eseményeket a síknegyed megfelelő ponthalmazaiként jelölhetjük ki. A C1>C2 eseményt, például, a síknegyed szögfelező alatti pontjaiból álló ponthalmaz adja meg, míg a C2>C1-10 eseményt a C2=C1-10 egyenes feletti pontokból álló halmaz jelöli ki. A két esemény összege a teljes pozitív síknegyedet jelenti, míg a szorzatuk a C2=C1 és C2=C1-10 egyenesek közötti pontok halmazát adják meg.
Ezek a példák tehát jól illusztrálják, hogy mind a kockadobás, mind pedig az ismeretlen kondenzátorok mérése által értelmezett véletlen események a halmazokkal analóg tulajdonságokkal jellemezhetők, és az eseményekhez rendelt esélyek meghatározásával értelmezhetjük a valószínűség fogalmát.
Az γ szimbólummal jelölt, egymást kölcsönösen kizáró elemi események Γ tere lehet megszámlálhatóan véges vagy végtelen diszkrét, korlátos vagy nemkorlátos kontinuum számosságú halmaz, amikor is egy tetszőleges eseményt az elemi események részhalmazaként határozzuk meg. Az -t biztos eseménynek nevezzük, mivel ezzel a véletlen kísérlet végrehajtása biztosan valamelyik elemi eseményt adó eredményre vezet. Az -n kívüli, ahhoz nem tartozó bármely eseményt nevezhetjük a véletlen kísérlet lehetetlen eseményének; egyértelműen az -ba nem tartozó Θ üres halmazzal azonosítjuk a lehetetlen eseményt.
Az A és B események összege az az esemény, amely mindazon elemi eseményekből áll, melyek legalább az egyiknek az elemei. Az események szorzatát azon elemi események alkotják, melyeket egyidejűleg mindkét esemény tartalmazza, míg az különbség az A azon elemi eseményeiből áll, melyek egyidejűleg nem elemei a B-nek. Ha a B esemény tartalmazza az A eseményt, azaz , akkor az A esemény maga után vonja a B esemény bekövetkezését. Ezt az implikáció relációjának nevezzük.
Mindezen előkészítés alapján bevezethetjük az eseményalgebra általános, precíz fogalmát.
8.1 definíció. Legyen Γ nem üres halmaz és jelölje A az Γ részhalmazaiból álló halmazt, amelyre teljesülnek az alábbi feltételek.
-
-
Ha és , akkor .
-
Ha , akkor az események megszámlálható összege is az eleme, azaz .
Akkor az A halmazrendszert eseményalgebrának, illetve pontosabban esemény σ-algebrának nevezzük.
Ha most feltételezzük, hogy az A eseményalgebra eseményei valamely véletlen kísérletek eredményeként jönnek létre, ahogy ezt a kockadobás és a négypólus kondenzátorainak mérései esetén láttuk, akkor e véletlen kísérletekhez szorosan hozzátartozik az egyes események esélyeivel kapcsolatos spekuláció. Például, mekkora az esélye annak, hogy éppen a hármas vagy a páros esemény jön ki, vagy mekkora az esélye annak, hogy a C1>C2 esemény valósul meg a mérések során? Egyetlen véletlen kísérlet eredményének megfigyelése nem ad megfelelő információt erről az esélyről, azonban a kísérlet egymástól független sokszoros megismétlése érdekes tulajdonságot mutat: valamely A esemény bekövetkezésének a száma az összes kísérlet számához viszonyítva, azaz relatív gyakorisága elég nagyszámú kísérlet esetén az eseményre jellemző tört érték körül állandósul. Így például, kockadobás esetén bármely elemi esemény, azaz az 1, 2, 3, 4, 5, és 6 számok kijöttének az összes dobás számához viszonyított aránya elég nagyszámú kísérlet esetén közel kerül az 1/6-hoz és tartósan ott is marad. Azt mondjuk, hogy a 3-as szám kijöttének gyakorisága elég nagyszámú dobás esetén 1/6, és ez a gyakorlatban megfigyelhető érték teremti meg a kapcsolatot a valószínűség absztrakt fogalmához.
8.2 definíció. Legyen A egy esemény σ-algebra, és annak tetszőleges eseményéhez rendeljünk hozzá egy valós számot az alábbi módon:
-
-
-
Tetszőleges, páronként diszjunkt eseményekre
.
Ekkor az függvényt valószínűségi függvénynek nevezzük, míg a , szám az A esemény valószínűsége. Általánosabban: az hármast Kolmogorov-féle valószínűségi mezőnek nevezzük, míg az a), b) és c) feltételek a valószínűség axiómiái.
Vezessük most be a feltételes valószínűség fogalmát: Az eseménynek egy feltételre vonatkozó feltételes valószínűségét a formulával értelmezzük. Ebből a feltételből kiindulva az előzővel analóg módon egy feltételes valószínűségi mezőt tudunk felépíteni, amely az előbbiekben meghatározottnak egy szűrését jelenti. Ez azt jelenti, hogy a feltétel nélküli valószínűségre levezetett összefüggések analóg módon érvényesek a feltételes valószínűségekre is.
A feltételes valószínűséggel az események függetlenségét is könnyen meghatározhatjuk: Az esemény független a eseménytől, ha . De akkor fennáll a reláció is, így , azaz az események egymástól független eseményeket alkotnak.
8.1 példa. A valószínűség klasszikus meghatározása. Kockadobás esetén az elemi eseményeket az {γk=k, k=1,2,3,4,5,6} számok megvalósulásai alkotják. Mivel bármelyik megvalósulásának az esélye azonos, ezért az elemi események valószínűségei: . Minden esemény – a lehetetlen eseménnyel együtt összesen 64 esemény lehetséges –, az elemi események halmaz-összegeiként alakulnak ki, ezért az összetett események valószínűségeit az alkotó elemi valószínűségek algebrai összegeiként kapjuk meg.
Ez azt jelenti, hogy ha az A eseményt m elemi esemény alkotja az módon, akkor az A esemény valószínűségét a . Így annak a valószínűségét, hogy a „páratlan” esemény valósul meg, azaz a következő dobásban egy páratlan szám jön ki, a
eredmény adja meg. Másik példaként a „legalább 3” esemény valószínűségét, azaz annak esélyét számolva, hogy a következő dobás eredménye három vagy annál nagyobb lesz, a
eredményt szolgáltatja. □
8.2 példa. Geometriai valószínűség. Tekintsük az 8-1. ábra (a,b) egyenes szakaszát, és jelöljük ki a belsejében az a≤c≤d≤b feltételeknek megfelelő (c,d) szakaszt. Tegyük fel, hogy teljesen véletlenül, találomra akarunk kijelölni egy pontot az (a,b) szakaszon. Mekkora a valószínűsége annak, hogy ez a pont a (c,d) szakaszra kerül?
Mindenek előtt vegyük észre, hogy mivel az (a,b) szakaszon belül minden véges hosszúságú szakasz pontjai megszámlálhatatlanul végtelen számosságú halmazt alkotnak, ezért egyetlen pontnak, ebben a feladatban lényegében egy elemi eseménynek a valószínűségére nincs értelme rákérdezni, ezért csak intervallumokkal lehet a feladatot kezelni.
A feladat kiírásában a teljesen véletlenül, találomra történő pont kijelölése azt jelenti, hogy az (a,b) szakasz bármelyik pontját ugyanolyan eséllyel találhatjuk el, azaz az (a,b) szakaszon belül nincs kitüntetett rész: bármelyik, bármekkora belső szakaszra történő találat csak attól függ, hogy az relatíve milyen hosszúságú, azaz az esély a szakaszok hosszával arányos. Ezt figyelembe véve azt mondhatjuk, hogy a (c,d) szakaszra történő találat valószínűségét a
módon fejezhetjük ki, ahol r>0 az arányossági tényező. Mivel ebben az esetben az (a,b) szakaszra történő találat a biztos eseményt jelenti, ezért írhatjuk, hogy annak valószínűsége
.
Innen az r értékét az kifejezés adja meg, ezért a (c,d) szakaszra történő találat valószínűségét a
aránnyal tudjuk kifejezni. □

8.1.2. Valószínűségi változók és valószínűségi eloszlások
A valószínűség precíz meghatározása az eseménytér és a véletlen kísérletek értelmezésén, azaz a valószínűségi mező fogalmán keresztül történik, azaz a rendszerek véletlen jelenségeinek elemzése során háttérként mindig megfelelő eseményteret és valószínűségi mezőt kell felvázolni. A véletlen jelenségek matematikai kezelésében azonban az eseménytéren értelmezett függvényekként definiált valószínűségi változók a valószínűségszámítás alapvető fogalmai közé tartoznak, ugyanakkor lehetővé teszik a véletlen hatások és folyamatok meglehetősen általános kezelését.
Az elemi események Γ halmazától függően folytonos és diszkrét valószínűségi változókat különböztetünk meg, és ezeket az alábbi módon határozhatjuk meg.
8.3 definíció. Legyen az elemi események Γ halmaza megszámlálhatlan, azaz kontinuum számosságú. Ekkor az , kontinuum számosságú értékkésszlettel rendelkező valós függvényt folytonos valószínűségi változónak nevezzük, ha minden valós számhoz létezik egy P valószínűséggel rendelkező esemény.
A folytonos valószínűségi változót meghatározó X függvény Ε értékkészletét alkothatják intervallumok, félegyenesek vagy akár a teljes egyenes pontjai. Ekkor minden A eseményt valamilyen φ feltétellel határozunk meg, melynek valószínűségét a P(φ) módon fejezzük ki. Itt a φ:X<α feltétel valószínűségét a P(φ)=P(X<α) kifejezéssel adjuk meg. Ezt a jelölést alkalmazva bevezethetjük a valószínűségi változók eloszlásfüggvényének fogalmát is az alábbi módon.
8.4 definíció. Az függvényt az X folytonos valószínűségi változó eloszlásfüggvényének nevezzük.
Egy folytonos változó eloszlásfüggvénye balról folytonos, monoton nemcsökkenő függvény. Ha az FX eloszlásfüggvény is folytonos, akkor létezik olyan nemnegatív fX(.) függvény, hogy
|
|
(8.1) |
és ha az eloszlásfüggvény differenciálható, akkor az
|
|
(8.2) |
függvényt az X valószínűségi változó sűrűségfüggvényének nevezzük. A sűrűségfüggvénnyel a normalizációs feltételt a
|
|
(8.3) |
formában írhatjuk.
Az fX(.) sűrűségfüggvény nemnegativitása következik az FX(.) monotonitásából, de a (8.1) egyenletből is következik, mivel tetszőleges a<b értékekre teljesülnie kell a
|
|
(8.4) |
egyenlőségnek. Ugyanakkor a (8.4)-ból azonban azt is látjuk, hogy folytonos valószínűségi változó esetén
azaz annak valószínűsége, hogy az X folytonos valószínűségi változó valamely c konkrét értéket vesz fel zérus. Ez azonban nem jelent lehetetlen eseményt, hanem csak nagyon kis valószinűségű eseményt, amit tetszőleges x=c esetén a
|
|
(8.5) |
formulával lehet kifejezni.
8.3 példa. Végezzük el a következő kísérletet. Vegyünk két azonos frekvenciájú szinuszjel feszültség-generátort, kapcsoljuk be azokat függetlenül egymást követően, és határozzuk meg a két színuszjel fáziskülönbségének valószínűségi sűrűségfüggvényét!
Mivel a bekapcsolások egymástól teljesen függetlenül történtek, ezért nincs fizikai alapja annak, hogy a két fázis közötti értékek közül bármelyiket vagy bármelyik intervallumot kiemeljük. Tehát azt kell feltételeznünk, hogy a fáziskülönbséget reprezentáló Φ véletlen változó sűrűségfüggvénye a (0,2π) intervallumban konstans értékű.
Felhasználva a
feltételt azt kapjuk, hogy a (0,2π) intervallumban. Ezt egyenletes eloszlásnak nevezzük.
Felhasználva a (8.1) összefüggést megkapjuk a véletlen fáziskülönbség eloszlásfüggvényét is
. □
8.5 definíció. Legyen az elemi események Γ halmaza megszámlálható számosságú. Ekkor az megszámlálható értékkésszlettel rendelkező valós függvényt diszkrét valószínűségi változónak nevezzük, ha minden valós számhoz létezik egy valószinűségű esemény.
Mivel most az elemi események teljes rendszert alkotnak, ezért a valószínűségekre érvényesek a és relációk, ahol a felső határra érvényes a feltétel, azaz a diszkrét események alkothatnak megszámlálhatóan véges vagy végtelen halmazt.
8.6 definíció. Az függvényt az X diszkrét valószínűségi változó eloszlásfüggvényének nevezzük.
A diszkrét valószínűségi változók eloszlásfüggvényei lépcsős függvények, melyekben az ugrások a valószínűségi változók xk értékeiben következnek be. Ezen ugrásokat a értékek adják meg, míg most a normalizációs feltételt a
|
|
(8.6) |
egyenlet szolgáltatja,.
8.4 példa. Tegyük fel, hogy két azonos mérőeszközt használunk a laborban, melyeknek egy adott időszakra vonatkozó meghibásodási valószínűségei 0.25 értékűek. Határozzuk meg azon X diszkrét valószínűségi változó eloszlásfüggvényét, amellyel az esetlegesen meghibásodó mérőeszközöket jellemezhetjük.
Az X valószinűségi változó három értéket vehet fel: x1=0, x2=1, x2=2, azaz az adott időszakban előfordulhat 1 vagy két eszköz meghibásodása, de az is lehet, hogy mindkét eszköz hibátlanul dolgozik.
A rendszer elemi eseményei az következők:
A1 – az első mérőeszköz meghibásodik
A2 – az első mérőeszköz hibátlanul működik
B1 – a második mérőeszköz meghibásodik
B2 – a második mérőeszköz hibátlanul működik
Ekkor az X valószínűségi változó egyes értékeinek a valószínűségei a következők (kihasználva, hogy az egyes elemi események között fennállnak az és relációk):
.
Összefoglalva, diszkrét valószínűségi változó értékei és valószínűségei:
|
xk |
0 |
1 |
2 |
|
P(xk) |
0.5625 |
0.375 |
0.0625 |
Ekkor az FX eloszlásfüggvény formája:
melyet a 8-3. ábra illusztrál.
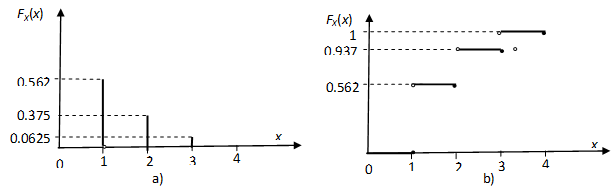
8.1.3. A valószínűségi változók jellemző paraméterei
A valószínűségi változók teljes leírását, akár diszkrét, akár folytonos változókról beszélünk, eloszlásaik, azaz eloszlásfüggvényeik és – ha léteznek – sűrűségfüggvényeik adják meg. Azonban mind a diszkrét, mind a folytonos függvényekkel történő munka meglehetősen összetett műveleket igényel, de sok esetben nem is szükséges e függvények által tartalmazott összes információ, mivel bizonyos gyakorlati feladatokban az is elégséges, ha az eloszlások egyes jellemző paramétereit ismerjük és használjuk fel. Ezek a jellemző paraméterek az eloszlásfüggvények különböző módon képzett funkcionáljai és azok kombinációi, amelyek közül a valószínűségi változók egyes függvényeinek várható értékei játszák a legfontosabb szerepet. Ehhez először valamely általános függvény várható értékét definiáljuk:
8.7 definíció. Az X valószínűségi változó g:X→R valós függvénye várható értékének nevezzük folytonos esetben az
|
|
(8.7) |
integrált, míg diszkrét esetben az
|
|
(8.8) |
összeget.
A g függvény formájától függően nagyon sok jellemző paramétert tudunk előállítani az (8.7) és (8.8) várható értékek alkalmazásával, minden esetben feltételezve, hogy az integrálok és összegzések véges értékeket adnak:
-
: az X változó α konstans szerinti n-ed rendű momentuma.
-
: az X változó n-ed rendű közönséges momentuma a μn jelöléssel.
-
: az X változó várható (átlagos) értéke (elsőrendű közönséges momentuma) a μ1=μX jelöléssel.
-
az X változó várható érték szerinti n-ed rendű centrális momentuma a jelöléssel.
-
: az X változó varianciája (szórásnégyzete) (a várható érték szerinti másodrendű centrális momentuma) a jelöléssel.
A felsorolt jellemzők közül a μX várható érték alapvető szerepét az adja, hogy egy véletlen kísérletsorozat esetén a megfigyelt értékek a várható (átlagos) érték körül ingadoznak. Ezen ingadozások mértékének legfontosabb jellemzője a variancia (szórásnégyzet) vagy a négyzetgyökkel kifejezett szórás. E két jellemző alkalmazásával a
|
|
(8.9) |
aránnyal az ingadozások relatív mértékét fogalmazzuk meg. Ugyanakkor e két jellemzővel végezhetjük el az X változó normálását is, ami az
művelettel az Y normált változót jelenti: az Y zérus várható értékű és egységnyi varianciájú valószínűségi változót jelöl.
Az elsőrendű közönséges momentum – várható érték –, valamint a másodrendű centrális momentum – szórásnégyzet – említett szerepei mellett azt mondhatjuk, hogy a valószínűségi eloszlások tulajdonságait az alacsonyrendű momentumokkal jellemezhetjük a legjobban. Így az eloszlások egyik fontos tulajdonságát, a szimmetrikusságot, azaz az eloszlás aszimetriájának mértékét jellemzi
|
|
(8.10) |
ferdeségi tényező. Ugyancsak két alacsonyrendű momentum felhasználásával képezzük a
|
|
(8.11) |
lapultsági tényezőnek nevezett mutatót.
A (8.10)-(8.11) aggregált jellemzők mind folytonos, mind diszkrét valószínűségi változók esetében értelmezhetők és használhatók. Az
|
|
(8.12) |
egyenlet xp megoldásával definiált p-ed rendű kvantilis azonban csak folytonos valószínűségi változók esetében adott egyértelműen. Ennek értelmezését a összefüggés adja meg. Jegyezzük meg, hogy a p=1/2-ed rendű kvantilisnek külön neve van: ezt az X valószínűségi változó mediánjának nevezzük.
A valószínűségi eloszlások modellezési alkalmazásaiban nagyon hasznos relációk a következő abszolút értékekre vonatkozó egyenlőtlenségek:
|
|
(8.13) |
Markov-egyenlőtlenség tetszőleges n esetén:
|
|
(8.14) |
Csebisev-egyenlőtlenség:
|
|
(8.15) |
8.8 definíció. Az X valószínűségi változó karakterisztikus függvényének nevezzük folytonos esetben az
|
|
(8.16) |
integrált, míg diszkrét esetben az
|
|
(8.17) |
összeget, ahol j az imaginárius egység.
Innen már látható, hogy a karakterisztikus függvény és a valószínűségi sűrűségfüvény Fourier-transzformációval összekötött függvény-párost alkotnak. Inverz irányban kapjuk a rendszertechnikából jól ismert Fourier-transzformációkat:
|
|
(8.18) |
és
.(8.19)
A karakterisztikus függvény tulajdonságai:
ahol a konjugált függvényt jelenti.
A karakterisztikus függvény fontos alkalmazásbeli tulajdonsága, hogy az ω változó szerinti n-edik differrenciálhányadossal generálni tudjuk az X valószínűségi változó n-edik közönséges momentumát a
|
|
(8.20) |
módon.
A karakterisztikus függvény alkalmazásával az X valószínűségi változó fontos jellemző-
inek egy másik fontos halmazát, a kumulánsokat is generálni tudjuk a
|
|
(8.21) |
módon. A momentumok és kumulánsok között jól meghatározott kapcsolatok vannak, amelyek lehetővé teszik közöttük az egyértelmű átszámításokat.
8.1.4. Többdimenziós valószínűségi vektor-változók és eloszlások
A gyakorlatban sok esetben találkozunk olyan problémával, amikor egyidejűleg több, különböző valószínűségi változóval modellezhető hatással és eseménnyel kell a vizsgálatot, elemzést végezni. Ha ezek a valószínűségi változók függetlenek egymástól, akkor önállóan kezelhetjük és vizsgálhatjuk azokat, és ha ugyanazon objektumokra fejtik ki hatásaikat, akkor az együttes hatást a problémától függően lineáris vagy nemlineáris szuperpozíciókkal összegezhetjük. Azonban gyakran előfordul, hogy már maguk a valószínűségi változókkal jellemzett tényezők között is erős kölcsönhatások vannak, így azokat nem lehet külön-külön kezelni, hanem egyetlen, de többdimenziós valószínűségi változóval tudjuk csak a problémát megfogalmazni. A rendszertechnikában többek között ilyen problémák, amikor a rendszerekre és rendszerelemekre történő hatásokat vizsgáljuk: a bemeneti és kimeneti valószínűségi változók között – éppen a rendszerre jellemző – szoros kapcsolatok vannak. Ekkor – mind folytonos, mind diszkrét esetben – az egydimenziós valószínűségi változók általánosításával kaphatjuk meg azokat az eszközöket, amelyeket fel tudunk használni az ilyen valószínűségi problémák vizsgálatára és elemzésére.
8.9 definíció. Az elemi események Γ halmazán értelmezett , n-változós valós függvényt n-dimenziós valószínűségi változónak nevezzük, ha minden valós számhoz létezik egy valószinűséggel rendelkező esemény.
Ha az elemi eseménytér és a függvény értékkészlete megszámlálható halmazokat alkotnak, akkor diszkrét valószínűségi változóról beszélünk, míg kontinuum számosságú halmazok folytonos változót jelentenek, Ehhez a vonatkozó valószínűségi eloszlásfüggvényt is specifikálhatjuk az alábbi módon.
8.10 definíció. Az , n-változós valós függvényt az valószínűségi vektor-változó együttes eloszlásfüggvényének nevezzük.
Az folytonos valószínűségi vektor-változó együttes sűrűségfüggvényét az
|
|
(8.22) |
módon lehet megadni, és a normalizációs feltételt az alábbi formában írhatjuk fel:
|
|
(8.23) |
Az együttes eloszlásfüggvényekből az egyes változók un. perem-eloszlásfüggvényeit a többi változó kiintergálásával kaphatjuk meg. Így az n-dimenziós esetben egy (n-1)-dimenziós perem-eloszlásfüggvényt és perem-sűrűségfüggvényt az
|
|
(8.24) |
és
|
|
(8.25) |
integrálokkal képezzük. Természetesen a többi változó peremeloszlását hasonló módon nyerjük. Ugyakkor az egyes változók szekvenciális kiintegrálásával sorban kapjuk az (n-2)-, (n-3)-,… -dimenziós eloszlás- és sűrűségfüggvényeket egészen a komponensek egydimenziós függvényeinek előállításáig. Jegyezzük meg, hogy a perem-eloszlásfüggvényekből nem tudjuk az együttes eloszlásfüggvényeket előállítani, mivel a perem-eloszlásfüggvények nem tartalmazzák az ehhez szükséges információkat. Természetesen ugyanilyen állítás érvényes a perem-sűrűségfüggvényekre.
Az n-dimenziós eloszlásfüggvények meghatározásából és a (8.24) relációból következnek az alábbi fontos tulajdonságok is:
mivel az xl<∞ feltétel mindig fennáll, ezért ezt a változót el is lehet hagyni. Ezzel szemben az xl<-∞ reláció lehetetlen eseményt reprezentál, ezért
.
Ugyanakkor az xi<∞ feltétel érvényes mindegyik változóra, ezért az
egyenlőség lényegében a biztos eseményt reprezentálja.
8.5 példa. Vegyük az (X,Y) folytonos valószínűségi vektor-változót, amely legyen un. egyenletes eloszlású a 8-4. ábra által bemutatott ellipszisen, azaz az együttes sűrűségfüggvény legyen konstans értékű az
módon. Határozzuk meg az X és Y változók perem-eloszlásainak sűrűségfüggvényeit!
Az együttes sűrűségfüggvényből jól látható, hogy az X változó értéktartománya a (-a,a) intervallum, ezért kifejezve az y értékét az
egyenletből az értékekhez jutunk, ezért az X változó perem-
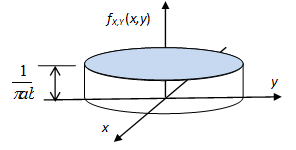
sűrűségfüggvényét az alábbi számításokkal kapjuk meg:
.
Hasonló meggondolással kaphatjuk meg az Y változó perem-sűrűségfüggvényét:
. □
8.6 példa. Tételezzük fel, hogy a kockadobást két azonos, de különböző színű – mondjuk piros és fehér – kocka egyidejű dobásával végezzük, amikor is a színek a véletlen kísérletek eredményeinek rendezett számpárosokként történő értékeléséhez kell. A két kocka egyidejű dobásával – tartva állandóan az „első szám piros kocka, második szám fehér kocka” sorrendben történő elszámolást – az (1;1), (1;2) … (6;5), (6,6) elemi eseményeket kaptuk. Egy ilyen kettős dobás eredményének a valószínűségét a
|
|
(8.26) |
módon számolhatjuk, mivel mind a 36 azonos valószínűségű esemény.
Ezzel lényegében egy diszkrét kétdimenziós valószínűségi vektor-változót határoztunk meg, melynek eloszlásfüggvényét az XPiros=X1 és XFehér=X2 általánosabb jelöléssel az
|
|
(8.27) |
formában írhatjuk fel.
Az egyes változók szerinti perem-sűrűségfüggvények:
és
. □
Több valószínűségi változó esetén természetszerűleg vetődik fel azok egymástól való függésének a vizsgálata is. Így az (X1,X2) folytonos két-dimenziós valószínűségi változó esetén a az X2 változónak az X1 változótól való feltételes valószínűségét az
|
|
(8.28) |
módon határozzuk meg, ahol az a két változó együttes sűrűségfüggvénye az pedig az abból előállítható perem-sűrűségfüggvény. Az (8.28) egyenletből rögtön következik a két valószínűségi változó függetlenségének a feltétele is. Ugyanis, ha az X2 változó független az X1 valószínűségi változótól, akkor , és így a (8.28) egyenletből a függetlenségre az
|
|
(8.29) |
feltételt kapjuk.
8.1.5. A többdimenziós valószínűségi vektor-változók jellemző paraméterei
A többdimenziós vektor-változók jellemző paramétereinek a tárgyalását is a két-dimenziós változókkal folytatjuk, mivel az összefüggések nyilván ezekben az esetekben a legegyszerűbbek, miközben a nagyobb dimenziókra történő általánosítások kézzelfoghatók.
8.11 definíció. A n-változós valós függvény várható értékének nevezzük folytonos valószínűségi változók esetében az
|
|
(8.30) |
integrált, míg diszkrét valószínűségi változókra az
|
|
(8.31) |
összeget.
Ha , akkor a
|
|
(8.32) |
számot az valószínűségi változók m1+m2+…+mn=m-ed rendű vegyes közönséges momentumának nevezzük.
A (8.32) n-dimenziós vegyes momentum-forma egyidejűleg ad meg kapcsolatokat n különböző valószínűségi változó között, amely így meglehetősen általános fogalom és a gyakorlatban kevésbé használatos. Viszont annál gyakrabban használjuk a (8.32) vegyes momentumok redukált változatait, amelyek többnyire két-két valószínűségi változó közötti, két-dimenziós momentumokkal kifejezett kapcsolatokat jelentik.
Ha speciális esetben az változók közül a két-változós függvényt vesszük, akkor, figyelembe véve az (8.30) összefüggést, ennek a függvénvnek a várható értékét az
|
|
(8.33) |
integrál fejezi ki. Ekkor a g függvény formájától függően az valószínűségi változók közötti kapcsolatok sok jellemzőjét és jellemző paraméterét tudjuk meghatározni mind az (8.31) folytonos, mind pedig az (8.31) diszkrét változók esetében:
-
: az Xk és Xl valószínűségi változók mk és ml, azaz mk+ml=m-ed rendű vegyes közönséges momentumai.
-
A függvény az Xk valószínűségi változó momentumát jelenti, melynek speciális esete az Xk változó várható értéke. Hasonlóan nyerjük a vegyes momentumok másik, az Xl valószínűségi változóra vonatkozó határeseteit.
-
: az Xk és Xl valószínűségi változók vegyes másodrendű közönséges momentumai.
-
: az Xk és Xl valószínűségi változók mk és ml, azaz mk+ml=m-ed rendű vegyes centrális momentumai. A vegyes centrális momentumok definíciójából következnek az alábbi egyenlőségek: a) ; b) ; c) .
-
: az Xk és Xl valószínűségi változók közötti kovariancia-együttható: ,. Rövidebb jelöléssel .
Független valószínűségi változók esetén , de rögtön hangsúlyozzuk ki, hogy a kovariancia-együttható zérus értékéből általában nem következik a valószínűségi változók függetlensége.
Az n-dimenziós valószínűségi vektor-változó bármelyik két változója között meghatározva a kovariancia-együtthatót a teljes kapcsolatrendszert a kovariancia-mátrixba tudjuk összefoglalni, melynek főátlójában sorban az egyes valószínűségi változók szórás-négyzetei (varianciái) jelennek meg az alábbi módon:
|
|
(.8.34) |
Mivel , így a kovariancia-mátrix szimmetrikus, de egyúttal pozitív szemidefinit, ami azt jelenti, hogy bármely vektor esetében teljesül a
|
|
(8.35) |
kvadratikus formára vonatkozó egyenlőtlenség. Ez természetesen az n=2 választás esetében is érvényes, amit a
formában írhatunk, és amelyből némi átalakítással – a és feltételek teljesülése esetén – a kovariancia-együtthatókra megkaphatjuk a
|
|
(8.36) |
Schvarz-egyenlőtlenséget. Erre támaszkodva definiáljuk a
|
|
(8.37) |
mennyiséget, melyet az Xk és Xl valószínűségi változók korreláció-együtthatójának nevezünk. A korreláció-együttható teljesíti a relációkat. Független valószínűségi változók esetén nyilván erre is teljesül a egyenlőség is.
Mind a kovariancia-, mind a korreláció-együttható fontos szerepet játszik a valószínűségi változók közötti összefüggések mérésében. A korreláció-együttható normált mennyiség, így ezzel tudjuk statisztikai jellegű kapcsolatoka jellemezni. A érték a két változó között közvetlen lineáris összefüggést jelent, míg – ahogy ezt már jeleztük – a zérus korrelációból a függetlenség csak akkor következik, ha egy kétdimenziós normális eloszlásről van szó. A negative értékek ellenkező irányú kapcsolatokat jelentenek.
8.12 definíció. Az n-dimenziós valószínűségi vektor-változó karakterisztikus függvényének nevezzük folytonos esetben a
|
|
(8.38) |
integrált, míg diszkrét esetben a
|
|
(8.39) |
összeget, ahol j az imaginárius egység.
Az n-dimenziós karakterisztikus függvény több, az egydimenzióshoz hasonló tualdonsággal rendelkezik:
a)
b)
c)
ahol a konjugált függvény jelenti.
Ha az n-dimenziós valószínűségi vektor-változó egyes komponensei függetlenek egymástól, akkor a (8.29) általánosításának megfelelően felírhatjuk az
|
|
(8.40) |
és
|
|
(8.41) |
feltételeket.
8.1.6. Gyakran használt diszkrét és folytonos eloszlások
A diszkrét és folytonos valószínűségi változók eloszlás- és sűrűségfüggvényei jól meghatározott tulajdonságokkal rendelkeznek, azonban általános függvény-formájukban meglehetősen nezézkesen kezelhetők. Azonban sok olyan konkrét, lényegében néhány paraméterrel meghatározott függvényt lehet használni, melyek rendelkeznek a valószínűségi eloszlás- és sűrűségfüggvények megadott tulajdonságaival, de paramétereik ismeretében könnyen előállíthatók és felhasználhatók a felmerülő gyakorlati problémák megoldásában. Ugyanakkor ezek a paraméterek kifejezhetők az eloszlások momentumaival is, ami sokat segíthet az eloszlás- és sűrűségfüggvények mérési adatokhoz való illesztésében.
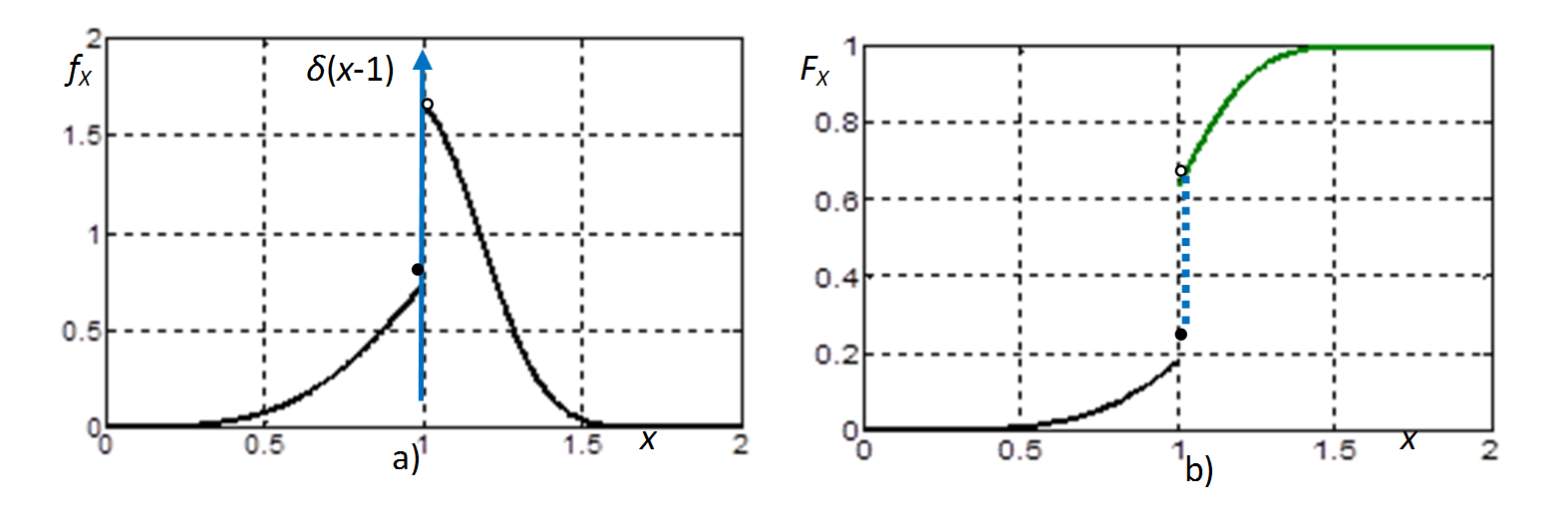
Elfajult eloszlás. Az elfajult (vagy unáris) eloszlású X valószínűségi változó egyetlen, x1 értékkel (elemi eseménnyel) rendelkezik a valószínűséggel. Ennek sűrűség-függvénye a disztribúciók (általánosított függvények) körében értelmezett δ(x-x0) Dirac-delta függvény, míg az eloszlásfüggvényt az 1(x-x0) Heaviside (egységugrás) függvény adja meg, ahogy ezt az 8-5. ábra illusztrálja.
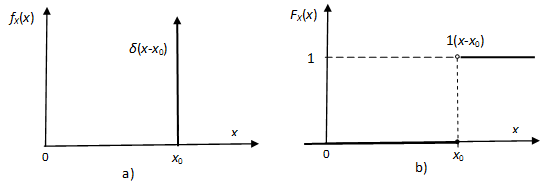
A karakterisztikus függvény a alakú, míg a momentumok:
.
Bináris eloszlás. A bináris X valószínűségi változó két, x1 és x2 értékkel (elemi eseménnyel) rendelkezik és , 0<p<1 valószínűségekkel.
A bináris valószínűségi változók fontos szerepet töltenek be a két stabilis állapottal jellemezhető multivibrátorok, mágneses vagy relés rendszerek, vagy akár a bináris számrendszert használó numerikus számítások statisztikai elemzéseiben. Itt a leggyakrabban az x1=0 és x2=1 jelöléseket használjuk.
Karakterisztikus függvény:
Momentumok:
.
Binomiális eloszlás. Vegyünk n független Xk, k=1,2…n, azonos bináris eloszlású valószínűségi változót a és , 0<p<1 valószínűségekkel. Jelölje Yn az Xn valószínűségi változók
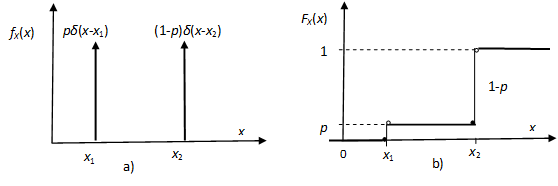
összegét. Mivel az Xk valószínűségi változók a 0 és 1 értékeket vehetik fel, így az Yn a 0 és n közötti egész értékeket vehet fel. Ekkor annak a valószínűsége, hogy az Yn az m, 0≤m≤n értéket veszi fel a
kifejezés adja meg, melynek magyarázata a következő: annak valószínűsége, hogy egy kísérletben éppen m egyes jön ki . Ez azonban különböző módon lehetséges, és mivel az összes konfiguráció egymástól független eseményt alkot, így az m db egyes esemény valószínűsége a két tényező szorzataként alakul ki.
Az eloszlás karakterisztikus függvénye a
Momentumok:
.
Poisson-eloszlás. A gyakorlatban nagyon sok probléma modellezéséhez használható fel a Poisson eloszlás, melynek meghatározása a következő: a λ>0 paraméterű, 0,1,2,…n,… értékeket felvevő valószínűségi eloszlást Poisson eloszlásnak nevezzük, ha a valószínűségi sűrűségfüggvény a
alakú.
Karakterisztikus függvény:
Momentumok:
.
Egyenletes eloszlás. Az X valószínűségi változó egyenletes eloszlású az (a,b) intervallumon, ha a sűrűségfüggvénye
.
Karakterisztikus függvény:
Momentumok:
.
Gauss-(normális) eloszlás. A másik, nagyon sok probléma modellezésére felhasználható valószínűségi eloszlás a normális, vagy Gauss-eloszlás. Az
valószínűségi sűrűségfüggvényű X valószínűségi változót normális eloszlásúnak nevezzük.
Könnyen ellenőrizhető, hogy a normális eloszlás sűrűségfüggvényében a μX az X valószínűségű változó várható értéke, míg σX a szórását jelenti.
Karakterisztikus függvény:
A normális eloszlás szimmetrikus eloszlás, melynek szimmetria centruma a μX várható érték. Érdekes tulajdonsága, hogy az összes páratlan rendű centrális momentuma zérus értékű, míg a páros rendű centrális momentumait a
képlettel lehet számolni.
A normális eloszlás egy fontos tulajdonsága, hogy a várható értékkel és varianciával jellemzett X1, X2,…Xn független normális eloszlású valószínűségi változók összege is normális eloszlású, melynek várható értékét és varianciáját a és összegek adják meg.
A normális eloszlás egy másik fontos tulajdonsága, hogy egy n-dimenziós (X1,X2,…Xn) normális eloszlású valószínűségi változó együttes sűrűségfüggvényét általános esetben is meg tudjuk adni analitikusan formában:
ahol az egyes komponensek vérható értékei, míg a mátrix az (8.34) kovariancia-mátrix inverze.
Gamma és exponenciális eloszlás. Az X valószínűségi változót gamma eloszlásúnak nevezzük, ha a sűrűségfüggvénye az
alakú. Ez két-paraméteres – a λ és p paraméterekkel rendelkező – eloszlás, melynek speciális esete az exponenciális eloszlás, melyet a p=1 paraméterérték esetén kapjuk az
Karakterisztikus függvény:
Momentumok:
.
Az exponenciális eloszlás karakerisztikes függvényét és momentumait is megkaphatjuk a p=1 behelyettesítéssel.
Weibull eloszlás. Ha az X valószínűségi változó exponenciális eloszlású, akkor az
valószínűségi változót Weibull eloszlásúnak nevezzük, melynek aűrűségfüggvénye
Momentumok:
.
8.1.7. Valószínűségi változók függvényei
A rendszertechnikában elsősorban a rendszerekre és rendszerelemekre történő hatásokat és az azokra reacióként kapott válaszokat vizsgáljuk. Ez a statikus vagy statikusként modellezhető rendszerek esetében a véletlen hatások modelljeit jelentő valószínűségi változókra kapott rendszerválaszokat jelenti. Mivel a statikus rendszerek gyakorlatilag időváltozó nélküli egy vagy többváltozós függvényekkel írhatók le, ezért a bemeneti és kimeneti valószínűségi változók között éppen ezek a – természetesen a rendszerre jellemző – függvénykapcsolatok adják meg. Most a valószínűségi változók egíüttes hatásait, valamint statikus jellegű a függvény-kapcsolataik tulajdonságait vizsgájuk meg.
Független valószínűségi változók összege. Két, egymástól független X és Y valószínűségi változó Z=X+Y összegének az eloszlását az alábbi módon határozhatjuk meg:
azaz az
|
|
(8.42) |
A (8.42) integrál a rendszertechnikában jól ismert függvény-konvolúció kifejezése, amely diszkrét valószínűségi változók esetén a
|
|
(8.43) |
kifejezéssel adott.
Független valószínűségi változók szorzata. Két egymástól független X és Y valószínűségi változó Z=XY szorzatának az eloszlását a feltételes valószínűségből közvetlenül kapjuk a változók függetlenségére vonatkozó
|
|
(8.44) |
feltételt, amit az
|
|
(8.45) |
formában is írhatunk.
Valószínűségi változók nemlineáris függvénykapcsolata.
Differenciálva ennek az egyenletnek jobbszélső elemét a esetben
összefüggéshez jutunk.
Azonban a 8-4. ábra alapján: ha , akkor
melyet differenciálva
azaz végeredményül az
|
|
(8.46) |
összefüggést kapjuk.
A (8.46) függvénykapcsolat az karakterisztikájú statikus rendszereknek az X valószínűségi változóval jellemzett véletlen hatásra történő reakcióját írja le, ami a rendszertechnikában a dinamika nélküli rendszerek vizsgálatában jól felhasználható összefüggés.
kifejezéssel adott, ahol U0 konstans érték, míg a Φ fázis valószínűségi változó.
Tételezzük fel, hogy a Φ valószínűségi változó egyenletes eloszlású, melynek sűrűségfüggvénye a korábban (8.3 példa) tárgyalt módon
.
Határozzuk meg az U valószínűségi változó sűrűséggvényét!
A feszültségfüggvény inverze
amely a (0,2π) intervallumban két-értékű függvéy. Írjuk ezt fel két tényleges függvény összegeként, azaz legyen a
és
össege, melynek így első differenciálhányadosai
Ekkor az U feszültség valószínűségi sűrűségfüggvénye az (8.46) alapján
.□
Többdimenziós valószínűségi változó függvényei. Legyen az n-dimenziós valószínűségi vektor-változó vegyes-sűrűségfüggvénye , és tekintsük e változók differenciálható függvényeit. Ha most az
|
|
(8.47) |
leképezésekkel meghatározott n-dimenziós valószínűségi vektor-változó sűrűségfüggvényét keressük, akkor ezt – az (8.46) összefüggés általánosításával – az
|
|
(8.48) |
összefüggés adja meg, ahol J az (8.47) leképezések Jacobi-mátrixa.
alakú. Határozzuk meg az R és Φ valószínűségi változók együttes sűrűségfüggvényét, ha a változók között a derékszögű koordináta-polárkoordináta
transzformáció teremt kapcsolatot.
Az alkalmazott transzformáció Jacobi mátrixa
így az R és Φ valószínűségi változók együttes sűrűségfüggvényét az
alakban kapjuk. Ez azt mutatja, hogy R és Φ valószínűségi változók egymástól függetlenek:
.
8.1.8. Valószínűségi változók entrópiája és információ-tartalma
A véletlen kísérletek lényege a bizonytalanság, melyek eredményeit esetenként meg lehet „saccolni” a helyzetre vonatkozó bizonyos tapasztalatok bírtokában, de a műszaki rendszerek esetében szükséges az ilyen bizonytalanságok mennyiségi értékelése is. E bizonytalanság kitünően használható mértéke az entrópia, amely a valószínűségi változók egyik legfontosabb leképezése, és a véletlen kísérletek eredményeinek bizonytalanságát (véletlenségét) a priori jellemzi.
8.13 definíció. Ha az X diszkrét valószínűségi változó a valószínűségekkel, akkor a
|
|
(8.49) |
függvényt az X valószínűségi változó entrópiájának nevezzük.
Jegyezzük meg, hogy a (8.49) függvényben tetszőleges a>1 alapú logaritmust használhatunk, mivel ez csak a mértékegységet befolyásolja. A leggyakrabban használt 2-es alap azért célszerű, mivel ekkor a két azonos valószínűségű változó entrópiája éppen
=1 bit értékű.
Könnyen belátható, hogy , és zérus csak abban az esetben lehet, ha egy esemény 1 valószínűségű, míg az összes többi valószínűsége zérus értékű. Ez éppen az az eset, amikor nincs semmi bizonytalanság abban, hogy milyen eredménye lesz a kísérletnek. Azonban az a kérdés is rögtön felvetődik, hogy az (8.49) entrópia mikor éri el a maximális értéket? A válasz egyértelmű: a maximális értéket az a valószínűségi változó adja, melyben az összes valószínűség azonos: .
Két, X1 és X2 diszkrét valószínűségi változó együttes entrópiája a
|
|
(8.50) |
kifejezéssel adott, amiből a feltételes valószínűség képletét felhasználva az X2 valószínűségi változónak az feltétel melletti entrópiáját kapjuk meg
|
|
(8.51) |
Innen az X2 valószínűségi változónak adott X1 feltétel melletti átlagos feltételes entrópiáját a
|
|
(8.52) |
formában írhatjuk. Összevetve az előbbi kifejezéseket azt látjuk, hogy
|
|
(8.53) |
amely természetesen a változók felcserélésével is igaz marad. Ugyanakkor, ha a szóban forgó változók függetlenek egymástól, akkor
|
|
(8.54) |
azaz az együttes entrópia a két entrópia összegeként adódik. Ha viszont a átlagos feltételes entrópiát hasonlítjuk össze az adott változó entrópiájával, a
|
|
(8.55) |
egyenlőtlenséghez jutunk. És mivel egyik változó sem kitüntetett, ezért itt is felcserélhetjük a változókat.
Vegyük most az X és Y diszkrét változók között a leképezést. Ekkor a két változó entrópiája között a
|
|
(8.56) |
egyenlőtlenség áll fenn. Ugyanis, ha a gk,l kölcsönösen egyértelmű leképezés, akkor, de csak akkor az egyenlőség érvényes. Viszont ha L<K, akkor a leképezés az entrópia csökkenésével jár együtt, mivel a teljes bizonyosság ekkor kevesebb elemen kerül elosztásra.
A kétdimenziós valószínűségi változóra vonatkozó (8.55) összefüggés természetesen hasonló módon általánosítható n-dimenziós változókra is, és ezt az általánosítást az ezekből következő többi összefüggésre is átvihetjük.
Így a (8.56) összefüggésből az egyenlőtlenségből eredő eltérést kiegészítve az
|
|
(8.57) |
egyenlőséghez jutunk, melyet az X1 változónak az X2 változóra vonatkozó információ menynyiségének nevezünk. Ezt az összefüggést úgy interpretálhatjuk, hogy az X1 valószínűségi változóval jellemzett kísérlet végrehajtása által kapott, az X2 változóra vonatkozó információ a (8.57) kifejezéssel csökkenti az X2 valószínűségi változó által tartalmazott bizonytalanságot. Ennek az összefüggésnek a tetszőleges n-dimenziós valószínűségi változókra való általánosítása alkotja az információs csatornák jellemzésének az alapját. Az előző összefüggésekből az is látható, hogy , azaz az információ pozítív mennyiség kivéve, ha a két változó független egymástól.
8.14 definíció. Ha az X folytonos valószínűségi változó az fX(x) valószínűségi sűrűségfügg-
vénnyel, akkor a
|
|
(8.58) |
függvényt a valószínűségi változó entrópiájának nevezzük.
A folytonos változókra a diszkrét változók összefüggéseihez hasonló összefüggéseket lehet értelmezni, bár meg kell jegyezni, hogy a folytonos változók entrópiája negatív értékeket is felvehet, ahogy ezt a Gauss-eloszlás esetében könnyen ellenőrizhetjük.
8.2. Sztochasztikus folyamatok
8.2.1. A sztochasztikus folyamatok fogalma
A valószínűségi jelenségeknek valószínűségi változókkal történő tárgyalásában minden hatást és eseményt időbeli megvalósításától függetlenűl vizsgáltunk és modelleztünk, még akkor is, ha azok valamilyen szekvenciában következtek be. Így a binomiális eloszlás ismertetésében nem vizsgáltuk, hogy azok egyidejűleg, egymástól független, bináris véletlen kísérletek révén alakulnak-e ki, vagy pedig időben egymást követően, egyazon véletlen kísérletet ismételjük-e meg n-szer. Ez az eljárás a gondolatkísérletek megfogalmazásán és alkalmazásán alapult, ami a statikus vagy statikusként modellezhető rendszerek esetében a véletlen hatások modelljeit jelentő valószínűségi változókra kapott rendszerválaszok vizsgálatában is használható volt.
Azonban a műszaki rendszerek jelentős része nem modellezhető statikus rendszerekként, mivel többnyire nem elhanyagolható dinamikával rendelkeznek, ezért sok esetben csak az időben, időbeli folyamatok keretében lehet azokat vizsgálni és értékelni. Ez természetesen a véletlen jelenségek esetében is érvényes, ezért a továbbiakban a valószínűségi jelenségek időbeli folyamatait és azoknak a rendszerekre való hatásait elemezzük.
8.15 definíció. Sztochasztikus folyamatnak nevezzük az x(ξ,γ) valós, kétváltozós függvényt, melyben ξ lehet időváltozó, térbeli változó vagy jelentheti azok együttesét, míg a γ valamely valószínűségi mező elemi eseményeit reprezentálja. Egy konkrét γ0 esemény esetén x(ξ,γ0) az x(ξ,γ) sztochasztikus folyamat egy realizációját jelenti.
Az ξ változó jellegétől függően az x(ξ,γ) sztochasztikus folyamat különböző fizikai jelenségek modelljeiként értelmezhető. Így a fizikából jól ismert Brown-mozgás leírásában a ξ változó időben változó térbeli koordinátát jelent, míg az elektroncsövekben és félvezető eszközökben kialakuló sörétzajnak, bár nyilván ennek is fontosak a térbeli eloszlásai, az eszközöket koncentrált paraméterű elemekként modellezve elsősorban időbeli változásait vizsgáljuk. A továbbiakban a véletlen folyamatok t időbeli változásaival foglalkozunk, mivel a rendszertechnikában elsősorban az időfüggvényekkel modellezett jelek hatásait vizsgáljuk, amikor is a folyamatok jövőbeli értékei függhetnek a múltbeli értékektől és más véletlen tényezőktől.
Az x(t,γ) sztochasztikus folyamatot – a valószínűségi változókhoz hasonlóan – X(t)-vel je-
löljük, ami azt jelzi, hogy tetszőleges, adott t’ időpontban az X(t’) mennyiség valószínűségi változó. Ha a t argumentum adott korlátos vagy nem-korlátos intervallumokban tetszőleges értékeket vehet fel, akkor folytonos idejű folyamatról beszélünk, ha azonban az értelmezési tartomány bármely korlátos intervallumában csak véges számú időpontban vesz fel értékeket, akkor diszkrét idejű sztochasztikus folyamatról van szó.
Sztochasztikus folyamatok együttesét n-dimenziós sztochasztikus folyamatnak nevezzük, míg az párost komplex változós folyamatként értelmezzük.
Vegyünk egy X(t) időben folytonos sztochasztikus folyamatot, melynek értékeit valamely adott valószínűségi mező határozza meg. Ha most n független véletlen kísérletet hajtunk végre, akkor azok eredményeként az X(t) sztochasztikus folyamat
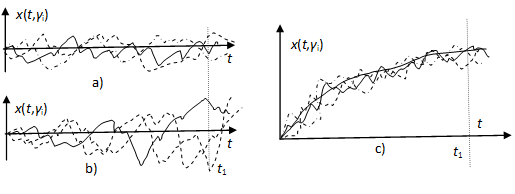
x(t,γ1), x(t,γ2), x(t,γ3), … x(t,γn)
egyes realizációit generáljuk, ahogy ezt a 8. ábra illusztrálja három különböző folyamat 3-3 realizációját mutatva. A 8-8. ábra/a realizációi azonos jellegű fluktuációkat mutatnak, a 8-8. ábra/b realizációi azonos szinten idővel növekvő amplitudójú kilengéseket mutatnak, míg a 8-8. ábra/c által bemutatott realizációk egy idővel növekvő szint körül állandósult amplitudóval fluktuálnak.
Mivel az X(t) folyamat tetszőleges t1 időpontban valószínűségi változó, ezért realizációinak a t1 időpontban megfigyelt értékei meghatározzák az X(t1) valószínűségi változó sűrűségfüggvénnyel jellemzett statisztikai tulajdonságait. Általában véve azonban, ez még kevés magának a sztochasztikus folyamatnak a statisztikai jellemzéséhez. Több információt nyerünk magáról a folyamatról, ha egy másik időpontban is kiértékeljük az X(t2) valószínűségi változót képezve az kétdimenziós vegyes sűrűség-függvényt. Folytatva ezt a kiértékelést az előzőektől különböző t3, …tN időpontokban az N-dimenziós valószínűségi változóhoz jutunk, melynek az vegyes sűrűségfüggvényét az X(t) sztochasztikus folyamat N-ed rendű sűrűségfüggvényének nevezzük. Jegyezzük meg, hogy ha az változók N-dimenziós normális eloszlásúak, akkor a sztochasztikus folyamatot normális vagy Gauss-folyamatnak nevezzük.
8.2.2. Momentumok és korreláció függvények
Egy sztochasztikus folyamatot akkor tekinthetünk statisztikusan meghatározottnak, ha a folyamat N-ed rendű sűrűségfüggvénye tetszőleges t1,t2,…tN időpontokra ismert. Ez a meghatározási általános esetben azonban nagyon nehéz alkalmazni, de többnyire nem is szükséges, mivel sok esetben, a valószínűségi változókhoz hasonlóan, kielégítő lehet a jellemző paraméterekkel, így a különböző a momentum-függvényekkel történő jellemzés is.
Az X(t) sztochasztikus folyamat átlagos értékének nevezzük a
|
|
(8.59) |
elsőrendű momentumfüggvényt. Ahogy ez látható, az átlagos érték változhat az időben. Ilyen esetet illusztrál a 8-8. ábra/c, amikor is a bemutatott realizációk az időben növekvő átlagérték körül ingadoznak, míg a 8-8. ábra/a és 8-8. ábra/b esetén az átlagértékek a konstans értékek.
Jegyezzük meg, hogy a továbbiakban, ha ez nem vezet félreértésre, az egyszerűbb képletek kedvéért az x(tk)=xk jelöléseket használjuk.
Sztochasztikus folyamatok esetében két, különféle közönséges másodrendű momentum-függvényt definiálunk: a
|
|
(8.60) |
másodrendű közönséges momentum-függvényt és a
|
|
(8.61) |
vegyes momentum-függvényt, ahol a t1 és t2 időpontokhoz tartozó másodrendű vegyes sűrűségfüggvény. A (8.61) típusú másodrendű momentum-függvény lényegében ugyanazon folyamat két különböző időpontban megjelenő valószínűségi változói közötti vegyes momentum.
A közönséges momentumok mellett a másodrendű centrális momentumok is fontos szerepet játszanak a sztochasztikus folyamatok jellemzésében: a
|
|
(8.62) |
a folyamat variancia-függvénye, míg a
|
|
(8.63) |
kétváltozós függvényt a folyamat kovariancia-függvényének nevezzük.
A kovariancia-függvények alapvető tulajdonságai:
-
-
, azaz szimmetrikus függvény
-
8.16 definíció. Az n-dimenziós sztochasztikus folyamat kovarianciamátrix-függvényének nevezzük a
|
|
(8.64) |
elemekből álló négyzetes mátrixot. A főátlóban lévő elemeket auto- kovariancia-, míg függvényeket keresztkovariancia-függvényeknek nevezzük.
A továbbiakban az autokovariancia-függvényeket – ha ez nem okoz félreértést – egyszerűen kovariancia-függvényeknek fogjuk nevezni.
8.2.3. Stacionárius folyamatok
Az előző szakaszban már említettük, hogy a sztochasztikus folyamatoknak az N-ed rendű sűrűségfüggvényekkel történő meghatározása általános esetben nagyon nehéz. Azonban a folyamatoknak vannak olyan speciális osztályai, melyek tulajdonságai lehetővé teszik a könnyebb meghatározást és ez által az alkalmazási lehetőségeik is jelentősen megnőnek.
8.17 definíció. Az X(t) sztochasztikus folyamatot stacionáriusnak nevezzük, ha tetszőleges τ esetén az valószínűségi változók valószínűségi eloszlása ugyanaz, mint az változók eloszlása.
Ez más szavakkal azt jelenti, hogy a stacionárius sztochasztikus folyamat tulajdonságai nem változnak az időtranszláció hatására, ami az
|
|
(8.65) |
feltétel teljesülését is jelenti.
A (8.65) összefüggés felhasználásával könnyen megmutatható, hogy egy stacionárius folyamat átlagértéke és varianciája időben konstans értékű. A (8.63) egyenlet alapján az is könnyen kimutatható, hogy ha τ=-t1 akkor
|
|
(8.66) |
azaz egy stacionárius folyamat kovariancia-függvénye csak az időpontok különbségétől, azaz az időtranszláció értékétől függ. A kovariancis-függvények általános tulajdonságaiból azt kapjuk, hogy stacionárius folyamat esetén , azaz a közvetlenül egymás közelében lévő időpontok értékei közötti korrelációs kapcsolatok a legerősebbek. Ekkor az egyenlőséget felhasználva értelmezhetjük a
|
|
(8.67) |
normált kovariancia-függvényt, amit a stacionárius folyamatok korreláció-függvényének nevezünk. Hasonlóan a valószínűségi változók analóg módon meghatározott jellemzőihez, a kovariancia- és korreláció-függvények a szochasztikus folyamatok esetében is fontos szerepet játszanak az egyes időpontokban megjelenő értékek közötti összefüggések mérésében.
Azonban a sztochasztikus folyamatok egy fontos osztálya, amikor is a t1 és t2 időpontokban felvett értékei függetlenek egymástól még a , ε nagyon kis pozitív szám, esetben is. Az ilyen folyamatok modelljét a független növekményű, azaz teljesen független folyamatok alkotják, melyek közül a rendszertechnikában fontos szerepet játszó fehérzajt emeljük ki.
8.18 definíció. Az X(t) Gauss-féle stacionárius sztochasztikus folyamatot fehérzajnak nevezzük, ha
-
,
-
ahol az Sf konstans a fehérzaj intenzitása.
A fehérzaj tehát zérus átlagértékű folyamat, amelyben az infinitezimális távolságban megjelenő értékek sem korreláltak, és mivel Gauss-folyamatról van, így egymástól függetlenek is. Ez a folyamat a Dirac-delta funkcionál miatt – az általánosított függvények osztályához hasonlóan – az általánosított sztochasztikus folyamatok körében kerül pontos meghatározásra. Egyszerűbben: egy normális stacionárius folyamatból, melynek korreláció-függvénye alakú, az α→ω határátmenettel lehet értelmezni.
Ahhoz, hogy a sztochasztikus folyamatokat alkalmazni tudjuk a fizikai jelenségek és műszaki rendszerek modellezésében, természetesen szükségesek módszerek, melyek lehetővé teszik a folyamatok olyan valószínűségi jellemzőinek megfigyelések és mérések alapján történő meghatározását, mint az átlegértékek, korreláció-függvények, valószínűségi eloszlások. Ebben az irányban jelentős lépés a stacionaritás feltétele, amely azt mutatja, hogy egy stacionárius folyamat átlagértéke, warianciája, általában a momentumai konstans értékűek, míg a kovariancia- és korreláció-függvények, azaz a momentum-függvények csak a két megfigyelési időpont távolságától függnek. Azonban még ebben az esetben is: az momentumok megbízható meghatározásához elég nagyszámú kísérletből származó x(t,γi) realizáció ugyanabban a t1 időpontban történő méréséből nyert statisztikai minta szükséges. Ezt a sokaság szerinti meghatározásnak nevezzük. Azonban egyes stacionárius folyamatok ergodicitási tulajdonsága jelentősen megkönnyíti a sztochasztikus folyamatokkal történő modellezési munkát.
8.19 definíció. Ha az X(t) stacionárius sztochasztikus folyamat kovariancia-függvényére érvényes az
|
|
(8.68) |
akkor a folyamat majdnem mindegyik realizációjára érvényes az
|
|
(8.69) |
egyenlőség.
Itt a „majdnem mindegyik” azt jelenti, hogy a realizációk (8.69) időintegrálja „1 valószínűséggel” megadja a folyamat átlagos értékét, amit valójában úgy értelmezhetünk, hogy tetszőleges realizáció (8.69) integráljával számolhatjuk ki a folyamat átlagértékét.
Figyelembe véve, hogy ha X(t) stacionárius sztochasztikus folyamat, akkor az X(t)∙X(t+τ) szorzat szintén stacionárius sztochasztikus folyamat, amelyre alkalmazhatjuk a (8.68) feltételt. Ez azt jelenti, hogy az X(t)∙X(t+τ) stacionárius folyamatra vonatkoztatva a (8.68) feltétel a
|
|
(8.70) |
alakot ölti, és ebben az esetben a (8.69) integrálkifejezés megfelelője az
|
|
(8.71) |
egyenlőség, amely a kovariancia- és korreláció-függvények időbeli realizációkkal történő számítási lehetőségét szolgáltatja.
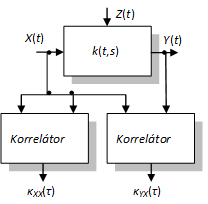
A (8.71) összefüggés egyszerű sémát ad a korreláció függvény számítására, melyet korrelátor blokkdiagramjaként a 8-9. ábra mutat be.

sztochasztikus folyamat korreláció-függvényét, melynek φ fázisa egyenletes eloszlású az
.
A folyamat átlagos értéke:
ahonnan , azaz a folyamat átlagértéke zérus értékű. Hasonló módon felhasználva a trigonometrikus függvények azonosságait a második momentumra az
eredményt kapjuk. Végül a kovariancia-függvényt a
számítások adják, amiből a miatt rögtön következik a korreláció-függvényre a
Azonban – nyilván a periodicitás következtében – a kovariancia-függvényre ezt az eredményt megkapjuk az időátlag képzésével is:
amely megegyezik az előzővel. □
Jegyezzük meg, hogy bár a függvény nem elégíti ki a (8.70) feltételt, a kovariancia-függvény mégis számolható az időátlagból is. Ennek az a magyarázata, hogy a (8.70) feltétel csak elégséges feltétel, így a szükségességről nem mond semmit.
Az adott feltételek mellett a folyamat sűrűségfüggvénye nem függ az időtől, azaz az
formában írható, ahol az effektív feszültség értéke . A valószínűségek alapján a kritikus feszültség túllépésének a valószínűségét a
módon számolhatjuk.
8.2.4. Harmonikus analízis és teljesítménysűrűség spektrum
A frekvenciafüggvényeket és frekvenciatartományt a valószínűségi eloszlás- és sűrűségfügg-vények Fourier-transzformációja, azaz a karakterisztikus függvények révén a valószínűségi változók vizsgálatában a valós tartománnyal egyenértékűen lehet felhasználni. Sőt, a frekvenciatartománybeli vizsgálat sok esetben egyszerűbb műveletekkel történik. Így a momentumokat a sűrűségfüggvények esetében integrálással kell számolnunk, míg a karakterisztikus függvények ismeretében azokat differenciálással és a zérus érték behelyettesítésével nyerhetjük.
A stacionárius sztochasztikus folyamatok esetében – a determinisztikus időfüggvények transzfomációja révén kapott időtartomány-frekvenciatartomány párosításnak megfelelően – a frekvenciatartománybeli vizsgálat az alábbi meghatározáson alapul:
8.20 definíció. Ha az X(t) stacionárius sztochasztikus folyamat folytonos kovariancia-függvénnyel rendelkezik, akkor a kovariancia-függvény előállítható a
|
|
(8.72) |
formában, amely transzformációnak az
|
|
(8.73) |
inverze is létezik.
Ez a definíció a sztochasztikus folyamatok egy nagyon fontos tételén, a Wiener-Hincsin tételen alapul, ahol az függvényt a folyamat spektrális sűrűségfüggvényének, sok esetben teljesítménysűrűség-függvényének nevezzük. A (8.72) és (8.73) összefüggések a kovariancia-függvény és a spektrális sűrűségfüggvény közötti kölcsönösen egyértelmű Fourier-transzformációját jelentik.
Jegyezzük meg, hogy a 8.20 definíció feltételei mellett az X(t) folyamat előállítható az
|
|
(8.74) |
formában, ahol a valós argumentumú folyamat, és amellyel az SXX spektrális sűrűségfüggvény szoros kapcsolatban van.
A spektrális sűrűségfüggvény alapvető tulajdonságai:
-
,
-
-
Mivel mind a kovariancia-függvény, mind a spektrális sűrűségfüggvény páros függvények, ezért a (8.72) és (8.73) transzformációk a
|
|
(8.75) |
és
|
|
(8.76) |
formában is írhatók.
A (8.71) tulajdonság a spektrális sűrűségfüggyvénynek a folyamat energetikai tulajdonságaival való kapcsolatát mutatja meg, mivel ergodikus folyamatok esetén (8.75) alapján valamely realizációra írhatjuk, hogy
|
|
(.8.77) |
azaz a folyamat időben átlagos teljesítményét szolgáltatja. A spektrális sűrűségfüggvényt ezért is nevezzük teljesítménysűrűség-függvénynek. Így, ha x(t) egy egységnyi ellenálláson átáramló villamos áramot jelöl, akkor (8.77) az ellenálláson kiváló átlagos teljesítményt adja meg. Összevetve a (8.71) és (8.77) kifejezéseket azt mondhatjuk, hogy a stochasztikus folyamat átlagos teljesítménye a harmonikus összetevők – a spektrum egyes összetevői – által reprezentált teljesítmények összegével egyenlő.
Ha most a speciális tulajdonságokkal rendelkező fehérzajt nézzük, akkor a kifejezést behelyettesítve a (8.72) kifejezésbe az
|
|
(8.78) |
eredményt kapjuk, ami azt jelenti, hogy a fehérzaj spektrális sűrűségfüggvénye a teljes (-∞,∞) intervallimban konstans értékű, és figyelembe véve a kovariancia-függvény szimmetria tulajdonságát az
|
|
(8.79) |
értékű. Így a fehérzaj átlagos teljesítménye végtelen nagy, tehát ez is azt jelzi, hogy fizikailag nem relizálható, de a modellezésben nagyon jól használható. Alkalmazása a rendszerelemzésben és tervezésben azzal (is) indokolható, hogy a fehérzaj a legnehezebben eliminálható zaj, azaz alkalmazása olyan zavart rendszert jelent, amelynél bármely valós zavaroknak kitett rendszer csak jobb lehet. Ráadásul a fehérzaj speciális tulajdonságai viszonylag könnyű számításokat jelent.
A modellezésben gyakran használjuk az
|
|
(8.80) |
korlátos spektrumú fehérzajt, melynek kovariancia-függvénye
|
|
(8.81) |
míg átlagos teljesítménye .
Az ergodikus stacionárius folyamatok időbeli realizációkat tartalmazó kifejezései minden-
hol a T→∞ határátmenettel adják meg az elméleti értékeket. Azonban bármelyik mérés csak véges időpontig tarthat, azért a kovariancia-függvényt a gyakorlatban a
|
|
(8.82) |
összefüggés segítségével kell megbecsülni. Természetesen a mérés idejét úgy kell megválasztani, hogy a (8.82) közelítés elégséges kis hibával teljesüljön.
Ergodikus folyamatok esetében a kovariancia-függvényt (8.82) alapján direkt úton becsülhetjük meg az időbeli realizációkból. Ugyanakkor figyelembe véve, hogy a (-T/2, T/2) véges intervallumon bármely realizáció Fourier-sorba fejthető, és ezt általánosítva azt mondhatjuk, hogy ezzel a (-T/2, T/2) intervallumon az X(t) sztochasztikus folyamat
|
|
(8.83) |
sorfejtéséhez jutunk, ahol a harmonikusok
|
|
(.8.84) |
komplex amplitudói véletlen változók. Ha az X(t) sztochasztikus folyamat átlagos értéke zérus, akkor mindegyik Uk zérus várható értékű valószínűségi változó. Figyelembe véve, hogy az amplitudók komplex mennyiségek, és felhasználva a (8.84) összefüggést, a k-adik amplitudóval az
|
|
(8.85) |
kifejezéshez jutunk. Mivel a T→∞ határértékkel a (8.85) jobboldala az SXX(ω)-hez tart, így a baloldal a kovariancia-függvény egy jó közelítését adja.
Határozzuk meg a folyamat spektrális sűrűségfüggvényét és idöben átlagos teljesítményét!
Alkalmazzuk a (8.73) definiáló egyenletet:
.
Jegyezzük meg, hogy az a→ω határátmenet a σ2 értékű konstans spektrális sűrűségfügg-vényhez vezet, amely természetesen a fehérzaj spektrális sűrűségfüggvényével azonos.
A folyamat átlagos teljesítménye pedig:
.
8.2.5. Folytonos idejű lineáris dinamikus rendszerek
Egy folytonos idejű lineáris dinamikus rendszer súlyfüggvénnyel képzett modelljét az X(s) sztochasztikus folyamat hatása alatt, idővariáns esetben az
|
|
(8.86) |
egyenlet írja le, ahol az X(s) folyamat realizációja, míg a súlyfüggvényre érvényes a
|
|
(8.87) |
feltétel. Ez a (8.87) feltétel a lineáris dinamikus rendszerek fizikai realizálhatóságát biztosítja, mivel azok nem lehetnek anticipatívek, azaz nem lehetnek jövőbelátók. Ha a rendszer idő-invariáns, melyet gyakran szintén stacionáriusnak nevezünk, akkor (8.86) az
|
|
(8.88) |
formába megy át. Az idővariáns és időinvariáns dinamikus rendszereket a 8-10. ábra mutatja be. Itt – az analógiák miatt – mind a folytonos idejű, mind a későbbiekben tárgyalandó diszkrét idejű rendszereket is illusztráltuk.
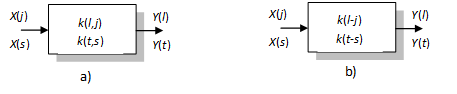
Szimbolikusan felírva a (8.86) egyenletet az X(t) bemeneti és Y(t) kimeneti sztochasztikus folyamatokra
|
|
(8.89) |
és képezve mindkét oldal várható értékét, az átlagértékekre a
|
|
(8.90) |
egyenlethez jutunk. Ha az X(t) stacionárius sztochasztikus folyamat, akkor =konstans, míg a kimeneti folyamat átlagértékét a
|
|
(8.91) |
összefüggés határozza meg, azaz a kimeneti folyamat átlagos értéke változik az időben: a kimenet nem stacionárius folyamat. Ha viszont maga a rendszer a (8.88) konvolúcióval van leírva, azaz a rendszer is stacionárius, akkor kimeneti átlagérték is konstans a
|
|
(.8.92) |
összefüggés szerint.
Felírva a (8.90) egyenletet a t’≠t időpontra is, összeszorozva az egyenletek mindkét oldalát és képezve a két oldal várható értékét az eredményt a
|
|
(8.93) |
egyenlet adja. Ismét feltételezve mind a bemeneti folyamat, mind a rendszer stacionárius mivoltát, a
|
|
(8.94) |
egyenletet kapjuk. Alkalmazva az integrálban a t-s=s1 és t’-s’=s2 változó-helyettesítéseket, a
|
|
(8.95) |
egyenletet adja. Mivel a (8.95) jobboldala csak a t-t’=τ különbségtől függ, ez a
|
|
(8.96) |
összefüggést eredményezi, azaz a kimeneti folyamat kovariancia-függvénye is csak a megfigyelési időpontok távolságától függ. Ez azt jelenti, hogy a kimeneti Y(t) folyamat szintén stacionárius.
Képezve a (8.96) egyenlet mindkét oldalának Fourier-transzformációját, a spektrális sűrűségfüggvényekre egyszerű számításokkal kapjuk az
|
|
(8.97) |
összefüggést, ahol a a konjugáltja, és amelyet az
|
|
(8.98) |
formában írhatunk. Itt a a lineáris rendszer frekvenciafüggvénye, amely lényegében a k(t-s) súlyfüggvény Fourier-transzformáltja. Ezt felhasználva a kimeneti folyamat teljesítményét a bemenet spektrális sűrűségfüggvényéből közevetlenül számolhatjuk:
|
|
(8.99) |
A (8.98) összefüggés egyszerűbb számítási lehetőséget jelent mint az időtartományban értelmezett kettős integral-kapcsolat, bár a jelenlegi numerikus számítási lehetőségek mellett ez már nem igazán fontos. Ugyanakkor a (8.98) és (8.99) egyenletek szemléletesebb képet adnak a jelenségekről, és a frekvenciamódszerek alkalmazásában sok esetben hasznos közelítő vázlatok segítségével könnyen értelmezhetők.
Ismét, az előzőekben bemutatott levezetések alapján, időinvariáns rendszerekben a bemeneti folyamatok kovariancia- (autokovariancia-) függvényeiből a kimenetek-bemenetek keresztkovariancia-függvényeit számolhatjuk a
|
|
(8.100) |
összefüggés segítségével. Ennek megfelelője a spektrális sűrűségüggvények körében az
|
|
(8.101) |
formában írható. Ezeket az összefüggéseket jól fel lehet használni a rendszerek átviteli tulajdoságainak a vizsgálatában, amihez kitünő eszköz a 8-11. ábra mérési elrendezése.
A lineáris dinamikus rendszerek átviteli tulajdonságainak vizsgálata azt mutatta, hogy a bemeneti és kimeneti kovariancia-függvények között, ahogy ezt a (8.93) és (8.96) egyenletek mutatják, mind az idővariáns, mind pedig az időinvariáns rendszerek esetében találunk direkt összefüggéseket. Nemlineáris rendszerekben ez már egyáltalán nincs így, még az olyan egyszerű esetben sem, amit az (8.46) nemlineáris leképezéssel reprezentálható statikus rendszer képvisel.
Itt a karakterisztikával jellemzett statikus rendszer az X(t) sztochasztikus folyamat realizációjának hatására pillanatszerűen reagál az
|
|
(8.102) |
módon, és így az Y(t) sztochasztikus reakció tulajdonságait tetszőleges időpontban az (8.102) összefüggés írja le.
Ha az X(t) folyamat stacionárius, akkor a kimenet átlagfüggvénye is konstans a
|
|
(8.103) |
összefüggésnek megfelelően. Ugyanakkor a kimenet kovariancia-függvényét – a nem-linearitás miatt – nem lehet a bemenet kovariancia-függvényével összekapcsolni, mivel általában csak a
|
|
(8.104) |
összefüggést tudjuk felírni, ahol a bemeneti folyamat másodrendű együttes sűrűségfüggvénye. Így tehát nemlineáris leképezések esetén általában nem találunk egyértelmű kapcsolatokat a bemeneti és kimeneti folyamatok kovariancia-függvényei között. Ha azonban a bemenet egyúttal Gauss-folyamat is, akkor a kovariancia-függvény ismeretében kifejezhető a másodrendű együttes sűrűségfüggvény is, így ekkor megadható a két kovariancia-függvény közötti direkt összefüggés is.
A 8-12. ábra által ábrázolt RC-szűrő frekvenciafüggvénye a T=RC időállandóval a
képlettel adott, ahonnan az abszolutérték négyzete
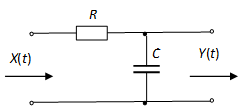
Aluláteresztő RC-szűrő (8.11 példa)
.
Felhasználva a (8.98) összefüggést a kimenet spektrális sürüségfüggvénye a
alakban írható. Ebből inverz Fourier-transzformációval kapjuk meg a kovariancia-függvényt
.
Ezt az integrált egy integráltáblázatból tudjuk meghatározni. Az eredmény :
így ebből a szűrő kimenet teljesítménye:
.
8.2.6. Diszkrét idejű sztochasztikus folyamatok és lineáris rendszerek
A műszaki gyakorlatban gyakran találkozunk időben diszkrét sztochasztikus folyamatokkal is. Ezek származhatnak időben folytonos folyamatok mintavételezéséből, véletlen jelenségek ismétlődő megfigyeléseiből, de vannak események és folyamatok, melyeknek inherens tulajdonsága az időben diszkrét jelleg. Ugyanakkor a digitális technika lényegében ilyen jellegű, azaz diszkrét idejű folyamatokkal, más néven sztochasztikus idősorokkal dolgozik.
Az időben diszkrét sztochasztikus folyamatok tulajdonságai és kezelése alapjában véve azonosak a folytonos idejű folyamatokéval, ezért az ott megismert értelmezések és összefüggések általában itt is érvényesek azzal, hogy az összefüggéseket és számításokat diszkrét változókkal kell felírni.
Egy időben diszkrét sztochasztikus folyamatot az módon jelölünk, melynek értelmezési tartományát alkotó időpontok között a véges, általában azonos időközök találhatók. A továbbiakban az egyszerűség kedvéért a jelölések helyett a jelöléseket használjuk.
Ha az folyamat stacionárius, akkor ebben az esetben is érvényesek az időben folytonos stacionárius folyamatokra bemutatott tulajdonságok. Így a
|
|
(8.105) |
átlagos (várható) érték időben konstans függvény, míg a
|
|
(8.106) |
kovariancia-függvény csak a megfigyelési időpontok távolságától függ, azaz
|
|
(8.107) |
Ez természetesen a
|
|
(8.108) |
képlettel definiált korreláció-függvényre is igaz, amit a
|
|
(8.109) |
formában írhatunk.
Vizsgáljuk most egy diszkrét idejű lineáris dinamikus rendszer viselkedését, melynek bemenet-kimenet modelljét idővariáns esetben az
|
|
(8.110) |
egyenlet írja le, ahol
|
|
(8.111) |
a rendszer diszkrét idejű súlyfüggvénye. Ha a rendszer időinvariáns, akkor (127) a
|
|
(8.112) |
formában írható.
Felírva a (8.112) egyenletet egy m≠l időpontra is, összeszorozva a két egyenletet és alkalmazva a (8.106) operációt mind a két oldalra, átalakítások után a kovariancia-függvényekre a
|
|
(8.113) |
egyenletet kapjuk, amely a (8.96) egyenlet megfelelője a diszkrét idejű stacionárius folyamatokra
Definiálva a diszkrét idejű stacionárius folyamatok diszkrét spektrális sűrűségfüggvényét (diszkrét teljesítménysűrűség spektrumát) az
|
|
(8.114) |
Fourier-transzformációval, melynek inverze a
|
|
(8.115) |
alakú, könnyen előállíthatjuk a spektrális sűrűségfüggvények közötti (8.101) összefüggést.
A lineáris dinamikus rendszerek bemeneti és kimeneti stacionárius folyamatai közötti (8.100) összefüggést most a
|
|
(8.116) |
egyenlet alkotja, ahol és a bemenet és kimenet kovariancia-(autokovariancia)- és keresztkovariancia-függvényei.
Ha a diszkrét idejű folyamatok egyben az ergodicitás tulajdonságával is rendelkeznek, akkor a jellemző paramétereket az időbeli realizációk határértékeiből számolhatjuk a folytonos idejű folyamatokra megadott (8.69) és (8.71) kifejezéseknek megfelelően. Végtelen nagy értékek természetesen most sem realizálhatók, ezért most is a (8.82) összefüggéshez hasonló, véges intervallumokon végzett becsléseket kell alkalmaznunk: a kovariancia függvény
|
|
(8.117) |
és keresztkovariancia-függvény
|
|
(8.118) |
ahol az átlagos értékek becslései:
és .
Egy lineáris dinamikus rendszer autokovariancia- és keresztkovariancia-függvényeinek a kapcsolatát a (8.116) egyenlet mutatja be. Felírva ezt az egyenletet az n véges felső határig
és elvégezve a kísérletet sorban a 0,1,2…n értékekre, és figyelembe véve az autokovariancia-függvény
szimmetria tulajdonságát a
egyenlethez jutunk, ahonnan a lineáris rendszer súlyfüggvényének egyes értékeit a
inverz egyenletrendszer határozza meg. □