9. fejezet - Laplace-transzformációhoz kapcsolódó levezetések
Vissza		Előre

9. fejezet - Laplace-transzformációhoz kapcsolódó levezetések

Tartalom

9.1. Néhány egyszerű függvény Laplace-transzformáltja

9.1.1. Az egységugrás Laplace-transzformáltja

f(t)=ε(t) 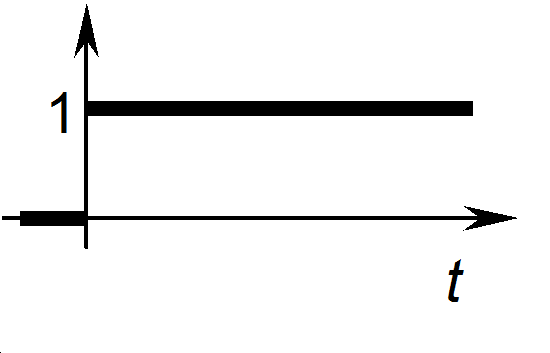F(s)=?

$F (s) = £ {ε (t)} = \int_{0}^{\infty} ε (t) \cdot e^{- s t} d t = {[\frac{e^{- s t}}{- s}]}_{0}^{\infty} = 0 - (- \frac{1}{s}) = \frac{1}{s}$

(9.1)

miután feltételünk volt, hogy Re{s}= > 0.

9.1.2. Az egységnyi sebességugrás Laplace-transzformáltja

f(t)=ε(t)t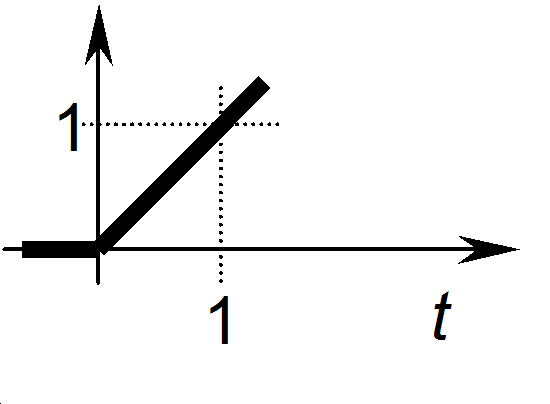F(s)=?

$F (s) = \int_{0}^{\infty} t \cdot e^{- s t} d t$

(9.2)

Az alábbi parciális integrálási szabályt alkalmazva:

$\begin{array}{l} \int u \cdot \dot{v} d t = u \cdot v - \int \dot{u} \cdot v d t \\ (\begin{array}{l} \frac{d}{d t} (u \cdot v) = \dot{u} \cdot v + u \cdot \dot{v} / \int \\ u \cdot v = \int \dot{u} \cdot v d t + \int u \cdot \dot{v} d t \\ u \cdot v - \int \dot{u} \cdot v d t = \int u \cdot \dot{v} d t \end{array}) \end{array}$ ,ahol $\begin{matrix} u (t) = t & \dot{v} (t) = e^{- s t} \\ \dot{u} (t) = 1 & v (t) = - \frac{e^{- s t}}{s} \end{matrix}$

(9.3)

Behelyettesítve:

$F (s) = \int_{0}^{\infty} t \cdot e^{- s t} d t = {[t \cdot \frac{e^{- s t}}{- s}]}_{0}^{\infty} - \int_{0}^{\infty} 1 \cdot \frac{e^{- s t}}{- s} d t = 0 - (- 0) + \frac{1}{s} \int_{0}^{\infty} e^{- s t} d t = \frac{1}{s} \cdot \frac{1}{s} = \frac{1}{s^{2}}$

(9.4)

9.1.3. Az exponenciális függvény Laplace-transzformáltja

Az $f (t) = e^{- \frac{t}{T}}$ időfüggvény Laplace transzformáltja:

$F (s) = \int_{0}^{\infty} e^{- \frac{t}{T}} \cdot e^{- s t} d t = \int_{0}^{\infty} e^{- (s + \frac{1}{T}) t} d t = {[\frac{e^{- (s + \frac{1}{T}) t}}{- (s + \frac{1}{T})}]}_{0}^{\infty} = \frac{1}{s + \frac{1}{T}} = \frac{T}{1 + s T}$

(9.5)

tehát az exponenciális függvénynek is algebrai függvény felel meg!

9.2. Fontosabb alkalmazási szabályok (műveletek)

A Laplace transzformáció tehát az f(t) valós változójú függvényhez a transzformációs összefüggés szerint az s komplex változójú függvényt rendeli.

Kérdés: az f(t) függvényen végzett alapvető műveletek miként érvényesülnek a transzformált tartományban?

9.2.1. LINEARITÁSI szabály

Adott f(t), amelynek Laplace transzformáltja {f(t)}=F(s)akkor {Kf(t)}=K{f(t)}=KF(s).

Adott f1(t), f2(t), amelyeknek Laplace transzformáltjai F1(s), F2(s)akkor {f1(t)+f2(t)}= {f1(t)}+ {f2(t)}=F1(s)+F2(s).

Mindkét törvényszerűség azzal igazolható, hogy a Laplace-transzformáció tulajdonképpen határozott integrál.

9.2.2. ELTOLÁSI szabály

Adott f(t), amelynek Laplace transzformáltja {f(t)}=F(s), ekkor f(t-) esetén a Laplace-transzformáció eredménye:

9.1. ábra - Laplace transzformáció eredménye

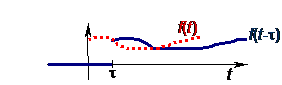
Legyen t-=z, ekkor t=z+, amiből dt=dz következik.

$\begin{array}{l} £ {f (t - τ)} = \int_{0}^{\infty} f (t - τ) e^{- s t} d t = \int_{0}^{\infty} f (z) e^{- (z + τ) s} d z = \int_{0}^{\infty} f (z) e^{- z s} e^{- τ s} d z = \\ = e^{- τ s} \int_{0}^{\infty} f (z) e^{- z s} d z = e^{- τ s} \cdot F (s) \end{array}$

(9.6)

9.2.3. HASONLÓSÁGI szabály

Adott f(t), amelynek Laplace transzformáltja {f(t)}=F(s), ekkor f(at) esetén a Laplace-transzformáció eredménye:

Legyen $a t = z$ , ekkor $t = \frac{z}{a}$ és $d t = \frac{1}{a} d z$ .

$£ {f (a \cdot t)} = \int_{0}^{\infty} f (a \cdot t) e^{- s t} d t = \int_{0}^{\infty} f (z) \cdot e^{- s \frac{z}{a}} \frac{1}{a} d z = \frac{1}{a} \int_{0}^{\infty} f (z) \cdot e^{- \frac{s}{a} z} d z = \frac{1}{a} F (\frac{s}{a})$

(9.7)

9.2.4. DIFFERENCIÁLÁS az időtartományban

Adott $f (t)$ , amelynek deriváltja $\frac{d}{d t} f (t) = \dot{f} (t)$ , és $ℒ {f (t)} = F (s)$ . Első lépésként, a már bemutatott, parciális integrálást alkalmaztuk a következő helyettesítéssel: $\dot{v} = \dot{f} (t)$ és $u = e^{- s t}, \Rightarrow v = f (t), \dot{u} = - s \cdot e^{- s t}$ , továbbá feltételezzük, hogy $s$ értékét megfelelően választjuk meg.

$ℒ {\dot{f} (t)} = \int_{- 0}^{\infty} \dot{f} (t) e^{- s t} d t = \int_{- 0}^{\infty} (\frac{d}{d t} (f (t) e^{- s t})) d t - \int_{- 0}^{\infty} f (t) (- s) e^{- s t} d t$

(9.8)

Vizsgáljuk meg (9.8) jobboldalának első tagját. Mivel létezik $f (t)$ Laplace-transzformáltja, ezért $f (\infty) \cdot e^{- s \infty} = 0$ . (9.8) második integráljából $- s$ kiemelhető, ami marad az pedig $f (t)$ Laplace-transzformáltja.

$ℒ {\dot{f} (t)} = {[f (t) e^{- s t}]}_{- 0}^{\infty} - \int_{- 0}^{\infty} f (t) (- s) e^{- s t} d t = s F (s) - f (- 0)$

(9.9)

Általánosan:

$ℒ [\frac{d^{n}}{d t^{n}} f (t)] = s^{n} F (s) - \sum_{i = 0}^{n - 1} {(s)}^{i} f^{(n - 1 - i)} (- 0)$

(9.10)

ahol $f^{(i)} (- 0)$ az $f (t)$ függvény $i$ -dik deriváltjának baloldali határértéke a $t = 0$ helyen.

9.2.5. INTEGRÁLÁS az időtartományban

Adott f(t), amelynek létezik a primitív függvénye, és $£$ {f(t)}=F(s).

Mi lesz az időtartománybeli integrál Laplace-transzformáltja?

$£ {\int_{0}^{t} f (τ) d τ} = \int_{0}^{\infty} \int_{0}^{t} f (τ) d τ e^{- s t} d t = {[- \int_{0}^{t} f (τ) d τ \frac{1}{s} e^{- s t}]}_{0}^{\infty} + \frac{1}{s} \int_{0}^{\infty} f (t) e^{- s t} d t = - 0 + 0 + \frac{1}{s} F (s)$

(9.11)

A feladatot parciális integrálással oldottuk meg, a következő helyettesítéseket alkalmazva: $u = \int_{0}^{t} f (τ) d τ$ , $\dot{v} = e^{- s t}$ . A kapott eredmény általánosítható, akkor $\frac{1}{s^{n}} F (s)$ lesz az eredmény.

Fontos következtetés: mivel a differenciálásnak illetve integrálásnak az s-el való szorzás illetve osztás felel meg, a differenciálegyenletek helyébe a transzformált tartományban algebrai egyenletek lépnek. Így a feladatok megoldása lényegesen egyszerűsödik.

9.2.6. Végérték tételek

A végérték tételek segítségével lehetőségünk van meghatározni a kezdeti és az állandósult állapotbeli értékeket anélkül, hogy az inverz transzformációt elvégeznénk. Elsőként határozzuk meg a kezdeti értéket. A tétel alkalmazható, ha a függvénynek létezik a nulla körüli Taylor sora:

$f (t) = a_{0} + a_{1} t + \frac{a_{2}}{2!} t^{2} + \dots = \sum_{i = 0}^{\infty} \frac{a_{i}}{i!} t^{i}$

(9.12)

Végezzük el az inverz transzformációt

$F (s) = \frac{a_{0}}{s} + \frac{a_{1}}{s^{2}} + \frac{a_{2}}{s^{3}} + \dots = \sum_{i = 0}^{\infty} \frac{a_{i}}{s^{i + 1}}$

(9.13)

A két sor összevetéséből kapjuk a következő összefüggést:

$f (+ 0) = \lim_{t \to 0} f (t) = \lim_{s \to \infty} s \cdot F (s) = a_{0}$

(9.14)

A tétel megfordítása $(\lim_{t \to \infty} f (t) = \lim_{s \to 0} s \cdot F (s))$ csak akkor igaz, ha F(s) si pólusaira teljesül a $Re (s_{i}) \leq 0$ feltétel. A legegyszerűbb a tételt akkor belátni, ha a pólusok egyszeresek. Ekkor a kifejtési tétel alapján:

$\lim_{t \to \infty} f (t) = \lim_{t \to \infty} \sum_{i = 1}^{n} K_{i} \cdot e^{s_{i} \cdot t} = 0,$

(9.15)

mivel az exponenciális függvény negatív valósrész esetén zérushoz tart. Az egyenlőség jobb oldala:

$\lim_{s \to 0} s \cdot F (s) = \lim_{s \to 0} \sum_{i = 1}^{n} s \frac{K_{i}}{s - s_{i}} = 0,$

(9.16)

szintén zérushoz tart. Igaz a tétel akkor is, ha valamely pólus valósrésze zérus, hiszen ekkor mindkét oldal Kk-hoz tart, ahol k a zérus valósrészű pólus indexe.

A többi eset számunkra nem túl érdekes, hiszen – mint a későbbiekben majd látni fogjuk – csak ekkor $(Re (s_{i}) < 0)$ stabil a rendszer.

Vissza		Előre
8. fejezet - Véletlen hatások és sztochasztikus folyamatok	Főoldal	10. fejezet - Ellenőrző kérdések