6. fejezet - Súrlódás modellek és kompenzációja
- 6.1. A súrlódás kezdeti modelljei
- 6.2. Súrlódási fajták, típusok
- 6.3. Súrlódással kapcsolatos általános megfigyelések
- 6.4. A súrlódás eredete
- 6.5. Egyszerű elemek
- 6.6. Komplex modellek
- 6.7. A dinamikus modellparaméterek tulajdonságainak összehasonlítása
6.1. A súrlódás kezdeti modelljei
Amikor meg szeretnénk vizsgálni az aktuális eredményeket és teóriákat, érdemes visszatekinteni a múltba és megvizsgálni, hogy elődeink hogyan értelmezték ugyanazt a problémát. Alább egy rövid összefoglalót adunk, összpontosítva csak a súrlódási modell fejlődésére a XX. század közepétől.
6.1.1. Az első súrlódási modell
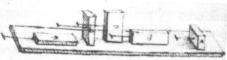
Érdekes, de talán nem meglepő, hogy az első súrlódási modell Leonardo Da Vinci-től (1452-1519) származik. Leonardo megmérte az erőket az objektumok között, mind horizontális, mind elhajló felület esetén, ezáltal felismerte a különbséget a csúszó és gördülő súrlódás között, valamint a kenés jótékony hatását. Ahogy a 6.1.ábra mutatja, Leonardo kíváncsi volt a látható területeken okozott hatásokra. Ezt írta a jegyzetébe: „A súrlódás azonos súly esetén egyenlő ellenállást okoz a mozgás kezdetén, habár a kapcsolat különböző szélességeken és hosszúságokon keresztül történik.” A fenti megfigyelés teljes összhangban van a súrlódás első kettő törvényével. Leonardo bevezette az első együtthatót a súrlódási erő és a szabályos terhelés arányaként, azonban feltételezte, hogy minden súrlódó testnek van súrlódási ellenállása, amely a súly negyedével egyenlő.
6.1.2. A többi tudományos megközelítés
Robert Hook-ot a híres Steven's szekere - ez egy hajóféle, amely kerekeken mozgott, vitorlával és megfelelő kötélzettel volt ellátva – inspirálta. Próbálta megfejteni a gördülő súrlódást, és felismert két dolgot: "Az első és legfontosabb a hajlékonyság, a kerekek súlya, amelyek gördülnek és nyomnak, és a második ezek részeinek a tapadása, ragadása a kerékhez;…". A jövőben különbséget tett a maradó, és a nem maradó alakváltozás szerepe között, és megfejtette az akadozás és tapadás kérdéseit.
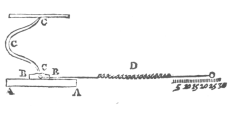
Guillaume Amontons (1673-1705) is részt vett számos súrlódással foglalkozó tudományos munkában. Kísérletei eredménye és azok értelemzései megjelentek a „Royal Academia”-ban 1699-ben. A készülék, amelyet Amontons használt a kísérleteiben a 6.2 ábrán látható. A tesztpéldányok, amelyeket AA és BB-vel jelöltünk, különböző rugókkal együtt voltak megterhelve, ezt jelzi a CCC, amíg az erőhatás le nem győzi a súrlódó erőt és el nem indítja a csúszást, amelyet a rugón (D) mérhetünk.
6.2. Súrlódási fajták, típusok
Az egymáshoz képest elmozduló anyag részecskéi között fellépő mozgásgátló hatást súrlódásnak nevezzük. Ebből következik, hogy a súrlódási erő ellentétes értelmű az elmozdulással.
Általánosságban két fő csoportra bontható a súrlódás jelensége:
-
külső súrlódás, ez a szilárd testek érintkező felületein lép fel;
-
belső súrlódás, mely az anyag belső részecskéinek relatív elmozdulásakor keletkezik.
Külső súrlódáskor három esetet különböztethetünk meg, attól függően, hogy milyen az elmozdulás jellege:
-
Csúszó súrlódás: amikor az egyik test egyik irányban csúszik a másik test felületén.
-
Forgási súrlódás: ilyenkor az egymással érintkező felületek egy körpályát írnak le, egy adott forgástengely körül. Ekkor az elmozdulással (forgással) szembeni ellenállás nyomatékként adható meg,
|
T = F |
(6.1) |
ahol F a két forgó testet terhelő erő, r pedig az elmozduló felületek sugara.
-
Gördülő súrlódás: az egymáson legördülő forgástest mozgását egy erő nyomatéka okozza. A gördülő ellenállási tényező a csúszási súrlódási együtthatónak csak kis százaléka.
A fenti összefüggésből következik, hogy a súrlódási erő vagy nyomaték nem csak a felületre normális erőtől, tehát a terheléstől függ, hanem a súrlódási tényezőtől is. A súrlódási tényezőt viszont számtalan hatás befolyásolja:
-
Anyagminőség: az anyag belső szerkezete, az anyag hővezetése, a súrlódó felületek rugalmassága ill. merevsége tartozik ide.
-
Felületi minőség: ezt jellemzi a felület érdessége, a súrlódó felületek állapota (Beilby, oxidációs, adszorpciós réteg).
-
Igénybevételi körülmények: ezen a csúszási sebességet, a terhelés nagyságát, az üzemi hőmérsékletet, és a súrlódó pár illesztését értjük.
A belső súrlódásra vonatkozó törvényszerűségek bonyolultabbak, de a súrlódási tényezőt itt is a Coulomb-féle összefüggéssel adjuk meg.
Az egymással érintkező felületek között többféle súrlódási állapotot szokás megkülönböztetni:
-
száraz vagy statikus súrlódás;
-
határréteg-súrlódás;
-
vegyes súrlódás;
-
folyadéksúrlódás;
-
az előző esetek kombinációja.
A következőkben ezeket az állapotokat tárgyaljuk részletesebben.
6.2.1. Száraz súrlódás
Ha szilárd testek egymáson kenőanyag nélkül mozognak, akkor száraz súrlódásról beszélünk. Valóságban száraz súrlódás nincs, mert mindig valami kevés kenőanyag marad a felületre tapadva. Elegendő, ha a felületre néhány molekulányi vastag levegő vagy gázréteg tapad, ez is csökkenti a súrlódási ellenállást. Az egymáson elmozduló felületek részben rugalmas, részben képlékeny alakváltozást szenvednek, a kiálló részek letöredezhetnek, vagy összehegedhetnek. A súrlódási tényező 0,3..1,3 között változik. Azért mégsem tárgyalhatjuk ezt a jelenséget olyan egyszerűen, mivel itt egy komplexebb folyamatról van szó.
Amikor két felület találkozik, és rajtuk erőt fejtünk ki, de nem történik csúszás, akkor a kapcsolódás durvasága, mint egyik fontos tulajdonság kerül előtérbe. A két test érintkezési felülete elasztikusan deformálódik, létrejön egy kezdeti csúszási elmozdulás, és mindkét felület határrétege képlékenyen deformálódik, kialakul a száraz vagy statikus súrlódás. Ahogy a mechanikából ismert, a kapcsolódások ilyenkor mindkét, tangenciális és normál irányban is deformálódhatnak. Amikor a tangenciális erőt először alkalmazzuk, akkor a tömeg egy kis elmozdulása figyelhető meg tangenciális irányban. Ez az elmozdulás 10-4…5 10-3 mm -es tartományban van, ami megszűnik, ha az anyagnak nincs csúszási hajlama. Az utóbbi esetben a test még kúszni fog a felületen, eleinte még meglehetősen kis sebességgel (kb. 105 mm/sec), ami ezután pedig lecsökken. Nagyon puha anyagoknál, mint pl. az indiumnál és a grafitnál ez a szakasz lassú és állandó csúszási sebesség alakul ki kb. 10-5 – 10-7 mm/sec tartományban.
Tanulmányozva a golyóscsapágyak forgását, Dahl észrevette, hogy az elmozdulás arányos az alkalmazott erővel, amíg el nem érjük a kritikus erőt, ahol az elszakadás történik. A tangenciális terhelés alatt a felületi réteg rugalmasan deformálódik, majd visszaáll eredeti helyzetébe, ha a terhelő erőt megszüntetjük. Dahl modellezte ezt a jelenséget, kis rugókkal helyettesítve a kapcsolódásokat a két megfelelő felület között. Amikor tangenciális erőt alkalmazunk, a rugók deformálódnak, és elmozdulás történik. A vonzási egyenlet a következő összefüggéssel adható meg :
|
Ft(x) = -ktx |
(6.2) |
Ahol az Ft a tangenciális erő, a kt a kapcsolódás keménysége, az x pedig az egyensúlyi helyzettől való kitérés. A kt, ami a tangenciális keménység, pedig a felületi réteg geometriájának, - más szóval a durvaság geometriája -, az anyag rugalmasságának és az alkalmazott normális erőnek a függvénye. Első közelítésben nézzük az elszakadási elmozdulást, ami konstans, ennélfogva a keménység megadható a következő egyenlettel :
|
|
(6.3) |
ahol az Fb az elszakadáshoz tartozó erő, és az x a felületi réteg maximális deformációja az elszakadás előtt. Ha a normális erő változó és a súrlódási együttható konstanssá válik, akkor a normális erő arányos lesz kt-vel.A kezdeti csúszási elmozdulást a mechanikai szakcikkekben "micro-slip"-nek is nevezik. Az átmenet a kezdeti csúszási elmozdulásból a csúszásba meglehetősen komplex. Nincs hirtelen átmenet a csúszásba, a csúszás először a kapcsolódás határán történik, majd tovább terjeszkedik a középpont irányába.
Kiterjedt vizsgálatokat végeztek, hogy különböző vegyi hatások hogyan csökkentik le a felület súrlódási tényezőjét. Ez a csökkenés különösen nagy volt grafit és molibdén-diszulfid felületen való alkalmazása esetén, mivel ezeknek az anyagoknak az a sajátossága, hogy kiegyenlítik az egyenlőtlenségeket, és tükörsima felületet hoznak létre.
6.2.2. Határréteg súrlódás
Ez a súrlódás akkor lép fel, amikor a súrlódó felületeken kb. 1…2 molekulányi vékonyságú folyadékréteg tapad meg, és ez bizonyos kenőhatást fejt ki. A súrlódási tényező értéke 0,1…0,3 között mozog.
A határkenés - így is nevezik - fő jellemzője még a nagyon kis sebesség, ennélfogva a folyadéksúrlódás nem is kap szerepet, ahogyan a sebesség is túl kicsi, hogy kialakuljon a folyadéksúrlódási réteg. Ebben az állapotban a határréteg biztosítja a kenést. Ennek folytonosnak és szilárdnak kell lennie, hogy fennmaradjon ez az állapot a kapcsolódási feszültség alatt is, és kis nyírófeszültségek ébredjenek a súrlódásnál.
Azt gondolhatjuk, a nyíróerőnek köszönhető, hogy két szilárd felület közötti határkenésnél a súrlódás nagyobb, mint a részleges vagy teljes folyadékkenésnél. Azonban ez nem mindig igaz. Nem feltétlenül szükséges, hogy a nyíróerő nagyobb legyen, mint a folyadék viszkózus ereje, gondoljunk például az üvegre. Nagyon sok anyagnál kisebb lesz a nyíróerő, mint a viszkózus áramlás ereje a folyadékban. Bizonyos határkenési állapotnál a súrlódási szint alatta marad a Coulomb súrlódásnál tapasztaltnak, és teljesen kiküszöböli a stick-slip-et (akadozó csúszást). Elméletileg a kenőanyag viszkozitásának nincs hatása ebben az esetben a súrlódásra. Csapágyakban a kenés kimaradása esetén előálló helyzet az, amikor ez a fajta, azaz határréteg súrlódás alakul ki, de mindig jelentkezik egy bizonyos mértékű hidrodinamikai hatás is.
6.2.3. Vegyes súrlódás
Ha az egymáson elmozduló felületek között kenőanyag is van, de nem annyi, hogy a felületek egymástól teljesen elváljanak, akkor vegyes vagy részleges súrlódás jön létre. Ez a súrlódási állapot lényegében a határréteg súrlódásból és a tiszta folyadéksúrlódásból tevődik össze. A kenést ekkor a felületre tapadó, igen vékony felületi kenőanyagréteg biztosítja, amely még a csúcsokon is csökkenti a súrlódást. A súrlódási tényező értéke attól függően változik, hogy milyen arányban vesz részt a kenésben a határréteg súrlódás és a teljes folyadéksúrlódás
= 0,05…0,1. Ebben a súrlódási állapotban igen könnyen bekövetkezhet a csúcsok berágódása, vagy összehegedése, mert aránylag kis csapágyhőmérsékletnél is több száz keletkezhet.
Részleges folyadékkenés tehát akkor alakul ki, amikor a folyadék az érintkezési zónákba kerül a mozgás miatt, csúszásnál vagy éppen forgásnál. A terhelés ráadásakor a nyomás keletkezésénél néha előfordul kis kenőanyag kiáramlás, de ezt a viszkozitás megakadályozza, mégpedig a vékony folyadékréteg formálásával. Ez persze függ a mozgás sebességétől, a kapcsolódás geometriájától, és a kenőanyag viszkozitásától. Amikor ez a vékony réteg nem vastagabb, mint a felületi érdességmagasság, akkor beszélünk részleges folyadékkenésről, ilyenkor szilárd rész találkozik szilárd résszel. Amikor a filmréteg elég vastag, és az elválás tökéletes, akkor a terhelést teljes egészében a folyadék veszi fel. A részleges folyadékkenést talán könnyebb megértenünk, ha a vízisíelő analógiájára gondolunk. Nulla sebességnél a síelő úszva maradhat csak fenn a vízen. A kritikus sebesség fölött a síelőt a síléc mozgása tartja fönt a vízen. Az álló és mozgó helyzet között van a hidrodinamikus tartomány.
Ezek a sebességek jelentik az analógiát a részleges folyadékkenésre. Azonban ez az analógia nem teljesen tökéletes, mivel az úszásnál nem szilárd-szilárd a kapcsolat, mozgásnál pedig a síelő a folyadék tehetelenségének és nem a viszkozitásnak köszönheti a támaszt, mint a folyadékkenés esetében. Amikor a síelő növelte sebességét, és elemelkedett, akkor a vele szemben fennálló ellenállások lecsökkentek, így engedve számára a még gyorsabb haladást. Ahogy a részleges folyadékkenésnél a sebességet növeljük, a szilárd-szilárd kapcsolat csökken, a súrlódás kisebb lesz, és növekedik a mozgó részek gyorsasága.
A határkenés nagyon fontos szerepet kap a stick-slip jelenségében. A határkenési állapot tényleges megfejtése a megfelelő molekulák felfedezése, amelyek korrodálás nélkül összekötik a nagy szilárdságú acélfelületeket. Több feltételt kellene, hogy kielégítsenek: elegendő szilárdságúak legyenek, ellenálljanak a csúszóerőknek, és kis nyíróerőhöz kis súrlódás tartozzon. Az ilyen molekulák növelik a kenőanyag terjedelmét (gépolaj vagy zsír) és jellemzően az összes molekula kevesebb, mint 2 %-át alkotják. A kenőanyag adalékok három általános osztályba sorolhatók: síkosító hatóanyagok, magas nyomású hatóanyagok, és kopás ellenes hatóanyagok. Száraz kenőanyagok, olyan mint a Teflon, a mechanizmusok számos variációiban működik. A legfontosabb feltétel az ilyen hatóanyagoknál a csillapítás, amelyek révén kialakulhat a teljes folyadékkenés. A részleges folyadékkenés modellje a tribológia tudományának egyik legnehezebb része. Manapság észrevehetjük, hogy a felületek érdességeinek, méreteinek és orientációjának részletessége egyre komplikáltabbá teszi a kapcsolódó felületek egymás közötti kölcsönhatásának analízisét.
6.2.4. Folyadéksúrlódás
Az egymáson elmozduló felületek között bizonyos körülmények között összefüggő olajhártya alakul ki, és ebben elegendően nagy a nyomás, amely a terhelés ellenére a két felületet szétválasztja egymástól, megszüntetve a fémes érintkezést. Mivel ilyenkor a két felület nem találkozik egymással, kopás sem jön létre. A súrlódási tényezőt ilyenkor a kenőanyag belső súrlódása határozza meg, amit folyadéksúrlódásnak nevezünk. Ebben az állapotban a súrlódási tényező értéke a kenőanyagban kialakult nyomástól, és a kenőanyag viszkozitásától függ, megközelítőleg = 0,001…0,01. A belső súrlódási ellenállás meghatározható, ha feltételezzük, hogy a kenőanyag áramlása lamináris, vagyis réteges (ld. 6.3. ábra).
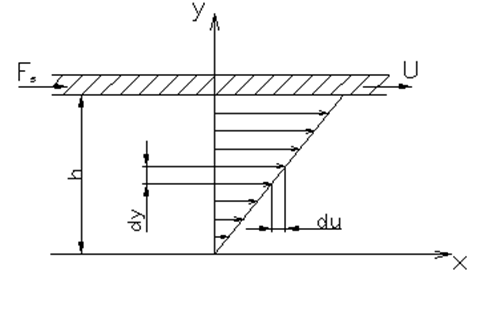
Áramlástani ismereteink szerint a csúszó felületek közötti csúsztató feszültség arányos a sebesség y tengelymenti változásával, a sebességgradienssel, azaz
|
|
(6.4) |
Az egyenletben az [Pa] egy arányossági tényező, amely a kenőanyag belső súrlódására jellemző, ezt a kenőanyag dinamikai viszkozitásának nevezzük. Ha ismerjük a két lap közötti sebességeloszlást, akkor meghatározható a felső síklap állandó mozgatásához szükséges erő, mely a következő összefüggéssel határozható meg,
|
|
(6.5) |
ahol dA a síklap elemi felülete és A a síklap felülete.
6.2.5. Az előző esetek kombinációja:
Az eddig tárgyalt esetek, súrlódási állapotfajták a valóságban mindig csak együttesen fordulnak elő, és határozzák meg a test súrlódási állapotát.
A következőkben az egyik legnagyobb problémát okozó jelenségről szeretnénk néhány szót szólni, amely általában egyenes vonalú mozgásnál, egymáson elcsúszó felületek elcsúszásakor következik be, főleg megmunkáló gépek ágyvezetékeinél, szánok mozgásainál. Ezt a jelenséget a szakirodalomban akadozó csúszásnak (stick-slip) nevezik.
6.2.6. Akadozó csúszási állapot (stick-slip)
Kis csúszási sebességnél a mozgás egyenlőtlen, ugrásszerűen változik, úgy is mondhatjuk, hogy oszcillál. Ez az ugrásszerű sebességváltozás olyan nagy mértékű is lehet, hogy egy-egy ilyen periódus alatt a sebesség zérusra csökkenhet. Ilyenkor a mozgás akadozóvá válik. Az akadozó csúszást az okozza, hogy a test rugalmas alakváltozást szenved, másrészt a nyugvásbeli és mozgásbeli súrlódási tényezők értéke különböző. Ezenkívül a mozgásbeli súrlódási tényező értéke és a sebesség között nem lineáris a kapcsolat. A mozgásbeli súrlódási tényező értéke mindig nagyobb, mint a nyugvásbeli súrlódási tényező értéke.
Az akadozó csúszás megértéséhez érdemes egy fizikai modellt elképzelnünk, ami két testből áll, ezek egymáson csúsznak, a felsőt pedig egy rugalmas elemmel, például egy rugóval hajtjuk. Amikor a felső elmozduló test az alsóra tapad, akkor a v sebesség zérusra csökken. Ekkor a rugalmas hajtóelem összenyomódik, így a rugóerő hirtelen nőni kezd, míg el nem éri és nagyobb nem lesz, mint a nyugvásbeli súrlódó erő. A test hirtelen megindul, a sebessége v, és a mozgásbeli súrlódó erő (F) pedig kisebb, mint a nyugvásbeli (F), a lengés megindul. A tapadás és csúszás periódikusan ismétlődik. Azt a sebességet, ahol nincs letapadás, kritikusnak vagy határsebességnek nevezzük.
6.3. Súrlódással kapcsolatos általános megfigyelések
A súrlódásról általánosságban beszélve, öt pontban összefoglalhatjuk a jól ismert tulajdonságokat [111]-nek megfelelően.
1. Bármelyik helyzetben, ahol a tangenciális erők eredője kisebb, mint az adott helyzethez tartozó specifikus erőparaméter, a súrlódási erő egyenlő értékű, és ellentétes irányú lesz az alkalmazott erők eredőjével, és tangenciális mozgás nem lép fel.
2. Amikor tangenciális mozgás következik be, akkor a súrlódási erő a felület relatív sebességének ellentétes irányában hat.
3. A súrlódási erő F arányos a normál F erővel. Ez a reláció segít abban, hogy definiáljuk a súrlódási állandót, :
|
F = F |
(6.6) |
Másképpen ez a törvény kifejezhető a konstans válaszszöggel, vagy súrlódási szöggel, , definíció szerint:
|
tan = |
(6.7) |
Talán érthetőbb a következő definíció: annak a lejtőnek a szöge, amire bármilyen tárgyat helyezve az ott nyugalomban marad, de ha ezt a szöget csak egy kicsivel is megnövelem, a tárgy le fog csúszni a lejtőről.
4. A súrlódás független az Aa látszólagos kapcsolati felülettől. Különböző méretű tárgyaknak ugyanaz a súrlódási tényezőjük.
5. A súrlódási erő független a v csúszási sebességtől. Ez azt mutatja, hogy a csúszás elkezdéséhez szükséges erő megegyezik a csúszás fenntartásához szükséges erővel, bármely megadott sebességnél.
Ezek a súrlódási tulajdonságok széles körben használtak a mindennapi életben, és a mérnöki gyakorlatban. Sajnos azonban, ennek ellenére tudjuk, hogy ezek egyszerű, és általában jó közelítések. A súrlódás kutatása még folyamatban van, és a tribológia még sok fel nem fedezett területet tartalmaz. Amiről már teljesen biztosak vagyunk, az az, hogy a valódi kép sokkal bonyolultabb, és többször meglepően különbözik a fent említett szabályoktól.
6.4. A súrlódás eredete
Az alább részletezett modell a XVIII. században keletkezett, Coulomb és Amontons tudományos eredményei óta még ma is sűrűn használják. A XX. század technológiai fejlődésének köszönhetően sok új eszköz és eljárás született a tribológiai kutatások segítésére, és segített a súrlódás újragondolásában.
A Coulomb típusú modell két hatalmas hibát hordoz. Egyfelől az egész modell alapjában a érdességi elméletre támaszkodik, és azt állítja, hogy a súrlódás csak a felszín érdességétől függ. Ennek oka viszonylag egyszerű. Akkoriban még hiányoztak azok a speciális felszerelések, és a kiegészítő tudás, hogy észrevegyék a súrlódás és az összetartó erő kapcsolatát. Másrészről, ez a modell nem szolgál meggyőző érvekkel a súrlódás disszipatív jellegére. De ezek az elképzelések azért jó irányba mutattak [140], és az igazi áttörés 1943-ban, a második világháború alatt következett be. Ausztráliában Bowden, és Tabor [24] kísérletsorozatai bizonyítékul szolgáltak a korábbi tapadási elméletre, és ez lehetőséget teremtett a súrlódási veszteségek magyarázatára.
Kísérleteik hasonló eredményekre vezettek más anyagpárok esetén is. A kísérletek eredményét kibővítve, két tulajdonságot adtak a súrlódáshoz [24], [25]. Rabinowicz későbbi munkái újabb két tulajdonságot mutattak ki. [111].
A súrlódás négy okra vezethető vissza:
-
A két felület közötti összetartó (adhéziós) erő.
-
A két felület egymásba vágódása.
-
A felület érdessége.
-
Elektromos összetevők.
Az előző fejezetben áttekintettük a súrlódás keletkezését, okait és megjelenési formáit. Ebben a fejezetben megpróbáljuk összefoglalni a súrlódás modellezésére használt különféle eljárásokat.
6.5. Egyszerű elemek
A statikus modellek leginkább egyszerű matematikai leírásai a súrlódás viselkedésének. Nem a súrlódás egészét, hanem csak egy részét, mint pl. a súrlódó erő nyugalomban, a súrlódás, mint az állandósult-állapot sebességfüggvénye stb. írjuk le.
6.5.1. Coulomb súrlódás
A legegyszerűbb és talán a leginkább ismert modell az úgynevezett Coulomb súrlódási modell. A modellben használt nagyfokú egyszerűsítések és elhanyagolások ellenére nagymértékben használja a mérnöki társadalom, amikor a dinamikus hatások elhanyagolhatóak. Mindazonáltal, a Coulomb modell az összes továbbfejlesztett modellnek alkotóeleme. A Coulomb súrlódó erő Fc állandó nagyságú erő, mely a mozgással ellentétes irányban hat:
Amikor
|
|
(6.8) |
|
|
(6.9) |
Ahol FN a felületeket összeszorító erő és a súrlódási tényező. A meghatározható különböző feltételekkel végzett mérésekből. A legnagyobb probléma a Coulomb modellel, hogy nem képes a nulla körüli sebességtartomány kezelésére. Ahhoz, hogy ezt a modellt alkalmazni tudjuk ezekre az esetekre, bevezetjük a 0 tényezőt. A mozgás kezdetekor felcseréli -t a (6.9) egyenletben, egészen addig, amíg el nem kezdődik a folyamat állandósult állapota. A és 0 értéke megtalálható a fontosabb fizika, vagy mérnöki táblázatokban, különböző anyagpárokra, száraz és síkosított esetekre.
Az első ilyen jellegű táblázat a XVIII. század elején készült. Megjegyzendő, hogy ez a legegyszerűbb és leggyorsabb módja a súrlódás számításának, de ez a módszer akár 20%-os pontatlansággal is járhat.
6.5.2. Viszkózus súrlódás
A viszkózus súrlódási elem modellezi a súrlódási erőt az elmozdulás sebességével arányosan.
Amikor
|
(2.10) |
(6.10) |
6.5.3. Statikus súrlódás
A statikus súrlódás erőkényszer.
Ha
|
|
(6.11) |
ahol Fs a statikus súrlódó erő, egy további terhelés az Fc -n a Coulomb súrlódási erőn.
6.5.4. Csúszás előtti elmozdulás
A csúszás előtti elmozdulást először Dahl tanulmányozta és modellezte [40]. A 2.2 képlet alapján:
|
|
(6.12) |
(2.12)
ahol Ff(x) a súrlódási erő a csúszás előtti elmozdulás függvénye, kt az anyag merevsége, és x az elmozdulás. kt anyagtulajdonság, de a (6.12) egyenletből számítható, ha x 1-50 [m] között van.
6.5.5. Az ébredő statikus súrlódás
Többféle modell áll rendelkezésre a jelenség leírásához. Kato elméleti modellje [85] a következő:
|
|
(6.13) |
ahol a végső statikus súrlódás, vagyis a statikus súrlódás nagysága nagyon hosszú idő után, nyugalomban, FC a Coulomb súrlódás a beragadás pillanatában, és m pedig tapasztalati paraméterek 0.04 és 0.64, illetve 0.36 és 0.67 között. Kis hosszú ébredési időt jelent. A nem-konformális kapcsolatot megvizsgálva Amstrong-Hélouvry a = 1.66 és m = 0.65 [6] –t állapította meg.
Egy másik modell, amelyet Amstrong-Hélouvry [6] dolgozott ki, megszünteti FC használatát a statikus súrlódás ébredésének pillanatában. Ennek a modellnek kevesebb a paramétere, mint a 2.13 egyenletének.
|
|
(6.14) |
ahol a statikus súrlódás szintje a csúszás n-dik ciklusának kezdete, a statikus súrlódás szintjének a vége az előző csúszásciklus végén, a végső statikus súrlódás, a kísérleti paraméter. Jegyezzük meg, különbözik a (6.13) egyenletben közölt mértékegységtől.
6.5.6. Súrlódási memória
A súrlódási memória egyszerűen időkéséssel modellezhető:
|
|
(6.15) |
ahol Ff(t) az azonnali súrlódási erő, Fvel() a súrlódás az állandósult-állapotbeli sebesség függvényében, és t a késleltető paraméter. A súrlódás időkésését mérve Hess és Soom [75] ezt 3 és 9 ms közöttinek találta a terheléstől és kenéstől függően. Ők szintén rámutattak, hogy a késés növekszik a kenőanyag viszkozitásának növekedésével, és a kapcsolati terhelés növekedésével. De úgy tűnik, hogy független az oszcillációs frekvenciától.
6.6. Komplex modellek
A komplex modelleket leggyakrabban egyszerű modellelemekből építik fel, hozzáadott tulajdonságokkal, amik kezelik a dinamikus viselkedést. Ma a tribológia tudománya még távol van attól, hogy kész képet adjon a súrlódás működéséről minden tekintetben, ezért ezek a modellek sokkal inkább tapasztalati kísérletekre építkeznek, mint mély tudományos háttérre.
6.6.1. Állandósult állapotú modellek
6.6.1.1. A Stribeck görbe
A Stribeck görbe a súrlódás egy összetettebb modellje, a súrlódás a sebesség függvénye. Azonban csak állandósult állapotban érvényes, tartalmazza a Coulomb és a viszkózus súrlódási modellt, mint beépített elemeket. Az alábbi modellt Hess és Soom [75] alkalmazta.
|
|
(6.16) |
ahol a Coulomb, viszkózus és statikus súrldást az FC, Fv és Fs jelöli. A vs a Stribeck görbe karakterisztikus sebessége. Hess és Soom rendszeres függőséget mutatott ki Fv és vs –en, mint kenő és terhelési paramétereken.
Egy másik megközelítés a Stribeck hatás modellezésére a linearizált exponenciáls kifejezés, amit Bo és Pavelescu alkalmazott [21]. A viszkózus súrlódás kifejezést Armstrong-Hélouvry [9] alkotta meg.
|
|
(6.17) |
ahol egy hozzáadott tapasztalati paraméter. Az irodalomban Bo és Pavelescu [21] -ra 0.5 –től 1-ig tartó értékeket adott meg. Armstrong-Hélouvry [6], [8] = 2, Fuller [57] javasolt = nagyon nagyot arra a rendszerre, ahol hatásos határkenés van. A = 2 értékre az exponenciális modell (6.17) egyenlete Gauss-i modellé alakul, ami közel egyenlő a Lorentz-i modellel az (6.16) egyenletben.
6.6.1.2. Tustin modell
A Stribeck görbe másik egyszerű reprezentációja a Tustin modell [144]. A modell az alapvető súrlódási jelenségekből építkezik, és egyszerűen egymásra helyezi őket. A három tulajdonság, a Coulomb súrlódás FC, a statikus súrlódás Fs és a viszkózus súrlódás Fv.
|
|
(6.18) |
A Tustin modellt linearizálva a következőket kapjuk:
|
|
(6.19) |
Ez a linearizált modell azonban csak 85 %-os pontossággal alkalmazható abban a tartományban, ahol a sebesség a négyzetgyökével összehasonlítható. Egyéb esetekben, amikor a rendszersebesség nem ilyen lassú, más modellt kell használni.
6.6.2. Dinamikus modellek
6.6.2.1. Hét-paraméteres súrlódási modell
Népszerű elképzelés, hogy „fésüljük” össze a már létező modelleket. Így működik a hét-paraméteres modell. A hét paraméterből mindegyik egy-egy súrlódási jelenséget ír le, ami a 6.2 táblázatban látható. Az értékük általában a mechanikai és kenési feltételektől függ, de tipikus értékeket a következő munkák alapján javasolok [6], [27], [57], [75], [85], [105].
A súrlódás adott.
Nincs csúszás (előcsúszási elmozdulás).
|
|
(6.20) |
Csúszás (Coulomb + viszkózus + Stribeck görbe súrlódás súrlódási memóriával)
|
|
(6.21) |
Ébredő statikus súrlódás:
|
|
(6.22) |
Ahol:
|
Ff() |
azonnali súrlódási erő |
|
FC |
(Φ) a Coulomb súrlódási erő |
|
Fv |
(Φ) a viszkózus súrlódási erő |
|
Fs |
a Stribeck súrlódás nagysága Stribeck súrlódás (a súrlódási erő elszakadásánál FC+Fs) |
|
Fsa |
az előző csúszási periódus végén a Stribeck súrlódás nagysága |
|
Fs |
(Φ) a Stribeck súrlódás nagysága hosszú idő után nyugalomban (az erő lassú alkalmazásával) |
|
kt |
(Φ) a statikus kapcsolat tangenciális keménysége |
|
vs |
(Φ) a Stribeck súrlódás karakterisztikus sebessége |
|
L |
(Φ) a súrlódási memória időkonstansa |
|
(Φ) átmeneti paraméter |
|
|
t2 |
az ébredési erő zérus sebesség mellett |
|
(Φ) |
A jelölt paraméterek súrlódási modell paraméterek, az egyéb változók pedig állapotváltozók. |
|
Paraméter tartomány |
A paraméterek függenek |
|
|
FC |
0.001 0.1FN |
a kenőanyag viszkozitásától, kapcsolati geometriától, terheléstől |
|
Fv |
0 very large |
a kenőanyag viszkozitásától, kapcsolati geometriától, terheléstől |
|
Fs |
0 0.1FN |
a határkenéstől, FC |
|
kt |
1/x(FC+Fs) x1 50 [m] |
az anyagtulajdonságoktól, a felület megmunkálásától |
|
vs |
0.00001 0.1 [m/s] |
a kapcsolati geometriától és terheléstől |
|
L |
1 50 [ms] |
a kenőanyag viszkozitásától, kapcsolati geometriától, terheléstől |
|
0 200 [s] |
a határkenéstől |
|
Súrlódási modell |
Becsült/megfigyelt működés |
|
Viszkózus |
Stabilitás minden sebességnél és sebesség irányváltásnál. |
|
Coulomb |
Nincs akadozó csúszás PD szabályozással. Nincsenek határciklusok PD szabályozással. |
|
Statikus + Coulomb + Viszkózus |
Megjósolja az akadozó csúszást bizonyos kezdeti feltételekkel, PD szabályozás esetén. Megjósolja a határciklusokat PID szabályozás használatakor. |
|
Stribeck |
Szükséges, hogy megjósoljuk a kezdeti feltételek, amelyek akadozó csúszáshoz vezetnek. |
|
Ébredő statikus súrlódás |
Szükséges, hogy pontosan megjósoljuk a sebesség és az akadozó csúszás amplitúdójának kapcsolatát. |
|
Súrlódási memória |
Szükséges, hogy pontosan megjósoljuk a merevség és az akadozó csúszás amplitúdója közötti kapcsolatot. |
|
Előcsúszási elmozdulás |
Szükséges, hogy a beragadás alatt pontosan megjósoljuk a kis elmozdulásokat (beleértve a sebesség irányváltásait is). |
Paraméter-azonosítás. A paraméterek, amelyek nemlineáris kapcsolatban vannak a súrlódó erővel, nem azonosíthatóak lineáris eljárással. Kim javasolt egy lehetséges, nem-lineáris azonosítási eljárást a hét-paraméteres modellre, az „Accelerated Evolutionary Programming (AEP)”-t [88] és megadja a leírását, amit alább részletezünk. Az AEP is egy sztohasztikus optimalizácós eljárás, tetszőleges függvény szélsőértékének keresésére. Az egyszerű optimalizációs eljárás a következő: határozza meg az n paraméteres rendezett halmaz értékeit.
|
|
(6.23) |
amelyek minimalizálják/maximalizálják a költségfüggvényt f(z). Az AEP egy genetikus algoritmus típusú eljárás, szülő/gyerek típusú kapcsolatot használnak a legpontosabb megoldás eléréséhez. Két változtatható operátort használ. Az egyik, az irányoperátor meghatározza az irányt a megoldás jóságának megfelelően. A másik egy zéró értékű Gauss-i operátor, a hozzáadott zavarásnál használják, így készül a leszármazott. Az AEP szintén használ egy további “kor” változót, hogy növelje a keresés változatosságát, és kiküszöbölje az egyének lokális minimumon való elhelyezkedését. A Gaussi operátor be van építve az irányoperátorba, és a változó „kor”-ba. Nem úgy, mint más generikus eljárások, az AEP csak egy gyereket készít a szülőktől. Az új szülők pedig egy egyenes versenyben választódnak ki a szülők és gyermekei közül. Egy leszármazott akkor kerül kiválasztásra, ha a gyermek megnyeri a szüleivel folytatott versenyt. Az AEP az evolúció irányát és a „kor”t egy vektorban helyezi el, ezzel növeli a konvergencia sebességét a változatosság elvesztése nélkül. Ezáltal az (6.23) kifejezés a következő formát veszi fel
|
|
(6.24) |
ahol az i-dik vektor, az evolúciós iránya a j-dik paraméternek, és agei jelöli az élettartamát egy egész típusú i-dik vektorban. A következő két szabályt a szülő zavarására alkalmazzuk, így készülnek a leszármazottak.
1-es szabály
Ha ,
akkor ,
különben ,
|
|
(6.25) |
2-es szabály
Ha ,
akkor ,
különben ,
,
|
|
(6.26) |
ahol jelöli a j-dik paramétert az i-dik vektorban a Np vektorok között a k-dik generációban, jelöli az evolúciós irányt a . A egy Gauss eloszlású véletlenszerű változó, ami a irányba mutat, és i, i = 1, 2 pozitív konstansok. Ha az 1-es szabály jelzi, hogy az újonnan létrejött gyermek tulajdonságai jobbak, akkor a keresés folytatódik az ígéretes irányba, beállítva az irány értékét, és egy véletlen számot generálva a hozzátartozó pozitív vagy negatív régióban. Egyébként a szülőt tartjuk meg, ekkor a „kor” változót eggyel növeljük. Amikor a 2-es szabály „különben” része érvényesül, a második esetben a Gauss eloszlású véletlen változó eltérése minden lépésnél egyre nagyobb lesz, mert a „kor” is benn van a végtermékben. Ezáltal sokkal valószínűbb, hogy az algoritmus nem ragad be a lokális minimumban, hanem talál egy globálisat.
Az AEP eljárás alkalmazása a következőképpen zajlik:
1. Inicializáció. A kezdeti populáció generálása az Np próbamegoldással, a megadott területen belüli egyenlő eloszlással, a különálló vektorokkal
|
|
(6.27) |
ahol és , véletlenszerűen inicializáltak, és az agei értéke 1.
2. Kiértékelés. A szülők kiértékelése a megadott költségfüggvény f(zi) szerint.
3. Mutáció. Minden Np szülő zi, létrehoz egy gyermeket az 1-es és 2-es szabály használatával.
4. Kiértékelés. Az új leszármazottak kiértékelése.
5. Egy az egyben típusú összehasonlítás. Ha az újonnan létrehozott gyermek jobb, mint a szülő, akkor a gyermeket választjuk ki, és elvetjük a szülőt, és fordítva. Az új Np szülők a tulajdonságaik alapján sorbarendezésre kerülnek.
|
0 tól 0-ig: |
t2 t2 + Ts |
|
0 tól 1-ig: |
compute Fs,b |
|
1 től 0-ig: |
Fs,a and t2 0 |
|
1 től 1-ig: |
Nincs működés (2.29) |
6. Végrehajtási ellenőrzés. Egészen addig folytatja a harmadik lépésig, amíg a végrehajtási idő le nem járt, vagy egy elfogadható megoldást nem találunk.
A legjobb út a paraméterazonosításhoz a kísérlet és az AEP párhuzamos futtatása, ugyanazokkal a bemeneti paraméterekkel. A paraméterek akkor tekinthetőek azonosítottnak, ha a valós és a számított értékek közötti eltérés megszűnik, vagy egy előre meghatározott érték alá süllyed. A használt szenzortól függően a bemeneti paraméter lehet elmozdulás vagy sebesség.
A hét-paraméteres modellhez először tudnunk kell a bemeneti v, vagy (dx/dt) és a t2 és Fs,a. állapotváltozókat. Ehhez definiáljuk az új állapotváltozót s-t, ami megmutatja, hogy a rendszer akad vagy csúszik.
|
|
(6.28) |
ahol vcritical a sebesség/pozíció szenzor felbontása, ami a valós rendszerbe van beépítve. Az s, t2 és Fs,a változásaitól függően a következők érvényesek.
Amikor s változik:
ahol Ts a mintavételezési idő.
Jelölje a z vektor az (6.21) egyenlet ismeretlen paramétereit.
|
|
(6.29) |
ahol az összes paraméter pozitív. A hiba a berendezés és az identifikációs kimenet között a következő:
|
, i = 1, 2, …, Ns |
(6.30) |
ahol jelöli a becsült értéket, z x(z,ti) a berendezés elmozdulása, x(,ti) az indentifikációs modell elmozdulása a ti, mintavételezési időben és Ns az összes mintaadat. A költségfüggvény négyzetes hibáját is figyelembe véve:
|
|
(6.31) |
Akkor a paraméter identifikációs problémát optimalizációs problémaként kezelhetjük:
|
|
(6.32) |
6.6.2.2. Állapotváltozós súrlódási modellek
A geofizikusok által a kövek határkenésénél végzett kutatások alapján megszületett az állapotváltozós súrlódási modell. [6], [16]. A konstans normál feszültség esetén, az általános forma magában foglal n db állapotváltozót i a következőképpen néz ki:
Ebből az ábrázolásból következik, hogy a sebesség hirtelen változása nem okoz hirtelen változást -ban, de annak deriváltjában már igen. Egy állapotváltozó esetén Ruina javasolja a következő súrlódási törvényt [16]:
|
|
(6.35) |
|
|
(6.36) |
Ahol a skaláris állapotváltozó, L a karakterisztikus csúszási hossz. A (v0/f0) pár megfelel bármilyen szabadon választott pontnak, az állandósult állapotbeli súrlódás-sebesség görbén. Az állandósult állapotbeli görbét a következő kifejezés adja meg:
|
|
(6.37) |
és az állandósult állapotbeli állapotváltozók összefüggenek az anyagjellemzőkkel.
Korlátok. Sajnos a modellstruktúra önmagában hordozza a korlátot az állapotváltozós modell használatakor. Teljes nyugalomban v/v0 értéke a (6.38) egyenletben zérussá válik, ami végtelen súrlódási erőt ad a logaritmus függvény használata miatt (ln 0 = ). Szimulációkban ez normális esetben problémát okoz az integrátor használatakor. Ezt elkerülendő egy kapcsolót alkalmazunk, ami nulla sebesség esetén is véges súrlódási erőt ad. De ha , ez azt jelenti, hogy a nagyon kis sebességek esetén a logaritmus függvény értéke, és ezzel együtt a súrlódási erő igen gyorsan változik, ez pedig a kiválasztott környezet méretétől függő hibát eredményez, emiatt ezt a modellt nem alkalmazzák alacsony sebességekre, mert nem ad kielégítő eredményt.
Paraméter-azonosítás. Dupont megadja a kísérleteihez használt mérőberendezések részletes leírását [49]. Persze egyéb más rendszert is lehet használni, és mi most nem ismertetjük részleteiben az eredeti elrendezést. Az első lépés az, hogy azonosítsuk az (6.36) és (6.37) paramétereit, majd felrajzoljuk a megadott rendszerre az állandósult állapotbeli sebesség-súrlódás görbét (vagy Stribeck görbét ). A sebesség változása a rendszer változásával is jár. Ezt fel lehet használni arra, hogy A és B értékeit kiszámítsuk. A rendszerválasz a t0 pillanatbeli sebességugrás által adott, ahol a pár (v1, f1) a kezdeti állandósult állapotnak megfelelő, a pár (v2, f2) az ugrásfüggvényre adott válasz után leírja az elért állandósult állapotot, amíg fmax jelöli a maximális súrlódási erőt a tranziens alatt. A paraméter A és B kiszámítható a következőképpen:
Az exponenciális csökkenése a állapotváltozónak, a sebességugrást követően a következő
|
|
(6.40) |
A 2.3-as táblázat mutatja az állapotváltozó modell paramétereit, amiket Dupont számított ki. A használt sikosítóanyag a következő volt. Paraffinolaj, maximális Saybolt viszkozitás 158, és a kereskedelemben kapható paszta. A tesztanyag hőkezelt, olajban edzett szerszámacél, 59 HRC keménységgel.
|
Paraméterek |
Száraz |
Paraffin olaj |
Határkenés |
|
A 103 |
2.8 0.5 |
0.0Φ |
1.1 0.1 |
|
B 103 |
9.4 1.1 |
11.1 2.5 |
4.0 0.4 |
|
L [m] |
64.7 14.3 |
22.4 4.3 |
19.2 1.4 |
The magnitude was less then the noise level of the measurement
.
6.6.2.3. Karnopp súrlódási modell
Néhány modellben a súrlódás nem folytonos függvénye az állandósult állapotbeli sebességnek. Ezekben az esetekben nem folytonos általános függvények integrálása problémákat okozhat, de a beágyazott kapcsolófüggvényekkel ez a probléma még kezelhető. De ehhez még hozzáadódik az, hogy az integrátornak meg kell tudni keresnie a nem folytonos pontokat a megadott intervallumban. Változtatható lépésközű, változtatható rendű (fokszámú) eljárásokra van ehhez szükség, melyek beépített elemek az összes kereskedelmileg elérhető szimulációs szoftverben. Azonban az esetek többségében nekünk fix lépésközű megoldásokat kell használnunk, mert a mintavételezési idő állandó.
A Karnopp [84] modell megoldja ezt problémát, a pseudo sebesség, és a nulla sebesség kis szomszédainak bevezetésével. DV amiben a sebesség zérusra van állítva. A pseudo sebesség, p(t), ahol az eredeti anyag momentumként van feltüntetve, a megszokott módon történő integrálása a következő:
|
|
(6.41) |
ahol Fa a rendszerre ható erő, Fm pedig a modellezett súrlódóerő. A rendszer sebességét a (2.43)-nak megfelelően állítják be, ahol M a rendszer tömege.
|
|
(6.42) |
(2.43)
A súrlódási törvény a következő:
|
|
(6.43) |
Ez magában foglalja a Coulomb, a statikus, és a viszkózus típusú erőket (FC, Fs, Fv ), de kiegészíthető egyéb alkalmas surlódás típussal (pl. Stribeck görbe).
6.6.2.4. LuGre modell
Nem úgy, mint a hét-paraméteres modell, a LuGre modell egy integrált, dinamikus súrlódási modell. Néhány forrás így is hivatkozik rá, „integrált dinamikus modell”. A név egy rövidítés, két egyetem, a Lund technológiai egyetem, és az INPG Grenoble egyetem nevéből ered, ami vendégül látta az együttműködő kutatókat. A LuGre modell a kapcsolat rugalmasságán alapul [33].
A z(t) változó a súrlódási állapotot jeleníti meg, és a két csúszó felület kapcsolódó pontjainak átlagos elhajlását jelenti. A pillanatnyi súrlódás Ff a következő:
|
|
(6.44) |
ahol 0 leírja a merevséget rugószerű viselkedés esetén, kis elmozdulásokra, és 1 megadja a negatív viszkózus súrlódás kifejezését. Az állapotváltozó kiegészíthető a következőképpen:
|
|
(6.45) |
ahol
|
|
(6.46) |
Az Fc, Fs és Fv a Coulomb, Stribeck, és statikus súrlódás. Bizonyos speciális esetekre, egy további kiegészítő elem, Fg adódik hozzá a kifejezéshez a gravitáció hatását kifejezendő (azokban az esetekben, ahol vertikális a megmunkálás tengelye), vagy mint erősítő offset. Az állandósult állapot a következő:
|
|
(6.47) |
Ennek a modellnek az előnye amellett, hogy mind lineáris, mind polárkoordináták esetén érvényes, az, hogy leírja a jelenséget mind lapos felületekre, mind forgó csapágyelemekre.
Paraméter-azonosítás. Az azonosítási eljárást a [2]-ben leírtak alapján végzik, az általános eljárást követve lineáris dinamikai rendszerek esetére. Megjegyzendő, hogy az eljárás magában foglalja Fg –t az (6.45)-(6.47) egyenleteknek megfelelően. A paraméterek Fs és 0 könnyen leolvashatóak a Dahl görbéről.
A feltételezés magával vonja, hogy Fs = F. Továbbá, ha , akkor és . Az (6.47) egyenlettel ezt összetéve, a következőket kapjuk:
|
|
(6.48) |
Euler közelítését használva az idő szerinti deriváltakra, a lineáris regresszió eredménye:
|
|
(6.49) |
Az [1] cikk szerzője állítja, hogy az algoritmus érzékeny a pozíció mérési zajára, és javasolja az interferometria használatát az induktív szenzorok helyett, hogy kiiktassuk az eltérést-n.
6.6.2.5. Módosított Dahl modell
Az eredeti Dahl modell [40], [20] előrejelzi a súrlódási késést a sebesség irányváltások között, és hiszterézis hurkokra vezet. Azonban nem tartalmazza a Stribeck effektust. Ennek korrigálására Canudas javasolta, hogy transzformálják át a Dahl modellt egy másodrendű lineáris állapot invariáns modellé, amelyik emulálja a Stribeck effektust, a súrlódási erő válaszának túllövésével. Ezzel együtt azonban eltűnt az elsőrendű modell disszipatív jellege is. A Canudas által módosított Dahl modell az első olyan modell, amelybe az állapotváltozók számának növekedése nélkül belekerült a Stribeck jelenség.
A súrlódási erő Ff leírva a következőkkel:
ahol az időállandó arányos az 1/vmint-vel az eredeti Dahl modellhez hasonlóan, z egy állapotváltozó, amit úgy kell értelmezni, mint egy belső súrlódási állapotjelzőt, vs a Stribeck görbe karakterisztikus sebessége, míg 1, 2 és 3 a pozitív konstansok, a Coulomb, Stribeck, valamint a viszkózus súrlódást fejezik ki.
Az állandósult állapotban a súrlódást a következő kifejezés adja:
|
|
(6.53) |
6.6.2.6. M2 modell
Az M2 modellt ugyanaz a kutatócsoport fejlesztette ki, mint a módosított Dahl modellt. Most még nincs ismertebb neve, az eredeti irodalomban is egyszerűen csak M2 modellnek hívják [33]. A modell két paraméterből áll, az Fs csúszósúrlódásból, és az Fd dinamikus súrlódásból. A két állapotot egy dinamikus s súlyozófaktor köti össze, ami a relatív sebességtől függ. Az Ff teljes súrlódás megadható a következő kifejezéssel
|
|
(6.54) |
Az s súlyozófaktor az alábbi egyenlet megoldásából kapható:
|
|
(6.55) |
ahol s az időállandó, ami a súrlódási időkésést is magában foglalja. Az s = 1 a csúszást jelenti, míg s = 0 a megakadást. Emiatt s úgy is értelmezhető, mint a „csúszás” mértéke [33].
Az úgynevezett Dahl effektus modellezi a csúszósúrlódás viselkedését, egy merev rugó alkalmazásával, a ds.csillapítással együtt. A csúszósúrlódás azonban korlátozott az elszakadási erő miatt, és a telítési függvény is megjelenik a következő formában:
|
|
(6.56) |
A telítést leirhatjuk a következő módon:
|
|
(6.57) |
ahol
|
|
(6.58) |
A változó egy belső változó, ami leírja a relatív elmozdulás kapcsolatát attól a ponttól, ahol az akadozó súrlódás megjelent. A második kifejezés értékét nullázza, ha a csúszás megkezdődik.
|
|
(6.59) |
A dinamikus súrlódás Fd a Coulomb és a viszkózus súrlódás kifejezésének kombinációja, 0 és 2.-vel jelölve.
ahol:
|
|
(6.62) |
6.7. A dinamikus modellparaméterek tulajdonságainak összehasonlítása
A 6.5 táblázat az összes beépített elem tulajdonságainak összehasonlítását mutatja.
|
Hét-paraméteres |
Állapot-változós |
Karnopp |
LuGre |
Módosított Dahl |
M2 |
|
|
Előcsúszási elmozdulás |
igen |
nem |
nem |
igen |
igen |
igen |
|
Coulomb súrlódás |
igen |
igen |
igen |
igen |
igen |
igen |
|
Viszkózus súrlódás |
igen |
igen |
igen |
igen |
igen |
igen |
|
Negatív viszkózus súrlódás |
igen |
ha A < B |
nem |
igen |
igen |
igen |
|
Ébredő statikus súrlódás |
igen |
nem |
igen |
igen |
igen |
igen |
|
Dwell Time |
igen |
nem |
nem |
igen |
igen |
igen |
|
Súrlódási memória |
igen |
igen |
nem |
igen |
igen |
igen |
A 6.6 táblázat leírja az egyes modellek bemeneti/kimeneti paramétereit.
|
Hét-paraméteres |
Állapot-változós |
Karnopp |
LuGre |
Módosított Dahl |
M2 |
|
|
Bemeneti paraméter |
v |
v |
F |
v |
v |
v |
|
Kimeneti paraméter |
Ff |
Ff |
Ff |
Ff |
Ff |
Ff |
|
Állapot-változós |
z(t) |
z(t) |
s |
|||
|
Modell paraméterek |
táblázat |
A, B, L, f0, v0 |
FC, Fs, Fv, Dv, m |
FC, Fs, Fv, vs, 0, 1 |
0, 1, 2, v0, |
0, 1, 2, s, r, v0, ks, ds |
|
Azonosítás meg-valósítható |
igen |
igen |
nem szükséges |
Igen |
nem |
nem |
2.5.4 Szimulációk bemutatása
Hogy egy teljesebb, áttekintést kapjuk az előzőekben felsorolt modellekről, egy sor szimulációt végeztünk el, hogy megvizsgáljuk a különböző dinamikus modellek viselkedését. A szimulációkat a MATLAB szoftvercsomag segítségével hajtottuk végre, és leginkább az előcsúszási elmozdulást, nulla sebesség átlépést, sebesség irányváltást, és az akadozó csúszást vizsgáltuk. Más szóval az alacsony sebességű zónákra koncentráltunk. Ezért az állapotváltozós modellt most nem vizsgáltuk.
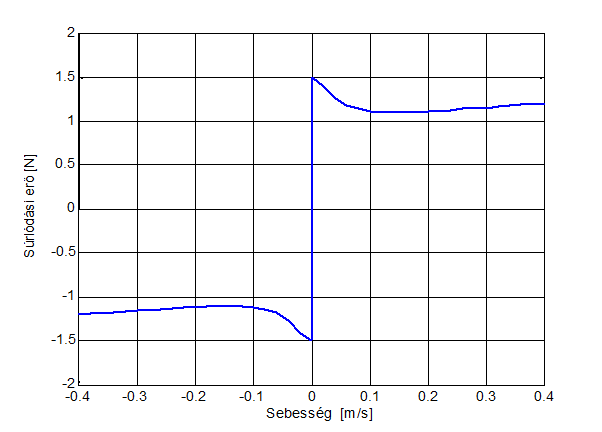
Azért, hogy összehasonlítható eredményeket kapjunk, az összes modellváltozók, és szimulációs paraméterek ugyanarra az értékre lettek beállítva. A 6-4. ábra mutatja az állandósult állapotbeli súrlódási görbét, vagy más néven a Stribeck görbét, amit a szimulációhoz használtunk, kivéve a Karnopp modellt. Itt az FC, Fv és Fs értékeit az állandósult állapotbeli görbe értékeihez hasonlóra állítottuk be.
6.7.1. Akadozó-csúszás típusú mozgás
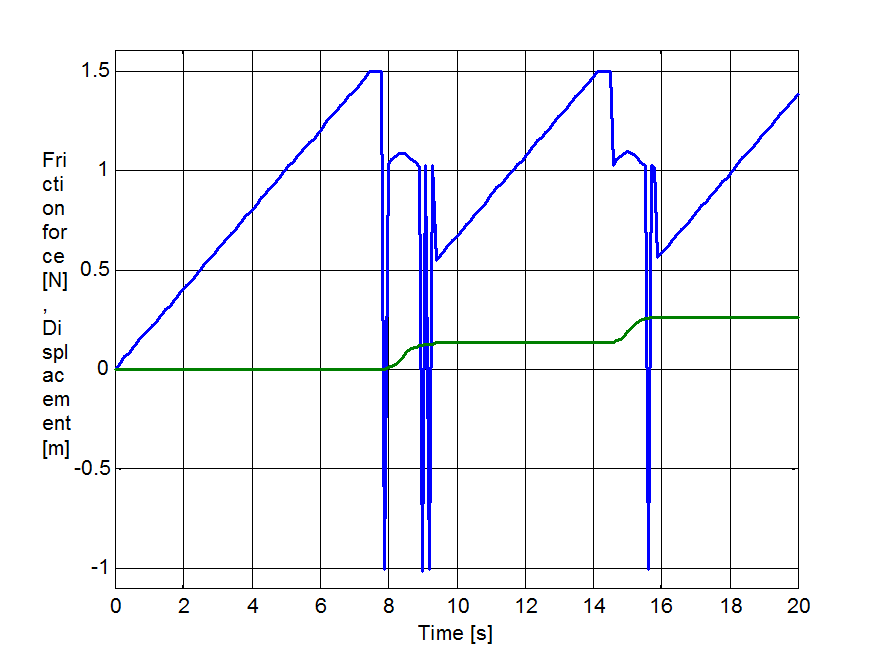
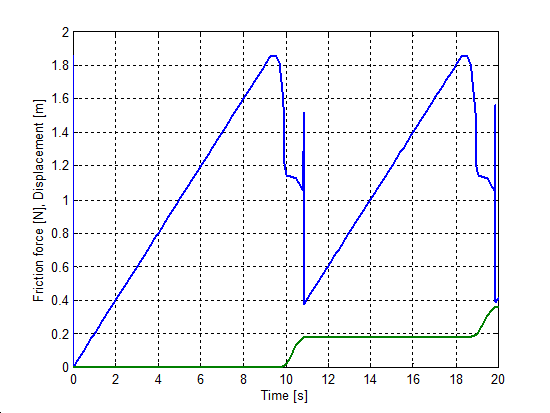
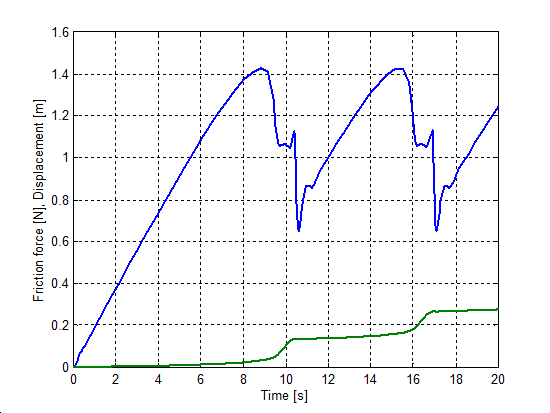
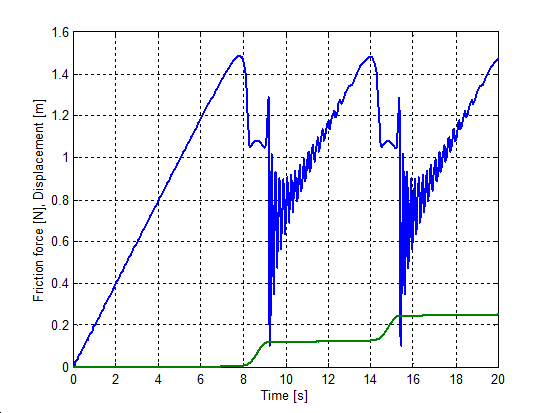
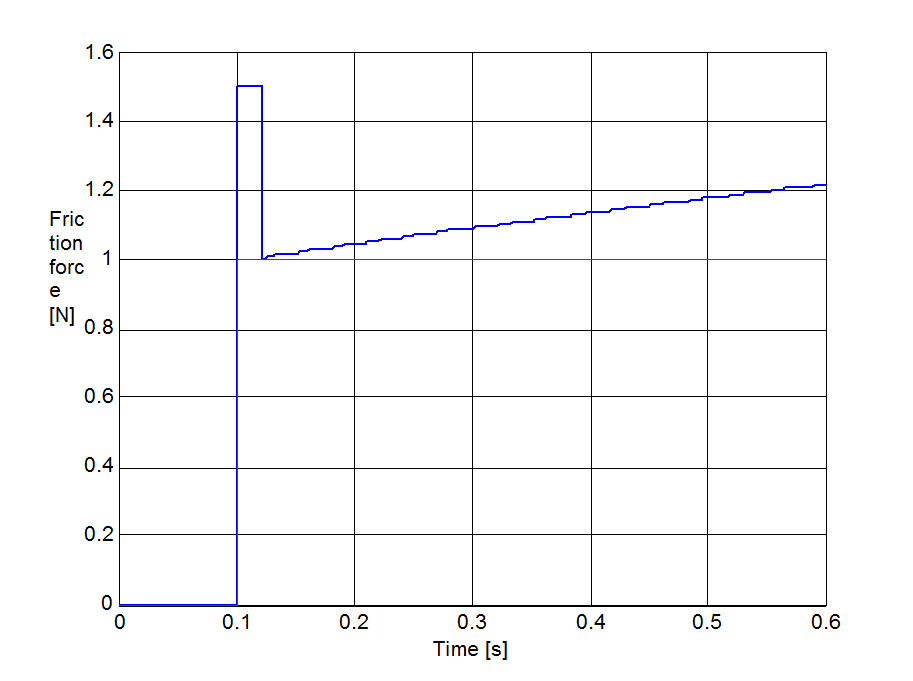
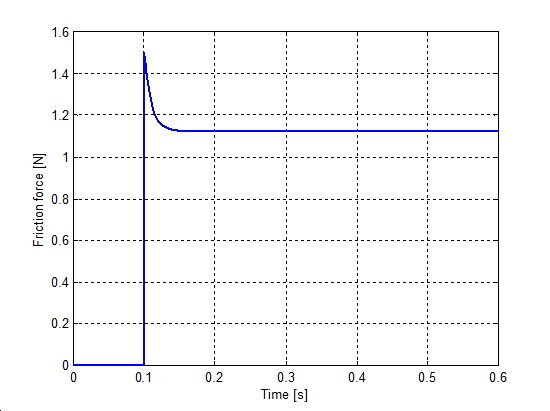
Egy rúgó által húzott egységnyi tömeg súrlódással, ez volt az akadozó csúszás szimulációjának kiindulási modellje. A rugó szabad vége konstans sebességgel mozgott. Mind a rendszer merevsége, mind a sebesség olyan módon volt megválasztva, hogy akadozó-csúszás keletkezzék. (vrugó = 0.02 m/s, krugó = 0.1 N/m). Ezek az értékek ugyanazok voltak a különböző modellek esetében.
A 6-5.-től 6-10-ig sorszámú ábrák mutatják a szimulációs eredményeket. A felső görbe az erő, az alsó pedig az elmozdulás az idő függvényében.
Mind a hét-paraméteres modell, mind a Karnopp, mind a LuGre modell esetében sima görbét kapunk. A Karnopp modell nem tartalmazza az időkésést, és a rendszer válasza bármilyen változásra azonnali. Ez az oka annak, hogy az erő értéke negatívvá válik a mozgás kezdetekor. Mind a módosított Dahl, mind az M2 modellek meg nem engedhető oszcillációt mutatnak, ami a súrlódási erőre szuperponálódik rá, amikor a tömeg beragad. De meg kell jegyeznünk, hogy az M2 modell esetében az eredeti forrás [33] sima görbét mutat. Valószínűleg ez speciális paraméterezéssel el is érhető.
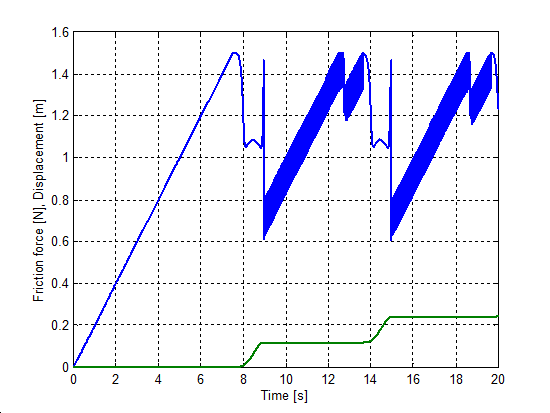
6.7.2. Zérus sebesség átmetszése
Az előzővel egyező rendszert állítottunk be a sebesség irányváltásainak szimulációjához. A rugó szabad vége Asin(t) szinuszosan változó sebességel lett rángatva, ahol A = 1 m/s volt. A szimulációval kapott súrlódási erő, sebesség, elmozdulás, és rugóerő időfüggvényeket 6.10-től 6-29-ig sorszámú ábrákon tekinthetjük meg. A vékony szaggatott vonal mutatja a sebességet, kivéve az elmozdulásnál, mert ott a szabad vég felöli elmozdulást ábrázoltuk.
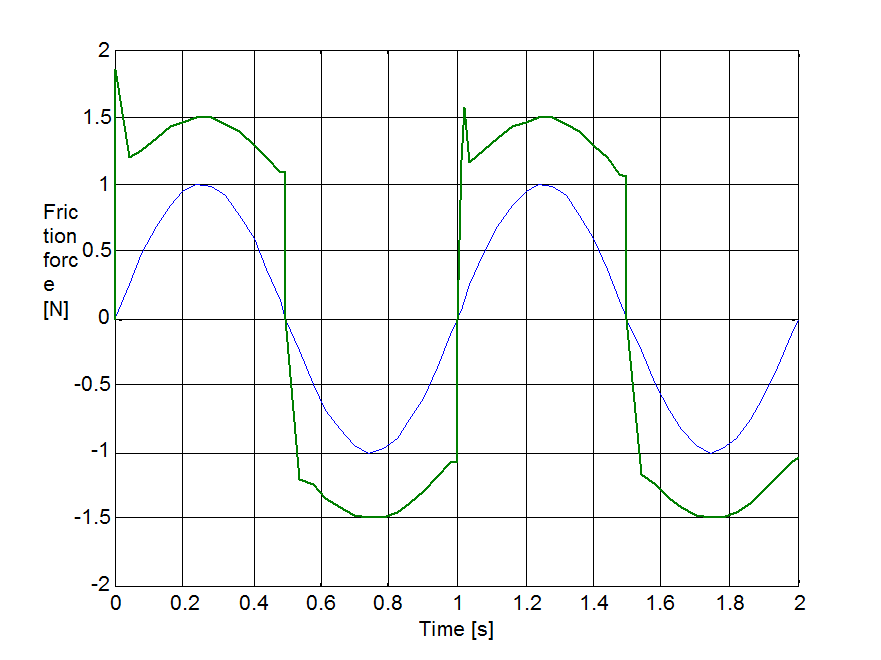
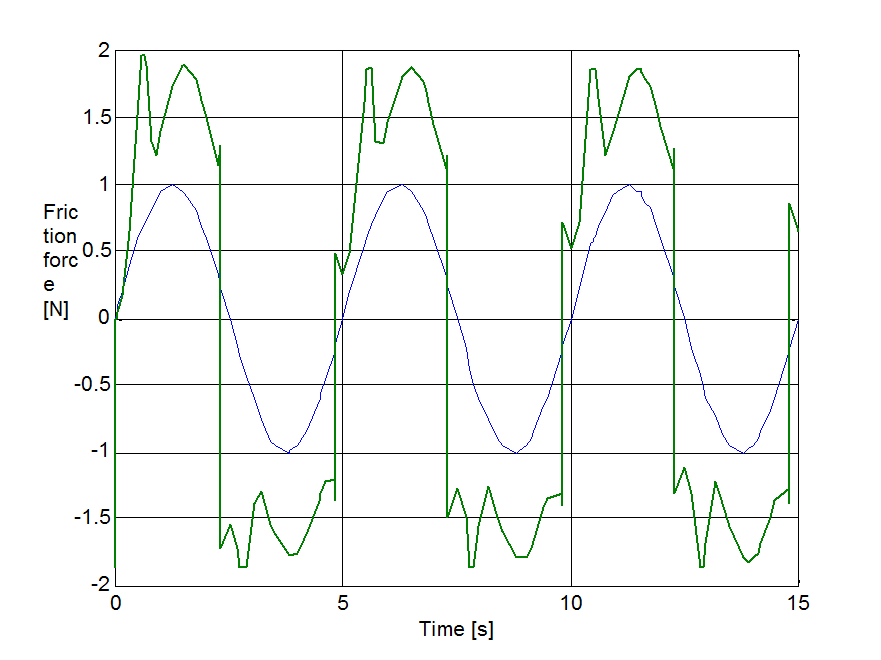
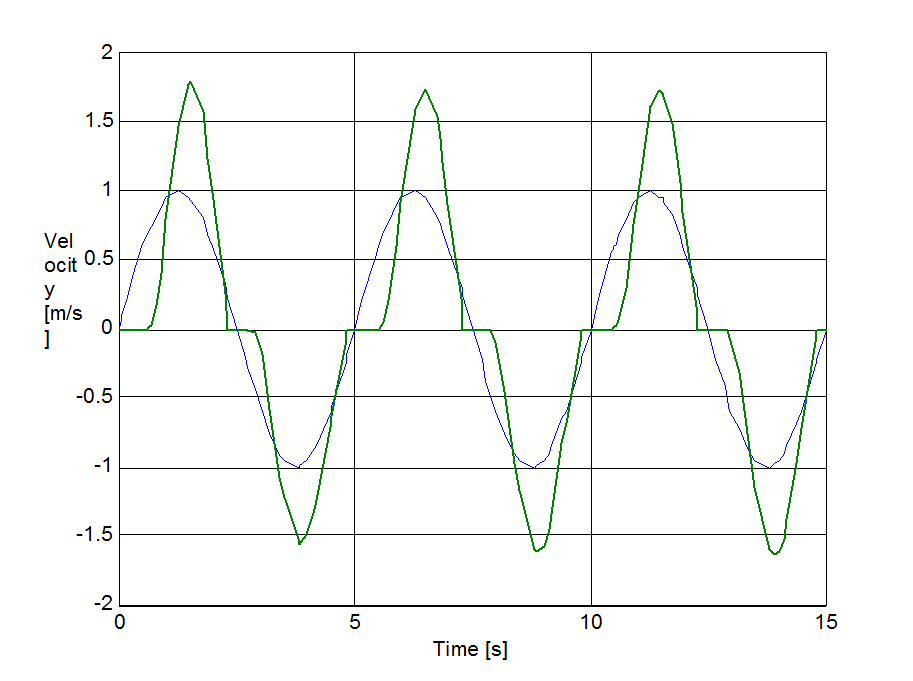
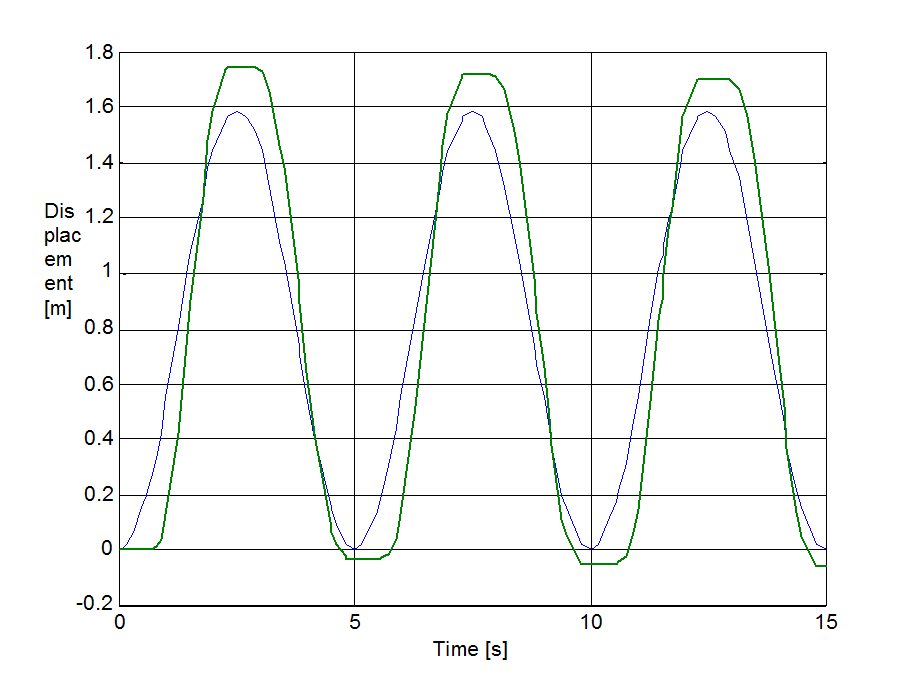
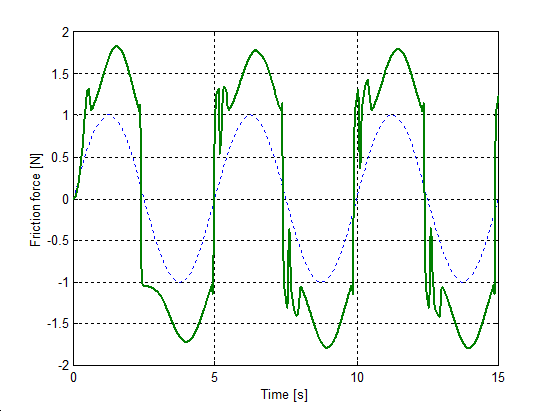
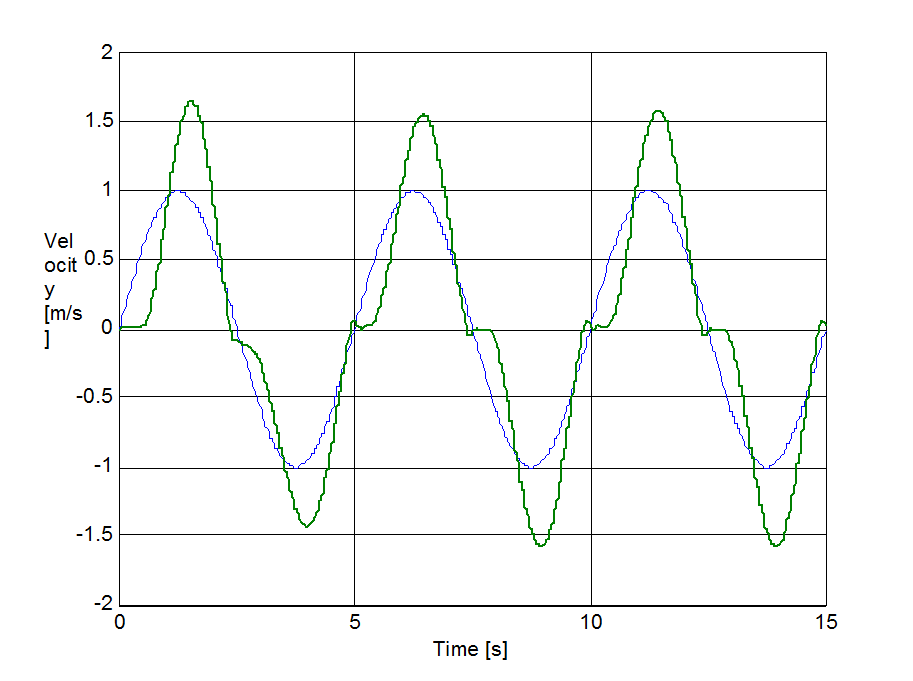
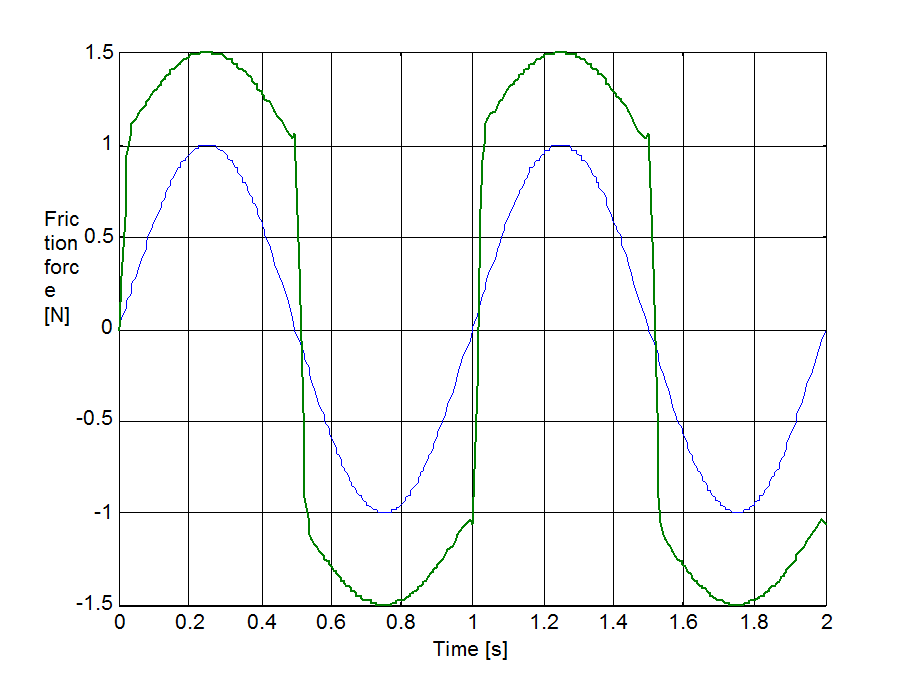
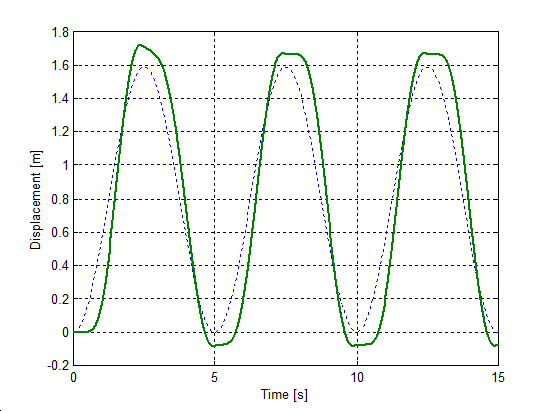
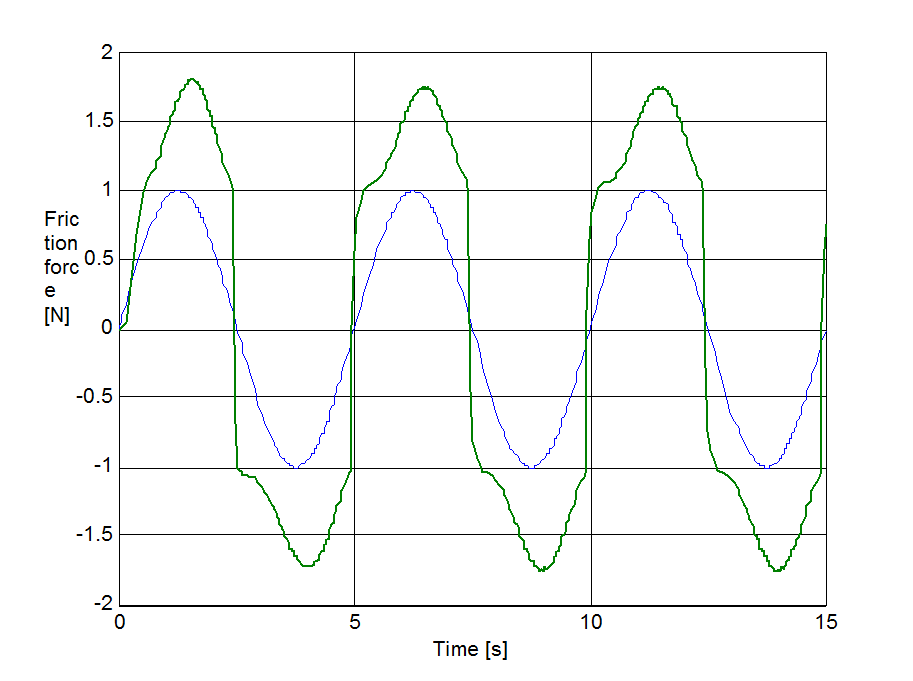
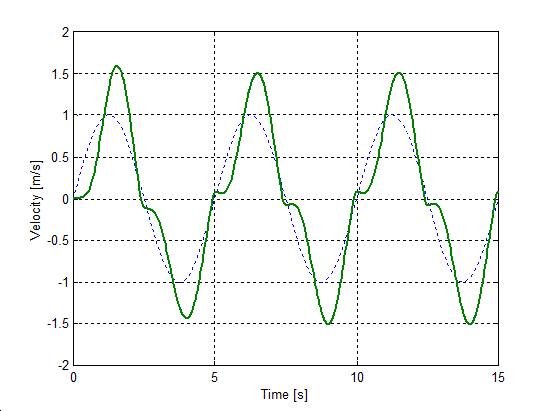
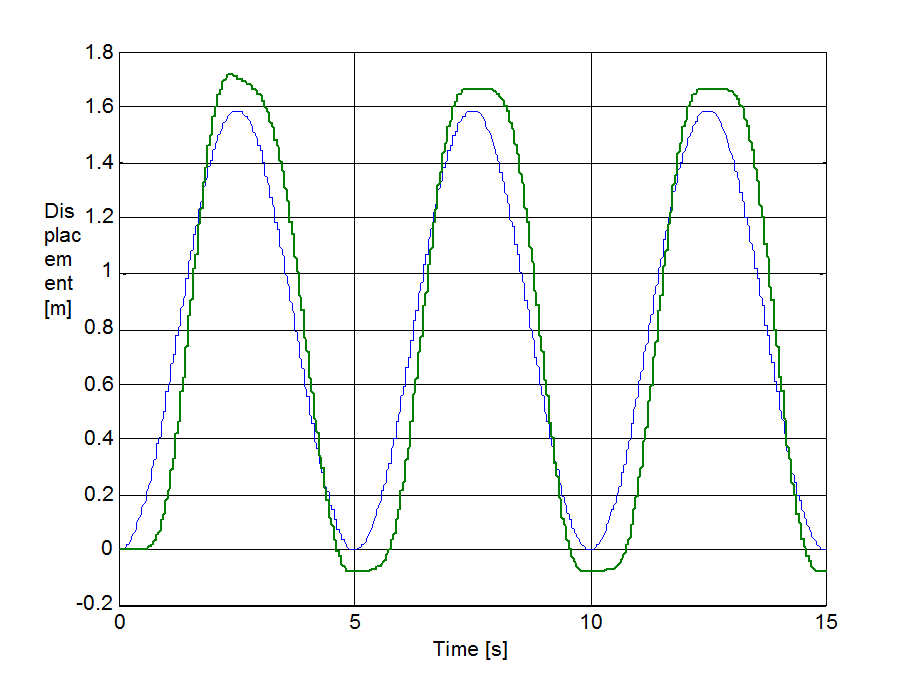
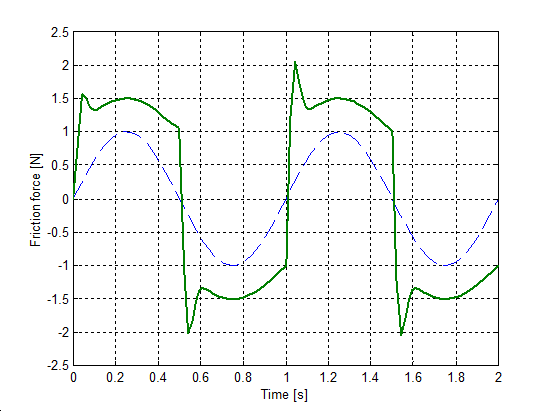
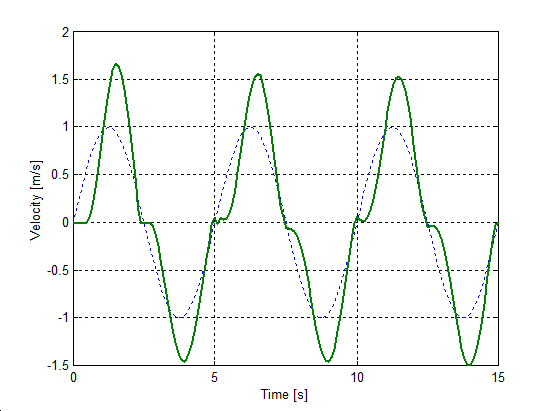
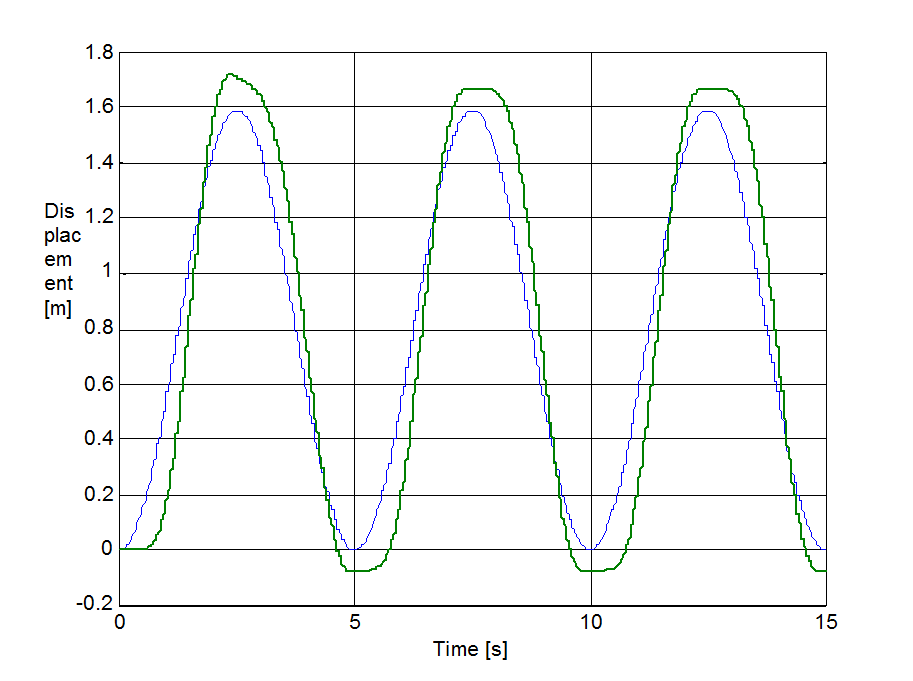
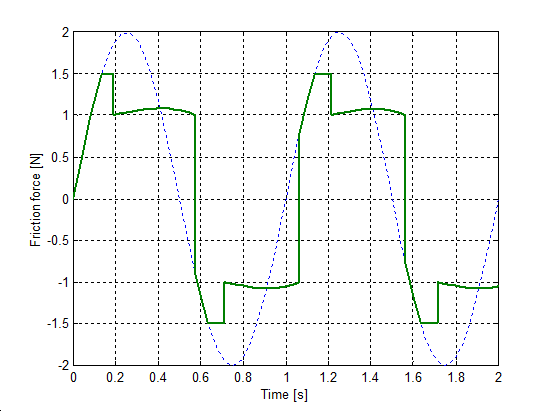
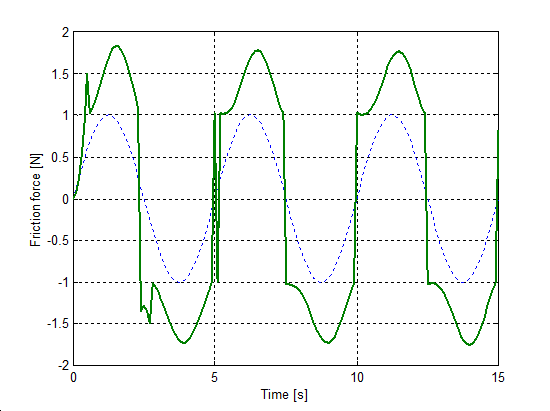
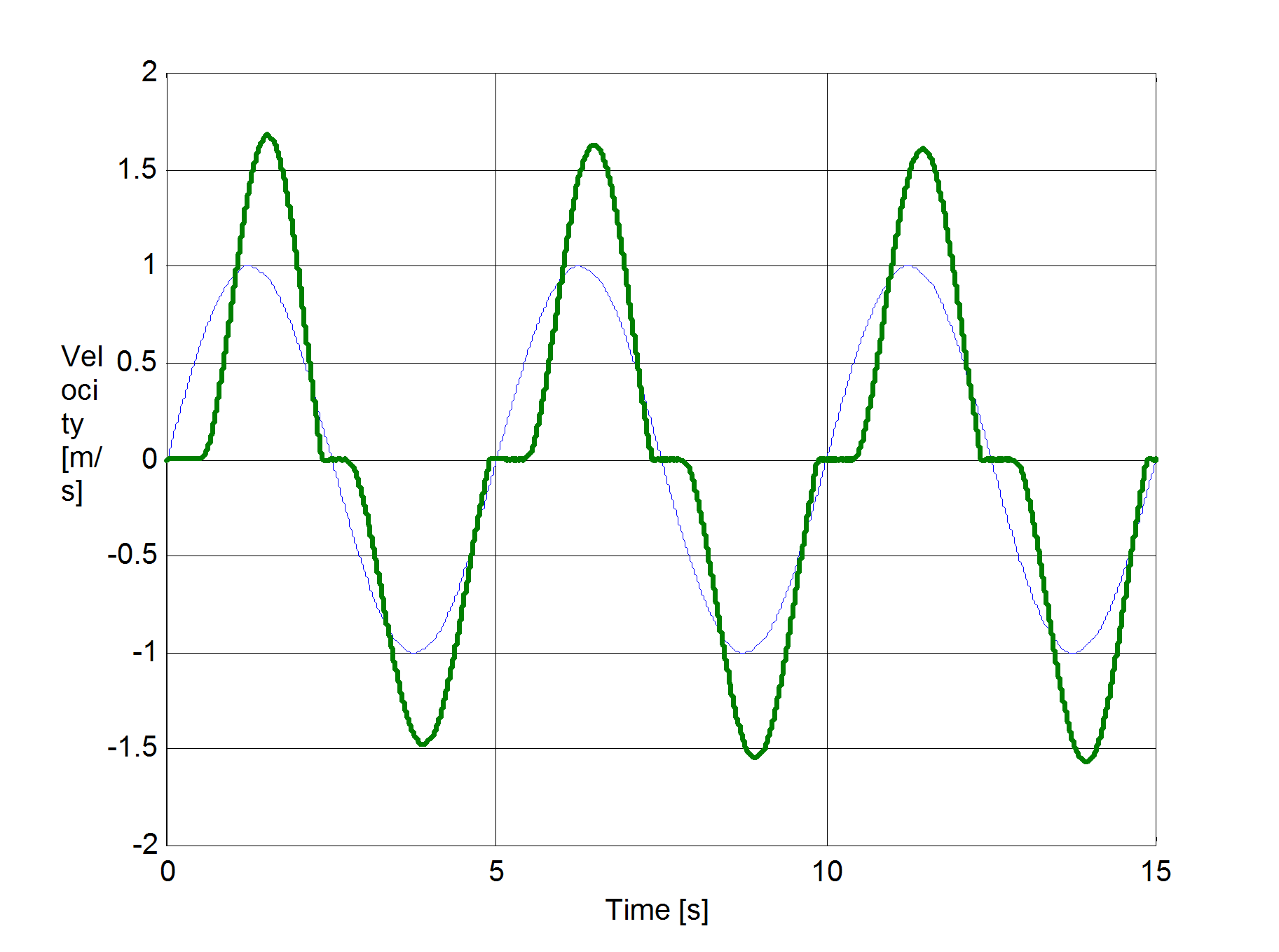
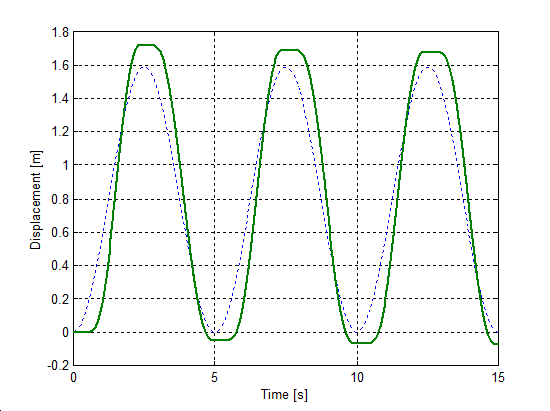
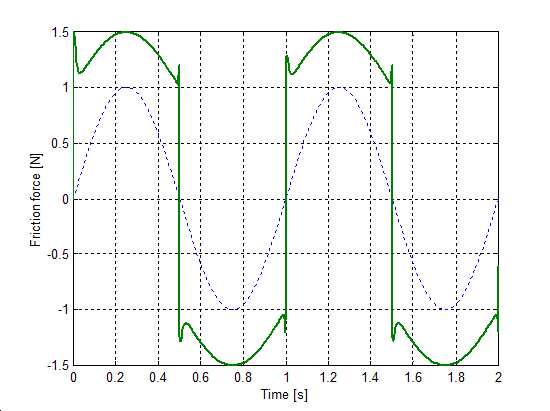
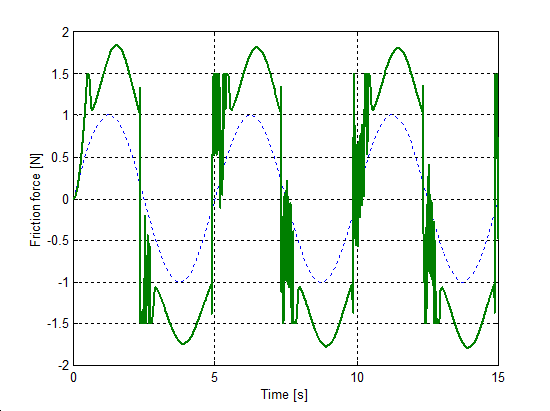
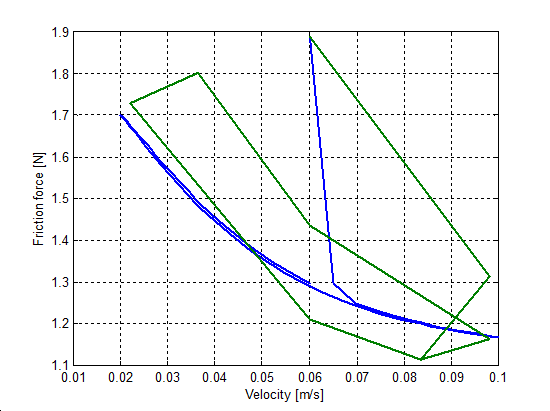
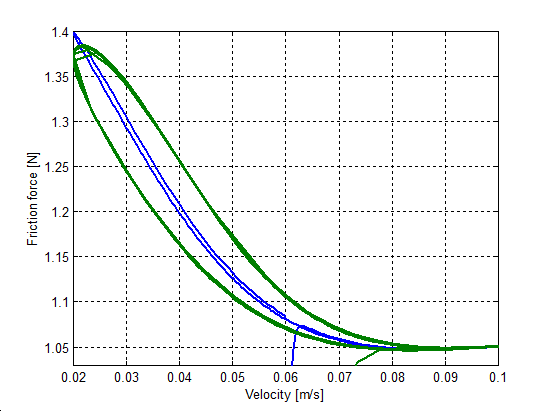
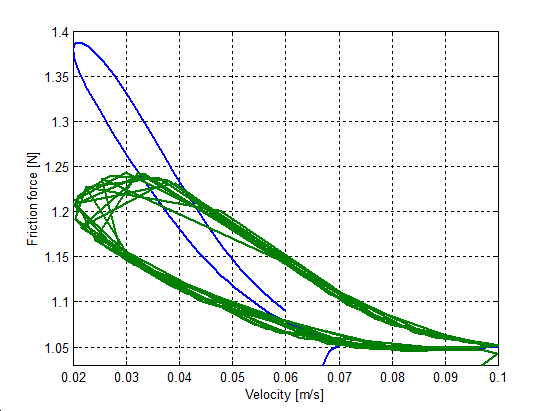
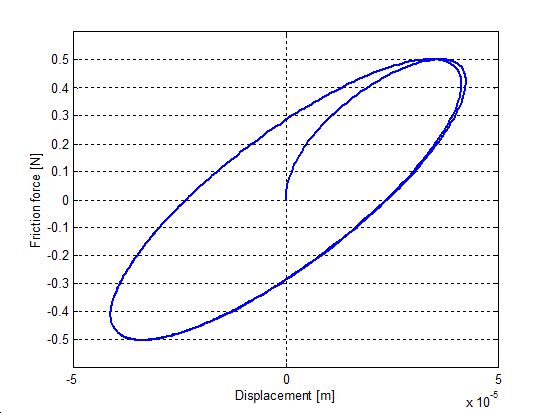
6.7.3. Hiszterézis hatás
Egy szimulációsorozatot végeztünk, hogy megmutassuk a hiszterézis jelenségét a sebesség függvényében, iránytól független mozgás esetén. A sebességet 0.06 + 0.04sin(t)-re állítottuk be, és két különböző t értékre végeztük el a szimulációt (0.1 és 1 Hz). Az 6-30-től 6-33-ig terjedő sorszámú ábrák mutatják az eredményt. Nagyobb értékek nagyobb hiszterézisgörbét mutatnak. Az átmeneti vonalak az állandósult állapotban nem lettek eltávolítva. A hiszterézis effektust minden esetben megfigyelhető, kivéve a Karnopp modellt. Ezért a görbe még sok ismétlés után is nyitott, habár t = 1 Hz esetén némi konvergenciát mutat. Ez a Karnopp modell nem dissszipatív jellege miatt van így.
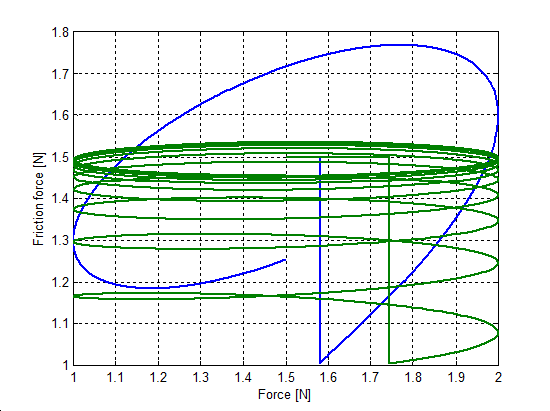
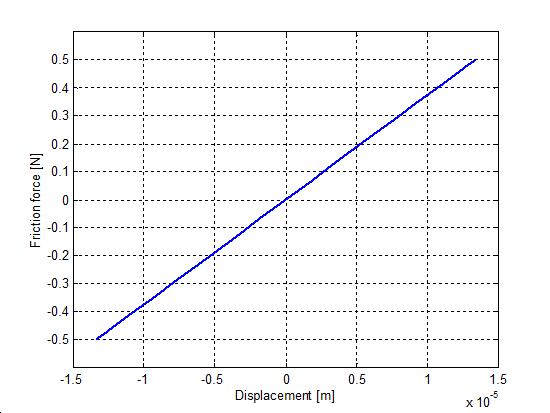
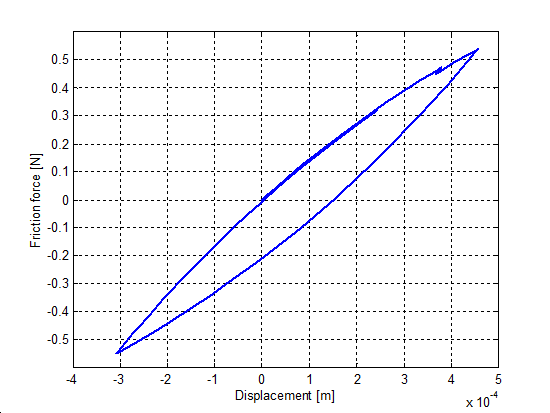
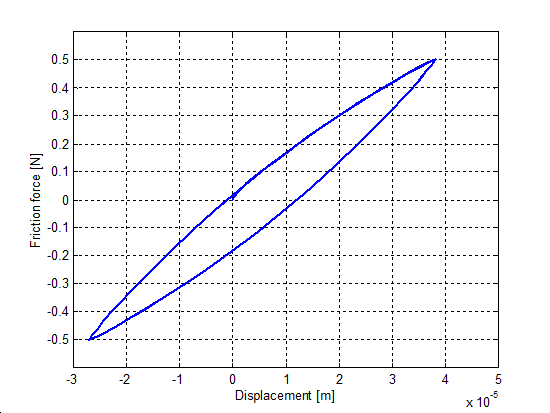
6.7.4. Rúgószerű stiction viselkedés
A zérus sebességnél javallott, hogy a modellek nem lineáris rugókarakterisztika jelleget mutassanak. Hogy ezt szimuláljuk, csak egy egészen kis erőt - kisebbet mint az elszakadási erő szintje - alkalmaztunk, minden esetben ugyanakkora nagysággal (F = 0.5 N). A fel- és leterhelési ciklusokat a szinusz függvény biztosította a megadott amplitúdóval, egységnyi tömegen. Az eredmény előcsúszási elmozdulás görbéket az 6.34-től 6.37-ig terjedő sorszámú ábrákon ábrázoltuk. Jegyezzük meg, hogy a Karnopp súrlódási modell nem tartalmazza ezt a tulajdonságot, nem úgy, mint a többi modell. A hét-paraméteres modell nem mutat hiszterézis jelenséget. Ennek az az oka, hogy a hét-paraméteres modell lineáris rugóelemet alkalmaz a Dahl effektus modellezésére. Érdekes lehet megjegyezni, hogy az M2 modell már az első ciklus után eléri az állandosult állapotát.
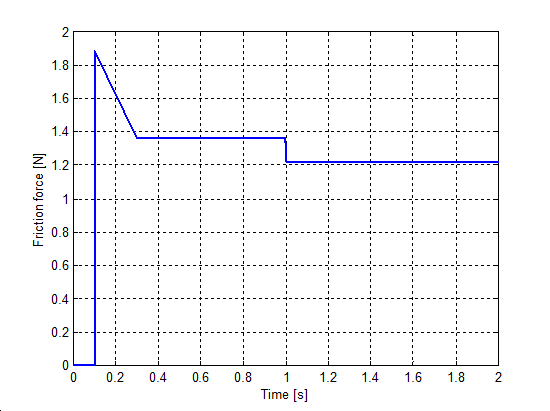
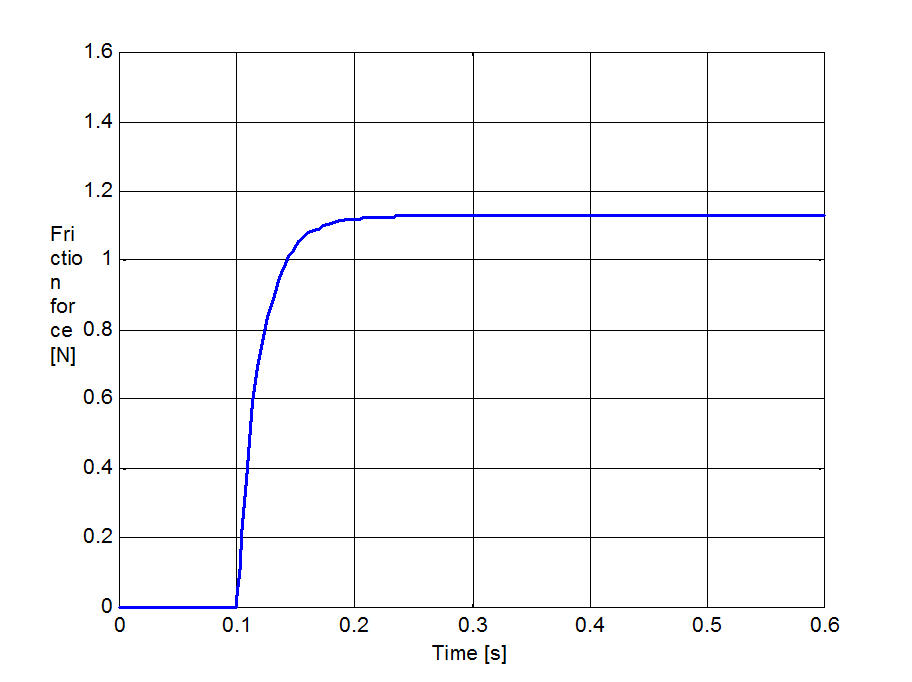
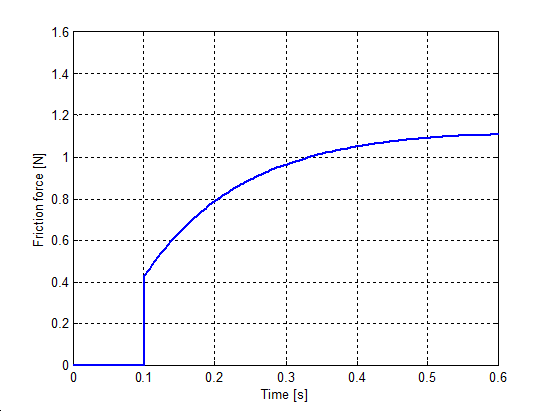
6.7.5. Rendszerválaszok
Az 6.38-től 6.42-ig terjedő sorszámú ábrák mutatják a különböző rendszerek átmeneti függvényeit, a válasz az
egység-sebességugrás bemenetre készült, kivéve a Karnopp modell esetében, ahol az ugrásfüggvény egységnyi erő volt.
6.7.6. Végső konklúzió a modellekre
Hat dinamikus súrlódási modellt mutattunk be részleteiben, ötöt vizsgáltunk meg különböző szimulációkban. Tulajdonságaik az alábbi táblázatban láthatóak. A Karnopp modellt eredetileg valós idejű használatra tervezték. A nulla körüli kis környezetben használva könnyen megoldható az integrálás véges mintavételezési ideje. Mindazonáltal ez a modell az 1980-as években lett kifejlesztve a mai fejlettebb szoftver-csomagok és a javított mintavételezési idő lehetővé teszi a bonyolultabb modellek valós-idejű használatát. A Karnopp modell szintén nem tartalmazza a disszipatív modellezést sem.
A hét-paraméteres modell a Karnopp modellel együtt korai, de sikeres próbálkozásai voltak a súrlódás modellezésének. Bár a hét-paraméteres modell tartalmazza az összes kívánt tulajdonságot a súrlódás pontos modellezéséhez, de annyira összetett, hogy nagyon nehéz ezt a modellt felhasználva működő szabályozási rendszert készíteni. Idáig a hét-paraméteres modell paramétereinek a kiszámítása is kihívás volt, talán ma már léteznek olyan új azonosító eljárások, mint például az AEP [88], amik remélhetőleg sikeresen használhatóak. A LuGre modell talán a legígéretesebb modell, ami nem csak tapasztalatilag, hanem elméletileg is alá van támasztva. Emellett sima súrlódási görbét ad, nem úgy, mint bizonyos esetekben az M2 modell, és sok esetben a módosított Dahl modell. Az állapottér modell a tudomány két területének összefogásából született: a geofizika, valamint a gépészet és a gépelemek. Végül nem maradt más kérdés, csak annak eldöntése, hogy melyik modellt kell használni. Alapjában ez a környezettől, a megengedhető hibától, a hibatűréstől, és a számítási teljesítményektől függ. A modellek számítási igény szerinti sorrendje a következő: Karnopp, módosított Dahl, állapottér modell, LuGre, hét-paraméteres, M2 modell.
|
Hét-paraméteres |
Állapot-változós |
Karnopp |
LuGre |
Módosított Dahl |
M2 |
|
|
Zero sebességen való átmenet |
igen |
nem |
igen |
igen |
igen |
igen |
|
Nagyon lassú sebességek |
igen |
nem |
igen |
igen |
igen |
igen |
|
Lassú sebességek |
igen |
igen |
igen |
igen |
igen |
igen |
|
Gyors sebességek |
igen |
igen |
igen |
igen |
igen |
igen |
|
Akadozó csúszás |
igen |
nem |
igen |
igen |
igen |
igen |
|
Disszipáció |
igen |
nem |
igen |
igen |
igen |