7. fejezet - Csúszómód alapú modell referenciás szabályozás
7.1. Bevezetés, zavaró-jel becslők rövid áttekintése
7.1.1. Inverz modellen alapuló zavaró-jel becslés
Először a mozgásszabályozás területén a kilencvenes években leggyakrabban alkalmazott „inverz modellen alapuló zavaró-jel becslés” elvét ismertetjük [10], [11], [12], [13], [14], [15], [16] kiemelve a gyakorlati alkalmazáskor felmerülő legnagyobb problémákat. Elsősorban ezek a problémák motiválták egy alapvetően módszer keresését.
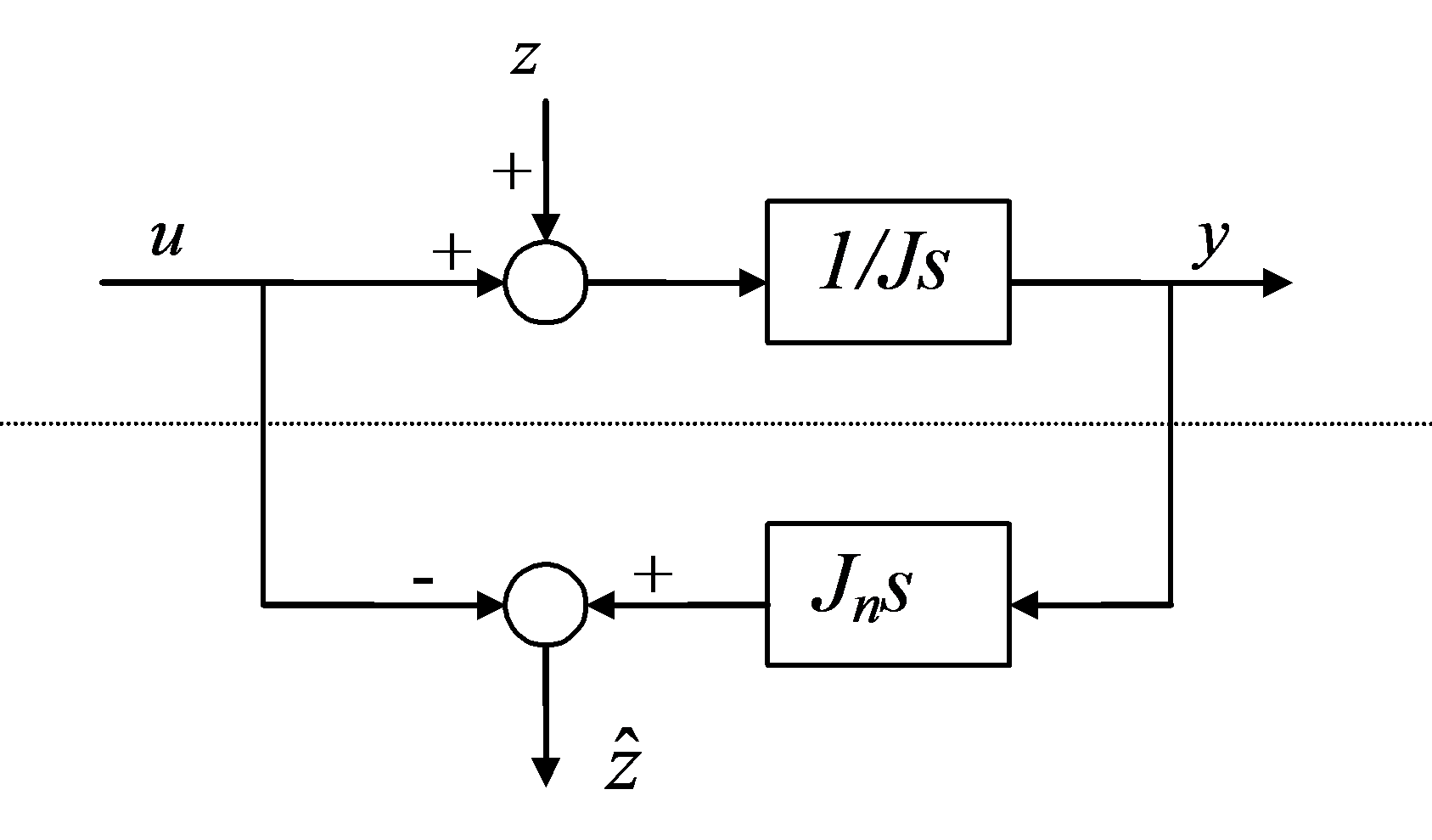
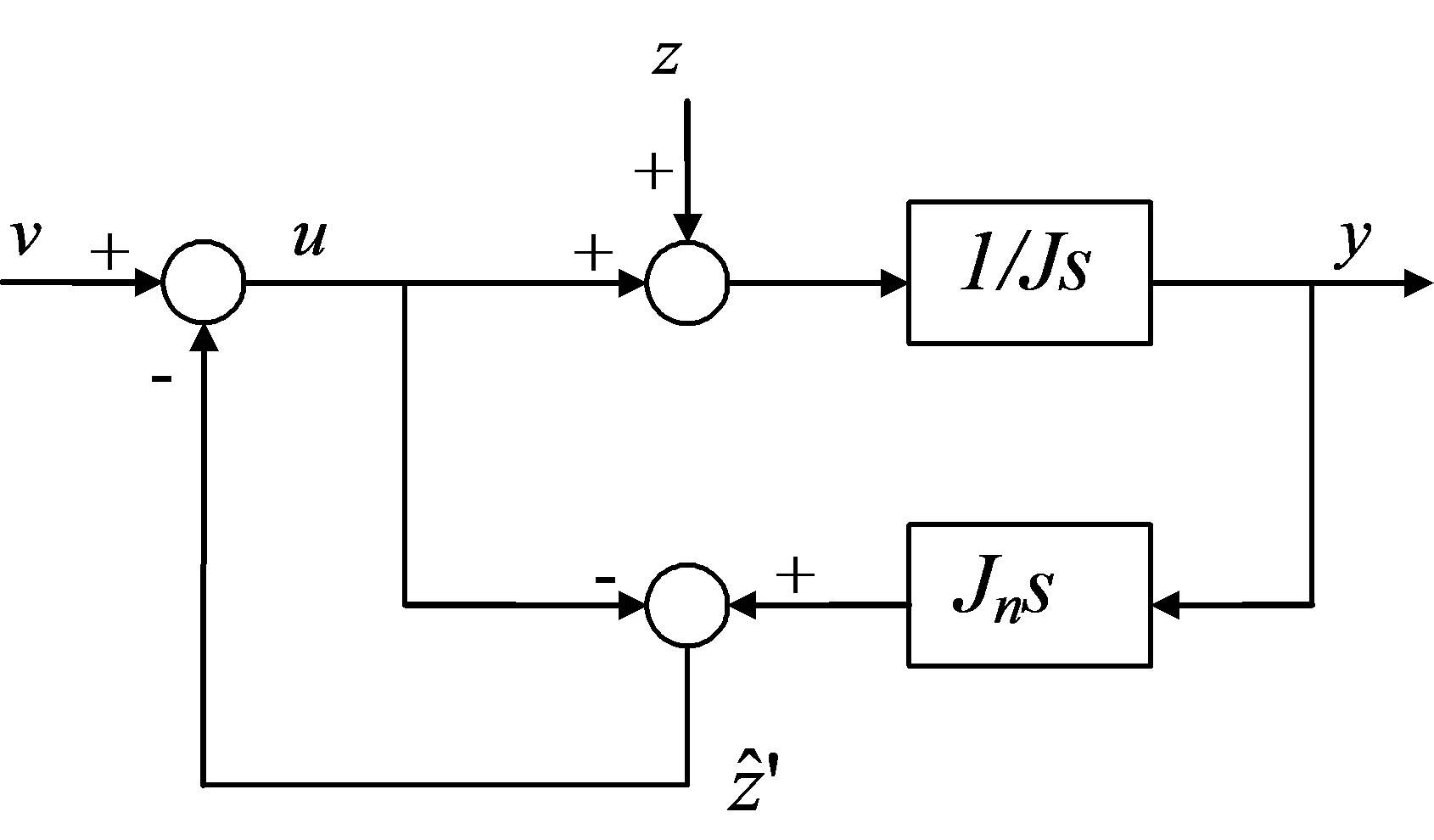
A 6-43. ábra egy nagyon egyszerű zavaró-jel becslő (disturbance observer) elvi működését mutatja be. 6-43. ábra/a felső része egy J tehetetlenségű motor egyszerűsített vázlata, míg az alsó rész a zavaró-jel becslő, amely a motor modelljének inverze. J és Jn a motor valós és névleges tehetetlenségi nyomatékai, z a bemeneten jelentkező zavaró-jel. Látható, hogy a becsült zavaró-jel, (az ábrán jelölve) nem csupán a valós zavaró-jel értékét tartalmazza, hanem a J paraméter eltéréséről is hordoz információt. A z zavaró-jel hatását a becsült zavaró-jel visszacsatolásával kompenzálhatjuk (ld. 6-43. ábra/b).
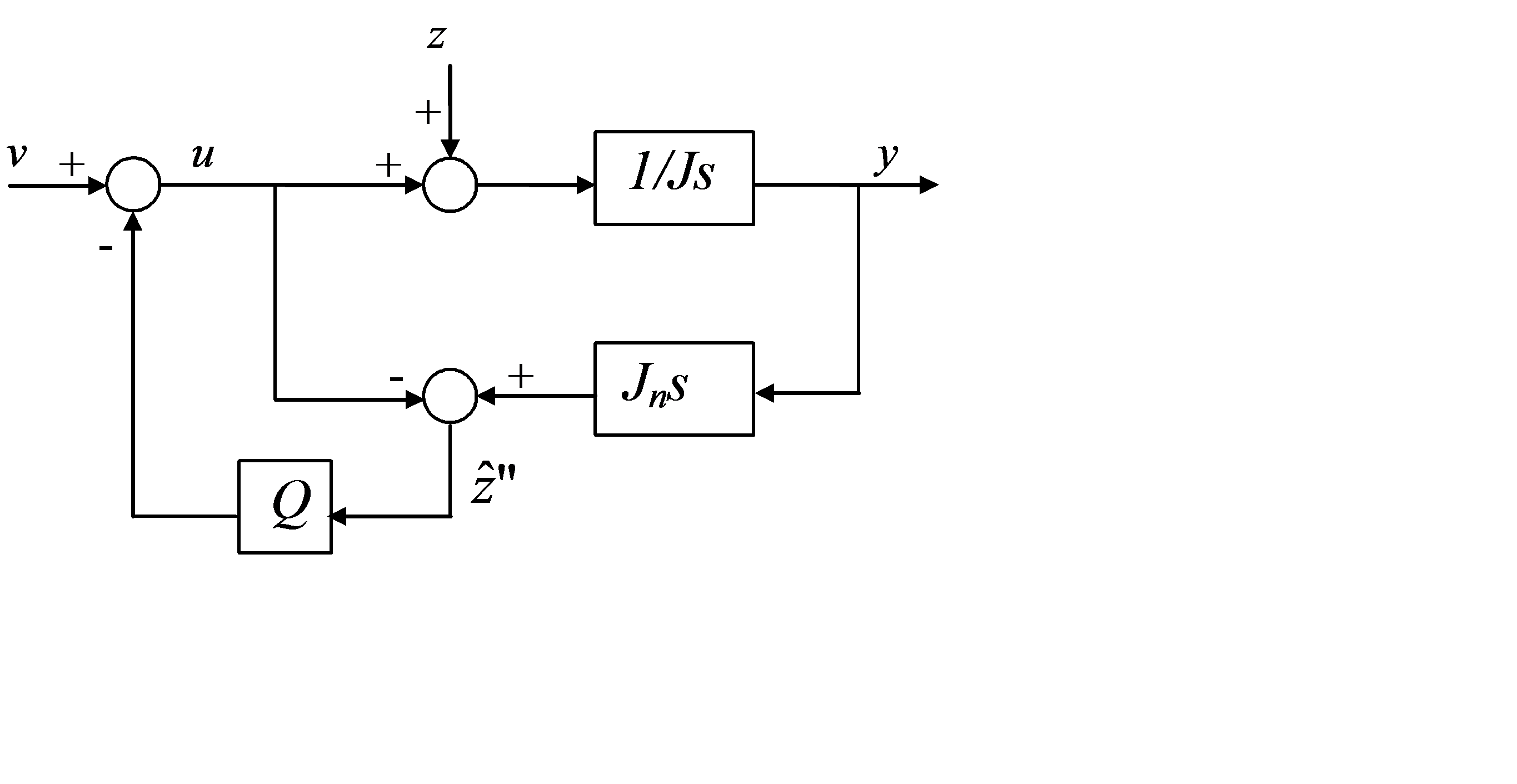
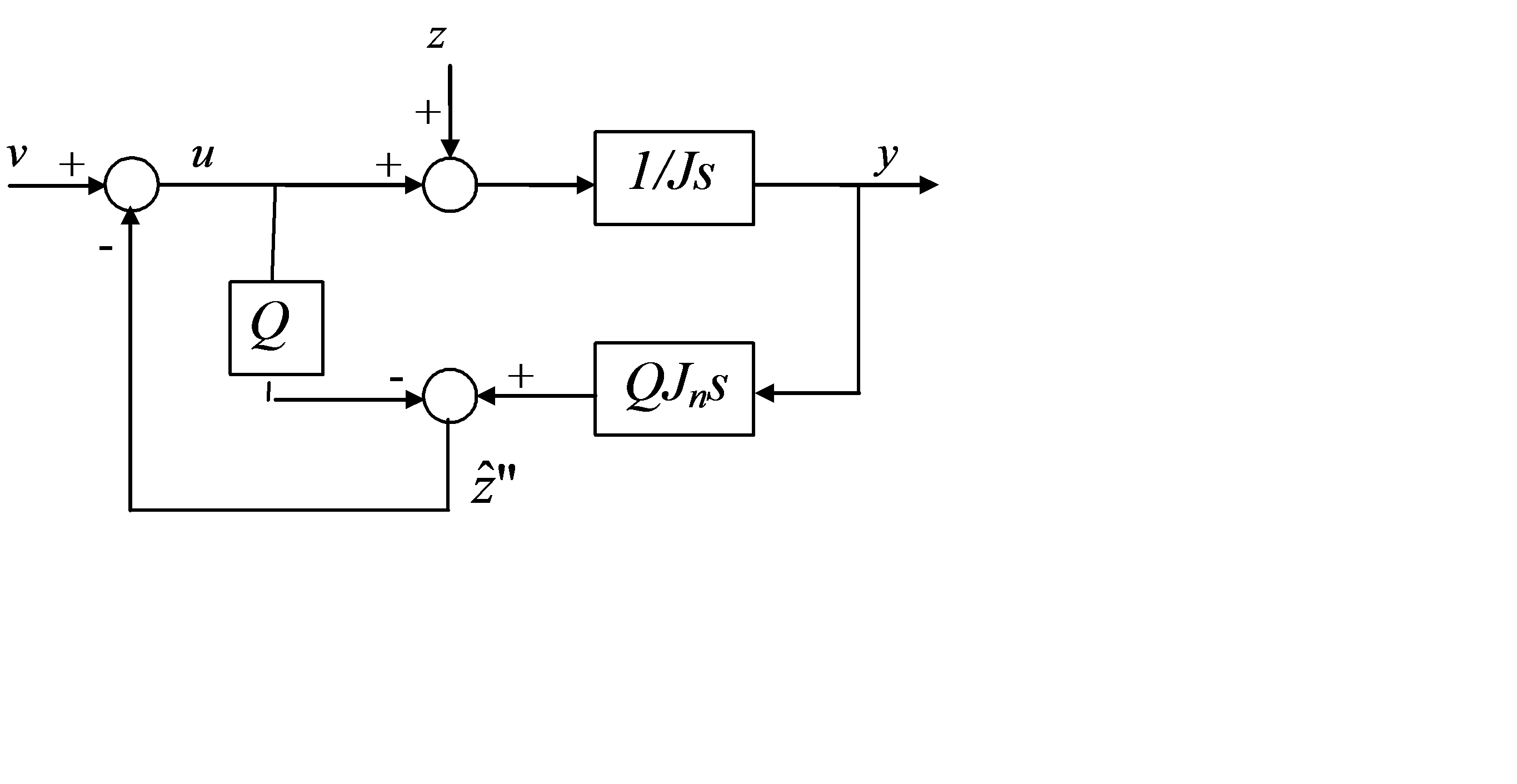
6-43. ábra A zavaró-jel becslők elvi vázlata
Egyszerű számítások után adódik, hogy az új, v bemenettől az y kimenő jelig az átviteli függvény 1/Jns, a zavaró-jeltől pedig nem függ az y. A gyakorlatban egy tiszta differenciáló tag komoly gondot okozhat, hiszen kiemeli a zajokat. Ennek kiküszöbölésére kerül a visszacsatoló ágba a Q aluláteresztő szűrő, ahogy azt a 6-43. ábra/c is mutatja. Q vágási frekvenciáját jóval nagyobbra kell választani, mint a szakasz meghatározó időállandójának reciproka (hogy a hasznos jelet nehogy kiszűrjük), ugyanakkor elegendően kicsire kell választani ahhoz, hogy a zajokat kellően elnyomja. Természetesen Q alul áteresztő szűrő összevonható a szakasz inverzével (ld. 6-43. ábra/d), a kettőt együtt célszerű realizálni. A zavaró-jel átvitelének értéke így , amely megfelelő tervezéssel elegendően kicsi lehet az alacsonyabb frekvenciás tartományban.
Ez a módszer általánosítható, de ekkor is megmarad az a probléma, hogy a legtöbb szabályozott szakasz integráló jellegű, ezért az inverze deriváló jellegű lesz. Az esetleges időkésleltetések további problémát jelentenek. A kilencvenes években cikkek sokasága foglalkozott azzal, hogy miként lehet egy olyan Q szűrőt megtervezni, amely széles tartományban gondoskodik az optimális működésről. Összefoglalásként megállapíthatjuk, hogy ennél a módszernél az a legnagyobb gond, hogy az inverz modellre alapul.
7.1.2. Modell referenciás szabályozás a külső és belső zavaró-jel becslésére
A továbbiakban ismét egy nagyon egyszerű estet vizsgálunk, ahol a szabályozott szakasz egy egyszerű arányos tag egy ismeretlen, de korlátos paraméter bizonytalansággal . Megjegyezzük, hogy ennek hatását tekintjük belső zavaró-jelnek.
Az alapelv nagyon egyszerű, az ideális és a perturbált szakasz kimenő jeleinek különbségét egy kellően nagy erősítéssel vissza csatoljuk a perturbált szakaszhoz. Ha K kellően nagy, akkor a két jel különbségnek kicsinek kell lennie, hogy visszacsatolt jel ne legyen túlzottan nagy, ez viszont azt jelenti, hogy a visszacsatolt jel információt tartalmaz a paraméter bizonytalanságról.
A 6-44. ábra/b-n az átalakított szabályozókör látható, melynek alapján már könnyen felírható a teljes átviteli függvény a bemenettől a kimenetig. Vizsgáljuk meg azt az esetet, amikor a K arányos tag értéke a végtelenbe tart.
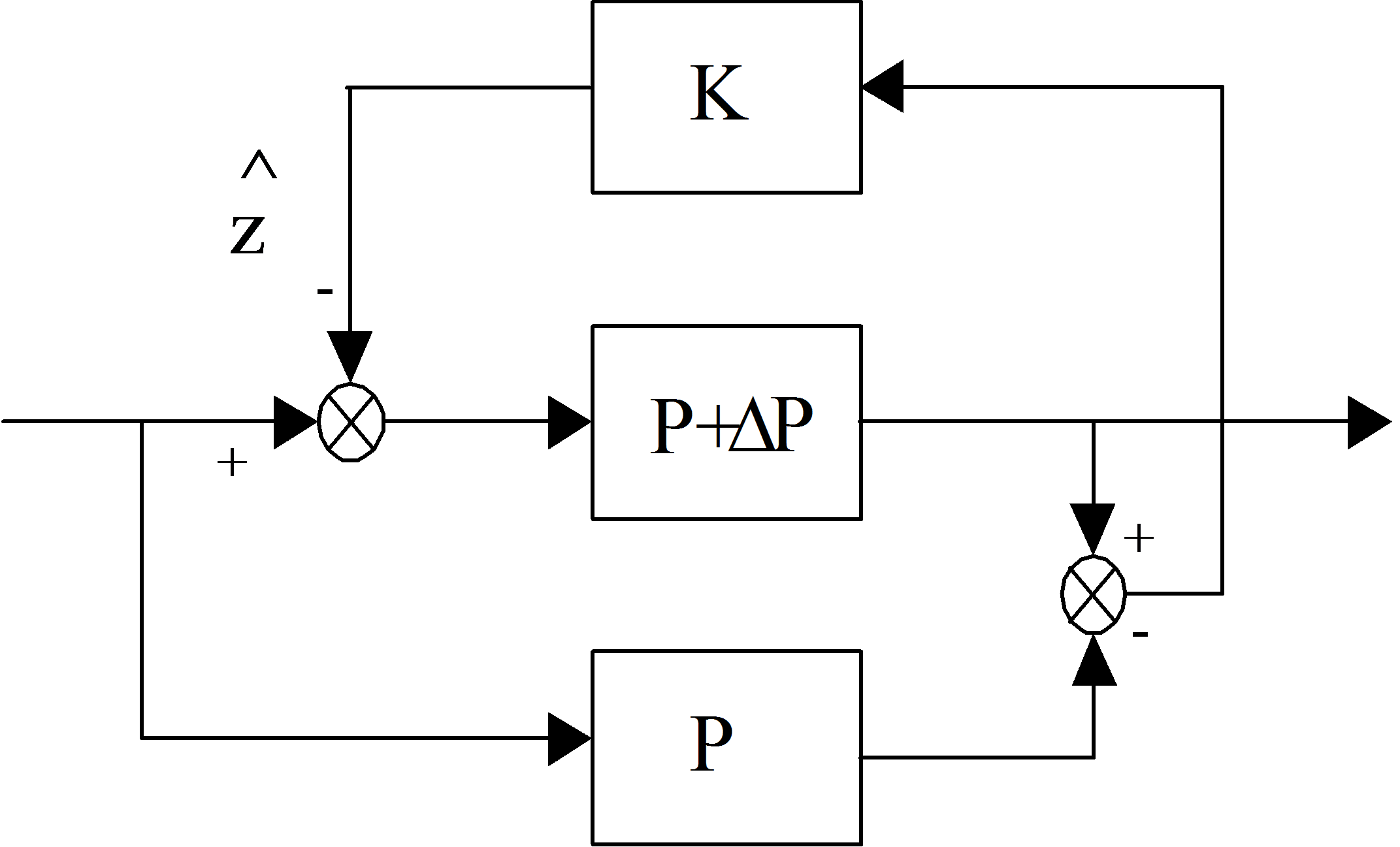
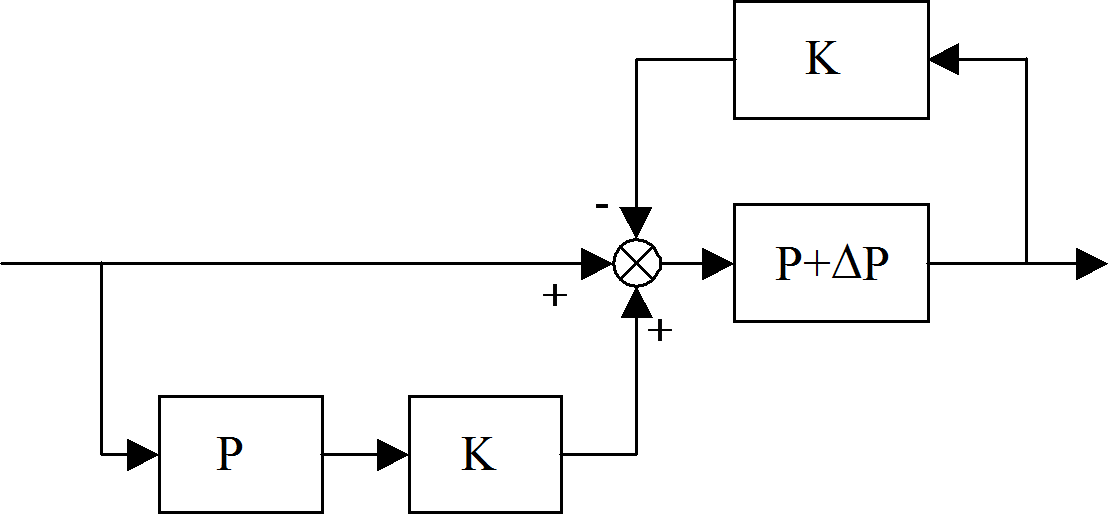
6-44. ábra/b-nak megfelelően a bemenet és a kimenet között az erősítés, a l’Hospital szabály alkalmazásával:
|
|
(6.66) |
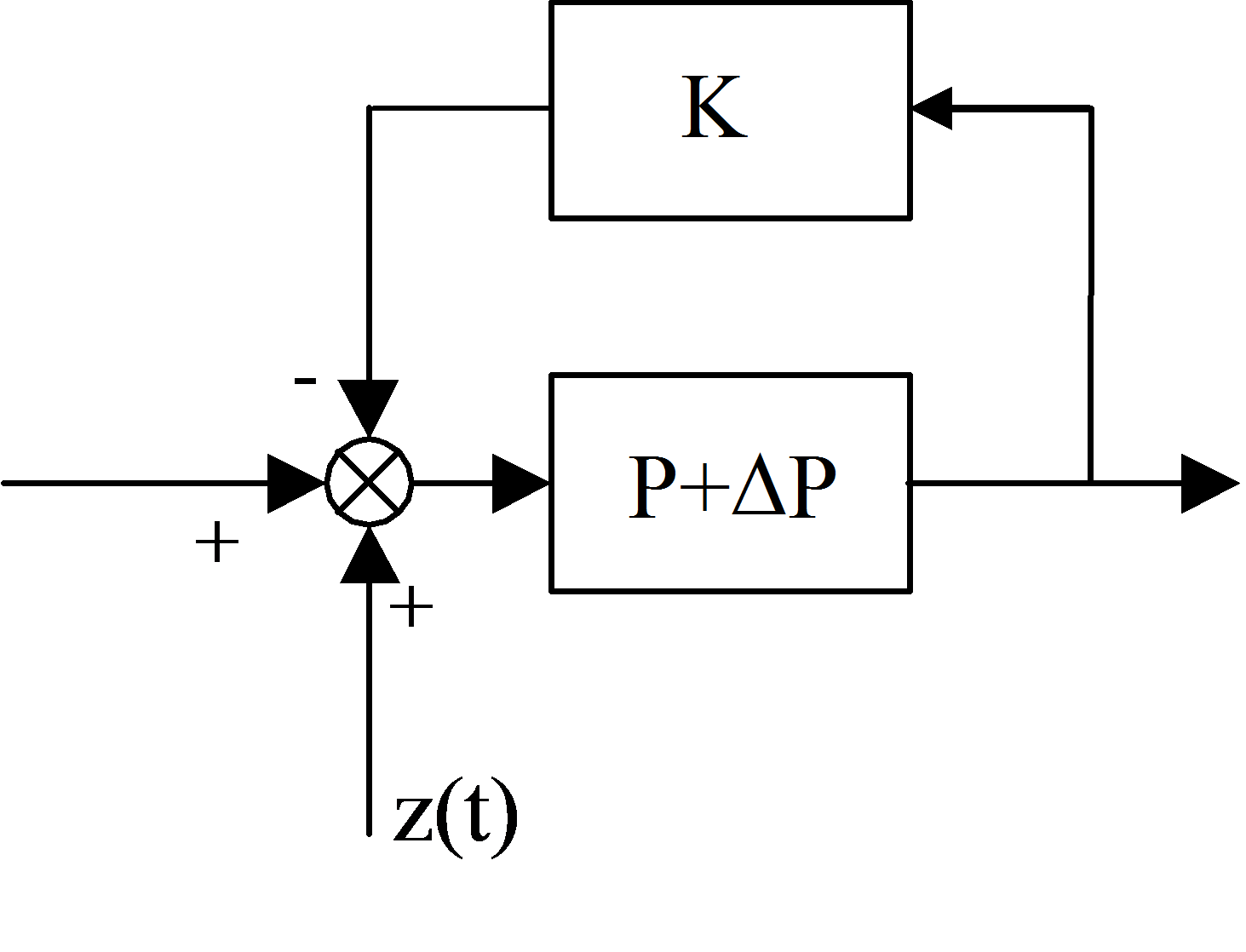
A 6-43. ábra-hoz hasonlóan adjunk z(t) korlátos zajt a perturbált szakasz bementére (lásd. 6-45. ábra). Az z(t) zaj hatása a kimenetre:
|
|
(6.67) |
Ez úgy értelmezhető, hogy a visszacsatolt jel információt hordoz mind a paraméter bizonytalanságról, mind a korlátos bemeneti zajról.
A módszer általánosítható akár több bemenetű, több kimenetű rendszerekre is, mint az a következő fejezetben láthatni fogjuk. A tervezés szempontjából az egyik legfontosabb kérdés, hogy mekkorára kell választani K értékét.
7.2. Csúszómód alapú modell referenciás szabályozás a külső és belső zavaró-jel becslésére
Reguláris állapotegyenlet alakjában adott egy perturbált LTI rendszer (6.68). Tegyük fel, hogy (6.68) kielégíti az ún. Drazenovic feltételt, más szavakkal csak azok az állapotváltozók perturbátak, amelyekre közvetlenül hat az u beavatkozó jel.
|
, |
(6.68) |
ahol és jelölik a rendszer mátrixokat, és a megfelelő korlátos paraméter-bizonytalanság, továbbá z(t) egy ismeretlen, de ugyancsak korlátos zavaró-jel, korlátos elsőrendű időbeni deriválttal. A ¯ jel a névleges, illetve más megközelítésben az előírt ideális értékeket jelöli. Az állapotváltozókat két csoportra osztjuk, x1-re, amelyre az u beavatkozó jel nem hat közvetlenül és x2-re, amelyre az u beavatkozó jel közvetlenül hat. Jelöljük a x2 perturbált állapotváltozók becsült értékét -vel, és tervezzünk egy részleges, nem folytonos megfigyelőt a következőképpen:
|
|
(6.69) |
A megfigyelőt elegendőt a perurbált állapotváltozóra megtervezni, mert ha megegyezik -vel, akkor ebből következik, hogy is megegyezik -gyel. A tag szerepe a (6.69) részleges megfigyelőben az, hogy képviselje, illetve elnyomja a paraméter-bizonytalanság és a zavaró-jel hatását. Egy szokásos Luenberger megfigyelő esetén
|
|
(6.70) |
Ismeretes, hogy L tervezése visszavezethető bármely állapot-visszacsatolás módszerre, általánosítva akár egy nem folytonos állapot visszacsatolásra is. Az ötlet az, hogy tervezünk egy nem folytonos jelet a (6.69) részleges megfigyelőhöz a csúszómód szabályozás elméletére alapozva. Továbbiakban a 2.3 pontban leírt lépéseket követve tervezzük meg a csúszómódban működő megfigyelőt.
A csúszómód szempontjából válasszuk állapotváltozónak az eredeti (6.68) rendszerben perturbált tényleges és megfigyelt állapotváltozóit.
|
|
(6.71) |
Ennek megfelelően a differenciálegyetrendszer a következő alakú lesz
|
|
(6.72) |
A célunk az, hogy legyen
|
. |
(6.73) |
Az m elemű vektor meghatározásához m feltételre, más szavakkal m darab a Hiba! A hivatkozási forrás nem található. hasonló skalár változóra, van szükség, amelyeket egy vektorba rendezhetünk. (6.73)-nak megfelelően legyen az m darab skalár változó a következő alakú
|
, |
(6.74) |
ahol egységmátrix. A 2.5 pontban láttuk, hogy több bemenetű több kimenetű rendszerek esetén alapvetően kétféle szemléletet követve juthatunk el a csúszómódhoz. Itt kövessük a lokális szemléletet, amikor a vektor minden elemére a többitől független alkalmazunk egy relés megfigyelőtörvényt.
|
ahol (i=1,2...m), |
(6.75) |
ahol i index az adott vektor i. elemét jelöli. A megfigyelőtörvény mellett szükségünk van egy szabályozási törvényre is. (6.68) második sorát összevetve (6.69)-tel észre vehetjük, hogy csúszómódban, amikor (6.73) teljesül, akkor információt tartalmaz a paraméter bizonytalanságról és külső zavaró-jelről, és ezt az információt ezek kompenzálására is felhasználhatjuk. Legyen az ideális rendszer számára előírt beavatkozó jel és válasszuk a következő szabályozási törvényt:
|
. |
(6.76) |
A következőkben azt kell belátnunk, hogy a (6.75) megfigyelőtörvény tényleg elvezet-e a csúszómód kialakulásához, továbbá tényleg tartalmaz-e információt a paraméter bizonytalanságról és külső zavaró-jelről. (6.72) és (6.76) alapján
|
. |
(6.77) |
(6.77)-ben nem folytonos. Visszatérve a 2.3-ban leírtakhoz, a csúszófelület mentén az ekvivalens vektor Hiba! A hivatkozási forrás nem található. alapján számítható ki.
|
. |
(6.78) |
Látható, hogy Hiba! A hivatkozási forrás nem található., illetve (6.78) úgy elégíthető ki, ha a nemfolytonos megfigyelőjel egy olyan ekvivalens megfigyelőjellel helyettesítjük, amelyet a következőképp kapunk meg
|
. |
(6.79) |
(6.79)-et behelyettesítve (6.77)-be és figyelembe véve, hogy
|
, |
(6.80) |
a következőt kapjuk
|
. |
(6.81) |
(6.81) úgy értelmezhető, hogy a (6.68) differenciálegyenlettel leírt eredeti rendszerre egy új, részlegesen megváltoztatott és zavaró-jeltől mentes dinamikát kényszerítünk a ekvivalens megfigyelőjel segítségével. Ekkor az eredeti állapotváltozókat a következő differenciálegyenlet írja le:
|
. |
(6.82) |
Mint később látni fogjuk bizonyos esetekben nem jelenet megkötést, hogy csak , és értéke választható meg tetszőlegesen.
A következő kérdés, hogy ekvivalens megfigyelőjel miként állítható elő, és meg kell vizsgálnunk, hogy teljesül-e a csúszómód kialakulásának feltétele. Hiba! A hivatkozási forrás nem található. feltételt alkalmazásához szükség van a -re.
|
|
(6.83) |
Tegyük fel, hogy a (6.75) megfigyelő törvényt alkalmazzuk.
|
|
(6.84) |
Hiba! A hivatkozási forrás nem található. feltétel teljesüléséhez az kell, hogy (6.84) minden sora ellenkező előjelű legyen, mint adott sora. (6.75)-ból következik, hogy minden sora megegyezik megfelelő sorainak előjelével. (6.84)-ben negatív előjellel szerepel, ezért Hiba! A hivatkozási forrás nem található. feltétel teljesítésének elégséges feltétele (6.84) és (6.79) alapján:
|
|
(6.85) |
Ez könnyen értelmezhető. A ekvivalens megfigyelőjel a végtelenül nagy frekvenciával kapcsolgatott középértéke. Ez egyben egy módszert is kínál arra vonatkozóan, hogy ekvivalens megfigyelőjel miként állítható elő. Ennek megfelelően ekvivalens megfigyelőjel előállítható átlagolásával pl. egy aluláteresztő szűrő (AÁSZ) segítségével.
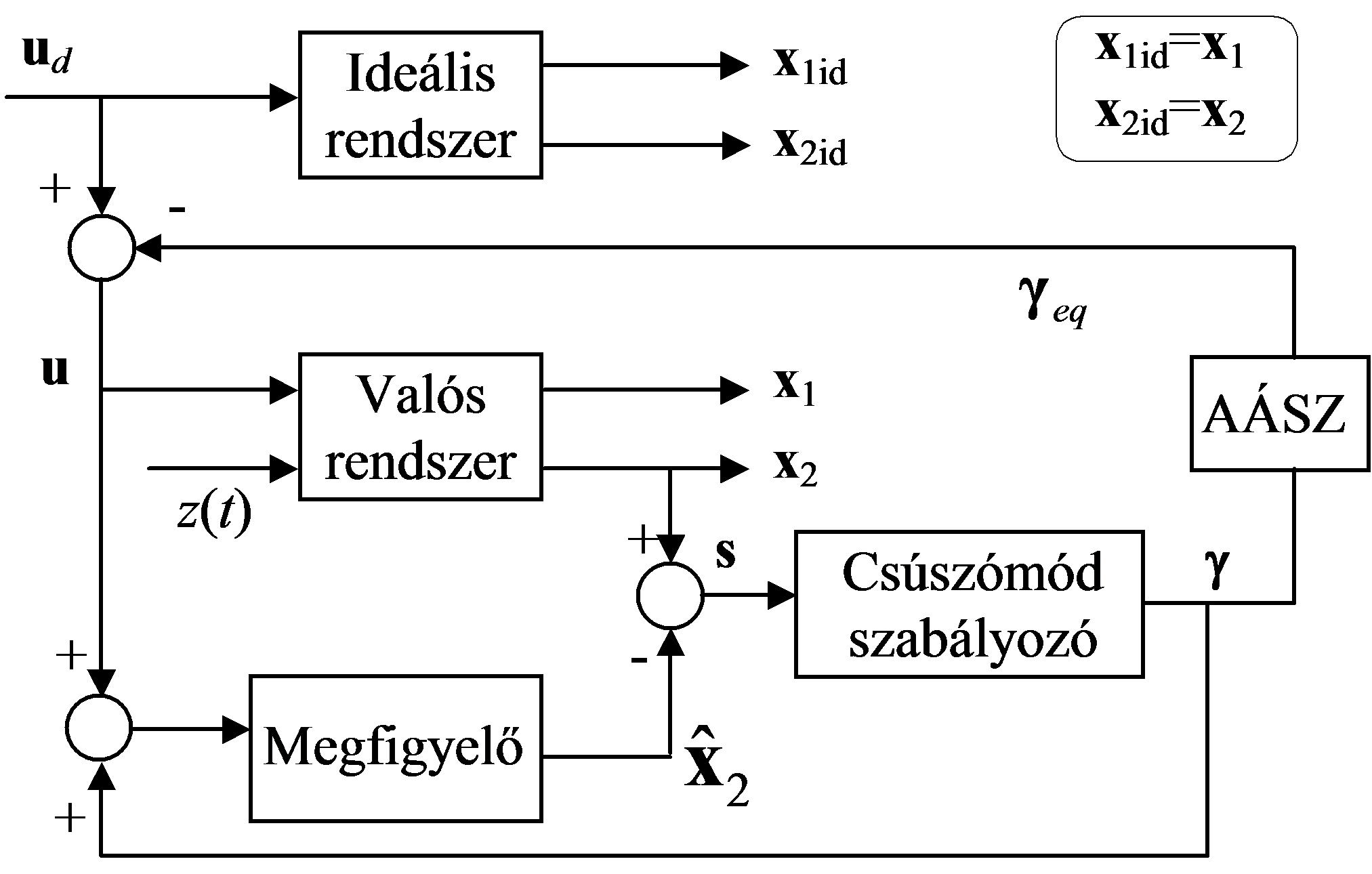
Összegezésül tekintsük a 6-46. ábra-t. A fentiekben beláttuk, hogy egy olyan rendszerre, amely (6.68) alakú differenciálegyenlettel írható le, egy új, részlegesen megváltoztatott valamint zavaró-jeltől mentes dinamikát kényszeríthetünk (ld. (6.81)) egy végtelenül nagy frekvenciával kapcsolgatott (6.75) típusú relés megfigyelőjel segítségével, ha a (6.85) feltétel teljesül.
7.2.1. Diszkrét idejű megvalósítás
Napjainkban a szabályozók többségét digitálisan valósítják meg. Két egymásnak ellentmondó elvárásunk van. Egyfelől (6.85) értelmében abszolút értékének kellően nagynak kell lennie, másfelől ha abszolút értéke nagy, akkor két mintavétel között a beavatkozás integrált hatása is nagy. Bekövetkezhet az, hogy minden mintavétel után előjelet vált, így a közép értéke nulla, annak ellenére, hogy a kompenzálandó jel nem nulla. Erre mutat példát a 6-47. ábra.Tételezzük fel, hogy a Tk mintavételi időpontok egyenletes eloszlásúak, látható, hogy az s alternál a nulla érték körül, annak ellenére, hogy a középértéke nem nulla. Ilyen esetben is alternál, ha a (6.75)-at alkalmazzuk.
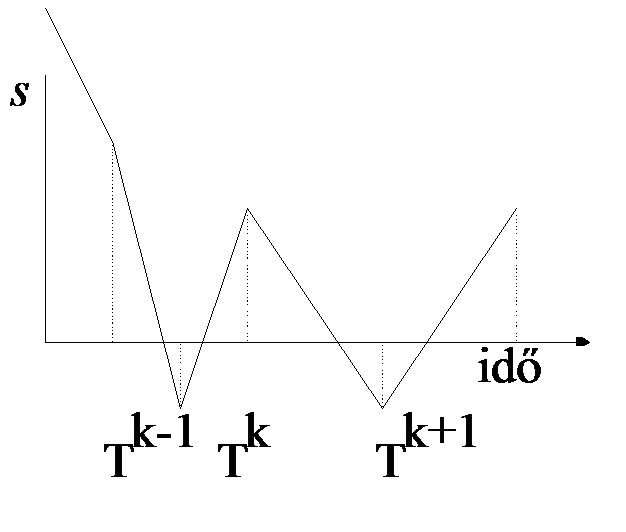
Mindenképp a (6.75) megfigyelő törvényen kell javítani. Az egyik lehetséges megoldás, ha abból indulunk ki, hogy a ekvivalens megfigyelőjel csak lassan változik. Ha feltételezzük, hogy ismerjük értékét egy k. időpillanatban, akkor a következő k+1. mintavételezési időpillanatban csak a változást kell megbecsülni, mintavételezési időpont sorszámát felső indexben jelöljük.
|
|
(6.86) |
Ebben az esetben abszolút értéke jelentősen lecsökkenthető. jelet továbbra is szűréssel állítjuk elő. Feltételezve, hogy folytonos és deriválható, abszolút értékét (6.85) helyett két mintavételi pont közötti maximális változása korlátozza
|
|
(6.87) |
ahol a két mintavétel között eltelt idő. A kísérleti berendezésünk tervezésénél (6.86)-et és (6.87)-öt alkalmaztuk.
A telemanipulációs alkalmazásoknál egy kicsit más szabályozási törvényt követtünk.
A csúszómód szabályozóknál a csattogás elkerülésének egyik módja a Ljapunov stabilitási kritériumon alapszik. Legyen egy pozitív definit Ljapunov függvény jelölt, amelyet a következő mádon választunk:
|
|
(6.88) |
A megfigyelő visszacsatolását úgy kell megválasztani, hogy Ljapunov függvény deriváltja kielégítse a következő feltételt:
|
|
(6.89) |
A fenti feltétel kielégíthető, ha sikerül egy olyan pozitív definit mátrixot találni, amelyre igaz a következő:
|
|
(6.90) |
Ekkor
|
|
(6.91) |
(6.72), (6.74) és (6.76) egyenletnek megfelelően:
|
|
(6.92) |
|
|
(6.93) |
A (6.93) megfigyelő törvény első tagja gondoskodik a csúszófelület csattogás mentes eléréséről, vagyis biztosítja a rendszer aszimptotikus stabilitását. De ez a tag nullává válik, amint a rendszer eléri a csúszófelületet. A (6.93) megfigyelési törvényben γeq tag nem ismert, ezt becsülnünk kell. Abból indulhatunk ki, hogy γeq csak lassan változik γeq értékét a k. mintavételi pontban γeq előző értékéből számíthatjuk.
|
|
(6.94) |
(6.94)-at behelyettesítve (6.93) diszkrét idejű alakjába kapjuk a következő diszkrétidejű szabályozási törvényt.
|
, |
(6.95) |
ahol és .
7.3. Csúszómód alapú modell referenciás szabályozás kísérleti alkalmazása
7.3.1. A kísérlet tervezése
Tekintsük a 3.4 pontban bevezetett és az előző fejezetben is vizsgált szervorendszert. Látható, hogy kielégíti az ún. Drazenovic feltételt
|
, |
(6.96) |
ahol
|
|
(6.97) |
Továbbá a súrlódás nem lineáris összetevőit képviseli. A kompenzáció célja az, hogy a rendszerre egy és paraméterű referencia modell dinamikáját kényszerítsünk. A megfigyelő egyenlete
|
, |
(6.98) |
A csúszómód szempontjából válasszuk állapotváltozónak a következőt.
|
|
(6.99) |
Legyen a csúszófelület
|
|
(6.100) |
Legyen a rendszer bemenő jele
|
|
(6.101) |
ahol az ideális rendszer bemenőjele. Alkalmazzunk egy relés megfigyelőtörvényt.
|
ahol |
(6.102) |
Ennek megfelelően
Az s() vektorfüggvénynek az vektortérre vonatkozó irány menti deriváltja az S felület két oldalán, ahol a a csúszómódra vonatkozó állapotváltozókat jelöli.
Ellenőriznünk kell a csúszómód kialakulásának feltételét
|
|
(6.107) |
(6.105), (6.106) és (6.107) összevetéséből következik, hogy a csúszómód kialakulásának feltétele
|
|
(6.108) |
Ha (6.108) teljesül, akkor a S felület pontjaiban a Hiba! A hivatkozási forrás nem található. definíció értelmében a trajektória változását leíró ekvivalens vektor a Hiba! A hivatkozási forrás nem található.-hoz hasonlóan a következő alakú
|
|
(6.109) |
Hiba! A hivatkozási forrás nem található., (6.105) és (6.106) alapján
|
|
(6.110) |
(6.110)-at (6.109)-be helyettesítve belátható, hogy a (6.86) rendszer dinamikai tulajdonságai megváltoztathatók a (6.101) szabályozási és (6.102) megfigyelő törvény segítségével a (6.108) feltétel teljesülése mellett
|
|
(6.111) |
A szabályozó hatásvázlatát a 6-48. ábra-n foglaltuk össze. Az ábrán a Megfigyelő nevű doboz egyben referencia modellnek is felfogható.
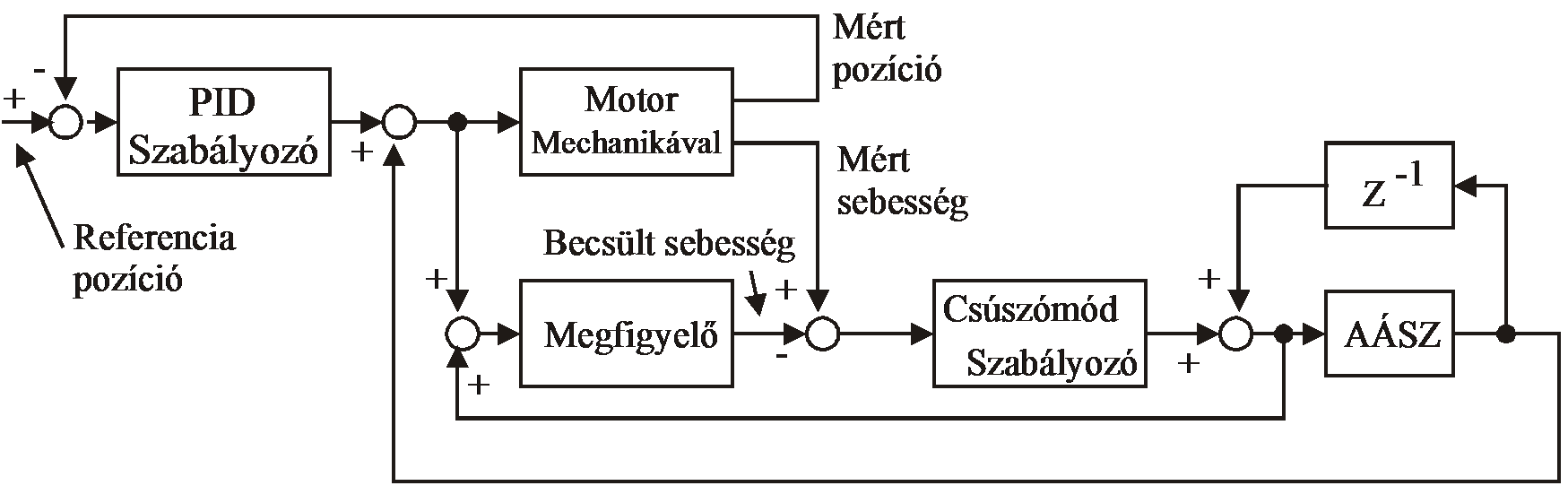
7.3.2. Mérési eredmények
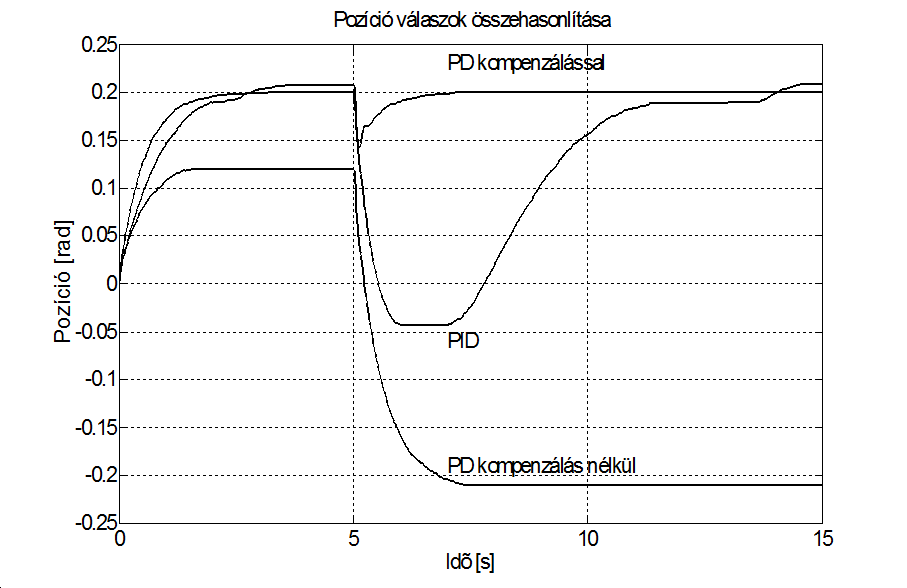
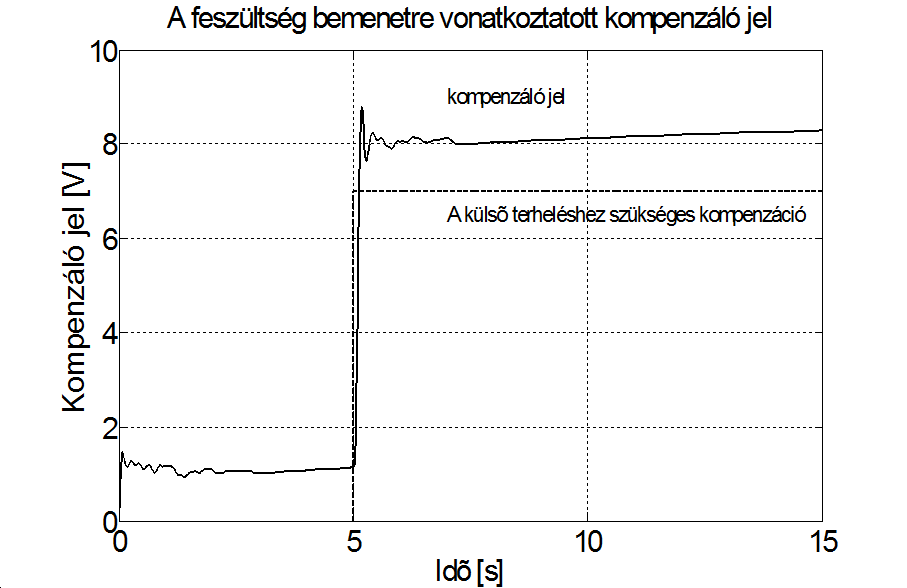
Ismét a pozíciószabályozás a cél. A zavarkompenzáció feladata az, hogy a nem lineáris súrlódást kompenzálva egy általunk meghatározott ideális dinamika követésére kényszerítse a tényleges rendszerünket. A kompenzálás képességeinek bemutatása érdekében egy olyan pozíciószabályozót választottunk, amely esetén kompenzáció nélkül az ideáli és a valós rendszer válasza szembetűnően eltér. Tekintsük a 6-49. ábra-t. A választásunk a PD szabályozóra esett, amely elvileg pozíciószabályozásnál súrlódás mentes esetben tudná kompenzálni az állandósult hibát, mivel ideális esetben a motoron belül van egy integráló hatás. Az arányos tagot és a referencia jelet is szándékosan nagyon kicsire választottuk P=15. (A referencia jel nagyságának is csak nem lineáris rendszereknél van jelentősége.) A PD szabályozó esetén, ahogy a motorra jutó feszültség a kritikus 1.2 V érték alá csökken, a motor beragad. A t=5sec időpillanatban szoftveresen egy terhelésrádobást hajtottunk végre, olyan módon, hogy a motor számára kiadott feszültség jelből levontunk 7 V-ot. A terhelés rádobás után a valós rendszer válasza még előjelben is különbözik az ideális rendszer válaszától. A 6-49. ábra-ból egyértelműen kitűnik, hogy kompenzáció nélkül ez a PD szabályozó nem tud megbirkózni a feladattal. Hangsúlyozzuk, hogy egy lényegesen nagyobb arányos taggal, különösen nagyobb referencia jelnél sokat lehetne javítani a szabályozás minőségén, de az a célunk, hogy a javasolt kompenzáció hatékonyságát mutassuk be. Ha ugyan ezt a kifejezetten rosszul megválasztott és kifejezetten rosszul behangolt PD szabályozót kiegészítjük a javasolt kompenzációval, akkor egy teljesen elfogadható működést érhetünk el. A terhelés rádobás előtti állandósult hiba 40%-ról lecsökkent 0.15 %-ra. A terhelés rádobás után ennél is nagyobb arányú a javulás, ekkor az állandósult hiba 205%-ról 0.4%-ra csökken. Összehasonlításul, megvizsgáltuk, hogy a (P és D értékeket változatlanul hagyva) milyen javulás érhető el egy olyan integráló tag hozzáadásával, amely a motoron kívül van. Lineáris rendszer és konstans alapjel esetén az integráló típusú szabályozások állandósult hibája nulla, de a súrlódás miatt a rendszerünk nem tekinthető lineárisnak; jól látható az ún. stick-slip jelenség. Terhelés rádobás előtt a váltakozó előjelű hiba 3.7% volt terhelés rádobás után 4.6%. A 6-50. ábra a kompenzáló jel időfüggvényét mutatja, az ábrán szaggatott vonallal jelöltük a külső terheléshez szükséges kompenzációt. Jól látható, hogy a terhelés rádobás előtt kialakult egy konstans kompenzáló jel, ez az a mozgás közben jelentkező Coulomb súrlódást kompenzálja, és ezért nem ragad be a rendszer a referencia jel elérése előtt, mint a kompenzáció nélküli PD szabályozásnál. A 6-49. ábra és 6-50. ábra összevetéséből az is látszik, hogy a kompenzáló jel gyorsabb változásokra képes, mint a pozíciójel, ez a használhatóság egyik fontos élőkövetelménye.
7.4. Csúszómód alapú modell referenciás szabályozás gyakorlati alkalmazásai
7.4.1. Egy 20 szabadsági fokú Érzékelő Kesztyű
Az Érzékelő Kesztyű a Tokió Egyetemen készült, és képes lefedni az emberi kéz szabadsági fokait csuklótól lefelé. Minden ujjhoz 4 szabadsági fok tartozik, amivel igen bonyolult és precíz mozgásokat is lehet a távoli környezet felé közvetíteni. Az érzékelő kesztyű fotója a 6-51. ábra-n látható. Ez a kép csak azokat a részeket mutatja, amelyek közvetlenül az emberi kézhez kapcsolódnak. Az izületeket állandó mágnessel gerjesztett egyenáramú motorok mozgatják. A motorokat nem szereltük fel a kesztyűre, mivel jelentősen megnövelte volna a kesztyű tömegét, és ez fárasztó lenne az operátor számára. A motorokat egy külön állványon kaptak helyet. A motorok Bowdenen keresztül hajtják az izületeket. A kesztyűn erőmérő cellákat is elhelyeztünk, hogy közvetlenül mérni tudjuk az operátor által kifejtett erőt.
A 6-52. ábra-n látható egy ujj mechanikai kialakítása. Az ábra az egy ujjra (finger) felszerelt egységet mutatja a két véghelyzetben. A véghelyzetek meghatározásánál ideális esetet feltételeztünk: minden ujjperc maximálisan 90 fokos elfordulásra képes. Minden ujjpercet egy csuklós mechanizmus fed le

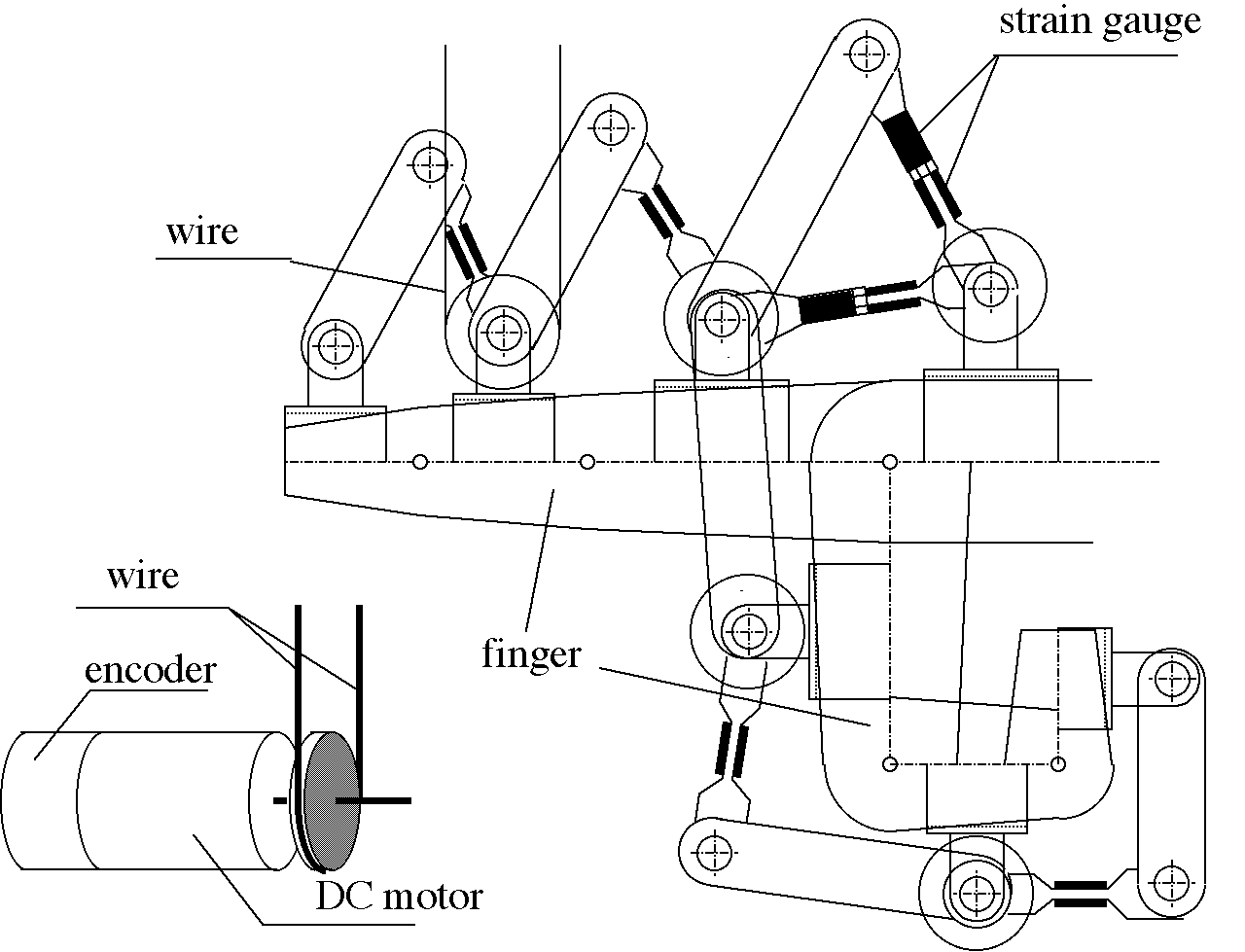
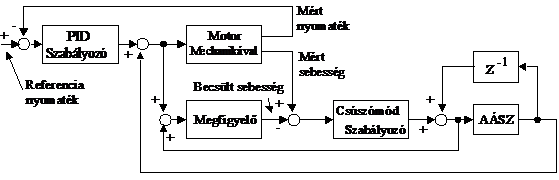
Az operátor szemszögéből az Érzékelő Kesztyű mozgatásához szükséges mindenfajta erő (beleértve a súrlódás legyőzéséhez és a mechanika mozgatásához, gyorsításához felhasznált erők) zavarásnak tekinthető. Nyilvánvaló, hogy az Érzékelő Kesztyű teljes dinamikáját csak végtelenül nagy teljesítménnyel lehetne kikompenzálni, ezért szükségszerű, hogy az operátor valamilyen minimális erőt érzékeljen az Érzékelő Kesztyű felöl, annak mozgatása érdekében, de lehetőség szerint ennek az erőnek olyan csekélynek kell lennie, amit az operátor már gyakorlatilag nem érzékel. A másik megközelítés az, hogy az érzékelő kesztyű számára előírunk valamilyen mesterséges dinamikát, csekély súrlódással. Például olyan dinamikát programozunk az operátornak, hogy azt az érzetet keltsük, mintha áramló folyadékban dolgozna. Az Érzékelő Kesztyű számára egy olyan modell követését kell előírni, amely egy megfelelően kis értékű erővel mozgatható és a szabályozó kör referencia jele a távoli környezetből közvetített nyomaték jel. Először japán hallgatók egyszerű PID szabályozást próbáltak ki, de nem nyújtott kielégítő eredményt. Egyik látogatásom során javasoltam, hogy próbálják ki, a tézisben szereplő csúszómód alapú modell referenciás szabályozást. A 6-53. ábra-n egy izületre vonatkozó szabályozás hatásvázlata látható. Az ábrán a Megfigyelő nevű doboz egyben referencia modellnek is felfogható. A csúszómód szabályozó célja, hogy a referencia modell követésére kényszerítse a rendszert. Ez a referencia modell független attól, hogy milyen egyéb szabályozási kör van körülötte. A nyomatékszabályozó PID típusú szabályozási kör, már csak a referencia modellt látja, mint szabályozott szakaszt. Ha a referencia modell lineáris, akkor a nyomaték szabályozás szamszőgéből egy egyszerű lineáris szabályozásról beszélhetünk.
A referencia modell behangolását egyetlen izület pozíció szabályozása segítségével végezzük el a kísérletben leírt pozíciószabályozáshoz hasonlóan. Első lépésként a kompenzáló eljárást kellett behangolni. Kompenzáció szempontjából nincs jelentősége, hogy az operátor milyen feladatot hajt végre, ezért a behangolásnál az operátort egy pozíciószabályozó hurok helyettesítette.
7.4.1.1. Operátor mutatóujjának szabad mozgásának vizsgálata
Szabad mozgáskor az a feladat, hogy az operátor minél kevesebbet érezzen a kesztyű dinamikájából, vagyis hogy az előre definiált szabad mozgás esetében érvényes virtuális impedanciát érezze. A nyomaték referencia jel nulla. A 6-54. ábra-n a szabad mozgás mérési eredményei láthatóak.
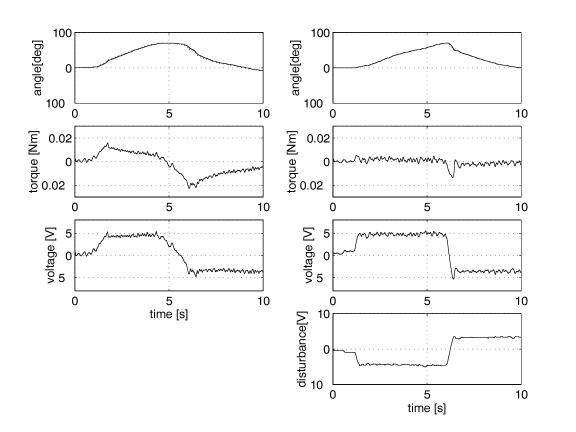
A legfelső sorban a szögelfordulás (angle) látható fok (deg) egységben. A mérést úgy végeztük, hogy a mutatóujj és a tenyér csatlakozásánál található csukló, tenyérre merőleges elmozdulását mértük vízszintes és derékszög között. A második sorban a mechanikában elhelyezett nyomaték mérő cella által mért nyomaték (torque) van. A harmadik sorban a motor bemenetére kapcsolt feszültséget (voltage) lehet látni, Volt [V] egységben. A bal oldali oszlop a tisztán PID szabályozással működik, zavarkompenzáció nélkül, míg a jobb oszlopban PID szabályozás van zavarkompenzációval. Ezért a jobb oszlopban az utolsó ábra a becsült zavaró-jelet mutatja.
Látható, hogy a referencia modell alkalmazása esetében a nyomaték jellege egyenletes és csak a nulla egy környezetében mozog. Egy nyomaték csúcs látható akkor, mikor az operátor az ujját az alsó véghelyzetből a felső alaphelyzetbe viszi vissza. Csak PID típusú szabályozás esetén egy állandó nyomaték hiba van. Ez azért van, mert a PID szabályozók csak viszonylag szűk tartományban képesek helyesen kompenzálni. Amikor az operátor ezen tartományon kívül dolgozik, akkor a szabályozás már nem képes megfelelően ellátni a feladatát.
7.4.2. Egy 6 szabadságfokú mikromanipulátor mestereszközének súrlódás kompenzációja
A probléma teljesen hasonló volt mint az érzékelő kesztyűnél. A japán hallgatók nem tudtak megbirkózni a 6-55. ábra-n látható erő visszacsatolásos mikromanipulátor mestereszközének súrlódás kompenzációjával. A probléma elsősorban a lineáris mozgásoknál jelentkezett, így csak ezzel foglalkoztunk. Egy rugós erőmérővel megmérve a mester kar mozgatásához kompenzáció nélkül akár 30 N erőre is szükség volt, ez semmiképp sem megfelelő precíziós mozgatási feladatok elvégzésére.

Referencia modellnek a következőt választottuk
|
|
(6.112) |
Figyelem, itt s a Laplas operátort jelöli, a referencia modell sebessége a referencia modellre ható erő. Ez a modell azt jelenti, hogy 0.1N erővel meglehetősen nagy, v=2.5 m/s sebesség érhető el, szemben azzal, hogy kompenzáció nélkül 10 N erővel meg sem tudjuk mozdítani a mester kart. Ebben az esetben mód nyílt arra is, hogy a csúszómód alapú modell referenciás szabályozást összevessük egy klasszikus modell referenciás adaptív szabályozással, ahol következő szabályozási törvényt alkalmaztuk
|
|
(6.113) |
ahol mesterkarra ható erő, p modell bemenőjelének erősítési tényezője és q sebesség jel visszacsatolásának erősítési tényezője. A két adaptációs törvény
|
|
(6.114) |
Ahol és az ún. tanulási paraméter. A klasszikus modell referenciás adaptív szabályozás hatásvázlata a 6-56. ábra-n látható.
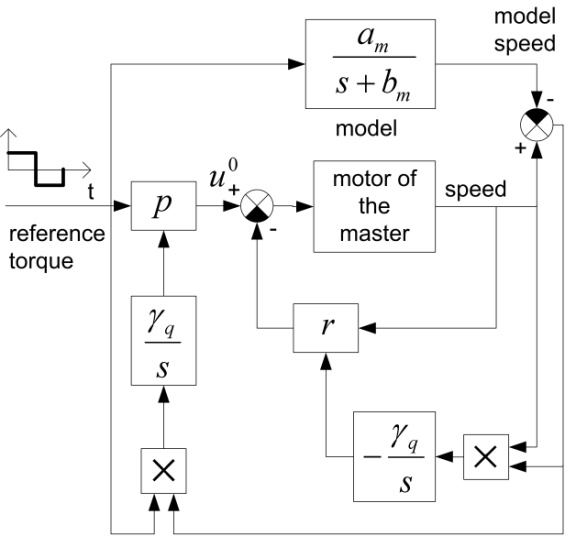
A modell követés behangolásához ismét a pozíciószabályozást használtuk a mérési eredményeket a 6-57. ábra és 6-58. ábra-n foglaltuk össze. Az X tengely mentén lehetett a legkönnyebben mozgatni a mesterkart, és az Y tengely mentén a legnehezebben. Az eredményeket táblázatosan is összefoglaltuk. Itt csak a japán hallgatók méréseire tudunk hagyatkozni, állításuk szerint a legjobban behangolt klasszikus modellreferenciás adaptív szabályozásnál a tézisben javasolt csúszómód alapú modell referenciás szabályozás jobb eredményt ad. Ha esetleg ez az állítás nem lenne igaz, akkor az mindenképp elmondható, hogy a tézisben javasolt módszer egyszerűbben megvalósítható és egyszerűbben behangolható.
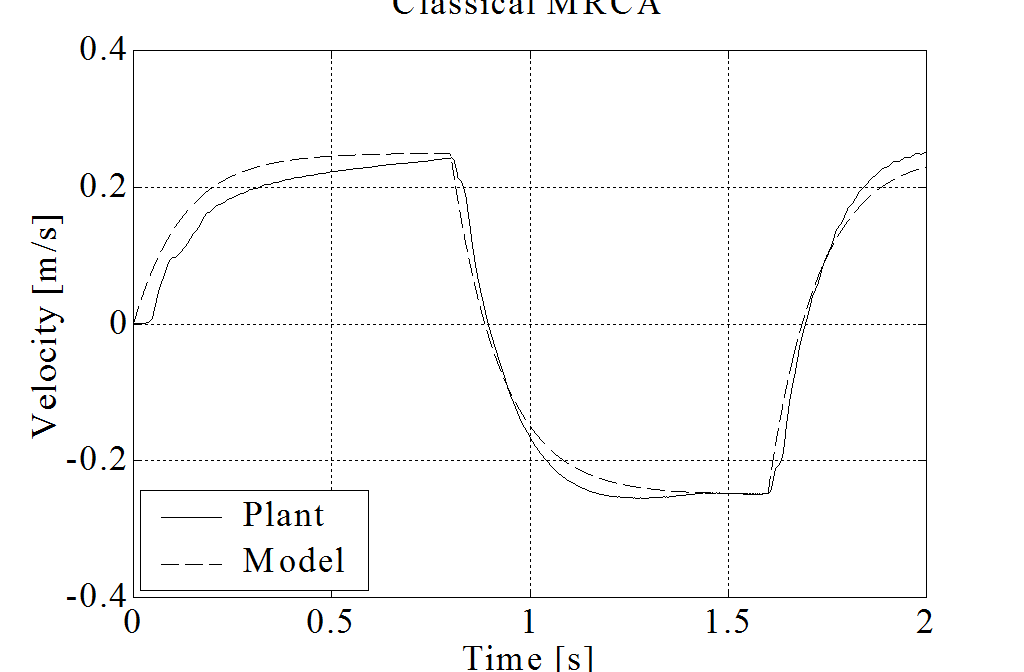
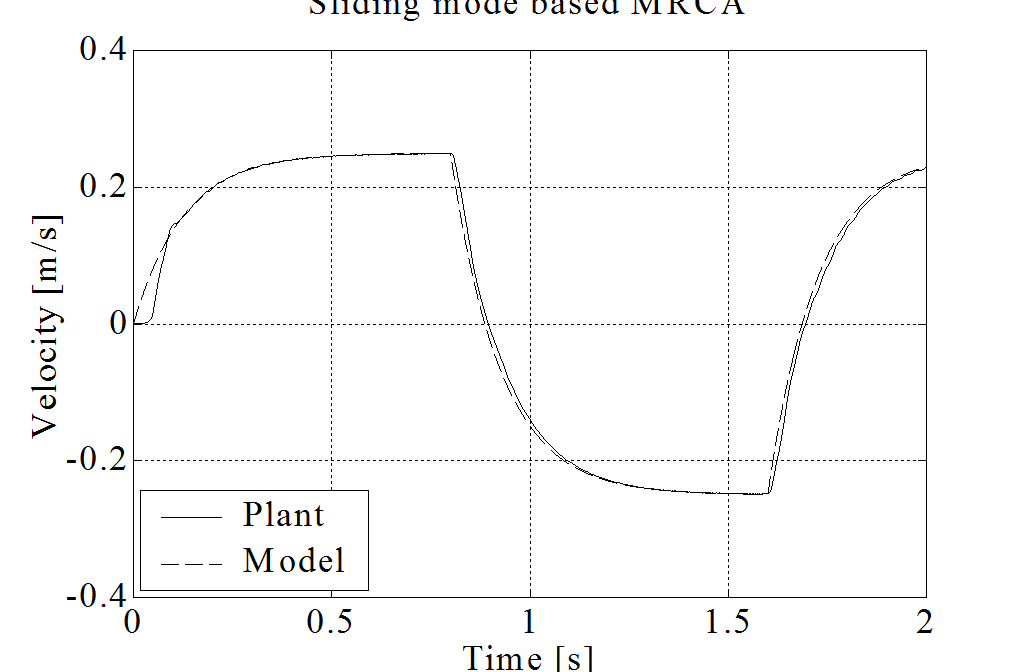
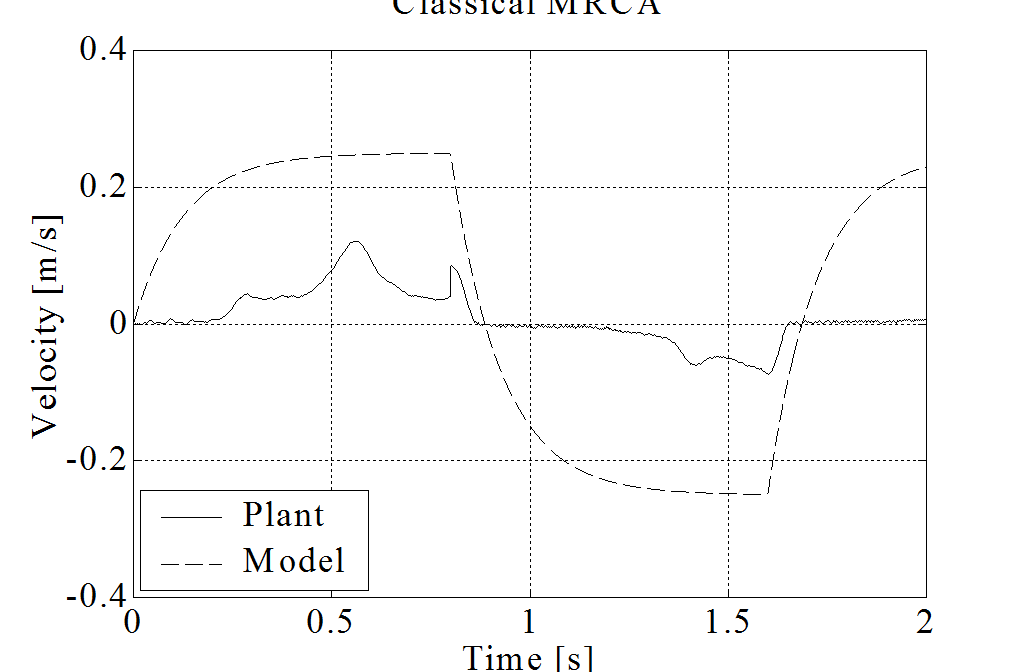
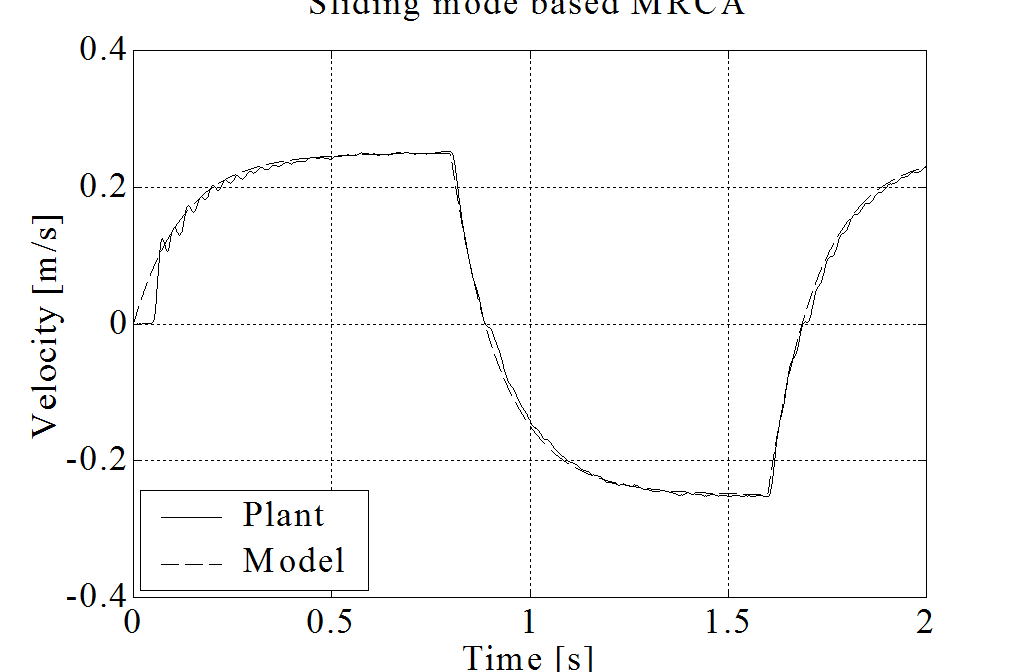
Mérési eredmények táblázatos összehasonlítása
|
Szabályozó \ tengely |
X |
Y |
Z |
|
Sszabályozás nélkül |
10 [N] |
32 [N] |
14 [N] |
|
Klasszikus modell referenciás adaptív szabályozás |
0.05 [N] |
0.07 [N] |
0.05 [N] |
|
Csúszómód alapú modell referenciás szabályozás |
0.001 [N] |
0.002 [N] |
0.005 [N] |