4. fejezet - Feladatok a visszacsatolt rendszer stabilitásával kapcsolatban
Vissza		Előre

4. fejezet - Feladatok a visszacsatolt rendszer stabilitásával kapcsolatban

Tartalom

4 . 1 feladat

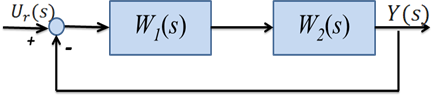
A rendszer hatásvázlata az alábbi ábrán látható. Az átviteli függvények: $W_{1} = \frac{1}{T s}$ és $W_{2} = \frac{1}{1 + 2 s + s^{2}}$ . Határozzuk meg milyen $T$ értékek esetén stabil a rendszer.

4.1. ábra - 4.1 feladat

Megoldás

Először meg kell határoznunk a visszacsatolt eredő átviteli függvényt:

$W_{c l} = \frac{W_{1} \cdot W_{2}}{1 + W_{1} \cdot W_{2}} = \frac{\frac{1}{T s} \cdot \frac{1}{1 + 2 s + s^{2}}}{1 + \frac{1}{T s} \cdot \frac{1}{1 + 2 s + s^{2}}} \cdot \frac{T s (1 + 2 s + s^{2})}{T s (1 + 2 s + s^{2})} = \frac{1}{1 + T s + 2 T s^{2} + T s^{3}}$

(4.1)

Ebből a karakterisztikus egyenlet:

$1 + T λ + 2 T λ^{2} + T λ^{3} = 0$

(4.2)

$\begin{array}{l} H = | \begin{matrix} 2 T & 1 & 0 \\ T & T & 0 \\ 0 & 2 T & 1 \end{matrix} | \\ H_{1} = 2 T > 0 \Rightarrow T > 0 \\ H_{2} = 2 T^{2} - T > 0 \\ T (2 T - 1) > 0 \\ T < 0 és T > 0.5 \\ H_{3} = H_{2} \end{array}$

(4.3)

ha $T > 0$ , akkor minden együttható pozitív
a Hurwitz determináns:

Mivel az együtthatók vizsgálatából azt kaptuk, hogy $T > 0$ , így a minden feltételt kielégítő megoldás: $T > 0.5$ .

4 . 2 feladat

Az 4-2. ábraán egy szabályozási kör látható, ahol a szabályozott szakasz átviteli függvénye

$W_{p} = \frac{1}{(1 + 10 s) (1 + 1 s) (1 + 0.1 s)}$

(4.4)

4.2. ábra - Szabályozási kör

Legyen a szabályozó átviteli függvénye:

$W_{c} = P$

(4.5)

$W_{c} = P \frac{(1 + 10 s)}{10 s}$

(4.6)

$W_{c} = P (1 + s)$

(4.7)

$W_{c} = P \frac{(1 + s)}{(1 + 0.1 s)}$

(4.8)

$W_{c} = P \frac{(1 + 10 s) (1 + s)}{10 s (1 + 0.1 s)}$

(4.9)

A fenti esetekben határozzuk meg, hogy milyen $P$ értékek esetén stabilis a rendszer.

Megoldás

A visszacsatolt rendszer eredő átviteli függvénye:

$W_{c l} (s) = \frac{W_{c} (s) W_{p} (s)}{1 + W_{c} (s) W_{p} (s)} = \frac{W_{x} (s)}{1 + W_{x} (s)}$

(4.10)

Behelyettesítve a szabályozó és a szabályozott szakasz átviteli függvényeit:

$W_{c l} = \frac{\frac{P}{(1 + 10 s) (1 + 1 s) (1 + 0, 1 s)}}{1 + \frac{P}{(1 + 10 s) (1 + 1 s) (1 + 0, 1 s)}} = \frac{\frac{P}{(1 + 10 s) (1 + 1 s) (1 + 0, 1 s)}}{\frac{P + (1 + 10 s) (1 + 1 s) (1 + 0, 1 s)}{(1 + 10 s) (1 + 1 s) (1 + 0, 1 s)}}$

(4.11)

$W_{c l} = \frac{P}{P + (1 + 10 s) (1 + 1 s) (1 + 0, 1 s)}$

(4.12)

A felnyitott kör átviteli függvénye:

$W_{x} = \frac{P}{(1 + 10 s) (1 + 1 s) (1 + 0, 1 s)} = \frac{N u m_{x} (s)}{D e n_{x} (s)}$

(4.13)

Ezáltal a karakterisztikus egyenlet a következő $p (s) = N u m_{x} (s) + D e n_{x} (s)$ , azaz

$p (s) = s^{3} + 11, 1 s^{2} + 11, 1 s + P + 1$

(4.14)

Tehát a karakterisztikus polinom együtthatói:

${[\begin{matrix} a_{3} & a_{2} & a_{1} & a_{0} \end{matrix}]}^{T} = {[\begin{matrix} 1 & 11, 1 & 11, 1 & P + 1 \end{matrix}]}^{T}$

(4.15)

Az együtthatók alapján a stabilitás szükséges feltétele, hogy minden egyes együttható legyen pozitív, így:

$P > - 1$

(4.16)

Harmadfokú polinom esetén a Hurwitz-mátrix a következő:

$H = [\begin{matrix} a_{2} & a_{0} & 0 \\ a_{3} & a_{1} & 0 \\ 0 & a_{2} & a_{0} \end{matrix}]$

(4.17)

A Hurwitz-mátrix alapján a szükséges determináns értéke:

$H_{2} = \det (H_{2}) = a_{2} a_{1} - a_{3} a_{0} = 123, 21 - (P + 1) > 0$

$122.21 > P$

(4.18)

A stabilitásvesztés feltétele $P_{\max} = 122.21$

Karakterisztikus egyenlet: $p_{a} (s) = s^{3} + 11, 1 s^{2} + 11, 1 s + P + 1$

A stabilitás feltétele: $- 1 < P < 122, 21$

Karakterisztikus egyenlet: $p_{b} (s) = s^{3} + 11 s^{2} + 10 s + P$

A stabilitás feltétele: $0 < P < 110$

Karakterisztikus egyenlet: $p_{c} (s) = s^{2} + 10, 1 s + P + 1$

A stabilitás feltétele: $- 1 < P < \infty$

Karakterisztikus egyenlet: $p_{d} (s) = s^{3} + 20, 1 s^{2} + 102 s + 10 P + 10$

A stabilitás feltétele: $- 1 < P < 204, 02$

Karakterisztikus egyenlet: $p_{e} (s) = 0, 1 s^{3} + 2 s^{2} + 10 s + P$

A stabilitás feltétele: $- 1 < P < 200$

Összefoglalva a táblázatból kiolvasható, hogy a D tag hozzáadásával a maximális körerősítés megnövelhető.

P tag	ideális PD tag	valóságos PD tag	PI tag	valóságos PID tag
$W_{c} = P$	$W_{c} = P (1 + s)$	$W_{c} = P \frac{(1 + s)}{(1 + 0.1 s)}$	$W_{c} = P \frac{(1 + 10 s)}{10 s}$	$W_{c} = P \frac{(1 + 10 s) (1 + s)}{10 s (1 + 0.1 s)}$
$P_{m a x} = 122$	$P_{m a x} = \infty$	$P_{m a x} = 204$	$P_{m a x} = 110$	$P_{m a x} = 200$

4 . 3 feladat

Az 4-2. ábraán egy szabályozási kör látható, ahol a szabályozott szakasz átviteli függvénye

$W_{p} = \frac{1}{(1 + 10 s) (1 + 1 s) (1 + 0.1 s)}$

(4.19)

4.3. ábra - Szabályozási kör

A legyen a szabályozó átviteli függvénye:

$W_{c} = P$

(4.20)

$W_{c} = P \frac{(1 + 10 s)}{10 s}$

(4.21)

$W_{c} = P (1 + s)$

(4.22)

$W_{c} = P \frac{(1 + s)}{(1 + 0.1 s)}$

(4.23)

$W_{c} = P \frac{(1 + 10 s) (1 + s)}{10 s (1 + 0.1 s)}$

(4.24)

A fenti esetekben határozzuk meg $P$ értékét úgy, hogy a fázistartalék kb. 50 legyen.

Megoldás

A felnyitott kör átviteli függvénye

$W_{x} (s) = \frac{P}{(1 + 10 s) (1 + 1 s) (1 + 0.1 s)}$

(4.25)

$φ_{t} = 180 - \tan^{- 1} (10 ω_{c}) - \tan^{- 1} (1 ω_{c}) - \tan^{- 1} (0.1 ω_{c})$

$P = (1 + 10 ω_{c} j) (1 + 1 ω_{c} j) (1 + 0.1 ω_{c} j)$

(4.26)

Behelyettesítve

$ω_{c} = 0.8811 r a d / s e c P = 11.8644 φ_{t} = 50.0564$

(4.27)

A felnyitott kör átviteli függvénye

$W_{x} (s) = \frac{P}{(10 s) (1 + 1 s) (1 + 0.1 s)}$

(4.28)

$φ_{t} = 180 - 90 - \tan^{- 1} (1 ω_{c}) - \tan^{- 1} (0.1 ω_{c})$

$P = (10 ω_{c} j) (1 + 1 ω_{c} j) (1 + 0.1 ω_{c} j)$

(4.29)

Behelyettesítve

$ω_{c} = 0.7221 r a d / s e c P = 8.9300 φ_{t} = 50.0368$

(4.30)

A felnyitott kör átviteli függvénye

$W_{x} (s) = \frac{P}{(1 + 10 s) (1 + 0.1 s)}$

(4.31)

$φ_{t} = 190 - \tan^{- 1} (10 ω_{c}) - \tan^{- 1} (0.1 ω_{c})$

$P = (1 + 10 ω_{c} j) (1 + 0.1 ω_{c} j)$

(4.32)

Behelyettesítve

$ω_{c} = 8.591 r a d / s e c P = 113.2673 φ_{t} = 50.001$

(4.33)

A felnyitott kör átviteli függvénye

$W_{x} (s) = \frac{P}{(1 + 10 s) (1 + 0.1 s) (1 + 0.1 s)}$

(4.34)

$φ_{t} = 180 - \tan^{- 1} (10 ω_{c}) - \tan^{- 1} (0.1 ω_{c}) - \tan^{- 1} (0.1 ω_{c})$

$P = (1 + 10 ω_{c} j) (1 + 0.1 ω_{c} j) (1 + 0.1 ω_{c} j)$

(4.35)

Behelyettesítve

$ω_{c} = 3.789 r a d / s e c P = 43.3448 φ_{t} = 50.0084$

(4.36)

A felnyitott kör átviteli függvénye

$W_{x} (s) = \frac{P}{(10 s) (1 + 0.1 s) (1 + 0.1 s)}$

(4.37)

$φ_{t} = 180 - 90 - \tan^{- 1} (0.1 ω_{c}) - \tan^{- 1} (0.1 ω_{c})$

$P = (10 ω_{c} j) (1 + 0.1 ω_{c} j) (1 + 0.1 ω_{c} j)$

(4.38)

Behelyettesítve

$ω_{c} = 3.6390 r a d / s e c P = 41.2089 φ_{t} = 50.0071$

(4.39)

MATLAB kód

T1=10;
T2=1;
T3=0.1;
 
om=0.8811;
ft=180-atand(om*T1)-atand(om*T2)-atand(om*T3);
P=1/abs(1/(1+T1*om*i)/(1+i*T2*om)/(1+i*T3*om));
 
om=0.7221;
ft=180-90-atand(om*T2)-atand(om*T3);
P=1/abs(1/(T1*om*i)/(1+i*T2*om)/(1+i*T3*om));
 
om=8.591;
ft=180-atand(om*T1)-atand(om*T3);
P=1/abs(1/(1+i*T1*om)/(1+i*T3*om));
 
om=3.789;
ft=180-atand(om*T1)-atand(om*T3)-atand(om*T2/10);
P=1/abs(1/(1+i*T1*om)/(1+i*T3*om)/(1+i*T2/10*om));
 
om=3.639
ft=180-90-atand(om*T2/10)-atand(om*T3)
P=1/abs(1/(T1*om*i)/(1+i*T2/10*om)/(1+i*T3*om))

Összefoglalva a táblázatból kiolvasható, hogy a D tag hozzáadásával a körerősítés megnövelhető.

P tag	ideális PD tag	valóságos PD tag	PI tag	valóságos PID tag
$W_{c} = P$	$W_{c} = P (1 + s)$	$W_{c} = P \frac{(1 + s)}{(1 + 0.1 s)}$	$W_{c} = P \frac{(1 + 10 s)}{10 s}$	$W_{c} = P \frac{(1 + 10 s) (1 + s)}{10 s (1 + 0.1 s)}$
$P = 11.8644$	$P = 113.2673$	$P = 43.3448$	$P = 8.9300$	$P = 41.2089$

4.1. Szabályozási körök szintézise I. - PID szabályozás tervezése

Ebben a fejezetben azt feltételezzük, hogy szabályozott szakasz $W_{P} (s)$ átviteli függvényének pólusai egyszeresek, és mind valós negatív számok és kellően távol vannak egymástól. A $W_{c} (s)$ átviteli függvénnyel rendelkező szabályozó az $E (s)$ hibajelből számítja ki $W_{P} (s)$ szabályozott szakasz $U (s)$ bemenőjelét (ld. 4-4. ábra). Feladatunk $W_{c} (s)$ meghatározása.

4.4. ábra - Szabályozási kör

4.1.1. P szabályozó

A P szabályozó egyenlete az időtartományban

$u (t) = P e (t)$

(4.40)

A szabályozó átviteli függvénye

$W_{C_P} (s) = P$

(4.41)

$P$ választásának szempontjai (ez minden PID típusú szabályozóra igaz)

Ha feltételesen stabilis a rendszer, akkor a fázistartalék megválasztása
Ha strukturálisan stabilis a rendszer, akkor gyorsaság megválasztása, fizikai korlátok figyelembe vétele

A $P$ szabályozó gyorsítja a rendszert (ld. 5.2.3 pont). Általában azt szeretnénk, ha $P$ minél nagyobb lenne, de ennek a stabilitás vagy a beavatkozó szerv fizikai korlátai szabnak határt. (Ha egy 10 V-os motorra 100000 V-ot kapcsolunk, akkor már nem beszélhetünk a motor gyorsaságáról, csak a tönkremeneteléről).

4.1.2. PI szabályozó:

A PI szabályozó egyenlete az időtartományban

$u (t) = P_{P I} e (t) + I_{P I} \int_{0}^{t} e (τ) d τ$

(4.42)

Laplace-transzformálva

$U (s) = P_{P I} E (s) + I_{P I} \frac{E (s)}{s} = P_{P I} (1 + \frac{1}{\frac{P_{P I}}{I_{P I}} s}) E (s) = P_{P I} \frac{1 + \frac{P_{P I}}{I_{P I}} s}{\frac{P_{P I}}{I_{P I}} s} E (s)$

(4.43)

A PI szabályozó tervezésére használt szokásos átviteli függvény alakja

$W_{C_P I} (s) = P (1 + \frac{1}{T_{I} s}) = P \frac{1 + T_{I} s}{T_{I} s}$

(4.44)

Ha a ferekvenciatartományban megtervezzük a szabályozót, akkor az időtartományban használt paramétereket a következőképpen írhatjuk fel

$P_{P I} = P; I_{P I} = \frac{P}{T_{I}}$

(4.45)

Ahogy korábban láttuk (ld. xxx) a felnyitott körben található integráló tag az állandósult hibát szünteti meg konstans referenciajel esetén.

Általános szabályként komondható, hogy az integráló tag időállandóját a szabályozott szakasz legnagyobb időállandójával azonos nagyságúra kell választani.

$T_{I} = T_{1}$ legyen (ahol $T_{1}$ a rendszer legnagyobb időállandója)ha $T_{I} < T_{1}$ stabilitási problémaha $T_{I} > T_{1}$ feleslegesen lassítjuk a rendszert

4.1.3. PD szabályozó

Az ideális PD szabályozó egyenlete az időtartományban

$u (t) = P_{P D} e (t) + D_{P D} \frac{d e (t)}{d t}$

(4.46)

Laplace-transzformálva

$U (s) = P_{P D} E (s) + s D_{P D} E (s) = P_{P D} (1 + \frac{D_{P D}}{P_{P D}} s) E (s)$

(4.47)

A szabályozó tervezéséhez használt átviteli függvény

$W_{C_P D i} (s) = P (1 + T_{D} s)$

(4.48)

(4.47) és (4.48) összevetéséből kiolvasható

$P_{P D} = P; D_{P D} = T_{D} P_{P D}$

(4.49)

Ideális deriváló tag nem valósítható meg. A deriválás a zajokat kiemeli (mérési zaj minden valós szabályozási körben jelen van). Ha akár analóg, akár digitális eszközzel deriválunk, akkor valamilyen módon gondoskodnunk kell a zajszűrésről. A szűrés egy újabb időállandót hoz be a rendszerbe. A legegyszerűbb alul-áteresztő szűrő átviteli függvénye: $\frac{1}{1 + T_{D}^{'} s}$ , ennek megfelelően egy megvalósítható PD szabályozó átviteli függvénye

$W_{C_P D} (s) = P \frac{1 + T_{D} s}{1 + T_{D}^{'} s}$

(4.50)

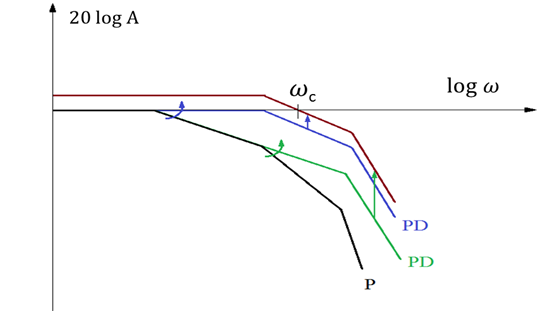
A $1 + T_{D} s$ szorzótényező a felnyitott kör átviteli függvényének számlálójában jelenik meg, ezért a D hatással a fázistartalékot növelhetjük, ezzel a szabályozó a beállás lengéseit csökkentheti.

$T_{D} = T_{2}$

(A 2. legnagyobb időállandóval egyezzen meg)

A szűrő csökkenti a fázistartalékot. Hogy a D tag fáziscsökkentő hatását ne veszítsük el, legyen $T_{D} ≫ T_{D}^{'}$ (általában egy nagyságrend különbség van közöttük).

PD szabályozót célszerű alkalmazni, ha maga a szabályozott szakasz integrátort tartalmaz. Tipikusan pozíció ígéret xxx

4.1.4. PID szabályozó

Az ideális PID tag kimenőjele az időtartományban

$u (t) = P_{P I D} e (t) + I_{P I D} \int_{0}^{t} e (τ) d τ + D_{P I D} \frac{d e (t)}{d t}$

(4.51)

Laplace-transzformálva

$U (s) = P_{P I D} E (s) + I_{P I D} \frac{E (s)}{s} + s D_{P I D} E (s)$

(4.52)

A szabályozó átviteli függvénye:

$W_{C_{P I D i}} (s) = P_{P I D} (1 + \frac{I_{P I D}}{s P_{P I D}} + \frac{D_{P I D}}{P_{P I D}} s) = P_{P I D} \frac{1 + \frac{P_{P I D}}{I_{P I D}} s + \frac{P_{P I D}}{I_{P I D}} \frac{D_{P I D}}{P_{P I D}} s^{2}}{\frac{P_{P I D}}{I_{P I D}} s}$

(4.53)

Az ideális PID szabályozó tervezéshez annak átviteli függvényét a következő alakban szokás felírni

$W_{C_P I D i} (s) = P \frac{(1 + T_{I} s) (1 + T_{D} s)}{T_{I} s}$

(4.54)

(4.53) és (4.54) összevetéséből

$I_{P I D} = \frac{P}{T_{I}}; D_{P I D} = T_{D} P; P_{P I D} = \frac{T_{I} + T_{D}}{T_{I}} P$

(4.55)

A valós PID szabályozó átviteli függvénye

$W_{C_P I D} (s) = P \frac{(1 + T_{I} s) (1 + T_{D} s)}{T_{I} s (1 + T_{D}^{'} s)}$

(4.56)

A szokásos választás

$T_{I} = T_{1}$ és $T_{D} = T_{2}$ , valamint $T_{D} = 10 T_{D}^{'}$
Az időállandók kiválasztása után $P$ -t addig növeljük, amíg stabilitási vagy fizikai korlátba nem ütközünk

Szabályozó elemek szerepe:

P tag: gyorsít (túlvezérel)
I tag: egységugrás esetén az állandósult hibát eltünteti (ha a szabályozott szakasz nem tartalmaz integrátort)
D tag: fázistartalékot növel (túllendülést csökkent, illetve nagyobb gyorsítást enged meg)

4.5. ábra - PID szabályozó hangolásának magyarázata

4.1.5. Kidolgozott feladatok PID szabályozók tervezésére

A szabályozott szakasz

$W_{P} (s) = \frac{1}{(1 + 0.1 s) (1 + 1 s) (1 + 10 s)}$

(4.57)

4 . 4 feladat PI szabályozó tervezése :

$W_{C_P I} (s) = P (1 + \frac{1}{T_{I} s}) = P \frac{1 + T_{I} s}{T_{I} s}$

(4.58)

Legyen

$T_{I} = 10$

(4.59)

Ha $P = 1$ , akkor

$W_{x} (s) = \frac{1}{(1 + 0.1 s) (1 + 1 s) 10 s}$

(4.60)

A felnyitott kör frekvencia átviteli függvénye:

$W_{x} (j ω) = \frac{1}{(1 + 0.1 j ω) (1 + 1 j ω) 10 j ω}$

(4.61)

$W_{x} (j ω)$ Bode-diagramja

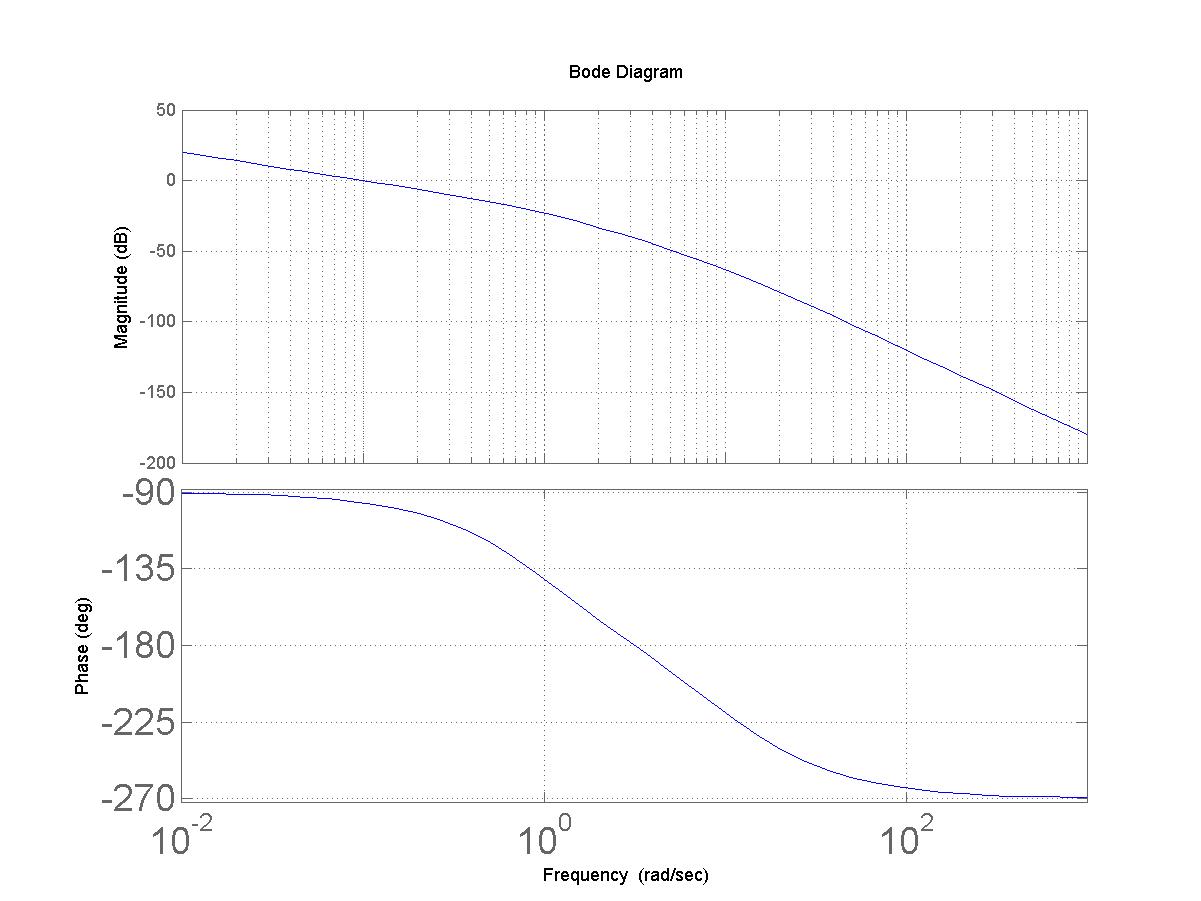
4.6. ábra - PI szabályozó felnyitott körének Bode-diagramja egységnyi körerősítéssel

Az ábráról leolvashatjuk, hogy egy adott fázistartalékhoz közelítőleg mekkora vágási körfrekvencia és körerősítés tartozik. Ha pl. 45̊ fázistartalékot szeretnénk, akkor a Bode diagramból kiolvasható, hogy a fázis akkor éri el a -135̊-ot, amikor a körfrekvencia valamivel kisebb, mint 1 és ekkor az amplitúdó kb. -20dB, vagyis $P$ értékét kb. 10-re kell beállítani ahhoz, hogy az amplitúdó diagram kb. ott metssze a 0dB tengelyt, ahol a fázisa kb. -135̊. Ez csak egy közelítő becslés. A konkrét számítás a következő.

A leolvasáshoz hasonlóan, először azt kell meghatározni, hogy milyen körfrekvencián éri el a frekvencia átviteli függvény azt a fázisszög értéket, amely a kiválasztott fázistartalékhoz tartozik (ez lesz a vágási körfrekvencia). pl. legyen kb. 45̊. Esetünkben a fázistartalék:

$φ_{t} = 180 - 90 - arctg (1 ω_{c}) - arctg (0.1 ω_{c})$

(4.62)

Legyen $ω_{c} = 0.85$ [rad/sec], ekkor

$φ_{t} = 180 - 90 - arctg (0.85) - arctg (0.085) = 44.7770$

(4.63)

Ez kellően közel van az előzetesen választott érékhez. A szükséges körerősítés, amely jelen esetben megegyezik $P$ értékével.

$P = \frac{1}{| \frac{1}{(1 + j 0.1 ω_{c}) (1 + j ω_{c}) j 10 ω_{c}} |} = | j 8.5 (1 + j 0.085) (1 + j 0.85) | = 11.1960$

(4.64)

Fel kell hívni a figyelmet arra, hogy ez egy számpélda, ahol a zsebszámológépünk sokkal nagyobb pontossággal számol, mint amire szükségünk van és amilyen pontossággal ismerjük a vizsgált rendszer paramétereit. A gyakorlatban az így kapott eredményeket kerekíteni szokás.

Szimulációval vizsgáljuk meg, hogy miként viselkedik a visszacsatolt rendszer, $P = 10$ választással, illetve ezt az értéket ötszörösére és ötödére változtatjuk. A referencia jel legyen 1.

4.7. ábra - PI szabályozó körerősítésének behangolása

Látható, ha P=10, akkor a fázistartalék 45̊. Egy 20%-nál kisebb túllendüléssel áll be a rendszer az állandósult értékre. Ha a körerősítést ötödére csökkentjük, akkor a beállás lassabb és nincs túllendülés. Ha a körerősítést ötszörösére növeljük, akkor gyorsabban reagál a rendszer, de beállást mégsem tekinthetjük gyorsabbnak, mert a jelentős lengések miatt sokkal később csökken a hiba tartósan egy megadott korlát alá (ezeknél a szimulációknál $T_{I} = 10$ ).

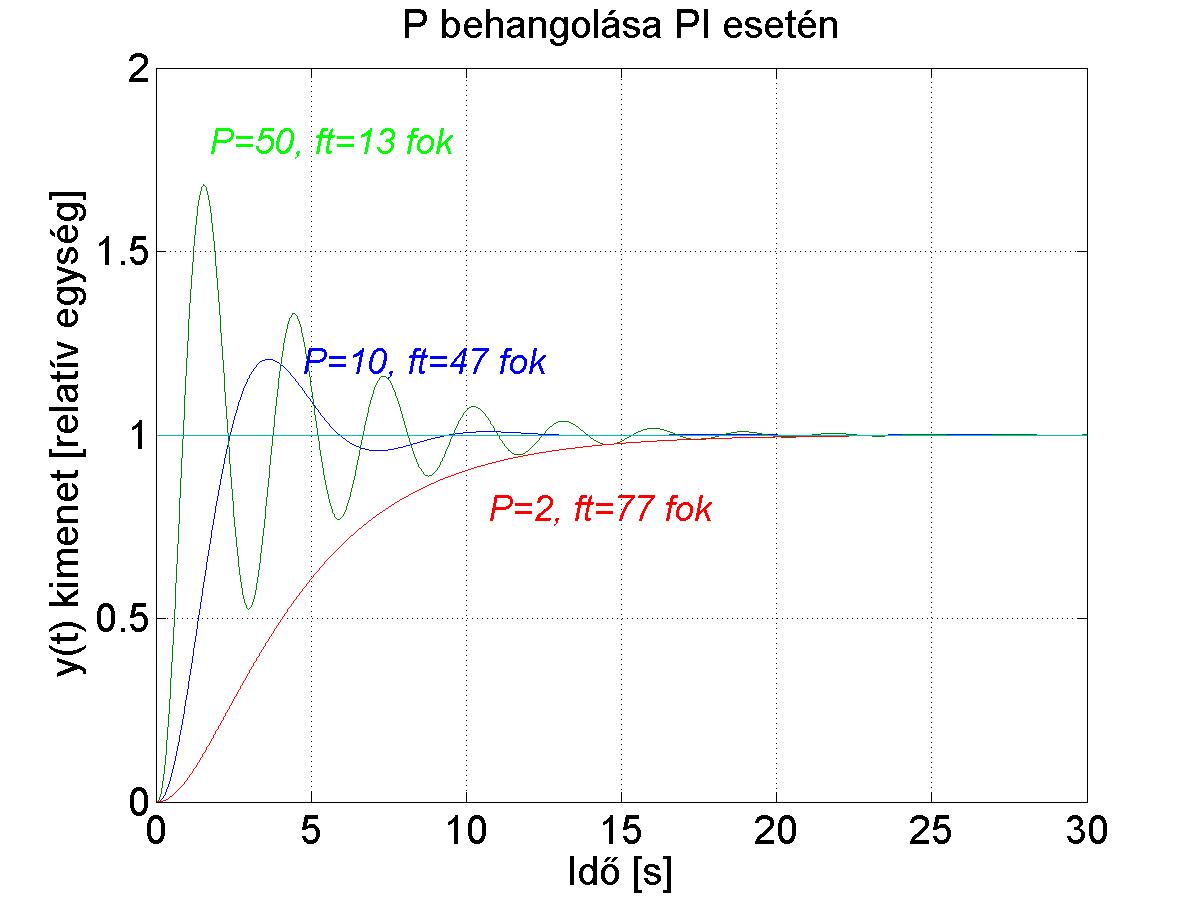
Vizsgáljuk meg a $T_{I}$ behangolásának hatását (ezeknél a szimulációknál $P = 10$ ). Alapértelmezésben $T_{I} = 10$ , és ezt az értéket ötödére, illetve ötszörösére változtatjuk.

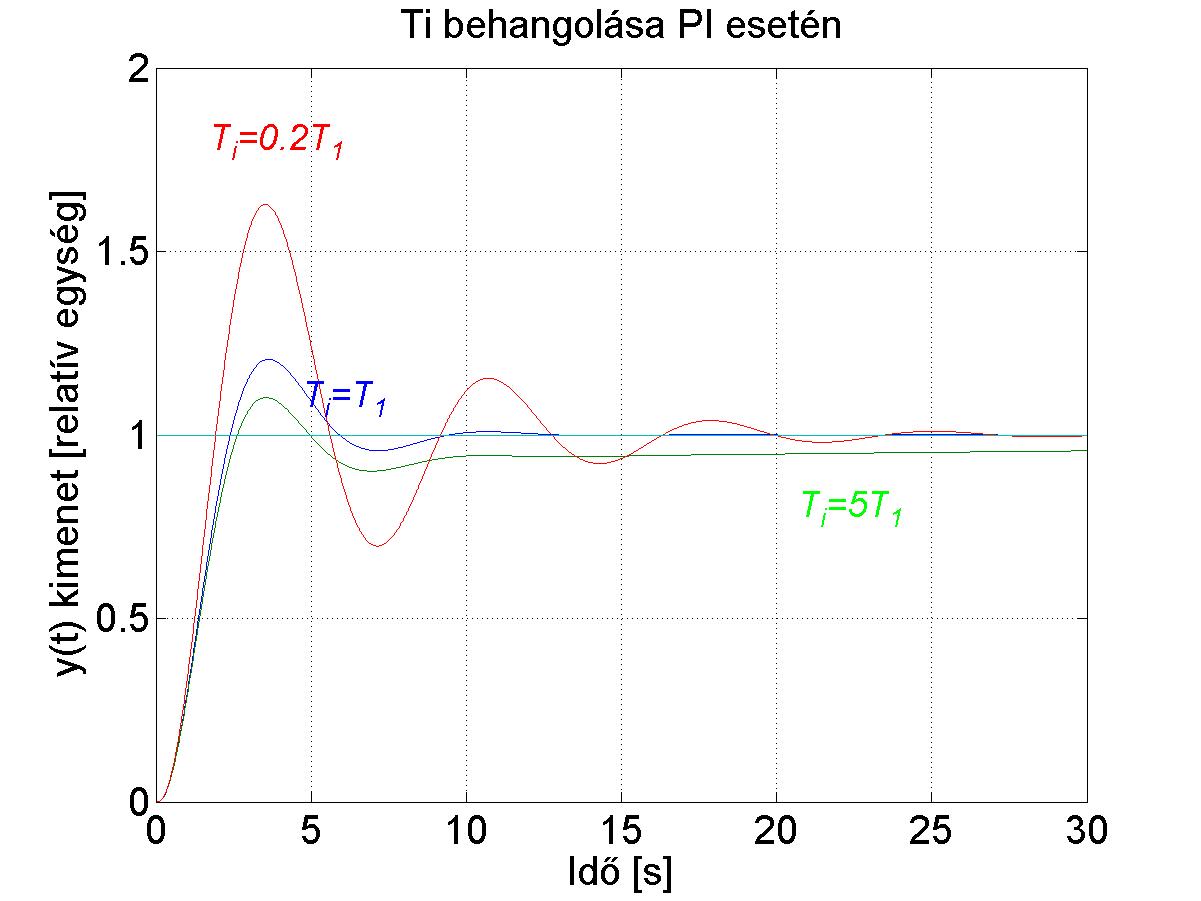
4.8. ábra - PI szabályozó időállandójának behangolása

Látható, ha $T_{I}$ értékét lecsökkentjük, akkor ezzel nem tudjuk gyorsítani a rendszert, mert ezt nem engedi a rendszer legnagyobb időállandója. Ha $T_{I}$ értéke nagyon nagy, akkor kisebb a túllövés, de az állandósult hiba csak lassan szűnik meg (egy feleslegesen nagy időállandót vittünk a rendszerbe).

4 . 5 feladat PD szabályozó :

$W_{C_P D} (s) = P \frac{1 + T_{D} s}{1 + T_{D}^{'} s}$

(4.65)

Legyen

$T_{D} = 1$ és $T_{D}^{'} = 0.1$

Ha $P = 1$ , akkor

$W_{x} (s) = \frac{1}{(1 + 0.1 s) (1 + 0.1 s) (1 + 10 s)}$

(4.66)

A felnyitott kör frekvencia átviteli függvénye:

$W_{x} (j ω) = \frac{1}{(1 + j 0.1 ω) (1 + j 0.1 ω) (1 + j 10 ω)}$

(4.67)

$W_{x} (j ω)$ Bode-diagramja

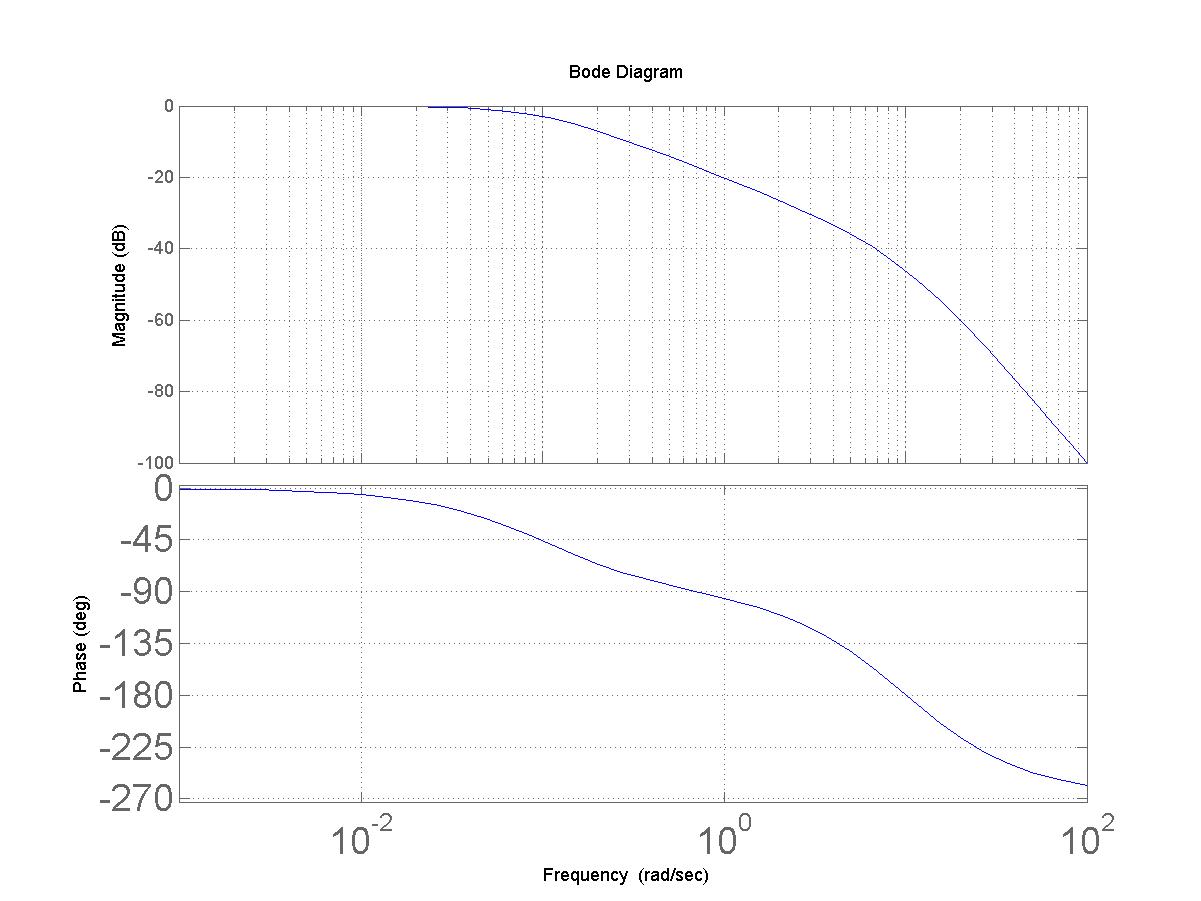
4.9. ábra - PI szabályozó felnyitott körének Bode-diagramja egységnyi körerősítéssel

Az ábráról leolvashatjuk, hogy ha a körerősítést 10-re növeljük (az amplitúdó diagramot 20dB-lel toljuk feljebb), akkor a vágási körfrekvencia 1 rad/sec és a fázis tartalék közel 90̊. A konkrét számítás a következő.

$φ_{t} = 180 - arctg (10 ω_{c}) - arctg (0.1 ω_{c}) - arctg (0.1 ω_{c})$

(4.68)

Legyen $ω_{c} = 1$ [rad/sec], ekkor

$φ_{t} = 180 - arctg (10) - arctg (0.1) - arctg (0.1) = 84.2894$

(4.69)

Ehhez tartozó körerősítés, amely jelen esetben megegyezik P értékével.

$P = \frac{1}{| \frac{1}{(1 + 10 ω_{c} j) (1 + 0.1 ω_{c} j) (1 + 0.1 ω_{c} j)} |}$

$= | (1 + 10 j) (1 + 0.1 j) (1 + 0.1 j) | = 10.1504$

(4.70)

Szimulációval vizsgáljuk meg, hogy miként viselkedik a visszacsatolt rendszer, $P = 10$ választással, illetve ezt az értéket ötszörösére és ötödére változtatjuk. Az ábrán szerepel még egy tiszta P szabályozó szimulációs eredménye is. A referenciajel legyen 1.

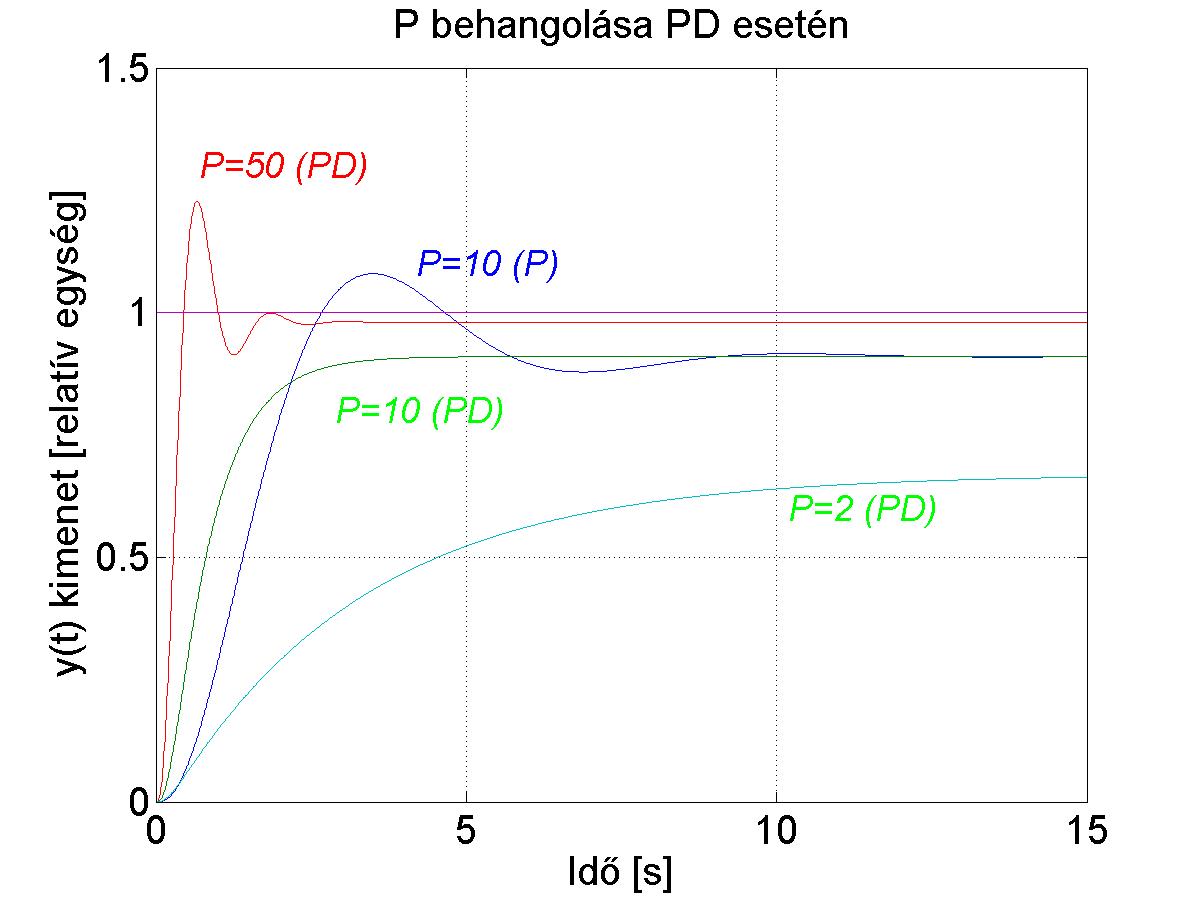
4.10. ábra - PD szabályozó körerősítésének behangolása

Látható, ha $P = 10$ , akkor a D tag nélkül a rendszer lengéssel áll be, a D taggal ezek a lengések eltűnnek, de az állandósult hiba megmarad és ez közel 10%. Ha a P értékét növeljük, akkor a D taggal együtt is megjelennek a lengések, a beállás gyorsabb és az állandósult hiba is kisebb. Ha csökkentjük a P értékét, akkor a beállás lassul, és az állandósult hiba megnő.

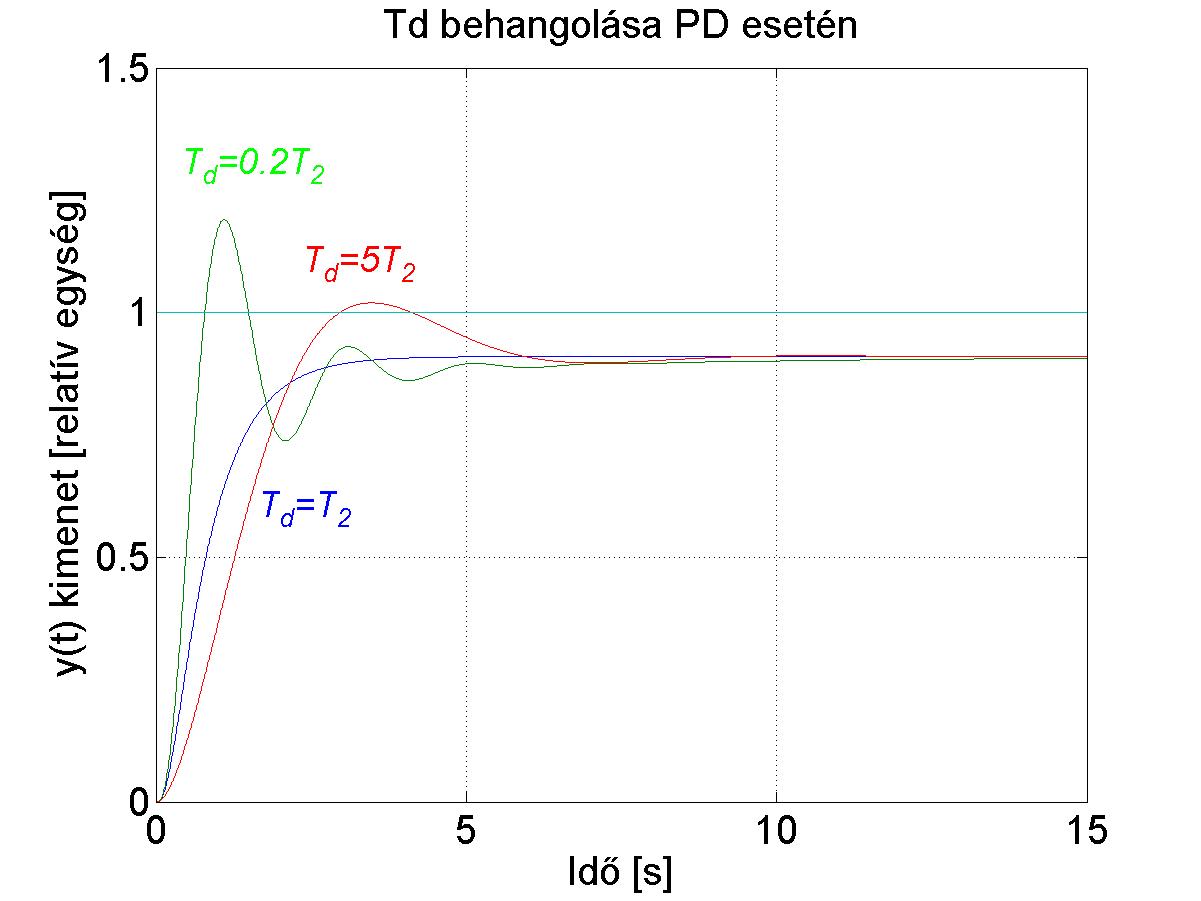
4.11. ábra - Szimuláció

Látható, ha $T_{D}$ értékét akár növeljük, akár csökkentjük a $T_{D} = T_{2}$ beállításhoz képest, a beállás csak rosszabb lesz.

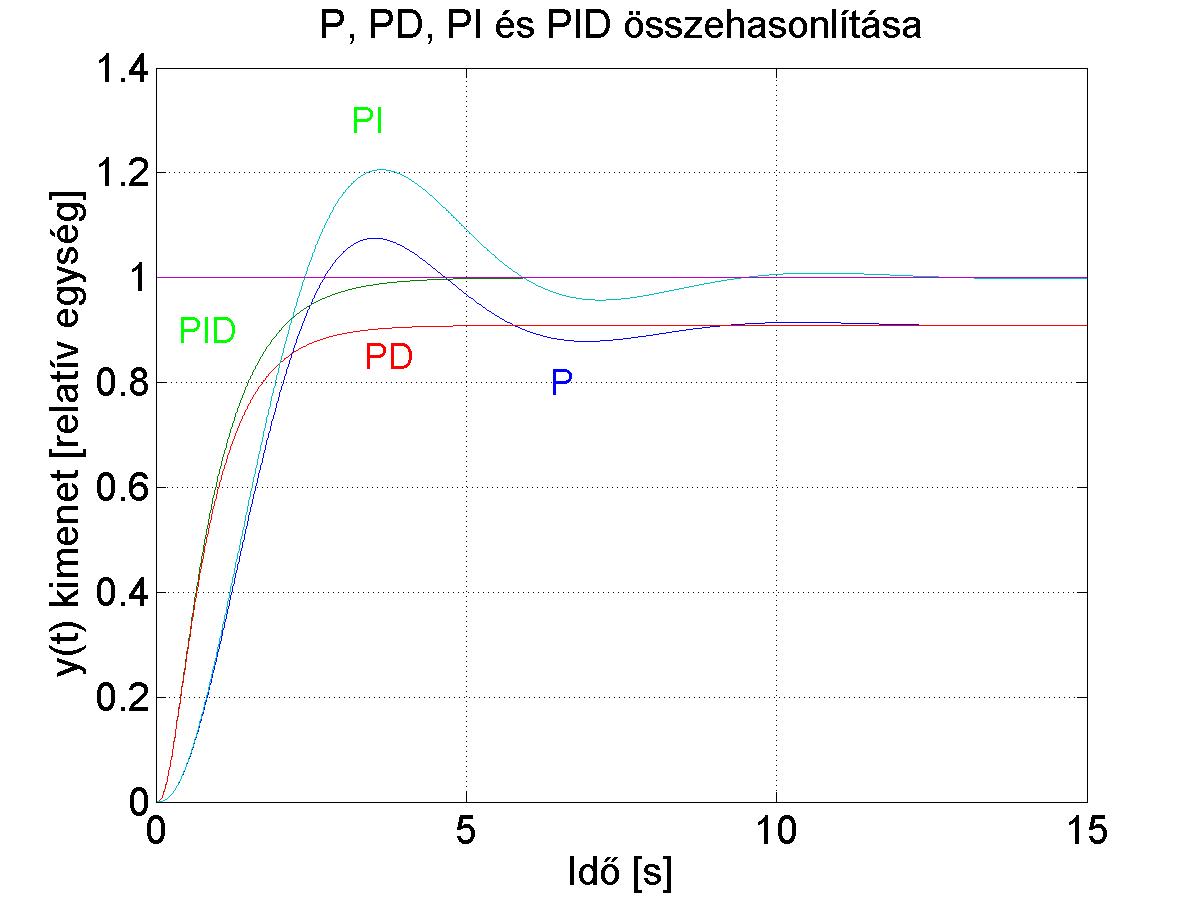
P, PI, PD és PID összehasonlítása: Mind a négy esetben a referenciajel egy egységugrás, és $P = 10$ . PD és PID esetén $T_{D} = T_{2}$ és $T_{D}^{'} = 0.1 T_{D}$ . PI és PID esetén $T_{I} = T_{1}$ .

A P leng és állandósult hibája is van, a PI az állandósult hibát tünteti el, de leng. A PD a lengést csökkenti (esetünkben el is tünteti), de van állandósult hibája. A PID nem is leng és nincs állandósult hibája. Természetesen PID szabályozó esetén is lehetnek lengések, ha P értékét nagyobbra választjuk. Ekkor a beállás is gyorsabb lesz. A PD szabályozókat leginkább akkor alkalmazzuk, ha a szabályozott szakasz már eleve tartalmaz integrátort. Tipikusan ilyen eset a pozíció szabályozás pl. robotoknál.

4.12. ábra - P, PI, PD és PID szabályozók összehasonlítása

4.1.6. PID szabályozók kísérleti behangolása

Vannak esetek, amikor a szabályozott szakasz paraméterei nem ismertek, ezért a PID szabályozót próbálgatással, kísérletileg kell behangolni. Több olyan módszer ismert, amely a próbálgatások hatékonyságát növeli. Az egyik legnépszerűbb módszert Ziegler és Nichols dolgozta ki [13]. Elsősorban időkésleltetéssel rendelkező rendszerekhez alkalmazható, de gyakorlatilag minden szabályozógyártó használta a módszert kisebb módosításokkal beállítási ajánlásaik elkészítéséhez. Népszerűségének oka az, hogy egyszerű megtanulni és elmagyarázni. A módszert egy egyenáramú szervomotor fordulatszám szabályozó körének kísérleti behangolásán keresztül mutatjuk be. A példában egy fordulatszám szabályozó behangolását mutatjuk be. A szabályozó algoritmus a motor armatúra áramának az alapjelét határozza meg. A program kiszámítja és kiadja a motor áramreferencia jelét, a motor áramszabályozóhurkához (amely az áramkorlátozást is megvalósítja) biztonsági okokból nem férünk hozzá. A motor tényleges árama a szabályozási idő leteltével éri el a referencia értéket, maga a rendszer két energiatárolós szakasznak tekinthető, ezért a motor önmagában strukturálisan stabilis (így a Ziegler-Nichols módszer nem lenne alkalmazható), de a fordulatszám jelet digitális szűréssel állítjuk elő, így a motor az alkalmazott harmad fokú szűrő algoritmussal együtt már egy öt energiatárolós rendszernek tekinthető. Természetesen ez csak akkor igaz, ha a szűrt jelet használjuk fel a hiba előállításához. Itt a program kódot nem az eredeti formájában, hanem a megértéshez szükséges leegyszerűsített formában ismertetjük.

4.1.6.1. Ziegler-Nichols módszer

A Ziegler-Nichols módszer alkalmazásának feltétele, hogy a szabályozási kör a stabilitás határán is működtethető legyen, ebből következik, hogy strukturálisan stabilis rendszereknél nem alkalmazható, vagyis a szabályozott szakasznak vagy időkésleltetéssel vagy legalább három energiatárolóval kell rendelkeznie.

A behangolás lépései

Kapcsoljuk a szabályozót csak P módra, avagy kapcsoljuk ki az I és D funkciókat. Esetenként annak eldöntése is szükséges lehet, hogy melyik a pozitív irány (hogyan kell a szabályozót bekötni)

A szabályozó P paraméterét nulla értékről kezdjük óvatosan növelni addig, amíg a kimenőjel állandó amplitúdóval nem kezd lengeni.

Az állandó amplitúdójú lengésekhez vezető erősítést tekintjük a kritikus $P_{c r}$ erősítésnek és a lengések $T_{c r}$ periódusidejét a kritikus periódusidőnek.

A különböző típusú PID szabályozók $P$ , $T_{I}$ és $T_{D}$ paramétereinek javasolt értékét egy táblázatból olvashatjuk ki, pontosabban a táblázatnak több, kismértékben eltérő változata ismert az irodalomban. Természetesen a választás attól is függ, hogy milyen túllendülést engedünk meg.

	P	TI	TD
P szabályozó	$P_{c r} / 2$
PI szabályozó	$P_{c r} / 2.2$	$T_{c r} / 1.2$
PID szabályozó	$P_{c r} / 1.7$	$T_{c r} / 2$	$T_{c r} / 8$

Alkalmazzuk a fenti lépéseket a kísérleti eszközünkre. A P szabályozó (4.40) formáját megvalósító programsor (megfelelő típus deklarációt feltételezve)

Ia_ref=P_par*error;

(4.71)

Az 4-14. ábraán két mérés eredménye látható, a baloldali ábrán a P paraméter értéke nem érte el a kritikus értéket, a jobb oldali ábrán már igen. .

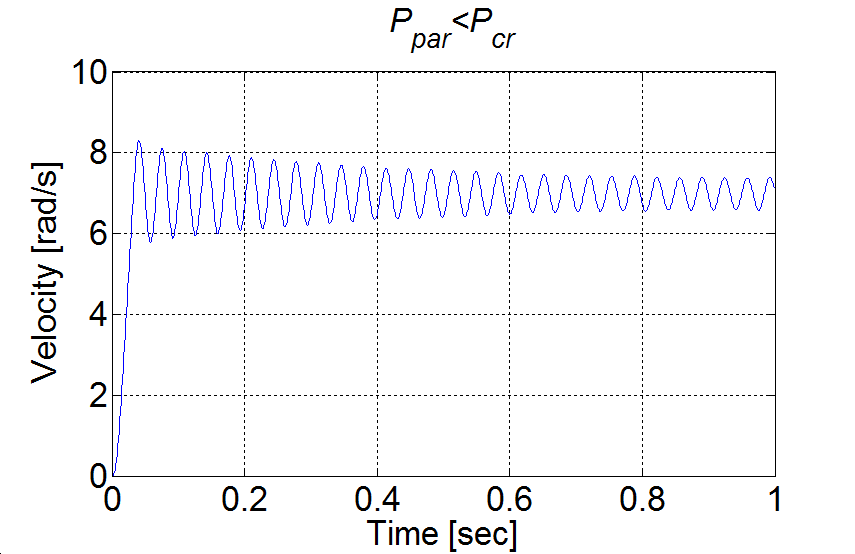
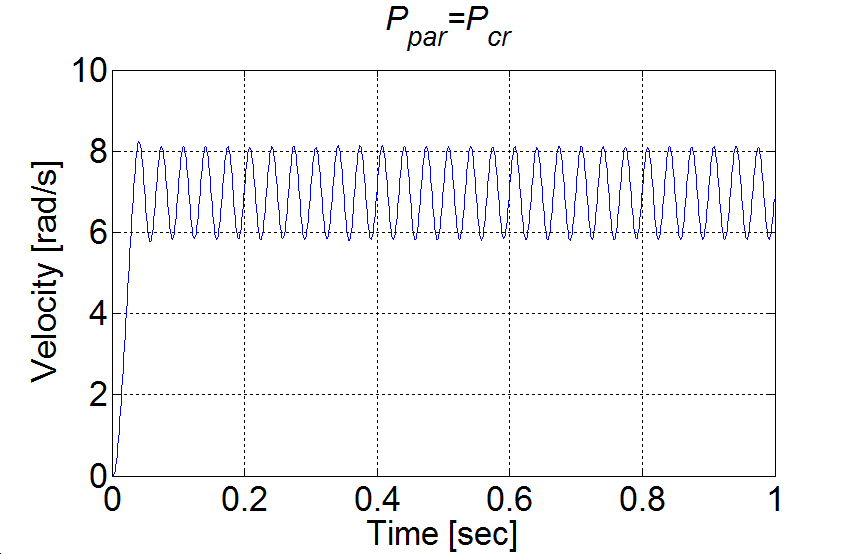
4.13. ábra - paraméter meghatározása ()

A $P_{c r} = 4.6$ , így a táblázat alapján a P szabályozó erősítésének értéke legyen $P = 2.3$ . E paraméterrel elvégzett mérés eredménye az 4-15. ábraán látható. Megfigyelhető, hogy a $P$ paraméter nem azonos a szakasz körerősítésével, az állandósult hiba 1% körül van.

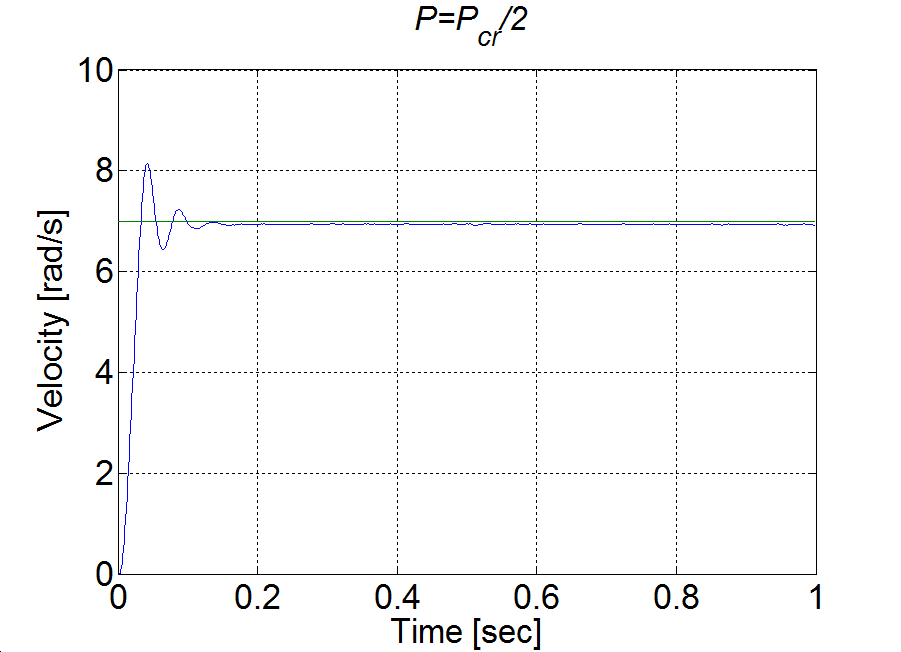
4.14. ábra - Ziegler- Nichols módszerrel behangolt P szabályozó működése

A PI szabályozó az (4.42) alakú egyenletét közelítőleg megvalósító két programsor (típus deklarálás és kezdeti értékadás nélkül)

error_int= error_int+error*T_s;

Ia_ref=P_par*error+ I_par*error_int;

(4.72)

A 4-14. ábraáról leolvasható, hogy 0.2 sec időtartamra kb. 6 periódus esik, ezért a periódusidő $T_{c r} \approx 33 m s$ . A PI szabályozó alkalmazásához a táblázatból kiolvasható értékek:

$P_{p a r} = \frac{P_{c r}}{2.2} = 2.16 I_{p a r} = \frac{P_{p a r}}{T_{c r}} 1.2 = 77.7$

(4.73)

A fenti paraméterekkel beállított PI szabályozóval elvégzett mérés eredménye az 4-16. ábraán látható.

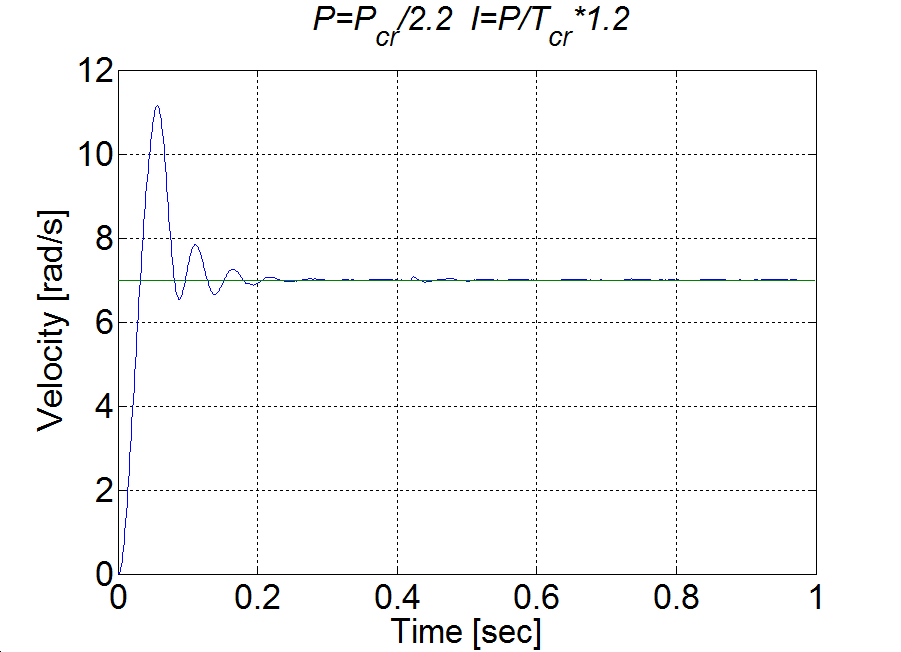
4.15. ábra - Ziegler- Nichols módszerrel behangolt PI szabályozó működése

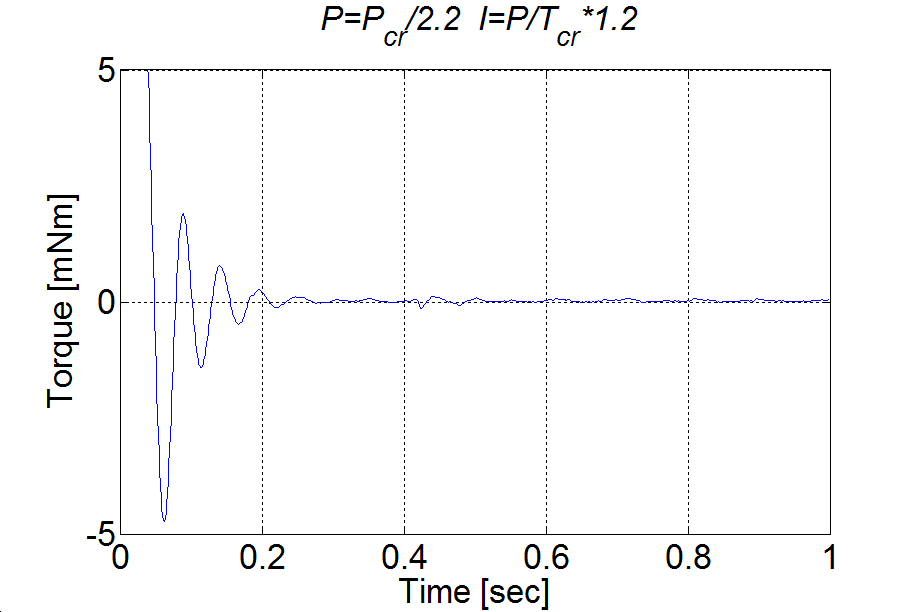
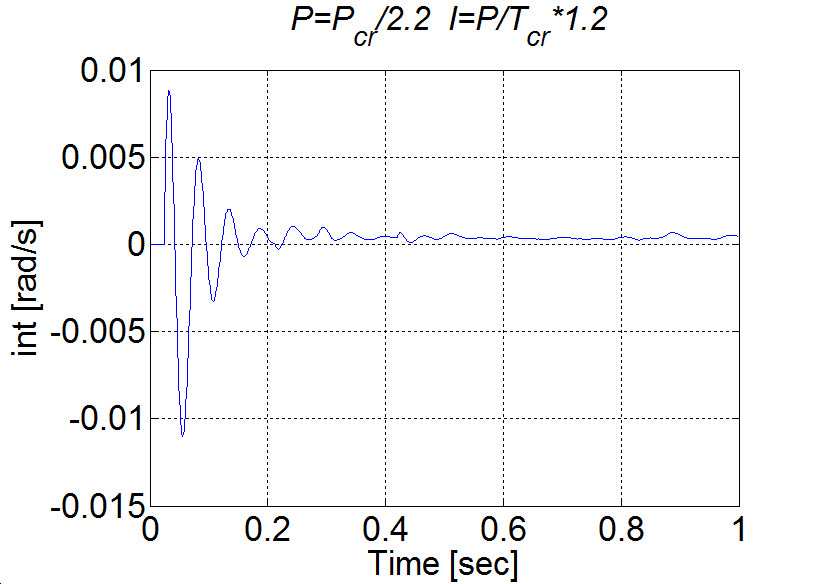
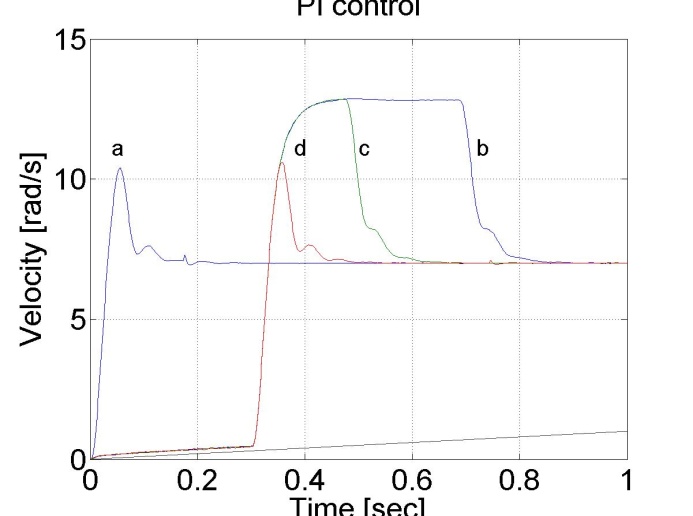
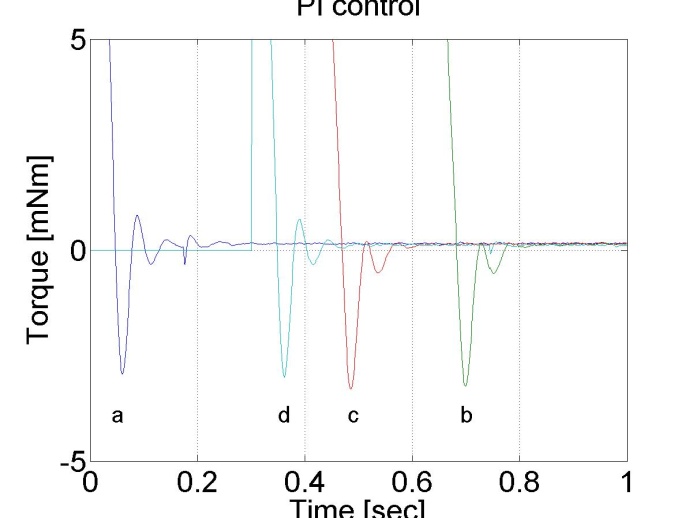
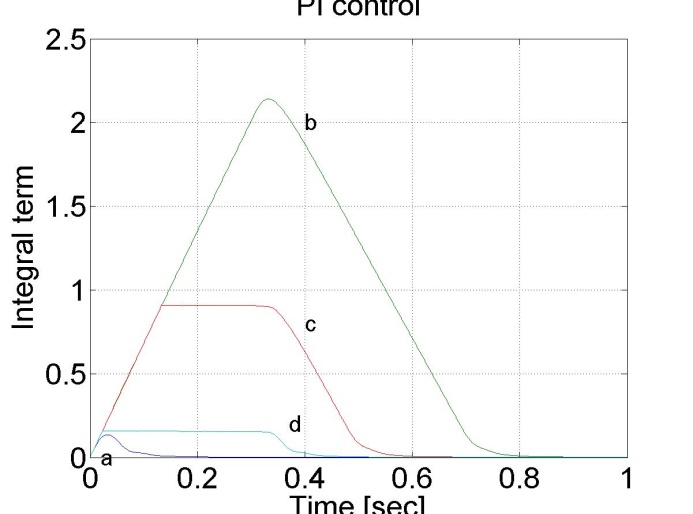
Jól látható, hogy a túllövés kb. 50% és a lengések amplitúdója nem az elvárt exponenciális burkológörbével csökken. Ennek oka nem magában a PI szalyozó működésében keresendő. Vizsgáljuk meg a a motor nyomatékát (ld. 4-17. ábra). A nyomaték a felfutási idő alatt telítődik. Ekkor a szabályozási kör felnyílik, de az integrátor az összegzést tovább folytatja a telítődés alatt is, más szavakkal akkor is, amikor a szabályozó működése szünetel. Ez alatt az idő alatt az integrátor értéke jelentősen megnövekdhet, amelyet csak ellentétes előjelű hibával lehet a kívánt értékre visszacsökkenteni, ezért jelentkezik egy jelentős túllövés.

4.16. ábra - A nyomaték időfüggvénye PI szabályozás esetén

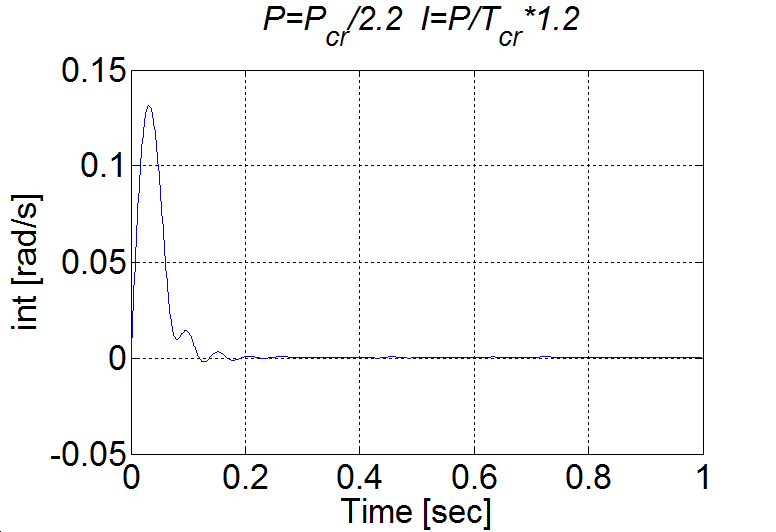
4.17. ábra - A hibaintegrál időfüggvénye PI szabályozás esetén

4.1.7. PID szabályozók telítődése

Az 4-16. ábraán látható túllövést csökkenthetjük azzal, ha az integrátort kikapcsoljuk a telítődés időtartamára.

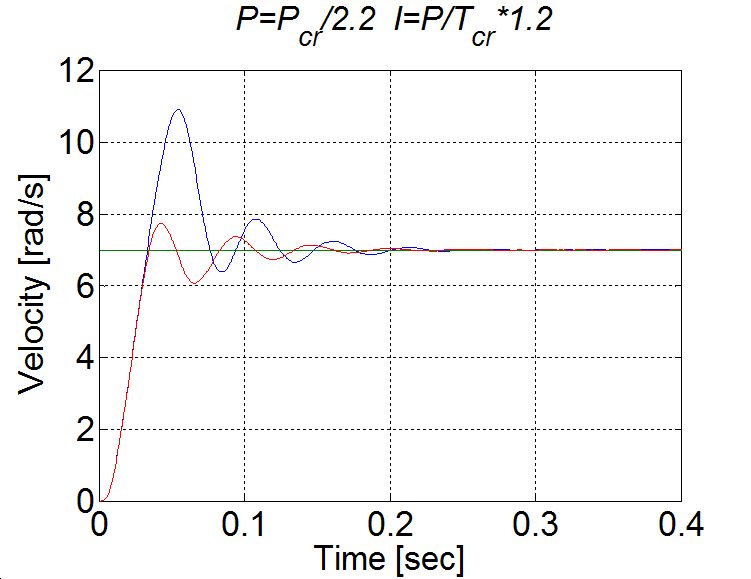
4.18. ábra - PI szabályozó telítődése

4.19. ábra - A hibaintegrál időfüggvénye PI szabályozás esetén

4.20. ábra - PID szabályozók telítődése

4.1.8. Stick-slip jelenség

A jelenség robotok pozíció szabályozásakor akkor fordul elő, ha a súrlódás miatt a mozgató mechanizmus referencia érték előtt vagy után beragad, különösen akkor fordul elő a referencia érték előtti beragadás, ha aszimptotikus beállás a cél és e miatt nincs túllövés. Így marad egy állandósult hibajel és az egy a mechanizmusra ható erőt eredményez. A mechanizmus azért nem tud elmozdulni, mert a relatívan kis hibából származó csekély beavatkozó erő kisebb, mint a tapadási surlódási erő maximuma. Ha a pozíciószabályozó körben van egy integrátor, akkor az folyamatosan integrálja a hibát és ez folyamatosan növeli a beavatkozás erejét. Egy idő elteltével az integrátor annyi hibát integrál össze, hogy az abból generált beavatkozó erő nagyobb lesz mint a maximális tapadási súrlódási erő, ekkor mechanizmus elmozdul, de a mozgás közben a súrlódási erő lecsökken a tapadási súrlódási erőhöz képest, így a mechanizmus garantáltan túllendül és a folyamat megismétlődik az ellentétes irányban. A jelenség jól mefigyelhető a 4-21. ábraán.

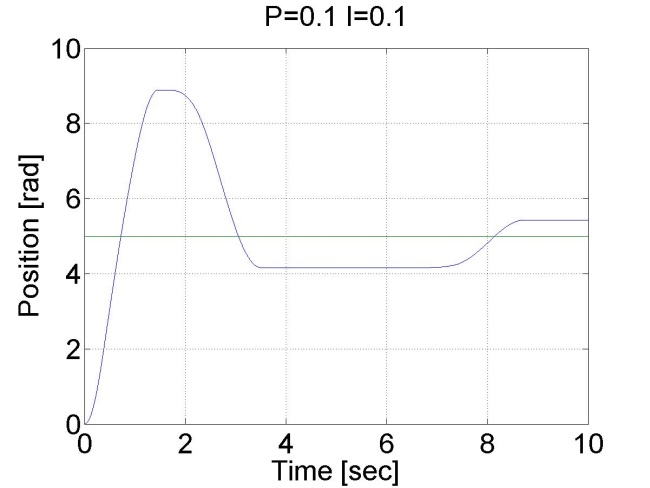
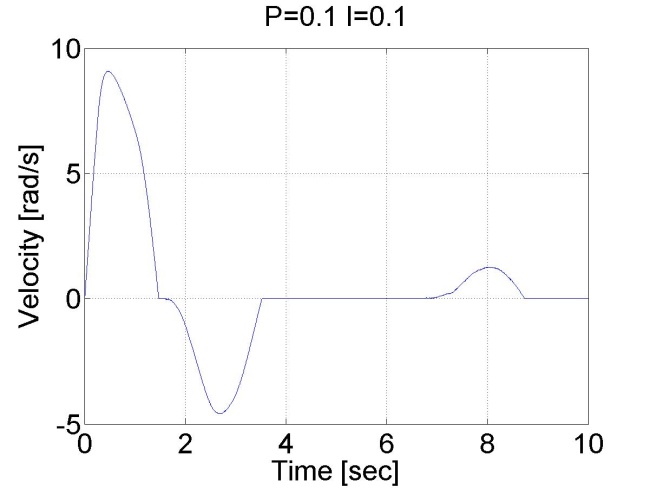
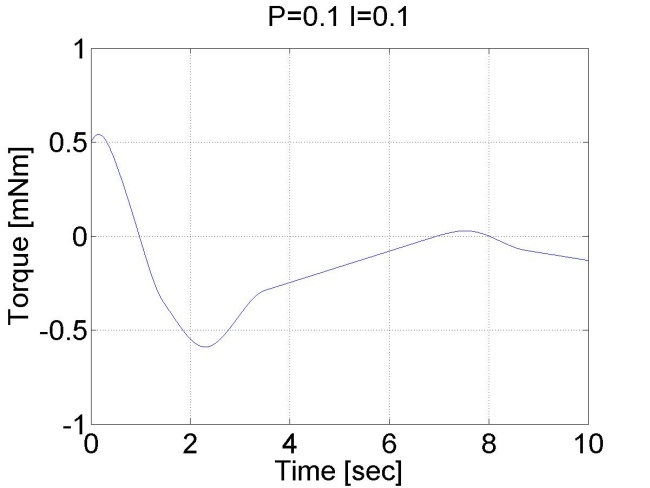
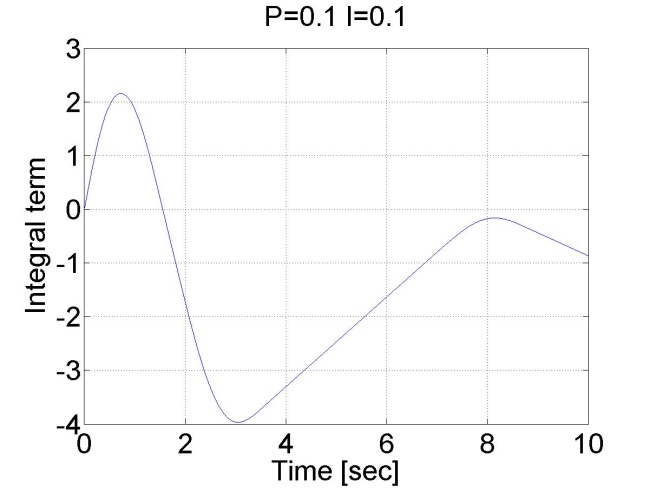
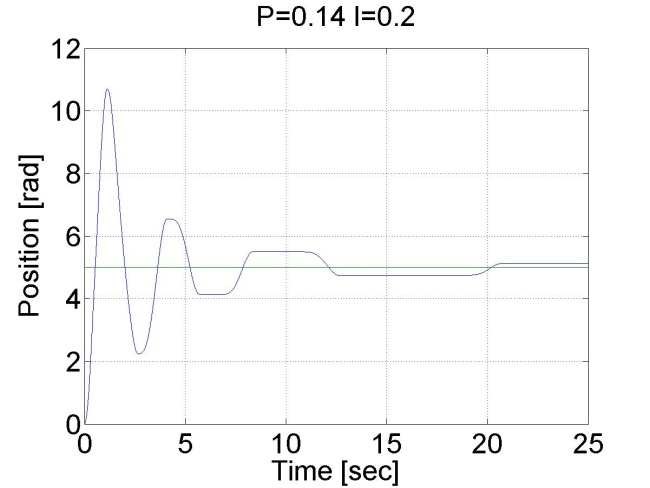
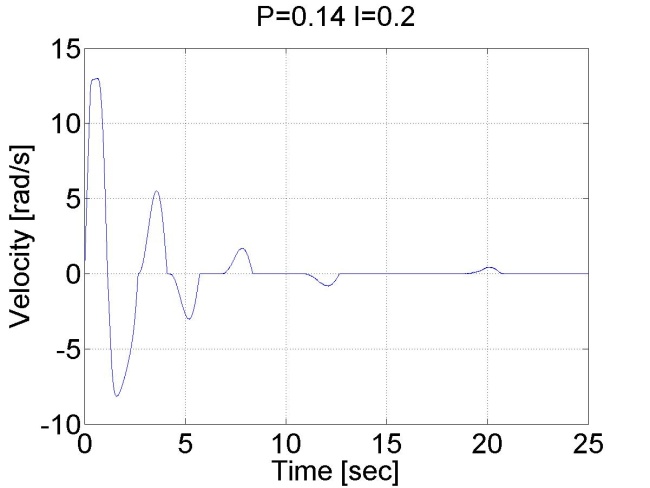
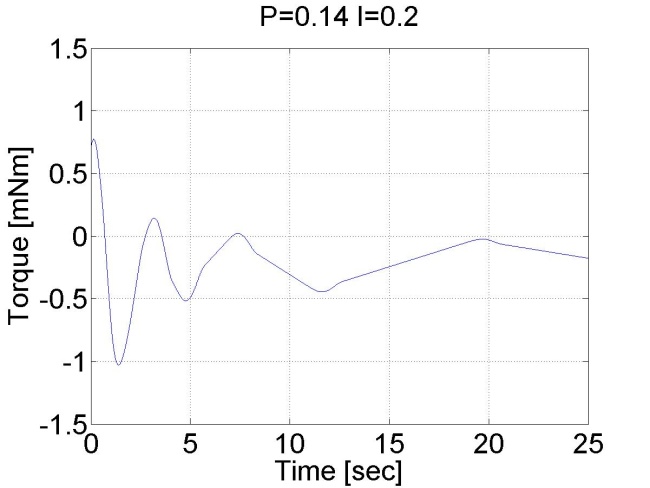
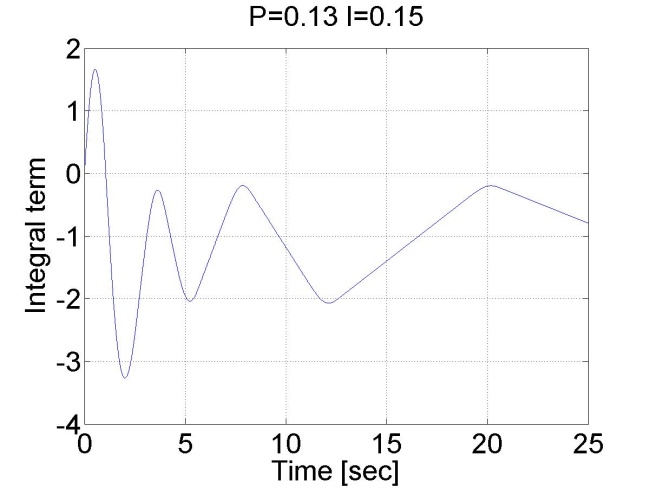
4.21. ábra - Stick-slip jelenség

4.2. Szabályozási körök szintézise II.

4.2.1. Kaszkád szabályozás

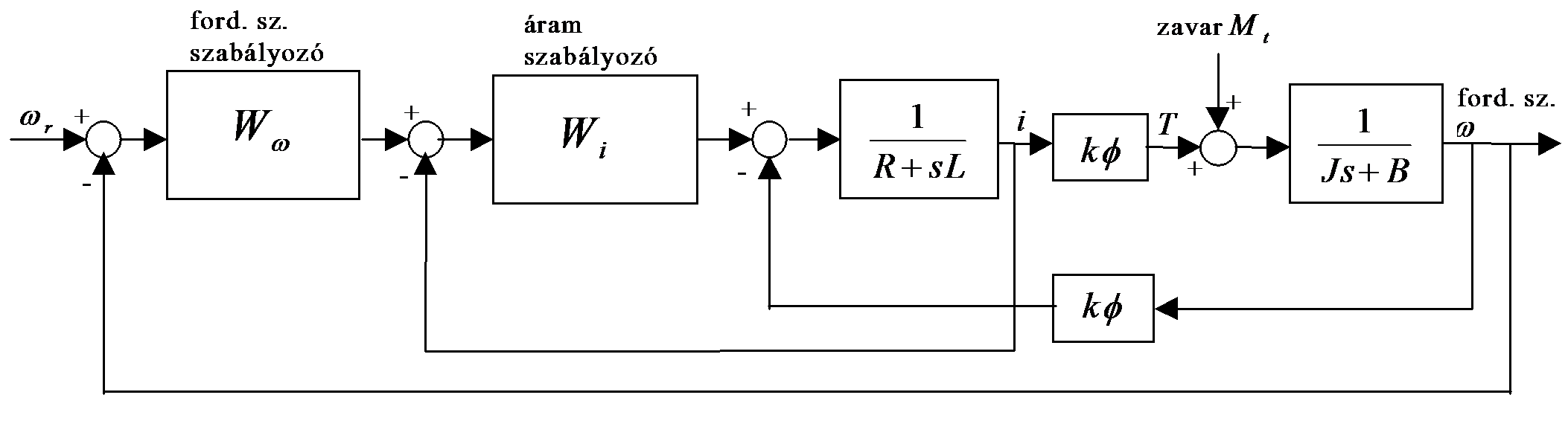
4 . 6 feladat Az egyenáramú motor hagyományos fordulatszabályozása

Az 4-22. ábra az egyenáramú motor szabályozókörét mutatja, amelyben a belső hurok, a $W_{i}$ szabályozóval az áramszabályozásról gondoskodik, míg a külső körben a $W_{ω}$ szabályozó a fordulatszám-szabályozó. Az áramszabályozásra egyrészt azért van szükség, mert Tv kicsi, ezért i könnyen megszalad, másrészt azért, hogy indítás, fékezés vagy hírtelen terhelésváltozás esetén a motor túláram ellen védve legyen. Ez természetesen korlátozza a motor gyorsító- és lassítónyomatékát, ezért úgy kell beállítani a szabályozót, hogy a motor dinamikai tulajdonságai feleljenek meg a követelményeknek. Mivel az áramszabályozás gyorsabban megy végbe, mint a fordulatszám-szabályozás (Tm>Tv), ezért az ub indukált feszültség hatása, tehát a motor belső visszacsatolása (k) a továbbiakban elhanyagolható. Ez a közelítés olyan kis hibát okoz a végeredményben, ami nem számottevő. Így a szabályozás leegyszerűsödik egy kéthurkú kaszkád-szabályozásra.

Ezen szabályozók általában PID típusúak, mivel ennél a legegyszerűbb szabályozási esetnél ez biztosítja a gyors és pontos, statikus hiba mentes beállást. Egy P, azaz arányos típusú szabályozó csak állandó hibával tudja követni az alapjelet, az integráló, úgynevezett első rendű jelleg viszont biztosítja az első rendű statikus hiba megszűnését, a differenciáló jelleg pedig a szabályozás gyorsaságát adja. Külön problémát jelent az arányos erősítés (Ad), az integrálási és differenciálási időállandók (Ti, Td) terhelésfüggő beállítása. Az adott hajtáshoz úgy kell beállítani ezeket a paramétereket, hogy az alapjelet túllendülés-mentesen, optimálisan rövid idő alatt érje el a hajtás.

4.22. ábra - Egyenáramú motor szabályozóköre

A $W_{i}$ áramszabályozó:

$W_{i} = A_{i} \frac{1 + s T_{i}}{s T_{i}}$

A szakirodalom ajánlása szerint a legcélszerűbben $T_{i} = T_{v}$ értékeket érdemes választani időállandóknak.

A felnyitott áramszabályozó kör átviteli függvénye:

$W_{I x} = A_{i} \frac{(1 + T_{i} s)}{T_{i} s} \cdot \frac{1}{R_{a}} \frac{1}{(1 + T_{v} s)} = A_{i} \frac{1}{R_{a}} \frac{1}{T_{i} s}$

Ez egy ún. strukturálisan stabilis felnyitott kör. A fázistartalék mindig 90 fok. A körerősítést a visszacsatolt szabályozási kör tulajdonságai alapján választhatjuk meg. A visszacsatolt áramszabályozó kör átviteli függvénye:

$W_{I v} = \frac{1}{1 + T_{I} s}$

ahol $T_{I} = \frac{T_{v}}{\frac{A_{i}}{R_{a}}}$ . A tervezés TI megválasztását jelenti.

A $W_{ω}$ fordulatszám-szabályozó is egy PI tag:

$W_{ω} = A_{ω} \frac{1 + s T_{ω}}{s T_{ω}}$

Így a szabályozási kör a következőképpen is felrajzolható:

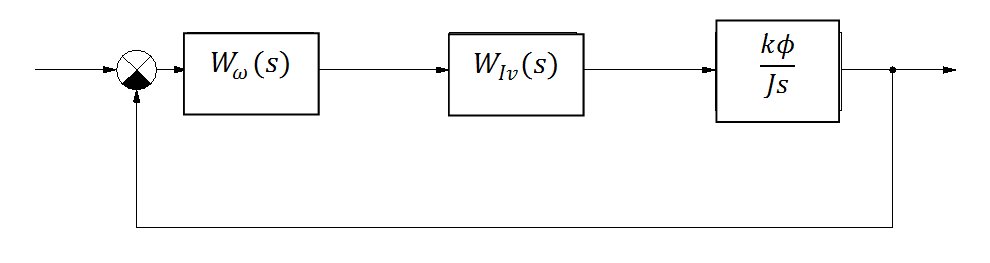
4.23. ábra - Külső, fordulatszám szabályozási kör

A viszkózus súrlódást elhanyagoljuk, ezért a felnyitott kör átviteli függvénye:

$W_{f x} = A_{ω} \frac{(1 + T_{ω} s)}{T_{ω} s} \cdot \frac{1}{(1 + T_{I} s)} \cdot \frac{k φ}{J_{m} s}$

A szabályozás még hiányzó paramétereit: A, TI, Tω. A frekvencia átviteli függvény Bode diagramja:

4.24. ábra - A frekvencia átviteli függvény Bode diagramja

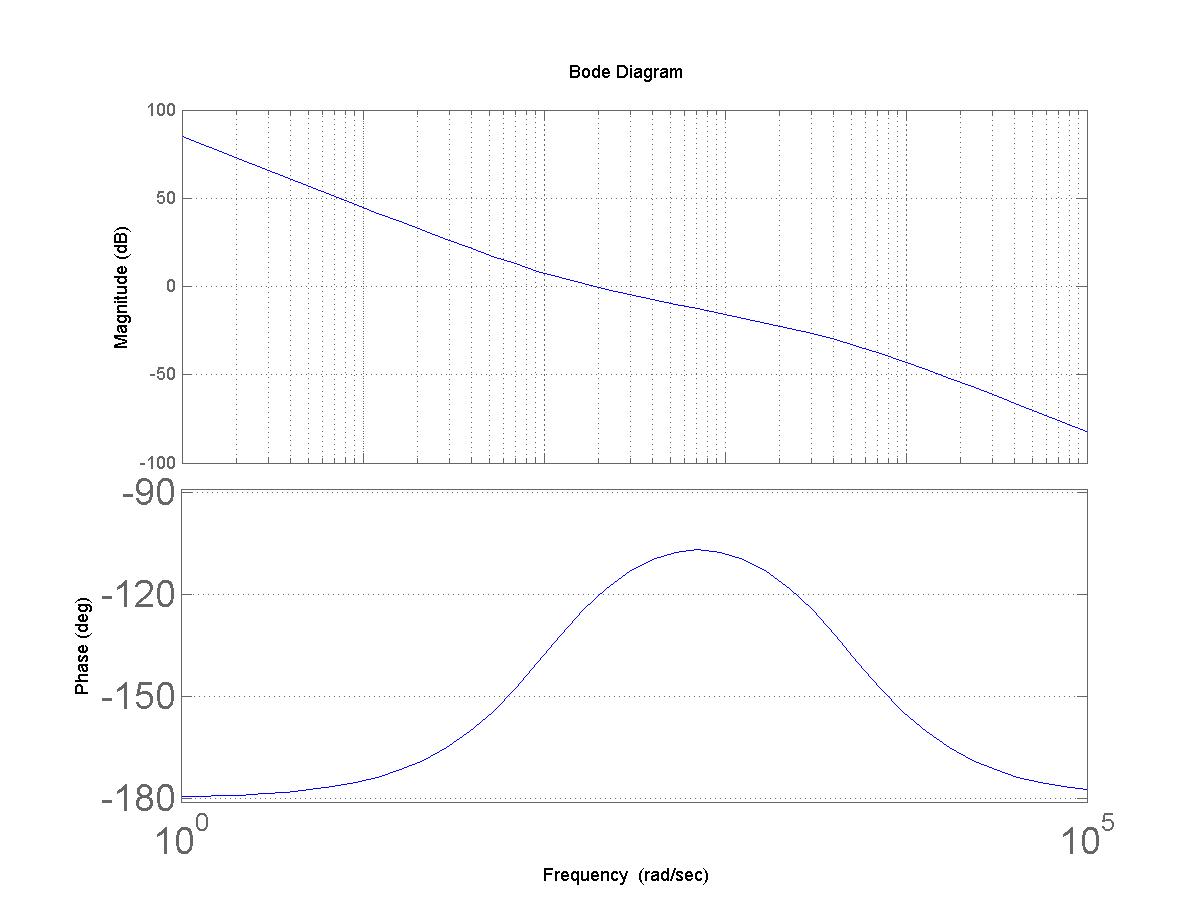
A frekvencia -180 fokról indul, és oda tér vissza. Optimális esetben a vágási körfrekvencia a fázis diagram csúcsához tartozik. TI és Tω. értékét célszerű Tv és Tm nagyságrendjében megválasztani. További megfontolások tehetők annak alapján is, hogy a rendszer válasza jellegre is különböző lehet, alapjel illetve terhelésugrás hatására.

4.2.2. Nem minimálfázisú rendszerek szabályozása

4.2.2.1. Időkésleltetett rendszerek szabályozása Ziegler-Nichols módszerrel

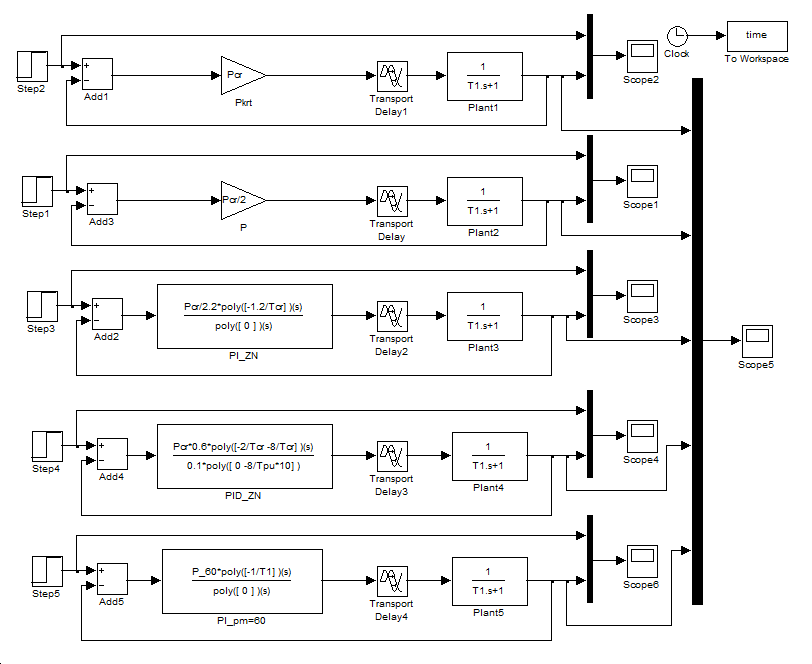
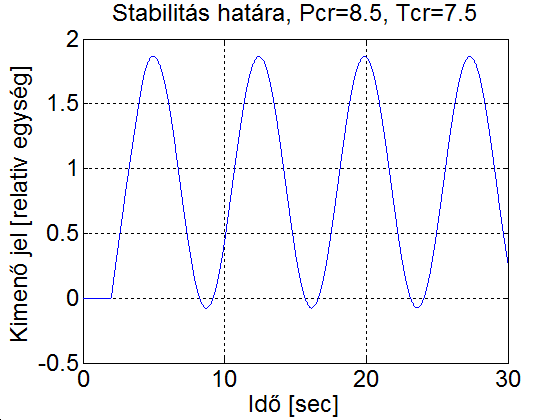
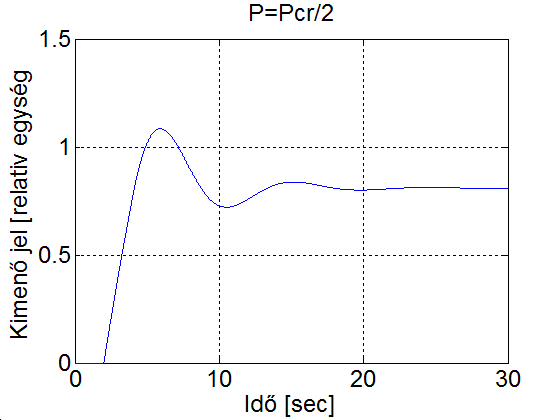
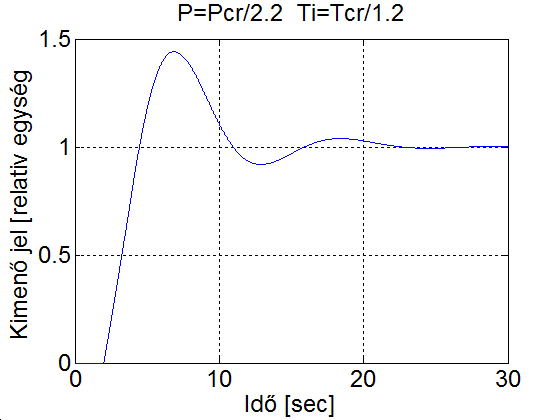
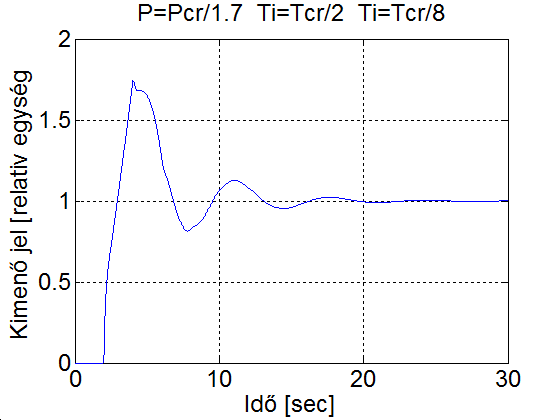
Legyen a szabályozott szakasz egyenergiatárolós, amelynek időállandója legyen $T 1 = 10$ és a rendszer időkésleltetése legyen $T h = 2$ . Próbálgatással a 4-25. ábra felső szabályozási körében a körerősítést addig növeljük, ameddig el nem jutunk a stabilitás határára (ld. 4-26. ábra). A kritikus körerősítés $P c r = 8.5$ és kritikus körerősítéshez tartozó periódusidő az ábráról leolvasva $T c r = 7.5$ . A P, PI és PID szabályozót a Ziegler- Nichols hangoló táblázat szerint behangolva a szimulációs eredmények a 4-27. ábra, 4-28. ábra és 4-29. ábra mutatja. Összehasonlításul $T i = T 1$ váéasztással 60 fokos fázistartalékkal végeztünk egy szimulációt (ld. 4-30. ábra)

A kirajzolást végző MATLAB kód

plot(time,yout(:,1))
set(gca, 'fontsize', [18]);
xlabel('Idő [sec]');
ylabel('Kimenő jel [relativ egység]');
title('Stabilitás határa, Pcr=8.5, Tcr=7.5');
grid
 
pause
plot(time,yout(:,2))
set(gca, 'fontsize', [18]);
xlabel('Idő [sec]');
ylabel('Kimenő jel [relativ egység');
title('P=Pcr/2');
grid
 
pause
plot(time,yout(:,3))
set(gca, 'fontsize', [18]);
xlabel('Idő [sec]');
ylabel('Kimenő jel [relativ egység');
title('P=Pcr/2.2  Ti=Tcr/1.2');
grid
 
pause
plot(time,yout(:,4))
set(gca, 'fontsize', [18]);
xlabel('Idő [sec]');
ylabel('Kimenő jel [relativ egység');
title('P=Pcr/1.7  Ti=Tcr/2  Ti=Tcr/8');
grid
 
pause
plot(time,yout(:,5))
set(gca, 'fontsize', [18]);
xlabel('Idő [sec]');
ylabel('Kimenő jel [relativ egység');
title('P=2.6180  Ti=T1');
grid

4.25. ábra - Ziegler-Nichols módszer alkalmazása

4.26. ábra - Stabilitás határa

4.27. ábra - P szabályozó

4.28. ábra - PI szabályozó

4.29. ábra - PI szabályozó

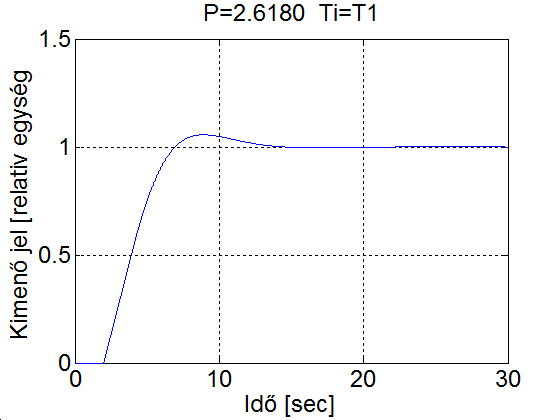
4.30. ábra - PI szabályozó 60 fok fázistartalék

4.2.2.2. A holtidős tag átviteli függvényének közelítése racionális törtfüggvénnyel

Strejc féle módszer gondolatmenete a következő: a $T_{h}$ holtidős tagot $n$ db egyenergiatárolós taggal helyettesítjük úgy, hogy minden egyenergítárolós tag időállandója $\frac{T_{h}}{n}$ nagyságú

$e^{- s T_{h}} \approx \frac{1}{{(1 + \frac{T_{h}}{n})}^{n}}$

(4.74)

Pade approximáció

$e^{- s T_{h}} \approx \frac{\prod_{i = 1}^{n} (1 - T_{p i} s)}{\prod_{i = 1}^{n} (1 + T_{p i} s)}$

(4.75)

4.2.2.3. Smith prediktor

A Smith Predictor egy klasszikus konfiguráció az időkésleltetés kompenzálására. Legyen a P(s) az elsőrendű szűrő Td időállandóval. A P0(s) a P(s) egy olyan modellje, amelyben az időkésleltetés kiesik

$P (s) = \frac{e^{- T_{d} s}}{T_{f} s + 1}$ , $P_{0} (s) = \frac{1}{T_{f} s + 1}$

( 4.76 )

A lenti ábrán (4-31. ábra) két hurok látható: a belső hurokban a kompenzáló jel v(t) tartalmaz egy y(t) prediktort. C0(s) egy PID szabályozó.

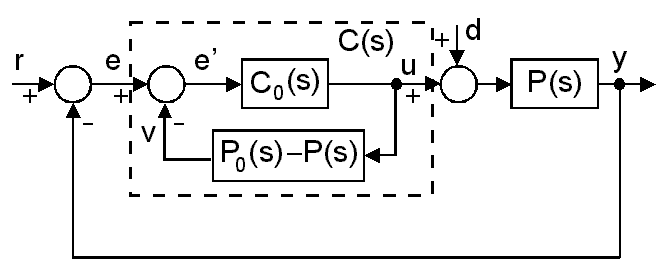
4.31. ábra - A Smith Predictros konfigurációja

A zárt hurok átviteli függvénye a következő

$W (s) = \frac{y (s)}{r (s)} = \frac{C (s) P (s)}{1 + C (s) P (s)} = \frac{C_{0} (s) P (s)}{1 + C_{0} (s) P_{0} (s)}$

( 4.77 )

Fontos megjegyezni, hogy a transzcendentális kifejezés eltűnik a zárt hurok átviteli függvényének karakterisztikus egyenletében. A gyakorlatban, a tökéletes model, P(s) nem ismert, tehát az időkésleltetés hatása teljes mértékben nem szüntethető meg, de a Smih Predictor redukálja annak hatását.

4 . 7 feladat szabályozó tervezése időkésleltetés esetén

Egy folytonos folyamat átviteli függvénye:

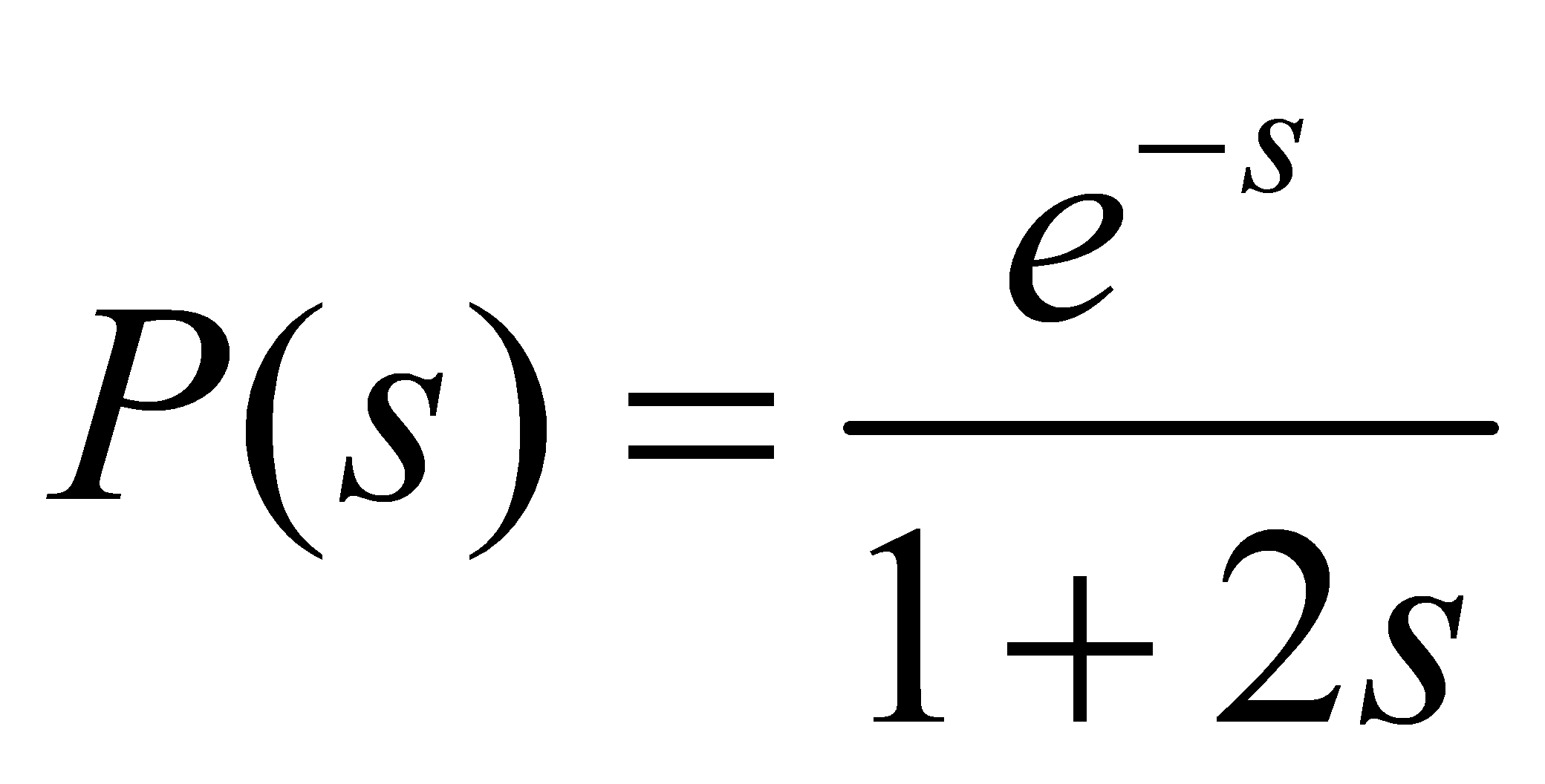
Soros szabályozási körben szabályozzuk a folyamatot.

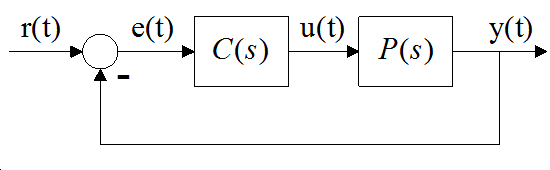
4.32. ábra - Smith prediktor

a.) P szabályozás alkalmazása esetén (C(s) = K) határozza meg K azon értékeit, melyekre a visszacsatolt kör stabilis.

b.) Tervezzen soros PI szabályozót úgy, hogy a visszacsatolt rendszer viselkedése tegyen eleget a következő feltételeknek:

egységugrás bemeneti jelet stacionárius állapotban hiba nélkül kövesse.
A fázistartalék 60̊ legyen.

Vissza		Előre
3. fejezet - Kvalitatív rendszerdinamika és rendszerek stabilitása	Főoldal	5. fejezet - Adaptív szabályozás