3. fejezet - Robotok statikai jellemzése

3. fejezet - Robotok statikai jellemzése
Vissza	I. rész - rész	Előre

A robotok mechanikai szempontból történő leírásának következő fontos eleme a statikai jellemzés, amelynek során a nyugalomban lévő robotokban ébredő erőkkel és forgatónyomatékokkal foglalkozunk. Ezt az indokolja, hogy sok esetben ismernünk kell, mekkora csuklóerők illetve nyomatékok szükségesek ahhoz, hogy a robot egy adott munkadarabot nyugalmi helyzetben meg tudjon tartani. A statikai leírást a 3.1. ábra segítségével követhetjük nyomon.

3.1. ábra -

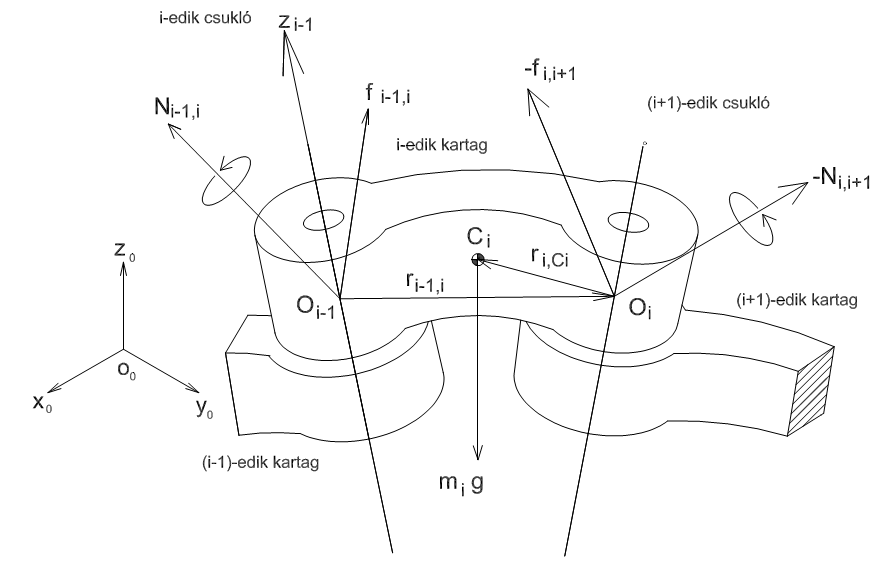
A kartagok, csuklók és koordináta rendszerek sorszámozása illetve indexelése az eddigi konvencióknak megfelelő. Írjuk fel először a nyugalomban lévő i‑edik kartagra az erők egyensúlyát kifejező egyenletet! Legyen az i‑edik kartag tömege $m_{i}$ , jelöljük továbbá az i‑edik kartag által az i‑edik kartagra kifejtett erőt $f_{i - 1, i}$ ‑vel az i‑edik kartag által az (i+1)‑edikre kifejtett erőt pedig $f_{i, i + 1}$ ‑gyel. Ekkor a következő egyenletet írhatjuk fel

$f_{i - 1, i} - f_{i, i, + 1} + m_{i} g = 0$ , $(i = 1... n)$ .

(3.1)

Ha a csuklókban ébredő forgatónyomatékokat (az erők leírásához hasonló indexelést alkalmazva) $N_{i - 1, i}$ ‑vel illetve $N_{i, i + 1}$ ‑gyel jelöljük, továbbá az 5. ábrán látható irányvektorokat figyelembe vesszük, akkor a forgatónyomatékok egyensúlyát az alábbi egyenlet fejezi ki

$N_{i - 1, i} - N_{i, i + 1} - (r_{i - 1, i} + r_{i, C i}) \times f_{i - 1, i} + (- r_{i, C i}) \times (- f_{i, i + 1}) = 0$ , $(i = 1... n)$ .

(3.2)

Ha a kiszemelt i‑edik kartag a legutolsó vagyis az n‑edik, akkor is alkalmazhatjuk a fenti két egyenletet, azzal a kikötéssel, hogy a környezetet formálisan (n+1)‑edik kartagként vesszük számításba. Az utolsó kartag által a környezetre kifejtett erőket és forgatónyomatékokat együttesen a továbbiakban egy hatelemű F vektorral fejezzük ki, azaz

$F = [\begin{matrix} f_{n, n + 1} \\ N_{n, n + 1} \end{matrix}]$ .

(3.3)

Bevezetjük továbbá az ún. ekvivalens csuklónyomatékok (angolul: equivalent joint torques) fogalmát. Az i‑edik csukló ekvivalens csuklónyomatéka erő, vagy nyomaték dimenziójú leehet. Nagysága egyenlő annak az erőnek vagy nyomatéknak a nagyságával, amelyet az i‑edik csukló aktuátora fejt ki a csuklótengely irányában, illetve a tengely körül. Az egyes csuklok ekvivalens csuklónyomatékaiból egy n (általában hat) elemű vektort képezhetünk

$τ = {[\begin{matrix} τ_{1} & τ_{2} & ... & τ_{n} \end{matrix}]}^{T}$ .

(3.4)

A $τ$ vektor egyes elemei a korábbi jelölésekkel a következőképpen fejezhető ki

prizmatikus csukló esetén

$τ_{i} = b_{i - 1}^{T} f_{i - 1, i}$ .

(3.5)

rotációs csukló esetén

$τ_{i} = b_{i - 1}^{T} N_{i - 1, i}$ .

(3.6)

Keressünk kapcsolatot a (3.3) egyenlettel definiált F és a (3.4) egyenlettel definiált $τ$ vektor között! Állításunk a következő

$τ = J^{T} F$ ,

(3.7)

ahol $J$ a korábbiakban bevezetett Jacobi‑mátrix.

A bizonyításhoz a virtuális munka elvét fogjuk felhasználni. Ha a rendszer eredetileg egyensúlyban van, akkor az egyensúlyhelyzetből az adott geometriai kényszereknek eleget tevő virtuális elmozdulásokkal kimozdítva a rendszeren végzett eredő munka zérus.

Tegyük fel ezek után, hogy a robotot valamekkora virtuális elmozdulásoknak vetjük alá, amit kifejezhetünk egyrészt a végpont

$δ p = [\begin{matrix} δ x_{e} \\ δ φ_{e} \end{matrix}]$ ,

(3.8)

másrészt a csuklókoordináták

$δ q = {[\begin{matrix} δ q_{1} & δ q_{2} & ... & δ q_{n} \end{matrix}]}^{T}$

(3.9)

elmozdulás vektorával.

Valamennyi erő és forgatónyomaték hatását figyelembe véve a végzett virtuális munka a következőképpen írható fel, azaz

$δ W = τ_{1} δ q_{1} + ... + τ_{n} δ q_{n} - f_{n, n + 1}^{T} δ x_{e} - N_{n, n + 1}^{T} δ φ_{e}$ ,

amelyből

$δ W = τ^{T} δ q - F^{T} δ p = τ^{T} δ q - F^{T} J δ q = (τ^{T} - F^{T} J) δ q$ ,

továbbá

$δ W = {(τ - J^{T} F)}^{T} δ q$ .

(3.10)

A levezetés során figyelembe vettük, hogy $δ p = J δ q$ . Mivel az (3.10)‑ben felírt $δ W$ virtuális munka tetszőleges $δ q$ virtuális elmozdulásra zérus kell, hogy legyen, ez csak akkor teljesülhet, ha

$τ - J^{T} F = 0$ .

(3.11)

A (3.11) összefüggést átrendezve valóban a bizonyítani kívánt (3.7) összefüggéshez jutunk.

A továbbiakban tovább fejlesztjük eredeti robotmodellünket. Mindeddig ugyanis – első közelítésként – feltételeztük, hogy a robot kartagjai ideális merev testek, csuklói és beavatkozó szervezi, azaz aktuátorai pedig kotyogásmentesek (holtjáték), továbbá feltételeztük azt is, hogy súrlódásmentesek. E feltételezések egyike sem külön teljesül igazából a valóságos robotoknál.

Modellünk pontosítása során elsőként a csuklókban elhelyezett aktuátorok korlátozott merevségének hatását fogjuk figyelembe venni. Szabályozástechnikai szempontból ugyanis döntő jelentőségű, hogy ha valamelyik $q_{i}$ csuklókoordináta az előírt értéktől valamekkora $Δ q_{i}$ értékkel eltér, akkor erre a szabályozóval ellátott aktuátor egy megfelelő $Δ τ_{i}$ csuklónyomaték változással reagáljon. Egyelőre lineáris közelítést fogunk alkalmazni, ami az esetek többségében elfogadható eredményt ad.

Minden egyes csuklóra tehát egy

$Δ τ_{i} = k_{i} Δ q_{i}$ ,

(3.12)

alakú lineáris összefüggést írunk fel, ahol $k_{i}$ tényezők egyfajta „rugóállandókként” értelmezhetők. A $k_{i}$ tényezőkből képezhetünk egy

$K = diag (k_{1}, k_{2},..., k_{n})$

(3.13)

diagonális mátrixot, amelyet csuklómerevségi mátrixnak nevezünk.

Most arra a kérdésre keressük a választ, hogyan érvényesül az ekvivalens csuklónyomatékok megváltozásának ( $Δ τ$ ‑nak) a hatása a robot és a környezet közötti kölcsönhatást kifejező F vektor megváltozásában. Az (3.7) összefüggés most értelemszerűen

$Δ τ = J^{T} Δ F$

(3.14)

alakban lesz érvényes. Másfelől a (3.12) és (3.13) egyenletek alapján írhatjuk, hogy

$Δ τ = K Δ q$ ,

(3.15)

ha kihasználjuk, továbbá a jól ismert $Δ p = J Δ q$ összefüggést. Ha a (3.12) egyenlettel definiált $k_{i}$ együtthatók egyike sem zérus (ami működésképes, szabályozott hajtásokkal ellátott robotoknál nyílván valóan fönnáll), akkor a K diagonális mátrix invertálható. A (3.12) - (3.15) egyenletek felhasználásával végül is a következő eredményt írhatjuk fel

$Δ p = C Δ F$ ,

(3.16)

ahol

$C = J K^{- 1} J^{T}$

(3.17)

a robot úgynevezett végpontra vonatkoztatott engedékenységi (angolul: compliance) mátrixa.

A C engedékenységi mátrixról jegyezzük meg, hogy az – K csuklómerevségi mátrixszal ellentétben – általában nem diagonális mátrix. Ez abból adódik, hogy a robot egyetlen csuklójának mozgása is a végpont több szabadságfokú mozgását eredményezheti.

Vissza	Fel	Előre
2. fejezet - Robotok geometriai és kinematikai jellemzése	Főoldal	4. fejezet - Robotok dinamikai jellemzése