4. fejezet - Robotok dinamikai jellemzése
A korábban bemutatottak alapján kijelenhető, hogy robotok kinematikai jellemzése során kizárólag a robot mozgások leírásának lehetőségeire szorítkoztunk, a mozgást létrehozó okok figyelmen kívül hagyásával. A robotmozgások mechanikai jellemzése a jelen alfejezetben teljesedik ki, amelynek során eljutunk a robot irányítás legalapvetőbb egyenletének felállításához és megismerkedünk egy elterjedt és hatékony számítási algoritmus elvi alapjaival, mely algoritmus számos robot irányítási feladat megvalósításakor igen eredményesen alkalmazható. A robotmozgások dinamikai tárgyalását egy tetszőlegesen megválasztott, i‑edik kartag mozgásának vizsgálatával kezdjük, az 4.1. ábra segítségével, amely a 3.1. ábra némileg módosított változata.
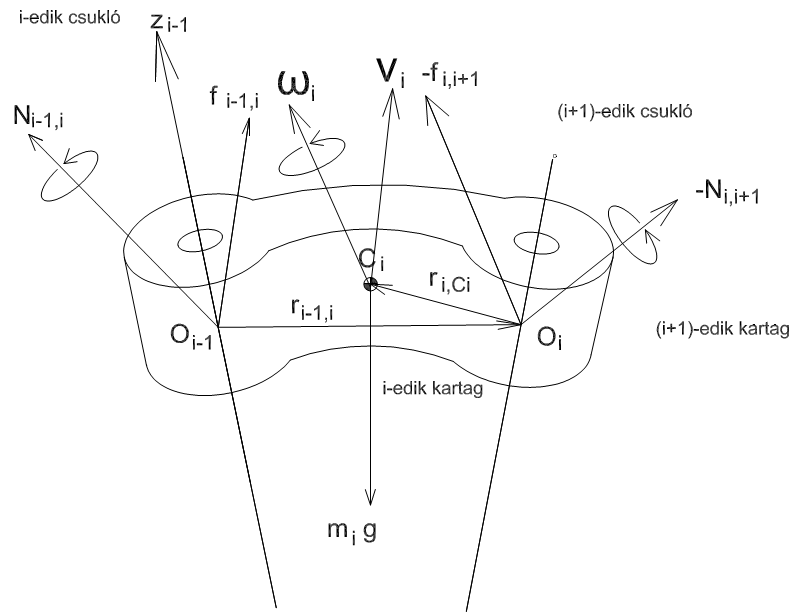
Elöljáróban megjegyezzük, hogy – akárcsak a kinematikai feladatok esetében – beszélhetünk direkt és inverz dinamikai feladatról. Az előbbinél adott ekvivalens csukló nyomatékok esetén vizsgáljuk a robot mozgását, az utóbbinál azt keressük, hogy az általunk megkövetelt robotmozgás az ekvivalens csuklónyomatékok milyen értékeivel valósítható meg.
A dinamikai egyenleteket először az ún. Newton–Euler- formalizmus szerint fogjuk felírni. Ez az eljárás lényegében a Newton axiómákon nyugvó mechanikai szemléletmódot követi.
Jelöljük az (4.1. ábra) ábrán látható módon ‑vel az i‑edik kartag tömegközéppontjának sebességvektorát és ‑vel a tömegközéppontja körüli forgásának szögsebesség vektorát! Az 4.1. ábra összes többi vektorának értelmezése megtalálható a 3.1. ábra leírásánál.
Ha az i‑edik kartagot gyorsuló vonatkoztatási rendszerként fogjuk fel, akkor az erőkre vonatkozó dinamikai egyenletet úgy nyerjük, hogy az (3.1) egyenlet jobb oldalát kiegészítjük a tehetetlenségi erővel (az idő szerinti deriváltakat a szokásoknak megfelelően, ahol csak lehetséges, az illető mennyiség betűjele fölé írt ponttal, illetve pontokkal fogjuk jelölni)
|
. |
(4.1) |
Kissé bonyolultabb úton juthatunk el a forgatónyomatékokra vonatkozó egyenlet az ún. Newton‑Euler‑egyenlet felírásához. Ehhez mindenekelőtt definiálnunk kell a robot kartagjainak tehetetlenségi tenzorát. Tetszőleges merev test tenzora alatt a következő 3×3‑as kvadratikus mátrixot értjük
|
, |
(4.2) |
ahol
|
, |
||
|
, |
||
|
, |
||
|
, |
||
|
, |
||
|
, |
ahol a test anyagának sűrűsége; a test tömegközpontjának koordinátái ( abban a koordinátarendszerben, amelyben a tehetetlenségi nyomatékot meg akarjuk határozni); x, y és z a test egyes anyagi pontjainak koordinátái (mint futókoordináták), dV pedig az elemi térfogat, mint integrálási változó. Természetesen valamennyi szereplő integrált a test teljes térfogatára ki kell terjeszteni.
Egy kis kitérőként emlékeztetünk arra, hogy egy rögzített tengely körül forgó merevtest forgási tehetetlensége egyetlen állandó skaláris adattal, az I tehetetlenségi nyomatékkal jellemezhető, továbbá ha a forgás ‑val jelölt szögsebessége nem állandó, a forgó mozgás fenntartásához szükséges N forgatónyomaték az alábbi egyenletből határozható meg
|
. |
(4.3) |
Bonyolultabbá akkor válik a helyzet (így a robotmozgások esetében is), ha a forgástengely, illetve forgáspont nem rögzített, hanem változó helyzetű. Ilyen esetben az (4.3)‑gyel felírt perdület tétel (impulzusmomentum‑tétel) csak olyan formában érvényes, ha a perdület teljes idő szerinti deriváltját képezzük, ami a következőképpen írható fel
|
. |
(4.4) |
A fenti összefüggés a mechanikai előtanulmányokból feltehetően ismert, hogy ha egy forgó koordinátarendszerben felírt vektor idő szerinti deriváltját képezzük egy rögzített koordinátarendszerben, akkor az így nyert derivált két tagból fog állni. Ezek közül az egyiknél a differenciáloperátor szerepét lényegében a szögsebesség vektorral balról történő vektoriális szorzás tölti be.
Ennyi előismeret birtokában felírhatjuk a forgatónyomatékokra vonatkozó dinamikai egyenletet
|
, |
(4.5) |
A fenti egyenletben magyarázatra lényegében csak a baloldal utolsó tagja szorul. Ez a tag nem más, mint az előbbiekben ismertetett effektusokból adódó ún. giroszkopikus nyomaték.
A (4.1) és (4.5) egyenletekből álló Newton‑Euler formalizmus rendelkezik mind előnyös, mind hátrányos tulajdonságokkal. A módszer javára írható, hogy az egyenletekben szereplő tagok mindegyikéhez jól körülhatárolható, szemléletes fizikai jelentés rendelhető hozzá. Számítástechnikai szempontból további előny, hogy ezen egyenletek alapján viszonylag egyszerű az adott feladat algoritmizálhatósága. Ugyanakkor hátrányként kell elkönyvelni azt a tényt, hogy az egyenletekben szereplő sebesség és szögsebesség vektorok nem alkotnak független rendszert, hiszen valamennyi kartag mozgása hatást gyakorol az összes további kartag mozgására.
Az említett hátrány kiküszöbölésére a robotikában is használatos az ún. Euler‑Lagrange formalizmus, mely a Newton‑Euler formalizmussal fizikailag teljesen egyenértékű dinamikai leírást tesz lehetővé.
A korábbi tanulmányokból ismert, hogy a Newton‑Euler formalizmus a dinamikai problémák energetikai megközelítésén alapul, és egyenleteiben ún. általánosított erők és általánosított koordináták, valamint az utóbbiak idő szerinti deriváltjai szerepelnek. Mind az általánosított erők, mind az általánosított koordináták független (nem csatolt) rendszert alkotnak, s lehetőség nyílik ún. zárt alakú dinamika egyenletek felállítására.
Ha a Lagrange-formalizmust robotokra kívánjuk alkalmazni, általánosított koordinátáknak a csuklókoordinátákat, általánosított erőknek pedig a ekvivalens csuklónyomatékokat választjuk, amikhez egyes esetekben még egy járulékos tag hozzáadódhat. A járulékos tagot jelöljük ‑vel.
Ha egy adott állapotban lévő mechanikai rendszer, pl. robot teljes kinetikus energiáját T‑vel, teljes potenciális energiáját pedig U‑val jelöljük, akkor a rendszer Lagrange függvénye definíciószerűen
|
|
(4.6) |
A robot minden egyes szabadságfokára felírhatjuk, az alábbi alakú, igen tömör Lagrange-féle mozgásegyenletet
|
, |
(4.7) |
ahol az i‑edik általánosított erő.
Fejtsük ki ezek után kissé részletesebben a fenti egyenlet egyes tagjait! Az i‑edik kartag kinetikus energiája
|
, |
(4.8) |
ahol minden szereplő mennyiség azonos jelentésű a korábban definiáltakkal. A robot teljes kinetikus energiája tehát
|
. |
(4.9) |
Az i‑edik kartag kinetikus energiájára felírt (4.8) összefüggés azonban az előbbiek értelmében nem zárt alakú egyenlet, hiszen az egyes ‑k és ‑k nem függetlenek egymástól. Célunk tehát most az, hogy a kartagok kinetikus energiájára (majd pedig potenciális energiájukra is) zárt alakú, a csuklókoordinátákat illetve azok deriváltjait tartalmazó összefüggéseket nyerjük.
A korábbi (2.39) és (2.43) egyenletekkel megteremtettük annak lehetőségét, hogy a végpont sebességének illetve szögsebességének vektorát az egyes csuklósebességekkel fejezzük ki, felhasználva a (2.38) szerint szétbontott Jacobi‑mátrixot.
Semmi akadálya nincs annak, hogy hasonló összefüggéseket írjunk fel bármely -edik kartag sebesség- illetve szögsebesség vektorára. Természetesen esetben az i‑edik kartag mozgását csak az azt megelőző csuklók mozgása befolyásolja, így az i‑edik kartagig bezárólag értelmezett Jacobi-mátrix – amit a továbbiakban ‑vel jelölünk – mindenképpen eltér az (2.38) szerintitől annyiban, hogy az utolsó (n+1) darab oszlopvektora nullvektor lesz, vagyis
|
. |
(4.10) |
Az (2.39) és (2.43) egyenletek analógiájára most már felírhatjuk, hogy
|
, |
(4.11) |
valamint
|
. |
(4.12) |
Továbbá a (4.11) és a (4.12) egyenleteket megadhatjuk ennél tömörebb alakban is
|
és . |
(4.13) |
A mátrix egyes elemeire felírhatjuk továbbá
|
, , |
(4.14) |
illetve
|
. |
(4.15) |
Megjegyezzük, hogy a vektor a (j-1)‑edik csuklótengely pozitív irányba mutató egységvektor; az vektor értelmezését.
Felhasználva az (4.8) – (4.15) összefüggéseket, a robot teljes kinetikus energiájára az alábbi kifejezés kapjuk
|
, |
(4.16) |
ahol
|
|
(4.17) |
a robot egészének tehetetlenségi nyomatéki tenzora, mely az egyes kartagok tehetetlenségi nyomatéki tenzoraihoz hasonlóan ugyancsak konfigurációfüggőek.
Ha -vel jelöljük a H mátrix ‑edik elmélet. Akkor az (4.16) egyenletet átírhatjuk a következő alakba
|
. |
(4.18) |
Egy kicsit egyszerűbb dolgunk van, ha a robot potenciális energiáját akarjuk kifejezni, ez ugyanis egyszerűbben alakban írható
|
|
(4.19) |
Továbbiakban azt a kérdést vizsgáljuk meg, mikor azonosíthatjuk az általánosított erőket az ekvivalens csukló nyomatékokkal, és mikor kell az utóbbiakat még egy, a korábbiakban már említett járulékos taggal kiegészíteni. A válasz az, hogy ha a robot végpontja a környezettel kölcsönhatásban van és a környezettet erővel ( hatelemű, erőket és nyomatékokat is magában foglaló vektor) hat a robot végpontjára, akkor állításunk szerint az általánosított erők
|
|
(4.20) |
alakban fejezhetők ki.
Állításunkat ismét a virtuális munka elvének felhasználásával bizonyítjuk be. Fejtsük ki, ugyanis az aktuátorok ekvivalens csuklónyomatékokat, a környezet pedig erőhatást, s tegyük fel, hogy a robot nyugalomban van! Ekkor bármely virtuális elmozdulás a csuklókoordináták térben ‑val, a végpont világkoordinátában ‑vel jelölhető. A végzett virtuális munka
|
. |
(4.21) |
Másfelől a virtuális munka az általánosított erők és a csuklókoordinátákban kifejezett virtuális elmozdulások szorzatának összegével egyenlő
|
. |
(4.22) |
Az (4.21) és (4.22) egyenletek jobb oldalának összevetésével az (4.20) állítás, bizonyítást nyert.
Most már minden szükséges részeredmény (a tejesség igénye nélkül, a robot teljes kinetikus és teljes potenciális energiájának kifejezése) rendelkezésünkre áll ahhoz, hogy felírhassuk a robot Euler‑Lagrange‑féle dinamikai egyenletét. Az (4.18) alapján az (4.7) egyenlet első tagja a következőképpen írható fel
|
. |
(4.23) |
A elemek a csuklókoordináták függvényei, ezért idő szerinti deriváltjuk a következőképpen is kiszámítható
|
. |
(4.24) |
Ami a robot potenciális energiáját illeti, az a csuklósebességektől független, vagyis értelemszerűen
|
, . |
(4.25) |
Az (4.7) egyenlet második tagjában a kinetikus és a potenciális energia csuklókoordináták szerinti parciális deriváltjai jelennek meg, és pedig
|
, |
(4.26) |
illetve
|
, |
(4.27) |
mivel az helyvektor szerinti parciális deriváltja könnyen belátható módon az (4.10)‑gyel definiált Jacobi‑mátrix oszlopvektorával egyenlő. Az (4.23) – (4.27) egyenleteket (4.7)‑ba helyettesítve végül is a következő egyenletet kapjuk
|
, |
(4.28) |
ahol
|
. |
(4.29) |
Az egész eddigi tananyag legfontosabb eredményének az (4.28) egyenletet tekinthetjük, amit joggal nevezhetünk a robotirányítás alapegyenletének is. Az egyenlet egyenes tagjaihoz a következő fizikai jelentést rendelhetjük hozzá:
-
a baloldal első tagja tartalmazza a kartag lineáris gyorsulásához szükséges erőt, illetve szöggyorsuláshoz szükséges forgatónyomatékot.
-
esetben a baloldal második tagja fejezi ki a kartag forgásakor fellépő centrifugális erőt
-
esetben a baloldal második tagja azt a Coriolis‑erőt fejezi ki, amely akkor lép fel, ha valamely kartag egy másik kartaghoz rögzített forgó koordinátarendszerhez képest haladó mozgást végez.
-
a baloldal harmadik tagja a kartagok saját súlyát, illetve az azokból adódó forgatónyomatékokat reprezentálja.
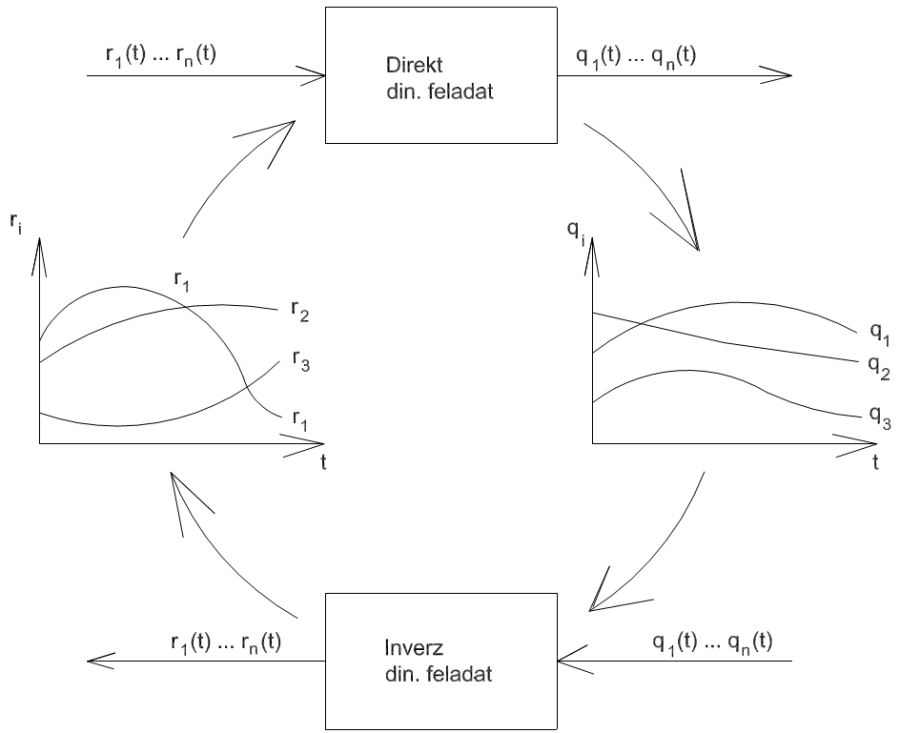
Az ábra felső részén látható téglalap az irányítóegységgel (esetleg számítógéppel) összekapcsolt robotot, mint komplex rendszert jelképezi. Ennek bemenő jeleit a mennyiségek, vagyis az ekvivalens csuklónyomatékok időfüggvényei alkotják, míg a kimenetek csuklókoordináták időfüggvények. Az alsó téglalap ugyanazt a rendszert jelképezi, mint a felső, azonban a ki- és bemenetek szerepet cseréltek. Az inverz dinamikai feladat megoldását tehát a következőképpen is megfogalmazhatjuk.
A robot használatának célja többnyire az, hogy a végpont (a robotkéz) egy általunk megkívánt, az elvégzendő feladat által meghatározott térbeli mozgást valósítson meg. Ennél fogva bemenőjelként az egyes csuklókoordináták időfüggvényeit írhatjuk fel. Az irányítórendszer (számítógép) feladata lényegében az egyes ekvivalens csuklónyomatékok időfüggvényeinek előállítása, vagyis az egyes értékek időpillanatról időpillanatra történő kiszámítása.
Az inverz dinamikai feladat megoldása általában sok számítástechnikai nehézséget rejt magában. Mint láttuk, az Euler‑Lagrange‑féle dinamikai egyenletek (4.28) szerinti alakja rendkívül tömör, kompakt módon írja le a robotmozgások dinamikáját.
Ha azonban valósidejű (angolul: real-time) számítógépes robotirányítást kívánunk megvalósítani, az Euler‑Lagrange formalizmus alkalmazása meglehetősen előnytelen, tekintettel arra, hogy az Euler‑Lagrange-egyenletekre alapozott algoritmusok számításigénye igen nagy. Ez esetben egy-egy feladat megvalósításához elvégzendő aritmetikai műveletek száma nagyjából a szabadságfokok számának harmadik-negyedik hatványával arányos. Ezért jóval célszerűbb a Newton‑Euler formalizmuson alapuló algoritmusok alkalmazása, ahol a számításigény csupán a szabadságfokok számának első hatványával arányos.
A 4.3. ábra egy Newton‑Euler formalizmuson alapuló rekurzív algoritmust szemléltet, ami tulajdonképpen a direkt kinematikai és az inverz dinamikai feladat kombinációjának tekinthető.
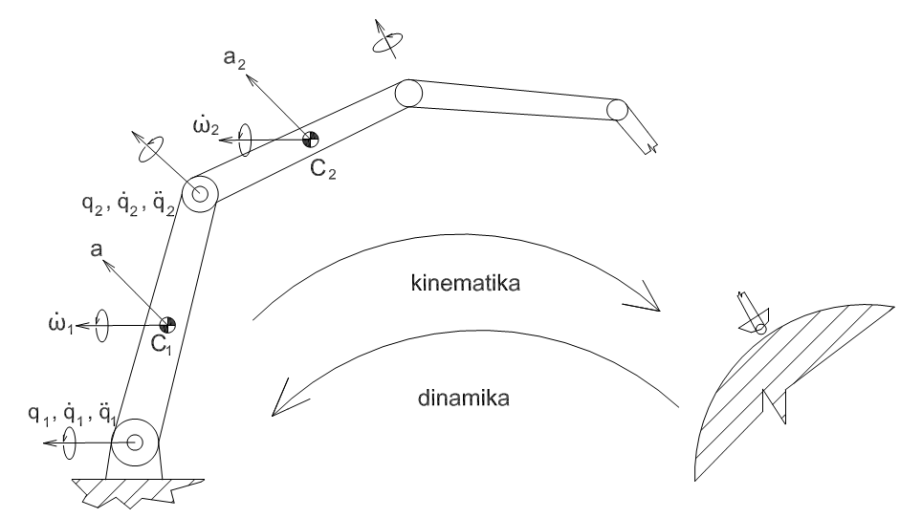
Az eljárás abból indul ki, hogy (mint teljesítendő követelményt) ismerjük, valamennyi csuklókoordináta időfüggvényét, így azok idő szerinti első és második deriváltját is – és a függvénynek – meghatározhatók, tehát ismertnek feltételezhetők.
Az eljárás első részében rendre meghatározzuk az (4.11), (4.12) és (4.13) egyenletekben szereplő kinetikai változókat. Például első lépésként ismeretében meghatározzuk az első kartagra jellemző , és így tovább. Az eljárás ezen első fázisát mindig folytatjuk, míg el nem jutunk az utolsó kartag kinetikai jellemzőinek értékeiig.
Ezután kerül sor az algoritmus dinamikai részének megvalósítására. Az (4.1) egyenletet helyettesítéssel a következő alakra hozhatjuk
|
, |
(4.30) |
ahol
|
. |
(4.31) |
Az eljárás rekurzív jellege most már világosan látható, hiszen az (4.30)‑hez teljesen hasonló módon megkaphatjuk ‑t ugyanis ismerjük értékét. A rekurzív eljárás dinamikai szakaszát tehát – most a forgatónyomatékot figyelembe vevő Newton‑Euler‑egyenleteket is felírva – a következő egyenletekkel jellemezhetjük.
|
, |
(4.32) |
|
|
. |
(4.33) |
A jelen fejezet befejezéseként egy konkrét, jól bevált számítási algoritmust fogunk ismertetni, ennek előkészítéseként azonban meg kell ismerkednünk néhány olyan jelenséggel, melyek akkor lépnek fel, ha valamilyen mozgást két, egymáshoz képest forgó mozgást végző koordinátarendszerben is le akarunk írni.
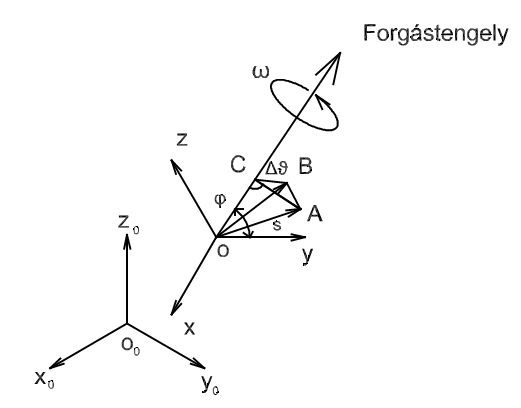
Vegyük fel a 4.4. ábra szerint egy, a környezethez képest nyugalomban lévő világ‑koordinátarendszert, valamint egy, az előbbihez képest szögsebességgel puszta forgó mozgást végző koordinátarendszert! Tekintsünk egy, az vonatkozási rendszerhez képest nyugvó (ezáltal a világ‑koordinátarendszerből szemlélve ugyancsak szögsebességgel forgó) tetszőleges s vektort! Keressük ezen s vektor idő szerinti deriváltját a világ‑koordinátarendszerben! Egy rövid időintervallumban az s vektor az koordinátarendszer
|
|
(4.34) |
szöggel fordul el.
Ha a (4.4. ábra) ábrán látható AOC szöget ‑vel jelöljük, akkor az vektor megváltozásának nagysága az ábra alapján
|
. |
(4.35) |
Az vektor merőleges mind a forgástengelyre, mind az vektorra, ennél fogva párhuzamos az vektorral. A határátmenetet képezve ezért kimondhatjuk, hogy az vektor idő szerinti deriváltja a világ‑koordinátarendszerből szemlélve
|
. |
(4.36) |
A (4.5. ábra) ábrán három koordinátarendszert láthatunk, melyeket egy képzeletbeli robot nulladik, i‑edik illetve (i+1)‑edik kartagjához rögzítettnek feltételezünk.
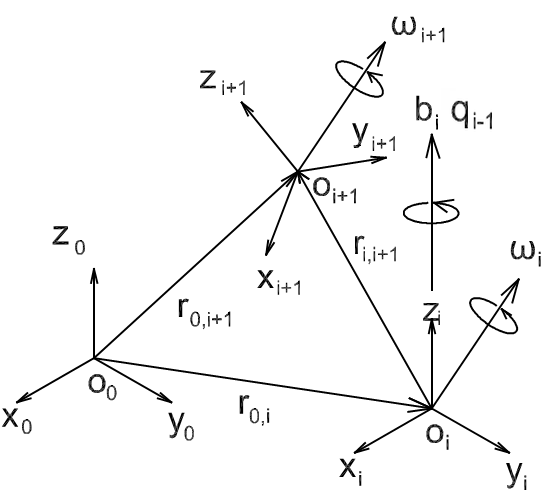
Az ábra alapján írhatjuk
|
|
(4.37) |
Célunk az, hogy az (4.37) egyenlet jobb oldalának idő szerinti deriváltját előállítsuk (világkoordinátákban), feltételezve, hogy az koordinátarendszer szögsebességgel forog az ‑hoz képest. A (4.37) egyenlet mindkét oldalának idő szerinti deriváltját képezve
|
. |
(4.38) |
Az és vektorok kezdőpontja a világ‑koordinátarendszer origója; jelöljük ezek idő szerinti deriváltjait ‑gyel illetve ‑vel. Az vektor ellenben az i‑edik koordinátarendszer origóját köti össze, ezért a világ‑koordinátarendszerben értelmezett időderiváltját nem képezhetjük a fenti egyszerű módon. Jelöljük -nel, -vel és -vel rendre azokat az egységvektorokat, amelyek az adott időpillanatban az i‑edik koordinátarendszer illetve tengelyeinek pozitív irányába mutatnak! Jelölje x, y, és z az vektornak a forgó koordinátarendszerben vett komponenseit! Ekkor a következő összefüggést írhatjuk fel
|
. |
(4.39) |
az pont ‑hez képesti mozgásából adódó sebességre vezessük be a következő jelölést
|
, |
(4.40) |
ahol a „rel” rövidítés a „relatív” szóra utal. A (4.39) egyenlet jobb oldalán a zárójelek közé tett második három tag a forgó koordinátarendszer forgásából származó sebességként értelmezhető.
Mivel az vektorok a forgó koordinátarendszerrel együtt forognak, a világkoordináták szerint értelmezett időderiváltjuk, a (4.36) összefüggés alapján számítható. Így a (4.36) egyenlet, valamint a (4.38) – (4.40) egyenletek figyelembevételével a következő összefüggésre juthatunk
|
. |
(4.41) |
A fenti eredmény általánosításaként megállapíthatjuk, hogy a rögzített és mozgó (forgó) koordinátarendszerekben érvényes differenciáloperátorok között formálisan a következő kapcsolat áll fenn
|
|
(4.42) |
Képezhetjük ezek után az vektor második deriváltját is a (4.42) differenciáloperátor ismételt alkalmazásával
|
|
(4.43) |
A fenti egyenlet bal oldala az (i+1)‑edik, jobb oldalának első tagja pedig az i‑edik kartag világkoordinátákban értelmezett lineáris gyorsulása; jelöljük ezeket rendre illetve . Ekkor némi átalakítással a (4.43) egyenletet a következő formába írhatjuk át
|
, |
(4.44) |
amely tehát magában foglalja az (i+1)‑edik kartag valamennyi (lineáris, Coriolis és centrifugális) gyorsulás összetevőjét.
4.1. Luh-Walker-Paul algoritmus
A mechanikai alapokat összefoglalása után megismerkedünk az ún. Luh‑Walker‑Paul‑féle algoritmussal, amely egy 1986‑ban kiadott amerikai szakkönyv szerint (akkoriban) a leghatékonyabbnak számított a robotdinamikai feladatok megoldása során.
Az algoritmus első részeként rekurzív kinematikai összefüggéseket fogunk felírni, amelyek különböző alakúak lesznek attól függően, hogy a vizsgált csukló prizmatikus (P), vagy rotációs (R).
Eszerint, ha az (i+1)‑edik csukló prizmatikus, akkor az (i+1)‑edik kartag szögsebessége illetve szöggyorsulása
|
, |
(4.45) |
|
|
. |
(4.46) |
Ha ellenben az (i+1)‑edik csukló rotációs, akkor az (i+1)‑edik kartag szögsebessége illetve szöggyorsulása
|
, |
(4.47) |
|
|
. |
(4.48) |
A lineáris sebességek és gyorsulások prizmatikus csukló esetén
|
, |
(4.49) |
|
|
. |
(4.50) |
Ha (4.49) és (4.50) egyenleteket visszahelyettesítjük a (4.41) illetve a (4.44) egyenletekbe a következő összefüggéseket kapjuk
|
, |
(4.51) |
|
|
. |
(4.52) |
Az ezeknek megfelelő összefüggések rotációs csukló esetén a következő alakban lesznek érvényesek
|
, |
(4.53) |
|
|
. |
(4.54) |
illetőleg a szükséges helyettesítések elvégzése után
|
, |
(4.55) |
|
|
. |
(4.56) |
Ezzel az algoritmus kinematikai részét illetően minden szükséges összefüggés rendelkezésünkre áll. Mielőtt rátérnénk a dinamikai szakasz ismertetésére, némi figyelmet kell, hogy szenteljünk annak a körülménynek, hogy a Newton‑Euler egyenletekben szereplő változók mind tömegközéppontra vonatkozó mennyiségekkel, ezzel szemben a jelen algoritmus csuklókra vonatkozó mennyiségekkel számol.
A két különböző reprezentáció közötti kapcsolatot az alábbi egyenletek adják meg
|
, |
(4.57) |
|
|
. |
(4.58) |
Az egyenletek értelmezését a 4.6. ábra segíti.
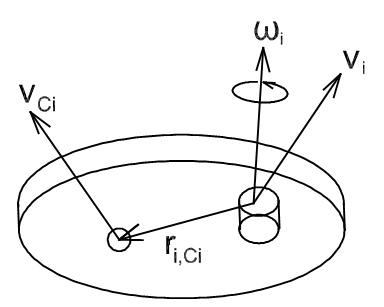
Tisztázásra szorul még az a kérdés, hogyan módosul a (4.5) egyenletben szereplő perdület (impulzusmomentum), ha azt nem tömegközéppontra vonatkoztatjuk. Mint ismeretes, minden kartag tehetetlenségi tenzora a kartag orientációjától függő mennyiség.
Jelöljük ‑val azt a 3×3‑as rotációs mátrixot, amelyik az i‑edik kartag koordinátarendszeréből a világ‑koordinátarendszerbe történő transzformálását valósítja meg, jelöljük továbbá az i‑edik kartag saját koordinátarendszerének origóján (tehát nem a tömegközéppontjára) értelmezett tehetetlenségi tenzorát ‑sal.
Energetikai megfontolásokkal (a forgásból adódó kinetikus energiák elemzésével) belátható, hogy a tehetetlenségi tenzor két fajta reprezentációja között az alábbi összefüggés érvényes
|
. |
(4.59) |
Most már valóban minden összefüggés rendelkezésünkre áll ahhoz, hogy a Luh‑Walker‑Paul‑algoritmust teljes egészében átlássuk.