2. fejezet - Mintavételes rendszerek szimulációja
- 2.1. Impulzusátviteli függvény és a mintavételes állapottér leírási mód
-
- 2.1.1. Differenciaegyenlet előállítása
- 2.1.2. Diszkrét idejű állapottér modell
- 2.1.3. Mintavételezés, Z–transzformáció
- 2.1.4. A Z–transzformáció tulajdonságai
- 2.1.5. Mintavételezett jelek Z-transzformációja
- 2.1.6. Mintavételes és folytonos rendszerek összekapcsolása, tartószervek (ZOH, FOH)
- 2.1.7. Mintavételezett adatokkal működő folytonos rendszer diszkrét modellje
- 2.1.8. Inverz Z–transzformáció
- 2.1.9. Impulzusátviteli függvény
- 2.2. Mintavételes rendszerek alapelemei
- 2.3. Mintavételes alapelemek összekapcsolása
-
- 2.3.1. Az impulzusátviteli függvény (SISO rendszer) megvalósítása digitális számítógépen
-
- 2.3.1.1. Az impulzusátviteli függvény megvalósítása soros kapcsolású alapelemekkel
- 2.3.1.2. Az impulzusátviteli függvény megvalósítása párhuzamos kapcsolású alapelemekkel
- 2.3.1.3. Impulzusátviteli függvény megvalósítása közvetlen programozással
- 2.3.1.4. Impulzusátviteli függvény megvalósítása M programozással
- 2.4. Állapottér leírású (MIMO) rendszer megvalósítása
- 2.5. Transzformációk a mintavételes rendszerekben
2.1. Impulzusátviteli függvény és a mintavételes állapottér leírási mód
Az impulzusátviteli függvény mintavételes rendszerekben megfelel a folytonos időben használt átviteli függvénynek. Az impulzusátviteli függvény formális definíciója hasonlít az átviteli függvényéhez, a kimenő jel transzformáltját kell elosztanunk a bemenő jel transzformáltjával.
Átviteli függvény esetén Laplace–transzformáltak,
|
|
(2.1) |
impulzusátviteli függvénynél Z-transzformált értékek hányadosáról van szó, adott h mintavételi időtartam mellett.
|
|
(2.2) |
2.1.1. Differenciaegyenlet előállítása
A K.Á.L.I. differenciálegyenlet h mintavételi időtartammal differenciaegyenletté alakítható. Az átalakításhoz az idő szerinti differenciálhányadosok közelítése szükséges. Az x(t) folytonos idejű jel idő szerinti első deriváltját többféle numerikus módszerrel közelíthetjük. Mindegyik közelítésnél felhasználjuk a z = e s·h operátort, hogy a Laplace–operátoros tartománybeli s operátorral való szorzási műveletet (idő szerinti differenciálás műveletét) megvalósítsuk a h mintavételi időtől függő z operátorral.
2.1.1.1. Előrehaladó differencia
Az előrehaladó differencia (Euler–módszer) a k·h pillanatbeli idő szerinti differenciálhányados értéket a (k+1)·h időpillanatbeli érték segítségével adja meg.
|
|
(2.3) |
A z eltolás operátor felhasználásával az idő szerinti differenciálásnak megfelelő közelítés
|
|
(2.4) |
Más módszerrel, bevezetve a függvényt
|
|
(2.5) |
Az alábbi helyettesítéssel és Laplace-transzformációval
|
|
(2.6) |
|
|
|
(2.7) |
Figyelembe véve, hogy
|
|
(2.8) |
Kapjuk a z és s operátor kapcsolatát az előrehaladó differencia-közelítésnél
|
|
(2.9) |
Ebből
|
|
(2.10) |
2.1.1.2. Hátrahaladó differencia
Hátrahaladó differencia módszer a k·h pillanatbeli idő szerinti differenciálhányados értékét a (k-1)·h időpillanatbeli érték segítségével adja meg
|
|
(2.11) |
A z eltolás operátor felhasználásával a differenciálásnak megfelelő közelítés
|
|
(2.12) |
A másik módszerrel
|
|
(2.13) |
Laplace transzformációval és s helyettesítésével
|
|
(2.14) |
Átrendezve
|
|
(2.15) |
A z és s operátor kapcsolata hátrahaladó differencia-közelítésnél
|
|
(2.16) |
Ebből
|
|
(2.17) |
2.1.2. Diszkrét idejű állapottér modell
Ha a folytonos idejű állapotegyenletet digitális számítógéppel szeretnénk megoldani, át kell alakítanunk diszkrét idejűvé. Feltételezzük, hogy az u (t) vektorbeli bemenő jelek csak a diszkrét k·h időpillanatokban változtatják meg értéküket.
A folytonos állapotegyenlet,
|
|
(2.23) |
diszkrét idejű állapotegyenletében
|
. |
(2.24) |
az idő szerinti differenciálhányadost közelíthetjük a következő differenciahányadossal
|
|
(2.25) |
A folytonos idejű állapotegyenlet megoldása
|
|
(2.26) |
Feltételezve, hogy két mintavételi időpont között a bemenő jel értéke nem változik, a 2.26. egyenletet felírhatjuk a (k+1). és a k. időpillanatra
|
|
(2.27) |
|
|
|
(2.28) |
A második egyenlet -szeresét kivonva az első egyenletből, és a helyettesítéssel
|
|
(2.29) |
Átrendezés után a diszkrét idejű állapotegyenletet kapjuk
|
|
(2.30) |
A folytonos kicsatolási egyenlet formája:
|
, |
(2.31) |
a diszkrét idejű kicsatolási egyenlet pedig a következő alakú:
|
. |
(2.32) |
A diszkrét idejű állapottér modell kapcsolata a folytonos idejű állapottér modellel
|
|
(2.33) |
|
|
|
(2.34) |
|
|
|
(2.35) |
|
|
|
(2.36) |
A mátrix kitevőjű exponenciális függvény meghatározása.
|
|
(2.37) |
-
Ha rendelkezésünkre áll a folytonos rendszer állapottér leírású alakban, akkor a Z-transzformációt a megadott h mintavételi időtartammal, a 2.33 és a 2.34 képletek alkalmazásával is elvégezhetjük.
-
A végtelen sor eleme k=70 indexértéknél az 1/70! értéke 10-100 nagyságrendű, tehát a végtelen sor helyett elegendő véges indexértékig számolni a sor elemeit.
2.1.3. Mintavételezés, Z–transzformáció
Az időben folytonos jel mintavételezését elképzelhetjük egy kapcsoló segítségével. A kapcsoló h időközönkénti bekapcsolásával (majd azonnali kikapcsolásával) a jelből impulzussorozat jellegű mintákat gyűjtünk. A mintavételezett jel értékét a következő mintavételi időpontig fenntartja az úgynevezett tartószerv, amely a mintavételezett jelet minden időpillanatban rendelkezésre álló folytonos jellé alakítja. A legegyszerűbb tartószerv a nulladrendű tartószerv (ZOH = Zero Order Hold), amely a mintavételezett jel értékét változatlanul tartja a következő mintavételezésig.
A h időközönkénti mintavételezést biztosító egységimpulzusokból (δ(t )) álló jelsorozatként adott mintavevő időfüggvénye
|
|
(2.38) |
Az x(t) folytonos jelből az x*(t) mintavételezett jelsorozatot előállító összefüggés tulajdonképpen moduláció, az impulzussorozat amplitúdóját moduláljuk az x(t ) jellel
|
|
(2.39) |
Mivel a rendszervizsgálatok során leggyakrabban a t < 0 tartományban zérusértékű jelekkel foglalkozunk, a mintavételezett jelet definiáló összefüggés
|
. |
(2.40) |
Az előző egyenlet második részének Laplace–transzformáltja
|
|
(2.41) |
Bevezetve a h idővel való eltolásnak megfelelő
|
|
(2.42) |
operátort, felírhatjuk az x(t ) jel Z-transzformáltját
|
|
(2.43) |
Mivel a Z-transzformáció során csak a jel mintavételi időpillanatbeli (t=k·h) értékeivel foglalkozunk, felírható
|
|
(2.44) |
Az inverz Z-transzformációval nem tudjuk a teljes x(t) jelet visszaállítani, mivel csak a t=k·h mintavételi időpontokban ismerjük az értékeit.
2.1.4. A Z–transzformáció tulajdonságai
Szorzás konstanssal:
|
|
(2.45) |
Linearitás:
|
|
(2.46) |
Szorzás -val {ahol a konstans érték}:
|
|
(2.47) |
Eltolási tétel:
|
|
(2.48) |
|
|
|
(2.49) |
|
|
(2.50) |
|
|
|
(2.51) |
ha akkor
|
|
(2.52) |
|
|
|
(2.53) |
|
|
|
(2.54) |
|
|
|
(2.55) |
|
|
|
(2.56) |
ha akkor
A komplex átalakítás tétele:
|
|
(2.57) |
|
Időtartományban |
Z-transzformált tartományban |
|---|---|
|
= |
|
|
= |
2.1.5. Mintavételezett jelek Z-transzformációja
|
x(t) |
x(s) |
{x[n·h]} |
x(z) |
|---|---|---|---|
|
1 |
1 |
||
|
Tuschák Róbert: Szabályozástechnika 3. Füzet; (1988) |
|||
2.1.6. Mintavételes és folytonos rendszerek összekapcsolása, tartószervek (ZOH, FOH)
Az x*(t) h időközönként mintavételezett jel, melynek értékei csak a k·h , k = 0,1,2, . . . időpillanatokban állnak rendelkezésre. Ahhoz, hogy ezt a jelet egy folytonos idejű rendszerben alkalmazni tudjuk, folytonos idejűvé kell alakítanunk. Ezt a feladatot egy tartószerv elnevezésű eszközzel lehet megvalósítani.
Elméletileg tetszőleges rendű tartószervet létre lehet hozni, de a szükséges korábbi értékek nagy száma és a realizálás (számítás) bonyolultsága miatt, leggyakrabban nulladrendű, esetleg elsőrendű tartószervet használunk.
2.1.6.1. A nulladrendű tartószerv
A nulladrendű tartószerv (ZOH = Zero Order Hold) segítségével a mintavételezett jelből úgy állítunk el folytonos idejű jelet, hogy a k. mintavételi időpillanatbeli értéket a (k+1). mintavételi időpillanatbeli érték megérkezéséig tartjuk. Rövid, nulla meredekségű függvénydarabokkal (vízszintesekkel) közelítjük az eredeti jelet. A visszaállított jel h mintavételi idő szélességű impulzusok (a k. pillanatban k·h magasságú téglalapok) sorozata.
A t=0 időpillanatban működésbe lépő, h ideig működő nulladrendű tartószerv időfüggvénye két egységugrással írható fel. Az első 1(t) egységugrás t=0-ban kezdődik. A második egységugrás negatív értékű, h idővel később kezdődik és amplitúdója -1 érték.
A nulladrendű tartószerv időfüggvénye
|
, |
(2.58) |
és ennek Laplace–transzformáltja
|
|
(2.59) |
Mivel a nulladrendű tartószerv bemenete Dirac–impulzus, a fenti Laplace–transzformált egyben a nulladrendű tartószerv átviteli függvénye (2.60)
|
|
(2.60) |
A nulladrendű tartószerv frekvencia-átviteli függvénye (2.61) s =jω formális helyettesítéssel
|
|
(2.61) |
2.1.6.2. Elsőrendű tartószerv
Az elsőrendű tartószerv (FOH = First Order Hold) a jel (k+1). időpillanatbeli értékét becsüli és a k. időpillanatbeli értékből a becsült értékbe vezető egyenessel közelíti a k. és a (k+1). időpillanat közötti folytonos értékeket. A módszer a (k+1). időpillanatbeli érték becsléséhez a már rendelkezésre álló (k-1). és k. időpillanatbeli értékeket összekötő egyenes meredekségét (a differenciahányadost) alkalmazza. A k. időpillanatbeli értékből ezzel a meredekséggel induló egyenes h idővel későbbi értéke adja a jel (k+1)·h időpillanatbeli közelítő értékét. Amikor megjelenik a jel tényleges (k+1)·h időpillanatbeli értéke, az elsőrendű tartószerv függőleges vonallal köti össze az azonos időpillanatbeli közelítő és valós jelértékeket.
Az elsőrendű tartószerv átviteli függvénye
|
|
(2.62) |
2.1.7. Mintavételezett adatokkal működő folytonos rendszer diszkrét modellje
A folytonos differenciálegyenlettel leírt rendszerek mintavételi időtartamának megállapítását a 1.8.1.2. szakasz fejezetben leírt elvek figyelembevételével kell megállapítani, a vizsgált rendszerben még figyelembe vett legkisebb időállandó segítségével.
Mintavételezett adatokkal működő folytonos rendszer általános felépítését a 2.1. ábra mutatja be. Az átalakítandó rendszert a G(s) időben folytonos átviteli függvénnyel írjuk le. A bementi jel, egy mintavételes jel u[k⋅h] amelyet például egy számítógépes irányító rendszer bocsájt ki. A folytonos rendszer időben folytonos jelet igényel bemeneti jelként. A tartószerv (jelformáló) a mintavételezett jelet időben folytonos jellé alakítja, és az u[k⋅h] mintavételes jelből, időben folytonos m(t) jelet hoz létre.

A mintavételezési időnél az m[t=k⋅h]-nak egyenlőnek kell lennie az u[k⋅h]-val. A mintavételezési pontok között egy tartószervvel polinomiális n-ed rendű extrapolációt alkalmazhatunk, amelyet a következő függvénnyel írhatunk le:
|
, |
(2.63) |
ahol
|
k·h |
a k. mintavételezési időpont, |
|
|
τ |
a két mintavételezés közötti folytonos jel független változója, , |
|
|
n |
a közelítés fokszáma. |
A legegyszerűbb és a leggyakrabban alkalmazott tartószerv a nullarendű tartószerv (ZOH = Zero Order Hold), amelynél
|
|
(2.64) |
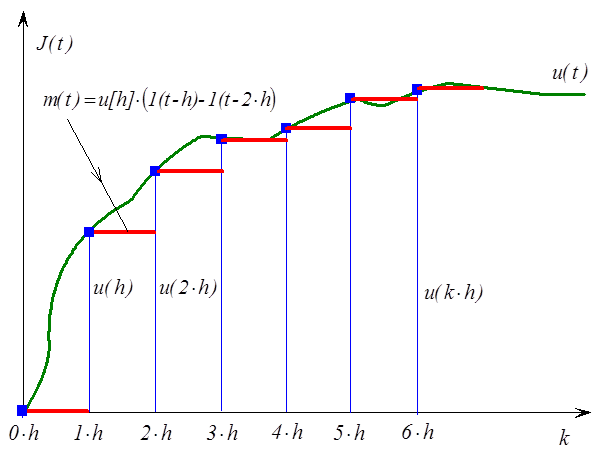
Ahogyan a (2.2. ábra) ábrán látható, a tartószerv kimenete m(t) függ az időben folytonos u(t) jeltől.
|
|
(2.65) |
Az előző egyenlet Laplace-transzformáltja a következő lesz
|
|
(2.66) |
Fontos, hogy az összefüggés a mintavételezett jel időben folytonos Laplace-transzformáltja
|
|
(2.67) |
Tehát, a nullarendű tartószerv (ZOH) átviteli függvényét a fennmaradó tört írja le, ezért a tartószerv átviteli függvénye:
|
|
(2.68) |
A diszkrét idejű átviteli függvény, amelyet impulzusátviteli függvénynek is nevezünk, tulajdonképpen a GZOH(s) nulladrendű tartószerv átviteli függvénye és a folyamat átviteli függvénye G(s) szorzatának Z-transzformáltja.
Ez az impulzusátviteli függvény a folytonos átviteli függvénnyel leírt rendszer transzformáltja mintavételes alakba a megadott h mintavételi időtartammal.
|
|
(2.69) |
A diszkrét idejű rendszer impulzusátviteli függvényének blokkdiagramját (2.3. ábra) ábra mutatja
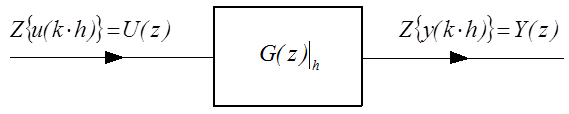
Egy mintavételes rendszer Z-transzformáltját a kimeneti jel Z-transzformáltjának Y(z) és a bemeneti jel Z-transzformáltjának U(z) hányadosaként definiáljuk, adott mintavételi időtartamnál.
|
|
(2.70) |
Megjegyzés:
Ha összehasonlítjuk a mintavételezett, időben folytonos jelek U(s) és a diszkrét idejű jelek U(z) Laplace-transzformáltjait
|
|
(2.71) |
és
|
|
(2.72) |
ismét megkapjuk az összefüggést a Laplace- és a Z-transzformáció közötti kapcsolatra
|
|
(2.73) |
és
|
|
(2.74) |
Fontos még megjegyezni, hogy
|
|
(2.75) |
ahol
|
folytonos időben h értékű késleltetés Laplace-transzformáltja. |
A Táblázat 2.3 a folytonos átviteli függvénnyel leírt rendszerek Z-transzformált impulzusátviteli függvényét adja meg adott h mintavételezési időtartammal.
|
G(s) |
G(z) |
|---|---|
|
, |
|
|
Tuschák Róbert: Szabályozástechnika 3. Füzet; (1988) |
|
2.1.8. Inverz Z–transzformáció
2.1.8.1. Táblázatból való visszakereséssel
Ilyenkor a Táblázat 2.2 x(z) oszlopát alkalmazzuk bementként, és az x(t) időfüggvényt határozzuk meg a táblázatból.
2.1.8.2. Résztörtekre bontással
A számítások eredményeként általában a kimenő jel Z-transzformáltját határozzuk meg, amely az Y(z). Az Y(z) a számítások elvégzése után általában egy számláló és nevező polinom z független változóval. Ha a számlálót és a nevezőt is gyöktényezős alakban írjuk fel a következő kifejezést kapjuk:
|
|
(2.76) |
Ezt bonthatjuk fel a nevező (Y(z)) gyökei () szerint felírt résztörtekre.
|
|
(2.77) |
alakra hozzuk, ahol
|
a számláló polinom gyökei (zérusai), |
||
|
a nevező polinom gyökei (pólusai), |
||
|
állandók. |
A meghatározott együtthatók segítségével a megoldás időtartományban
|
|
(2.78) |
|
|
|
(2.79) |
alakú lesz.
Egy tag rekurzív formulává történő visszaalakításánál az alakú kifejezésben az értékek a meghatározó paraméterek, n pedig az elemek száma.
A résztörtekre bontás a nevező többszörös gyökei (pólusai) esetén is alkalmazható, ilyenkor a reziduum tétel segítségével határozzuk meg a függvényt.
2.1.8.3. Sorba fejtéssel
Az Y(z) függvényt, amely általában egy számláló (NUM(z)) és egy nevező (DEN(z)) polinomok hányadosaként jelenik meg, z-1 hatványsorba fejtjük.
|
|
(2.80) |
A z-1 hatványsor együtthatói a diszkrét számsorozat mintavételi időpontokban felvett értékeit adják. Ha Y(z) racionális törtfüggvény, a sorfejtést a számláló nevezővel való osztásával végezhetjük.
2.1.8.4. Inverz Z-transzformáció diszkrét konvolúcióval
A mintavételes rendszereknél a diszkrét konvolúciós összeget ugyanúgy alkalmazhatjuk az inverz Z-transzformáció meghatározásához, mint a folytonos rendszereknél a konvolúciós integrált az inverz Laplace-transzformáció esetén.
Az inverz Z-transzformációhoz alkalmazzuk az Y(z) függvényt, amelyet bontsunk fel két Z-transzformált függvény szorzatára, (amelyek egyszerűbbek Y(z)-nél)!
|
|
(2.81) |
Így Y(z) kifejezhető, a szorzatban szereplő Y 1 (z) és Y 2 (z) függvények z-1 hatványaival felírt sorainak sorozatával.
|
|
(2.82) |
A két függvénysor összeszorzásával a következő függvényt kapjuk:
|
|
(2.83) |
Az y[k] általánosan felírható függvénye időtartományban:
|
|
(2.84) |
ami nem más, mint y 1 [k] és y 2 [k] diszkrét konvolúció függvénye.
Ezt az inverz Z-transzformációs eljárást akkor érdemes alkalmazni, ha az y 1 [k] és y 2 [k] már eleve idősorozatként áll rendelkezésünkre.
A diszkrét konvolúciót általánosan a következő összefüggéssel határozhatjuk meg:
|
|
(2.85) |
A * a konvolúciós szorzat, amelynek definícióját a 2.84 képlettel adtuk meg.
2.1.9. Impulzusátviteli függvény
A G(s) átviteli függvényű rendszer impulzusátviteli függvényét az egységimpulzusra adott válasz, a súlyfüggvény (impulzusválasz) segítségével is felírhatjuk. A g(t) súlyfüggvény az átviteli függvény inverz Laplace–transzformáltja (mivel a Dirac–delta Laplace transzformáltja egy).
|
|
(2.86) |
A k·h mintavételi időpillanatokban tekintsük a súlyfüggvény értékeit, és helyettesítsük be a Z-transzformáció definíciós összefüggésébe (2.44)
|
|
(2.87) |
Stabil rendszerek impulzusátviteli függvényében a végtelen sor (2.87) konvergens. Sorba kapcsolt impulzusátviteli függvénnyel adott elemek eredő impulzusátviteli függvényét az impulzusátviteli függvények szorzásával adhatjuk meg. Ugyanez mintavételes rendszereknél nem feltétlenül igaz, mindig tekintettel kell lennünk a mintavevő(k) elhelyezésére.
2.1.9.1. Impulzusátviteli függvény z pozitív hatványaival G(z)
A mintavételes rendszerek leírásánál megvalósított állandó együtthatós differenciaegyenlet időben előrelépéses felírási móddal a következő alakban adható meg
|
|
(2.88) |
ahol
|
a 0d …a nd |
az előrelépéses differenciaegyenlet kimenő jelének időben eltolt értékeihez tartozó együtthatók, |
|
|
b 0d …b md |
az előrelépéses differenciaegyenlet bemenő jelének időben eltolt értékeihez tartozó együtthatók, |
|
|
y[(k+i)·h] |
a rendszer kimenő jele a (k+i)·h időpillanatban, |
|
|
n |
a kimenő jel legnagyobb időbeni eltolásának indexe, |
|
|
u[(k+j)·h] |
a rendszer bemenő jele a (k+j)·h időpillanatban, |
|
|
m |
a bemenő jel legnagyobb időbeni eltolásának indexe, |
|
|
h |
mintavételi időtartam [idő dimenzió], |
|
|
k |
az aktuális számítási időpont indexe (t=k·h). |
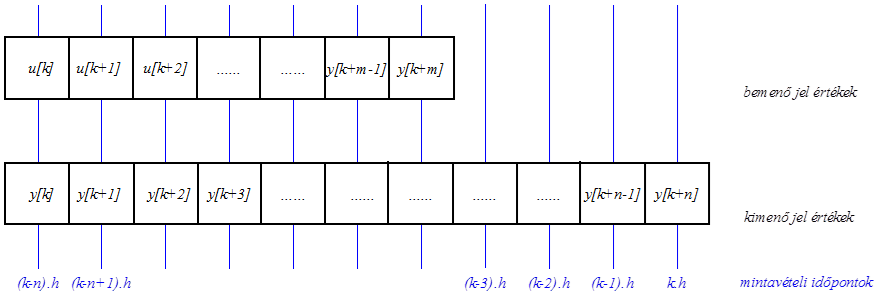
Az időben előrelépéses differenciaegyenlethez a bemeneti és a kimeneti jelek adott mintavételi időpontbeli értékeit a (2.4. ábra) ábrán láthatjuk. Az ábrán látható, hogy a számításhoz (k-n)·h időponttal korábbi állapotból a bemenő és a kimenő jel mintavételes értékei valóban „előre lépnek” az időben.
Az impulzusátviteli függvényt a rendszer előrelépéses differenciaegyenletének Z- transzformációjával (a 2.49 összefüggés szerint az időbeni eltolás Z-transzformációjával), a korábbi bementi és kimeneti jelértékeket nullának feltételezve felírhatjuk, hogy
|
|
(2.89) |
ahol
|
az előrelépéses differenciaegyenlet kimenő jelének időben eltolt értékeihez tartozó együtthatók, |
||
|
az előrelépéses differenciaegyenlet bemenő jelének időben eltolt értékeihez tartozó együtthatók, |
||
|
n |
a nevezőben z legnagyobb pozitív hatványkitevője, |
|
|
m |
a számlálóban z legnagyobb pozitív hatványkitevője, |
|
|
h |
mintavételi időtartam [idő dimenzió]. |
Fizikailag megvalósítható rendszereknél a számláló és a nevező legmagasabb hatványkitevőjű tagjai között igaznak kell lennie a következő relációnak .
2.1.9.2. Impulzusátviteli függvény z negatív hatványaival G(z-1)
Ha a differenciaegyenletet a jelenlegi időponthoz képest időben visszalépő értékek segítségével írjuk fel, akkor a differenciaegyenlet visszalépéses algoritmusát kapjuk.
Az állandó együtthatós differenciaegyenlet időben visszalépéses felírási móddal
|
|
(2.90) |
ahol
|
a visszalépéses differenciaegyenlet kimenő jelének időben eltolt értékeihez tartozó együtthatók, |
||
|
a visszalépéses differenciaegyenlet bemenő jelének időben eltolt értékeihez tartozó együtthatók, |
||
|
y[(k-i)·h] |
a rendszer kimenő jele a (k-i)·h időpillanatban, |
|
|
n |
a kimenő jel legnagyobb időbeni eltolásának indexe, |
|
|
u[(k-j)·h] |
a rendszer bemenő jele a (k-j)·h időpillanatban, |
|
|
m |
a bemenő jel legnagyobb időbeni eltolásának indexe, |
|
|
h |
mintavételi időtartam [idő dimenzió], |
|
|
k |
az aktuális számítási időpont indexe (t=k·h). |
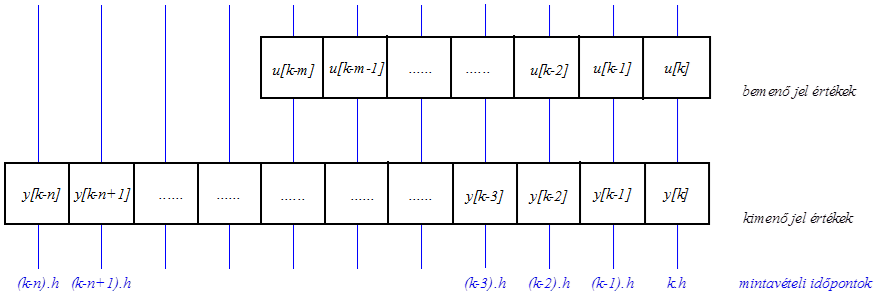
A impulzusátviteli függvényt felírhatjuk a rendszer visszalépéses differenciaegyenletének Z-transzformációjával a 2.48 összefüggés szerint a időbeni eltolás Z-transzformációjával.
|
|
(2.91) |
ahol
|
a visszalépéses differenciaegyenlet kimenő jelének időben eltolt értékeihez tartozó együtthatók, |
||
|
a visszalépéses differenciaegyenlet bemenő jelének időben eltolt értékeihez tartozó együtthatók, |
||
|
n |
a kimenő jel legnagyobb időbeni eltolásának indexe; a nevezőben z legnagyobb pozitív hatványkitevője, |
|
|
m |
a bemenő jel legnagyobb időbeni eltolásának indexe, a számlálóban z legnagyobb pozitív hatványkitevője, |
|
|
h |
mintavételi időtartam [idő dimenzió]. |
2.1.9.3. G(z) átalakítása G(z-1) alakra
Egy vizsgált mintavételes rendszer előrelépéses differenciaegyenlete alapján felírható impulzusátviteli függvény (adott mintavételi időtartamnál), amely számlálóbeli valamint nevezőbeli polinom-együtthatókkal rendelkezik.
Fizikailag megvalósítható rendszernél teljesülnie kell a következő relációnak .
|
|
(2.92) |
Ugyanez a mintavételes rendszer visszalépéses differenciaegyenlete alapján szintén felírható egy impulzusátviteli függvény (adott mintavételi időtartamnál), amely számlálóbeli és nevezőbeli polinom-együtthatókkal rendelkezik. A számlálóban lévő együtthatókat -től -ig kiegészítettük olyan együtthatókkal, amelyek nem szerepeltek a korábban felírt visszalépéses differenciaegyenlet algoritmusban, most viszont fontos szerepük lesz.
|
|
(2.93) |
Mivel ugyanarról a mintavételes rendszerről van szó, a két impulzusátviteli függvénynek ugyanarra a bemenő jelsorozatra ( u[k] ) ugyanazt a kimenő jelsorozatot ( y[k] ) kell kiadnia. Ezen feltétel biztosításához a pozitív hatványkitevőjű G(z) impulzusátviteli függvény együtthatóiból a következő módon kell a G(z -1 ) impulzusátviteli függvény együtthatóit képeznünk.
A G(z) impulzusátviteli függvény nevezőjének legmagasabb fokú z tagjával elosztjuk a számlálót és a nevezőt is, az így létrejövő átviteli függvény z negatív hatványai szerint fogja leírni az impulzusátviteli függvényt. Az együtthatók értékadását a (Táblázat 2.4 és a Táblázat 2.5) táblázat tartalmazza.
|
…. |
|
…. |
|
…. |
Mintapélda:
Határozzuk meg a következő G(z) impulzusátviteli függvényből a G(z -1 ) impulzusátviteli függvényt!
|
|
(2.94) |
Megoldás:
A G(z) impulzusátviteli függvény legmagasabb nevezőbeli z hatványával, z 2 -el elosztva a számlátót és a nevezőt a közetkező impulzusátviteli függvényt kapjuk:
|
|
(2.95) |
2.1.9.4. 1G(z-1) átalakítása G(z) alakra
Egy vizsgált mintavételes rendszer visszalépéses differenciaegyenlete alapján felírható impulzusátviteli függvény (adott mintavételi időtartamnál), amely számlálóbeli
és nevezőbeli polinom-együtthatókkal rendelkezik.
A mintavételes rendszer differenciaegyenlete:
|
|
(2.96) |
Ugyanez a mintavételes rendszer előrelépéses differenciaegyenlete alapján szintén felírható egy impulzusátviteli függvény (adott mintavételi időtartamnál), amely számlálóbeli és nevezőbeli polinom-együtthatókkal rendelkezik. A számlálóban lévő együtthatókat -től -ig kiegészítettük olyan együtthatókkal, amelyek nem szerepeltek a korábban felírt előrelépéses differenciaegyenlet algoritmusban, most viszont fontos szerepük lesz.
|
|
(2.97) |
Mivel ugyanarról a mintavételes rendszerről van szó, a két impulzusátviteli függvénynek ugyanarra a bemenő jelsorozatra ( u[k] ) ugyanazt a kimenő jelsorozatot ( y[k] ) kell kiadnia. Ezen feltétel biztosításához a negatív hatványkitevőjű G(z -1 ) impulzusátviteli függvény együtthatóiból a következő módon kell a G(z) impulzusátviteli függvény együtthatóit képeznünk.
Határozzuk meg a G(z -1 ) impulzusátviteli függvény nevezőjének legnagyobb abszolút értékű, negatív kitevőjét (n<0 érték)! Ezt követően osszuk el a számlálót és a nevezőt is z n -el! Így létrejön az az átviteli függvény, amely z pozitív hatványai szerint fogja leírni az impulzusátviteli függvényt. Az együtthatók értékadását a (Táblázat 2.6 és a Táblázat 2.7) táblázat tartalmazza.
|
…. |
|
…. |
|
…. |
Mintapélda:
Határozzuk meg a következő G(z -1 ) impulzusátviteli függvényből G(z) impulzusátviteli függvényt:
|
|
(2.98) |
Megoldás:
A G(z) impulzusátviteli függvény nevezőjének legmagasabb abszolút értékű kitevője = 2-vel. A számlátót és a nevezőt szorozva z +2 -el a közetkező függvényt kapjuk:
|
|
(2.99) |
2.2. Mintavételes rendszerek alapelemei
A mintavételes rendszereket leíró differenciaegyenletben a következő alapműveletek szerepelnek:
-
jelkomponensek összeadása, kivonása,
-
jelkomponensek szorzása, osztása állandó értékkel (az együtthatókkal),
-
jelkomponensek eltolása időben korábbi irányba egy mintavételi időtartammal.
Az alapelemek fizikai megvalósításánál a digitális rendszertechnika alapelemeket alkalmazva logikai áramkörökkel, programozható logikai áramkörrel (FPGA), illetve (mikro)számítógépes algoritmussal valósíthatjuk meg a műveleteket.
A differenciaegyenlet alapműveleteinek hardveres megvalósítása
Az összeadás, kivonás, szorzás és osztás műveletét ezeknél a számításoknál alapvetően lebegőpontos számokkal kell megvalósítani. Ezeknek a műveleteknek a megvalósítása logikai áramkörökkel bonyolult, mivel nagyszámú logikai áramkört tartalmazó kapcsolást eredményez, amely költség, méretek és teljesítményigény szempontjából sokkal drágább, bonyolultabb például a (mikro)számítógépes „szoftveres” megvalósításnál.
Az aritmetikai műveletek logikai áramkörökkel történő megvalósítása napjainkban programozható logikai áramkörök segítségével történik. Ezeket az áramköröket Programozható Logikai Tömböknek (angol elnevezése FPGA = Field Programable Gate Array ) nevezzük és nagyszámú, több millió „alapelemet” tartalmaznak, amelyek egy program segítségével tetszőleges kialakítású logikai áramkör megvalósítását biztosítják. Így az alapelemek összekapcsolásával létrehozhatunk ciklusutasítást, feltételes végrehajtást, aritmetikai műveleteket méghozzá úgy, hogy a megvalósított műveletek úgy jönnek létre, mintha egy számítógépes programból létrehoztuk volna az adott algoritmust megvalósító logikai áramkört. Ezek a logikai áramkörökkel megvalósított műveletek, nem sorban egymás után hajtódnak végre, mint soronként egymás után végrehajtott mikroszámítógépes utasításoknál, hanem minden számítási blokkban párhuzamosan működnek. Ezért ezekkel a programozható logikai áramkörökkel megvalósított műveletek, ugyanolyan bonyolultságú algoritmus esetén, sokkal gyorsabban futnak (50…200-szor), mintha a feladatot egy nagy sebességű mikroszámítógépen futtatnánk.
Természetesen a Programozható Logikai Tömbök segítségével létre lehet hozni a mintavételes rendszerek differenciaegyenletének számításához még szükséges úgynevezett shift regisztereket (számértékeket tartalmazó tömböket) is, amelyeknél egy ciklusutasításban elvégzett értékátadással megvalósítható az adatok mintavételi értékeinek mozgatása meghatározott irányban.
Az FPGA áramkörök alkalmazása napjainkban egyre szélesebb körű. A párhuzamos, több szálon futó programozás biztosításához és az elkészített program teszteléséhez egyre több fejlesztőeszköz áll rendelkezésre.
A differenciaegyenlet alapműveleteinek szoftveres megvalósítása
A mintavételes rendszerek jelfeldolgozási feladatainak megoldásában jelenleg az a gyakorlat, hogy az adatok beolvasását, feldolgozását és visszajuttatását a valós rendszerbe, egy (vagy több) különböző szerkezeti felépítésű mikroszámítógép segítségével valósítják meg. A mikroszámítógépek alapvetően egész típusú aritmetikával, és ezek végrehajtását biztosító utasításokkal rendelkeznek.
Szükség van tehát a számításoknál alapvető igényként megjelenő lebegőpontos számítási műveletek létrehozására.
Ez történhet nagy szóhosszúságú, egész típusú adatokban virtuális tizedespont kijelöléssel és az így kialakított számábrázolási formátumban az összes művelet elvégzésével. Ez a számábrázolási forma kihasználja az összes „gépi utasítás szinten” rendelkezésre álló aritmetikai műveletet, és a szokásos számalkalmazási tartományban megfelelő pontossággal valósítja meg a műveleteket.
Az igazi megoldást az jelenti, hogy a jelfeldolgozásra alkalmazott processzor gépi kódú utasításaiként megvalósítjuk a lebegőpontos adatfeldolgozás műveleteit. Alapműveletekről van szó: összeadás, kivonás, szorzás és osztás, melyeket általában egy magas szintű programozási nyelv (leggyakrabban C programnyelvi) környezetében biztosítanak a fejlesztők számára. Majd az elkészült jelfeldolgozó programot lefordítják az adott processzor (mikroprocesszor) gépi kódú (natív) utasításaira.
A mintavételezett jelek (bemenő és kimenő jel) tömbjein végzett műveleteket (mintavételezett értékek léptetését (shiftelését) szintén megvalósíthatjuk az adott processzor (mikroprocesszor) utasításait alkalmazó magas szintű nyelven.
2.2.1. Mintavételes rendszerek alapműveletei
Ebben a részben áttekintjük a mintavételes rendszerek azon alapműveleteit, amelyeket a mintavételes rendszer differenciaegyenletének digitális számítógépes megoldásánál alkalmazunk.

A (2.6. ábra) ábrán szereplő „ M ” művelet a következők közül kerülhet ki:
-
összeadás ( + ),
-
kivonás ( - ),
-
szorzás ( * ),
-
osztás ( / ).
A két bementi érték (u1[k] és u2[k]) a rendszer differenciaegyenletében a mintavételi időpontokban megjelenő jelek értéke a k. mintavételi időpontban.
A műveleti elem nem hisztórikus tulajdonságú , vagyis a bemeneteire érkezett adatokból nem tárolja egyik értéket sem a további számításokhoz.
A számítási blokkdiagramokban néhány oyan műveletvégző elem és szimbólum is található, amelyek nem a (2.6. ábra) ábrán látható általános leírási formátumúak. Ezek a következők:
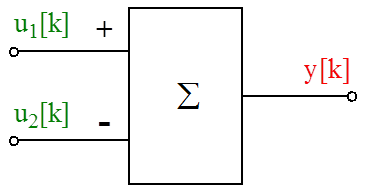
A (2.7. ábra) ábrán látható műveletvégző egyég a következő műveletet végzi el, ahol a bementek jelszorzó tulajdonságát (előjelét) is megadhatjuk:
|
|
(2.100) |
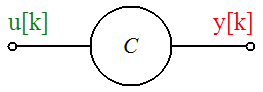
A (2.8. ábra) ábrán látható műveletvégző egyég a következő műveletet végzi el, ahol c konstans érték:
|
|
(2.101) |
2.2.2. Időbeni eltolást végző elem (shift művelet) megvalósítása mintavételes rendszerekben
A mintavételes rendszer differenciaegyenletében a bemenő és kimenő jelek adott mintavételi időpontokban felvett értékeket tartalmazó tömbök. A tömbben szereplő jelértékeket minden mintavételi időpontban megszorozzuk a differenciaegyenlet megfelelő indexű jeleinek együtthatóival, majd kifejezzük a kimenő jel legnagyobb mintavételezési eltolási értékét y[k·h]-t (visszalépéses differenciaegyenlet felírás esetén). Ez a megoldás jellegre nagyon hasonlít a folytonos differenciálegyenletek számítási egyenletének meghatározására, ahol a kimenő jel legnagyobb idő szerinti differenciálértékét fejezzük ki a kimenő jel, alacsonyabb fokú deriváltjaival és a bemenő jellel valamint annak idő szerinti deriváltjaival.
A mintavételes rendszer visszalépéses differenciaegyenletének rekurzív számítási algoritmusa , a megadott mintavételes bemenő jelsorozatra a következő:
|
|
(2.102) |
A számítások elvégezhetőségéhez olyan műveletvégző elemeket – shift regisztereket – kell alkalmaznunk, amelyek biztosítják, hogy a bemenő és a kimenő jel értékei minden mintavételi időpontban egy indexértékkel változtassák meg a pozíciójukat. Ez csak úgy valósítható meg, hogy a legrégebben tárolt adatot megszüntetjük, a felszabaduló helyre pedig a (2.9. ábra) ábrán bemutatott művelet végrehajtási sorrendjében átmásoljuk a korábbi adatokat, és a k·h időpontnál megüresedett helyre bemásoljuk a jel aktuális értékét. A bemenő jelnél az u[k·h] értéket a bemeneti jelek mintavételezett értékeit tartalmazó shift regiszterbe, a kimenő jelnél pedig a 2.102 egyenlettel meghatározott, y[k·h] kimenő jel értéket a kimeneti jelek mintavételezett értékeit tartalmazó shift regiszterbe másoljuk.
![Az x új [k] bemenő jel beléptetése az időbeni eltolás tömbbe(végrehajtása a k·h időpontban történik.)](images/image_II_9.png)
Az időbeni eltolás elem (shift művelet) hisztórikus tulajdonságú , azaz pillanatnyi kimeneti értékét meghatározza, hogy milyenek voltak a korábbi bementi értékek. A t=0 időpillanatban (k=0 mintavételezési indexértéknél) beállíthatjuk az időbeni eltolás elem összes állapotváltozójának (tárolt tömbelemének) kezdeti értékét .
2.2.3. Időbeni késleltetés megvalósítása mintavételes rendszerekben
Mintavételes rendszerekben az időbeni késleltetés csak a mintavételi időtartam egész számú többszöröse lehet, hiszen csak a mintavételi időpontokban történik meg a rendszer differenciaegyenletével új kimeneti jelérték meghatározása. Az időbeni késleltetést egy shift regiszter segítségével valósíthatjuk meg, amelynél egy paraméterrel (késleltetési index) megadjuk, hogy a bemeneti jel hány mintavételi időtartammal késleltetett értékét szeretnénk kimeneti adatként megkapni. A shift regiszter működését megvalósító programnak figyelembe kell vennie, hogy a késleltetési index nem lehet nagyobb, mint a shift regiszter mérete (a vektor lefoglalt elmeinek száma), vagyis annak maximális indexű késleltetett eleme.
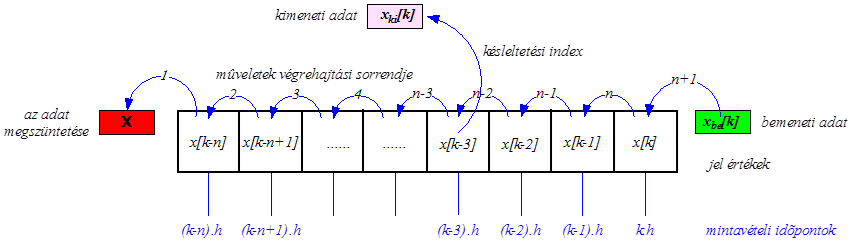
A mintavételezett adatok a (2.10. ábra) ábrán bemutatott módon az x be [k] bemeneti értékkel juttatják be a késleltető elembe adataikat, és a késleltetési index elnevezésű paraméterrel megadott indexű elemet olvassuk ki x ki [k] kimeneti adatként. Mivel az adatok időbeni eltolása (shiftelése) csakis a mintavételezéskor történik, a bementi jel késleltetése a késleltetési index szorzata a h mintavételi idővel. Ha nagyobb késleltetésre van szükségünk, több késleltető elemet kapcsolhatunk sorba, hogy az előírt késleltetési időtartamot megvalósítsuk.
Ha a késleltetési index=1 a bemeneti mintavételes jelet egy mintavételi időtartammal, h-val késleltetjük, amelynek ábrázolása a számítási blokkdiagramban a (2.11. ábra) ábrán látható.
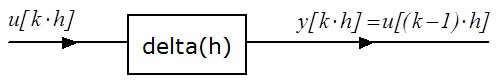
2.2.4. Mintavételes rendszerek nemlineáris elemei
A mintavételes nemlineáris elemek típusait az 1.8.3.4. szakasz fejezetben részletesen bemutattuk.
2.3. Mintavételes alapelemek összekapcsolása
2.3.1. Az impulzusátviteli függvény (SISO rendszer) megvalósítása digitális számítógépen
2.3.1.1. Az impulzusátviteli függvény megvalósítása soros kapcsolású alapelemekkel
Az impulzusátviteli függvény pozitív z hatványkitevőkkel:
|
|
(2.103) |
Ha a számlálót és a nevezőt is osztjuk z n -el, a G(z -1 )-et kapjuk:
|
|
(2.104) |
A számlálót és a nevezőt z csökkenő hatványai szerinti sorban felírva:
|
|
(2.105) |
Bevezetve azt a jelölésmódot, amelynél az együtthatók indexei a z negatív hatványkitevőt is megjelenítik, G(z -1 )-re a következő összefüggést kapjuk:
|
|
(2.106) |

A 2.12. ábra az impulzusátviteli függvény soros kapcsolású elemekre való felbontását mutatja, ahol
|
q |
a sorba kapcsolt elemek darabszáma. |
Ez alapján a G(z -1 ):
|
|
(2.107) |
ahol
-
a mintavételes elsőrendű tag átviteli függvénye (1. verzió):
(2.108)
-
a mintavételes elsőrendű tag átviteli függvénye (2. verzió):
(2.109)
illetve
-
a mintavételes másodrendű tag átviteli függvénye:
(2.110)
Az egyes tagok megvalósítása:
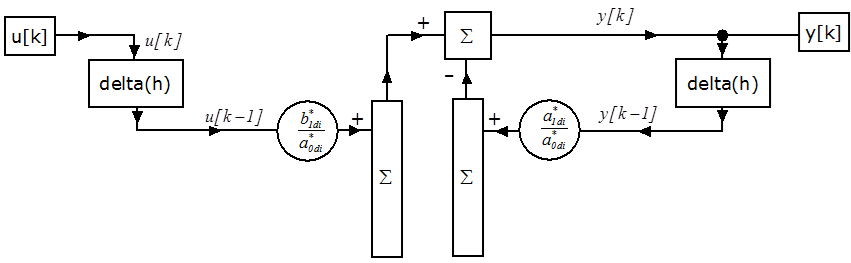
A mintavételes elsőrendű tag impulzusátviteli függvénye (1. verzió):
|
|
(2.111) |
A mintavételes elsőrendű tag differenciaegyenlete (1. verzió):
|
|
(2.112) |
amelyből
|
|
(2.113) |
A mintavételes elsőrendű tag számítási blokkdiagramja (1. verzió):
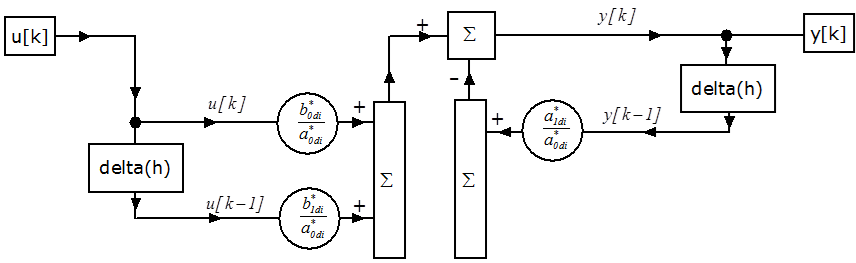
A mintavételes elsőrendű tag impulzusátviteli függvénye (2. verzió):
|
|
(2.114) |
A mintavételes elsőrendű tag differenciaegyenlete (2. verzió):
|
|
(2.115) |
amelyből
|
|
(2.116) |
A mintavételes elsőrendű tag számítási blokkdiagramja (2. verzió):
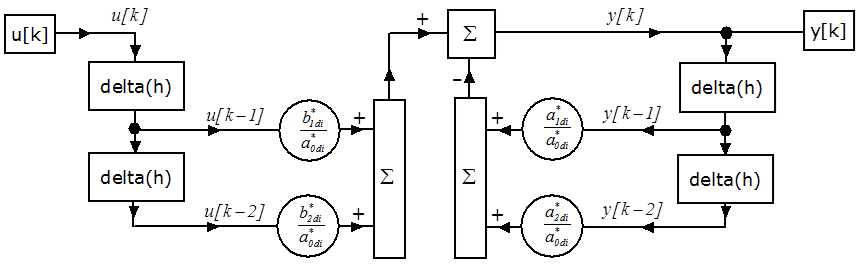
A mintavételes másodrendű tag impulzusátviteli függvénye:
|
|
(2.117) |
A mintavételes másodrendű tag differenciaegyenlete:
|
|
(2.118) |
amelyből
|
|
(2.119) |
A mintavételes másodrendű tag számítási blokkdiagramja:
Mintapélda:
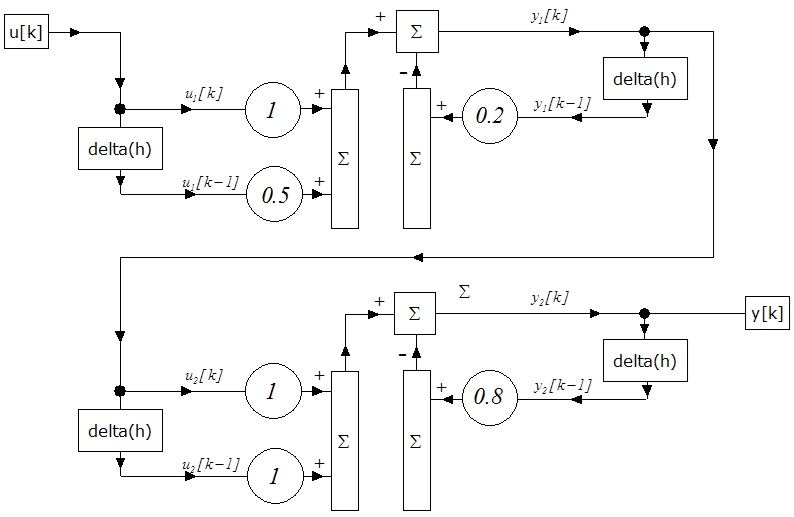
Határozzuk meg a következő impulzusátviteli függvény szimulációs blokkdiagramját!
|
|
(2.120) |
Megoldás:
|
|
(2.121) |
|
|
|
(2.122) |
|
|
|
(2.123) |
|
|
|
(2.124) |
|
|
|
(2.125) |
A mintapélda számítási blokkdiagramja:
2.3.1.2. Az impulzusátviteli függvény megvalósítása párhuzamos kapcsolású alapelemekkel
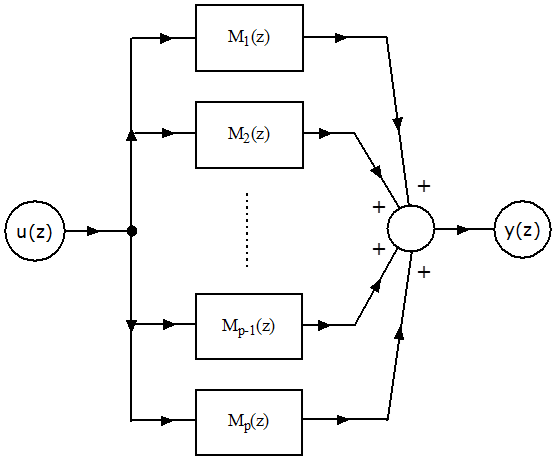
A 2.16. ábra a mintavételes impulzusátviteli függvény párhuzamos kapcsolású elemekre való felbontását , ahol
|
p |
a párhuzamosan kapcsolt elemek darabszáma |
Ekkor:
|
|
(2.126) |
ahol
-
a mintavételes elsőrendű tag átviteli függvénye (1. verzió):
(2.127)
-
a mintavételes elsőrendű tag átviteli függvénye (2. verzió):
(2.128)
illetve
-
a mintavételes másodrendű tag átviteli függvénye:
(2.129)
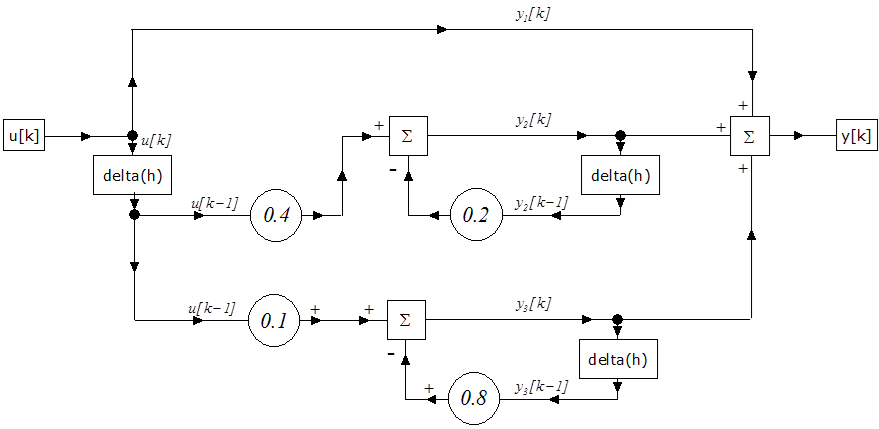
Mintapélda:
Határozzuk meg a következő impulzusátviteli függvény szimulációs blokkdiagramját:
|
|
(2.130) |
Megoldás:
|
|
(2.131) |
átalakítva z -1 hatványaira
|
|
(2.132) |
|
|
|
(2.133) |
|
|
|
(2.134) |
|
|
|
(2.135) |
A mintapélda számítási blokkdiagramja:
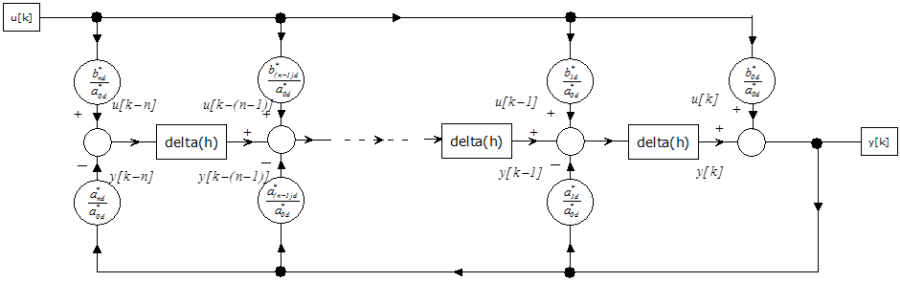
2.3.1.3. Impulzusátviteli függvény megvalósítása közvetlen programozással
A G(z) impulzusátviteli függvény számítási blokkdiagramját akarjuk meghatározni
|
|
(2.136) |
A számlálót kiegészítjük bm+1..bn elemekkel, amelyek mindegyike 0.0 értékű:
|
|
(2.137) |
Ha a számlálót és a nevezőt is elosztjuk z n -el, a következő G(z -1 ) függvényt kapjuk:
|
|
(2.138) |
A számlálót és a nevezőt z csökkenő hatványai szerinti sorban felírva:
|
|
(2.139) |
Bevezetve azt a jelölésmódot, amelynél az együtthatók indexei a z negatív hatványkitevőt is megjelenítik, a G(z -1 )-re a következő összefüggést kapjuk
|
|
(2.140) |
|
|
|
(2.141) |
|
|
|
(2.142) |
Kifejezzük Y(z -1 )-et, amely a kimenő jelének mintavételes értéke a k·h-ik időpontban (ez a késleltetés nélküli kimenő jel értéke)
|
|
(2.143) |
Inverz Z-transzformáció után a rendszer differenciaegyenlete
|
|
(2.144) |
A differenciaegyenlet számítási blokkdiagramja a (2.19. ábra) ábrán látható.
Mintapélda:
Határozzuk meg a következő impulzusátviteli függvény szimulációs blokkdiagramját!
|
|
(2.145) |
Megoldás:
A G(z) függvényt átalakítva z -1 hatványaira
|
|
(2.146) |
Az inverz Z-transzformációt elvégezve a differenciaegyenlet
|
|
(2.147) |
A mintapélda számítási blokkdiagramja:
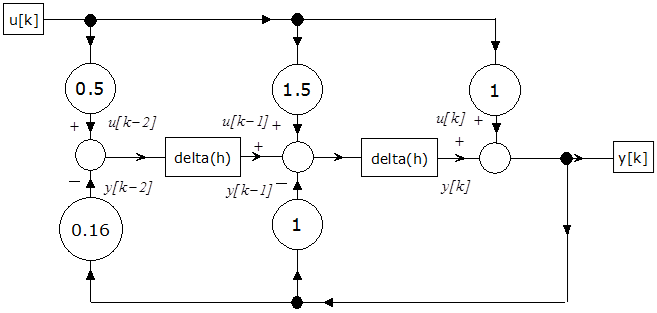
2.3.1.4. Impulzusátviteli függvény megvalósítása M programozással
A G(z) impulzusátviteli függvény számítási blokkdiagramját akarjuk meghatározni M programozással
|
|
(2.148) |
A számlálót kiegészítjük bm+1..bn elemekkel, amelyek mindegyike 0.0 értékű.
|
|
(2.149) |
Ha a számlálót és a nevezőt is elosztjuk z n -el a következő G(z -1 ) függvényt kapjuk
|
|
(2.150) |
A számlálót és a nevezőt z csökkenő hatványai szerinti sorban felírva
|
|
(2.151) |
Bevezetve azt a jelölésmódot, amelynél az együtthatók indexei a z negatív hatványkitevőt is megjelenítik, a G(z -1 )-re a következő összefüggést kapjuk
|
|
(2.152) |
Egy új bevezetett változóval M(z -1 )-vel kifejezzük Y(z -1 )-t:
|
|
(2.153) |
ahol
|
|
(2.154) |
|
|
|
(2.155) |
így
|
|
(2.156) |
Mintapélda:
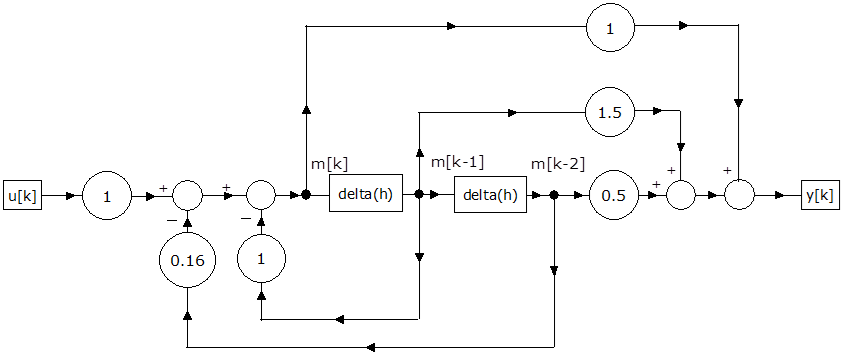
Határozzuk meg a következő impulzusátviteli függvény szimulációs blokkdiagramját!
|
|
(2.157) |
Megoldás:
A G(z) függvényt átalakítva z-1 hatványaira
|
|
(2.158) |
|
|
|
(2.159) |
|
|
|
(2.160) |
|
|
|
(2.161) |
Az inverz Z-transzformáció után az y[k] és az m[k] jelek az időtartományban
|
|
(2.162) |
|
|
|
(2.163) |
A mintapélda számítási blokkdiagramja:
2.4. Állapottér leírású (MIMO) rendszer megvalósítása
2.4.1. Az impulzusátviteli függvény meghatározása mintavételes állapottér mátrixok segítségével
A mintavételes állapottér leírású rendszer
|
|
(2.164) |
|
|
a mintavételes állapottér leírási mód mátrixai, |
|
|
u [k] |
a bemenő jelek vektora, |
|
|
y [k] |
a kimenő jelek vektora, |
|
|
x [k] |
az állapotváltozók vektora, |
|
|
k |
a mintavételezési idő indexe (t=k*h). |
Az impulzusátviteli függvény z pozitív hatványai szerint felírt alakja:
|
|
(2.165) |
Az impulzusátviteli függvény a mintavételes állapottér mátrixokkal a következő egyenletekből határozható meg:
|
|
(2.166) |
|
|
|
(2.167) |
|
|
|
(2.168) |
|
|
|
(2.169) |
|
|
|
(2.170) |
meghatározása a következő végtelen sor segítségével történik:
|
|
(2.171) |
ahol
|
-hez (+végtelenhez) tart. |
|
|
(2.172) |
|
|
|
(2.173) |
|
|
|
(2.174) |
ahol
|
|
a folytonos rendszer állapottér mátrixai. |
2.4.2. Mintavételes állapottér mátrixok meghatározása az impulzusátviteli függvény segítségével
A z pozitív hatványaival felírt impulzusátviteli függvény
|
|
(2.175) |
Állítsuk elő ebből a rendszer differenciaegyenletét inverz Z-transzformációval!
|
|
(2.176) |
A kimenő jelet y[k]-t választva állapotváltozóként
|
|
(2.177) |
és a bemenő jel együtthatóit kiegészítve b m+1 ..b n -ig 0.0 értékű együtthatókkal, a mintavételes állapottér egyenlet leírási mód (fázisváltozós kanonikus formában):
|
|
(2.178) |
|
|
|
(2.179) |
|
|
… |
||
|
… |
||
|
|
(2.180) |
|
|
|
(2.181) |
|
|
|
(2.182) |
A kimenő jel pedig a következő formulával adható meg
|
|
(2.183) |
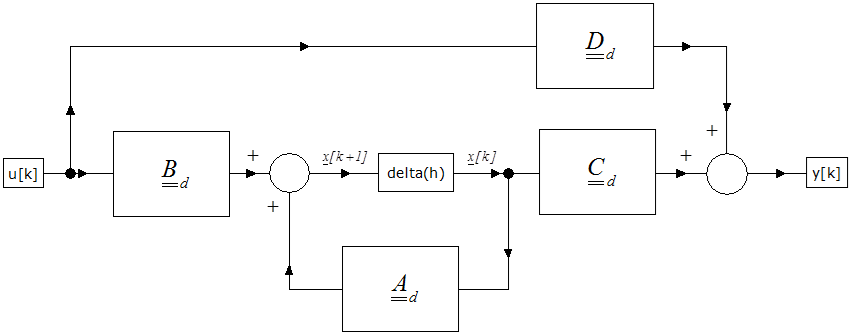
A mintavételes állapottér leírási mód mátrixos formában
|
|
(2.184) |
|
|
|
(2.185) |
A mintavételes állapottér rendszer számítási blokkdiagramja
Mintapélda:
Határozzuk meg a következő impulzusátviteli függvény szimulációs blokkdiagramját!
|
|
(2.186) |
Megoldás:
A z pozitív hatványkitevőivel felírva az impulzusátviteli függvény:
|
|
(2.187) |
A z tartományból visszatérve a mintavételes időtartományba, a mintavételes állapottér egyenlet a következő alakú lesz:
|
|
(2.188) |
|
|
|
(2.189) |
|
|
|
(2.190) |
Mátrixos alakban
|
|
(2.191) |
|
|
|
(2.192) |
Az impulzusátviteli függvény együtthatóinak behelyettesítésével a mintavételes állapotegyenlet:
|
|
(2.193) |
|
|
|
(2.194) |
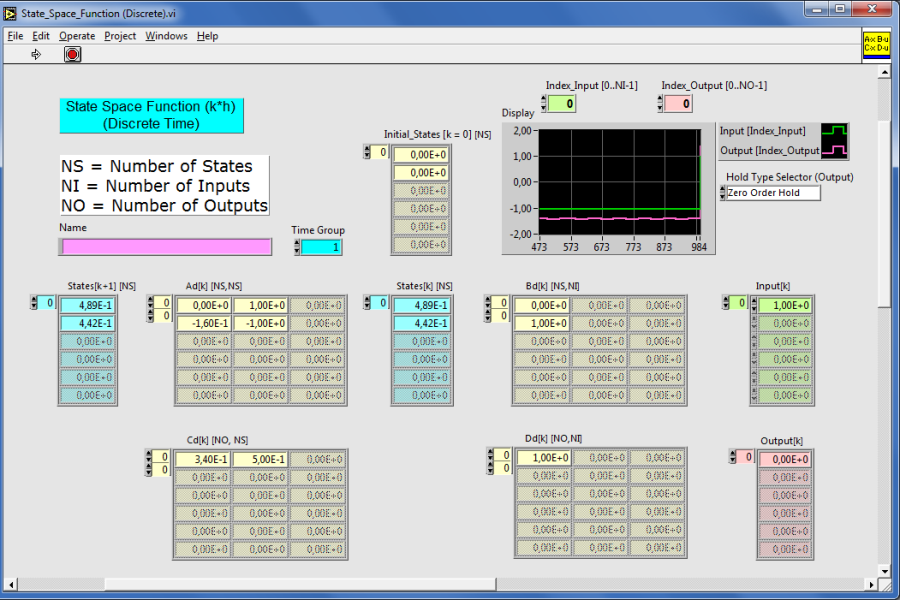
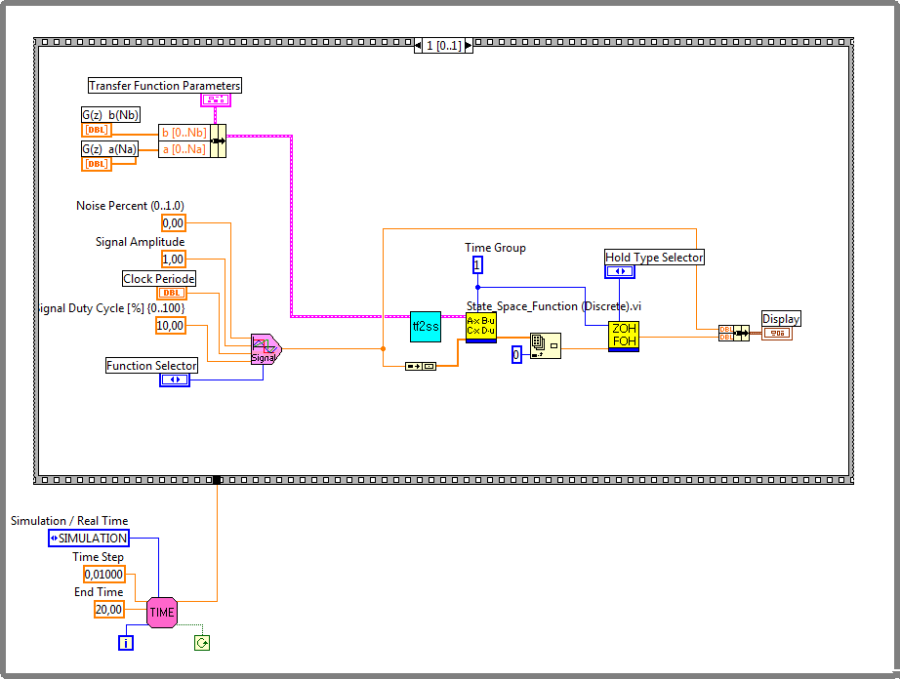
2.5. Transzformációk a mintavételes rendszerekben
2.5.1. Az impulzusátviteli függvény (tf) transzformációi
2.5.1.1. Az impulzusátviteli függvény állandósult állapotbeli erősítése
Az impulzusátviteli függvényt z növekvő hatványai szerint felírva
|
|
(2.195) |
A Z-transzformáció végérték tételét alkalmazva
|
|
(2.196) |
Ha a bemenő jel 1(t), akkor állandósult állapotban az egységnyi nagyságú bemenő jelre adott válaszfüggvényből megkapjuk A p_mintavételes -t, a G(z) impulzusátviteli függvény állandósult állapotbeli erősítését.
|
|
(2.197) |
A G(z) impulzusátviteli függvényben – mind a számlálóban, mind a nevezőben – az z és z magasabb kitevős hatványai mind az egy (1) értékhez tartanak, ezért
|
|
(2.198) |
A G(z) impulzusátviteli függvény állandósult állapotbeli erősítése (A p_mintavételes ) az impulzusátviteli függvény számlálója együtthatóinak összege, osztva a nevező együtthatóinak összegével.
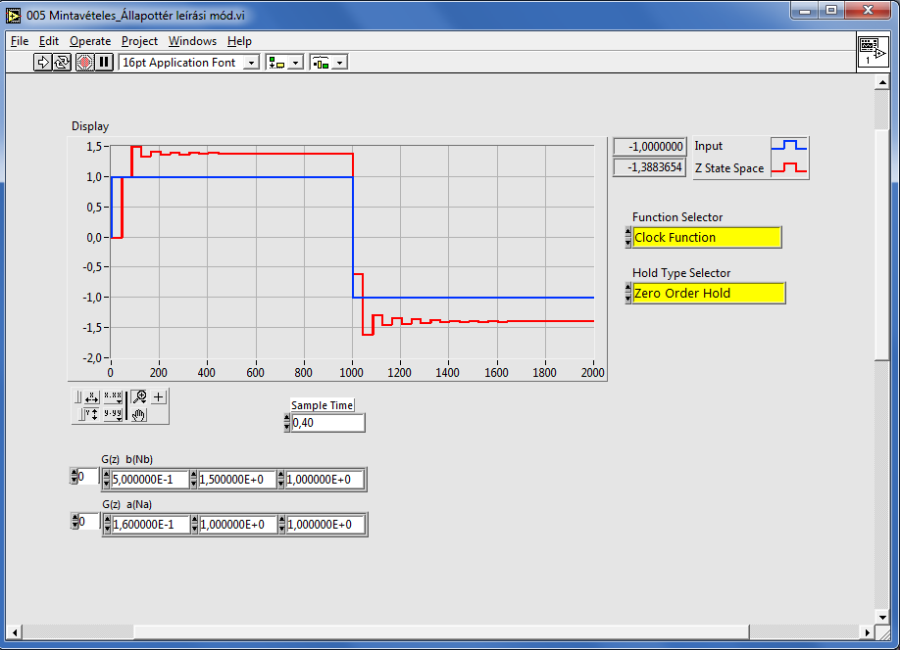
Az állandósult állapotbeli erősítés meghatározására LabVIEW MathScript-ben a dcgain() függvény használható:
|
dcgain (sys), |
(2.199) |
ahol
Mintapélda:
Egy polinomiális alakú impulzusátviteli függvénnyel megadott rendszer állandósult erősítési tényezőjét szeretnénk meghatározni.
A h a mintavételi időtartam, amely mintavételes rendszer esetén nem nulla!
NUM=[1]
DEN=[1, -0.5, 0.6, -0.5]
h=0.3
sys=tf(NUM, DEN, h)
Ap_mintaveteles=dcgain(sys)
>>
NUM =
1
DEN =
1 -0.5 0.6 -0.5
h =
0.3
Transfer Function
Input:1 Output:1
1,000
------------------------------
1,000z^3-0,500z^2+0,600z-0,500
Sampling time: 0,300000
Ap_mintaveteles =
1.6667
2.5.1.2. Impulzusátviteli függvény transzformációja zérus-pólus-erősítés alakból polinomiális alakba
A zérus-pólus-erősítés impulzusátviteli függvény a következő alakú:
|
|
(2.200) |
Az átalakításnál a gyöktényezős alakban felírt számlálóból z hatványainak megfelelő polinomiális alakot hozunk létre, majd a számlálóban szereplő polinom minden együtthatóját megszorozzuk a zérus-pólus-erősítés alakú impulzusátviteli függvény K d erősítési tényezővel.
Hasonlóan elvégezzük a nevező z hatványainak megfelelő polinom előállítását is, ezek után rendelkezésünkre állnak a polinomiális alakú impulzusátviteli függvény együtthatói.
|
|
(2.201) |
A zérus-pólus-erősítés alakú impulzusátviteli függvényből a polinomiális alakú impulzusátviteli függvény alakba az átalakítás következő LabVIEW MathScript függvénnyel végezhető el:
|
[d, e] = zpk_to_tf (a, b, c), |
(2.202) |
|
zpk_to_tf |
a zérus-pólus-erősítés alakú impulzusátviteli függvényből a polinomiális alakú impulzusátviteli függvény átalakítást végző függvény neve LabVIEW MatScript-ben, |
|
|
a |
a zérus-pólus-erősítés alakú impulzusátviteli függvény zérusai, |
|
|
b |
a zérus-pólus-erősítés alakú impulzusátviteli függvény pólusai, |
|
|
c |
a zérus-pólus-erősítés alakú impulzusátviteli függvény erősítése (Kd), amely skalár érték, |
|
|
d |
a polinomiális alakú impulzusátviteli függvény számlálójában a z hatványok együtthatói, |
|
|
e |
a polinomiális alakú impulzusátviteli függvény nevezőjében a z hatványok együtthatói. |
Mintapélda:
Egy zérusaival, pólusaival és erősítési tényezőjével megadott impulzusátviteli függvényt sys_zpk_d-t szeretnénk átalakítani polinomiális impulzusátviteli függvény alakra sys_poly_d-re.
A h a mintavételi időtartam, amely mintavételes rendszer esetén nem nulla!
zeros_d=[0.26]
poles_d=[0.1, 0.2, 0.33]
k_d = [1]
h=0.3
sys_zpk_d=zpk(zeros_d, poles_d, k_d, h)
[NUM_d, DEN_d] = zpk_to_tf(zeros_d, poles_d, k_d)
sys_poly_d=tf(NUM_d, DEN_d, h)
step(sys_poly_d, 5)
sys_zpk_d = zpk(zeros_d, poles_d, k_d, h)
[NUM_d, DEN_d] = zpk_to_tf(zeros_d, poles_d, k_d)
sys_poly_d=tf(NUM_d, DEN_d, h)
step(sys_poly_d, 5)
zeros_d =
0.26
poles_d =
0.1 0.2 0.33
k_d =
1
h =
0.3
Zero-Pole-Gain Model
Input:1 Output:1
1,000(z-0.26)
-------------------------
(z-0.1) (z-0.2) (z-0.33)
Sampling time: 0,300000
NUM_d =
1 -0.26
DEN_d =
1 -0.63 0.119 -0.0066
Transfer Function
Input:1 Output:1
1,000z-0,260
------------------------------
1,000z^3-0,630z^2+0,119z-0,007
Sampling time: 0,300000
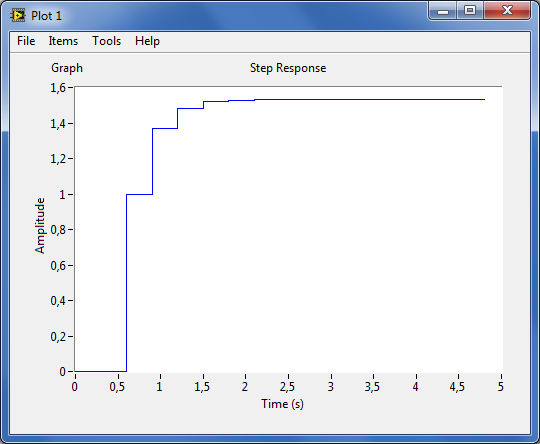
2.5.1.3. Impulzusátviteli függvény transzformációja állapottér modell alakból polinomiális alakba
Az állapottér alakban felírt rendszer Z-transzformáció után a következő egyenleteket eredményezi:
|
|
(2.203) |
|
|
|
(2.204) |
Az állapotegyenletből (2.203) kifejezhetjük az állapotváltozók vektorát. Amennyiben az állapotváltozók kezdeti értéke zérus (), a számítás egyszerűsödik.
|
|
(2.205) |
|
|
|
(2.206) |
Az így kifejezett állapotváltozó vektort behelyettesíthetjük a kicsatolási egyenletbe, hogy megkapjuk a kimenő jel Laplace–transzformáltját:
|
|
(2.207) |
A kapott kifejezés jobb oldalán kiemelhetjük a bemenő jel U(z)-t és eloszthatjuk vele az egyenlet mindkét oldalát, hogy megkapjuk a SISO rendszer impulzusátviteli függvényét az állapottér modell segítségével:
|
|
(2.208) |
Mintapélda:
Állapottér alakban mátrixokkal megadott rendszert szeretnénk átalakítani polinomiális impulzusátviteli függvény alakra sys_poly_d-re (LabVIEW MathScript-ben).
A h a mintavételi időtartam, amely mintavételes rendszer esetén nem nulla!
Ad = [ 0.9843, 0.2799, 0.0277;
-0.1386, 0.818, 0.1413;
-0.7065, -0.9865, 0.1114]
Bd =[0.0031
0.0277
0.1413]
Cd = [1, 0, 0]
Dd = [0]
h=0.3
sys_ss_d = ss(Ad, Bd, Cd, Dd, h)
[sys_poly_d] = tf(sys_ss_d)
>>
Ad =
0.9843 0.2799 0.0277
-0.1386 0.818 0.1413
-0.7065 -0.9865 0.1114
Bd =
0.0031
0.0277
0.1413
Cd =
1 0 0
Dd =
0
h =
0.3
State Space Model
a
0.9843 0.2799 0.0277
-0.1386 0.818 0.1413
-0.7065 -0.9865 0.1114
b
0.0031
0.0277
0.1413
c
1 0 0
d
0
Sampling time: 0,300000
Transfer Function
Input:1 Output:1
0,003z^2+0,009z+0,001
------------------------------
1,000z^3-1,914z^2+1,204z-0,223
Sampling time: 0,300000
2.5.2. Zérus-pólus-erősítés függvény (zp) transzformációi
2.5.2.1. Zérus-pólus függvény erősítése (Kd)
Az impulzusátviteli függvényt z pozitív hatványaival felírva
|
|
(2.209) |
Meghatározva a számláló m darab és a nevező n darab gyökét, felírhatjuk a G(s) impulzusátviteli függvény gyöktényezős alakját. Mivel a gyökök meghatározásánál a legmagasabb fokú tagok együtthatóinak mind a számlálóban, mind pedig a nevezőben 1-nek kell lennie. Így a számlálóból és a nevezőből ki kell emelni a legmagasabb z hatványok együtthatóit- ezek hányadosa lesz K d az erősítés értéke.
|
|
(2.210) |
|
|
|
(2.211) |
2.5.2.2. Polinomiális alakú impulzusátviteli függvény átalakítása zérus-pólus-erősítés alakúvá
A polinomiális alakú impulzusátviteli függvény a következő függvénnyel írható le:
|
|
(2.212) |
Az átalakításnál kiemeljük a számlálóból és a nevezőből z legmagasabb hatványainak együtthatóit b md -et és a nd -et. A pólus-zérus-erősítés impulzusátviteli függvény K d erősítési tényezője, melynek meghatározását a 2.5.2.1. szakasz fejezetben ismertettük. Ezután meghatározzuk a számláló és a nevező gyökeit, és felírjuk az impulzusátviteli függvény gyöktényezős alakját a K d erősítési tényezővel.
|
|
(2.213) |
A polinomiális alakú impulzusátviteli függvényből zérus-pólus-erősítés impulzusátviteli függvény alakba az következő függvénnyel történik az átalakítás LabVIEW MathScript-ben:
|
[c, d, e] = tf_to_zpk (a, b) |
(2.214) |
ahol
Mintapélda:
Egy polinomiális impulzusátviteli függvényt sys_poly_d-t szeretnénk átalakítani zérusaival, pólusaival és erősítési tényezőjével megadott impulzusátviteli függvény alakra sys_zpk_d-re (LabVIEW MathScript-ben).
A h a mintavételi időtartam, amely mintavételes rendszer esetén nem nulla!
NUM_d = [0.14, 0.256]
DEN_d = [0.8, 0.72, 0.3]
h=0.3
sys_poly_d = tf(NUM_d, DEN_d, h)
[zeros_d, poles_d, kd] = tf_to_zpk(NUM_d, DEN_d)
sys_zpk=zpk(zeros_d, poles_d, kd, h)
>>
NUM_d =
0.14 0.256
DEN_d =
0.8 0.72 0.3
h =
0.3
Transfer Function
Input:1 Output:1
0,140z+0,256
---------------------
0,800z^2+0,720z+0,300
Sampling time: 0,300000
zeros_d =
-1.8286
poles_d =
-0.45 + 0.4153i
-0.45 - 0.4153i
kd =
0.175
Zero-Pole-Gain Model
Input:1 Output:1
0,175(z+1.8286)
--------------------------------
(z+0.45-0.4153i)(z+0.45+0.4153i)
Sampling time: 0,300000
2.5.2.3. Állapottér modell alakú impulzusátviteli függvény átalakítása zérus-pólus-erősítés alakúvá
A 2.208 egyenlettel megadtuk, hogyan lehet állapottér alakból polinomiális impulzusátviteli függvény alakba átalakítani a rendszerleíró egyenletet. Ebben az esetben is ezt kell alkalmaznunk. Az előző 2.5.2.2. szakasz fejezetben bemutatott eljárással meghatározhatjuk a impulzusátviteli függvény polinomiális alakjából a zérus-pólus-erősítés impulzusátviteli függvény alakot.
Mintapélda:
Állapottér alakban mátrixokkal megadott rendszert szeretnénk átalakítani zérus-pólus-erősítés alakú impulzusátviteli függvény alakra sys_zpk_d-re (LabVIEW MathScript-ben).
A h a mintavételi időtartam, amely mintavételes rendszer esetén nem nulla!
Ad =[ 0, 1, 0
0, 0, 1
-5, -6, -5]
Bd = [0; 0; 1]
Cd = [1, 0, 0]
Dd = [0]
h=0.3
[zeros_d, poles_d, kd]=ss_to_zpk(Ad, Bd, Cd, Dd, h)
sys_zpk_d=zpk(zeros_d, poles_d, kd, h)
>>
Ad =
0 1 0
0 0 1
-5 -6 -5
Bd =
0
0
1
Cd =
1 0 0
Dd =
0
h =
0.3
zeros_d =
empty matrix 0 by 1
poles_d =
-0.6214 + 0.9719i
-0.6214 - 0.9719i
-3.7573 + 0i
kd =
1
Zero-Pole-Gain Model
Input:1 Output:1
1,000
-----------------------------------------------
(z+3.7573) (z+0.6214-0.9719i)(z+0.6214+0.9719i)
Sampling time: 0,300000
2.5.3. Állapottér (ss) transzformációk
2.5.3.1. Átalakítás polinomiális alakú impulzusátviteli függvényből állapottér modellbe
A polinomiális alakú impulzusátviteli függvényből a fázisváltozós alakú állapottér modell létrehozását a 2.5.3.1. szakasz fejezetben mutattuk be. Ezt a számítási eljárást alkalmazva állapottér számításra alkalmas modellt hozhatunk létre.
Mintapélda:
Polinomiális impulzusátviteli függvény alakról hozzunk létre állapottér alakú mátrixokat, melyekkel leírjuk a vizsgált rendszert (LabVIEW MathScript-ben)!.
A h a mintavételi időtartam, amely mintavételes rendszer esetén nem nulla!
NUM_d = [0.445]
DEN_d = [0.132, 0.512, 0.36, 0.5]
h=0.3
sys_poly_d = tf(NUM_d, DEN_d, h)
[Ad, Bd, Cd, Dd] = tf_to_ss (NUM_d, DEN_d)
>>
NUM_d =
0.445
DEN_d =
0.132 0.512 0.36 0.5
h =
0.3
Transfer Function
Input:1 Output:1
0,445
------------------------------
0,132z^3+0,512z^2+0,360z+0,500
Sampling time: 0,300000
Ad =
-3.8788 -2.7273 -3.7879
1 0 0
0 1 0
Bd =
1
0
0
Cd =
0 0 3.3712
Dd =
0
2.5.3.2. Átalakítás zérus-pólus-erősítés alakú impulzusátviteli függvényből állapottér modellbe
Ennél az átalakítási eljárásnál felhasználunk korábban bemutatott transzformációs eljárásokat. Első lépésben a zérus-pólus-erősítés alakú impulzusátviteli függvényből polinomiális impulzusátviteli függvény alakot hozunk létre, majd alkalmazzuk a 2.5.3.1. szakasz fejezetben bemutatott eljárást.
Mintapélda:
A zérus-pólus-erősítés alakú impulzusátviteli függvényből hozzunk létre állapottér alakú mátrixokat, melyekkel leírjuk a vizsgált rendszert (LabVIEW MathScript-ben)!
A h a mintavételi időtartam, amely mintavételes rendszer esetén nem nulla!
zeros_d = [-0.123, 0.32, -0.1]
poles_d = [+0.4, +0.456, +0.3]
kd = 3
h=0.3
sys_zpk_d = zpk(zeros_d, poles_d, kd, h)
[Ad, Bd, Cd, Dd] = zpk_to_ss(zeros_d, poles_d, kd)
step(sys_zpk_d, 10)
>>
zeros_d =
-0.123 0.32 -0.1
poles_d =
0.4 0.456 0.3
kd =
3
h =
0.3
Zero-Pole-Gain Model
Input:1 Output:1
3,000(z+0.123) (z-0.32) (z+0.1)
--------------------------------
(z-0.4) (z-0.456) (z-0.3)
Sampling time: 0,300000
Ad =
1.156 -0.4392 0.0547
1 0 0
0 1 0
Bd =
1
0
0
Cd =
3.177 -1.4948 0.1524
Dd =
3