2. fejezet - Mechanikai rendszerek modellezése fizikai elvek alapján
2.1. Modellezési elvek
A modellezés célja:
-
a rendszerek tulajdonságainak, viselkedésének elemzése, megértése (analízis),
-
a rendszerek jövőbeli állapotának megjóslása (predikció),
-
rendszertervezési feladatok megoldása (szintézis),
-
rendszerek minősítése (validálás).
A modell típusának kiválasztása, vagyis szimuláció vagy irányítás a cél, során figyelembe kell venni az alábbi szempontokat:
-
cél szempontjából lényeges vonások,
-
alkalmazható modellezési eljárások,
-
rendelkezésre álló ismeretanyag,
-
az esetleges megvalósítás módja, költségei.
Szimulációs cél esetén a rendszer viselkedésének minél pontosabb reprodukálása az irányadó. A bonyolultságnak csak a futtatási idővel szemben támasztott követelmények szabnak határt. Irányítási cél esetén csak azok a rendszertulajdonságok érdekesek, amik az irányítási célt befolyásolják. A bonyolultságnak az elérhető irányítástervezési eljárások lehetőségei szabnak gátat.
A modell jellege a modellezésnél használt módszerek és eszközök függvénye. Ezzel összefüggésben a modellezés kiindulási pontjai szerint a valós fizikai rendszerről szerzet információk forrásai lehetnek elméleti ismeretek illetve gyakorlati ismeretek és feltevések. Az elméleti ismeretek sorába tartoznak az egyes jelenségekről alkotott (fizikai, kémiai, stb.) elméletek által szolgáltatott leírások, amelyek általában (közönséges/parciális) differenciálegyenletek formájában öltenek testet. A gyakorlati ismeretek a rendszerről megfigyelések és mérések által gyűjtött adatok összessége, az elméleti modellekben szereplő egyes paraméterek mért értékeinek ismerete. A feltevések sorába tartozik az alkalmazott modell megbízhatóságáról, érvényességi tartományáról alkotott vélemény.
Osztályozhatjuk még a modellezésnél felhasznált információt azok dinamikája szerint. Így megkülönböztethetünk statikus és dinamikus ismereteket: a statikus ismeretek jellegüknél fogva magukba foglalják a törvények (egyenletek) típusait, a struktúra -- állapotok, egyenletek, tagok -- számát illetve paraméterek (együtthatók) értékének ismeretét. A dinamikus ismeret az időbeli működés leírására koncentrál.
A felhasznált információ forrása lehet a priori: ilyen például az előzetes elemzés, a kapcsolatok feltárása, a modellezés céljának és a pontossági igényeknek meghatározása, a modell típusának megválasztása. Ha ez a forrás a posteriori, akkor a feladat a rendszerről megfigyelések és mérések által gyűjtött információ alapján a modell megalkotása és pontosítása, illetve a modell megbízhatósági/érvényességi tartományának vizsgálata. Általában ekkor beszélünk modell identifikációról és validációról. Amikor a struktúra nem, vagy csak részben, adott struktúra-identifikációról, míg ha a struktúra adott akkor paraméter-identifikációról beszélünk.
A lehetséges modellosztályokat tekintve megkülönböztethetünk statikus és dinamikus modelleket: statikus modell időben nem változó állapotot ír le: a rendszer állapotát algebrai egyenletekkel, vagy idő szerinti deriváltakat nem tartalmazó (parciális) differenciál-egyenletekkel írható le. Elterjedt még a stacionárius, állandósult, illetve egyensúlyi modell kifejezés is. A dinamikus modell a vizsgált rendszer, folyamat jellemzőinek időbeni változását írja le, ami legtöbbször egy közönséges vagy parciális differenciálegyenlet, vagy egyenletrendszer. Lehetséges, hogy a tárgyalás nem az időtartományában, hanem valamely célszerűen megválasztott transzformált tartományában (frekvencia tartomány) valósul meg.
Az egyik legfontosabb osztályozó elv a lineáris illetve nemlineáris viselkedés megkülönböztetése: lineáris modell esetén a folyamatot leíró egyenletrendszer kielégíti a szuperpozíció elvét. A szuperpozíció elvéből következik, hogy lineáris matematikai modellek alakja csak homogén, lineáris egyenlet, illetve egyenletrendszer lehet. Egy nemlineáris modell használatakor a rendszerben lejátszódó folyamatot leíró egyenletek legalább egyike nemlineáris függvényt is tartalmaz. A nemlineáris modellek az egyszerűbb vizsgálat és tervezés érdekében valamilyen linearizálási eljárással lineáris modellekké alakíthatók át.
A modellben szereplő jelek természete szerint modellezhetünk folytonos illetve diszkrét időben: folytonos idejű modell esetén a modellezett rendszert vagy folyamatot leíró jellemzők, független és függő változók a vizsgált idő alatt bármelyik pillanatban vehetnek fel valamilyen értéket: a bemeneti és kimeneti jelei egyaránt folytonos idejű jelek. A folytonos paraméterű/folytonos állapotterű modellekben a változók egy adott tartományon, értékhatáron belül bármilyen értéket felvehetnek. A diszkrét idejű modellben a jellemzők csak adott, konkrét időpillanatokban vehetnek fel értékeket. Diszkrét paraméterű/diszkrét állapotterű modellek esetén a változók csak meghatározott diszkrét értékeket vehetnek fel.
A modellek ezen kívül még lehetnek determinisztikus vagy sztochasztikusak: determinisztikus modell esetén a modellekben szereplő jellemzők, valamint maguk a változók egyértelmű függvényekkel térben és időben egyaránt megadhatók. Sztochasztikus modell esetén a modellek jellemzői csak bizonyos valószínűségi összefüggések felhasználásával adhatók meg.
2.2. Newton-Lagrange-Hamilton modellezés
A Lagrange módszer a rendszer modelljét általánosított elmozdulás és sebesség komponensekkel fogalmazza meg:
|
|
(1) |
ahol a kinetikai (mozgási) energia, a potenciális (helyzeti) energia, a disszipációs (csillapítás által elnyelt) energia és egy külső erő. A kinetikus energia a sebességvektoron kívül a helyzetvektortól is függhet, míg a potenciális energia egyedül a helyzetvektortól függ. A kinetikus energia és a potenciális energia különbsége az úgynevezett Lagrange állapotfüggvényt adja meg:
|
|
(2) |
A Lagrange egyenlet felírható az egyes komponensekre bontott alakban is, azaz komponensre felírva:
|
|
(3) |
Példa 1.1
Példaként az 1. ábrán látható két tömegű lengőrendszer modelljét írjuk fel. A lengőrendszer komponensei: az és tömegek, a és rugók, valamint a csillapítás. A rendszert a elmozdulás gerjeszti, ennek hatására a két tömeg elmozdulása és .
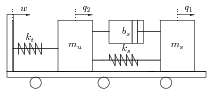
A modellezési feladat megoldása: első lépésében írjuk fel a Lagrange egyenlet komponenseit:
• Kinetikus energia egy tömegre: a
formula alapján a rendszer két tömegére
|
|
(4) |
adódik.
• Potenciális energia egy tömegre:
ezért a rendszerre:
|
|
(5) |
adódik.
• Disszipációs energia a rendszerre:
|
|
(6) |
A számítási műveletek az egyes komponensekre ( és ) bontott alakban a következők:
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
Végül a két tömegű lengőrendszer modellje a Lagrange egyenlet alapján:
|
|
(11) |
|
|
(12) |
Megjegyezzük, hogy a Newtoni mechanikában a rendszer modelljét erő és nyomaték egyensúlyi egyenletekkel fogalmazzuk Newton törvényeinek felhasználásával.
2.3. Átviteli függvény
Egy lineáris időinvariáns rendszer modelljének leírása lineáris, állandó együtthatós közönséges differenciál egyenlettel történik:
|
|
(13) |
ahol és együtthatók konstansok, nem függnek az időtől. Tekintsük a differenciálegyenlet Laplace transzformáltját ( - transzformált) zérus kezdeti feltételekkel. Ekkor a következő egyenlethez jutunk:
|
|
(14) |
ahol .
A racionális törtfüggvényt a rendszer átviteli függvényének nevezzük. Az átviteli függvény tehát a kimenőjel és a bemenőjel zérus kezdeti feltételekkel vett - transzformáltjainak hányadosa.
|
|
(15) |
Az alábbiakban néhány alaptag átviteli függvényét írjuk fel.
• Arányos tagok: Az egyenletből hiányoznak a bemenőjel és kimenőjel differenciálhányadosai.
|
|
(16) |
• Integráló tagok. Az egyenletben bemenőjel nulladik és a kimenőjel első differenciálhányadosa szerepel.
|
|
(17) |
• Differenciáló tagok: Az egyenletben kimenőjel nulladik és a bemenőjel első differenciálhányadosa szerepel.
|
|
(18) |
• Tárolós tagok: Az egyenletben a kimenőjelnek annyiad rendű differenciálhányadosa szerepel, ahány energiatárolót tartalmaz a tag. Ez a tag biztosítja a rendszerben lévő további dinamikák formalizálását.
Példa 1.2
Tekintsük a 1.2 ábrán látható egyszerűsített gépjármű felfüggesztési modellt, melynek adatai a következők: , , k= . Írjuk fel a mechanikai rendszer modelljét.
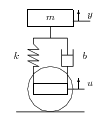
A feladat megoldása: A rendszer differenciálegyenlete:
|
|
(19) |
Alakítsuk át az egyenleteket Laplace transzformációval:
|
|
(20) |
Végül az átviteli függvény
|
|
(21) |
formában adódik.
2.4. Modellezés mért jelek alapján
A modell rendszerint egy differenciálegyenlet formájában ölt testet. Irányításelméleti alkalmazásokban ezek közönséges differenciálegyenletek, vagy darabonként közönséges differenciálegyenletek (kapcsolt rendszerek, impulzív rendszerek).
Amikor a teljes modellt a priori ismeretek alapján állítjuk fel, amik lehetnek fizikai elvek (Hamilton, Lagrange formalizmus, megmaradási elvek, mérlegegyenletek), akkor fehér doboz (white-box) modellezésről beszélünk. A módszer előnye, hogy a modell fizikai paramétereinek valós tartalma, jelentése van, hátránya viszont, hogy a modell felépítése általában rendkívül bonyolult. Ezen túlmenően a modell-bizonytalanságok kezelése is eléggé problematikus.
Ennek ellenpontja a fekete doboz (black-box) modellezés, amikor is a modell felállításához csak kísérletekkel, mérésekkel lehet információkat szerezni. Ilyen információ forrása lehet például a vizsgálójelekre adott rendszerválaszok (például az átmeneti függvény) elemzése. Elsősorban lineáris időinvariáns (LTI) rendszermodellek esetén használatos. Ha nincs más alapinformáció, akkor kiindulásként, mint matematikai modell, például polinommal történő közelítést biztosító egyenleteket lehet felhasználni. Az black-box modellek lényeges előnye a viszonylagos egyszerűségük; hátrányuk viszont, hogy a paramétereknek általában nincs valós fizikai jelentése.
E két véglet között helyezkedik el a szürke doboz (grey-box) modellezés, ami az előző két módszer kombinációja. Főleg nemlineáris jelenségek modellezésére használatos. Ekkor a struktúra adott -- de nem feltétlenül valamiféle egzakt levezetés eredménye. A (sztatikus) nemlinearitások leírásakor gyakran heurisztikus ismeretek épülnek be a modellbe. A műszaki gyakorlatban legtöbbször ez az eset fordul elő. Hátránya az, hogy a struktúra és a parametrizálás általában nem örződik meg a szokásos diszkretizálási eljárásokban.
Példaként tekintsük az úgynevezett kvázi változó paraméterű lineáris (qLPV) modellezést és paraméterezés: gyakran az
|
|
(22) |
nemlineáris rendszert az
|
|
(23) |
alakban szeretnénk felírni. Ez az átírás azonban általában nem egyértelmű:
|
|
(24) |
ahol
|
|
(25) |
Példa 1.3
|
|
(26) |
|
|
(27) |
|
|
(28) |
ahol
|
|
(29) |
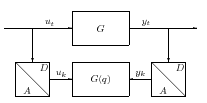
Amikor a rendszer modelljének konstruálása a bemenőjelek és a kimenő jelek mért (mintavételezett) adatai alapján történik, az eljárást modell identifikációnak nevezzük. A mért jelek közötti kapcsolat az alábbi alakban írható fel:
|
|
(30) |
ahol az úgynevezett eltolás operátor, modell leírja a rendszer bemenete és kimenete közötti kapcsolatot, azaz a mintavételezett rendszer átviteli függvényét.
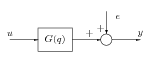
Egy zajjal terhelt lineáris időinvariáns rendszer modelljét mutatja a 4 ábra. A zajos rendszer modellje:
|
|
(31) |
ahol eltolás operátor, zaj (zavarás).
A rendszeridentifikáció végrehajtása több lépésben történik:
-
Bemenő és kimenő jelek mérése, mintavételezése, szűrése, feldolgozása (transzformációja).
-
Modell struktúrájának becslése fizikai megfontolások alapján.
-
Modell paramétereinek becslése.
-
Modell ellenőrzése, tesztelése, validálása.
-
Diszkrét modell transzformálása folytonos alakra.
A rendszermodell általános alakja:
|
|
(32) |
ahol átviteli függvény és az eltolás operátor. Például:
|
|
(33) |
ahol és polinomok az eltolás operátor szerint a következő alakúak:
|
|
(34) |
|
|
(35) |
A modell ARX struktúrája
|
|
(36) |
ahol
|
|
(37) |
|
|
(38) |
A modell struktúráját a kimenet korábbi kimeneteinek száma, a korábbi bemenetek száma és a bemenőjel eltolása határozza meg:
|
|
(39) |
ahol a modell paraméterei. Átrendezve:
|
|
(40) |
A paraméterbecslés eredménye:
|
|
(41) |
ahol a modell becsült paraméterei. A paraméterbecslés modellje kifejtve a következő:
|
|
(42) |
A modell alapján a kimenőjel -edik értékére becslés adható:
|
|
(43) |
Az előrejelzés hibája:
|
|
(44) |
minden -re.
Az n-edrendű ARX modell alakja:
|
|
(45) |
Vezessük be a következő jelölést:
|
|
(46) |
|
|
(47) |
ahol a mért jelek, a paraméterek halmaza. A kimenőjel:
|
|
(48) |
|
|
(49) |
|
|
(50) |
|
|
(51) |
A modell kompakt alakja:
|
|
(52) |
ahol
|
|
(53) |
|
|
(54) |
|
|
(55) |
|
|
(56) |
Az LS becslés azt a paramétervektort keresi, amelynél az hiba négyzetösszege a legkisebb. Az LS kritériumot a következő alakban definiáljuk:
|
|
(57) |
ami skaláris szorzat alakban is felírható:
|
|
(58) |
ahol a paramétereket tartalmazó vektor. Az LS becslés egy optimalizáló eljárás, melynek során a paraméterbecslési eljárás eredményét a következő költségfüggvény minimalizálásával kapjuk:
|
|
(59) |
Az LS kritérium kifejtve:
|
|
(60) |
|
|
(61) |
A minimum parciális deriválttal számítható:
|
|
(62) |
Az optimális megoldás:
|
|
(63) |
|
|
(64) |
amit az LS becslésre vonatkozó normálegyenletnek nevezzük.
A gyakorlati alkalmazásokból ismert tény, hogy a becslési hiba az idő fügvényében egyre nagyobb értékeket vesz fel. Ezért a becslési hiba súlyozását is érdemes bevinni a kritériumba.
|
|
(65) |
ahol , illetve súlyozó tényező. Abban a tartományban, ahol nagyra választjuk, a becslés pontosabb lesz, mint ahol kisebbre választjuk. A normálalak összefüggése a következőképpen változik.
|
|
(66) |
|
|
(67) |
Ezt a kifejezést a súlyozott LS becslésre vonatkozó normálegyenletnek nevezzük.
A becsült modell validáció vizsgálatára a gyakorlatban elterjedt módszer a hiba statisztikai vizsgálata, amikor is olyan kérdésekre várunk választ, mint: milyen a mért jel előrejelzett jellel való illesztése, illetve mennyire mondható el az jelről a fehérzaj tulajdonság.
Az identifikált modell tulajdonságait a rendszer tulajdonságaival való összehasonlítása. A vizsgálat mind idő, mind frekvenciatartományban elvégezhető.
Példa 1.4
Tegyük fel, hogy adott egy paramétereiben nem ismert másodfokú rendszer.
|
|
(68) |
ahol , és .
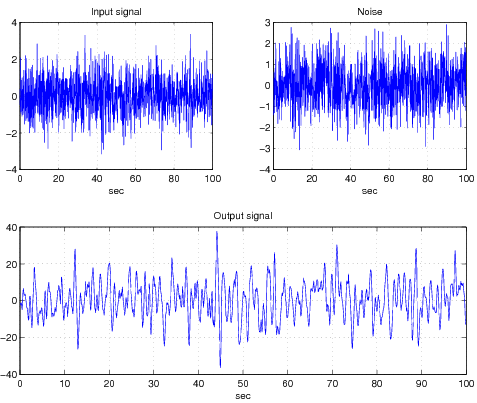
Tegyük fel, hogy a másodfokú rendszer bemenő és kimenő jeleit lépésenként mérjük. A mért mintát illusztrálja a 1.4 ábra.
A feladat megoldása: A modellt s következő ARX struktúrában keressük:
|
|
(69) |
ahol és . A paraméterbecslést legkisebb négyzetes módszerrel hajtjuk végre.
|
|
(70) |
|
|
(71) |
Kiszámítjuk az előrejelzett kimenetet és ezt a mért kimenethez hasonlítjuk. Elvégezzük a hiba kimenet (reziduál) elemzését.
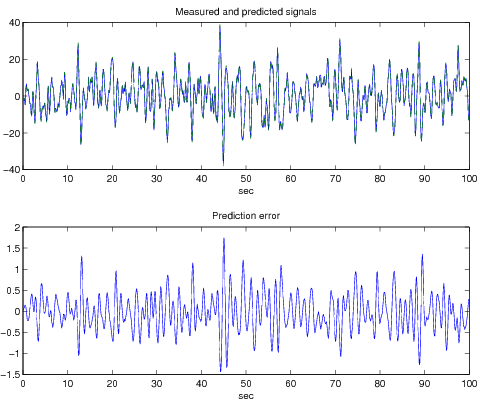
Hiba átlag: , szórás: . A modell által generált jel és a mért jel illesztése az eltérés jelével együtt a 1.4 ábrán látható.