3. fejezet - Rendszerek modellezése állapottérben
Vissza		Előre

3. fejezet - Rendszerek modellezése állapottérben

Tartalom

3.1. Az állapottér elmélet alapjai

A rendszer állapota egy $t_{0}$ időpontbeli információ (olyan jelek ismerete), amelyből az $u (t)$ , $t \geq t_{0}$ bemenőjel ismeretében a rendszer válasza minden $t \geq t_{0}$ időpontra meghatározható.A rendszer válasza a jövőbeli, $t \geq t_{0}$ időpontra vonatkozó állapotokat és a kimenőjeleket jelenti. A rendszer állapotait leíró jeleket, illetve ezek függvényeit, a rendszer állapotváltozóinak nevezzük.

Példa 2.1

Tekintsük az alábbi felfüggesztési rendszert. Az $u$ erő hatására az $m$ tömeg függőleges irányban ( $y$ ) elmozdul. Írjuk fel az erő és az elmozdulás közötti kapcsolatot. A feladat numerikus adatai: $m = 1 k g$ , $k = 4 \frac{N s}{m}$ , $c = 3 \frac{N}{m}$ .

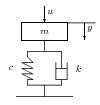
3.1. ábra - Lengő rendszer modellje

A feladat megoldása: A rendszer differenciálegyenlete:

$m \ddot{y} = - k \dot{y} - c y + u,$

(72)

$\ddot{y} = - 4 \dot{y} - 3 y + u .$

(73)

Állapotváltozók megválasztásának egy természetes módja a következő:

$x_{1} = y, x_{2} = \dot{y} .$

(74)

Ezzel a választással az állapotegyenletek alakja:

${\dot{x}}_{1} = \dot{y} = x_{2}$

(75)

${\dot{x}}_{2} = \ddot{y} = - 4 \dot{y} - 3 y + u = - 4 x_{2} - 3 x_{1} + u$

(76)

$y = x_{1},$

(77)

míg az állapottér reprezentáció:

$[\begin{array}{l} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{array}] = [\begin{array}{l} 0 & 1 \\ - 3 & - 4 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}] + [\begin{array}{l} 0 \\ 1 \end{array}] u$

(78)

$y = [\begin{array}{l} 1 & 0 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}]$

(79)

Természetesen egy másik állapottér megválasztás is lehetséges:

$x_{1} = 3 y, x_{2} = 4 \dot{y} .$

(80)

Ezzel a választással az állapotegyenletek alakja

${\dot{x}}_{1} = 3 \dot{y} = \frac{3}{4} x_{2}$

(81)

${\dot{x}}_{2} = 4 \ddot{y} = - 16 \dot{y} - 12 y + 4 u = - 4 x_{2} - 4 x_{1} + 4 u$

(82)

$y = \frac{1}{3} x_{1},$

(83)

a hozzá tartozó állapottér reprezentáció pedig:

$[\begin{array}{l} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{array}] = [\begin{array}{l} 0 & \frac{3}{4} \\ - 4 & - 4 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}] + [\begin{array}{l} 0 \\ 4 \end{array}] u$

(84)

$y = [\begin{array}{l} \frac{1}{3} & 0 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}]$

(85)

Fentiek alapján látható, hogy a bemenőjelek és kimenőjel közötti kapcsolat állapottér reprezentációja többféle alakban felírható és az állapottér alakja nem egyértelmű.

Az állapotegyenlet, mint egy elsőrendű differenciálegyenlet megoldása két lépésben történik. Előbb megoldjuk a homogén egyenletet, majd megkeressük az inhomogén egyenlet egy partikuláris megoldását. A homogén egyenlet alakja:

$\dot{x} (t) = A x (t),$

(86)

az $x (0) = x_{0}$ kezdeti feltétellel és megoldása:

$x (t) = e^{A t} x_{0},$

(87)

ahol az $e^{A t}$ mátrix-exponenciális függvényt a következőképpen értelmezzük:

$e^{A t} = I + A t + \frac{A^{2} t^{2}}{2!} + \frac{A^{3} t^{3}}{3!} + \dots .$

(88)

Például diagonál reprezentációk esetén, azaz $e^{A_{d} t}$ ( $A_{d} \in ℝ^{2 \times 2}$ ) választással ennek alakja: $e^{A_{d} t} = [\begin{array}{l} e^{λ_{1} t} & 0 \\ 0 & e^{λ_{2} t} \end{array}] .$

Az inhomogén egyenlet alakja:

$\dot{x} (t) = A x (t) + b u (t)$

(89)

ahol $x (0) = x_{0}$ egyenlet megoldása a következő:

$x (t) = \int_{0}^{\infty} e^{A (t - τ)} b u (τ) d τ .$

(90)

A fentiek alapján az elsőrendű differenciálegyenlettel leírt állapotegyenlet megoldása:

$x (t) = e^{A t} x_{0} + \int_{0}^{\infty} e^{A (t - τ)} b u (τ) d τ$

(91)

$y (t) = c^{T} x (t) .$

(92)

Példa 2.2

Határozzuk meg a $[\begin{array}{l} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{array}] = [\begin{array}{l} 0 & 1 \\ - 2 & - 3 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}] + [\begin{array}{l} 0 \\ 1 \end{array}] u$ rendszer válaszát egységugrás bemenet esetén.

A feladat megoldása:

1. lépés A homogén rész megoldása:

$\dot{x} = A x$

(93)

$s X (s) - x (0) = A X (s)$

(94)

$X (s) = {(s I - A)}^{- 1} x (0)$

(95)

A példában:

${(s I - A)}^{- 1} = \frac{a d j (s I - A)}{d e t (s I - A)} = \frac{[\begin{array}{l} s + 3 & 1 \\ - 2 & s \end{array}]}{s^{2} + 3 s + 2} = [\begin{array}{l} \frac{s + 3}{s^{2} + 3 s + 2} & \frac{1}{s^{2} + 3 s + 2} \\ \frac{- 2}{s^{2} + 3 s + 2} & \frac{s}{s^{2} + 3 s + 2} \end{array}]$

(96)

A homogén rész megoldása a mátrix tagjainak inverz Laplace transzformációjával történik:

$[\begin{array}{l} x_{1} (t) \\ x_{2} (t) \end{array}] = [\begin{array}{l} 2 e^{- t} - e^{- 2 t} & e^{- t} - e^{- 2 t} \\ - 2 e^{- t} + 2 e^{- 2 t} & - e^{- t} + 2 e^{- 2 t} \end{array}] [\begin{array}{l} x_{1} (0) \\ x_{2} (0) \end{array}]$

(97)

2. lépés Az inhomogén rész megoldása zérus kezdeti érték feltételezésével:

$\dot{x} = A x + b u$

(98)

$s X (s) = A X (s) + b U (s)$

(99)

$X (s) = {(s I - A)}^{- 1} b U (s)$

(100)

A példában:

${(s I - A)}^{- 1} b U (s) = \frac{a d j (s I - A)}{d e t (s I - A)} b \frac{1}{s}$

$= \frac{[\begin{array}{l} s + 3 & 1 \\ - 2 & s \end{array}] [\begin{array}{l} 0 \\ 1 \end{array}]}{s^{3} + 3 s^{2} + 2 s} = \frac{[\begin{array}{l} 1 \\ s \end{array}]}{s^{3} + 3 s^{2} + 2 s} = [\begin{array}{l} \frac{1}{s^{3} + 3 s^{2} + 2 s} \\ \frac{1}{s^{2} + 3 s + 2} \end{array}]$

(101)

Az inhomogén rész megoldása a mátrix tagjainak inverz Laplace transzformációjával történik:

$[\begin{array}{l} x_{1} (t) \\ x_{2} (t) \end{array}] = [\begin{array}{l} 0.5 - e^{- t} + 0.5 e^{- 2 t} \\ e^{- t} - e^{- 2 t} \end{array}]$

(102)

A teljes megoldás:

(103)

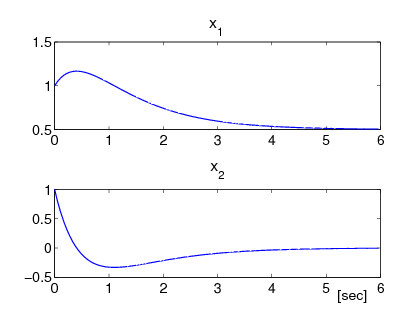
Ha a kezdeti értékek zérusok, azaz $x_{1} (0) = 0$ és $x_{2} (0) = 0$ :

$[\begin{array}{l} x_{1} (t) \\ x_{2} (t) \end{array}] = [\begin{array}{l} 0.5 - e^{- t} + 0.5 e^{- 2 t} \\ e^{- t} - e^{- 2 t} \end{array}]$

(104)

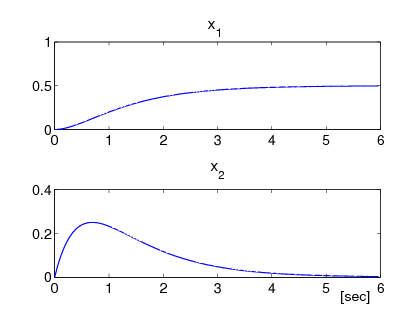
Ha a kezdeti értékek egységnyiek, azaz $x_{1} (0) = 1$ és $x_{2} (0) = 1$ , akkor:

$[\begin{array}{l} x_{1} (t) \\ x_{2} (t) \end{array}] = [\begin{array}{l} 0.5 - 1.5 e^{- 2 t} + 2 e^{- t} \\ - 2 e^{- t} + 3 e^{- 2 t} \end{array}]$

(105)

zérus kezdeti értékeknem zérus kezdeti értékek

3.2. ábra - Átmeneti függvények különböző kezdeti értékek esetén

3.1.1. Állapottér és átviteli függvény kapcsolata

Általánosan egy lineáris dinamikus rendszer állapottér reprezentációját a következő alakban írhatjuk:

$\dot{x} = A x + b u$

(106)

$y = c^{T} x,$

(107)

Az állapottér reprezentáció alapján a rendszer átviteli függvényét a Laplace transzformáció alkalmazásával kapjuk meg:

$s X (s) - x (0) = A X (s) + b U (s),$

(108)

ebből az állapot Laplace transzformáltja:

$X (s) = {(s I - A)}^{- 1} b U (s) + {(s I - A)}^{- 1} x (0),$

(109)

ahol $x (0)$ a kezdő állapot a $t = 0$ időpontban. Az $x (0) = 0$ feltétel mellett

$Y (s) = c^{T} X (s) = c^{T} {(s I - A)}^{- 1} b U (s) .$

(110)

A $G (s)$ átviteli függvény:

$G (s) = \frac{Y (s)}{U (s)} = c^{T} {(s I - A)}^{- 1} b .$

(111)

Az átviteli függvény pólusai tehát az

$det (s I - A) = 0$

(112)

egyenlet gyökei.

3.1.2. Irányíthatósági állapottér reprezentációk

Az irányíthatósági alakú állapottér reprezentáció a 9 ábrával illusztrálható és az alábbi alakban írható fel:

$[\begin{array}{l} {\dot{x}}_{1} \\ {\dot{x}}_{2} \\ {\dot{x}}_{3} \end{array}] = [\begin{array}{l} - a_{2} & - a_{1} & - a_{0} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}] + [\begin{array}{l} 1 \\ 0 \\ 0 \end{array}] u$

(113)

$y = [\begin{array}{l} b_{2} & b_{1} & b_{0} \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}]$

(114)

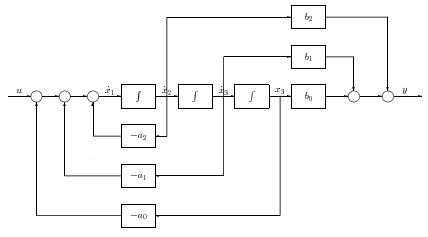
3.3. ábra - Az irányíthatósági alak illusztrációja

Induljunk ki egy általános rendszerből, melynek átviteli függvényét az alábbi alakban fogalmaztuk meg:

$Y (s) = \frac{b (s)}{a (s)} U (s),$

(115)

ahol $a (s)$ és $b (s)$ polinomiális függvények, például $b (s) = b_{1} s + b_{0}$ és $a (s) = s^{2} + a_{1} s + a_{0}$ . A bemenőjel Laplace transzformáltja $U (s)$ és a kimenőjel Laplace transzformáltja $Y (s)$ közötti kapcsolatot ekkor a következőképp írhatjuk:

$Y (s) = b (s) a^{- 1} (s) U (s) .$

(116)

Vezessük be a $ξ (s)$ változót az alábbi módon:

$ξ (s) = a^{- 1} U (s) .$

(117)

Ekkor a bemenőjel és a kimenőjel Laplace transzformáltja:

$Y (s) = b (s) ξ (s) = [b_{1} s + b_{0}] ξ (s) é s$

(118)

$U (s) = a (s) ξ (s) = [s^{2} + a_{1} s + a_{0}] ξ (s) .$

(119)

Inverz Laplace transzformációval a differenciálegyenlet:

$y = b_{1} \dot{ξ} + b_{0} ξ$

$u = \ddot{ξ} + a_{1} \dot{ξ} + a_{0} ξ$

(120)

Vezessük be a következő új változókat, amelyeket állapotváltozóknak nevezünk:

$x_{1} = \dot{ξ}, x_{2} = ξ .$

(121)

Figyelembe véve, hogy ${\dot{x}}_{1} = \ddot{ξ}$ és ${\dot{x}}_{2} = \dot{ξ} = x_{1}$ , az alábbi elsőrendű differenciál egyenletekhez jutunk, melyek az állapotdinamika egyenletrendszerét alkotják:

${\dot{x}}_{1} = - a_{1} x_{1} - a_{0} x_{2} + u$

(122)

${\dot{x}}_{2} = x_{1}$

(123)

Az állapotváltozókból a rendszer kimenőjele a következőképp kapható meg. Ez az úgynevezett megfigyelési egyenlet.

$y = b_{1} x_{1} + b_{0} x_{2}$

(124)

Az állapotegyenletek mátrixos alakban felírva:

${\dot{x}}_{c} = A_{c} x_{c} + b_{c} u$

(125)

$y = c_{c}^{T} x_{c}$

(126)

ahol

$A_{c} = [\begin{array}{l} - a_{1} & - a_{0} \\ 1 & 0 \end{array}], b_{c} = [\begin{array}{l} 1 \\ 0 \end{array}], c_{c}^{T} = [\begin{array}{l} b_{1} & b_{0} \end{array}] .$

(127)

Vizsgáljuk meg egy két állapotú rendszerben, hogy az irányíthatósági alak egyértelműségét. Induljunk ki az (125)-(126) kétállapotú általános leírásból. Az átviteli függvény és az állapottér reprezentáció közötti összefüggés alapján írjuk fel az átviteli függvényt:

$G (s) = c^{T} {(s I - A)}^{- 1} b$

$= [\begin{array}{l} b_{1} & b_{0} \end{array}] {[\begin{array}{l} s + a_{1} & a_{0} \\ - 1 & s \end{array}]}^{- 1} [\begin{array}{l} 1 \\ 0 \end{array}]$

$= \frac{[\begin{array}{l} b_{1} & b_{0} \end{array}] [\begin{array}{l} s & - a_{0} \\ 1 & s + a_{1} \end{array}] [\begin{array}{l} 1 \\ 0 \end{array}]}{s^{2} + a_{1} s + a_{0}}$

$= \frac{b_{1} s + b_{0}}{s^{2} + a_{1} s + a_{0}}$

(128)

Az átviteli függvény alapján jól látható, hogy az irányíthatósági alak egyértelműen felírható. Az $A_{c}$ mátrix első sorának elemei az átviteli függvény nevezőjének együtthatóiként, míg a $c_{c}^{T}$ vektor elemei az átviteli függvény számlálójának együtthatóiként jelennek meg.

3.1.3. Megfigyelhetőségi állapottér reprezentációk

Az irányíthatósági alak és a megfigyelhetőségi alak felírási módja között a dualitás teremt kapcsolatot. A két állapottér ekvivalens alakjai:

$A_{o} = A_{c}^{T},$

(129)

$b_{o} = c_{c},$

(130)

$c_{o}^{T} = b_{c}^{T},$

(131)

Vizsgáljuk meg az irányíthatósági és a megfigyelhetőségi alakok ekvivalenciáját. Írjuk fel az átviteli függvényt mindkét esetben egy kétállapotú állapottér reprezentáció esetére. Az irányíthatósági alakot (125) és (125) szerint vesszük:

$G (s) = [\begin{array}{l} b_{1} & b_{0} \end{array}] {[\begin{array}{l} s + a_{1} & a_{0} \\ - 1 & s \end{array}]}^{- 1} [\begin{array}{l} 1 \\ 0 \end{array}]$

$= \frac{b_{1} s + b_{0}}{s^{2} + a_{1} s + a_{0}}$

(132)

Vizsgáljuk meg a megfigyelhetőségi alakot is. Az állapotegyenletek mátrixos alakban felírva:

${\dot{x}}_{o} = A_{o} x_{o} + b_{o} u$

(133)

$y = c_{o}^{T} x_{o}$

(134)

ahol

$A_{o} = [\begin{array}{l} - a_{1} & 1 \\ - a_{0} & 0 \end{array}], b_{o} = [\begin{array}{l} b_{1} \\ b_{0} \end{array}], c_{o}^{T} = [\begin{array}{l} 1 & 0 \end{array}] .$

(135)

Vizsgáljuk meg egy két állapotú rendszerben, hogy az irányíthatósági és a megfigyelhetőségi alakok ekvivalensek. Induljunk ki az (125)-(126) kétállapotú általános leírásból. Az átviteli függvény és az állapottér reprezentáció közötti összefüggés alapján írjuk fel az átviteli függvényt:

$G (s) = c^{T} {(s I - A)}^{- 1} b$

$= [\begin{array}{l} 1 & 0 \end{array}] {[\begin{array}{l} s + a_{1} & - 1 \\ a_{0} & s \end{array}]}^{- 1} [\begin{array}{l} b_{1} \\ b_{0} \end{array}]$

$= \frac{[\begin{array}{l} 1 & 0 \end{array}] [\begin{array}{l} s & 1 \\ - a_{0} & s + a_{1} \end{array}] [\begin{array}{l} b_{1} \\ b_{0} \end{array}]}{s^{2} + a_{1} s + a_{0}}$

$= \frac{b_{1} s + b_{0}}{s^{2} + a_{1} s + a_{0}}$

(136)

Az átviteli függvények alapján jól látható, hogy az irányíthatósági alak és a megfigyelhetőségi alakok ekvivalensek.

3.1.4. Diagonális állapottér reprezentációk

Az diagonális alakú állapottér reprezentáció a 10 ábrával illusztrálható és az alábbi alakban írható fel:

$[\begin{array}{l} {\dot{x}}_{1} \\ {\dot{x}}_{2} \\ {\dot{x}}_{3} \end{array}] = [\begin{array}{l} - λ_{1} & 0 & 0 \\ 0 & - λ_{2} & 0 \\ 0 & 0 & - λ_{3} \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}] + [\begin{array}{l} r_{1} \\ r_{2} \\ r_{3} \end{array}] u$

(137)

$y = [\begin{array}{l} c_{2} & c_{1} & c_{0} \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}]$

(138)

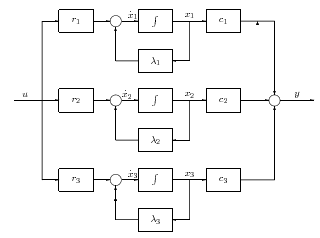
3.4. ábra - A diagonális alak illusztrációja

Tegyük fel, hogy adott egy rendszer kimenete az átviteli függvényének parciális tört alakú felbontásával:

$Y (s) = \frac{b (s)}{a (s)} U (s) = [\frac{r_{1}}{s - λ_{1}} + \frac{r_{2}}{s - λ_{2}}] U (s),$

(139)

ahol $λ_{1}$ , $λ_{2}$ az $s^{2} + a_{1} s + a_{0} = 0$ karakterisztikus egyenlet gyökei, $r_{1}$ , $r_{2}$ pedig a $λ_{1}$ , $λ_{2}$ gyökökhöz (a $b (s) / a (s)$ átviteli függvény pólusaihoz) tartozó rezidumok:

$r_{1} = lim_{s \to λ_{1}} (s - λ_{1}) \frac{b_{1} s + b_{0}}{(s - λ_{1}) (s - λ_{2})} = \frac{b_{1} λ_{1} + b_{0}}{λ_{1} - λ_{2}}$

(140)

$r_{2} = lim_{s \to λ_{2}} (s - λ_{2}) \frac{b_{1} s + b_{0}}{(s - λ_{1}) (s - λ_{2})} = \frac{b_{1} λ_{2} + b_{0}}{λ_{2} - λ_{1}} .$

(141)

Megjegyezzük, hogy ennél a felírásnál $λ_{1}$ és $λ_{2}$ konvex pólusok is lehetnek. Vezessük be új változóként az $X_{1} (s)$ , $X_{2} (s)$ változókat, melyekre

$X_{1} (s) = \frac{r_{1}}{s - λ_{1}} U (s)$

(142)

$X_{2} (s) = \frac{r_{2}}{s - λ_{2}} U (s)$

(143)

$Y (s) = X_{1} (s) + X_{2} (s)$

(144)

amiből az alábbi egyenletek írhatók fel:

$(s - λ_{i}) X_{i} (s) = r_{i} U (s)$

(145)

$s X_{i} (s) = λ_{i} X_{i} (s) + r_{i} U (s), i = 1, 2.$

(146)

Az állapotegyenletek mátrixos alakban felírva:

${\dot{x}}_{d} = A_{d} x_{d} + b_{d} u$

(147)

$y = c_{d}^{T} x_{d},$

(148)

ahol az $(A_{d}, b_{d}, c_{d}^{T})$ jelölésben a $d$ index az $A_{d}$ mátrix diagonális alakjára utal,

$A_{d} = [\begin{array}{l} λ_{1} & 0 \\ 0 & λ_{2} \end{array}], b_{d} = [\begin{array}{l} r_{1} \\ r_{2} \end{array}], c_{d}^{T} = [\begin{array}{l} 1 & 1 \end{array}] .$

(149)

Vizsgáljuk meg egy két állapotú rendszerben a diagonális alak egyértelműségét. Induljunk ki az (147)-(148) kétállapotú általános leírásból. Mivel sem $b_{d}$ sem $c_{d}$ alakjára nézve nincs megkötés, ezért ezeket válasszuk meg a következőképpen:

$b_{d} = [\begin{array}{l} r_{1} \\ r_{2} \end{array}], c_{d}^{T} = [\begin{array}{l} m_{1} & m_{2} \end{array}] .$

(150)

Az átviteli függvény és az állapottér reprezentáció közötti összefüggés alapján írjuk fel az átviteli függvényt:

$G (s) = c_{d}^{T} {(s I - A_{d})}^{- 1} b_{d}$

$= [\begin{array}{l} m_{1} & m_{2} \end{array}] {[\begin{array}{l} s - λ_{1} & 0 \\ 0 & s - λ_{2} \end{array}]}^{- 1} [\begin{array}{l} r_{1} \\ r_{2} \end{array}]$

$= \frac{[\begin{array}{l} m_{1} & m_{2} \end{array}] [\begin{array}{l} s - λ_{2} & 0 \\ 0 & s - λ_{1} \end{array}] [\begin{array}{l} r_{1} \\ r_{2} \end{array}]}{s^{2} - (λ_{1} + λ_{2}) s + λ_{1} λ_{2}}$

$= \frac{(m_{1} r_{1} + m_{2} r_{2}) s - (m_{1} r_{1} λ_{1} - m_{2} r_{2} λ_{1})}{s^{2} - (λ_{1} + λ_{2}) s + λ_{1} λ_{2}}$

(151)

Az átviteli függvény alapján látható, hogy a diagonális alak felírása nem egyértelmű. Habár az átviteli függvény nevezője alapján $A_{d}$ egyértelműen felírható (a pólusok sorrendjének megválasztásától eltekintve), $b_{d}$ és $c_{d}^{T}$ elemeinek megválasztása nem egyértelmű.

Példa 2.3

Határozzuk meg a 1.2 ábrán látható egyszerűsített gépjármű felfüggesztési modelljét irányíthatósági alakban. A feladata numerikus adatai: $m = 200 k g$ , $b = 100 N s / m$ , k= $9000 N / m$ .

A feladat megoldása: a 1.2 példa megoldása alapján induljunk ki az átviteli függvény alakból:

$G = \frac{0.5 s + 45}{s^{2} + 0.5 s + 45}$

(152)

Vezessünk be egy új változót:

$Z = \frac{1}{s^{2} + 0.5 s + 45} U$

(153)

Inverz Laplace transzformációval:

$\ddot{z} = - 0.5 \dot{z} - 45 z + u$

(154)

Az állapotváltozókat a $z$ deriváltjai csökkenő rendje szerint választjuk: $x_{1} = \dot{z}$ és $x_{2} = z$ . Ekkor az állapotok deriváltjai: ${\dot{x}}_{1} = \ddot{z} = - 0.5 x_{1} - 45 x_{2} + u$ és ${\dot{x}}_{2} = \dot{z} = x_{1}$ . A kimeneti jel: $y = 0.5 \dot{z} + 45 z = 0.5 x_{1} + 45 x_{2}$ . Az állapottér reprezentáció irányíthatósági alakban:

$[\begin{array}{l} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{array}] = [\begin{array}{l} - 0.5 & - 45 \\ 1 & 0 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}] + [\begin{array}{l} 1 \\ 0 \end{array}] u$

(155)

$y = [\begin{array}{l} 0.5 & 45 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}]$

(156)

3.1.5. Állapottér transzformációk

Vizsgáljuk azt az esetet, amikor egy adott $x$ állapotvektorból egy új $\bar{x}$ állapotvektort képezünk az alábbi módon:

$\bar{x} = T x$

(157)

ahol $T \in ℝ^{n \times n}$ egy $n \times n$ méretű nemszinguláris transzformációs mátrix, és $\bar{x} \in ℝ^{n}$ , $x \in ℝ^{n}$ . Ha az $x$ állapotvektor az $(A, b, c^{T})$ állapottér reprezentációhoz tartozik, azaz

$\dot{x} = A x + b u$

(158)

$y = c^{T} x,$

(159)

Határozzuk meg az $\bar{x}$ állapotvektor

$\dot{\bar{x}} = \bar{A} \bar{x} + \bar{b} u$

(160)

$y = {\bar{c}}^{T} \bar{x}$

(161)

egyenletekben szereplő $(\bar{A}, \bar{b}, {\bar{c}}^{T})$ mátrixokat. Mivel $x = T^{- 1} \bar{x}$ , ezt behelyettesítve az állapotegyenletbe kapjuk, hogy

$T^{- 1} \dot{\bar{x}} = A T^{- 1} \bar{x} + b u$

(162)

$y = c^{T} T^{- 1} \bar{x},$

(163)

azaz

$\dot{\bar{x}} = T A T^{- 1} \bar{x} + T b u$

(164)

$y = c^{T} T^{- 1} \bar{x},$

(165)

Állapottér reprezentációk közötti kapcsolat

$\bar{A} = T A T^{- 1},$

(166)

$\bar{b} = T b,$

(167)

${\bar{c}}^{T} = c^{T} T^{- 1} .$

(168)

Az $A$ és $\bar{A}$ mátrixok közötti fenti kapcsolatot hasonlósági transzformációnak nevezzük. Egy rendszer adott dimenziós állapottér reprezentációi egymásból hasonlósági transzformációval kaphatók.

Az irányíthatósági alakú állapottér reprezentációt előállító transzformációs mátrix alakja:

$T_{c} = {(C_{n} (A, b) τ (a))}^{- 1},$

(169)

ahol n dimenziós állapottér esetén $C_{n} (A, b)$ az irányíthatósági mátrix:

$C_{n} (A, b) = [\begin{array}{l} b & A b & A^{2} b & ..., \end{array}]$

(170)

és $τ (a)$ egy $n \times n$ dimenziós Toeplitz-mátrix:

$τ (a) = [\begin{array}{l} 1 & a_{n - 1} & a_{n - 2} & \dots & a_{1} \\ 0 & 1 & a_{n - 1} & \dots & a_{2} \\ \dots & 1 & \dots \\ 0 & 0 & 0 & \dots & 1, \end{array}]$

(171)

amelynek elemei a karakterisztikus egyenlet együtthatói:

$det (s I - A) = s^{n} + a_{n - 1} s^{n - 1} + a_{n - 2} s^{n - 2} + \dots + a_{1} s + a_{0} .$

(172)

Ekkor az irányíthatósági állapottér alak

${\bar{A}}_{c} = T_{c} A T_{c}^{- 1}, {\bar{b}}_{c} = T_{c} b, {\bar{c}}_{c}^{T} = c^{T} T_{c}^{- 1} .$

(173)

A diagonális alakú állapottér reprezentációt előállító transzformációs mátrix alakja:

$T_{d} = {(C_{n} (A, b) τ (a) n)}^{- 1},$

(174)

ahol $n$ egy $n \times n$ dimenziós Vandermonde-mátrix:

$n = [\begin{array}{l} λ_{1}^{n - 1} & λ_{2}^{n - 1} & ... & λ_{n}^{n - 1} \\ ... \\ λ_{1}^{2} & λ_{2}^{2} & ... & λ_{n}^{2} \\ λ_{1} & λ_{2} & ... & λ_{n} \\ 1 & 1 & ... & 1 \end{array}]$

(175)

A diagonális állapottér alak:

${\bar{A}}_{d} = T_{d} A T_{d}^{- 1}, {\bar{b}}_{d} = T_{d} b, {\bar{c}}_{d}^{T} = c^{T} T_{d}^{- 1} .$

(176)

Példa 2.4

Határozzuk meg az alábbi rendszer irányíthatósági alakját előállító transzformációs mátrixot.

$A = [\begin{array}{l} - 2 & 0 & - 4 \\ 1 & - 1 & 0 \\ 0 & 1 & 0 \end{array}], b = [\begin{array}{l} 1 \\ 0 \\ 0 \end{array}] c^{T} = [\begin{array}{l} 0 & 0 & 1 \end{array}]$

(177)

A feladat megoldása: az irányíthatósági alak transzformációs mátrixa:

$T = {(C τ)}^{- 1},$

(178)

ahol $det (s I - A_{c}) = s^{3} + 3 s^{2} + 2 s + 4$

$C = [\begin{array}{l} b & A b & A^{2} b \end{array}] = [\begin{array}{l} 1 & - 2 & 4 \\ 0 & 1 & - 3 \\ 0 & 0 & 1 \end{array}], τ = [\begin{array}{l} 1 & 3 & 2 \\ 0 & 1 & 3 \\ 0 & 0 & 1 \end{array}]$

(179)

$T = {(C τ)}^{- 1} = {[\begin{array}{l} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}]}^{- 1} = [\begin{array}{l} 1 & - 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}] .$

(180)

Az irányíthatósági alak:

$A_{c} = [\begin{array}{l} - 3 & - 2 & - 4 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}], b_{c} = [\begin{array}{l} 1 \\ 0 \\ 0 \end{array}], c_{c}^{T} = [\begin{array}{l} 0 & 0 & 1 \end{array}] .$

(181)

3.2. Irányíthatóság és megfigyelhetőség

Állapot megfigyelhetőség: adott $(A, b, c^{T})$ . Mi a feltétele annak, hogy az $x (t)$ állapotokat minden a $t \geq t_{0}$ időpontra meghatározhassuk a rendszer jövőbeli input és output függvényeinek ismeretében?

Definíció 2.1

Az $O_{n} (c^{T}, A)$ mátrixot a rendszer megfigyelhetőségi mátrixának nevezzük.

$O_{n} = {[\begin{array}{l} c^{T} & c^{T} A & ⋮ & c^{T} A^{n - 1} \end{array}]}^{T} .$

(182)

Tétel 2.1 Kálmán-féle rangfeltétel

Egy $(c^{T}, A)$ pár megfigyelhető akkor és csak akkor, ha megfigyelhetőségi mátrixuk rangja megegyezik az állapottér dimenziójával, azaz

$r a n g {O_{n} (c^{T}, A)} = n .$

(183)

Állapot irányíthatóság: adott $(A, b, c^{T})$ , és $x (t)$ a $t = t_{0} = 0$ időpontban. Mi a feltétele annak, hogy találjunk olyan $u (t)$ , $t \geq t_{0}$ irányítást, amely a rendszert véges $T$ idő alatt az $x (0)$ állapotból egy tetszőleges $x (T)$ , $x (T) \neq x (0)$ állapotba vigye?

Definíció 2.2

Az $C_{n} (Φ, b)$ mátrixot a diszkrét idejű rendszer irányíthatósági mátrixának nevezzük.

$C_{n} = [\begin{array}{l} b & A b & \dots & A^{n - 1} b \end{array}]$

(184)

Tétel 2.2 Kálmán-féle rangfeltétel

Egy $(A, b)$ pár akkor és csak akkor irányítható, ha irányíthatósági mátrixuk rangja megegyezik az állapottér dimenziójával, azaz

$r a n g {C_{n} (A, b)} = n .$

(185)

Definíció 2.3

Egy rendszer $(\tilde{A}, \tilde{b}, {\tilde{c}}^{T})$ állapottér reprezentációja minimál reprezentáció, ha együttesen irányítható és megfigyelhető, azaz

$r a n g {C_{n} (\tilde{A}, \tilde{b})} = r a n g {O_{n} ({\tilde{c}}^{T}, \tilde{A})} = n .$

(186)

A minimál reprezentációkhoz tartozó állapotér dimenziója a legkisebb az összes olyan $(A, b, c^{T})$ állapottér reprezentációkat tekintve, amelyekre

$c^{T} {(s I - A)}^{- 1} b = {\tilde{c}}^{T} (s I - \tilde{A}) \tilde{b} = \frac{b (s)}{a (s)},$

(187)

ahol $b (s) / a (s)$ a rendszer átviteli függvénye.

Kálman féle dekompozíció: az irányíthatóság és megfigyelhetőség koncepciója lehetővé teszi, hogy megértsük egy lineáris rendszer struktúráját.

Lineáris rendszerek négy alrendszerre bonthatók:

(a) $S_{c o}$ irányítható és megfigyelhető

(b) $S_{c \bar{o}}$ irányítható és nem megfigyelhető

(d) $S_{\bar{c o}}$ nem irányítható és nem megfigyelhető

$[\begin{array}{l} {\dot{x}}_{c o} \\ {\dot{x}}_{c \bar{o}} \\ {\dot{x}}_{\bar{c} o} \\ {\dot{x}}_{\bar{c o}} \end{array}] = [\begin{array}{l} A_{11} & 0 & A_{13} & 0 \\ A_{21} & A_{22} & A_{23} & A_{24} \\ 0 & 0 & A_{33} & 0 \\ 0 & 0 & A_{43} & A_{44} \end{array}] [\begin{array}{l} x_{c o} \\ x_{c \bar{o}} \\ x_{\bar{c} o} \\ x_{\bar{c o}} \end{array}] + [\begin{array}{l} B_{1} \\ B_{2} \\ 0 \\ 0 \end{array}] u$

$y = [\begin{array}{l} C_{1} & 0 & C_{2} & 0 \end{array}] x + D u$

Példa 2.5

Vizsgáljuk az alábbi diagonális állapottér reprezentáció megfigyelhetőségét és irányíthatóságát:

$\dot{x} = [\begin{array}{l} λ_{1} & 0 \\ 0 & λ_{2} \end{array}] x + [\begin{array}{l} r_{1} \\ r_{2} \end{array}] u,$

(188)

$y = [\begin{array}{l} 1 & 1 \end{array}] x .$

(189)

A feladat megoldása: a megfigyelhetőségi mátrix alakja:

$O_{2} (c^{T}, A) = [\begin{array}{l} c^{T} \\ c^{T} A \end{array}] = [\begin{array}{l} 1 & 1 \\ λ_{1} & λ_{2} \end{array}] .$

(190)

A rangfeltételt a következőképp vizsgálhatjuk: $r a n g {O_{2} (c^{T}, A)} = 2$ akkor, ha $det {O_{2} (c^{T}, A) \neq 0$ . Az adott feladatban: $det {O_{2} (c^{T}, A)} = λ_{2} - λ_{1}$ , azaz a megfigyelhetőség teljesül, ha akkor és csak akkor, ha $λ_{2} \neq λ_{1}$ .

Az irányíthatósági mátrix:

$C_{2} (A_{d}, b_{d}) = [\begin{array}{l} r_{1} & λ_{1} r_{1} \\ r_{2} & λ_{2} r_{2} \end{array}] .$

(191)

Az irányíthatósági mátrix rangja éppen $2$ ha

$det {C_{2} (A_{d}, b_{d})} = r_{1} r_{2} λ_{2} - r_{1} r_{2} λ_{2} = r_{1} r_{2} (λ_{2} - λ_{1}) \neq 0,$

(192)

azaz $r_{1} \neq 0, r_{2} \neq 0 é s λ_{1} \neq λ_{2} .$

Példa 2.6

Vizsgáljuk meg az alábbi állapottér reprezentációval adott rendszer irányíthatóságát és megfigyelhetőségét.

$A = [\begin{array}{l} 0 & 1 & 0 \\ 1 & 0 & - 1 \\ - 1 & - 2 & - 4 \end{array}], b = [\begin{array}{l} 0 \\ 0 \\ 1 \end{array}], c^{T} = [\begin{array}{l} 1 & 0 & 0 \end{array}] .$

(193)

A feladat megoldása: Írjuk fel az irányíthatósági mátrixot:

$C_{3} = [\begin{array}{l} b & A b & A^{2} b \end{array}] = [\begin{array}{l} 0 & 0 & - 1 \\ 0 & - 1 & 4 \\ 1 & - 4 & 18 \end{array}]$

(194)

Megfigyelhetőség ellenőrzése: egy mátrix rangja elemi mátrixműveletekkel vizsgálható. A teljes rang vizsgálata a mátrix determinánsának kiszámításával is meghatározható: $d e t C_{3} = 1$ . A rendszer tehát irányítható. Írjuk fel a megfigyelhetőségi mátrixot:

$O_{3} = [\begin{array}{l} c^{T} \\ c^{T} A \\ c^{T} A^{2} \end{array}] = [\begin{array}{l} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & - 1 \end{array}]$

(195)

Mivel $d e t O_{3} = 3$ , ezért a rendszer megfigyelhető.

Vissza		Előre
2. fejezet - Mechanikai rendszerek modellezése fizikai elvek alapján	Főoldal	4. fejezet - Rendszerek elemzése idő és frekvencia tartományban