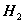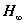Irányításelmélet
Szerzői jog © 2014 Dr. Bokor József, Dr. Gáspár Péter, Dr. Szabó Zoltán

A tananyag a TÁMOP-4.1.2.A/1-11/1-2011-0042 azonosító számú „ Mechatronikai mérnök MSc tananyagfejlesztés ” projekt keretében készült. A tananyagfejlesztés az Európai Unió támogatásával és az Európai Szociális Alap társfinanszírozásával valósult meg.

A kiadásért felel a(z): BME MOGI
Felelős szerkesztő: BME MOGI
ISBN 978-963-313-175-6
2014
Tartalom
- 1. Bevezetés
- 2. Mechanikai rendszerek modellezése fizikai elvek alapján
- 3. Rendszerek modellezése állapottérben
- 4. Rendszerek elemzése idő és frekvencia tartományban
- 5. Stabilitásvizsgálat
- 6. Minőségi tulajdonságok elemzése
- 7. Bizonytalanságok modellezése
- 8. PID szabályozások tervezése
- 9. Irányítástervezés állapot-visszacsatolással
- 10. Lineáris kvadratikus szabályozótervezés
- 11. Megfigyelőtervezés és szeparációs elv
- 12. H2 irányítások tervezése
- 13. Hinf. szabályozók tervezése
- 14. Rekonfiguráló és hibatűrő irányítások tervezése
-
- 14.1. Robusztus stabilitás, robusztus performancia
- 14.2. Robusztus stabilitás vizsgálat
- 14.3. Kis erősítések tétele
- 14.4. Robusztus performancia analízis
- 14.5. Struktúrált bizonytalanság
- 14.6. Struktúrált szinguláris érték
- 14.7. Struktúrált szinguláris érték: analízis
- 14.8. Struktúrált szinguláris érték: szintézis
- 15. Nemlineáris irányítások
- 16. Mintavételezett rendszerek irányítása
- 17. Irányítási rendszerek implementálása, beágyazott rendszerek
- 18. Irodalomjegyzék
Az ábrák listája
- 2.1. Kéttömegű lengőrendszer
- 2.2. Gépjármű felfüggesztés modellje
- 2.3. Identifikálandó modell
- 2.4. Zajjal terhelt modell
- 2.5. Mért bemenő és kimenő jelek
- 2.6. Becslési hiba elemzése
- 3.1. Lengő rendszer modellje
- 3.2. Átmeneti függvények különböző kezdeti értékek esetén
- 3.3. Az irányíthatósági alak illusztrációja
- 3.4. A diagonális alak illusztrációja
- 4.1. Lengőrendszer modellje
- 4.2. A 3.1 példa megoldása komplex pólusok esetén
- 4.3. A 3.1 példa megoldása valós pólusok esetén
- 4.4. Frekvencia függvény illusztrációja
- 4.5. 2TP tag frekvencia diagramjai valós pólusok esetén
- 4.6. 2TP tag frekvencia diagramjai komplex pólusok esetén
- 4.7. hatása a Bode diagramra
- 4.8. A 3.3 példa megoldása valós pólusok esetén
- 4.9. A 3.3 példa megoldása komplex pólusok esetén
- 5.1. Nyquist stabilitási kritérium
- 5.2. Nyquist stabilitási kritérium
- 5.3. Nyquist stabilitási kritérium
- 6.1. Időtartományi jellemzők
- 6.2. Időtartományi jellemzők
- 6.3. Időtartományi jellemzők
- 6.4. Időtartományi jellemzők
- 7.1. Példa egy felfüggesztési rendszer modellezésére
- 7.2. Az additív bizonytalanság struktúrája
- 7.3. Bizonytalanság a Nyquist diagramon
- 7.4. A multiplikatív bizonytalanság struktúrája
- 7.5. Bizonytalanság a Bode diagramon
- 7.6. Bizonytalanságok modellezése
- 7.7. A bizonytalan rugóállandó modellezése
- 7.8. A bizonytalan tömeg modellezése
- 7.9. struktúra
- 7.10. struktúra
- 8.1. Soros kompenzátor felépítése
- 8.2. Soros kompenzátor felépítése
- 8.3. Soros kompenzátor felépítése
- 8.4. PID szabályozó struktúrája
- 8.5. Arányos tag hatása
- 8.6. Arányos tag hatása
- 8.7. Arányos tag hatása
- 8.8. PID szabályozó struktúrája
- 8.9. Referenciajel súlyozás
- 8.10. Referenciajel súlyozás
- 8.11. Referenciajel súlyozás
- 8.12. Tuningolás, hangolás
- 9.1. A visszacsatolt (zárt) rendszer blokkdiagramja
- 10.1. A tervezés frekvencia tartományban
- 11.1. Állapotmegfigyelő
- 11.2. Állapotmegfigyelő
- 12.1. Általános rendszerstruktúra
- 12.2. DF zárt kör
- 12.3. DF transzformációja FI-be
- 12.4. felírása két alrendszerrel
- 14.1. struktúra
- 14.2. Kis erősités kapcsolat
- 14.3. Súlyozott kis erősités kapcsolat
- 14.4. Robusztus performancia es stabilitás
- 14.5. Robust performance analysis
- 14.6. Egy lengőrendszer dinamikájának modellezése
- 14.7. A parametrikus bizonytalanságok modellezése
- 14.8. Lengőrendszer modellezése parametrikus bizonytalanságokkal
- 14.9. Lengőrendszer modellje
- 14.10. Lengőrendszer modellje a bizonytalanságokkal
- 14.11. Parametrikus bizonytalanságok hatása a Bode diagramra
- 14.12. iteráció
- 16.1. Számítógéppel irányított rendszer blokkvázlata
- 16.2. A zérus és elsőrendű tartók működésének illusztrációja
- 16.3. Időben diszkrét és folytonos rendszer időtartományi görbéje
- 16.4. Folytonos és diszkrét idejű rendszerek pólusainak kapcsolata
- 17.1. Komplex rendszer moduljai
- 17.2. Jármű pozícióérzékelés és navigáció
- 17.3. Egyszerű beavatkozó szerv illusztrációja
- 17.4. Gépjármű fékrendszer illusztrációja
- 17.5. Gépjármű fékrendszer blokksémája
- 17.6. ESP működése
- 17.7. Egy reaktor sematikus ábrája
- 17.8. Az Ethernet megvalósítása
- 17.9. Beágyazott rendszer illusztrációja