9. fejezet - Irányítástervezés állapot-visszacsatolással
Vissza		Előre

9. fejezet - Irányítástervezés állapot-visszacsatolással

Tartalom

9.1. Pólusallokációs módszer

9.1. Pólusallokációs módszer

Adott egy rendszer $n$ -dimenziós $(A, b, c^{T})$ állapottér reprezentációja:

$\dot{x} = A x + b u$

$y = c^{T} x .$

(333)

A rendszer karakterisztikus polinomja:

$a (s) = det (s I - A) = s^{n} + a_{n - 1} s^{n - 1} + \dots + a_{1} s + a_{0} .$

(334)

Módosítsuk a rendszer dinamikáját az $x (t)$ állapot visszacsatolásával, azaz legyen a bemenőjel

$u = - k^{T} x + r,$

(335)

ahol $r (t)$ egy külső alap-, vagy referencia jel a $k$ pedig az állapot visszacsatolás erősítési tényezője:

$k^{T} = [\begin{array}{l} k_{n - 1} & \dots & k_{0} \end{array}] .$

(336)

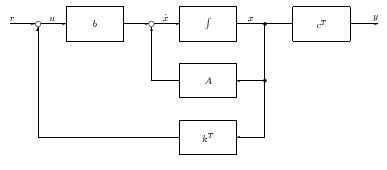
9.1. ábra - A visszacsatolt (zárt) rendszer blokkdiagramja

Behelyettesítve a bemenőjel alakját az állapotegyenletbe, a zárt rendszer állapotegyenlete a következő lesz:

$\dot{x} = (A - b k^{T}) x + b r$

(337)

$y = c^{T} x,$

(338)

amiből a zárt rendszer karakterisztikus egyenletére azt kapjuk, hogy

$α (s) = det (s I - A + b k^{T}) = s^{n} + α_{n - 1} s^{n - 1} + \dots + α_{1} s + α_{0} .$

(339)

Az alábbiakban megmutatjuk, hogy a $k$ erősítés megfelelő megválasztásával a zárt rendszer karakterisztikus polinomja tetszőlegesen beállítható, ha az $(A, b, c^{T})$ rendszer irányítható.

Mivel minden irányítható állapottér reprezentáció irányítható alakra hozható, tegyük fel hogy az alábbi rendszert irányítható alakra hoztuk.

$\dot{x} = A_{c} x + b_{c} u$

$y = c_{c}^{T} x .$

(340)

Ekkor a visszacsatolással módosult állapotmátrix:

$A_{c} - b_{c} k^{T} =$

$= [\begin{array}{l} - (a_{n - 1} + k_{n - 1}) & \dots & - (a_{1} + k_{1}) & - (a_{0} + k_{0}) \\ 1 & 0 & 0 \\ 0 & ⋱ & ⋮ \\ 0 & \dots & 1 & 0 \end{array}]$

(341)

A zárt rendszer karakterisztikus polinomja:

$α (s) = det (s I - A_{c} + b_{c} k^{T})$

$= s^{n} + (a_{n - 1} + k_{n - 1}) s^{n - 1} + \dots + (a_{1} + k_{1}) s + (a_{0} + k_{0}),$

(342)

Ha a zárt rendszer pólusait előírjuk, akkor rögzítjük a ${\bar{p}}_{1}, \dots, {\bar{p}}_{n}$ pólusokat, amiből az $\bar{a} (s)$ karakterisztikus polinom számítható:

$α (s) = (s - {\bar{p}}_{1}) \dots (s - {\bar{p}}_{n})$

$= s^{n} + α_{n - 1} s^{n - 1} + \dots + α_{1} s + α_{0} .$

(343)

Ebben a kifejezésben $α_{i}$ -k az állapot visszacsatolással módosított karakterisztikus polinom együtthatói. A $k_{i}$ , $a_{i}$ és $α_{i}$ együtthatók közötti kapcsolat:

$α_{i} = a_{i} + k_{i}, i = 0, \dots, n - 1.$

(344)

A kompenzátor elemeinek számítása:

$k_{i} = α_{i} - a_{i}, i = 0, \dots, n - 1.$

(345)

ahol $a_{i}$ -k az eredeti, míg $α_{i}$ -k a módosított karakterisztikus polinom együtthatói.

A tervezés során tehát előbb meghatározzuk az eredeti rendszer, majd a tervezett rendszer karakterisztikus polinomját. Az eredeti rendszer karakterisztikus polinomja:

$det (s I - A) = s^{n} + a_{n - 1} s^{n - 1} + \dots + a_{1} s + a_{0}$

(346)

A tervezett zárt rendszer karakterisztikus polinomja:

$det (s I - A + b k^{T}) = s^{n} + α_{n - 1} s^{n - 1} + \dots + α_{1} s + α_{0}$

(347)

Az együtthatók közötti összefüggések:

$a_{i} + k_{i} = α_{i}$

(348)

Az állapot visszacsatolás értékei:

$k_{i} = α_{i} - a_{i}$

(349)

Ha a rendszer irányítható, de nem irányíthatósági alakban adott, akkor egy $T$ nem szinguláris transzformációs mátrix segítségével irányíthatósági alakra hozható. Az irányíthatósági alakban jelöljük $A_{c}$ és $b_{c}$ -vel az állapotegyenlet együtthatóit.A tervezés ebben az irányíthatósági alakban történik, ami azt jelenti, hogy a tervezés eredményeként egy olyan $k_{c}$ állapot-visszacsatolást tervezünk, amely az irányíthatósági állapottér reprezentációra működik.

A tervezett állapot visszacsatolt erősítőt vissza kell transzformálni az eredeti rendszer állapotterére. A transzformálás összefüggése az alábbi:

$k^{T} = k_{c}^{T} \cdot T$

(350)

A tervezési lépések a következők:

(a) Az irányíthatóság ellenőrzése. Ha a rendszer nem irányítható, akkor az állapot visszacsatolás módszere nem alkalmazható.

(b) A rendszert irányíthatósági alakra hozzuk, azaz meghatározzuk $T$ nem szinguláris mátrixot, amely a rendszert irányíthatósági alakúra hozza.

$T = {(C (A, b) τ (a))}^{- 1}$

(351)

Ha a rendszer eleve irányíthatósági alakban adott, akkor $T$ mátrixot egységmátrixnak választjuk, azaz $T = I$ .

Megjegyezzük, hogy az új állapottérbe való transzformálás tényleges elvégzésére nincs szükség, elegendő a transzformációs mátrix meghatározása.

$a = {[\begin{array}{l} a_{n - 1} & \dots & a_{1} & a_{0} \end{array}]}^{T} .$

(352)

Ezután meghatározzuk a tervezett rendszer karakterisztikus polinomját:

$α = {[\begin{array}{l} α_{n - 1} & \dots & α_{1} & α_{0} \end{array}]}^{T} .$

(353)

Ezekhez a műveletekhez az eredeti rendszer $A$ mátrixát és a szabályozott rendszertől megkövetelt új pólusokat kell felhasználni.

(d) A kompenzátor komponenseit kiszámítjuk:

$k_{c}^{T} = [\begin{array}{l} k_{n - 1} & \dots & k_{1} & k_{0} \end{array}]$

(354)

ahol $k_{n - 1} = α_{n - 1} - a_{n - 1}$ ,..., $k_{1} = α_{1} - a_{1}$ , $k_{0} = α_{0} - a_{0}$

(e) Meghatározzuk az eredeti rendszerre vonatkozó erősítés együtthatóit.

$k^{T} = k_{c}^{T} \cdot T$

(355)

Az irányítójel az alábbi:

$u = - k_{n - 1} x_{1} - \dots - k_{1} x_{n - 1} - k_{0} x_{n} + r$

(356)

Megjegyzés 8.1 A fenti lépéseket egyetlen összefüggésbe sűríthetjük:

${(α - a)}^{T} = k^{T} C (A, b) τ (a)$

(357)

ahol a $T = {(C (A, b) τ (a))}^{- 1}$ az irányíthatósági alak előállítására szolgáló transzformációs mátrix. Az állapotvisszacsatolt erősítő:

$k^{T} = {(α - a)}^{T} τ {(a)}^{- 1} C {(A, b)}^{- 1}$

(358)

Az összefüggést az állapotvisszacsatolás erősítésének meghatározására szolgáló Bass Gura formulának nevezzük.

Összefoglalás:

(a) A pólusallokációs módszer alkalmazásának feltétele:

* Az állapotvektor elemei mértek legyenek.

* Az állapottér reprezentáció teljesítse az irányíthatósági feltételt.

* A szabályozott rendszer pólusai adottak legyenek.

(b) A pólusallokációs módszer előnyei:

* A módszer végrehajtása egyszerű mátrix műveletekkel történik.

* A szabályozott rendszer stabilis.

* Az irányítójel tetszőlegesen nagy lehet.

* A pólusok elhelyezkedése és a minőségi tulajdonságok közötti kapcsolat bonyolult, heurisztikus szabályokra és mérnöki intuíciókra hagyatkozva kell a pólusok helyét előírni.

* A szabályozott rendszer minőségi tulajdonságai az állapot-visszacsatolt erősítő megtervezése után utólagosan vizsgálandók.

Példa 8.1

Adott a

$G (s) = \frac{2 s + 3}{s^{2} + 9 s + 20}$

(359)

átviteli függvénnyel jellemzett rendszer. Írja fel a rendszer állapottér reprezentációját diagonális alakban! Tervezzen az így felírt állapottér reprezentációhoz állapot-visszacsatolást a $p_{1} = - 2 + i$ , $p_{2} = - 2 - i$ pólusokkal!

A feladat megoldása:

Diagonális alak előállítása:

$G = \frac{2 s + 3}{s^{2} + 9 s + 20} = \frac{2 s + 3}{(s + 4) (s + 5)}$

(360)

$r_{1} = lim_{s \to - 4} (s + 4) \frac{2 s + 3}{(s + 4) (s + 5)} = - 5,$

(361)

$r_{2} = lim_{s \to - 5} (s + 5) \frac{2 s + 3}{(s + 4) (s + 5)} = 7.$

(362)

Vezessük be új változóként az $X_{1} (s)$ , $X_{2} (s)$ változókat, ahol

$X_{1} (s) = \frac{r_{1}}{s - λ_{1}} U (s) = \frac{- 5}{s + 4} U (s),$

(363)

$X_{2} (s) = \frac{r_{2}}{s - λ_{2}} U (s) = \frac{7}{s + 5} U (s)$

(364)

$Y (s) = X_{1} (s) + X_{2} (s)$

(365)

Az állapottér reprezentáció diagonális alakban:

$[\begin{array}{l} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{array}] = [\begin{array}{l} - 4 & 0 \\ 0 & - 5 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}] + [\begin{array}{l} - 5 \\ 7 \end{array}] u$

(366)

$y = [\begin{array}{l} 1 & 1 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}]$

(367)

Az eredeti rendszer karakterisztikus polinomja:

$s^{2} + 9 s + 20 \Rightarrow a_{1} = 9; a_{0} = 20$

(368)

Szabályozott rendszer karakterisztikus polinomja:

$(s - λ_{1}) (s - λ_{2}) = s^{2} + 4 s + 5 \Rightarrow α_{1} = 4; α_{0} = 5$

(369)

Állapotvisszacsatolás erősítései: $k_{1} = - 5; k_{0} = - 17$

$k_{c}^{T} = [\begin{array}{l} - 5 & - 15 \end{array}]$

(370)

Ha a rendszer irányítható, de nem irányíthatósági alakban adott, akkor egy $T$ nem szinguláris transzformációs mátrix segítségével irányíthatósági alakra hozható.

$x_{c} = T x$

ahol $T = T_{c}$ a transzformációs mátrix. Az állapotvisszacsatolt-erősitő összefüggése: a hasonlósági transzformáció alapján az alábbi:

$k^{T} = k_{c}^{T} \cdot T .$

(371)

Transzformációs mátrix:

$T^{- 1} = C τ = [\begin{array}{l} - 5 & - 25 \\ 7 & 28 \end{array}]$

(372)

ahol

$C = [\begin{array}{l} - 5 & 20 \\ 7 & - 35 \end{array}], τ = [\begin{array}{l} 1 & 9 \\ 0 & 1 \end{array}],$

(373)

$det (s I - A) = s^{2} + 9 s + 20.$

(374)

Transzformációs mátrix:

$T = \frac{1}{35} [\begin{array}{l} 28 & 25 \\ - 7 & - 5 \end{array}]$

(375)

Az eredeti állapottérbe transzformálva:

$k^{T} = k_{c}^{T} T = \frac{1}{35} [\begin{array}{l} - 5 & - 15 \end{array}] [\begin{array}{l} 28 & 25 \\ - 7 & - 5 \end{array}]$

(376)

$= [\begin{array}{l} - 1 & - 1.4286 \end{array}]$

(377)

Vissza		Előre
8. fejezet - PID szabályozások tervezése	Főoldal	10. fejezet - Lineáris kvadratikus szabályozótervezés