8. fejezet - PID szabályozások tervezése
Vissza		Előre

8. fejezet - PID szabályozások tervezése

Tartalom

8.1. Tervezés frekvencia tartományban

Soros kompenzátor tervezése előírt fázistartalék elérése érdekében történik. A tervezési elv ismertetése érdekében első lépésben arányos soros kompenzátor tervezését mutatjuk be.

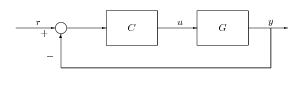
8.1. ábra - Soros kompenzátor felépítése

A zárt rendszer átviteli függvénye:

$G_{C} = \frac{G_{E}}{1 + G_{H}}$

(285)

ahol $G_{H}$ a hurokátviteli függvény és $G_{E}$ az előrevezető ág eredő átviteli függvénye.

Vizsgáljuk meg első lépésben egy arányos kompenzátor tervezését. Kihasználjuk azt, hogy egy C=A arányos tag amplitúdója $20 l o g_{10} A$ , míg fázisa $0$ a teljes frekvencia tartományban. Következtetés: Egy arányos tag az amplitúdó függvényt önmagával párhuzamosan eltolja, mégpedig $A > 1$ esetén felfelé, míg $A < 1$ esetén lefelé, ugyanakkor a fázisfüggvényt nem módosítja.

A soros kompenzátort úgy kell megválasztani, hogy $ω_{c}$ vágási körfrekvenciához tartozó fázisszög éppen az előírt legyen.

Olvassuk le a fázisszöghöz tartozó amplitúdó értékét és jelöljük ezt előjelhelyesen $x$ -szel Az arányos soros kompenzátort úgy kell megválasztani, hogy az amplitúdó függvényt önmagával párhuzamosan $x$ -szel eltolja (miközben a fázisfüggvényt változatlanul hagyja).

Tehát $C = A$ -t a következőképpen kell megválasztani:

$20 l o g_{10} A = - x$

(286)

ahol $x$ az ábráról leolvasott érték, s ebből $A$ kiszámítható:

$A = 10^{- \frac{x}{20}} .$

(287)

Összefoglalva a soros kompenzátor tervezés lépései a következők:

(a) $C = 1$ választással felrajzoljuk a felnyitott hurok Bode diagramját.

(b) Leolvassuk a $φ_{t}$ -hez tartozó $x$ előjeles értékét és kiszámítjuk $C = A$ soros kompenzátor értéket.

Megjegyzés: Ha az amplitudó függvényt lefelé kell eltolni, akkor $A < 1$ , míg ha felfelé, akkor $A > 1$ erősítést várunk.

Ha a cél egy dinamikus kompenzátor tervezése, akkor a tervezést megpróbáljuk visszavezetni arányos soros kompenzátor tervezésére:

$C (s) = A C_{0} (s)$

(288)

ahol $C_{0} (s)$ a kompenzátor átviteli függvényének ismert komponense.

Például:

$C (s) = \frac{1}{T_{i} s} = \frac{1}{T_{i}} \frac{1}{s}$

(289)

azaz $A = \frac{1}{T_{i}}$ és $C_{0} (s) = \frac{1}{s}$ . A felnyitott hurok átviteli függvénye a következő:

$G_{H} (s) = A G C_{0} (s) = A G_{m} (s)$

(290)

ahol $G_{m} (s) = G (s) C_{0} (s)$ . Ha a rendszer átviteli függvényét a $C_{0}$ komponenssel módosítjuk, akkor $G_{m} (s)$ átviteli függvényhez jutunk.

A tervezés során a $G_{m} (s)$ átviteli függvénnyel adott rendszert tekintjük szabályozandó rendszernek, amihez egy $A$ arányos kompenzátort kell terveznünk.Természetesen a tervezett soros kompenzátort $C (s) = A C_{0} (s)$ alakú.

Példa 7.1

Legyen az irányítandó rendszer átviteli függvénye:

$G = \frac{5}{s^{3} + 3 s^{2} + 2 s} .$

(291)

Tervezzünk $30$ fokos fázistartalékot biztosító arányos soros kompenzátort.

A feladat megoldása: Válasszunk kiindulásként $C = 1$ arányos soros kompenzátort:

$G_{H} = G C = \frac{5}{s^{3} + 3 s^{2} + 2 s} .$

(292)

Szerkesszük meg a felnyitott hurok Bode diagramját.

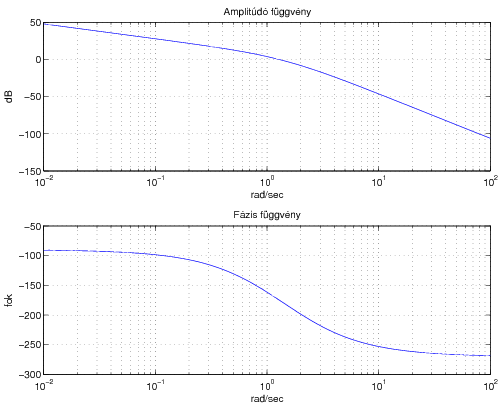
8.2. ábra - Soros kompenzátor felépítése

Változtassuk meg $C$ -t úgy, hogy a fázistartalék $30$ fokos legyen, azaz $φ_{t} = 30$ és a fázisszög $ω_{c}$ -nél: $φ = - 150$ . Kihasználjuk azt, hogy egy C=A arányos tag amplitúdója $20 l o g_{10} A$ , míg fázisa $0$ a teljes frekvencia tartományban.

• Jelen esetben $A = 0.43$ arányos soros kompenzátor oldja meg a feladatot ( $30$ fokos fázistartalékot biztosít).

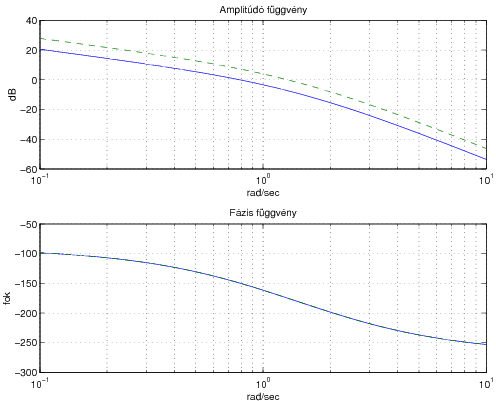
8.3. ábra - Soros kompenzátor felépítése

Példa 7.2

Legyen az irányítandó rendszer átviteli függvénye:

$G = \frac{5}{s^{2} + 3 s + 2}$

(293)

Tervezzünk jelkövetést biztosító soros kompenzátort, amelyik $30$ fokos fázistartalékot is garantál.

A feladat megoldása: A jelkövetés akkor biztosítható, ha a soros kompenzátor integráló tulajdonságú. Emiatt a soros kompenzátort a következő alakban választjuk meg:

$C = \frac{A_{i}}{s}$

(294)

A felnyitott hurok átviteli függvénye a következő:

$G_{H} = C G = \frac{A_{i}}{s} G = A_{i} \frac{G}{s}$

(295)

Ha a rendszer átviteli függvényét $\frac{G}{s}$ -nek tekintjük, akkor a továbbiakban egy arányos soros kompenzátort kell terveznünk az $1$ . példában leírtakhoz hasonló módon.

A következőkben megvizsgáljuk, hogy a modell alapján megtervezett szabályozó vajon stabilizálja-e a valós rendszert. Ehhez a modell bizonytalansági struktúráiból indulunk ki.

Tekintsük a bizonytalanságot additív struktúrában.

$G (s) = G_{N} (s) + Δ_{A} (s),$

(296)

A továbbiakban feltesszük, hogy a rendszer névleges modelljén kívül ismerjük a szabályozó modelljét. Tegyük fel, hogy a $G_{H N} (s) = C (s) G_{N} (s)$ kompenzált névleges rendszer stabilis. Vizsgáljuk meg, hogy a $G_{H} (s) = C (s) G (s)$ aktuális rendszer stabilitásához milyen feltételnek kell teljesülnie.

Tétel 7.1 Legyen $G_{N} (s)$ az ismert névleges modell, amelyet a tervezett $C (s)$ soros kompenzátor stabilizál. Tegyük fel, hogy a névleges modell és az aktuális rendszer közötti additív hiba felső korlátját a teljes $ω$ frekvencia tartományban ismerjük. Ekkor a névleges modellre tervezett szabályozó az aktuális rendszer stabilitását is biztosítja, ha a következő feltétel teljesül:

$\frac{1}{d_{A} (ω)} > | \frac{C (i ω)}{1 + G_{H N} (i ω)} |, \forall ω .$

(297)

Ez a robusztus stabilitás feltétele additív hiba struktúra esetén.

Tekintsük a bizonytalanságot multiplikatív struktúrában.

$G (s) = G_{N} (s) (1 + Δ_{M} (s)),$

(298)

Tétel 7.2 Legyen $G_{N} (s)$ az ismert névleges modell, amelyet a tervezett $C (s)$ soros kompenzátor stabilizál. Tegyük fel, hogy a névleges modell és az aktuális rendszer közötti multiplikatív hiba felső korlátját a teljes $ω$ frekvencia tartományban ismerjük. Ekkor a névleges modellre tervezett szabályozó az aktuális rendszer stabilitását is biztosítja, ha a következő feltétel teljesül:

$\frac{1}{d_{M} (ω)} > | \frac{G_{H N} (i ω)}{1 + G_{H N} (i ω)} |, \forall ω .$

(299)

Ez a robusztus stabilitás feltétele multiplikatív hiba struktúra esetén.

8.2. PID struktúra

A PID egy arányos, egy integráló és egy differenciáló tag párhuzamos kapcsolata. A PID szabályozó tervezésekor az erősítéseket és az időállandókat kell megfelelően beállítani (hangolni). Megjegyezzük, hogy a valóságban időtárolós differenciáló tag van az ideális differenciáló tag helyett.

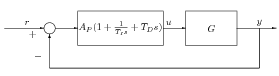
8.4. ábra - PID szabályozó struktúrája

A szabályozó átviteli függvénye:

$K = A_{P} (1 + \frac{1}{T_{I} s} + T_{D} s)$

(300)

ahol $A_{P}$ az arányos tag erősítése, $T_{I}$ az integráló tag időállandója, $T_{D}$ a differenciáló tag időállandója.

Az $u (t)$ jel és $e (t) = r (t) - y (t)$ hibajel közötti kapcsolat:

$u (t) = A_{P} (e (t) + \frac{1}{T_{I}} \int_{0}^{t} e (τ) d τ + T_{D} \frac{d e (t)}{d t})$

(301)

Zérus kezdeti feltételekkel Laplace transzformálva:

$U (s) = A_{P} (1 + \frac{1}{T_{I} s} + T_{D} s) E (s)$

(302)

Példaként tekintsük a $G = \frac{1}{{(s + 1)}^{3}}$ átviteli függvényű rendszert, amit különböző arányos taggal szabályoztunk. $A_{P} = 1; 2; 5.$

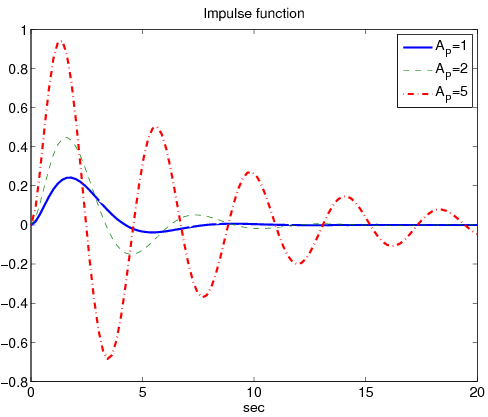
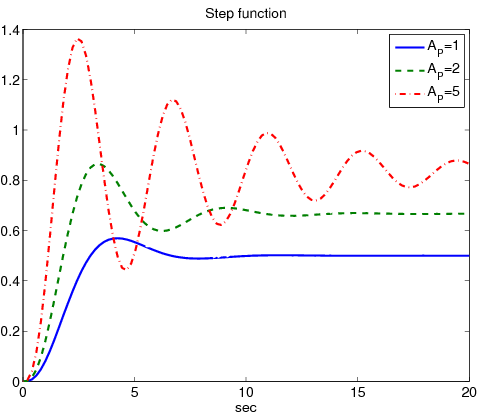
8.5. ábra - Arányos tag hatása

Növekvő erősítések mellett a szabályozási eltérés csökken ugyan, de a válaszfüggvény oszcillációja jelentősen növekszik. Tekintsük ugyanazt a $G = \frac{1}{{(s + 1)}^{3}}$ átviteli függvényű rendszert. Ezúttal PI taggal végeztük a szabályozást. Rögzítsük az arányos tagot $A_{P} = 1$ -re és változtassuk az integráló tag $T_{I}$ időállandóját. $T_{I} = 1; 2; 5$ .

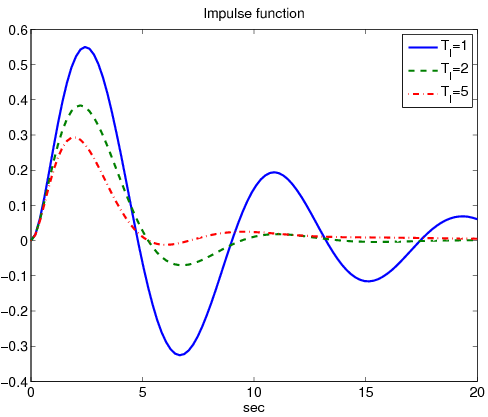
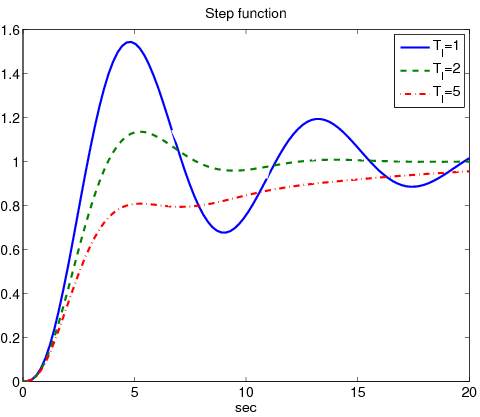
8.6. ábra - Arányos tag hatása

Az integráló hatás eredményeként az állandósult állapotú hiba eltűnik. A válaszfüggvény oszcillációja $T_{I}$ növekedésével jelentősen csökkenthető, viszont ezzel együtt a beállási idő jelentősen növekszik.Tekintsük ugyanazt a $G = \frac{1}{{(s + 1)}^{3}}$ átviteli függvényű rendszert. Ezúttal PID taggal végeztük a szabályozást. Rögzítsük az arányos tagot $A_{P} = 3$ -ra, rögzítsük az integráló tag $T_{I}$ időállandóját $T_{I} = 2$ -re és változtassuk a differenciáló tag $T_{D}$ időállandóját. $T_{D} = 0.1; 0.7; 1.4$ .

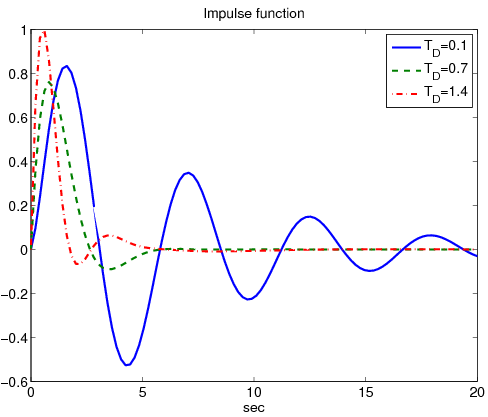
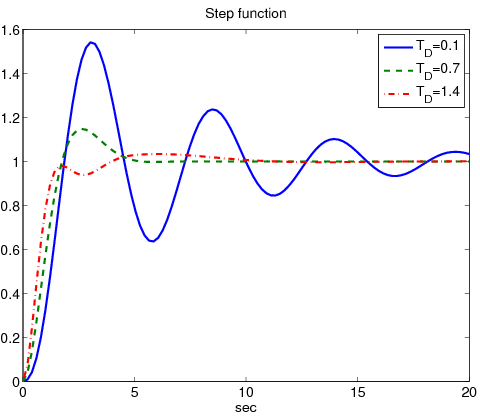
8.7. ábra - Arányos tag hatása

A $T_{D}$ növekedésével a beállási idő jelentősen csökkenthető és a lengések jelentősen csillapíthatók. A differenciáló hatás a szabályozást gyorsítja.

A PID szabályozó egy arányos, egy integráló és egy differenciáló tag párhuzamos kapcsolataként értelmezhető.

$K = A_{P} (1 + \frac{1}{T_{I} s} + T_{D} s)$

(303)

A PID szabályozó egy másik alakja egy arányos, egy PI tag és egy PD tag soros kapcsolataként értelmezhető. Ekkor az egyes komponensek egymással kölcsönhatásban vannak.

$K = A_{P'} (1 + \frac{1}{T_{I'} s}) (1 + T_{D'} s)$

(304)

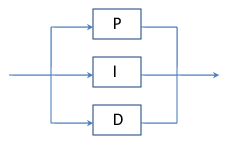
8.8. ábra - PID szabályozó struktúrája

A kétféle felírás között a következő kapcsolat írható fel. A klasszikus alak komponensei:

$A_{P} = A_{P'} \frac{T_{I'} + T_{D'}}{T_{I'}}$

(305)

$T_{I} = T_{I'} + T_{D'}$

(306)

$T_{D} = \frac{T_{I'} T_{D'}}{T_{I'} + T_{D'}}$

(307)

A soros alak komponensei:

$A_{P'} = \frac{A_{P}}{2} (1 \pm \sqrt{1 - 4 T_{d} / T_{i}})$

(308)

$T_{I'} = \frac{T_{I}}{2} (1 \pm \sqrt{1 - 4 T_{d} / T_{i}})$

(309)

$T_{D'} = \frac{T_{I}}{2} (1 \mp \sqrt{1 - 4 T_{d} / T_{i}})$

(310)

Megjegyzés: A soros alak felírásának feltétele, hogy $T_{i} � 4 T_{d}$ . A klasszikus alak általánosabb, mint a soros alak. Gyakran a tervezés (tuningolás) szempontjából a soros alak ledvezőbb. A két felírás P, PI, PD típusú struktúrák esetén ekvivalens. Különböző PID struktúrák választása esetén a két felírás paraméterei különböznek, azokat az összefüggéseknek megfelelően kell számítani.

A PID struktúra egy másik elterjedten használt alakja:

$G = A_{P}' + \frac{A_{I'}}{s} + A_{D'} s$

(311)

Ez az alak a klasszikus $K = A_{P} (1 + \frac{1}{T_{I} s} + T_{D} s)$ PID alakkal ekvivalens.

A két alak közötti kapcsolat:

$A_{P'} = A_{P}$

(312)

$A_{I'} = \frac{A_{P}}{T_{I}}$

(313)

$A_{D'} = A_{P} T_{D}$

(314)

és az időállandók: $T_{I'} = \frac{A_{P'}}{A_{I'}}$ , $T_{D'} = \frac{A_{D'}}{A_{P'}}$ .

A PID szabályozók tervezésekor a következő négy szempontot kell figyelembe venni:

- Zajszűrés.

- Referenciajel súlyozás.

- Beavatkozó telítődése.

- Tuningolás, hangolás.

8.3. PID tervezési módszer

8.3.1. Zajszűrés

A deriválási művelet mindig érzékeny a zajra.

Tekintsük az alábbi példát: Tegyük fel, hogy a jel a következő alakú:

$y (t) = sin t + n (t),$

(315)

ahol a zaj $n (t) = a_{n} sin (ω_{n} t)$ alakú, $ω$ frekvenciájú szinusz jel. A deriválást elvégezve:

$\frac{d y (t)}{d t} = cos t + n (t),$

(316)

ahol $n (t) = a_{n} ω cos (ω_{n} t)$ . Az eredmény azt mutatja, hogy habár az $n$ zaj hatása az $y$ eredeti jelre $1 / a_{n}$ , de a derivált alakban ez az arány $ω / a_{n}$ . A zaj aránya tetszőlegesen nagy lehet, ha $ω$ nagy értékű. Deriválási művelet esetén a magas frekvenciás komponens hatását csökkenteni kell. Ennek érdekében az $A_{P} T_{D} s$ ideális PD tag helyett egy egytárolós komponenssel módosított tagot alkalmazunk:

$D = \frac{A_{P} T_{D} s}{1 + s \frac{T_{D}}{N}}$

(317)

A komponens erősítése a nagyfrekvencia tartományban $N A_{P}$ értékre van korlátozva. Következésképpen megakadályozzuk, hogy az $n$ zaj $y$ jelre való hatása túl nagy értékre növekedjen.

A PID szabályozó általános alakja a következőképpen módosul:

$K (s) = A_{P} (1 + \frac{1}{T_{I} s} + \frac{T_{D} s}{1 + \frac{T_{D}}{N} s})$

(318)

Nagyfrekvenciás tartományban az erősítés értéke:

$lim_{s \to \infty} K (s) = A_{P} (1 + N)$

(319)

$N$ növelésével a sávszélesség növekszik, ami stabilitási szempontból kedvezőtlen. Emiatt további elsőrendű szűrőket alkalmazunk:

$F (s) = \frac{1}{{(1 + s T_{f})}^{n}}$

(320)

ahol $T_{f}$ a filter állandója, ami kölcsönhatásban van a szabályozó időállandóival. $T_{f}$ célszerű megválasztása $T_{f} = T_{D} / N$ .

Egy példa a szűrő lehetséges megválasztására:

$K (s) = A_{P} (1 + \frac{1}{T_{I} s}) (1 + T_{D} s) \frac{1}{{(1 + s \frac{T_{D}}{N})}^{2}}$

(321)

8.3.2. Referenciajel súlyozás

Gyorsan változó alapjel (egységugrás) esetén a szabályozó jelen impulzusszerű gyors válaszok jelenhetnek meg. Ezt a nemkívánatos jelenséget a referenciajel szűrésével oldhatjuk meg. Egy másik megoldási lehetőség a referenciajel megfelelő erősítésével történhet, amit referenciajel súlyozási eljárásnak nevezzük. A klasszikus PID esetén az $u (t)$ jel:

$u (t) = A_{P} (e (t) + \frac{1}{T_{I}} \int_{0}^{t} e (τ) d τ + T_{D} \frac{d e (t)}{d t})$

(322)

A módosított PID szabályozó esetén az $u (t)$ jel:

$u (t) = A_{P} ((b r (t) - y (t)) + \frac{1}{T_{I}} \int_{0}^{t} e (τ) d τ + T_{D} (c \frac{d r (t)}{d t} - \frac{d y (t)}{d t}))$

(323)

Az integrátort közvetlenül a hibajelre alkalmazzuk, viszont az arányos komponenst és a deriválás komponensét a súlyozott referenciajel és a kimenőjel különbségére alkalmazzuk. A bemenőjel összefüggése:

$u (t) = A_{P} ((b r (t) - y (t)) + \frac{1}{T_{I}} \int_{0}^{t} (r (τ) - y (τ)) d τ + T_{D} (c \frac{d r (t)}{d t} - \frac{d y (t)}{d t}))$

(324)

$U (s) = A_{P} (b + \frac{1}{s T_{I}} + c s T_{D}) R (s) - A_{P} (1 + \frac{1}{s T_{I}} + s T_{D}) Y (s)$

(325)

Az összefüggés azt mutatja, hogy a szabályozó struktúra elvileg két-szabadságfokú, melyeket egyrészt a referenciajelre, másrészt a kimenőjelre kell alkalmazni: $U (s) = U_{1} (s) - U_{2} (s)$ , ahol

$U_{1} (s) = A_{P} (b + \frac{1}{s T_{I}} + c s T_{D}) R (s) = C_{r} (s) R (s)$

(326)

$U_{2} (s) = A_{P} (1 + \frac{1}{s T_{I}} + s T_{D}) Y (s) = C_{y} (s) Y (s)$

(327)

A referenciajel értékét egyrészt $b$ erősítéssel, másrészt $c$ erősítéssel módosítjuk.

$U_{1} (s) = A_{P} (b + \frac{1}{s T_{I}} + c s T_{D}) R (s) = C_{r} (s) R (s)$

(328)

$U_{2} (s) = A_{P} (1 + \frac{1}{s T_{I}} + s T_{D}) Y (s) = C_{y} (s) Y (s)$

(329)

Megfelelő megválasztásukkal (hangolásukkal) a nagy tranziensek és túllendülések elkerülhetők.

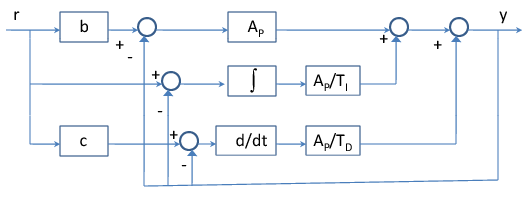
8.9. ábra - Referenciajel súlyozás

Példa 7.3

Példaként tekintsük a $G = \frac{1}{{(s + 1)}^{3}}$ átviteli függvényű rendszert, amit PID kompenzátorral szabályoztunk: $A_{P} = 3; T_{I} = 2; T_{D} = 0.5$ . A példában a súlyokat rendre $b = 0; b = 0.5; b = 1$ és $c = 0$ értékekre választottuk. Az ábra a $b$ erősítés hatását mutatja.

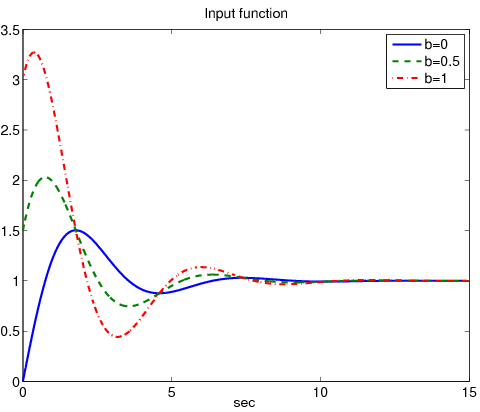
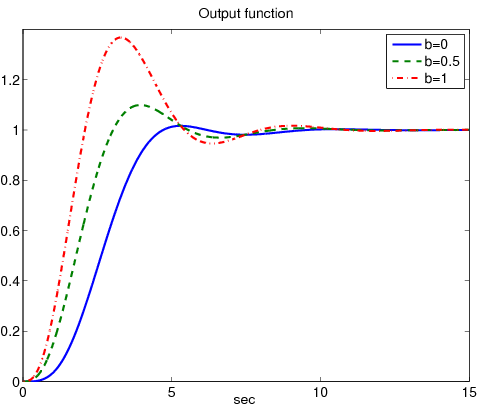
8.10. ábra - Referenciajel súlyozás

A legkisebb túllendülést $b = 0$ esetén értük el, ami azt jelenti, hogy a referenciajelet az arányos komponensbe nem vittük be. Növekvő $b$ mellett a túllendülés növekszik.

8.3.3. Beavatkozó telítődése

Minden beavatkozó elemnek vannak korlátai. Ha a beavatkozó működése során telítésbe megy, akkor a rendszer nyílt hurokként működik, hiszen a beavatkozó nem tud nagyobb értéket generálni, bármit is kíván a szabályozó. Ha a szabályozó integrátort tartalmaz és az aktuátor telítésbe megy, akkor a rendszer kimenetén egyre nagyobb érték jelenik meg, azaz nagy tranziensek keletkeznek. Több módszer van a windup elkerülésére.

- Referenciajel korlátozás: Annak érdekében, hogy elkerüljük az integrátor által okozott növekvő tranziensű jeleket, a referenciajel értékét korlátozzuk. Ez a megoldás konzervatív eredményhez és gyenge minőségi tulajdonságokhoz vezet.

- Sebesség algoritmus: Az algoritmus kiszámítja az irányítójel változásának (sebességének) értékét. Abban az esetben, ha az aktuátor telítésbe ment, az integrátorra adott jelet korlátozzuk, s ezzel megakadályozzuk a tranziensek növekedését. Tulajdonképpen az irányítójel változásának értékét korlátozzuk.

- Beavatkozójel számítása: Ha az aktuátor telítésbe megy, akkor az integrál jel értékét kiszámítjuk és módosítjuk annak érdekében, hogy a kimenetének korlátozását figyelembe vegyük.

Az ábrán látható szabályozó egy további visszacsatolást tartalmaz, ami a beavatkozóra kiadott jel és a számított jel közötti különbségét alkalmazza. A két jel között egy sebességjel korlátozás van.

- Ha a nincs telítés, akkor a hibajel zérus és a visszacsatolásnak nincs hatása. Ha a jel telítésbe megy, akkor a nem zérus hibajelet a visszacsatoláson keresztül a szabályozó figyelembe veszi.

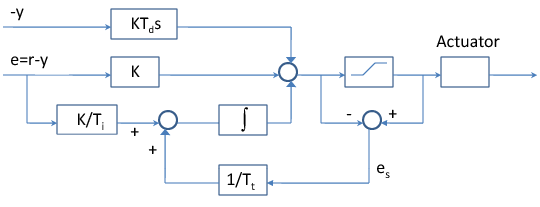
8.11. ábra - Referenciajel súlyozás

Az integrátor bemenete: $\frac{1}{T_{t}} e_{s} + \frac{K}{T_{i}} e,$ ahol $e = r - y$ a követési hiba, $e_{s} = u - v$ a szaturációs blokk bemenete és kimenete közötti eltérés.

Az integrátor bemenete:

$\frac{1}{T_{t}} e_{s} + \frac{K}{T_{i}} e,$

(330)

ahol $e$ a követési hiba. Állandósult állapotban az integrátor bemenetén zérus van, ezért az állandósult állapotú jel értéke $e_{s} = - \frac{K T_{t}}{T_{i}} e$ . Mivel

$e_{s} = u - v,$

(331)

az irányítójel értéke:

$v = u_{l i m} + \frac{K T_{t}}{T_{i}} e$

(332)

ahol $u_{l i m}$ az irányítójel telítési értéke. Ez azt jelenti, hogy a $v$ jel a telítési értékre beáll és azt csak rövid ideig haladja meg. A visszacsatolásban alkalmazott $T_{t}$ időállandó megválasztása az integrátorra való hatás dinamikáját szabja meg.

8.3.4. Tuningolás, hangolás

A szabályozó hangolásának egyik legegyszerűbb módszere a felnyitott hurok átmeneti függvénye alapján dolgozik. PI és PID szabályozóra a hurokerősítés az I hatás kiiktatásával történik. $L$ az úgynevezett lappangási idő (holtidő és késleltetés), míg $T$ a felfutási idő.

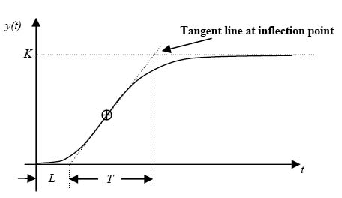
8.12. ábra - Tuningolás, hangolás

Az ábráról leolvasott értékek alapján a hurokerősítés, az integrálási időállandó és a deriválási időállandó beállítható.

	$A_{P}$	$T_{I}$	$T_{D}$
P	$A_{P} � T / L$	$\infty$	$0$
PI	$A_{P} � 0.9 T / L$	$T_{I} > 3.3 L$	$0$
PD	$A_{P} � 1.2 T / L$	$\infty$	$T_{D} < 0.25 L$
PID	$A_{P} � 1.2 T / L$	$T_{I} > 2 L$	$T_{D} < 0.5 L$

- PI szabályozásban a hurokerősítést a P szabályozáshoz képest célszerű lecsökkenteni. Ennek az oka, hogy a PI kompenzáció a $- 20 d B / d e k$ meredekségű szakaszt a kisfrekvenciák irányába tolja el az amplitudó görbét. A stabilitási tartalék növeléséhez emiatt a hurokerősítést célszerű kissé lecsökkenteni.

- PD és PID szabályozások esetén a hurokerősítés valamelyest növelhető a P szabályozáshoz képest. Ennek oka, hogy a PD és PID kompenzáció esetén a $- 20 d B / d e k$ meredekségű szakasz a nagyobb frekvenciák tartományában is folytatódik. A stabilitási tartalék még megfelelő marad, ha a hurokerősítést kissé növeljük.

A szabályozó hangolásának Ziegler-Nichols módszere a szabályozási kör belengetése alapján dolgozik. A módszer lényege, hogy a szabályozást a hurokerősítés növelésével az állandósult lengés állapotába hozzuk. A stabilitás határhelyzetében megmérjük a lengések $T_{k}$ periódusidejét és a beállított $A_{k}$ kritikus hurokerősítést. A meghatározott értékek alapján a hurokerősítés, az integrálási időállandó és a deriválási időállandó beállítható.

	$A_{P}$	$T_{I}$	$T_{D}$
P	$A_{P} � 0.5 A_{k}$	$\infty$	$0$
PI	$A_{P} � 0.45 A_{k}$	$T_{I} > 0.8 T_{k}$	$0$
PID	$A_{P} � 0.6 A_{k}$	$T_{I} > 0.5 T_{k}$	$T_{D} < 0.125 T_{k}$

Vissza		Előre
7. fejezet - Bizonytalanságok modellezése	Főoldal	9. fejezet - Irányítástervezés állapot-visszacsatolással