7. fejezet - Bizonytalanságok modellezése
Vissza		Előre

7. fejezet - Bizonytalanságok modellezése

Tartalom

7.1. Bizonytalanságok modellezése

A dinamikus jelenségek leírására közönséges vagy parciális differenciál-egyenleteket használunk. Az egyenletek alakja és struktúrája, a bennük szereplő paraméterek általában nem ismertek teljesen pontosan vagy ha azok időben változnak, a változásuk általában nem ismert.

Mivel a valódi rendszer modelljének pontos alakja a gyakorlati feladatokban nem ismert, s emiatt helyette annak közelítő, úgynevezett névleges (nominális) modelljét használjuk. A modell és a valós rendszer közötti eltérést több tényező okozza:

Az eltérés oka egyrészt modellezési eljárás következménye (pl. a felharmonikusokat, illetve a magasabb fokszámú együtthatókat elhanyagoljuk),
másrészt a rendszer működése során bekövetkező változások (pl. a normál üzem során a modell paraméterei változnak, az anyag kifáradás során változnak a rendszer paraméterei, sőt akár a struktúrája).
A fizikai rendszerekre külső zavarás hat. Még ha tudjuk is a hatásmechanizmust, a zavarás maga, annak nagysága, előre nem ismert és nem a mi irányításunk alatt van.
Nem mindig tudjuk kiadni azt az irányítójelet, amit szeretnénk.
A mérések sem pontosak (mérési zaj hatása).

Ezen hatások modellezésekor célszerű megkülönböztetni az állandóan jelen levő modell bizonytalanságot a külső zavarástól. Zavarások (disturbances) körébe tartozik tipikusan a rendszerre ható külső zavarás, az irányítójel hibája, a mérési zaj. Az irányítás célja, hogy a zavarások hatását csökkentse a mérnöki szempontból érdekes (esetleg fiktív) kimenő jelekre -- ez egy tipikus performancia követelmény.

Modell bizonytalanság (uncertainty) a modellben meglevő parametrikus bizonytalanságok és a nem modellezett dinamika hatása. Egy speciális eset a qLPV modellek ütemezési változói, amik ismertek a végrehajtás során de nem ismertek tervezéskor: a tervezés számára bizonyos szempontból bizonytalan paraméterként viselkednek. Az irányítás célja stabilitás és performancia garantálása adott nagyságú feltételezett modell bizonytalanság mellett.

Kétféle modell-bizonytalanságot különböztethetünk meg: strukturális és strukturálatlan modell-bizonytalanságot. A struktúrált bizonytalanság modellezésekor a bizonytalansági blokk struktúrálása (például blokk-diagonális) növelheti a modell pontosságát és használhatóságát az irányítás-tervezés szempontjából. Tipikusan struktúrált a grey-box modellezés során kapott modellben előforduló paramétereknek a bizonytalansága: a paraméter értéke pontosan nem ismert, de a bizonytalanság mértéke általában jól becsülhető.

Példa 6.1

Egy gépjármű felfüggesztési modelljének megkonstruálásakor több tényezőt kell figyelembe venni.

a rugózott tömeg változik az utasok tömegének módosulásával,
a felfüggesztés rugó vagy csillapítás karakterisztikája módosul,
kerékabroncs dinamikája változik.

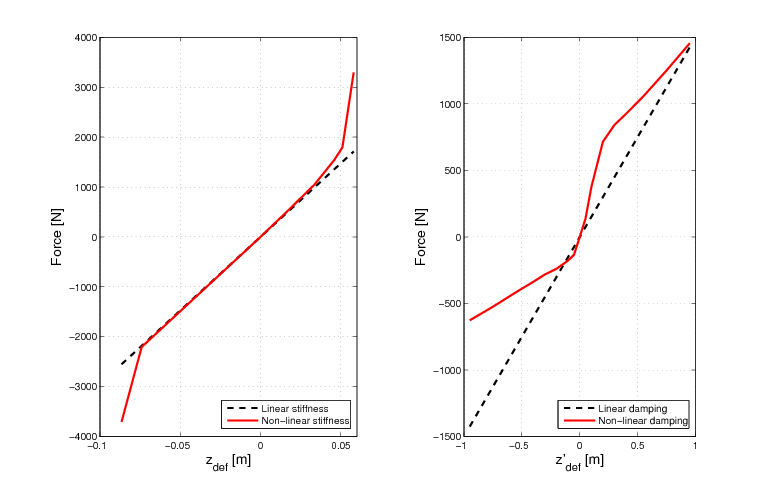
7.1. ábra - Példa egy felfüggesztési rendszer modellezésére

Példa 6.2

A modellezés során a nemlinearitások hatásait célszerű figyelembe venni. A mechanikai rendszerek irányítására alkalmazott lineáris irányítási algoritmusokkal megvalósított szabályozási rendszer tulajdonságait nagymértékben leronthatják a mechanikai rendszerben jelenlevő (nemfolytonos) nemlinearitások. Néhány jellemző példa: szaturáció, surlódás, holtsáv, kotyogás, hiszterézis.

7.2. Bizonytalansági modellek

7.2.1. Nemmodellezett dinamika

A mechanikai rendszerek irányítására alkalmazott lineáris vagy folytonos nemlineáris irányítási algoritmusokkal megvalósított szabályozási rendszer tulajdonságait nagymértékben leronthatják a mechanikai rendszerben jelenlevő (nemfolytonos) nemlinearitások. Tipikus nemlinearitások a szaturáció, surlódás,holtsáv, kotyogás, hiszterézis.

Számos irányítási alkalmazásnál az irányított rendszerben a nemlinearitás pontatlanul ismert vagy akár ismeretlen. Ha a linearizáláson alapuló technika kevésbé alkalmazható, a nemlinearitás hatásának kompenzálásához a szabályozót módosítani kell. Az alkalmazott technika alapján ez lehet robusztus szabályozás, amikor a szabályozót úgy tervezzük meg, hogy pontatlanul ismert nemlinearitás esetén is garantálja a zárt rendszer stabilitását és a szabályozási pontosságot, performanciát, vagy adaptív szabályozás, amikor a szabályozót kibővítjük olyan formában, hogy irányítás közben becsülje meg az ismeretlen nemlinearitást, paramétert.

A modell és a rendszer közötti hiba meghatározására általános megoldás nincs, különböző szerkezetű lehetőségek közül az additív, illetve a multiplikatív hiba struktúra a legismertebb.

A $G (s)$ aktuális rendszer és a $G_{N} (s)$ névleges rendszer közötti eltérést additív hiba struktúrának nevezzük, ha a következő összefüggés teljesül:

$G (s) = G_{N} (s) + Δ_{A} (s),$

(275)

ahol $Δ_{A} (s)$ az additív hiba átviteli függvénye. Az additív hiba ismeretlen.

7.2. ábra - Az additív bizonytalanság struktúrája

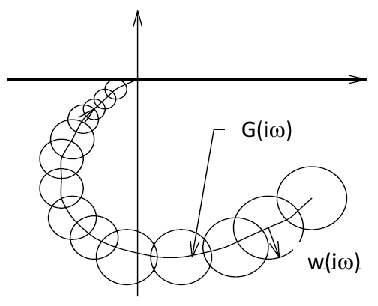
A $Δ_{A} (s)$ ismeretlen méretű additív hiba átviteli függvényt egy ismert korláttal rendelkező $Δ$ bizonytalansággal kifejezhetjük és frekvencia függvényét Nyquist diagramon ábrázolhatjuk:

$Δ_{A} (s) = Δ (s) w (s),$

(276)

ahol $ω$ skalár függvény. Az aktuális $G (i ω)$ rendszer Nyquist diagramja a névleges $G_{N} (i ω)$ rendszer Nyquist diagramjával és a bizonytalanságot leíró $w (i ω)$ függvénnyel illusztrálható.

7.3. ábra - Bizonytalanság a Nyquist diagramon

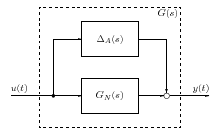
A $G (s)$ aktuális rendszer és a $G_{N} (s)$ névleges rendszer közötti eltérést multiplikatív hiba struktúrájúnak nevezzük, ha a következő összefüggés teljesül:

$G (s) = G_{N} (s) (1 + Δ_{M} (s)),$

ahol $Δ_{M} (s)$ a multiplikatív hiba átviteli függvénye.

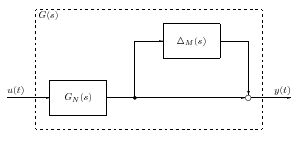
7.4. ábra - A multiplikatív bizonytalanság struktúrája

A $Δ_{M} (s)$ ismeretlen méretű additív hiba átviteli függvényt egy ismert korláttal rendelkező $Δ$ bizonytalansággal kifejezhetjük és frekvencia függvényét Bode diagramon ábrázolhatjuk:

$Δ_{M} (s) = Δ (s) w (s),$

(277)

ahol $ω$ skalár függvény. Az aktuális $G (i ω)$ rendszer Bode diagramja a névleges $G_{N} (i ω)$ rendszer Bode diagramjával és a bizonytalanságot leíró $w (i ω)$ függvénnyel illusztrálható.

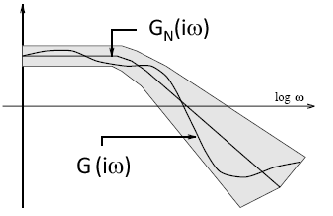
7.5. ábra - Bizonytalanság a Bode diagramon

7.2.2. Parametrikus bizonytalanság

Gyakran a bizonytalanságok egy része a rendszert leíró modell paramétereinek változásával is megfogalmazható.

7.6. ábra - Bizonytalanságok modellezése

Például az $A$ rendszermátrixban lévő $k$ rugóállandó és $b$ csillapítási együtthatók változnak. Ezek a paraméterek a mátrix több elemében is előfordulhatnak.

A bizonytalan rugóállandó paramétere a következőképpen modellezhető:

$k_{s} = {\bar{k}}_{s} (1 + d_{k s} δ_{k s}),$

(278)

ahol ${\bar{k}}_{s}$ a névleges rugóállandó, $d_{k s}$ a névleges értéktől való eltérést mutatja, míg $δ_{k s}$ paraméterről azt tudjuk, hogy a $[- 1 1]$ intervallumba esik. A bizonytalan rugóállandó $M - Δ$ struktúrája a 33 ábrán látható.

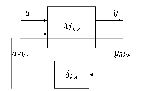
7.7. ábra - A bizonytalan rugóállandó modellezése

$k_{s} = {\bar{k}}_{s} (1 + d_{k_{s}} δ_{k_{s}}) = {\bar{k}}_{s} + {\bar{k}}_{s} d_{k_{s}} δ_{k_{s}}$ A jelek közötti kapcsolatok:

$[\begin{array}{l} y \\ y_{δ k s} \end{array}] = [\begin{array}{l} {\bar{k}}_{s} & 1 \\ d_{k s} {\bar{k}}_{s} & 0 \end{array}] [\begin{array}{l} u \\ u_{δ k s} \end{array}],$

(279)

ahol $u_{δ k s} = δ_{k s} y_{δ k s} = δ_{k s} d_{k s} {\bar{k}}_{s} u$ .Emiatt $y = ({\bar{k}}_{s} + δ_{k s} d_{k s} {\bar{k}}_{s}) u$ . Az ismert komponenseket tartalmazó blokk: $M_{k s} = [\begin{array}{l} {\bar{k}}_{s} & 1 \\ d_{k s} {\bar{k}}_{s} & 0 \end{array}]$

Ha egy bizonytalan paraméter a nevezőben van, akkor a következőképpen járunk el.

$\frac{1}{m_{s}} = \frac{1}{{\bar{m}}_{s} (1 + d_{m s} δ_{m s})}$

(280)

ahol ${\bar{m}}_{s}$ a névleges tömeg, $d_{m s}$ a névleges értéktől való eltérést mutatja, míg $δ_{m s}$ paraméterről azt tudjuk, hogy a $[- 1 1]$ intervallumba esik. A bizonytalan rugóállandó $M - Δ$ struktúrája a 34 ábrán látható.

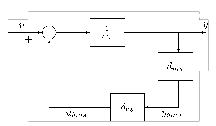
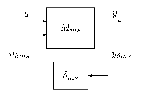
7.8. ábra - A bizonytalan tömeg modellezése

$\frac{1}{m_{s}} = \frac{1}{{\bar{m}}_{s} (1 + d_{m s} δ_{m s})} = \frac{1}{{\bar{m}}_{s}} - \frac{d_{m s}}{{\bar{m}}_{s}} δ_{m s} {(1 + d_{m s} δ_{m s})}^{- 1}$

(281)

A jelek közötti kapcsolatok:

$[\begin{array}{l} y \\ y_{δ m s} \end{array}] = [\begin{array}{l} \frac{1}{{\bar{m}}_{s}} & - \frac{d_{m_{s}}}{{\bar{m}}_{s}} \\ 1 & - d_{m_{s}} \end{array}] [\begin{array}{l} u \\ u_{δ m s} \end{array}],$

(282)

ahol $u_{δ m s} = δ_{m s} y_{δ m s}$ .Mivel $y_{δ m s} = u - d_{m s} u_{δ m s}$ , ezért $u_{δ m s} = {(1 + d_{m s} δ_{m s})}^{- 1} δ_{m s} u$ .

Emiatt $y = \frac{1}{{\bar{m}}_{s}} u - \frac{d_{m_{s}}}{{\bar{m}}_{s}} u_{δ m s} = (\frac{1}{{\bar{m}}_{s}} - \frac{d_{m s}}{{\bar{m}}_{s}} δ_{m s} (1 + d_{m s} δ_{m s})^{- 1}) u$ . Az ismert komponenseket tartalmazó blokk: $M_{m s} = [\begin{array}{l} \frac{1}{{\bar{m}}_{s}} & - \frac{d_{m_{s}}}{{\bar{m}}_{s}} \\ 1 & - d_{m_{s}} \end{array}]$ .

7.9. ábra - struktúra

7.3. M- $Δ$ struktúra

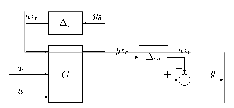
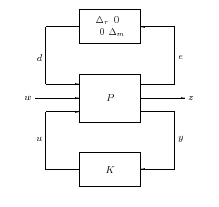
A szabályozott rendszer komponensei az előzőek alapján a modell és a szabályozó, valamint a minőségi specifikációkkal és bizonytalanságokkal kapcsolatos információk. A 35 ábrán látható úgynevezett $P - K - Δ$ struktúrájú modellt használjuk a szabályozó tervezéséhez.

$[\begin{array}{l} e \\ z \\ y \end{array}] = [\begin{array}{l} P_{11} & P_{12} & P_{13} \\ P_{21} & P_{22} & P_{23} \\ P_{31} & P_{32} & P_{33} \end{array}] [\begin{array}{l} d \\ w \\ u \end{array}]$

(283)

Ha figyelembe vesszük a szabályozó hatását, azaz az irányítójel és a mért jel közötti kapcsolatot $u = K y$ , akkor az úgynevezett M- $Δ$ struktúrához jutunk.

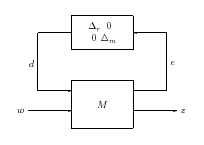
7.10. ábra - struktúra

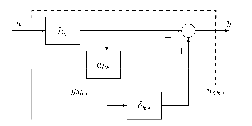
A 36. ábrán látható $M - Δ$ modellt a szabályozott rendszer elemzéséhez használjuk.

$[\begin{array}{l} e \\ z \end{array}] = [\begin{array}{l} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array}] [\begin{array}{l} d \\ w \end{array}]$

(284)

Vissza		Előre
6. fejezet - Minőségi tulajdonságok elemzése	Főoldal	8. fejezet - PID szabályozások tervezése