6. fejezet - Minőségi tulajdonságok elemzése
Vissza		Előre

6. fejezet - Minőségi tulajdonságok elemzése

Tartalom

6.1. Minőségi jellemzők

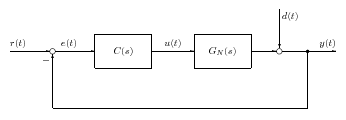
A minőségi kritériumok vizsgálata mindig a szabályozott rendszer (zárt kör) vizsgálatával történik: A zárt rendszer átviteli függvénye:

$G_{C} = \frac{G_{E}}{1 + G_{H}}$

(250)

ahol $G_{H}$ a hurokátviteli függvény és $G_{E}$ az előrevezető ág eredő átviteli függvénye. Az alábbiakban az időtartományi és frekvencia tartományi jellemzőket soroljuk fel.

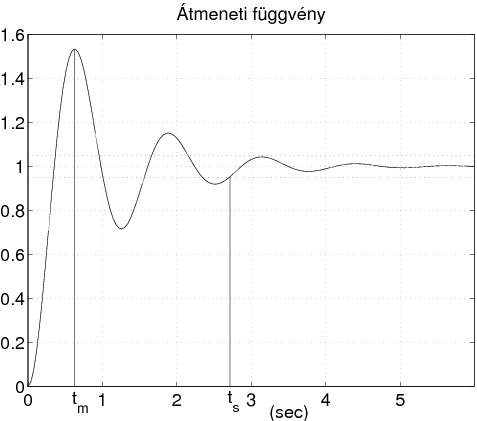
6.1. ábra - Időtartományi jellemzők

6.1.1. Időtartományi jellemzők

A rendszer állandósult állapotban felvett értékét beállási értéknek nevezzük, amit $y_{s s}$ -sel jelölünk.
A szabályozási idő ( $t_{s}$ ) annak időtartama, amely eltelte után a rendszer kimenete a beállási értéktől $5 %$ -nál nagyobb mértékben nem tér el.
A szabályozási eltérés a megkívánt érték és az állandósult állapotbeli érték különbsége: $y_{s s} - y_{d}$ ,
túllendülési idő ( $t_{m}$ ): a kimeneti jel maximális értékének időpontja,
túllendülés mértéke ( $p$ ): százalékban kifejezett viszonyszám, ami a maximális és beállási érték közötti különbség beállási értékhez való viszonyát fejezi ki: $p = \frac{y_{max} - y_{s s}}{y_{s s}} \cdot 100 %$

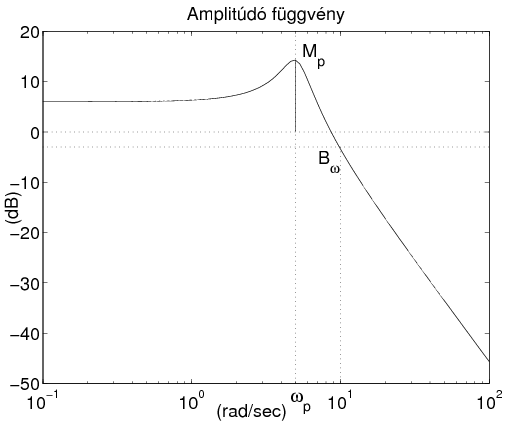
6.1.2. Frekvencia tartományi jellemzők

rezonancia csúcs $M_{p}$ : az amplitúdó görbe maximális értéke,
rezonancia frekvencia $ω_{p}$ : a rezonancia csúcshoz tartozó frekvencia érték,

6.2. ábra - Időtartományi jellemzők

A sávszélesség fogalmát a kiegészítő érzékenységi függvény segítségével a következőképp adhatjuk meg. A rendszer sávszélessége az a $ω \leq ω_{B}$ frekvencia tartomány, amelyben a $| T (i ω) |$ kiegészítő érzékenységi függvény Bode diagramja $- 3 d B$ -re csökken.

6.2. Érzékenységfüggvény

Vizsgáljuk a zárt rendszer kimenetét különböző bemenetek esetén:

$Y (s) |_{D \equiv 0} = \frac{G_{H} (s)}{1 + G_{H} (s)} R (s) = T (s) R (s)$

(251)

$Y (s) |_{R \equiv 0} = \frac{1}{1 + G_{H} (s)} D (s) = S (s) D (s)$

(252)

ahol $G_{H} (s) = G (s) C (s)$ .

6.3. ábra - Időtartományi jellemzők

Bevezetjük a szabályozási körben értelmezett $S$ érzékenységi függvényt és a $T$ kiegészítő érzékenységi függvényt:

$T (s) = \frac{G_{H} (s)}{1 + G_{H} (s)}$

(253)

$S (s) = \frac{1}{1 + G_{H} (s)}$

(254)

Az érzékenységi függvény azt mutatja meg, hogy a zavaró jellemző hogyan befolyásolja a zárt rendszer kimenetét.

$S (s) = \frac{1}{1 + G_{H} (s)}$

(255)

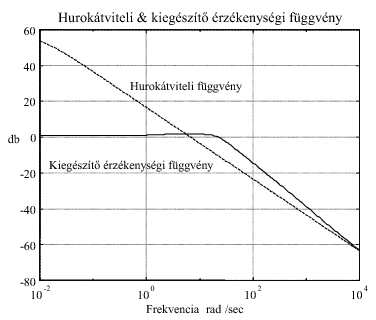
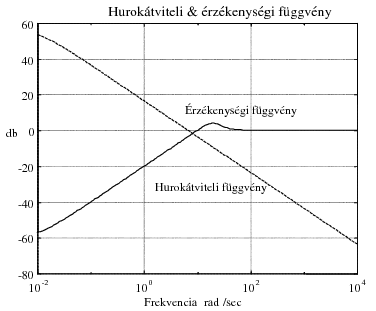
Az $S (i ω)$ érzékenységi függvény közelítő ábrázolását Bode-diagramon a felnyitott hurok $G_{H} (i ω)$ frekvenciafüggvénye alapján a következőképp végezhetjük el.

Az érzékenységi függvény definíció szerint:

$| S (i ω) | = | \frac{1}{1 + G_{H} (i ω)} | \forall ω .$

(256)

Kis és nagy körfrekvenciákra a következő közelítést használhatjuk:

$| S (i ω) | \approx {\begin{array}{l} \frac{1}{| G_{H} (i ω) |} & h a | G_{H} (i ω) | ? 1 a z a z h a ω = ω_{c} \\ 1 & h a G_{H} (i ω) | = 1 a z a z h a ω ? ω_{c} \end{array}$

(257)

A kiegészítő érzékenységi függvény a referencia jel és a kimenő jel közötti átviteli függvény.

$T (s) = \frac{G_{H} (s)}{1 + G_{H} (s)} .$

(258)

A $T (i ω)$ kiegészítő érzékenységi függvény közelítő ábrázolását Bode-diagramon a felnyitott hurok $G_{H} (i ω)$ frekvenciafüggvénye alapján a következőképp végezhetjük el. A kiegészítő érzékenység függvény definíció szerint:

$| T (i ω) | = | \frac{G_{H} (i ω)}{1 + G_{H} (i ω)} | \forall ω,$

(259)

Kis és nagy körfrekvenciákra a következő közelítést használhatjuk:

$| T (i ω) | \approx {\begin{array}{l} 1 & h a | G_{H} (i ω) | ? 1 \\ | G_{H} (i ω) | & h a | G_{H} (i ω) | = 1 \end{array}$

(260)

Az érzékenységi és kiegészítő érzékenységi függvények közötti összefüggés az alábbi:

$S (s) + T (s) = 1.$

(261)

6.4. ábra - Időtartományi jellemzők

6.3. Aszimptotikus jelkövetés

Követő szabályozásoknál a kimenőjelnek a referencia jeltől való eltérését követési hibának nevezzük:

$e (t) = y (t) - r (t) .$

(262)

Vizsgáljuk meg, hogy adott $r (t)$ referencia jelre aszimptotikusan mekkora lesz az eltérés, azaz a követési hiba. A követési hiba jel és a referencia jel Laplace-transzformáltjai közötti kapcsolatot az $S (s)$ érzékenységi függvény írja le. Alkalmazva a határérték tételeket:

$lim_{t \to \infty} e (t) = lim_{s \to 0} s E (s) = lim_{s \to 0} s S (s) R (s) .$

(263)

Vizsgálhatjuk a tipikus referencia jelek, mint egységugrás vagy egység sebesség ugrás jelek aszimptikus követését.

6.3.1. 1. eset: Egységugrás bemenetre adott válaszfüggvény

Vizsgáljuk meg a válaszfüggvényt $r (t) = 1 (t)$ , $R (s) = 1 / s$ bemenetre. Ekkor

$lim_{t \to \infty} e (t) = lim_{s \to 0} s \frac{1}{1 + G_{H} (s)} \frac{1}{s} = lim_{s \to 0} \frac{1}{1 + G_{H} (s)} .$

(264)

Ha $G_{H} (s)$ arányos jellegű, azaz ha $G_{H} (s) = G_{H 0} (s)$ , akkor

$lim_{s \to 0} \frac{1}{1 + G_{H 0} (s)} = \frac{1}{1 + K},$

(265)

ahol $K$ a hurokerősítési tényező. A követési hiba értéke függ a hurokerősítési tényező értékétől.

Ha $G_{H} (s)$ integráló jellegű, azaz ha $G_{H} (s) = G_{H 0} (s) / s$ ,

$G_{H 0} (s) |_{s = 0} < \infty$ alakú, akkor

$lim_{s \to 0} s \frac{1}{1 + G_{H 0} (s) / s} \frac{1}{s} = lim_{s \to 0} \frac{s}{s + G_{H 0} (s)} = 0,$

(266)

tehát a követési hiba aszimptotikusan zérus.

Ha $G_{H} (s)$ 2 típusú (kétszeres integrátort tartalmaz), azaz ha $G_{H} (s) = G_{H 0} (s) / s^{2}$ , $G_{H 0} (s) |_{s = 0} < \infty$ alakú, akkor

$lim_{s \to 0} s \frac{1}{1 + G_{H 0} (s) / s^{2}} \frac{1}{s} = lim_{s \to 0} \frac{s^{2}}{s^{2} + G_{H 0} (s)} = 0,$

(267)

tehát a követési hiba aszimptotikusan zérus.

6.3.2. 2. eset: Egységsebesség bemenetre adott válaszfüggvény

Vizsgáljuk meg a válaszfüggvényt $r (t) = t (t)$ , $R (s) = 1 / s^{2}$ bemenetre. Ekkor

$lim_{t \to \infty} e (t) = lim_{s \to 0} s \cdot \frac{1}{1 + G_{H} (s)} \cdot \frac{1}{s^{2}} = lim_{s \to 0} \frac{1}{s} \cdot \frac{1}{1 + G_{H} (s)} .$

(268)

Ha $G_{H} (s)$ arányos jellegű, azaz ha $G_{H} (s) = G_{H 0} (s)$ ,

akkor

$lim_{s \to 0} \frac{1}{s} \cdot \frac{1}{1 + G_{H 0} (s)} = \infty,$

(269)

azaz a kimenet nem korlátos.

Ha $G_{H} (s)$ integráló jellegű, azaz ha $G_{H} (s) = G_{H 0} (s) / s$ ,

$G_{H 0} (s) |_{s = 0} < \infty$ alakú, akkor

$lim_{s \to 0} \frac{1}{s} \cdot \frac{1}{1 + G_{H 0} (s) / s} = lim_{s \to 0} \frac{1}{s} \cdot \frac{s}{s + G_{H 0} (s)} = \frac{1}{1 + K},$

(270)

tehát a követési hiba aszimptotikusan nem zérus értékhez tart.

6.4. Zavarkompenzálás

Az aszimptotikus zavarkompenzálást az aszimptotikus alap- vagy referencia jelkövetéshez hasonlóan vizsgálhatjuk. Tipikus zavaró jelek, mint egységugrás, egység sebességugrás jelek, a zavaró jel hatását a kimenő jelben zérus referencia jel feltételezése mellett vizsgáljuk. Ehhez felírjuk a kimenő jel és a zavaró jel Laplace - transzformáltjai közötti összefüggéseket és alkalmazzuk a határérték tételeket.

A kimenő és a zavaró jel közötti átviteli függvény az $S (s)$ érzkenységi függvény. Ennek alapján a kimenőjel Laplace - transzformáltja

$Y (s) |_{R \equiv 0} = S (s) D (s) = \frac{1}{1 + G_{H} (s)} D (s) .$

(271)

Alkalmazva a határérték tételt:

$lim_{t \to \infty} y (t) |_{r \equiv 0} = lim_{s \to 0} s \frac{1}{1 + G_{H} (s)} D (s) .$

(272)

Legyen például $d (t) = 1 (t)$ , $D (s) = 1 / s$ .

6.4.1. 1. eset: Arányos rendszer vizsgálata

Vizsgáljuk meg az arányos rendszer viselkedését. A hurokátviteli függvény alakja $G_{H} (s) = G_{H 0} (s)$ . Ekkor

$lim_{s \to 0} s \frac{1}{1 + G_{H 0} (s)} \frac{1}{s} = \frac{1}{1 + K}$

(273)

ahol $K$ a hurokerősítés tényező. Tehát a zavaró jel hatása megjelenik a kimeneten.

6.4.2. 2. eset: Integráló rendszer vizsgálata

Legyen például $d (t) = 1 (t)$ , $D (s) = 1 / s$ és tegyük fel, hogy a hurokátviteli függvény integráló alakú, azaz $G_{H} (s) = G_{H 0} (s) / s$ . Ekkor

$lim_{s \to 0} s \frac{s}{s + G_{H 0} (s)} \frac{1}{s} = 0$

(274)

tehát a zavaró jel hatását a rendszer aszimptotikusan teljesen elnyomja, kompenzálja. Megjegyezzük, hogy a 2-típusú integráló tulajdonságú rendszer is kompenzálja a hibajelet.

Vissza		Előre
5. fejezet - Stabilitásvizsgálat	Főoldal	7. fejezet - Bizonytalanságok modellezése