10. fejezet - Lineáris kvadratikus szabályozótervezés
Vissza		Előre

10. fejezet - Lineáris kvadratikus szabályozótervezés

Tartalom

Az irányítástervezés során gyakran szeretnénk egy irányítás paramétereit úgy megválasztani, hogy valamilyen előre meghatározott minőségi tulajdonság (performancia előírás) teljesüljön. Az optimalizálási feladatokban olyan paraméterek választása a cél ami maximalizál vagy minimalizál egy adott kritérium-függvényt. Ebben a fejezetben megmutatjuk, hogyan lehet megválasztani azokat a paramétereket amik optimalizálnak egy adott kvadratikus specifikációt és amelyek a lehető legkisebb költséggel maximalizálják a megkívánt performanciát.

Tekintsük az alábbi kritérium-függvényt

$min_{u (\cdot)} \int_{0}^{T} L (x, u) d t + V (x (T))$

(378)

a következő dinamikus feltételek mellett

$\dot{x} = f (x, u), x = ℝ^{n},$

(379)

ahol az $x (0)$ kezdeti feltétel adott és $u \in ℝ^{m}$ . Ez egy korlátozások melletti optimalizálási feladat, ahol egy olyan megengedett $(x (t), u (t))$ trajektóriát keresünk ami minimalizálja a perem pontokban korlátozott $J$ költségfüggvényt

$J = \int_{0}^{T} L (x, u) d t + V (x (T)), ψ (x (T)) = 0.$

(380)

Az $L (x, u)$ tag az integrál költség míg $V (x (T))$ a végső, terminális költség. A $ψ : ℝ^{n} \mapsto ℝ^{q}$ függvény a terminális korlátozások egy halmazát határozza meg. A korlátozások menlleti optimalizálási feladatoknál szokásos módon egy

$H = L + λ^{T} f = L + \sum_{i = 1}^{n} λ_{i} f_{i},$

(381)

Hamilton függvényt definiálunk, ahol bevezetjük az időfüggő $λ$ társváltozókat.

Tétel 9.1 (Maximum elv) Ha $(x_{*}, u_{*})$ optimális akkor létezik $λ_{*} (t) \in ℝ^{n}$ és $ν_{*} \in ℝ^{q}$ úgy, hogy

${\dot{x}}_{i} = \frac{\partial H}{\partial λ_{i}} - {\dot{λ}}_{i} = \frac{\partial H}{\partial x_{i}}$

(382)

adott $ψ (x (T)) = 0$ , $x (0)$ peremfeltételekkel, ahol $λ (T) = \frac{\partial V}{\partial x} (x (T)) + ν^{T} \frac{\partial ψ}{\partial x}$ és

$H (x_{*} (t), u_{*} (t), λ_{*} (t)) \leq H (x_{*} (t), u, λ_{*} (t))$

(383)

minden $u \in Ω$ esetén.

A maximum elv nemlineáris dinamikák esetén is alkalmazható valamint abban az esetben is ha a szabályozó bemenet egy $Ω$ halmaz által van korlátozva. Korlátozások néklül, $Ω = ℝ^{m}$ , és differenciálható $H$ esetén az optimalitás egy szükséges feltétele, hogy

$\frac{\partial H}{\partial u} = 0.$

(384)

Ha $u_{*} = argmin H (x, u, λ)$ létezik, akkor felhasználható mint optimális szabályozó jel.

A bizonyítás elve a következő: a Lagrange féle multiplikátorok módszerét alkalmazva a költségfüggvény alakja

$\tilde{J} (x, u, λ, ν) = J (x, u) + \int_{0}^{T} - λ^{T} (t) (\dot{x} (t) - f (x, u)) d t + ν^{T} ψ (x (T)) =$

$= \int_{0}^{T} (L (x, u) - λ^{T} (t) (\dot{x} (t) - f (x, u)) d t + V (x (T)) + ν^{T} ψ (x (T)),$

(385)

ami a Hamilton függvény felhasználásával

$\tilde{J} (x, u, λ, ν) = \int_{0}^{T} (H (x, u) - λ^{T} (t) \dot{x}) d t + V (x (T)) + ν^{T} ψ (x (T))$

(386)

alakba írható. Az optimális megoldás környezetében linearizálva, azaz $x (t) = x_{*} (t) + δ x (t)$ , $u (t) = u_{*} (t) + δ u (t)$ , $λ (t) = λ_{*} (t) + δ λ (t)$ és $ν = ν_{*} + δ ν$ esetén, kapjuk, hogy

$δ \tilde{J} = \tilde{J} (x_{*} + δ x, u_{*} + δ u, λ_{*} + δ λ, ν_{*} + δ ν) - \tilde{J} (x_{*}, u_{*}, λ_{*}, ν_{*}) \approx$

$\approx \int_{0}^{T} (\frac{\partial H}{\partial x} δ x + \frac{\partial H}{\partial u} δ u - λ^{T} δ \dot{x} + (\frac{\partial H}{\partial λ} - {\dot{x}}^{T}) δ λ) d t +$

$+ \frac{\partial V}{\partial x} δ x (T) + ν^{T} \frac{\partial ψ}{\partial x} δ x (T) + δ ν^{T} ψ (x (T), u (T)),$

(387)

ahol a deriváltak az optimális megoldás mentén értendők.

Parciális integrálással elimináljuk a $δ \dot{x}$ -tól való függést

$- \int_{0}^{T} λ^{T} δ \dot{x} d t = - λ^{T} (T) δ x (T) + λ^{T} (0) δ x (0) + \int_{0}^{T} λ^{T} δ x d t .$

(388)

Mivel $x (0) = x_{0}$ adott, az első tag eltűnik és kapjuk, hogy

$δ \tilde{J} \approx \int_{0}^{T} [(\frac{\partial H}{\partial x} + λ^{T}) δ x + \frac{\partial H}{\partial u} δ u + (\frac{\partial H}{\partial λ} - {\dot{x}}^{T}) δ λ] d t +$

$+ (\frac{\partial V}{\partial x} + ν^{T} \frac{\partial ψ}{\partial x} - λ^{T} (T)) δ x (T) + δ ν^{T} ψ (x (T), u (T)) .$

(389)

Az optimalitáshoz megköveteljük,hogy $δ \tilde{J} = 0$ minden $δ x, δ u, δ λ$ és $δ ν$ esetén, így megkapva a tétel feltételeit.

A továbbiakban a lineáris kvadratikus (LQ) optimális szabályozási feladatot tekintjük: a dinamikus rendszer lineáris időinvariáns és a költségfüggvény kvadratikus, azaz

$\dot{x} = A x + B u, x (0) = x_{0},$

(390)

$J = \int_{0}^{T} (x^{T} Q x + u^{T} R u) d t + x^{T} (T) P_{f} x (T),$

(391)

ahol $Q \geq 0$ az állapothibát bünteti, $R > 0$ a szabályozó bemenetet és $P_{f} > 0$ a végső állapotot súlyozza.

A $Q$ és $R$ tervezési paraméterek meghatározzák az állapotok lineáris kombinációinak és az input energia fontosságát (súlyát):

- A funkcionálban szereplő $x^{T} Q x$ tag a rendszer minőségi jellemzőit súlyozza, a rendszer teljes energiáját bünteti egy $Q \geq 0$ súlymátrix segítségével

- A funkcionálban szereplő $u^{T} R u$ tag a rendszerbe betáplált szabályozó energiát súlyozza, $R > 0$ mátrix segítségével.

Gyakran a feladatot úgy módosítjuk, hogy egy adott $(x_{d}, u_{d})$ pálya követése legyen az elérendő cél, a költségfüggvényt ehhez a $(x - x_{d})$ és $(u - u_{d})$ tagokkal írjuk át. Van, amikor célszerű a végső $x (T) = x_{f}$ pontot is előírni, ilyenkor egy általánosabb $ψ_{i} (x (T)) = 0, i = 1, \dots, q$ megszorítást használhatunk. Amikor minden komponensre megszorítás van, azaz $q = n$ , a vonatkozó specifikáció alakja $ψ_{i} (x (T)) = x_{i} (T) - x_{i, f}$ lesz. Ilyenkor $V (x (T))$ elhagyható, mivel értéke rögzített.

Fontos eset, amikor $T = \infty$ és $V = 0$ , azaz a végtelen horizontú LQ feladat.

10.1. Lineáris kvadratikus regulátor

10.1.1. Véges horizontú LQR

A véges horizontú lineáris kvadratikus regulátor(LQR) feladat alakja

$\dot{x} = A x + B u, x (0) = x_{0}$

(392)

az alábbi költségfüggvénnyel:

$\tilde{J} = \frac{1}{2} \int_{0}^{T} (x^{T} Q x + u^{T} R u) d t + \frac{1}{2} x^{T} (T) P_{f} x (T),$

(393)

ahol $Q \geq 0, R > 0, P_{f} \geq 0$ .

A feladathoz tartozó $H$ Hamilton függvény

$H = \frac{1}{2} x^{T} Q x + \frac{1}{2} u^{T} R u + λ^{T} (A x + B u) .$

(394)

A maximum elv alkalmazásával az alábbi szükséges feltételeket kapjuk:

$\dot{x} = {(\frac{\partial H}{\partial λ})}^{T} = A x + B u, x (0) = x_{0},$

(395)

$- \dot{λ} = {(\frac{\partial H}{\partial x})}^{T} = Q x + A^{T} λ, λ (T) = P_{f} x (T)$

(396)

$0 = \frac{\partial H}{\partial u} = R u + λ^{T} B .$

(397)

Innen az optimális irányítás alakja

$u = - R^{- 1} B^{T} λ .$

(398)

Az optimális irányítás előállításához egy peremértékfeladatot kell megoldani $x (0)$ és $λ (T)$ peremfeltételekkel, ami általában egy nehéz feladat.

A társváltozót a $λ (t) = P (t) x (t)$ alakban keressük, így

$\dot{λ} = \dot{P} x + P \dot{x} = \dot{P} x + P (A x - B R^{- 1} B^{T} P) x,$

(399)

azaz

$- \dot{P} = P A + A^{T} P - P B R^{- 1} B^{T} P + Q, P (T) = P_{f},$

(400)

amit Riccati differenciál egyenletnek nevezünk.

10.1.2. Végtelen horizontú LQR feladat

A $T = \infty$ esetben a $P_{f} = 0)$ feltételből adódik a költségfüggvény alakja:

$J = \int_{0}^{\infty} (x^{T} Q x + u^{T} R u) d t .$

(401)

Mivel $λ$ végső értékére nincs megszorítás, a $P (t)$ helyett állandó $P$ mátrixot véve kapjuk a

$P A + A^{T} P - P B R^{- 1} B^{T} P + Q = 0$

(402)

algebrai Riccati egyenletet, és a hozzá tartozó

$u = - R^{- 1} B^{T} P x$

(403)

szabályozót.

Míg $R > 0$ feltételnek mindég teljesülni kell, tipikusan $Q \geq 0$ . A $Q = C_{z}^{T} C_{z}$ alakot véve a költségfüggvény

$J = \int_{0}^{\infty} ∥ C_{z} x ∥^{2} + u^{T} R u d t .$

(404)

Az optimális irányítás létezéséhez az $(A, C_{z})$ párnak detektálhatónak kell lenni.

Tétel 9.2 Tekintsük a

$\dot{x} = A x + B u, x (0) = x_{0},$

(405)

lineáris rendszert a

$J = \int_{0}^{\infty} x^{T} Q x + u^{T} R u d t, Q = C_{z}^{T} C_{z}, R > 0.$

(406)

költségfüggvénnyel, ahol az $(A, B)$ pár stabilizálható és az $(A, C_{z})$ megfigyelhető.

Az optimális szabályozó alakja

$u = - R^{- 1} B^{T} P x,$

(407)

ahol $P > 0$ a

$P A + A^{T} P - P B R^{- 1} B^{T} P + Q = 0.$

(408)

algebrai Riccati egyenlet stabilizáló megoldása. A minimális költség $J^{*} = x^{T} (0) P x (0)$ .

Bizonyítás 9.1 Ha $A$ stabil a

$A^{T} P + P A + Q = 0$

(409)

Lyapunov egyenletnek egyértelmű megoldása van: $P = \int_{0}^{\infty} e^{A^{T} t} Q e^{A t} d t$ , minden $Q = Q^{T}$ esetén. Ha $Q > 0$ vagy $Q \geq 0$ és $(A, Q)$ megfigyelhető, akkor $P > 0$ .

Ha $A$ stabil akkor az $u = 0$ -hoz tartozó megoldás $x (t) = e^{A t} x (0) \to 0$ . Ha $(A, B)$ stabilizálható, akkor van $F$ stabilizáló visszacsatolás melyre $e^{(A + B F) t} x_{0} \to 0$ . E pálya mentén

$J_{min} \leq J (x_{0}, 0) = \int_{0}^{\infty} x {(t)}^{*} Q x (t) d t < \infty$

(410)

$(J_{min} < J (x_{0}, F x) = \int_{0}^{\infty} x {(t)}^{*} (Q + F^{T} R F) x (t) d t < \infty),$

(411)

vagyis az optimális költség véges..

Egy t $P = P^{T}$ -vel minden $u$ -ra, melyre $x \to 0$ tekintsük a $V (x) = x^{T} P x$ kvadratikus funkcionált. Mivel

$\int_{0}^{\infty} \frac{d (x^{T} P x)}{d t} = \int_{0}^{\infty} {\dot{x}}^{T} P x + x^{T} P \dot{x} d t = - x {(0)}^{T} P x (0),$

(412)

minden stabil pálya mentén a

$\int_{0}^{\infty} x^{T} (A^{T} P + P A) x + 2 x^{T} P B u d t = - x {(0)}^{T} P x (0)$

(413)

költség invariáns a visszacsatolásra. Teljes négyzetté való kiegészítéssel kapjuk, hogy

$u^{T} R u + 2 x^{T} P B u = {(u - u_{o})}^{T} R (u - u_{o}) - x^{T} P B R^{- 1} B^{T} P x,$

(414)

ahol $u_{o} = - R^{- 1} B^{T} P x$ választással $P$ -re előírható, hogy kielégítse az

$A^{T} P + P A + Q - P B R^{- 1} B^{T} P = 0$

(415)

algebrai Riccati egyenletet. Ekkor az optimális irányítás $u_{o}$ és az optimális költség $J (x_{0}, u_{o}) = x_{0}^{T} P x_{0}$ .

A megfigyelhetőség szerepének illusztrálására tekintsük a stabil $A_{c l} = A - B R^{- 1} B^{*} P$ zárt kört. Ekkor algebrai Riccati egyenletből

$A_{c l}^{T} P + P A_{c l} + Q + P B R^{- 1} B^{T} P = 0,$

(416)

vagyis a zárt kör pályája mentén

$x^{T} P x = - x_{0}^{T} P x_{0} - \int_{0}^{t} x^{T} (τ) P B R^{- 1} B P x (τ) d τ - \int_{0}^{t} x^{T} (τ) Q x (τ) d τ .$

(417)

Így $0 \leq x^{T} P x \leq x_{0}^{T} P x_{0}$ . Ha $P$ nemszinguláris lenne, létezne egy $ξ_{0} \neq 0$ kezdeti érték, melyre $Q ξ (t) = 0 (C_{z} ξ (t) = 0)$ , ami ellent mond $z = C_{z} x$ megfigyelhetőségének. .

Másrészt ha $P > 0$ és $(λ, x_{0})$ egy sajátvektor, sajátérték párja $A_{c l}$ -nek, akkor

$2 Re (λ) x_{0}^{T} P x_{0} = - x_{0}^{T} P B R^{- 1} B^{T} P x_{0} - x_{0}^{T} Q x_{0},$

(418)

azaz $Re (λ) \leq 0$ . Feltéve, hogy $λ = j ω$ , következik, hogy $B^{T} P x_{0} = 0$ és $Q x_{0} = 0$ , vagyis $A x_{0} = 0$ .Ebből $Q e^{A t} x_{0} = 0$ adódna, ami ellentmond $z$ megfigyelhetőségének. Tehát a pozitív definit megoldás stabilizáló a megfigyelhetőségi feltétel mellett.

Az egyértelműség kimutatásához tekintsünk $P_{1}$ és $P_{2}$ megoldásokat úgy, hogy $A_{1} = A - B R^{- 1} B^{*} P_{1}$ és $A_{2} = A - B R^{- 1} B^{*} P_{2}$ stabilis.

Következik, hogy

$(P_{1} - P_{2}) A_{1} + A_{2}^{*} (P_{1} - P_{2}) = 0.$

(419)

A $ℒ (X) = A X + X B$ Sylvester operátor akkor és csak akkor szinguláris ha $A$ és $- B$ közös sajátértékekkel rendelkezik. Mivel $A_{1}$ és $A_{2}$ stabil, ezért az egyedüli megoldás $P_{1} - P_{2} = 0$ .

10.1.3. Általános végtelen horizontú LQR feladat

Általános $z = C_{z} x + D_{z u} u$ performancia jelet tekintve a költségfüggvény a

$J = \int_{0}^{\infty} x^{T} Q x + 2 x^{T} S u + u^{T} R u d t$

(420)

alakot veszi fel.

Ennek a feladathoz ugyancsak az algebrai Riccati egyenlet stabilizáló $P \geq 0$ megoldása

$A^{T} P + P A + Q - (P B + S) R^{- 1} (B^{T} P + S^{T}) = 0$

(421)

szolgáltatja az optimális szabályozót:

$u_{o} = - R^{- 1} (B^{T} P + S^{T}) x$

(422)

a $J (x_{0}, u_{o}) = x_{0}^{T} P x_{0}$ optimális költséggel.

Példa 9.1

Tervezzen LQ optimális szabályozást a

$G (s) = \frac{2}{s - 1}$

(423)

átviteli függvénnyel leírt rendszerre, ha az irányíthatósági állapottér reprezentációjában mérjük a rendszer állapotait a következő költségfüggvény minimalizálásával:

$J = \frac{1}{2} \int_{0}^{\infty} (y^{2} + r u^{2}) d t,$

(424)

ahol az $r = 3.2$ súly adott. Tervezze meg a $q$ súly értékét! Tervezze meg az optimális állapotvisszacsatolást!

A feladat megoldása:

Az állapottér reprezentáció irányíthatósági alakban:

$\dot{x} = - x + u$

(425)

$y = 2 x$

(426)

A feladatot visszavezetjük az optimalizálás standard alakjára az $y = 2 x$ összefüggés felhasználásával:

$J = \int_{o}^{\infty} (4 x^{2} + 3.2 u^{2}) d t$

(427)

azaz az állapotokat súlyozó mátrix $q = 4$ .

A Riccati egyenlet megoldása:

$A^{T} P + P A - P b r^{- 1} b^{T} P + Q = 0, P > 0$

(428)

ahol $A = - 1$ , $b = 1$ , $Q = 4$ , $r = 3.2$ . A megoldás: $P = 1.6$ .

Az állapot-visszacsatolt erősítő:

$k^{T} = r^{- 1} b^{T} P = 0.5,$

(429)

azaz az optimális irányítójel: $u = - 0.5 x + v$ .

Az LQ megoldás robusztussága

- A zárt rendszer mindig stabil lesz. Az LQ tervezés a szabályozott rendszer pólusait automatikusan a bal oldali félsíkba helyezi.

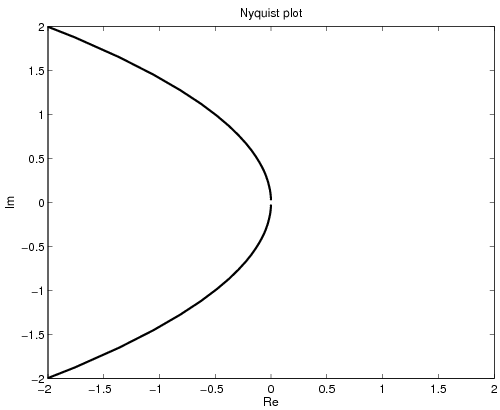
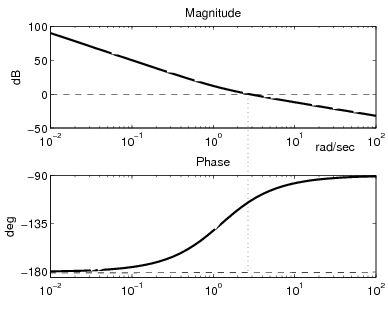
- Az LQ optimális megoldás a végtelen erősítési tartalékot és a $60^{\circ}$ -os fázistartalékot biztosít.

$G M = \infty$

(430)

$P M � 60^{\circ}$

(431)

Példa 9.2

Tervezzünk optimális állapot visszacsatolást LQ módszerrel a következő rendszerhez:

$\dot{x} = [\begin{array}{l} 0 & 1 \\ 0 & 0 \end{array}] x + [\begin{array}{l} 0 \\ 1 \end{array}] u$

(432)

A tervezési paraméterek: $Q = [\begin{array}{l} 1 & 0 \\ 0 & 0 \end{array}]$ és $r = 0.1$ .

A feladat megoldása:

(a) Riccati egyenlet megoldása:

$A^{T} P + P A - P b r^{- 1} b^{T} P + Q = 0.$

(433)

A CARE megoldása: $P = [\begin{array}{l} 0.7953 & 0.3162 \\ 0.3162 & 0.2515 \end{array}]$ .

(b) $k$ számítása:

$k = r^{- 1} b^{T} P .$

(434)

Az optimális állapotvisszacsatolás:

$k^{T} = [\begin{array}{l} 3.1623 & 2.5149 \end{array}]$ és

az optimális irányítójel: $u = - 3.1623 x_{1} - 2.5149 x_{2}$ .

10.1. ábra - A tervezés frekvencia tartományban

$G M = \infty$

(435)

$P M = {65.5}^{\circ} (2.76 r a d / s e c)$

(436)

10.2. Pólusok és zérusok

A szabályozott rendszer pólusai a $d e t (s I - A + b K) = 0$ karakterisztikus egyenlet megoldásai. A Hamilton mátrix tartalmazza az optimális irányítás megoldásait, így sajátértékei az optimális megoldás pólusait is megadják.

$H = [\begin{array}{l} A & - \frac{1}{r} b b^{T} \\ - Q & - A^{T} \end{array}]$

(437)

Felhasználva a $det [\begin{array}{l} A & B \\ C & D \end{array}] = det (A) det (D - C A^{- 1} B)$ összefüggést, felírhatjuk a Hamilton mátrixra vonatkozó karakterisztikus egyenletet:

$det [\begin{array}{l} s I - A & \frac{1}{r} b b^{T} \\ Q & s I + A^{T} \end{array}]$

(438)

$= det (s I - A) det (s I + A^{T} - \frac{1}{r} Q (s I - A)^{- 1} b b^{T}) = 0$

(439)

A karakterisztikus egyenlet (a levezetést mellőzve) a következő alakra hozható:

$det (s I - A) det (- s I - A^{T}) \cdot$

(440)

$\cdot det [\begin{array}{l} r + b^{T} {(- s I - A^{T})}^{- 1} Q {(s I - A)}^{- 1} b \end{array}] = 0$

(441)

A Hamilton rendszer pólusai tartalmazzák a zárt rendszer pólusait, valamint a pólusok ellenkező előjelű értékeit egyaránt.

Vizsgáljuk meg, hogy a szabályozó tervezésben alkalmazott súlyozás hogyan hat a szabályozott rendszer pólusaira. Válasszuk meg az irányítójelre adott súlyt a következőképpen:

$r = ρ r_{0},$

ahol $r_{0}$ rögzített és $ρ$ értékét változtatjuk.

Válasszuk az irányítójelre adott súlyt nagy értékre: $ρ \to \infty$ .

Az irányítási feladatot minél kisebb irányítójellel kívánjuk megoldani.

A karakterisztikus egyenlet a következő alakhoz tart:

$det (s I - A) det (- s I - A^{T}) det (ρ r_{0}) = 0$

(442)

A szabályozott rendszer pólusai megközelítik az eredeti rendszer stabil pólusait, valamint az eredeti rendszer nemstabil pólusainak a képzetes tengelyre való tükörképét.

Válasszuk az irányítójelre adott súlyt kis értékre: $ρ \to 0$ .

Az irányítási feladatban nincs előírás az irányítójel nagyságára nézve.

A karakterisztikus egyenlet a következő alakhoz tart:

$det (s I - A) det (- s I - A^{T}) \cdot$

(443)

$\cdot det [\begin{array}{l} b^{T} {(- s I - A^{T})}^{- 1} Q {(s I - A)}^{- 1} b \end{array}] = 0$

(444)

Átalakítva:

$det [\begin{array}{l} b^{T} a d j (- s I - A^{T}) Q a d j (s I - A) b \end{array}] = 0$

(445)

A szabályozott rendszer pólusai megközelítik az eredeti rendszer bal félsíkra eső zérusait vagy az eredeti rendszer jobb oldali zérusainak a képzetes tengelyre való tükörképét, illetve végtelenül nagy negatív értéket vesznek fel.

Példa 9.3

Tervezzünk optimális állapot visszacsatolást LQ módszerrel a következő rendszerhez:

$\dot{x} = [\begin{array}{l} 1 & - 1 \\ 3 & - 4 \end{array}] x + [\begin{array}{l} 1 \\ 0 \end{array}] u$

(446)

$y = [\begin{array}{l} 1 & 0 \end{array}] x$

(447)

A rendszer pólusai $p = [\begin{array}{l} 0.302; & - 3.302 \end{array}]$ , zérusai $z = - 4$ . A tervezési paraméterek: $Q = [\begin{array}{l} 1 & 0 \\ 0 & 0 \end{array}]$ és $r = ρ$ változó. Megjegyzés: Az első állapotváltozót tekintjük kimenetnek, a többi állaptváltozóra $0$ súlyt alkalmazunk a tervezésben.

A feladat megoldása:

- $ρ \to \infty$ választással a Hamilton mátrix sajátértékei: $p_{H} = [\begin{array}{l} \pm 3.302; & \pm 0.302 \end{array}]$ , míg a tervezett szabályozott rendszer pólusai: $p_{z} = [\begin{array}{l} - 3.302; & - 0.302 \end{array}]$ ,

- $ρ \to 0$ választással a Hamilton mátrix sajátértékei: $p_{H} = [\begin{array}{l} \pm 9.99 \cdot 10^{4}; & \pm 4 \end{array}]$ , míg a tervezett szabályozott rendszer pólusai: $p_{z} = [\begin{array}{l} - 9.99 \cdot 10^{4}; & - 4 \end{array}]$ ,

Példa 9.4

Tervezzünk optimális állapot visszacsatolást LQ módszerrel a következő nem minimálfázisú rendszerhez:

$\dot{x} = [\begin{array}{l} 1 & - 1 \\ 3 & 4 \end{array}] x + [\begin{array}{l} 1 \\ 0 \end{array}] u$

(448)

$y = [\begin{array}{l} 1 & 0 \end{array}] x$

(449)

A rendszer pólusai $p = [\begin{array}{l} 2.500 \pm 0.866 \end{array}]$ , zérusai $z = 4$ (pozitív). A tervezési paraméterek: $Q = [\begin{array}{l} 1 & 0 \\ 0 & 0 \end{array}]$ és $r = ρ$ változó. Megjegyzés: Az első állapotváltozót tekintjük kimenetnek, a többi állaptváltozóra $0$ súlyt alkalmazunk a tervezésben.

A feladat megoldása:

- $ρ \to \infty$ választással a Hamilton mátrix sajátértékei:

$p_{H} = [\begin{array}{l} 2.500 \pm 0.866 i; & - 2.500 \pm 0.866 i \end{array}]$ ,

míg a tervezett szabályozott rendszer pólusai: $p_{z} = [\begin{array}{l} - 2.500 \pm 0.866 i \end{array}]$ ,

- $ρ \to 0$ választással a Hamilton mátrix sajátértékei:

$p_{H} = [\begin{array}{l} \pm 9.99 \cdot 10^{4}; & \pm 4 \end{array}]$ ,

míg a tervezett szabályozott rendszer pólusai: $p_{z} = [\begin{array}{l} - 9.99 \cdot 10^{4}; & - 4 \end{array}]$ ,

A módszer alkalmazásának feltétele:

- Az állapotvektor elemei mértek legyenek.

- Az állapottér reprezentáció teljesítse az irányíthatósági feltételt.

A módszer előnyei:

- A szabályozott rendszer stabilis.

- A szabályozással szemben megfogalmazott minőségi követelmények a $Q$ és $r$ súlyok megválasztásával beépíthetők a szabályozás tervezésbe.

A módszer hátrányai:

- A különböző minőségi követelmények közötti ellentmondások és konfliktusok miatt a súlyok megválasztása bonyolult feladat. A súlyok tervezése során törekedni kell a minőségi követelmények közötti összhang megteremtésére. Emiatt az elért minőségi tulajdonságokat utólagosan ellenőrizni kell.

- A Riccati egyenlet megoldása numerikusan nehéz feladat.

Vissza		Előre
9. fejezet - Irányítástervezés állapot-visszacsatolással	Főoldal	11. fejezet - Megfigyelőtervezés és szeparációs elv