11. fejezet - Megfigyelőtervezés és szeparációs elv
Vissza		Előre

11. fejezet - Megfigyelőtervezés és szeparációs elv

Tartalom

11.1. Tervezési feladat
11.2. Állapotmegfigyelő tervezése
11.3. Dinamikus állapotvisszacsatolás

11.1. Tervezési feladat

Az eddigiekben feltételeztük, hogy a rendszer állapotát mérni tudjuk. Az állapot ismerete szükséges az állapot-visszacsatolt szabályzó tervezéséhez. Ha nem ismerjük az $x (t)$ állapotvektort, akkor egy olyan $\hat{x} (t)$ (azonos dimenziójú) mennyiséget képzünk, mely aszimptotikusan közelíti az eredeti állapotot, tehát

$\hat{x} (t) \to x (t)$

(450)

miközben $t \to \infty$ .

Ha ismert $(A, b, c^{T})$ akkor

$\dot{\hat{x}} (t) = A \hat{x} (t) + b u (t)$

(451)

$\hat{y} (t) = c^{T} \hat{x} (t)$

(452)

$\hat{x} (t) |_{(t = 0)} = {\hat{x}}_{0}$

(453)

ahol az állapot-becslés hibája $e (t) = x (t) - \hat{x} (t)$ minden $t \in [0, \infty)$ . Az állapotbecslés hibájának időbeli változását annak differenciál egyenlete adja meg:

$\dot{e} (t) = \dot{x} (t) - \dot{\hat{x}} (t)$

(454)

Levezethető, hogy $e (t) |_{(t = 0)} = {\hat{e}}_{0}$ kezdeti értékkel egy homogén lineáris differenciál-egyenlet:

$\dot{e} (t) = A e (t) .$

(455)

Vizsgáljuk az egyenlet megoldását:

$s . e (s) - e_{0} = A e (s)$

(456)

$e (s) = {(s I - A)}^{- 1} e_{0} \Rightarrow ℒ^{- 1} {{(s I - A)}^{- 1} e_{0}}$

(457)

$e (s) = e^{A t} e_{0}$

(458)

Ha $e_{0}$ nem zérus, akkor az állapothiba lecseng, feltéve hogy az $A$ mátrix stabil azaz, $R e (λ_{i}) < 0$ , $i = 1.. n$ . és így $e (t) \to 0$ miközben $t \to \infty$ .

Megjegyzés: Ha $A$ instabil, illetve ha a tervező befolyásolni akarja az

állapothiba lecsengését, akkor visszacsatolást kell alkalmazni.

Az állapotegyenlet:

$\dot{\hat{x}} (t) = A \hat{x} (t) + b u (t) + ℓ {y (t) - \hat{y} (t)}$

(459)

ahol $ℓ = {\begin{array}{l} [ℓ_{n - 1} & ℓ_{n - 2} & ℓ_{0}] \end{array}}^{T}$ , $ℓ$ -nek $n$ sora van. Ekkor az állapothiba

$\dot{e} (t) = \dot{x} (t) - \dot{\hat{x}} (t)$

(460)

$= (A - ℓ c^{T}) e (t),$

(461)

ha adott $e (t) |_{(t = 0)} = {\hat{e}}_{0}$ akkor $e^{(A - ℓ c^{T}) t} e_{0}$ . Így az $A$ minden elemét módosítani tudjuk, és minden sajátértékét tetszőlegesen meg tudjuk választani.

11.2. Állapotmegfigyelő tervezése

A megfigyelhetőségi és az irányíthatósági alakok között a dualitás teremt kapcsolatot. A két állapottér ekvivalens állapotterek:

$A_{o} = A_{c}^{T},$

(462)

$b_{o} = c_{c},$

(463)

$c_{o}^{T} = b_{c}^{T},$

(464)

A megfigyelő tervezés adott $(A_{o}, b_{o}, c_{o}^{T})$ esetén, ismert ${\bar{a}}_{0}, {\bar{a}}_{1},, {\bar{a}}_{n - 1},$ mellett $ℓ_{i} = {\bar{a}}_{i} - a_{i}$ ( $i = 0,, (n - 1)$ ) megválasztásával történik.

A módosult állapotmátrix alakja a következő:

${\bar{A}}_{o} = A_{o} - ℓ c^{T} =$

$[\begin{array}{l} - a_{n - 1} & 1 & 0 & 0 \\ - a_{n - 2} & 0 & 1 & 0 \\ ⋮ \\ - a_{0} & 0 & 0 & 0 \end{array}] - [\begin{array}{l} ℓ_{n - 1} \\ ℓ_{n - 2} \\ ⋮ \\ ℓ_{0} \end{array}] [\begin{array}{l} 1 & 0 & 0 \end{array}]$

(465)

A megfigyelő $ℓ$ erősítésére vonatkozó összefüggést dualitással kapjuk, ahol elvégezzük az alábbi megfeleltetéseket:

$A \to A^{T},$

(466)

$b \to c^{T},$

(467)

$k \to ℓ,$

(468)

amivel ellenőrizhető, hogy $C (A, b) \to O {(A^{T}, c)}^{T}$ .

$ℓ^{T} = k^{T} = {(α - a)}^{T} τ {(a)}^{- 1} O {(A^{T}, c)}^{T}$

(469)

A dualitási elvből levezetett és a megfigyelő tervezésére vonatkozó Bass Gura formula az alábbi:

$ℓ = O {(A^{T}, c)}^{- 1} τ {(a)}^{- T} (α - a)$

(470)

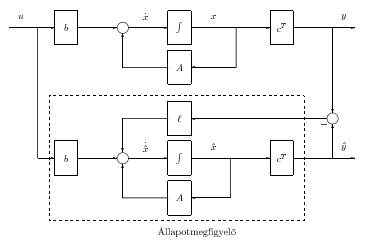
ahol $α$ a megfigyelő karakterisztikus egyenletének együtthatóiból képzett vektor. Az állapotmegfigyelővel ellátott körben a megfigyelő, mint dinamikus rendszer

$\dot{\hat{x}} (t) = A_{o} \hat{x} (t) + b_{o} u (t)$

(471)

$\hat{y} (t) = c_{o}^{T} \hat{x} (t)$

(472)

11.1. ábra - Állapotmegfigyelő

Példa 10.1

Tervezzen megfigyelőt az alábbi megfigyelhetőségi állapottér reprezentációban ismert rendszerre:

$A_{o} = [\begin{array}{l} - 4 & 1 \\ - 3 & 0 \end{array}] b_{o} = [\begin{array}{l} 1 \\ 2 \end{array}] c_{o}^{T} = [\begin{array}{l} 1 & 0 \end{array}]$

(473)

A tervezést pólusallokációs módszerrel végezze el $p_{1} = - 1$ és $p_{2} = - 2$ pólusokkal. Írja fel a megfigyelő állapotegyenletét! Adja meg a megfigyelő állapotegyenletének $ℓ$ vektorát!

A feladat megoldása:

Az eredeti rendszer karakterisztikus polinomja:

$det (s I - A_{o}) = s^{2} + 4 s + 3$

$a_{1} = 4; a_{0} = 3$

A megfigyelt rendszer karakterisztikus polinomja:

$\begin{array}{l} (s - λ_{1}) (s - λ_{2}) & = & (s + 1) (s + 2) = s^{2} + 3 s + 2 \end{array}$

${\bar{a}}_{1} = 3; {\bar{a}}_{0} = 2$

Az eredeti és tervezett karakterisztikus polinom együtthatók alapján az megfigyelő erősítései a következők: $ℓ_{1} = - 1; ℓ_{0} = - 1$

$ℓ = [\begin{array}{l} - 1 \\ - 1 \end{array}]$

(474)

Példa 10.2

Tervezzen megfigyelőt $p_{1} = - 1$ és $p_{2} = - 3$ pólusokkal az alábbi állapottér reprezentációban ismert rendszerre:

$A_{c} = [\begin{array}{l} 4 & - 3 \\ 1 & 0 \end{array}] b_{c} = [\begin{array}{l} 1 \\ 0 \end{array}] c_{c}^{T} = [\begin{array}{l} 1 & 2 \end{array}]$

(475)

A megfigyelő tervezését az állapotvisszacsatolásnál megismert elvek alapján végezzük el. Az irányíthatósági alakból a megfigyelhetőségi alak közvetlenül megkapható:

$A_{o} = [\begin{array}{l} 4 & 1 \\ - 3 & 0 \end{array}] b_{o} = [\begin{array}{l} 1 \\ 2 \end{array}] c_{o}^{T} = [\begin{array}{l} 1 & 0 \end{array}]$

(476)

A megfigyelő tervezését az $A_{o}$ és $b_{o}$ mátrixok alapján végezzük el pólusallokációs módszerrel. Vegyük észre, hogy ez a rendszer nem irányíthatósági alakú, ezért a transzformációs mátrixot meg kell határozni.

A rendszer karakterisztikus polinomja:

$det (s I - A_{c}) = s^{2} - 4 s + 3$

(477)

$a_{1} = - 4; a_{0} = 3$

A szabályozott rendszer karakterisztikus polinomja:

$\begin{array}{l} (s - λ_{1}) (s - λ_{2}) & = & (s + 1) (s + 3) = s^{2} + 4 s + 3 \end{array}$

(478)

${\bar{a}}_{1} = 4; {\bar{a}}_{0} = 3$

Az eredeti és tervezett karakterisztikus polinomok együtthatói alapján az erősítések a következők: $k_{o}^{T} = [\begin{array}{l} 8 & 0 \end{array}]$ . Az erősítő a megfigyelhetőségi alakra alkalmazható, ezért át kell transzformálni az eredeti állapottérbe.

A transzformációs mátrix számítása:

$T^{- 1} = C τ = [\begin{array}{l} b_{o} & A_{o} b_{o} \end{array}] [\begin{array}{l} 1 & {\bar{a}}_{1} \\ 0 & 1 \end{array}]$

$= [\begin{array}{l} 1 & 6 \\ 2 & - 3 \end{array}] [\begin{array}{l} 1 & - 4 \\ 0 & 1 \end{array}] = [\begin{array}{l} 1 & 2 \\ 2 & - 11 \end{array}]$

(479)

$T = \frac{a d j (T^{- 1})}{d e t (T^{- 1})} = \frac{[\begin{array}{l} - 11 & - 2 \\ - 2 & 1 \end{array}]}{- 15} = [\begin{array}{l} 0.7333 & 0.1333 \\ 0.1333 & - 0.0667 \end{array}]$

(480)

Az erősítő számítása:

$k_{c}^{T} = k_{o}^{T} T = [\begin{array}{l} 5.8667 & 1.0667 \end{array}]$

(481)

A dualitás elvét használva a megfigyelő értéke:

$ℓ_{c} = k_{c} = [\begin{array}{l} 5.8667 \\ 1.0667 \end{array}]$

(482)

11.3. Dinamikus állapotvisszacsatolás

A szabályozást a becsült állapotvisszacsatolással képezve kimenőjel visszacsatolásról beszélünk.

$u (t) = - k^{T} \hat{x} (t) + r (t)$

(483)

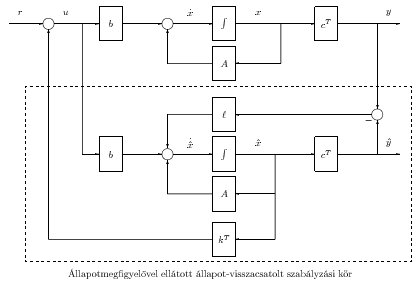
Kombinált állapot visszacsatolást és megfigyelőt tartalmazó szabályozó struktúra:

Rendszer

$\dot{x} = A x + b u$

(484)

$y = c^{T} x$

(485)

Megfigyelő

$\dot{\hat{x}} = A \hat{x} + b u + l (y - \hat{y})$

(486)

$\hat{y} = c^{T} \hat{x}$

(487)

Irányítás:

$u = - k^{T} \hat{x} + r$

(488)

A becsült állapot dinamikája:

$\dot{\hat{x}} = A \hat{x} + b u + l (y - \hat{y})$

$= A \hat{x} - b k^{T} \hat{x} + b r + l y - l c^{T} \hat{x}$

$= (A - b k^{T} - l c^{T}) \hat{x} + l y + b r$

(489)

A becslés hibája: $e = x - \hat{x}$ ,

továbbá a hiba dinamikája: $\dot{e} = \dot{x} - \dot{\hat{x}}$ .

Részletesen kifejtve:

$\dot{e} = (A x + b u) - [A \hat{x} - b k^{T} \hat{x} - l c^{T} \hat{x} + l c^{T} x]$

$= (A - l c^{T}) x - (A - l c^{T}) \hat{x}$

$= (A - l c^{T}) e$

(490)

11.2. ábra - Állapotmegfigyelő

Kombináljuk ezt az egyenletet a rendszer állapot egyenletével:

$[\begin{array}{l} \dot{x} \\ \dot{e} \end{array}] = [\begin{array}{l} A & 0 \\ 0 & A - l c^{T} \end{array}] [\begin{array}{l} x \\ e \end{array}] + [\begin{array}{l} b \\ 0 \end{array}] u$

(491)

Figyelembe véve a control inputot:

$u = - k^{T} \hat{x} + r$

(492)

az állapotegyenlet:

$\dot{x} = A x - b k^{T} \hat{x} + b r$

$= A x - b k^{T} x + b k^{T} e + b r$

$= (A - b k^{T}) x + b k^{T} e + b r$

(493)

Kombinált rendszer:

$[\begin{array}{l} \dot{x} \\ \dot{e} \end{array}] = [\begin{array}{l} A - b k^{T} & b k^{T} \\ 0 & A - l c^{T} \end{array}] [\begin{array}{l} x \\ e \end{array}] + [\begin{array}{l} b \\ 0 \end{array}] r$

(494)

A zárt rendszer karakterisztikus polinomja:

$det [\begin{array}{l} s I - A + b k^{T} & - b k^{T} \\ 0 & s I - A + l c^{T} \end{array}] =$

$= det (s I - A + b k^{T}) det (s I - A + l c^{T})$

(495)

A szabályozott rendszer karakterisztikus egyenlete a következő két egyenlettel (és azok megoldásával) azonos:

$det (s I - A + b k^{T}) = 0$

(496)

$det (s I - A + l c^{T}) = 0$

(497)

Következtetés:

A szabályozott rendszer pólusai az LQ rendszer karakterisztikus egyenletének és a megfigyelő rendszer karakterisztikus egyenletének megoldásai.

Tétel 10.1 A megfigyelővel és állapot-visszacsatolt szabályzóval ellátott zárt rendszer karakterisztikus polinomja

$d e t (s I - A_{z}) = \underset{á l l a p o t - v i s s z a c s a t o l á s}{\underset{�}{d e t (s I - A + b k^{T})}} \cdot \underset{m e g f i g y e l ő}{\underset{�}{d e t (s I - A + ℓ c^{T})}}$

(498)

Következmény 10.1 Az állapot-visszacsatolt szabályzó és a megfigyelő függetlenül tervezhető. Az optimális állapot visszacsatolás és a megfigyelő tervezés egymástól függetlenül végrehajtható. A szabályozott rendszer struktúrájában az egyes tervezési eredményeket kombináljuk.

- $k^{T}$ megválasztásával az állapotvisszacsatolást tervezzük és a pólusokat az alábbi értékekbe helyezzük:

$R e_{} [λ_{i} (A - b k^{T})] < 0, i = 1, 2, \dots, n$

(499)

- $l$ megfigyelő tervezésével a pólusokat a következő helyekre tesszük:

$R e_{} [λ_{i} (A - l c^{T})] < 0, i = 1, 2, \dots, n$

(500)

Vissza		Előre
10. fejezet - Lineáris kvadratikus szabályozótervezés	Főoldal	12. fejezet - H2 irányítások tervezése