12. fejezet - H2 irányítások tervezése
Vissza		Előre

12. fejezet - H2 irányítások tervezése

Tartalom

12.1. Speciális irányítási feladatok
12.2. Teljes információs (FI) szabályozó
12.3. H2 optimális DF és OE szabályozók
12.4. Egyszerűsített OF optimális irányítás

Az előzőekben bemutattuk az LQR probléma megoldását statikus állapot visszacsatolással. A gyakorlatban azonban nem mindig áll rendelkezésre a teljes állapot. Ezért módosítani szükséges a probléma kitűzését arra az esetre, ha csak dinamikus kimenet-visszacsatolás megengedett. A klasszikus sztochasztikus irányításelmélet keretei között ez vezet el a lineáris kvadratikus Gauss eloszlást feltételező (LQG) feladathoz.

Tekintsük az alábbi performancia funkcionált

$J (u) = \int_{0}^{\infty} (x^{T} (t) Q x (t) + u^{T} (t) R u (t)) d t$

(501)

ahol $Q$ és $R$ adott szimmetrikus pozitív definit mátrixok valamint $u (t)$ az irányító bemenet. Az állapotegyenlet valamint az $y (t)$ megfigyelési egyenlet a következő:

$\dot{x} = A x + B u + w,$

(502)

$y = C x + D u + v$

(503)

ahol $w$ és $v$ független fehér zaj folyamatok. A cél egy $K$ irányítás tervezése az $y$ megfigyelések alapján, ahol az $u$ irányító jel minimalizálja a $J (u)$ kritériumfüggvény várható értékét.

A továbbiakban ennek a feladatnak a determinisztikus változatával foglalkozunk, az úgynevezett optimális $ℋ_{2}$ irányítástervezéssel, aminek kiindulópontja az 53 ábrán látható általános rendszerstruktúra.A $ℋ_{2}$ feladat során egy olyan $K$ irányítás tervezése a cél, ami egyrészt stabilizálja a zárt hurkot valamint minimalizálja a $∥ ℱ_{l} (P, K) ∥_{2}$ rendszer normát.

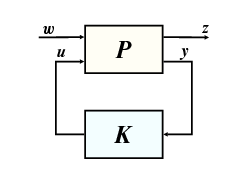
12.1. ábra - Általános rendszerstruktúra

Az alábbiakban egy megoldást adunk a $ℋ_{2}$ kimenet-visszacsatolásos feladatra. A levezetés először a kimenet-visszacsatolásos feladatot több specifikus, egyszerüsített feladatra vezeti vissza amelyek valamilyen módon mind az úgynevezett teljes információjú $ℋ_{2}$ probléma variációi. Ez utóbbi feladat megoldását egy klasszikus optimális irányítási problémára vezetjük vissza.

12.1. Speciális irányítási feladatok

A $ℋ_{2}$ feladat megoldása az egyszerüsített kimenet-visszacsatolásos -- output feedback (OF) -- probléma megoldásán alapszik, amihez az alábbi általános rendszerstruktúra tartozik:

$P (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ C_{1} & 0 & D_{12} \\ C_{2} & D_{21} & 0 \end{array}]$

(504)

ahol

$D_{12}^{T} (\begin{array}{l} C_{1} & D_{12} \end{array}) = (\begin{array}{l} 0 & I \end{array}),$

(505)

$(\begin{array}{l} B_{1} \\ D_{21} \end{array}) D_{21}^{T} = (\begin{array}{l} 0 \\ I \end{array}) .$

(506)

A $C$ és $D$ rendszermátrixokra kirótt speciális feltételek, (505) és (506), az egyszerüsített feladat ortogonalitási feltételei. Meg lehet mutatni, hogy a általános kimenet-visszacsatolásos problémát mindig vissza lehet vezetni erre a specifikus formára. Az egyszerűsített probléma lehetővé teszi számunkra, hogy világosabban mutassunk rá az optimális $ℋ_{2}$ irányítás alapvető tulajdonságaira.

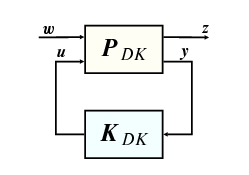
Az egyszerűsített probléma három másik specifikus feladattal van összefüggésben: teljes információs (full information) (FI), előrecsatolt zavarás (disturbance feedforward) (DF), és kimenet becslés (output estimation) (OE). Ebben a részben megfogalmazzuk ezeket a feladatokat és kimutatjuk egymáshoz való viszonyukat. Minden esetben feltételezzük az ortogonalitási feltételek teljesülését.

A teljes információs (FI) feladathoz tartozó általános rendszerstruktúra alakja

$P_{F I} (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ C_{1} & D_{11} & D_{12} \\ I & 0 & 0 \\ 0 & I & 0 \end{array}],$

(507)

vagyis az irányítás mind a teljes $x$ állapotot mind a $w$ zavaró bemenetet felhasználhatja.

A előrecsatolt zavarás (DF) feladathoz tartozó általános rendszerstruktúra alakja

$P_{D F} (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ C_{1} & D_{11} & D_{12} \\ C_{2} & I & 0 \end{array}],$

(508)

vagyis a $w$ zavaró bemenet közvetlenül mérhető.

A kimenet becslési (OE) feladathoz tartozó általános rendszerstruktúra alakja

$P_{O E} (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ C_{1} & D_{11} & I \\ C_{2} & D_{21} & 0 \end{array}],$

(509)

ami egy állapotmegfigyelővel hozható összeffüggésbe.

Az alábbi alakból

$P_{D F}^{T} = [\begin{array}{l} A^{T} & C_{1}^{T} & C_{2}^{T} \\ B_{1}^{T} & D_{11}^{T} & I \\ B_{2}^{T} & D_{12}^{T} & 0 \end{array}]$

(510)

nyilvánvaló, hogy az OE és DF feladatok egymás algebrai duálisai. Mivel

${(ℱ_{ℓ} (P, K))}^{T} = ℱ_{ℓ} (P^{T}, K^{T}),$

(511)

$K$ akkor és csak akkor stabilizálja $P$ -t ha $K^{T}$ stabilizálja $P^{T}$ -t. Mivel a DF és OE problémák duálisak, a DF megoldását fel tudjuk használni az OE szabályozó előállítására.

Az FI és DF feladatok abban az értelemben azonosak, hogy ha mindketten ugyan azzal a szabályozóval stabilizálhatók, akkor a zárt körök megegyeznek. Mivel a FI és a DF feladatok egyenértékűek az FI megoldását fel tudjuk használni a DF szabályozó megkonstruálására.

Lemma 11.1 Tegyük fel, hogy $A - B_{1} C_{2}$ asszimptotikusan stabilis. Ekkor

$ℱ_{ℓ} (P_{D F}, K_{D F}) = ℱ_{ℓ} (P_{F I}, K_{D F} (\begin{array}{l} C_{2} & I \end{array}))$

(512)

$ℱ_{ℓ} (P_{F I}, K_{F I}) = ℱ_{ℓ} (P_{D F}, ℱ_{ℓ} ({\hat{P}}_{D F}, K_{F I})),$

(513)

ahol

${\hat{P}}_{D F} = [\begin{array}{l} A - B_{1} C_{2} & B_{1} & B_{2} \\ 0 & 0 & I \\ I & 0 & 0 \\ - C_{2} & I & 0 \end{array}] .$

(514)

Bizonyítás 11.1 Az első tulajdonság az alábbi összefüggésnek a következménye:

$P_{D F} = (\begin{array}{l} I & 0 & 0 \\ 0 & C_{2} & I \end{array}) P_{F I} .$

(515)

12.2. ábra - DF zárt kör

A második tulajdonság kimutatásához $P_{D F}$ és ${\hat{P}}_{D F}$ Redheffer szorzatát kell meghatározni:

$\frac{d x}{d t} = A x + B_{1} w + B_{2} \hat{z},$

(516)

$\frac{d \hat{x}}{d t} = (A - B_{1} C_{2}) \hat{x} + B_{1} y + B_{2} u,$

(517)

$z = C_{2} x + D_{11} w + D_{12^{\hat{Z}}},$

(518)

$\hat{z} = u,$

(519)

$y = C_{2} x + w,$

(520)

$\hat{y} = (\begin{array}{l} {\hat{y}}_{1} \\ {\hat{y}}_{2} \end{array}) = (\begin{array}{l} \hat{x} \\ - C_{2} \hat{x} + y \end{array}),$

(521)

ahol $x$ a $P_{D F}$ állapot vektora és $\hat{x}$ a ${\hat{P}}_{D F}$ állapot vektora. A transzformáció sematikus vázlata a 11.1 ábrán látható.

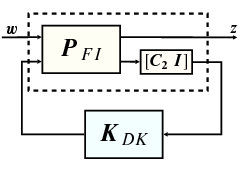
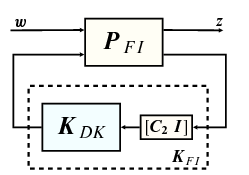
12.3. ábra - DF transzformációja FI-be

Az $e = x - \hat{x}$ hibavektor bevezetésével a transzformált állapotegyenletek a következők:

$\frac{d x}{d t} = A x + B_{1} w + B_{2} u,$

(522)

$\frac{d e}{d t} = (A - B_{1} C_{2}) e,$

(523)

$z = C_{1} x + D_{11} w + D_{12} u,$

(524)

$\hat{y} = (\begin{array}{l} \hat{x} \\ - C_{2} \hat{x} + y \end{array}) = (\begin{array}{l} x - e \\ C_{2} e + w \end{array}) .$

(525)

Mivel feltettük, hogy $A - B_{1} C_{2}$ stabilis és $e (0) = 0$

$ℛ_{ℓ} (P_{D F}, {\hat{P}}_{D F}) (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ C_{1} & D_{11} & D_{12} \\ I & 0 & 0 \\ 0 & I & 0 \end{array}] = P_{F I} (s),$

(526)

vagyis

$ℱ_{ℓ} (P_{F I}, K_{F I}) = ℱ_{ℓ} (ℛ_{ℓ} (P_{D F}, {\hat{P}}_{D F}), K_{F I}) = ℱ_{ℓ} (P_{D F}, ℱ_{ℓ} ({\hat{P}}_{D F}, K_{F I})) .$

(527)

Összefoglalásként, mindhárom feladat megoldása visszavezethető egy alkalmas teljes információs (FI) probléma megoldására.

12.2. Teljes információs (FI) szabályozó

Ahhoz, hogy a $∥ ℱ_{ℓ} (P_{F I}, K) ∥_{2}$ rendszernormát minimalizáljuk a stabilizáló $K$ szabályozók függvényében, véges horizontú feladok megoldását állítjuk elő, amik konvergálnak az optimális $ℋ_{2}$ szabályozóhoz.

A véges $T$ horizontú feladat költségfüggvénye

$J (u, T, Ψ) = \int_{0}^{T} z^{T} z d t + x^{T} (T) Ψ x (T) .$

(528)

ahol $Ψ \geq 0$ . A megjelenő második tag a hiányzó $x_{T}$ cél állapottal van összefüggésben. Mivel $z = C_{1} x + u$ , a költségfüggvény az alábbi alakra hozható:

$J (u, T, Ψ) = \int_{0}^{T} (x^{T} C_{1}^{T} C_{1} x + u^{T} u) d t + x^{T} (T) Ψ x (T),$

(529)

ami megegyezik az LQ/LQG performancia kritériummal, ha $Q = C_{1}^{T} C_{1}$ és $R = I$ .A szükséges optimalitási feltételek egy teljes négyzetté alakítással kaphatók a $C_{1}^{T} D_{12} = 0$ , $D_{12}^{T} C_{1} = 0$ és $D_{12}^{T} D_{12} = I$ egyszerüsítő ortogonalitási feltételek mellett.

Az LQ szabályozó levezetése során már látott módon bevezetjük az $X (t) = X (t, T, Ψ) \geq 0$ mátrix függvényt, $X (T) = Ψ$ , ami ki kell hogy elégítse az alábbi differenciál egyenletet:

$- \frac{d X}{d t} = A^{T} X + X A - X B_{2}^{T} B_{2} X + C_{1}^{T} C_{1} .$

(530)

Ekkor az

$u_{o p t} = - B_{2}^{T} X x$

(531)

választással a performancia funkcionál alakja

$J (u, T, Ψ) = \int_{0}^{T} (w^{T} B_{1}^{T} X x + x^{T} X B_{1} w) d t .$

(532)

Ahhoz, hogy az optimális FI $ℋ_{2}$ szabályozót megkapjuk a véges horizontú megoldások határértékeként, a terminális feltétel $Ψ$ mátrixát minden $T$ -re alkalmasan kell megválasztani.

Legyen $K$ olyan, amire $A - B_{2} K$ asszimptotikusan stablilis. Ekkor van hozzá $V (x) = x^{T} Ψ x$ Lyapunov függvény, azaz $Ψ \geq 0$ amire

$Ψ (A - B_{2} K) + {(A - B_{2} K)}^{T} Ψ + C_{1}^{T} C_{1} + K^{T} K = 0.$

(533)

Ez az egyenlet átírható az alábbi formába:

$Ψ A + A^{T} Ψ - Ψ B_{2} B_{2}^{T} Ψ + C_{1}^{T} C_{1} = - {(K - B_{2}^{T} Ψ)}^{T} (K - B_{2}^{T} Ψ) \leq 0,$

(534)

vagyis $Ψ$ kielégíti az

$Ψ A + A^{T} Ψ - Ψ B_{2} B_{2}^{T} Ψ + C_{1}^{T} C_{1} \leq 0$

(535)

egyenlőtlenséget. Kimutatható, hogy az $(A, (\begin{array}{l} C_{1} \\ Ψ \end{array}))$ pár detektálható.

Ezzel a $Ψ$ választással legyen $X_{T} (t)$ az alábbil Riccati differenciál egyenlet megoldása:

$- \frac{d}{d t} X_{T} (t) = X_{T} A + A^{T} X_{T} - X_{T} B_{2} B_{2}^{T} X_{T} + C_{1}^{T} C_{1}, X_{T} (T) = Ψ .$

(536)

Ekkor

$- \frac{d^{2}}{d t^{2}} X_{T} = {\dot{X}}_{T} A + A^{T} {\dot{X}}_{T} - {\dot{X}}_{T} B_{2} B_{2}^{T} X_{T} - X_{T} B_{2}^{T} B_{2} {\dot{X}}_{T} =$

$= {\dot{X}}_{T} (A - B_{2} B_{2}^{T} X_{T}) + {(A - B_{2} B_{2}^{T} X_{T})}^{T} {\dot{X}}_{T},$

(537)

amely egyenlet megoldása

$\frac{d}{d t} X_{T} (t) = Φ (t, T) [\frac{d}{d t} X_{T} (T)] Φ^{T} (t, T) \geq 0$

(538)

ahol $X_{T} (T) = Ψ$ és $Φ (t, T)$ a $- {(A - B_{2} B_{2}^{T} X_{T})}^{T}$ mátrixhoz tartozó alapmegoldás.Ekkor $\frac{d}{d t} X_{T} (t) \geq 0$ és mivel $X_{T} (T) \geq 0$ az $X_{T} (t)$ mátrixfüggvény monoton nem-csökkenő $t$ -ben.

A renszer időinvarianciáját felhasználva minden $τ > 0$ -ra

$X_{T + τ} (t) = X_{T} (t - τ) .$

(539)

Így $X_{T} (t)$ egy monoton nem-növekvő függvény $T$ -ben.

Mivel a Riccati egytenlet minden megoldására $X_{T} (t) \geq 0$ és $X_{T} (t) \leq Ψ$ bármely $t \leq T$ esetén, az $X_{T} (t)$ mátrixfüggvény egyenletesen korlátos minden $T$ -re.Ezért létezik a $Π (t) = {lim}_{T \to \infty} X_{T} (t)$ határérték. Az időinvariancia miatt minden $t_{1}$ és $t_{2}$ esetén

$Π (t_{1}) = lim_{T \to \infty} X_{T} (t_{1}) = lim_{T \to \infty} X_{T + t_{2} - t_{1}} (t_{2}) = Π (t_{2}) .$

(540)

Ebből következik, hogy a határérték egy konstans $Π$ mátrix, ami kielégíti. az alábbi algebrai Riccati egyenletet

$Π A + A^{T} Π - Π B_{2}^{T} B_{2} Π + C_{1}^{T} C_{1} = 0.$

(541)

A konstrukcióból hátra van még a stabilitás kimutatása. Először $A - B_{2} B_{2}^{T} X_{T} (0)$ stabilitását bizonyítjuk.Az egyszerűség kedvéért $X_{T}$ jelölje az $X_{T} (0)$ mátrixot és $F_{T} = - B_{2} X_{T}$ .

Tekintsük az alábbi Lyapunov differencál egyenletet:

$X_{T} (A + B_{2} F_{T}) + {(A + B_{2} F_{T})}^{T} X_{T} + F_{T}^{T} F_{T} + C_{1}^{T} C_{1} + {\dot{X}}_{T} = 0$

(542)

ahol ${\dot{X}}_{T} = \frac{d}{d t} X_{T} (t) |_{t = 0}$ . $X_{T}$ egy megfigyelgetősegi Gram mátrix, így $X_{T} \geq 0$ és ${\dot{X}}_{T} \geq 0$ .Ismert, hogy $A + B_{2} F_{T}$ minden instabil módusa nem megfigyelhető ${(\begin{array}{l} F_{T}^{T} & C_{1}^{T} & {\dot{X}}_{T} \end{array})}^{T}$ -ra.

Legyen $(λ, x)$ az $A + B_{2} F_{T}$ egy instabil nem megfigyelhető módusa, azaz

$(A - B_{2} F_{T}) x = λ x, Re (λ) \geq 0,$

(543)

$(\begin{array}{l} F_{T} \\ C_{1} \\ {\dot{X}}_{T} \end{array}) x = 0.$

(544)

A Lyapunov egyenletet kétoldalról szorozva $x^{*}$ és $x$ vektorokkal adódik, hogy $0 = (λ + \bar{λ}) x^{*} X_{T} x$ .Ebből következik, hogy $λ + \bar{λ} = 0$ vagy $X_{T} x = 0$ .

Az első esetben a Lyapunov egyenletet $x$ -el szorozva adódik, hogy $A^{T} X_{T} x = - j ω X_{T} x$ .Azonban $(A, B_{2})$ stabilizálható, vagyis minden instabil mód irányítható.Ebből következik, hogy $X_{T} x = 0$ .

Tegyük fel tehát, hogy $X_{T} x = 0$ .A Riccati egyenletet $x$ -el jobbról szorozva adódik, hogy ${\dot{X}}_{T} x = 0$ , amiből következik, hogy $X_{T} (t) x = 0$ bármely $t \leq T$ esetén, azaz $Ψ x = 0$ .Tehát $(λ, x)$ instabil de megfigyelhető $(\begin{array}{l} C_{1} \\ Ψ \end{array})$ -re, ami ellentmond a rendszer detektálhatóságának és $Ψ$ megválasztásának.Így $A - B_{2} B_{2}^{T} X_{T}$ asszimptotikusan stabilis. Folytonossági megfontolás alapján

$Re (λ_{i} (A - B_{2} B_{2}^{T} Π)) \leq 0$

(545)

minden $i$ -re. Ki kell még mutatnunk, hogy egyenlőség nem állhat fenn.

Feltéve, hogy létezik $ω$ és $x$ úgy, hogy

$(A - B_{2} B_{2}^{T} Π) x = j ω x,$

(546)

a Riccati egyenletből következik, hogy

$0 = x^{*} (Π A + A^{T} Π - Π B_{2} B_{2}^{T} Π + C_{1}^{T} C_{1}) x =$

$= x^{*} Π (A - B_{2} B_{2}^{T} Π) x + x^{*} (A^{T} - Π B_{2} B_{2}^{T}) Π x + x^{*} (Π B_{2} B_{2}^{T} Π) x + x^{*} C_{1}^{T} C_{1} x =$

$= x^{*} Π λ x + x^{*} \bar{λ} Π x + x^{*} (Π B_{2} B_{2}^{T} Π) x + x^{*} C_{1}^{T} C_{1} x = ∥ B_{2} Π x ∥_{2}^{2} + ∥ C_{1} x ∥_{2}^{2} .$

(547)

azaz, $C_{1} x = 0$ és $B_{2}^{T} Π x = 0$ , ezért $A x = j ω x$ .Mivel $(A, C_{1})$ detektálható ezért $C_{1} x$ nem tűnhet el, ami ellentmondás. Tehát a határérték egy asszimptotikusan stabilis megoldást ad.

Végezetül meg kell mutatni, hogy a határérték egy $ℋ_{2}$ optimális szabályozó.Jelölje $K_{2}$ ezt a határérték szabályozót.

Az FI rendszer és egy tetszőleges

$K (s) = [\begin{array}{l} \hat{A} & {\hat{B}}_{1} & {\hat{B}}_{2} \\ \hat{C} & {\hat{D}}_{1} & {\hat{D}}_{2} \end{array}]$

(548)

szabályozó az alábbi zárt kört eredményezi:

$\frac{d}{d t} (\begin{array}{l} x \\ \hat{x} \end{array}) = \bar{A} (\begin{array}{l} x \\ \hat{x} \end{array}) + \bar{B} w = (\begin{array}{l} A + B_{2} {\hat{D}}_{1} & B_{2} \hat{C} \\ {\hat{B}}_{1} & \hat{A} \end{array}) (\begin{array}{l} x \\ \hat{x} \end{array}) + (\begin{array}{l} B_{1} + B_{2} {\hat{D}}_{2} \\ {\hat{B}}_{2} \end{array}) w,$

(549)

$z = \bar{C} (\begin{array}{l} x \\ \hat{x} \end{array}) + \bar{D} w = (\begin{array}{l} C_{1} & 0 \\ D_{12} {\hat{D}}_{1} & D_{12} \hat{C} \end{array}) (\begin{array}{l} x \\ \hat{x} \end{array}) + (\begin{array}{l} 0 \\ D_{12} {\hat{D}}_{2} \end{array}) w .$

(550)

A $ℋ_{2}$ norma

$∥ ℱ_{ℓ} (P_{F I}, K) ∥_{2} = Trace ({\bar{B}}^{T} \bar{Q} \bar{B})$

(551)

ahol $\bar{Q}$ a rendszer megfigyelhetőségi Gram mátrixa ami kielégíti az alábbi Lyapunov egyenletet

${\bar{A}}^{T} \bar{Q} + \bar{Q} \bar{A} + {\bar{C}}^{T} \bar{C} = 0.$

(552)

Legyen

$\bar{X} = (\begin{array}{l} X & 0 \\ 0 & 0 \end{array})$

(553)

ahol $X$ kielégíti a következő algebrai Riccati egyenletet

$X A + A^{T} C - X B_{2} B_{2}^{T} X + C_{1}^{T} C_{1} = 0.$

(554)

Ekkor $\bar{Q} - \bar{X}$ kielégíti az alábbi Lyapunov egyenletet

$(\bar{Q} - \bar{X}) \bar{A} + {\bar{A}}^{T} (\bar{Q} - \bar{X}) + (\begin{array}{l} {({\hat{D}}_{1} + B_{2}^{T} X)}^{T} \\ \hat{C} \end{array}) (\begin{array}{l} {\hat{D}}_{1} + B_{2}^{T} X & \hat{C} \end{array}) = 0.$

(555)

Itt $(\bar{Q} - \bar{X})$ a $(\bar{A}, (\begin{array}{l} {\hat{D}}_{1} + B_{2}^{T} X & \hat{C} \end{array}))$ rendszer megfigyelhetőségi Gram mátrixa.Mivel $\bar{A}$ asszimptotikusan stablilis, ez a Gram mátrix pozitív definit, tehát $\bar{Q} \geq \bar{P}$ .

Kimutattuk tehát, hogy minden $K$ FI szabályozóra

$∥ ℱ_{ℓ} (P, K) ∥_{2} = Trace ({\bar{B}}^{T} \bar{Q} {\bar{B}}^{T}) \geq Trace ({\bar{B}}^{T} \bar{X} \bar{B}) .$

(556)

$K_{2}$ választással, azaz ${\hat{D}}_{1} = - B_{2}^{T} X$ és $\hat{C} = 0$ esetén $\bar{Q} = \bar{X}$ . Ekkor

$min_{K} ∥ ℱ_{ℓ} (P, K) ∥_{2} = Trace ({\bar{B}}^{T} \bar{X} \bar{B}) = Trace (B_{1}^{T} X B_{1}),$

(557)

tehát ez egy $ℋ_{2}$ optimális irányítás.

12.3. H2 optimális DF és OE szabályozók

Mint azt már láttuk az optimális DF és OE szabályozók megkaphatók egy FI feladat megoldásaként.

Feltéve, hogy $A - B_{1} C_{2}$ asszimptotikusan stabilis, ha $K_{F I} = [F_{2} 0]$ stabilizálja $P_{F I}$ -t, akkor $K_{D F} = ℱ_{ℓ} ({\hat{P}}_{D F}, K_{F I})$ stabilizálja $P_{D F}$ -et, ahol

${\hat{P}}_{D F} (s) = [\begin{array}{l} A - B_{1} C_{2} & B_{1} & B_{2} \\ 0 & 0 & I \\ I & 0 & 0 \\ - C_{2} & I & 0 \end{array}] .$

(558)

A zárt kör egyenletei

$\frac{d}{d t} \hat{x} = (A - B_{1} C_{2}) \hat{x} + B_{1} y + B_{2} u =$

$= (A - B_{1} C_{2} + B_{2} F_{2}) \hat{x} + B_{1} y,$

(559)

$\hat{z} = F_{2} \hat{x},$

(560)

így

$K_{D F} (s) = [\begin{array}{l} A + B_{2} F_{2} - B_{1} C_{2} & B_{1} \\ F_{2} & 0 \end{array}],$

(561)

ahol $F_{2}$ az FI feladat optimális állapot visszacsatolása.

Az OE feladat megoldása az OE és DF problémák dualitását felhasználva adódik:

${[ℱ_{ℓ} (P_{O E}, K_{O E})]}^{T} = ℱ_{ℓ} (P_{D F}^{T}, K_{D F}^{T}) .$

(562)

Következik, hogy

$K_{O E}^{T} (s) = [\begin{array}{l} A^{T} + C_{2}^{T} L_{2}^{T} - C_{1}^{T} B_{2}^{T} & C_{1}^{T} \\ L_{2}^{T} & 0 \end{array}],$

(563)

ahol $L_{2} = - C_{2}^{T} Y$ és $Y$ kielégíti az algebraic Riccati egyenletet

$A Y + Y A^{T} - Y C_{2}^{T} C_{2} Y + B_{1} B_{1}^{T} = 0.$

(564)

Így az eredeti OE feladat megoldása

$K_{O E} (s) = [\begin{array}{l} A + L_{2} C_{2} - B_{2} C_{1} & L_{2} \\ C_{1} & 0 \end{array}] .$

(565)

12.4. Egyszerűsített OF optimális $H_{2}$ irányítás

Az egyszerüsített OF rendszer alakja

$P_{O F} (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ C_{1} & 0 & D_{12} \\ C_{2} & D_{21} & 0 \end{array}]$

(566)

ahol az ortogonalitási feltételek

$C_{1}^{T} D_{12} = 0, B_{1} D_{21}^{T} = 0,$

(567)

$D_{21} D_{21}^{T} = I, D_{12}^{T} D_{12} = I$

(568)

fennállnak.

A szabályozó tervezésénél hasznos úgy tekinteni a rendszert mint amit egy teljes sztatikus $u_{*} = - B_{2}^{T} X x = F_{2} x$ állapotirányítás és egy zavarás vezérel. A zavarás szerepe, hogy kompenzálja a teljes állapot ismeretének hiányát.

Az FI irányítás minimalizálja $z = C_{1} x + D_{12} w$ energia normáját minden $w \in ℒ_{2}$ zavaró jelre. Hogy az $u$ eltérésének hatását az $u_{*}$ hatásától a kimeneten vizsgálhassuk, bevezetjük az új

$v = u - F_{2} x = u - u_{*}$

(569)

bemenetet, aminek segítségével átírjuk az állapotegyenleteket:

$\dot{x} = A x + B_{1} w + B_{2} u,$

(570)

$v = - F_{2} x + u,$

(571)

$y = C_{2} x + D_{21} w .$

(572)

A kapott rendszer

$P_{t m p} (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ - F_{2} & 0 & I \\ C_{2} & D_{21} & 0 \end{array}],$

(573)

a $(\begin{array}{l} w \\ u \end{array})$ bemenetet képezi le a $(\begin{array}{l} v \\ y \end{array})$ kimenetre.Vegyük észre, hogy $P_{t m p}$ az OE alakban adott.

A $w, v$ , és $z$ jeleket összekötő állapotegyenletek

$\dot{x} = A x + B_{1} w + B_{2} u = A x + B_{1} w + B_{2} (v + F_{2} x) =$

$= (A + B_{2} F_{2}) x + B_{1} w + B_{2} v,$

(574)

$z = C_{2} x + D_{12} u + C_{2} x + D_{12} (v + F_{2} x) =$

$= (C_{2} + D_{12} F_{2}) x + D_{12} v$

(575)

amik az alábbi rendszert határozzák meg

$P_{1} (s) = [\begin{array}{l} A + B_{2} F_{2} & B_{1} & B_{2} \\ C_{1} + D_{12} F_{2} & 0 & D_{12} \end{array}] .$

(576)

$P_{O F}$ felbontását erre a két alrendszerre a 56 ábra szemlélteti.

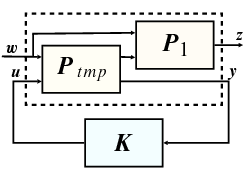
12.4. ábra - felírása két alrendszerrel

Mivel $P_{t m p}$ az OE alakban adott, már tudjuk, hogyan határozzuk meg azt a szabályozót ami minimalizálja a $ℱ_{ℓ} (P_{t m p}, K)$ zárt kör $ℋ_{2}$ normáját. A kérdés az, hogy ez a szabályozó minimalizálja-e $ℱ_{ℓ} (P, K)$ normáját is.

A válaszhoz írjuk át a zárt kör egyenleteit az új $v (t)$ változó figyelembe vételével:

$\dot{x} = A x + B_{1} w + B_{2} u = (A + B_{2} F_{2}) x + B_{1} w + B_{2} v =$

$= A_{F} x + B_{1} w + B_{2} v,$

(577)

$z = (C_{1} + D_{12} F_{2}) x + D_{12} v = C_{F} x + D_{12} v .$

(578)

ahol $A_{F} = A + B_{2} F_{2}$ and $C_{F} = C_{1} + D_{12} F_{2}$ .

Mivel a $z$ kimenet két hatás eredménye, a linearitás miatt írható, $z = z_{w} + z_{v}$ ahol $z_{w}$ a $w$ jel hatásának eredménye, feltéve, hogy $v = 0$ .A $z_{v}$ jel hasonló módon van definiálva.

A $z_{w}$ jelet meghatározó rendszer alakja

$P_{c} (s) = [\begin{array}{l} A_{F} & B_{1} \\ C_{F} & 0 \end{array}],$

(579)

míg a $z_{v}$ jel, amit $v = ℱ_{ℓ} (P_{t m p}, K)$ generál, az alábbi rendszer által van meghatározva

$z_{v} = U ℱ_{ℓ} (P_{t m p}, K) w$

(580)

ahol

$U (s) = [\begin{array}{l} A_{F} & B_{2} \\ C_{F} & D_{12} \end{array}] .$

(581)

Mivel $z = z_{w} + z_{v}$ kapjuk, hogy

$z = (P_{c} + U ℱ_{ℓ} (P_{t m p}, K)) w = ℱ_{ℓ} (P, K) w .$

(582)

Könnyű leellenőrizni, hogy $U$ egy $2$ -es normát megtartó leképezés, tehát egy belső függvény, és $U^{:} P_{c}$ instabil.Ez utóbbi belátásához ki kell mutatni, hogy $U^{:} P_{c} \in ℛ ℋ_{2}^{⊥}$ . Az $U^{:}$ és $P_{c}$ alakjaiból következik, hogy

$U^{:} P_{c} (s) = [\begin{array}{l} A_{F} & 0 & B_{1} \\ - C_{F}^{T} C_{F} & - A_{F}^{T} & 0 \\ D_{12}^{T} C_{F} & B_{2}^{T} & 0 \end{array}] .$

(583)

A $T = (\begin{array}{l} I & 0 \\ - X & I \end{array})$ hasonlósági transzformáció alkalmazásával, ahol $X$ kielégíti az FI feladathoz tartozó algebrai Riccati egyenletet és kihasználva, hogy $U$ egy belső függvény, vagyis

$D_{12}^{T} C_{F} + B_{2}^{T} X = 0$

(584)

$A_{F} X + {XA}_{F}^{T} + C_{F}^{T} C_{F} = 0,$

(585)

a transzformált rendszer állapotegyenleteire

$U^{:} P_{c} (s) = [\begin{array}{l} A_{F} & 0 & I \\ 0 & - A_{F}^{T} & X B_{1} \\ 0 & B_{2}^{T} & 0 \end{array}],$

(586)

adódik, azaz

$U^{:} P_{c} (s) = [\begin{array}{l} - A_{F}^{T} & X B_{1} \\ B_{2}^{T} & 0 \end{array}] .$

(587)

Ebből következik, hogy $U^{:} P_{c} \in ℛ H_{2}^{⊥}$ .

A két rendszer ortogonalitásából következik, hogy

$∥ ℱ_{ℓ} (P, K) ∥_{2}^{2} = ∥ P_{c} + U ℱ_{ℓ} (P_{t m p}, K) ∥_{2}^{2} = ∥ P_{c} ∥_{2}^{2} + ∥ U ℱ_{ℓ} (P_{t m p}, K) ∥_{2}^{2} =$

$= ∥ P_{c} ∥_{2}^{2} + ∥ ℱ_{ℓ} (P_{t m p}, K) ∥_{2}^{2},$

(588)

ezért az optimális irányításnak ki kell elégíteni az alábbi egyenletet

$min_{K} ∥ ℱ_{ℓ} (P, K) ∥_{2}^{2} = ∥ P_{c} ∥_{2}^{2} + min_{K} ∥ ℱ_{ℓ} (P_{t m p}, K) ∥_{2}^{2} .$

(589)

A zárt kör $ℋ_{2}$ normáját minimalizáló $K$ szabályozó a hozzárendelt $ℱ_{ℓ} (P_{t m p}, K)$ zárt kör minimalizálásával adódik, ahol

$P_{t m p} (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ - F_{2} & 0 & I \\ C_{2} & D_{21} & 0 \end{array}],$

(590)

ami egy optimális OE feladat.

Tétel 11.1 Az egyszerüsített OF feladat optimális szabályozója

$K_{O F} (s) = [\begin{array}{l} A + L_{2} C_{2} + B_{2} F_{2} & L_{2} \\ - F_{2} & 0 \end{array}],$

(591)

ahol $L_{2} = - Y C_{2}^{T}$ , $F_{2} = - B_{2}^{T} X$ , és $X$ valamint $Y$ kielégíti az alábbi FI és OE algebrai Riccati egyenletet:

$A^{T} X + X A - X B_{2} B_{2}^{T} X + C_{1}^{T} C_{1} = 0,$

(592)

$A Y + Y A^{T} - Y C_{2}^{T} C_{2}^{T} Y + B_{1} B_{1}^{T} = 0.$

(593)

Mivel az (592), (593) algebrai egyenletek nem csatoltak, ezért az OF szabályozó $F_{2}$ és $L_{2}$ erősítéseit egymástól függetlenül meg tudjuk határozni. $F_{2}$ a teljes állapotvisszacsatolás erősítése míg $L_{2}$ a Luenberger megfigyelőhöz tartozó erősítés.Az optimális kimenet visszacsatolásos $ℋ_{2}$ szabályozó alakja egy úgynevezett megfigyelő alapú szabályozó, ahol a megfigyelőt gyakran Kalman szűrőnek nevezzük.Így az optimális kimenet visszacsatolásos $ℋ_{2}$ szabályozó tervezése során fenn áll a szeparációs elv.

Vissza		Előre
11. fejezet - Megfigyelőtervezés és szeparációs elv	Főoldal	13. fejezet - Hinf. szabályozók tervezése

12. fejezet - H2 irányítások tervezése

12.1. Speciális irányítási feladatok

12.2. Teljes információs (FI) szabályozó

12.3. H2 optimális DF és OE szabályozók

12.4. Egyszerűsített OF optimális H 2 irányítás

12.4. Egyszerűsített OF optimális $H_{2}$ irányítás