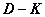14. fejezet - Rekonfiguráló és hibatűrő irányítások tervezése
Vissza		Előre

14. fejezet - Rekonfiguráló és hibatűrő irányítások tervezése

Tartalom

14.1. Robusztus stabilitás, robusztus performancia

Mivel a rendszerre ható külső körülmények változhatnak, valamint az érzékelők és beavatkozó szervek tulajdonságai is módosulhatnak, kisebb hibák léphetnek fel, stb. szükség van rekonfiguráló és hibatűrő irányítások tervezése. Ezen a tulajdonságok az elérésének egy módja lehet növelni a szabályozó robusztusságát ezekre a tényezőkre és a modellezési hibákra. Az alábbiakban a feladat megoldásának ezt a stratégiáját fejtjük ki részletesebben.

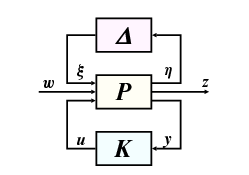
A szabályozási feladatot az 57 ábrán bemutatott $P - K - Δ$ struktúrában fogalmazzuk meg amit az alábbi egyenletek írnak le

$(\begin{array}{l} η \\ z \\ y \end{array}) = P (\begin{array}{l} ξ \\ w \\ u \end{array}) = (\begin{array}{l} P_{11} & P_{12} & P_{13} \\ P_{21} & P_{22} & P_{23} \\ P_{31} & P_{32} & P_{33} \end{array}) (\begin{array}{l} ξ \\ w \\ u \end{array}) .$

(676)

ahol $η, ξ$ jelek a bizonytalanságok leírására szolgálnak, $w, z$ az általánosított rendszerstruktúra zavarás és performancia jelei, $u, y$ a szabályozó bemenet és a mért kimenet.

14.1. ábra - struktúra

A bizonytalansági halmaz, $Δ$ , stabil átmenetfüggvényekből áll. A perturbált kör a

$ξ = Δ η$

(677)

bizonytalanság hatására lakul ki, ahol $Δ \in Δ$ és alakja a következő:

$(\begin{array}{l} η \\ z \end{array}) = ℱ_{u} (P, Δ) (\begin{array}{l} w \\ u \end{array}) =$

(678)

$= (\begin{array}{l} P_{22} & P_{23} \\ P_{32} & P_{33} \end{array}) + (\begin{array}{l} P_{21} \\ P_{31} \end{array}) Δ {(I - P_{11} Δ)}^{- 1} (\begin{array}{l} P_{12} & P_{13} \end{array}) (\begin{array}{l} w \\ u \end{array}) .$

(679)

Az $u = K y$ szabályozót a nominális (perturbálatlan) rendszerre kötve kapjuk, hogy

$(\begin{array}{l} z \\ y \end{array}) = ℱ_{l} (P, K) (\begin{array}{l} ξ \\ w \end{array}) =$

(680)

$= (\begin{array}{l} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array}) + (\begin{array}{l} P_{13} \\ P_{23} \end{array}) K {(I - P_{33} K)}^{- 1} (\begin{array}{l} P_{31} & P_{32} \end{array}) (\begin{array}{l} ξ \\ w \end{array}) .$

(681)

A szabályozott, $u = K y$ , és perturbált, $ξ = Δ η$ , kör alakja

$ℱ_{u} (ℱ_{l} (P, K), Δ) = ℱ_{l} (ℱ_{u} (P, Δ), K) .$

(682)

Mivel a zárt körök jól definiáltak kell, hogy legyenek és nem függhetnek $Δ$ és $K$ sorrendjétől, néhány feltételezéssel kell élnünk:

(a) Létezik $u = K y$ szabályozó, ami stabilizálja a nominális ( $Δ = 0$ ) rendszert ( $P$ ).

(b) A bizonytalansági halmaz

$Δ = {Δ (s) \in ℛ ℋ_{\infty} | Δ (i ω) \in Δ_{c} m i n d e n ω \in ℝ \cup^{} {\infty} e s e t é n},$

(683)

ahol $Δ_{c}$ komplex mátrixok egy halmaza, ami tartalmazza $0$ -t, ami meghatározza a bizonytalanságok méretét és struktúráját.Feltesszük, hogy ez a halmaz csillag alakú, vagyis $Δ_{c} \in Δ_{c} \Rightarrow τ Δ_{c} \in Δ_{c}$ minden $τ \in [0, 1]$ esetén.

(c) A bizonytalanságok és az általánosított rendszerstruktúra kötése jól definiált, vagyis $I - P_{11} (\infty) Δ_{c}$ invertálható minden $Δ_{c} \in Δ_{c}$ esetén.

Ezek a feltételek jórészt automatikusan teljesülnek a szokásos, intervallum, gömb, stb. típusú bizonytalansági halmazokra.

Általában normalizáló súlyozásokat alkalmazunk, amit azután figyelembe veszünk $P$ összeállításánál: ha $\hat{Δ}$ bizonytalansággal akarunk dolgozni, ahol $Δ = W_{1} \hat{Δ} W_{2}$ valós racionális $W_{1}$ és $W_{2}$ súlyokkal, akkor $P$ helyett $\hat{P}$ rendszert kell tekintenünk, ahol

$\hat{P} = (\begin{array}{l} W_{2} P_{11} W_{1} & W_{2} P_{12} & W_{2} P_{13} \\ P_{21} W_{1} & P_{22} & P_{23} \\ P_{31} W_{1} & P_{32} & P_{33} \end{array}) .$

(684)

14.2. Robusztus stabilitás vizsgálat

Vezessük be a

$ℱ_{l} (P, K) = (\begin{array}{l} M & N_{12} \\ N_{21} & N_{22} \end{array}),$

(685)

jelölést, ahol $M$ a bizonytalanság által látott átviteli függvény.

Tétel 13.1 Ha $K$ stabilizálja $P$ -t és ha $I - M Δ$ minden $Δ \in Δ$ esetén stabilan invertálható akkor $K$ robusztusan stabilizálja $ℱ_{u} (P, Δ)$ -t a $Δ$ bizonytalanságra nézve.

Bizonyítás 13.1 Ki kell mutatnunk, hogy

$(\begin{array}{l} z \\ y \end{array}) = ℱ_{u} (P, Δ) (\begin{array}{l} w \\ u \end{array}),$

(686)

$u = K v + v_{1}, v = y + v_{2}$

(687)

egy stabil rendszer.

Mivel $K$ stabilizálja $P$ -t, ez a rendszer írható mint

$(\begin{array}{l} η \\ z \\ u \\ v \end{array}) (\begin{array}{l} M & N_{12} & H_{13} & H_{14} \\ N_{21} & N_{22} & H_{23} & H_{24} \\ H_{31} & H_{32} & H_{33} & H_{34} \\ H_{41} & H_{42} & H_{43} & H_{44} \end{array}) (\begin{array}{l} ξ \\ w \\ v_{1} \\ v_{2} \end{array}), ξ = Δ η,$

(688)

ahol minen blokk stabil.

Következik, hogy

$(\begin{array}{l} z \\ u \\ v \end{array}) = (\begin{array}{l} N_{22} & H_{23} & H_{24} \\ H_{32} & H_{33} & H_{34} \\ H_{42} & H_{43} & H_{44} \end{array}) + (\begin{array}{l} N_{21} \\ H_{31} \\ H_{41} \end{array}) Δ {(I - M Δ)}^{- 1} (\begin{array}{l} N_{12} & H_{13} & H_{14} \end{array}) (\begin{array}{l} w \\ v_{1} \\ v_{2} \end{array}) .$

(689)

Mivel mind $Δ$ mind pedig ${(I - M Δ)}^{- 1}$ stabil ez egy stabil átviteli függvényt határoz meg.

A bizonyításból következik, hogy azt kell leelenőrizni, hogy $I - M Δ$ stabilisan invertálható, vagyis $det (I - M (s) Δ (s)) \neq 0$ minden $s \in ℂ^{0} \cup^{} ℂ^{+} \cup^{} {\infty}$ esetén. Ez a feladat bonyolult, mivel az egész jobb fél síkon kell a feltételt ellenőrizni.

A következő állítás megmutatja, hogy általában elég $I - M (s) Δ_{c}$ invertálhatóságát a komplex tengelyen ( $s = i ω$ , ahol $ω \in ℝ \cup^{} {\infty}$ ) ellenőrizni és elegendő csak a $Δ_{c} \in Δ_{c}$ halmazra.

Tétel 13.2 Tegyük fel, hogy $M$ egy stabil átviteli mátrix.

Ha $det (I - M (i ω) Δ_{c}) \neq 0$ minden $Δ_{c} \in Δ_{c}, ω \in ℝ \cup^{} {\infty}$ esetén, akkor $I - M Δ$ stabilisan invertálható minden $Δ \in Δ$ esetén.

Bizonyítás 13.2 A bizonyítás ellentmondásra való visszavezetéssel történik: tegyük fel, hogy létezik $Δ_{1} \in Δ$ amire $I - M Δ_{1}$ -nek $s_{1}$ egy zárusa $ℂ^{+}$ -ban, ahol $s_{1}$ nincs benne $ℂ^{0} \cup^{} {\infty}$ -ben.

Ha kimutatjuk, hogy létezik $s_{0} \in ℂ^{0}$ és $τ_{0} \in [0, 1]$ amire

$det (I - M (s_{0}) (τ_{0} Δ_{1} (s_{0}))) = 0,$

(690)

akkor ellentmondásra jutunk, mert $τ_{0} Δ_{1} \in Δ$ és $s_{0} \in ℂ^{0}$ .

Ehhez tekintsük az

$M Δ_{1} = [\begin{array}{l} A & B \\ C & D \end{array}],$

(691)

átviteli mátrixot, azaz

$I - M (τ Δ_{1}) = [\begin{array}{l} A & B \\ - τ C & I - τ D \end{array}] .$

(692)

Bevezetve a $A (τ) = A + B {(I - τ D)}^{- 1} τ C$ jelölést a Schur formulából

$det (I - M (s) (τ Δ_{1} (s))) = \frac{det (I - τ D)}{det (s I - A)} det (s I - A (τ))$

(693)

adódik. $s = \infty$ és $Δ = τ Δ_{1}$ esetén következik, hogy $det (I - τ D) \neq 0$ minden $τ \in [0, 1]$ -ra.Mivel $A$ stabilis $det (s_{1} I - A) \neq 0$ , így $det (s_{1} I - A (1)) = 0$ vagy $s_{1} \in λ (A (1))$ .

Mivel $A (τ)$ folytonosan függ $τ \in [0, 1]$ -tól, létezik egy folytonos komplex értékű $s (.)$ függvény $[0, 1]$ -en úgy, hogy $s (1) = s_{1}, det (s (τ) I - A (τ)) = 0$ minden $τ \in [0, 1]$ -ra.

$A (0) = A$ stabilis, így $s (0)$ benne van $ℂ^{-}$ -ban. Így a folytonos $Re (s (τ))$ függvény teljesíti $Re (s (0)) < 0$ és $Re (s (1)) > 0$ . Ezért léteznie kell egy $τ_{0} \in (0, 1)$ értéknek amire $Re (s (τ_{0})) = 0$ . Ekkor $s_{0} = s (τ_{0})$ és $τ_{0}$ miatt

$det (I - M (s_{0}) (τ_{0} Δ_{1} (s_{0}))) = 0,$

(694)

ami a keresett ellentmondás.

A fenti két állítást összegezve kapjuk a következő robusztus stabilitási eredményt:

Következmény 13.1 Ha $K$ stabilizálja $P$ -t és $d e t (I - M (i ω) Δ_{c}) \neq 0$ minden $Δ_{c} \in Δ_{c}$ és minden $ω \in ℝ \cup^{} {\infty}$ esetén, akkor $K$ robusztusan stabilizálja $ℱ_{u} (P, Δ)$ -t a $Δ$ bizonytalansági halmazra nézve.

A fordított állítás általában nem igaz. Egy konkrét esetben a teszt nem konzervatív voltát megpróbálhatjuk úgy igazolni, hogy egy destabilizáló $Δ \in Δ$ perturbációt keresünk.

14.3. Kis erősítések tétele

A robusztus stabilitási analízis egy alapvető eszköze a kis erősítések tétele, ami kimondja, hogy ha a hurokátviteli szorzat normája egynél kisebb, akkor a visszacsatolás stabilis. Ez az eredmény a fixpont tétel egy következménye.

Egy $S : X \mapsto X$ rendszert, ahol $X$ egy Banach tér (például $ℒ_{2} [0, T]$ vagy $ℒ_{2} [0, \infty$ )) kontraktív, ha a (Lipschitz) indukált normája $1$ -nél kisebb, azaz létezik $γ < 1$ úgy, hogy

$∥ S w - S \tilde{w} ∥_{S} \leq γ ∥ w - \tilde{w} ∥_{S}$

(695)

minden $w, \tilde{w} \in X$ esetén. A fixpont tétel alapján egy kontraktív $S$ rendszerhez létezik és egyértelmű $w \in S$ amire $w = S w$ .

14.2. ábra - Kis erősités kapcsolat

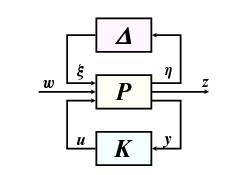
Tétel 13.3 (Kis erősítések tétele) Tegyük fel, hogy a $G_{1} : ℒ_{2 e} \mapsto ℒ_{2 e}$ valamint a $G_{2} : ℒ_{2 e} \mapsto ℒ_{2 e}$ rendszereknek véges erősítése van, amire $γ (G_{1}) γ (G_{2}) < 1$ .

Ekkor a visszacsatolt kapcsolat stabilis, azaz minden $u_{1}, u_{2} \in ℒ_{2} [0, \infty)$ esetén létezik es egyértelmű $e_{1}, e_{2} \in ℒ_{2} [0, \infty)$ , lásd a 58 ábrát.

Bizonyítás 13.3 Legyen $u_{1 T} = P_{T} u_{1}$ es $u_{2 T} = P_{T} u_{2}$ , definiáljuk az $S$ rendszert mint

$S e_{2 T} = u_{2 T} + P_{T} (G_{1} (u_{1 T} + P_{T} (G_{2} e_{2 T}))) .$

(696)

Mivel

$∥ S e_{2 T} - S {\hat{e}}_{2 T} ∥_{2, [0, T]} \leq γ (G_{1}) ∥ G_{2} e_{2 T} - G_{2} {\hat{e}}_{2 T} ∥_{2, [0, T]} \leq$

$\leq γ (G_{1}) γ (G_{2}) ∥ e_{2 T} - {\hat{e}}_{2 T} ∥_{2, [0, T]}$

(697)

és $γ (G_{1}) γ (G_{2}) < 1$ következik, hogy $S$ kontraktív $ℒ_{2} [0, T]$ -on. Így létezik és egyértelmű $e_{2 T} \in ℒ_{2} [0, T]$ úgy, hogy $e_{2 T} = S e_{2 T}$ minden $T$ -re, azaz

$e_{2 T} = u_{2 T} + P_{T} (G_{1} (u_{1 T} + P_{T} (G_{2} e_{2 T}))) .$

(698)

Mivel a $G_{i}$ rendszerek kauzálisak, következik, hogy

$e_{2 T} = P_{T} (u_{2} + G_{1} (u_{1} + G_{2} e_{2})) = P_{T} e_{2},$

(699)

ahol $e_{2}$ kielégíti a visszacsatolási egyenleteket.Mivel $T$ tetszőleges, minden $u_{1}$ és $u_{2} \in ℒ_{2 e}$ , esetén létezik és egyértelmű $e_{2} \in ℒ_{2 e}$ .Hasonló gondolatmenettel adódik $e_{1}$ létezése.

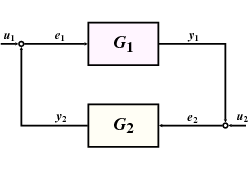
A gyakorlatban sokszor az eredeti visszacsatolás nem teljesíti a tétel feltételeit. Ilyenkor a zárt kör stabilitását megkaphatjuk a kis erősítések tételének alkalmazásával egy módosított elrendezésre, aminek a stabilitási tulajdonságai viszont azonosak az eredeti rendszerével.

14.3. ábra - Súlyozott kis erősités kapcsolat

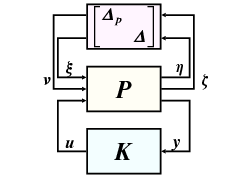
A leggyakrabban alkalmazott transzformáció stabilan invertálható súlyfüggvényeket alkalmazva módosítja a kapcsolást az 59 ábrán látható módon.

Következmény 13.2 Legyen $G_{1}, G_{2}$ stabil rendszer.Ekkor a visszacsatolt rendszer stabilis ha létezik egy $W$ , $W^{- 1}$ stabilis rendszer úgy, hogy $γ (W G_{1}) γ (G_{2} W^{- 1}) < 1$ .

14.4. Robusztus performancia analízis

14.4. ábra - Robusztus performancia es stabilitás

Definiáljuk a

$\tilde{Δ} = {(\begin{array}{l} Δ & 0 \\ 0 & Δ_{p} \end{array}) | ∥ Δ ∥ \leq 1, ∥ Δ_{p} ∥ \leq 1}$

(700)

halmazt. A kis erősítések tételét alkalmazva megkaphatjuk a $Δ$ -ra vonatkozó robusztus performancia eredményt:

- $I - M_{11} Δ$ invertálható és $∥ ℱ_{u} (M, Δ) ∥ < 1$ minden $∥ Δ ∥ \leq 1$ esetén,

akkor és csak akkor ha a robusztus stabilitási feltétel minden $\bar{Δ} = diag {Δ_{p}, Δ}$ -ra fennáll, ahol $Δ \in Δ$ és $∥ Δ_{p} ∥_{\infty} < 1$ , lásd az 59 ábrát, azaz

- $I - M \tilde{Δ}$ invertálható minden $∥ \tilde{Δ} ∥ \leq 1$ esetén,

ahol $M = ℱ_{l} (P, K)$ .

Megvizsgálva, hogy

$I - M \tilde{Δ} = I - (\begin{array}{l} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array}) (\begin{array}{l} Δ & 0 \\ 0 & Δ_{p} \end{array}) = (\begin{array}{l} I - M_{11} Δ & - M_{12} Δ_{p} \\ - M_{21} Δ & I - M_{22} Δ_{p} \end{array}),$

(701)

adódik, hogy

$I - M \tilde{Δ} = (\begin{array}{l} I & 0 \\ - M_{21} Δ {(I - M_{11} Δ)}^{- 1} & I \end{array}) (\begin{array}{l} I - M_{11} Δ & - M_{12} Δ_{p} \\ 0 & I - ℱ_{u} (M_{11}, Δ) Δ_{p} \end{array}) .$

(702)

$I - M Δ$ invertálható ha $I - ℱ_{u} (M_{11}, Δ) Δ_{p}$ invertálható.Feltevéseink szerint $∥ ℱ_{u} (M_{11}, Δ) ∥ < 1$ .

válasszuk $\tilde{Δ} = (\begin{array}{l} Δ & 0 \\ 0 & 0 \end{array})$ -t. Ekkor

$I - M \tilde{Δ} = (\begin{array}{l} I - M_{11} Δ & 0 \\ - M_{21} Δ & I \end{array})$

(703)

invertálható, tehát $I - M_{11} Δ$ invertálható minden $∥ Δ ∥ \leq 1$ esetén.

Mivel $I - M \tilde{Δ}$ invertálható, a kis erősítések tételéből következik, hogy $∥ ℱ_{u} (M_{11}, Δ) ∥ < 1$ minden $∥ Δ ∥ \leq 1$ esetén.

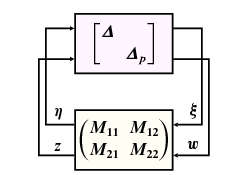
Összefoglalva: a robusztus performancia ekvivalens egy robusztus stabilitási feladattal, ami egy nomináis $M$ zárt körre és struktúrált bizonytalanságra vonatkozik, lásd a 61, ábrát. Mivel a bizonytalansági halmaz struktúrált, a kis erősítések tételénél kevésbé konzervatív eredmények keresése válik szükségessé.

14.5. ábra - Robust performance analysis

14.5. Struktúrált bizonytalanság

A bizonytalan rendszereket egy nominális LTI rendszer és egy visszacsatolt bizonytalan blokk együttesével modellezzük, ahol először a $Δ$ bizonytalansági halmazra az operátor egységgömböt választottuk. Ez az eset jól kezelhető a kis erősítések tételével. A továbbiakban ezt a technikát terjesztjük ki más szerkezetű bizonytalansági halmazok esetére.

Példa 13.1

Tekintsük az alábbi bizonytalansági blokkot

$Δ = (\begin{array}{l} δ & 0 \\ 0 & δ \end{array}), | δ | \leq 0.1.$

(704)

ahol a normalizáló súly $W = 10$ ( $∥ W Δ ∥_{\infty} \leq 1$ ). Ekkor a kis erősítések tételének feltételeit kielégiti $Δ = (\begin{array}{l} 0 & 0.1 \\ 0 & 0 \end{array})$ vagy $Δ = \frac{1}{\sqrt{2}} (\begin{array}{l} 0.1 & 0.1 \\ 0.1 & 0.1 \end{array})$ is. Ezért ebben az esetben a kis erősítések tétele igen konzervatív stabilitási eredményre vezet.

Egy igen fontos struktúrált bizonytalansági osztály a blokk diagonális bizonytalanságok halmaza.

Példa 13.2

Tekintsünk egy egy bemenetű és két kimenettel rendelkező $y = G u$ rendszert, ahol

$G = (\begin{array}{l} G_{1} \\ G_{2} \end{array})$

(705)

és $G_{1}$ valamint $G_{2}$ bizonytalanságát

$G_{1} = G_{0, 1} + W_{01} Δ_{1}, ∥ Δ_{1} ∥_{\infty} \leq 1$

(706)

$G_{2} = G_{0, 2} + W_{02} Δ_{2}, ∥ Δ_{2} ∥_{\infty} \leq 1,$

(707)

írja le, vagyis

$G = (\begin{array}{l} G_{0, 1} \\ G_{0, 2} \end{array}) + (\begin{array}{l} W_{01} & 0 \\ 0 & W_{02} \end{array}) (\begin{array}{l} Δ_{1} & 0 \\ 0 & Δ_{2} \end{array}) (\begin{array}{l} I \\ I \end{array}) =$

$= G_{0} + W_{1} (\begin{array}{l} Δ_{1} & 0 \\ 0 & Δ_{2} \end{array}) W_{2} .$

(708)

Ebben az esetben is a bizonytalanságot egy struktúrált, blokk diagonális

$Δ = (\begin{array}{l} Δ_{1} & 0 \\ 0 & Δ_{2} \end{array}), ∥ Δ_{i} ∥_{\infty} \leq 1, i = 1, 2$

(709)

halmaz, ami csak egy részhalmaza a strukturálatlan, normakorlátos halmaznak.

Blokk diagonális bizonytalansági struktúrák létrehozásának egyik módja az egyes $Δ$ bizonytalanságok kiemelése a rendszerből és az így kapott összekötés LFT alakra való hozása.

A továbbiakban azt az elvet illusztráljuk egy néhány konkrét példán keresztül.

Példa 13.3

Input-output multiplikatív bizonytalanság:

$z = (I + Δ_{i}) G (I + Δ_{o}) w \Leftrightarrow (\begin{array}{l} ζ_{i} \\ ζ_{o} \\ z \end{array}) = (\begin{array}{l} 0 & G & G \\ 0 & 0 & I \\ I & G & G \end{array}) (\begin{array}{l} ξ_{i} \\ ξ_{o} \\ w \end{array}),$

(710)

$(\begin{array}{l} ξ_{i} \\ ξ_{o} \end{array}) = (\begin{array}{l} Δ_{i} & 0 \\ 0 & Δ_{o} \end{array}) (\begin{array}{l} ζ_{i} \\ ζ_{o} \end{array})$

(711)

A $Δ$ kiemelésének menete:

- $Δ_{i}$ elkülönítése:

$z = G (I + Δ_{o}) w + ξ_{i}, ζ_{i} = G (I + Δ_{o}) w,$

(712)

$ξ_{i} = Δ_{i} ζ_{i},$

(713)

- $Δ_{o}$ elkülönítése:

$z = G w + ξ_{i} + G ξ_{o}, ζ_{i} = G w + G ξ_{0}, ζ_{o} = w$

(714)

$ξ_{i} = Δ_{i} ζ_{i}, ξ_{o} = Δ_{o} ζ_{o} .$

(715)

Példa 13.4

Faktorizált bizonytalanság ( $G_{o}$ invertálható ):

$z = (G_{i} + Δ_{i}) {(G_{o} + Δ_{o})}^{- 1} w \Leftrightarrow (\begin{array}{l} ζ \\ z \end{array}) = (\begin{array}{l} 0 & - G_{o}^{- 1} & G_{o}^{- 1} \\ I & G_{i} G_{o}^{- 1} & G_{i} G_{o}^{- 1} \end{array}) (\begin{array}{l} ξ_{i} \\ ξ_{o} \\ w \end{array}),$

(716)

$(\begin{array}{l} ξ_{i} \\ ξ_{o} \end{array}) = (\begin{array}{l} Δ_{i} \\ Δ_{o} \end{array}) ζ$

(717)

Az alábbi relációk

$z = (G_{i} + Δ_{i}) ξ, (G_{o} + Δ_{o}) ξ = w$

(718)

felírhatók mint

$z = G_{i} ξ + ξ_{i}, ζ = ξ, G_{o} ξ + ξ_{o} = w, ξ_{i} = Δ_{i} ζ, ξ_{o} = Δ_{o} ζ$

(719)

amiből $ξ$ -t eliminálva és figyelembe véve, hogy $ξ = G_{o}^{- 1} (w - ξ_{o})$ adódik

$z = G_{i} G_{o}^{- 1} w - G_{i} G_{o}^{- 1} ξ_{o} + ξ_{i}, ζ = G_{o}^{- 1} w - G_{o}^{- 1} ξ_{o}, ξ_{i} = Δ_{i} ζ, ξ_{o} = Δ_{o} ζ .$

(720)

Parametrikus bizonytalanságokra tekintsük az alábbi példákat:

Példa 13.5

Tekintsük a rugózott tömeg moddeljét: $m \ddot{y} = - k y + f$ .

$G (s) = (\begin{array}{l} 0 & 1 & 0 \\ - k / m & 0 & 1 / m \\ 1 & 0 & 0 \end{array}), {\dot{x}}_{2} = - \frac{k_{n}}{m} x_{1} + \frac{1}{m} u - \frac{δ_{k}}{m} x_{1}$

(721)

A bizonytalan rugóállandó $k = k_{n} + δ_{k}$ (additív bizonytalansági modell).

Ekkor az állapotegyenletek

${\dot{x}}_{1} = x_{2},$

(722)

${\dot{x}}_{2} = - \frac{k_{n}}{m} x_{1} - \frac{W_{k}}{m} η + \frac{1}{m} u$

(723)

$ξ = x_{1}$

(724)

$y = x_{1}$

(725)

$η = W_{k}^{- 1} δ_{k} ξ, a h o l ∥ W_{k}^{- 1} δ_{k} ∥ \leq 1.$

(726)

Példa 13.6

Tekintsük az 13.6 ábrán látható tömeg-csillapító-rugó rendszert ( $m$ tömeg, $k$ csillapítási együttható, $c$ rugóállandó).

Differenciálegyenlete:

$m \ddot{x} + c \dot{x} + k x = F$

(727)

ahol $x$ a tömeg elmozdulása, $F$ erő a rendszer gerjesztése.

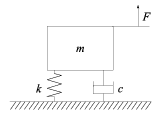
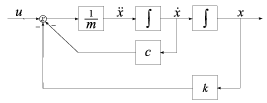
14.6. ábra - Egy lengőrendszer dinamikájának modellezése

A blokkdiagram a rendszer névleges modelljét illusztrálja. A valós rendszerben a fizikai paraméterek egyrészt nem ismertek pontosan, másrészt üzem közben változnak. Ismerjük viszont ezek átlagos értékét és becslésünk van az átlagos értéktől való eltérésükre.

$m = \bar{m} (1 + p_{m} δ_{m})$

(728)

$c = \bar{c} (1 + p_{c} δ_{c})$

(729)

$k = \bar{k} (1 + p_{k} δ_{k})$

(730)

A példában legyenek $\bar{m} = 3$ , $\bar{c} = 1$ , $\bar{k} = 2$ a névleges értékek, $p_{m} = 0.4$ , $p_{c} = 0.2$ , $p_{k} = 0.3$ és $- 1 � δ_{m}, δ_{c}, δ_{k} � 1$ reprezentálja, hogy a rendszer modellje, csillapítása és rugóállandója rendre $40 %$ , $20 %$ , $30 %$ bizonytalanságú.

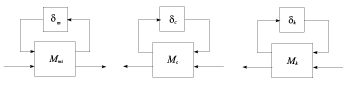
14.7. ábra - A parametrikus bizonytalanságok modellezése

A parametrikus bizonytalanságok a következőképpen írhatók fel:

$\frac{1}{m} = \frac{1}{\bar{m}} - \frac{p_{m}}{\bar{m}} δ_{m} {(1 + p_{m} δ_{m})}^{- 1} = F_{U} (M_{m}, δ_{m})$

(731)

$c = \bar{c} (1 + p_{c} δ_{c}) = F_{U} (M_{c}, δ_{c})$

(732)

$k = \bar{k} (1 + p_{k} δ_{k}) = F_{U} (M_{k}, δ_{k})$

(733)

ahol $M_{m} = [\begin{array}{l} - p_{m} & 1 \\ - p_{m} / \bar{m} & 1 / \bar{m} \end{array}]$ , $M_{c} = [\begin{array}{l} 0 & p_{c} \bar{c} \\ 1 & \bar{c} \end{array}]$ , $M_{k} = [\begin{array}{l} 0 & p_{k} \bar{k} \\ 1 & \bar{k} \end{array}]$ Megjegyzés: A kapcsolatokat felső bizonytalanság blokkal vettük figyelembe. A rendszer jelei közötti összefüggések ezek szerint a következőképpen alakulnak:

$[\begin{array}{l} y_{m} \\ \ddot{x} \end{array}] = [\begin{array}{l} - p_{m} & 1 \\ - p_{m} / \bar{m} & 1 / \bar{m} \end{array}] [\begin{array}{l} u_{m} \\ u - v_{c} - v_{k} \end{array}]$

(734)

ahol

$[\begin{array}{l} y_{c} \\ v_{c} \end{array}] = [\begin{array}{l} 0 & p_{c} \bar{c} \\ 1 & \bar{c} \end{array}] [\begin{array}{l} u_{c} \\ \dot{x} \end{array}]$

(735)

$[\begin{array}{l} y_{k} \\ v_{k} \end{array}] = [\begin{array}{l} 0 & p_{k} \bar{k} \\ 1 & \bar{k} \end{array}] [\begin{array}{l} u_{k} \\ x \end{array}]$

(736)

$u_{m} = δ_{m} y_{m}$

(737)

$u_{c} = δ_{c} y_{c}$

(738)

$u_{k} = δ_{k} y_{k}$

(739)

továbbá $v_{c} = u_{c} + \bar{c} x_{2}$ és $v_{k} = u_{k} + \bar{k} x_{1}$ .

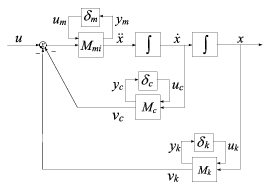
14.8. ábra - Lengőrendszer modellezése parametrikus bizonytalanságokkal

Válasszuk az állapotokat a következőképpen: $x_{1} = x$ , $x_{2} = \dot{x} = {\dot{x}}_{1}$ , $y = x_{1}$ , azaz ${\dot{x}}_{2} = \ddot{x} = {\ddot{x}}_{1}$ .

${\dot{x}}_{1} = x_{2}$

(740)

${\dot{x}}_{2} = - \frac{p_{m}}{\bar{m}} u_{m} + \frac{1}{\bar{m}} (u - v_{c} - v_{k})$

(741)

$y_{m} = - p_{m} u_{m} + (u - v_{c} - v_{k})$

(742)

Ezek után felírhatjuk a parametrikus bizonytalanságokat tartalmazó rendszer modelljét:

$[\begin{array}{l} {\dot{x}}_{1} \\ {\dot{x}}_{2} \\ y_{m} \\ y_{c} \\ y_{k} \\ y \end{array}] = [\begin{array}{l} 0 & 1 & 0 & 0 & 0 & 0 \\ - \frac{\bar{k}}{\bar{m}} & - \frac{\bar{c}}{\bar{m}} & \frac{\bar{-} p_{m}}{\bar{m}} & - \frac{1}{\bar{m}} & - \frac{1}{\bar{m}} & \frac{1}{\bar{m}} \\ - \bar{k} & - \bar{c} & - p_{m} & - 1 & - 1 & 1 \\ 0 & p_{c} \bar{c} & 0 & 0 & 0 & 0 \\ p_{k} \bar{k} & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \\ u_{m} \\ u_{c} \\ u_{k} \\ u \end{array}]$

(743)

A lengőrendszer modellje $G_{m d s}$ kizárólag az ismert $\bar{m}$ , $\bar{k}$ , $\bar{c}$ névleges paraméterektől és az ismert $p_{m}$ , $p_{c}$ , $p_{k}$ bizonytalnsági felső becslésektől függ. Így $G_{m d s}$ ismert és nem tartalmaz bizonytalanságokat.

$G_{m d s} = [\begin{array}{l} A & B_{1} & B_{2} \\ C_{1} & D_{11} & D_{12} \\ C_{2} & D_{21} & D_{22} \end{array}]$

(744)

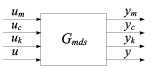
14.9. ábra - Lengőrendszer modellje

ahol $A = [\begin{array}{l} 0 & 1 \\ - \frac{\bar{k}}{\bar{m}} & - \frac{\bar{c}}{\bar{m}} \end{array}]$ , $B_{1} = [\begin{array}{l} 0 & 0 & 0 \\ - p_{m} & - \frac{p_{c}}{\bar{m}} & - \frac{p_{k}}{\bar{m}} \end{array}]$ , $B_{2} = [\begin{array}{l} 0 \\ - p_{m} & \frac{1}{\bar{m}} \end{array}]$ ,

$C_{1} = [\begin{array}{l} - \frac{\bar{k}}{\bar{m}} & - \frac{\bar{c}}{\bar{m}} \\ 0 & \bar{c} \\ \bar{k} & 0 \end{array}]$ , $D_{11} = [\begin{array}{l} - p_{m} & - \frac{p_{c}}{\bar{m}} & - \frac{p_{k}}{\bar{m}} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}]$ , $D_{12} = [\begin{array}{l} \frac{1}{\bar{m}} \\ 0 \\ 0 \end{array}]$ ,

$C_{2} = [\begin{array}{l} 1 & 0 \end{array}]$ , $D_{21} = [\begin{array}{l} 0 & 0 & 0 \end{array}]$ , $D_{22} = [\begin{array}{l} 0 \end{array}]$ .

A bizonytalanságokat tartalmazó $δ$ paramétereket egy külön blokk tartalmazza.

$[\begin{array}{l} u_{m} \\ u_{c} \\ u_{k} \end{array}] = [\begin{array}{l} δ_{m} & 0 & 0 \\ 0 & δ_{c} & 0 \\ 0 & 0 & δ_{k} \end{array}] [\begin{array}{l} y_{m} \\ y_{c} \\ y_{k} \end{array}]$

(745)

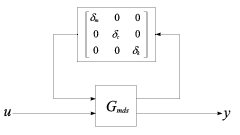
14.10. ábra - Lengőrendszer modellje a bizonytalanságokkal

A bizonytalan paraméterek hatása a 13.6. ábrán látható Bode diagramokon jól láthatók.

14.11. ábra - Parametrikus bizonytalanságok hatása a Bode diagramra

A modellezés célja, hogy megkapjuk az általánosított rendszer struktúrát, ahol az összes súlyfüggvény a $P$ általánosított rendszerbe van beillesztve, míg a bizonytalanságokat a blokk-diagonális $Δ$ tartalmazza, ami egy $Δ$ halmaz eleme, ahol:

$Δ (s) = diag (p_{1} I, \dots, p_{n_{r}} I, δ_{1} (s) I, \dots, δ_{n_{d}} (s) I, Δ_{1} (s), \dots, Δ_{n_{f}} (s)) .$

(746)

és ahol minden bokk normalizált.

14.6. Struktúrált szinguláris érték

Az $M \in ℂ^{n \times n}$ mátrixok esetén a $μ (M)$ struktúrált szinguláris érték definíciójában figyelembe veszünk egy feladatfüggő $Δ$ bizonytalansági struktúrát, ami az adott probléma sajátosságaitól és performancia követelményeitől függ. A vizsgált struktúrák az egységgömb megszorítását jelentik valamely $(Δ)$ tulajdonságok mentén, amikre feltesszük, hogy ha $Δ$ -ra teljesül $(Δ)$ , akkor $γ Δ$ -ra is teljesülni fog minden $γ \in [0, 1] (γ > 0)$ esetén, azaz $Δ$ csillag szerkezetű (kúp).

Tipikus példa a $(Δ)$ tulajdonságra a blokk-diagonális struktúra: aminek két típusát tekintjük -- ismédlődő skalár és teljes blokkú, vagyis

$Δ_{s, f} = {∥ Δ ∥ \leq 1, | Δ = diag (δ_{1} I_{r_{1}}, \dots, δ_{s} I_{r_{s}}, Δ_{s + 1}, \dots, Δ_{s + f}),$

(747)

$δ_{i} \in ℂ, Δ_{k} \in ℂ^{m_{k} \times m_{k}}}$

(748)

ahol a nemnegatív $s$ és $f$ egészek az ismétlődő skalár blokkok számát illetve a teljes blokkok számát jelentik.

Értelemszerűen fenn kell állnia az $\sum_{i = 1}^{s} r_{i} + \sum_{j = 1}^{f} m_{j} = n$ összefüggésnek. Az egyszerűség kedvéért a jelölésből elhagyjuk $s, f$ -t.

Gyakran normakorlátos $Δ$ halmazzal van dolgunk

$B_{Δ} = {Δ \in Δ : \bar{σ} (Δ) \leq 1} .$

(749)

Definíció 13.1 Az $M$ LTI operátorhoz rendelt és a $Δ$ halmazra vonatkoztatott $μ_{Δ} : s t a b l e \to [0, \infty)$ struktúrált szinguláris érték $μ_{Δ} (M) = s u p_{ω} μ_{Δ} (M (i ω))$ ahol

$μ_{Δ} (M (i ω)) =$

$= (\begin{array}{l} 0 hanincsolyan Δ \in Δ amire & det (I - Δ (i ω) M (i ω)) = 0, \\ \frac{1}{inf_{Δ \in Δ} {\bar{σ} (Δ (i ω)) | det (I - Δ (i ω) M (i ω)) = 0}} & egyébként . \end{array}$

(750)

A definíció jelentése a $u = M v, v = Δ u$ visszacsatolt kör esetén kézenfekvő: $1 / μ_{Δ} (M)$ annak a struktúrált $Δ$ bizonytalanságnak a normája ami destabilizálja a zárt kört.

A definíció egyenes következménye, hogy minden $Δ$ és $α \in ℂ$ esetén $μ_{Δ} (I) = 1$ valamint $μ_{Δ} (α M) = | α | μ_{Δ} (M)$ .Azonban, ha a blokkstruktúra nem triviális akkor $μ_{Δ} (M)$ nem normája $M$ -nek, mivel a háromszög egyenlőtlenség nem teljesül.

Lemma 13.1

$μ_{Δ} (M) = max_{Δ \in B_{Δ}} ρ (Δ M)$

(751)

Bizonyítás 13.4 Minden $α \in ℂ$ esetén $μ Δ (α M) = | α | μ Δ (M)$ , így csak két esetet kell vizsgálnunk: $μ_{Δ} (M) = 1$ akkor és csak akkor, ha $m a x_{Δ \in B_{Δ}} ρ (Δ M) = 1$ valamint $μ_{Δ} (M) = 0$ akkor és csak akkor, ha $m a x_{Δ \in B_{Δ}} ρ (Δ M) = 0$ . Ezek az esetek a definíció egyszerű következményei.

A lemmából, a spektrálsugár és a $max$ függvények folytonosságából valamint $B_{Δ}$ kompaktságából következik, hogy a $μ : ℂ^{n \times n} \to ℝ_{+}$ függvény folytonos.

Általában nem könnyű a $μ$ értékét kiszámítani. A továbbiakban a $μ$ függvény néhány olyan tulajdonságát soroljuk fel, amit haszonnal lehet a számításokban és becslésekben felhasználni.

- ha $Δ_{1} \neq Δ_{2}$ , általában $μ_{Δ_{1}} (M) \neq μ_{Δ_{2}} (M)$ .

- ha $Δ_{1} \subseteq Δ_{2}$ akkor $μ_{Δ_{1}} (M) \leq μ_{Δ_{2}} (M)$ .

- $ρ (M) \leq μ_{Δ} (M) \leq \bar{σ} (M)$ . ( $ρ (M)$ az $M$ spektrál sugara)

Valóban, ha $Δ_{1} = {δ I_{n} | δ \in ℂ}$ akkor $μ_{Δ_{1}} (M) = ρ (M)$ és $Δ_{2} = {Δ | Δ \in ℂ^{n \times n}}$ esetén $μ_{Δ_{2}} (M) = \bar{σ} (M)$ , míg tetszőleges $Δ$ esetén $Δ_{1} \subseteq Δ \subseteq Δ_{2}$ .

Sajnos ezek a becslések általában nagyon durvák,mivel $ρ$ valamint $\bar{σ}$ közti különbség tetszőlegesen nagy lehet.A becsléseket szűkíteni lehet $M$ olyan transzformációinak a felhasználásával amik nem befolyásolják $μ_{Δ} (M)$ értékét, azonban hatással vannak $ρ$ és $\bar{σ}$ értékére.

- ${max}_{Q \in Q} ρ (Q M) \leq μ_{Δ} (M) \leq {inf}_{D \in Θ} \bar{σ} (D M D^{- 1})$ ahol

$Q = {Q \in Δ | Q^{*} Q = I}, é s$

(752)

$Θ = {diag (D_{1}, \dots, D_{s}, d_{1} I_{m_{1}}, \dots, d_{f} I_{m_{f}}) |$

$D_{j} \in ℂ^{r_{i} \times r_{i}}, D_{i} = D_{i}^{*} > 0, d_{j} > 0}$

(753)

Valóban: mivel $det (I - M Δ) = det (I - Q M \tilde{Δ})$ ahol $\tilde{Δ} = Δ Q^{*}$ adódik, hogy $μ_{Δ} (Q M) = μ_{Δ} (M)$ minden $Q \in Q$ -ra. Másrészt $D Δ = Δ D$ ha $D \in Θ$ így $det (I - M Δ) = det (I - D M Δ D^{- 1}) = det (I - D M D^{- 1} Δ)$ .

Ezért $μ_{Δ} (M) = μ_{Δ} (D M D^{1}) \leq \bar{σ} (D M D^{- 1})$ , vagyis $μ_{Δ}$ invariáns a diagonális skálázásra.

- $β > 0$ esetén a

${D \in Θ : \bar{σ} (D^{\frac{1}{2}} M D^{- \frac{1}{2}}) < β}$

(754)

halmaz konvex.

Valóban:

$\bar{σ} (D^{\frac{1}{2}} M D^{- \frac{1}{2}}) < β \Leftrightarrow λ_{max} (D^{- \frac{1}{2}} M^{*} D^{\frac{1}{2}} D^{\frac{1}{2}} M D^{- \frac{1}{2}}) < β^{2} \Leftrightarrow$

$\Leftrightarrow D^{- \frac{1}{2}} M^{*} D^{\frac{1}{2}} D^{\frac{1}{2}} M D^{- \frac{1}{2}} - β^{2} I < 0 \Leftrightarrow M^{*} D M - β^{2} D < 0.$

(755)

Az utolsó feltétel egy lineáris mátrixegyenlőtlenség (LMI), ami egy konvex feltétel $D$ -ben.

- azon $Δ$ struktúrák esetén, amikre $2 s + f \leq 3$ : $μ_{Δ} (M) = {inf}_{D \in D} \bar{σ} (D M D^{- 1})$ .

Ha $s + f > 3$ akkor az egyenlőség általában nem teljesül.

A leírtakat az alábbi példa szemlélteti: legyen $M = (\begin{array}{l} 1 & a \\ \frac{1}{a} & 1 \end{array}), a \in ℝ$ és tekintsünk egy

$Δ = {Δ = (\begin{array}{l} δ_{1} & 0 \\ 0 & δ_{2} \end{array}) | δ_{1}, δ_{2} \in ℂ}$

(756)

bizonytalansági halmazt. Mivel $det (λ I - M) = λ^{2} - 2 λ$ és $det (λ I - M^{*} M) = λ^{2} - (2 + a^{2} + (1 / a)^{2}) λ$ akkor $ρ (M) = 2$ valamint $\bar{σ} (M) = | a + (1 / a) | \geq 2$ .

Mivel $det (I - M Δ) = 1 - δ_{1} - δ_{2}$ és $\bar{σ} (Δ) = {max}_{i = 1, 2} {| δ_{1} |, | δ_{2} |}$ :

$min_{Δ \in Δ} {\bar{σ} (Δ) | det (I - M Δ) = 0} = min_{δ_{1}, δ_{2} \in ℂ} {max_{i = 1, 2} {| δ_{1} |, | δ_{2} |} | 1 - δ_{1} - δ_{2} = 0} = \frac{1}{2} .$

(757)

Így $μ_{Δ} (M) = 2$ . Másrészt:

$Q = {I_{2}}, Θ = {D = diag (d, 1), d > 0}$

(758)

ezért

$max_{Q \in Q} ρ (Q M) = ρ (M) = 2,$

(759)

$\bar{σ} (D W^{- 1}) = | a d + \frac{1}{a d} | \Rightarrow inf_{D \in D} \bar{σ} (D M D^{- 1}) = 2,$

(760)

ami ebben a speciális esetben igazolja az állítás helyességét.

Eddig komplex skaláris blokkokat tekintettünk. Azonban a parametrikus bizonytalanságok tipikusan valós értékűek, amit figyelembe kell vennünk:

$Δ (s) = diag (p_{1} I, \dots, p_{n_{r}} I, δ_{1} (s) I, \dots, δ_{n_{c}} (s) I, Δ_{1} (s), \dots, Δ_{n_{f}} (s)) .$

(761)

Ez a struktúra elvezet a kevert (valós/komplex) $μ$ fogalmához. Ekkor a $D$ skálázás alkalmazása helyett felső becslést kaphatunk a kevert $μ$ -re, ha az úgynevezett $D, G$ skálázást használjuk:

$μ_{Δ} (M) \leq inf_{D \in Θ, G \in Γ, 0 \leq β} {β | M^{*} D M + j (G M - M^{*} G) - β^{2} D}$

(762)

ahol

$Θ = {diag (D_{1}, \dots, D_{n_{r} + n_{c}}, d_{1} I_{m_{1}}, \dots, d_{f} I_{m_{f}}) |$

$D_{j} \in ℂ^{r_{i} \times r_{i}}, D_{i} = D_{i}^{*} > 0, d_{j} > 0},$

(763)

$Γ = {diag (G_{1}, \dots, G_{n_{r}}, 0, \dots, 0) | G_{i} = G_{i}^{*} \in ℂ^{r_{i} \times r_{i}}},$

(764)

és $j^{2} = - 1$ .

Ez általában egy kvázi-konvex problémára vezet. Ha $M$ egy-rangú mátrix, akkor $μ$ megegyezik a felső becslésével.

14.7. Struktúrált szinguláris érték: analízis

A következő állítás alapvető szerepet játszik a $μ$ alapú robusztussági analízisben. Tekintsük a $Δ_{1} \in B_{Δ_{1}}$ és $Δ_{2} \in B_{Δ_{2}}$ bizonytalanságokat valamint a következő blokk-diagonális $Δ$ struktúrát:

$Δ = {(\begin{array}{l} Δ_{1} & 0 \\ 0 & Δ_{2} \end{array}) : Δ_{1} \in Δ_{1}, Δ_{2} \in Δ_{2}} .$

(765)

Tétel 13.4 (Fő hurok tétel)

$μ_{Δ} (M) < 1 \Leftrightarrow {\begin{array}{l} μ_{Δ_{2}} (M_{22}) < 1 \\ max_{Δ_{2} \in B_{Δ_{2}}} μ_{Δ_{1}} (ℱ_{l} (M, Δ_{2})) < 1 \end{array}$

(766)

Bizonyítás 13.5 Mivel

$det (I - M Δ) = det (\begin{array}{l} I - M_{11} Δ_{1} & - M_{12} Δ_{2} \\ - M_{21} Δ_{1} & I - M_{22} Δ_{2} \end{array}),$

(767)

$μ_{Δ} (M) < 1$ -ből következik, hogy $μ_{Δ_{2}} (M_{22}) < 1$ . Ezért

$det (I - M Δ) =$

(768)

$= det (I - M_{22} Δ_{2}) det (I - M_{11} Δ_{1} - M_{12} Δ_{2} (I - M_{22} Δ_{2})^{- 1} M_{21} Δ_{1})$

(769)

azonosságból következik, hogy

$det (I - M Δ) = det (I - M_{22} Δ_{2}) det (I - ℱ_{l} (M, Δ_{2}) Δ_{1}) .$

(770)

$μ$ definícióját felhasználva a bal oldal akkor és csak akkor nem zérus $Δ \in B_{Δ}$ esetén, ha $μ_{Δ} (M) < 1$ .Hasonlóan a jobb oldal akkor és csak akkor nem tűnik el, ha $μ_{Δ_{2}} (M_{22}) < 1$ és $μ_{Δ_{1}} (ℱ_{l} (M, Δ_{2})) < 1$ minden $Δ_{2} \in B_{Δ_{2}}$ -ra.

Tekintsünk most egy általánosított $P$ rendszerstruktúrát és egy stabilizáló $K$ szabályozót, azaz

$(\begin{array}{l} η \\ z \end{array}) = ℱ_{l} (P, K) (\begin{array}{l} ξ \\ w \end{array}) = N (\begin{array}{l} ξ \\ w \end{array}) =$

$= (\begin{array}{l} M & N_{12} \\ N_{21} & N_{22} \end{array}) (\begin{array}{l} ξ \\ w \end{array}),$

(771)

és $ξ = Δ η$ ahol $Δ$ stabil bizonytalanság, amire $Δ (j ω) \in Δ_{c}$ minden $ω \in ℝ \cup^{} {\infty}$ esetén.

Ekkor a $K$ robusztusan stabilizál, ha

$μ_{Δ_{c}} (M (j ω)) \leq 1$

(772)

minden $ω \in ℝ \cup^{} {\infty}$ esetén.

A $K$ szabályozó teljesíti a nominális performancia kritériumot,ha

$∥ N_{22} (j ω) ∥ \leq 1$

(773)

minden $ω \in ℝ \cup^{} {\infty}$ esetén.

A Fő hurok tétel alapján a performancia robusztus, ha

$μ_{\tilde{Δ}} (N (j ω)) \leq 1$

(774)

minden $ω \in ℝ \cup^{} {\infty}$ esetén, ahol $\tilde{Δ} = diag (Δ, Δ_{p})$ .

14.8. Struktúrált szinguláris érték: szintézis

Az analízis feltételek fényében egy robusztus stabilitást és performanciát garantáló szabályozó tervezéséhez minimalizálni kell egy struktúrált szinguláris értéket egy adott struktúrált bizonytalansági halmazon és minden frekvencián. Ez egy nemkonvex nemlineáris feladat, amire még nem született minden igényt kielégítő megoldó algoritmus. Egy, a gyakorlatban számos feladat esetében hatékonynak bizonyult heurisztikus algoritmus az úgynevezett $D - K$ -iteráció (vagy $D - G - K$ iteráció, valós bizonytalanságok kezelése esetén).

Tekintsük az alábbi bizonytalansági struktúrát:

$Δ_{c} = {∥ Δ ∥ \leq 1, | Δ = diag (δ_{1} I_{r_{1}}, \dots, δ_{s} I_{r_{s}}, Δ_{s + 1}, \dots, Δ_{s + f}),$

(775)

$δ_{i} \in ℂ, Δ_{k} \in ℂ^{m_{k} \times m_{k}}} .$

(776)

A $Δ_{c}$ -nek megfelelő $D$ skálázó mátrixok halmaza

$Θ = {diag (D_{1}, \dots, D_{s}, d_{1} I_{m_{1}}, \dots, d_{f} I_{m_{f}}) |$

$D_{j} \in ℂ^{r_{i} \times r_{i}}, D_{i} = D_{i}^{*} > 0, d_{j} > 0} .$

(777)

Ekkor a $\tilde{Δ}$ -hoz rendelt skálázó mátrixok halmaza

$\tilde{D} = {(\begin{array}{l} D & 0 \\ 0 & I \end{array}), | D \in Θ} .$

Ezekkel a skálázó szűrőkkel

$μ_{\tilde{Δ}} (N (j ω)) \leq inf_{D \in \tilde{D}} ∥ D^{- 1} N (j ω) D ∥_{\infty},$

(778)

így minden stabilizáló szabályozóra, ami teljesíti a

$inf_{D \in \tilde{D}} ∥ D^{- 1} N (j ω) D ∥_{\infty} \leq 1$

(779)

feltételt minden $ω \in ℝ \cup^{} {\infty}$ esetén, garantált a robusztus performancia. Ezért a $μ$ -t direktbe optimalizáló szabályozó tervezése helyett a felső becslést minimalizáljuk a $\tilde{D}$ segítségével.

Ezt a feladatot az alábbi kritérium fogalmazza meg: minimizáljuk

$sup_{ω \in ℝ \cup^{} {\infty}} ∥ D {(ω)}^{- 1} ℱ_{l} (P, K) (i ω) D (ω) ∥_{\infty}$

(780)

minden $P$ -t stabilizáló $K$ szabályozóra, és minden frekvencián a $\tilde{D}$ -beli $D (ω)$ skálázó mátrixokra. Ha ez a minimum kisebb mint egy, akkor a tervezés sikeres.

14.8.1. A $D - K$ iteráció

14.12. ábra - iteráció

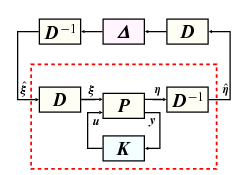
Sajnos az (780) feladatban nem tudunk egyszerre minimalizálni a $K$ szabályozó és frekvenciafüggő $D (ω)$ skálázó mátrixok függvényében. Ezért egy iterációt alkalmazunk: fixen tartjuk a $D (ω)$ skálát és (780) minimumát keressük a stabilizáló szabályozók halmazán. A második lépésben a $K$ szabályozót tratjuk fixen és (780) minimumát keressük a $D (ω)$ skálák függvényében. Ezt az eljárást nevezzük $D / K$ -iterációnak, lásd még az 68 ábrát.

$D / K$ -iteráció algoritmusa:

Rögzítjük az iterációk maximális számát, MAXIT, és egy $ε > 0$ tolerancia szintet. Választunk egy $D \in \tilde{D}$ skálafüggvényt.

A rögzített $D$ -vel megkeressük $K$ -t, az optimális $H_{\infty}$ szabályozót amire $γ < γ_{i n f} + ε$ úgy, hogy fennáll a $∥ D N D^{- 1} ∥ < γ H_{\infty}$ becslés. Ha $γ < δ^{- 1}, K$ a keresett robusztus szabályozó, ha nem, akkor tovább megyünk a $2$ . lépésre.

Rögzített $K$ szabályozóval egy új $D$ skálázó szűrőt számolunk ki, minimalizálva $\bar{σ} [D (j ω) N (j ω) D (j ω)^{- 1}]$ értékét $D (j ω)$ függvényében.

Amennyiben minden $ω$ frekvencián $\bar{σ} [D (j ω) N (j ω) D (j ω)^{- 1}] < δ^{- 1}$ akkor $K$ a keresett robusztus szabályozó, ha nem, tovább megyünk a $3$ . lépésre.

Ha elértük MAXIT-et, akkor az algoritmus nem szolgáltatott megoldást. Ellenkező esetben tovább megyünk az $1$ . lépésre.

Az első lépés egy standard $H_{\infty}$ optimális szabályozási feladat megoldása.A második lépésben minimalizálni kell $\bar{σ} [D (j ω) N (j ω) D (j ω)^{- 1}]$ értékét, amit egy numerikus optimalizálással érünk el egy ${ω_{i}}$ rácson, ahol a racionális $D$ skálázó szűrőt közelítjük. A közelítés pontossága általában növeli a szűrő rendjét, így a keletkező szabályozó rendjét is. Ezért gyakran szükséges a $μ$ -optimális szabályozókat helyettesíteni egy redukált rendű szub-optimális szabályozóval.

Vissza		Előre
13. fejezet - Hinf. szabályozók tervezése	Főoldal	15. fejezet - Nemlineáris irányítások