1. fejezet - AZ OPTIMUMKERESÉS
A legkülönbözőbb termelési folyamatok megtervezésénél és megszervezésénél a mérnökök célja mindig az optimális eredmény elérése. Az ipari gyártási folyamatok, a mezőgazdasági termelés, az energiatermelés, vagy a vegyszer- és gyógyszergyártás egyaránt több szempontból lehet optimális: lehet a termelt mennyiség maximumára, vagy a termék minőségének maximális szintjére, vagy a ráfordítások minimalizálására törekedni. Mindegyik célt más-más úton lehet megközelíteni. Mivel a legtöbb esetben bonyolult és összetett folyamatokról van szó, elkerülhetetlenül szükség van kísérletekre, amelyekből megismerhetjük a körülmények hatását a vizsgált folyamatra.
A faktoriális kísérleti tervek módszerét R.A. Fisher dolgozta ki Angliában az 1920-as években. Ez a módszer segített a kísérletezőnek megtalálni a kísérleti eredményre ható legfontosabb faktorokat, azok lehetséges összes kombinációját, mindezeknek a hatását a kísérleti eredményre, és megtalálni az optimális eredményt hozó faktor-kombinációt.
1.1. A teljes kísérleti mező feltérképezése
Kezdetben a kísérletek megtervezésénél a teljes kísérleti mező feltérképezésével próbálták megismerni a maximális eredmény eléréséhez szükséges körülményeket. Ez azt jelentette, hogy feltárták azokat a hatásokat (faktorokat), amelyek befolyásolhatták az eredményt (optimalizációs paramétert), majd a faktorok minden lehetséges értéke (faktor-szint) mellett kísérleteket végeztek. Először kiválasztották az egyik faktort és annak a szintjeit változtatták lehetőleg nem túl nagy lépésekben, miközben a többi faktor szintjét változatlan értéken tartották, és minden faktor-szint mellett egy vagy több kísérletet végeztek. Ezután egy másik, majd egy harmadik faktort változtatva és a többit változatlan értéken tartva újabb és újabb kísérleteket végeztek. A kísérleteket végül is minden faktor-szint kombináció (kísérleti beállítás) mellett elvégezték, és így ki tudták választani az optimális faktor-szint kombinációt (1.1. ábra).
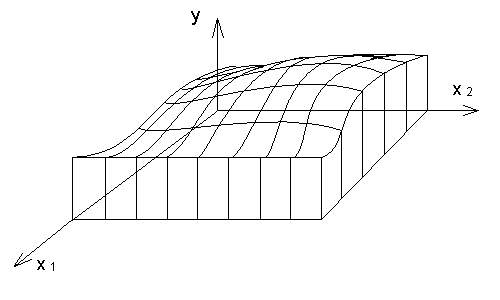
Ez 2 faktor és 10-10 faktorszint mellett (1.1. ábra) 100 kísérletet, 3 faktor és 10-10 faktorszint esetén 1000 kísérletet jelentett. A mezőgazdaságban viszont jóval több, mint 3 faktor lehetséges (pl. a különböző vetőmagok, földminőségek, műtrágyák mennyisége és minősége, öntözés mennyisége és időpontja, stb.), Ezen kívül ráadásul egy-egy kísérlet lebonyolítása egy teljes év lehet. Az ilyen módszerű kísérletezés tehát megengedhetetlenül költségesnek és hosszadalmasnak bizonyult. Hasonlóképpen nehéz a helyzet a vegyiparban és a gyógyszeriparban, ahol szintén sok faktor hatásával kell számolni.
1.2. A Gauss-Seidel módszer
A Gauss-Seidel módszer alkalmazásával lényegesen lecsökkenthető az optimum megtalálásához szükséges kísérletek száma. A módszert két faktor esetére mutatjuk be az 1.2. ábrán.
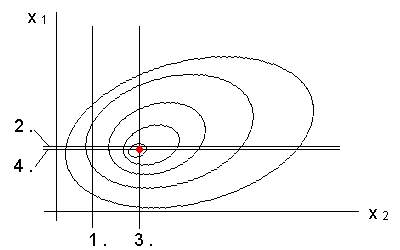
Az 1.2. ábrán a két vízszintes tengelyen az x1 és x2 faktort ábrázoljuk, a rajzra merőleges függőleges tengelyen helyezkedik el az y válasz függvény, amely esetünkben legyen maga az optimalizációs paraméter. Az első kísérletsorozatban csak az x1 paraméter értékeit változtatjuk, a lehetséges összes érték tartományában. A kapott eredmények egy y(x1) görbén helyezkednek el (az 1.2. ábrán felülnézetben az x1x2 síkon az 1. egyenes). Ezek közül kiválasztjuk azt az x1-et, amelyikhez a legnagyobb y (a legkedvezőbb kísérleti eredmény) tartozik és most, a második kísérlet sorozatban ezt az x1 érték lesz változatlan, míg az x2 értékét változtatjuk a lehetséges értékek tartományában. Az így elvégzett kísérletek eredményei az y(x2) egyenes fölött helyezkednek el (az ábrán a 2. egyenes). Most kiválasztjuk azt az x2 értéket, amelyikhez a legnagyobb y tartozik, és az előző két lépést váltogatva (3. egyenes, 4. egyenes), 3-4 kísérlet sorozat elvégzése után eljutunk az optimálisnak tekinthető eredményhez.
Ez 2 faktor és 10-10 faktor-szint esetén csak 30-40 kísérlet elvégzését jelenti az előző módszerrel elvégzendő 100 kísérlet helyett. A módszer értelemszerűen alkalmazható 3, vagy több faktor esetén is.
1.3. Box és Wilson módszere
Először az 1920-as évek végén vetette fel az angol statisztikus, Ronald Fischer, hogy célszerű lenne az összes faktort egyidejűleg variálni.
Box és Wilson 1951-ben Angliában publikálta hasonló módszerét. A módszer alapgondolata az, hogy egymás után végrehajtott egyszerű kísérletsorozatokkal meg kell állapítani, hogy a faktor-szintek milyen irányú módosítása visz közelebb az optimális beállításhoz. Az optimumot a legmeredekebb lejtés, vagyis a gradiens irányában kell keresni. Ezért ezt a módszert gradiens-módszernek is nevezik. Az egyes kísérletsorozatokban mindig minden faktor-szintet egyidejűleg változtatni kell. Az eljárást 2 faktor-szint esetére az 1.3. ábrán mutatjuk be. Az 1. lépésben az x1 faktor növekvő és az x2 faktor csökkenő értékei hoztak javulást a kísérleti eredményben. A 2. lépésben csak az x1 faktor növelése hozott javulást. A 3. lépésben romlott a kísérleti eredmény, ebből kiderült, hogy már átléptük az optimumot.
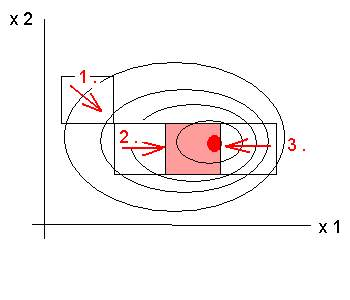
A Box-Wilson módszer alkalmazásával jelentős idő- és költségmegtakarítást érhetünk el. Van azonban egy fontos feladat, amelyet a kísérletek megtervezése előtt meg kell oldani. Meg kell választani, hogy a kísérleti mező melyik pontján kezdjük el a kísérleteket, és mekkora lépésekkel (faktorszint változtatásokkal) végezzük az egyes kísérleteket. Első sorban igyekezni kell az optimumhoz minél közelebbről indulni, azaz valamilyen módon minél pontosabban megbecsülni az optimális kísérleti beállítást. Ezután minden faktornál akkora „lépés-közt” kell választani, amely sem túl kicsi, sem túl nagy. Túl kicsi lépésköz esetén ugyanis szükségtelenül sok kísérletet kell elvégezni az optimum megtalálásához, túl nagy lépésköz esetén viszont megeshet, hogy „átugorjuk” az optimumot. A teljes kísérleti mező feltérképezése esetén ilyen hibát nem követhetünk el, és a Gauss-Seidel optimumkeresési módszer alkalmazása esetén is kisebb az esély hasonló tévedésre.
A Box-Wilson módszer alkalmazása esetén tehát néhány előkísérlettel előzetes („a priori”) ismeretekre kell szert tenni.
A továbbiakban a Box-Wilson módszer különböző alkalmazásával fogunk foglalkozni.